Substrate Activation Efficiency in Active Sites of Hydrolases Determined by QM/MM Molecular Dynamics and Neural Networks
Abstract
1. Introduction
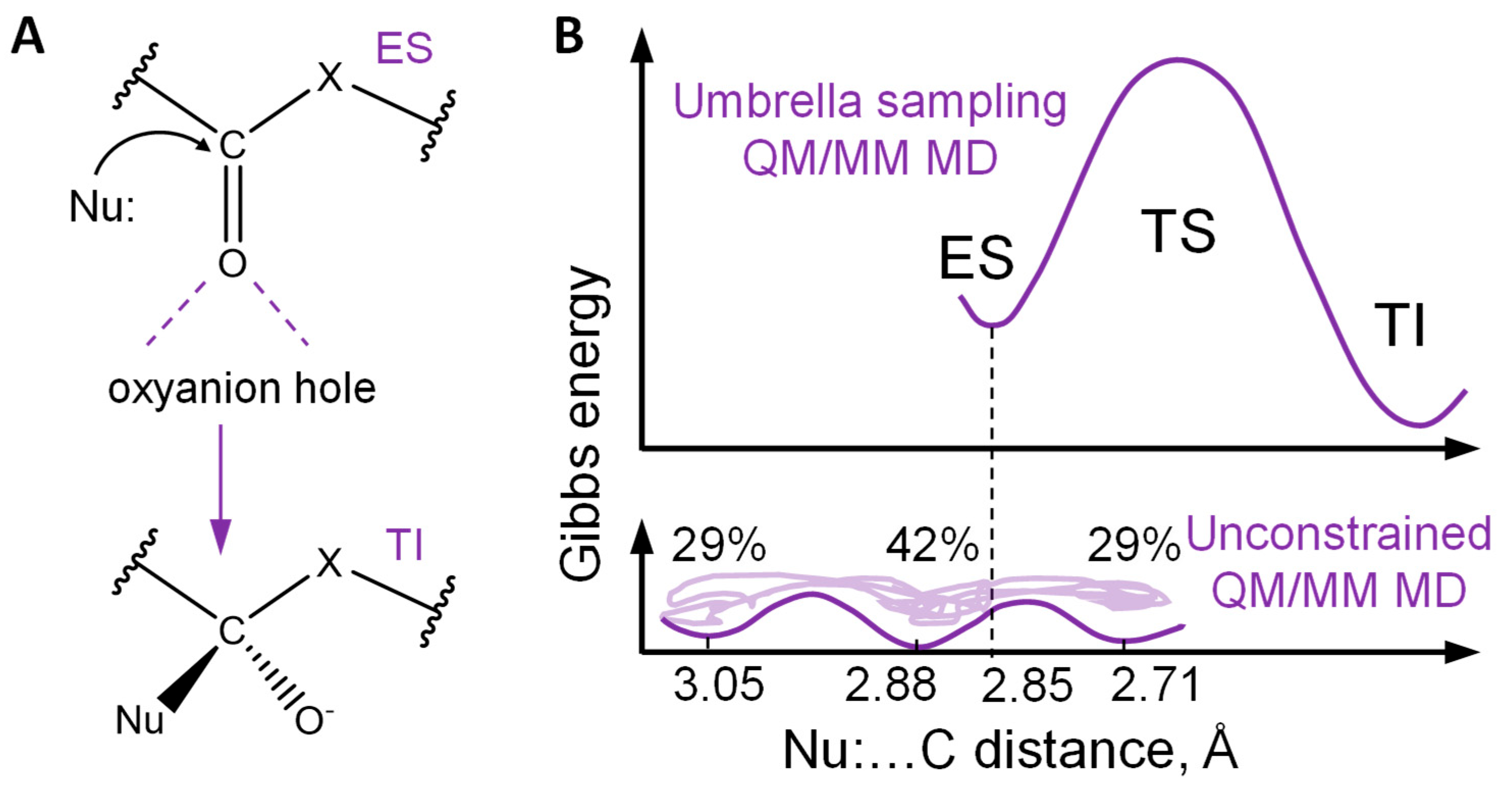
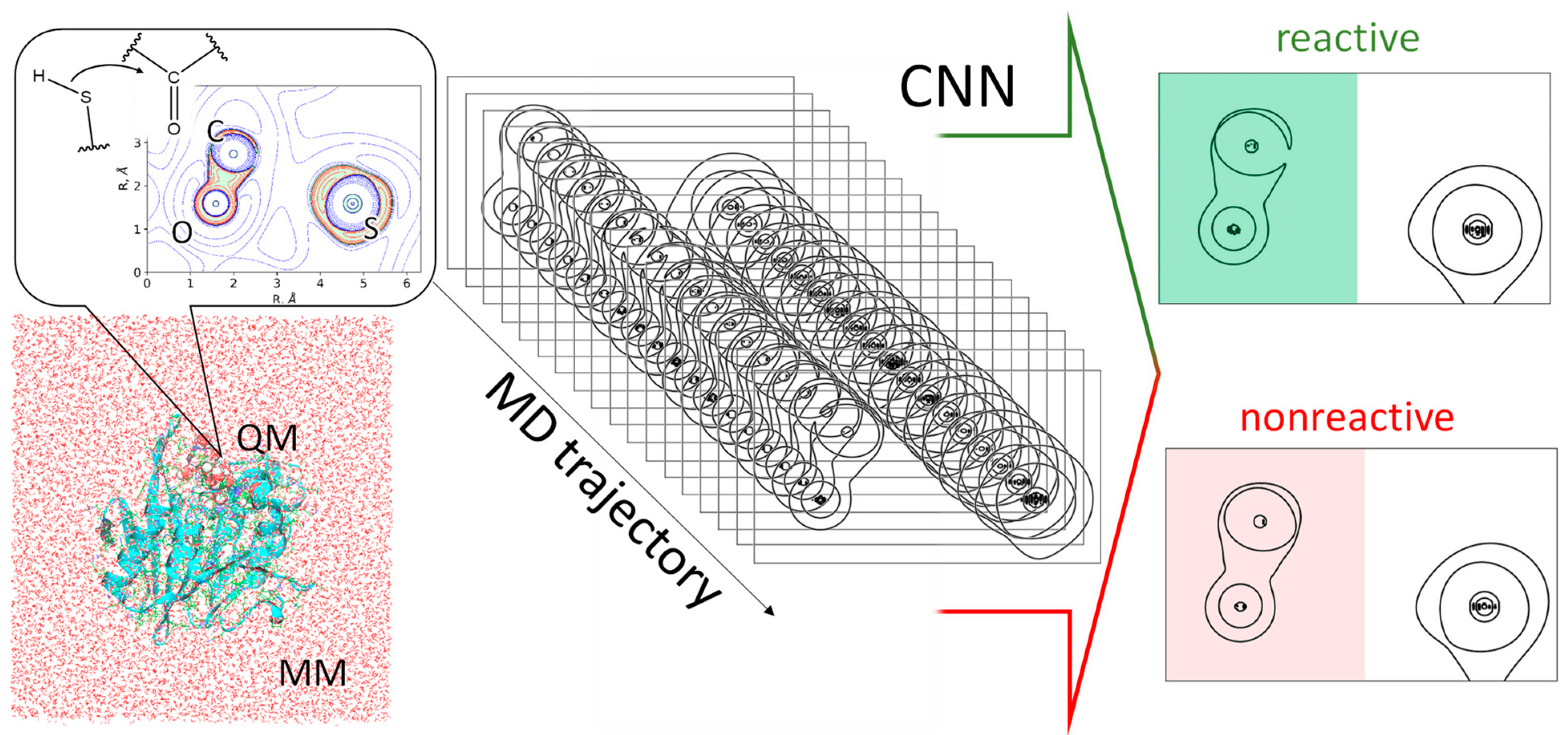
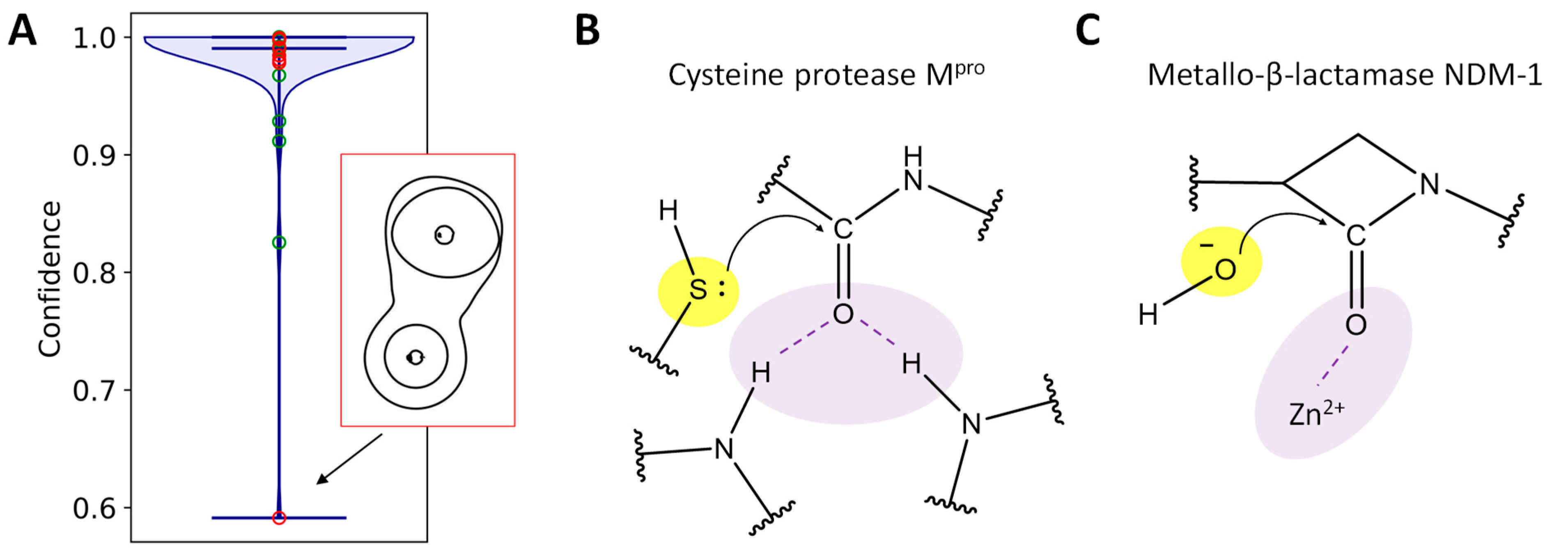
2. Results and Discussion
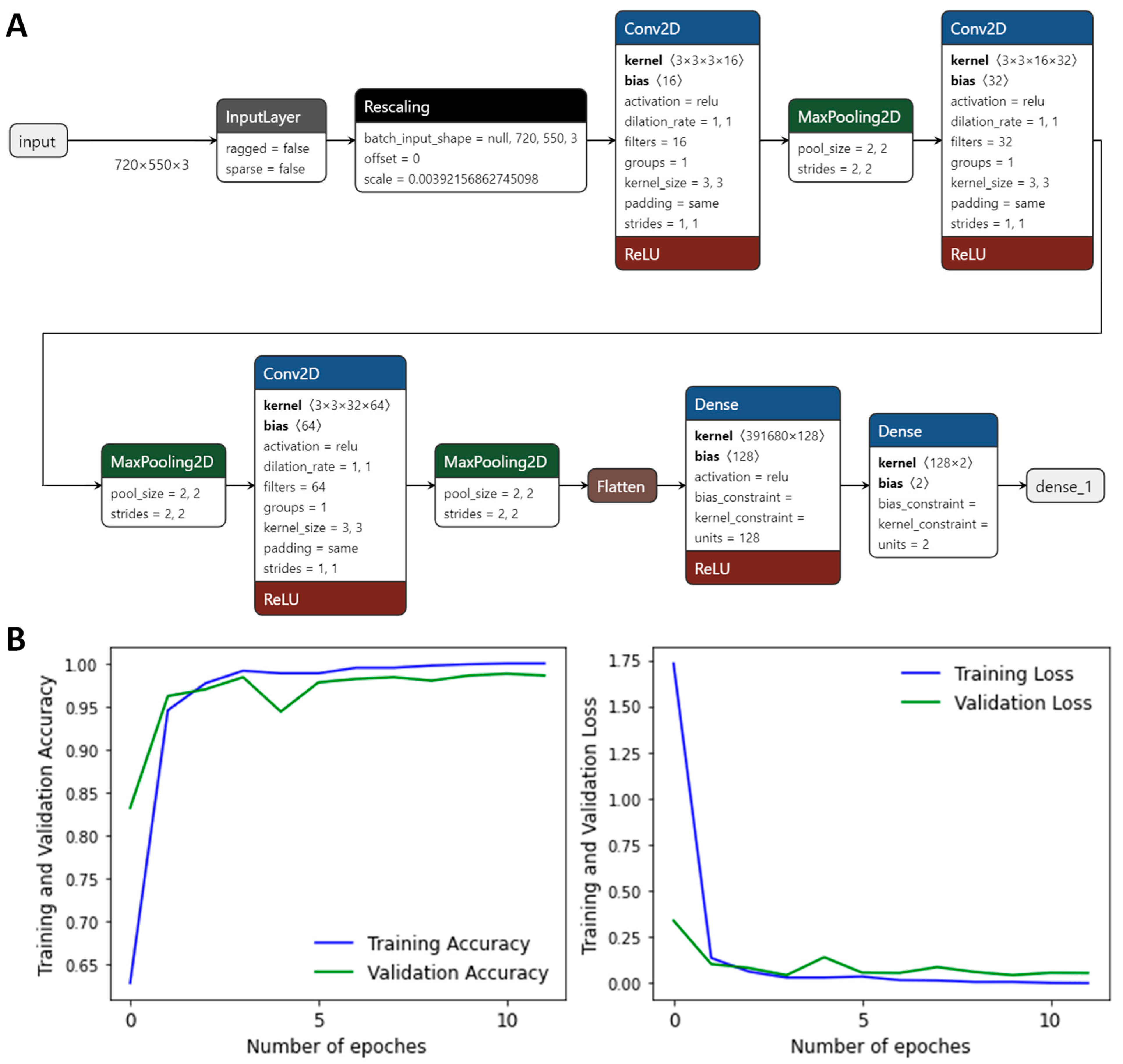
3. Models and Methods
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wolfenden, R.; Snider, M.J. The Depth of Chemical Time and the Power of Enzymes as Catalysts. Acc. Chem. Res. 2001, 34, 938–945. [Google Scholar] [CrossRef] [PubMed]
- Schramm, V.L. Enzymatic Transition States and Drug Design. Chem. Rev. 2018, 118, 11194–11258. [Google Scholar] [CrossRef] [PubMed]
- Kamerlin, S.C.L.; Chu, Z.T.; Warshel, A. On Catalytic Preorganization in Oxyanion Holes: Highlighting the Problems with the Gas-Phase Modeling of Oxyanion Holes and Illustrating the Need for Complete Enzyme Models. J. Org. Chem. 2010, 75, 6391–6401. [Google Scholar] [CrossRef] [PubMed]
- Simón, L.; Goodman, J.M. Hydrogen-Bond Stabilization in Oxyanion Holes: Grand Jeté to Three Dimensions. Org. Biomol. Chem. 2012, 10, 1905. [Google Scholar] [CrossRef]
- Amyes, T.L.; Richard, J.P. Specificity in Transition State Binding: The Pauling Model Revisited. Biochemistry 2013, 52, 2021–2035. [Google Scholar] [CrossRef]
- Krivitskaya, A.V.; Khrenova, M.G. Boronic Acids as Prospective Inhibitors of Metallo-β-Lactamases: Efficient Chemical Reaction in the Enzymatic Active Site Revealed by Molecular Modeling. Molecules 2021, 26, 2026. [Google Scholar] [CrossRef]
- Krivitskaya, A.V.; Khrenova, M.G. Influence of the Active Site Flexibility on the Efficiency of Substrate Activation in the Active Sites of Bi-Zinc Metallo-β-Lactamases. Molecules 2022, 27, 7031. [Google Scholar] [CrossRef]
- Khrenova, M.G.; Tsirelson, V.G.; Nemukhin, A.V. Dynamical Properties of Enzyme–Substrate Complexes Disclose Substrate Specificity of the SARS-CoV-2 Main Protease as Characterized by the Electron Density Descriptors. Phys. Chem. Chem. Phys. 2020, 22, 19069–19079. [Google Scholar] [CrossRef]
- Khrenova, M.G.; Nemukhin, A.V.; Tsirelson, V.G. Discrimination of Enzyme–Substrate Complexes by Reactivity Using the Electron Density Analysis: Peptide Bond Hydrolysis by the Matrix Metalloproteinase-2. Mendeleev Commun. 2020, 30, 583–585. [Google Scholar] [CrossRef]
- Carroll, M.T.; Cheeseman, J.R.; Osman, R.; Weinstein, H. Nucleophilic Addition to Activated Double Bonds: Predictions of Reactivity from the Laplacian of the Charge Density. J. Phys. Chem. 1989, 93, 5120–5123. [Google Scholar] [CrossRef]
- Grier, D.L.; Streitwieser, A. Electron Density Analysis of Substituted Carbonyl Groups. J. Am. Chem. Soc. 1982, 104, 3556–3564. [Google Scholar] [CrossRef]
- Wang, T.; Xiang, G.; He, S.; Su, L.; Wang, Y.; Yan, X.; Lu, H. DeepEnzyme: A Robust Deep Learning Model for Improved Enzyme Turnover Number Prediction by Utilizing Features of Protein 3D-Structures. Brief. Bioinform. 2024, 25, bbae409. [Google Scholar] [CrossRef] [PubMed]
- Hua, C.; Lu, J.; Liu, Y.; Zhang, O.; Tang, J.; Ying, R.; Jin, W.; Wolf, G.; Precup, D.; Zheng, S. Reaction-Conditioned De Novo Enzyme Design with GENzyme. arXiv 2024, arXiv:2411.16694. [Google Scholar] [CrossRef]
- Ming, Y.; Wang, W.; Yin, R.; Zeng, M.; Tang, L.; Tang, S.; Li, M. A Review of Enzyme Design in Catalytic Stability by Artificial Intelligence. Brief. Bioinform. 2023, 24, bbad065. [Google Scholar] [CrossRef]
- Casadevall, G.; Duran, C.; Osuna, S. AlphaFold2 and Deep Learning for Elucidating Enzyme Conformational Flexibility and Its Application for Design. JACS Au 2023, 3, 1554–1562. [Google Scholar] [CrossRef]
- Markus, B.; Gruber, C.C.; Andreas, K.; Arkadij, K.; Stefan, L.; Gustav, O.; Elina, S.; Radka, S. Accelerating Biocatalysis Discovery with Machine Learning: A Paradigm Shift in Enzyme Engineering, Discovery, and Design. ACS Catal. 2023, 13, 14454–14469. [Google Scholar] [CrossRef] [PubMed]
- Hossack, E.J.; Hardy, F.J.; Green, A.P. Building Enzymes through Design and Evolution. ACS Catal. 2023, 13, 12436–12444. [Google Scholar] [CrossRef]
- Buller, R.; Damborsky, J.; Hilvert, D.; Bornscheuer, U.T. Structure Prediction and Computational Protein Design for Efficient Biocatalysts and Bioactive Proteins. Angew. Chem. Int. Ed. 2025, 64, e202421686. [Google Scholar] [CrossRef]
- Yang, J.; Li, F.-Z.; Arnold, F.H. Opportunities and Challenges for Machine Learning-Assisted Enzyme Engineering. ACS Cent. Sci. 2024, 10, 226–241. [Google Scholar] [CrossRef]
- Jin, Z.; Du, X.; Xu, Y.; Deng, Y.; Liu, M.; Zhao, Y.; Zhang, B.; Li, X.; Zhang, L.; Peng, C.; et al. Structure of Mpro from SARS-CoV-2 and Discovery of Its Inhibitors. Nature 2020, 582, 289–293. [Google Scholar] [CrossRef]
- Phillips, J.C.; Braun, R.; Wang, W.; Gumbart, J.; Tajkhorshid, E.; Villa, E.; Chipot, C.; Skeel, R.D.; Kalé, L.; Schulten, K. Scalable Molecular Dynamics with NAMD. J. Comput. Chem. 2005, 26, 1781–1802. [Google Scholar] [CrossRef] [PubMed]
- Denning, E.J.; Priyakumar, U.D.; Nilsson, L.; Mackerell, A.D. Impact of 2′-Hydroxyl Sampling on the Conformational Properties of RNA: Update of the CHARMM All-Atom Additive Force Field for RNA. J. Comput. Chem. 2011, 32, 1929–1943. [Google Scholar] [CrossRef] [PubMed]
- Best, R.B.; Zhu, X.; Shim, J.; Lopes, P.E.M.; Mittal, J.; Feig, M.; MacKerell, A.D. Optimization of the Additive CHARMM All-Atom Protein Force Field Targeting Improved Sampling of the Backbone ϕ, ψ and Side-Chain χ1 and χ2 Dihedral Angles. J. Chem. Theory Comput. 2012, 8, 3257–3273. [Google Scholar] [CrossRef]
- Vanommeslaeghe, K.; Hatcher, E.; Acharya, C.; Kundu, S.; Zhong, S.; Shim, J.; Darian, E.; Guvench, O.; Lopes, P.; Vorobyov, I.; et al. CHARMM General Force Field (CGenFF): A Force Field for Drug-like Molecules Compatible with the CHARMM All-Atom Additive Biological Force Fields. J. Comput. Chem. 2010, 31, 671–690. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of Simple Potential Functions for Simulating Liquid Water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Toward Reliable Density Functional Methods without Adjustable Parameters: The PBE0 Model. J. Chem. Phys. 1999, 110, 6158. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Seritan, S.; Bannwarth, C.; Fales, B.S.; Hohenstein, E.G.; Isborn, C.M.; Kokkila-Schumacher, S.I.L.; Li, X.; Liu, F.; Luehr, N.; Snyder, J.W.; et al. TeraChem: A graphical processing unit-accelerated electronic structure package for large-scale ab initio molecular dynamics. WIREs Comput. Mol. Sci. 2021, 11, e1494. [Google Scholar] [CrossRef]
- Melo, M.C.R.; Bernardi, R.C.; Rudack, T.; Scheurer, M.; Riplinger, C.; Phillips, J.C.; Maia, J.D.C.; Rocha, G.B.; Ribeiro, J.V.; Stone, J.E.; et al. NAMD Goes Quantum: An Integrative Suite for Hybrid Simulations. Nat. Methods 2018, 15, 351–354. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual Molecular Dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Matta, C.F.; Bader, R.F.W. Atoms-in-Molecules Study of the Genetically Encoded Amino Acids. III. Bond and Atomic Properties and Their Correlations with Experiment Including Mutation-Induced Changes in Protein Stability and Genetic Coding. Proteins Struct. Funct. Bioinform. 2003, 52, 360–399. [Google Scholar] [CrossRef] [PubMed]
- Bader, R.F.W.; Popelier, P.L.A.; Chang, C. Similarity and Complementarity in Chemistry. J. Mol. Struct. Theochem 1992, 255, 145–171. [Google Scholar] [CrossRef]
- Grobelny, D.; Teater, C.; Galardy, R.E. The Ketone Cinnamoyl-(1-13C-Phe)-CGly-Pro-Pro Is a Tetrahedral Transition State Analog Inhibitor of C. histolyticum Collagenase. Biochem. Biophys. Res. Commun. 1989, 159, 426–431. [Google Scholar] [CrossRef] [PubMed]
- Shi, Z.; Boyd, R.J. Stereoselectivity of Nucleophilic Addition to Substituted Cyclohexanones: A Structure and Charge Density Study. J. Am. Chem. Soc. 1993, 115, 9614–9619. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F. Multiwfn: A Multifunctional Wavefunction Analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Polyakov, I.V.; Meteleshko, Y.I.; Mulashkina, T.I.; Varentsov, M.I.; Krinitskiy, M.A.; Khrenova, M.G. Substrate Activation Efficiency in Active Sites of Hydrolases Determined by QM/MM Molecular Dynamics and Neural Networks. Int. J. Mol. Sci. 2025, 26, 5097. https://doi.org/10.3390/ijms26115097
Polyakov IV, Meteleshko YI, Mulashkina TI, Varentsov MI, Krinitskiy MA, Khrenova MG. Substrate Activation Efficiency in Active Sites of Hydrolases Determined by QM/MM Molecular Dynamics and Neural Networks. International Journal of Molecular Sciences. 2025; 26(11):5097. https://doi.org/10.3390/ijms26115097
Chicago/Turabian StylePolyakov, Igor V., Yulia I. Meteleshko, Tatiana I. Mulashkina, Mikhail I. Varentsov, Mikhail A. Krinitskiy, and Maria G. Khrenova. 2025. "Substrate Activation Efficiency in Active Sites of Hydrolases Determined by QM/MM Molecular Dynamics and Neural Networks" International Journal of Molecular Sciences 26, no. 11: 5097. https://doi.org/10.3390/ijms26115097
APA StylePolyakov, I. V., Meteleshko, Y. I., Mulashkina, T. I., Varentsov, M. I., Krinitskiy, M. A., & Khrenova, M. G. (2025). Substrate Activation Efficiency in Active Sites of Hydrolases Determined by QM/MM Molecular Dynamics and Neural Networks. International Journal of Molecular Sciences, 26(11), 5097. https://doi.org/10.3390/ijms26115097







