Artificial Intelligence in Molecular Optimization: Current Paradigms and Future Frontiers
Abstract
1. Introduction
2. Definition of Molecular Optimization
3. Current Approaches and Barriers
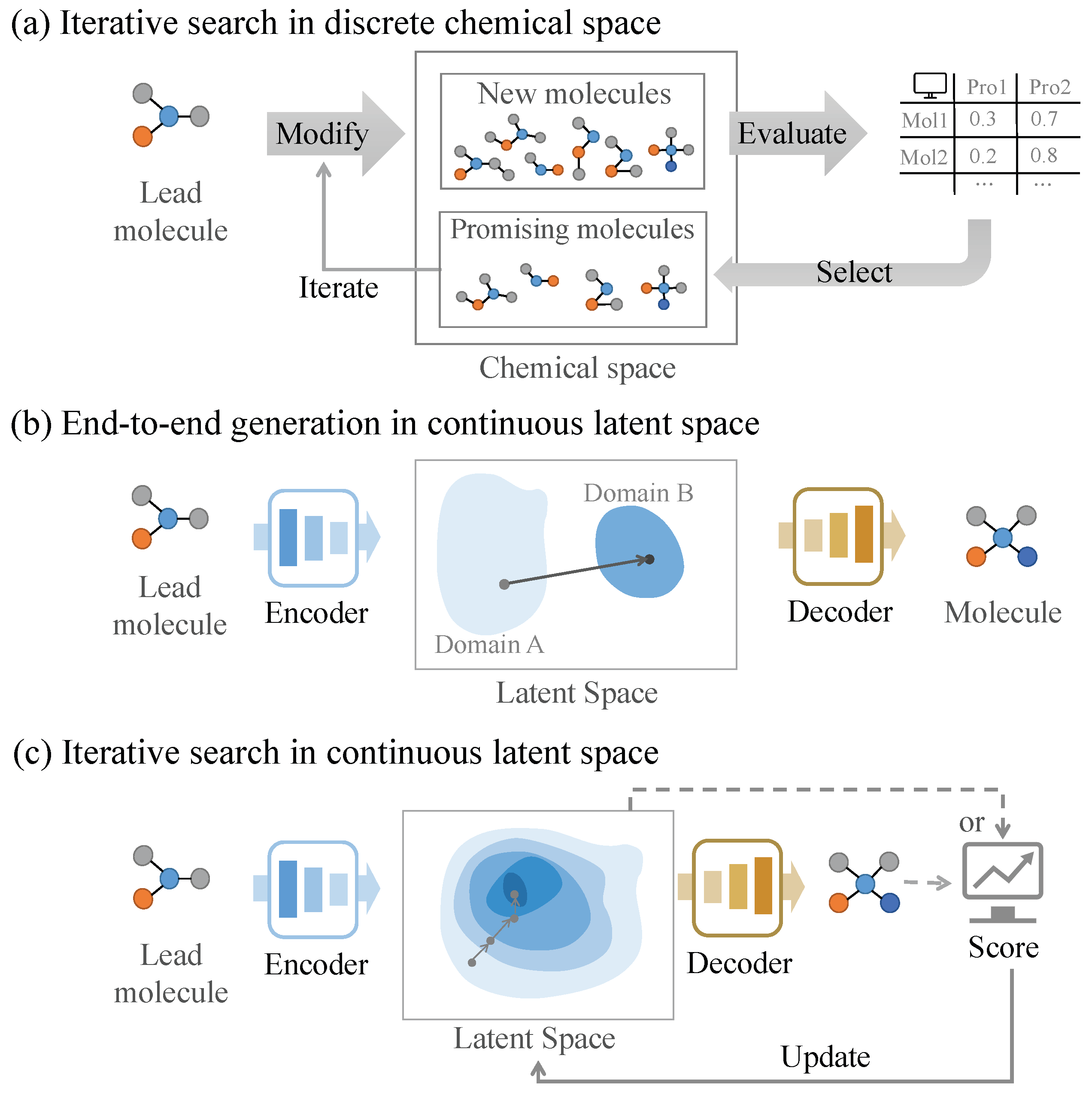
3.1. Molecular Optimization in Discrete Chemical Spaces
3.1.1. GA-Based Molecular Optimization Methods
| Category | Model | Molecular Representation | Data Type | Optimization Objective | Citation |
|---|---|---|---|---|---|
| Iterative search in discrete space | STONED | SELFIES | Unpaired | Multi-property | [31] |
| MolFinder | SMILES | Unpaired | Multi-property | [32] | |
| GB-GA-P | Graph | Unpaired | Multi-property | [33] | |
| GCPN | Graph | Unpaired | Single-property | [34] | |
| MolDQN | Graph | Unpaired | Multi-property | [35] | |
| End-to-end generation in continuous space | CMG | SMILES | Paired | Multi-property | [36] |
| T&S polish | Graph | Paired | Multi-property | [25] | |
| Mol-CycleGAN | Graph | Unpaired | Single-property | [37] | |
| UGMMT | SMILES | Unpaired | Single property | [38] | |
| IPCA | SMILES | Unpaired | Multi-property | [39] | |
| GPMO | SMILES | Paired | Multi-property | [40] | |
| VJTNN | Graph | Paired | Single-property | [22] | |
| SCVAE | Graph | Paired | Single-property | [41] | |
| Modef | Graph | Paired | Multi-property | [42] | |
| CFOM | SMILES | Unpaired | Single-property | [43] | |
| TamGen | SMILES | Unpaired | Single-property | [44] | |
| Iterative search in continuous space | QMO | SMILES | Unpaired | Multi-property | [45] |
| DST | Graph | Unpaired | Multi-property | [46] | |
| LIMO | SELFIES | Unpaired | Multi-property | [47] | |
| InversionGNN | Graph | Unpaired | Multi-property | [48] | |
| MOMO | SMILES | Unpaired | Multi-property | [49] | |
| DecompOpt | 3D | Unpaired | Multi-property | [50] | |
| GCDM | 3D | Unpaired | Multi-property | [51] | |
| Retmol | SMILES | Unpaired | Multi-property | [52] | |
| MO-LSO | Graph | Unpaired | Multi-property | [53] | |
| Prompt-MolOpt | SMILES | Paired | Multi-property | [54] | |
| Drugassist | SMILES | Unpaired | Multi-property | [55] |
3.1.2. RL-Based Molecular Optimization Methods
3.1.3. Analysis of Molecular Optimization Methods in Discrete Space
3.2. Molecular Optimization in Continuous Latent Spaces
3.2.1. End-to-End Generation Methods
3.2.2. Iterative Search Methods
3.2.3. Analysis of Molecular Optimization Methods in Continuous Space
3.3. Optimization Performance Comparison
- Task 1: PlogP optimization task
- Task 2: QED optimization task
- Task 3: Multi-property optimization task
4. Crucial Considerations and Future Opportunities
4.1. Reasonable Molecular Representation
4.1.1. Informative Molecular Representations
4.1.2. Modifiable Molecular Representations
4.2. Appropriate Datasets
4.2.1. Types of Molecular Datasets
4.2.2. Challenges and Suggestions in Obtaining Datasets
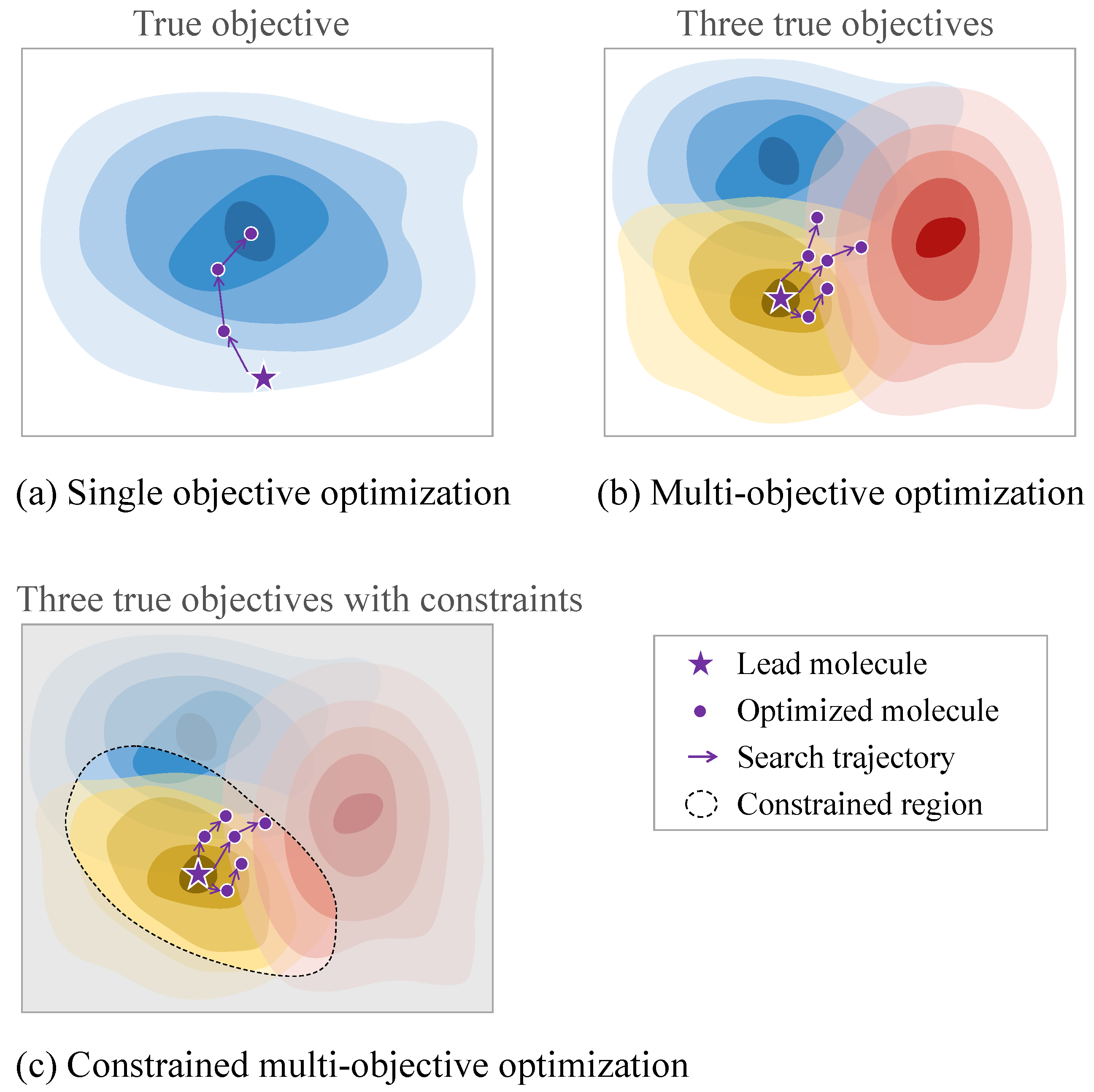
4.3. Optimization Properties
4.3.1. Common Molecular Properties
4.3.2. Multi-Property Optimization
4.3.3. Challenges in Practical Molecular Optimization Tasks
4.4. Optimization Algorithms
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, S.; Xie, J.; Ye, R.; Xu, D.D.; Yang, Y. Structure-aware dual-target drug design through collaborative learning of pharmacophore combination and molecular simulation. Chem. Sci. 2024, 15, 10366–10380. [Google Scholar] [CrossRef] [PubMed]
- Qi, Y.; Zhao, H.; Lei, Y. Organic molecular design for high-power density sodium-ion batteries. Chem. Commun. 2025, 61, 2375–2386. [Google Scholar] [CrossRef] [PubMed]
- Godinez, W.J.; Ma, E.J.; Chao, A.T.; Pei, L.; Skewes-Cox, P.; Canham, S.M.; Jenkins, J.L.; Young, J.M.; Martin, E.J.; Guiguemde, W.A. Design of potent antimalarials with generative chemistry. Nat. Mach. Intell. 2022, 4, 180–186. [Google Scholar] [CrossRef]
- Caburet, J.; Boucherle, B.; Bourdillon, S.; Simoncelli, G.; Verdirosa, F.; Docquier, J.D.; Moreau, Y.; Krimm, I.; Crouzy, S.; Peuchmaur, M. A fragment-based drug discovery strategy applied to the identification of NDM-1 β-lactamase inhibitors. Eur. J. Med. Chem. 2022, 240, 114599. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Fan, S.; Dong, M.; Li, J.; Kong, C.; Zhuang, J.; Meng, X.; Lu, S.; Zhao, Y.; Wu, C. Structure-guided design of CPPC-paired disulfide-rich peptide libraries for ligand and drug discovery. Chem. Sci. 2022, 13, 7780–7789. [Google Scholar] [CrossRef]
- Huang, Z.; Weng, X.; Ou-Yang, L. GFLearn: Generalized Feature Learning for Drug-Target Binding Affinity Prediction. IEEE J. Biomed. Health Inform. 2025; Online ahead of print. [Google Scholar] [CrossRef]
- Yang, L.; Guo, Q.; Zhang, L. AI-assisted chemistry research: A comprehensive analysis of evolutionary paths and hotspots through knowledge graphs. Chem. Commun. 2024, 60, 6977–6987. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, L.; Wang, Y.; Zou, J.; Yang, R.; Luo, X.; Wu, C.; Yang, W.; Tian, C.; Xu, H.; et al. Generative deep learning enables the discovery of a potent and selective RIPK1 inhibitor. Nat. Commun. 2022, 13, 6891. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Q.; Wen, H.; Gerbaud, V.; Jin, S.; Shen, W. Multi-objective optimization strategy for green solvent design via a deep generative model learned from pre-set molecule pairs. Green Chem. 2024, 26, 412–427. [Google Scholar] [CrossRef]
- Zhu, Y.; Wu, J.; Hu, C.; Yan, J.; Hou, T.; Wu, J. Sample-efficient multi-objective molecular optimization with gflownets. Adv. Neural Inf. Process. Syst. 2023, 36, 79667–79684. [Google Scholar]
- Wang, X.; Du, Z.; Guo, Y.; Zhong, J.; Song, K.; Wang, J.; Yu, J.; Yang, X.; Liu, C.Y.; Shi, T.; et al. Computer-aided molecular design and optimization of potent inhibitors disrupting APC–Asef interaction. Acta Pharm. Sin. B 2024, 14, 2631–2645. [Google Scholar] [CrossRef]
- Bos, P.H.; Houang, E.M.; Ranalli, F.; Leffler, A.E.; Boyles, N.A.; Eyrich, V.A.; Luria, Y.; Katz, D.; Tang, H.; Abel, R.; et al. AutoDesigner, a De Novo Design Algorithm for rapidly exploring large chemical space for lead optimization: Application to the design and synthesis of d-Amino acid oxidase inhibitors. J. Chem. Inf. Model. 2022, 62, 1905–1915. [Google Scholar] [CrossRef] [PubMed]
- Sridharan, B.; Goel, M.; Priyakumar, U.D. Modern machine learning for tackling inverse problems in chemistry: Molecular design to realization. Chem. Commun. 2022, 58, 5316–5331. [Google Scholar] [CrossRef]
- Ai, C.; Yang, H.; Liu, X.; Dong, R.; Ding, Y.; Guo, F. MTMol-GPT: De novo multi-target molecular generation with transformer-based generative adversarial imitation learning. PLoS Comput. Biol. 2024, 20, e1012229. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Zhang, O.; Jiang, C.; Zhao, H.; Zhang, X.; Chen, M.; Liu, Y.; Su, Q.; Wu, Z.; Wang, X.; et al. Deep lead optimization enveloped in protein pocket and its application in designing potent and selective ligands targeting LTK protein. Nat. Mach. Intell. 2025, 7, 448–458. [Google Scholar] [CrossRef]
- Chan, H.S.; Shan, H.; Dahoun, T.; Vogel, H.; Yuan, S. Advancing drug discovery via artificial intelligence. Trends Pharmacol. Sci. 2019, 40, 592–604. [Google Scholar] [CrossRef] [PubMed]
- Zhavoronkov, A.; Ivanenkov, Y.A.; Aliper, A.; Veselov, M.S.; Aladinskiy, V.A.; Aladinskaya, A.V.; Terentiev, V.A.; Polykovskiy, D.A.; Kuznetsov, M.D.; Asadulaev, A.; et al. Deep learning enables rapid identification of potent DDR1 kinase inhibitors. Nat. Biotechnol. 2019, 37, 1038–1040. [Google Scholar] [CrossRef]
- Skinnider, M.A. Invalid SMILES are beneficial rather than detrimental to chemical language models. Nat. Mach. Intell. 2024, 6, 437–448. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, J.; Cao, Z.; Barati Farimani, A. Molecular contrastive learning of representations via graph neural networks. Nat. Mach. Intell. 2022, 4, 279–287. [Google Scholar] [CrossRef]
- Liu, S.; Sui, J.; Luo, B.; Zhang, J.; Xiang, X.; Yang, T.; Luo, Y.; Liu, J. Discovery of 5-(Piperidin-4-yl)-1, 2, 4-oxadiazole derivatives as a new class of human caseinolytic protease p agonists for the treatment of hepatocellular carcinoma. J. Med. Chem. 2024, 67, 10622–10642. [Google Scholar] [CrossRef]
- Koziarski, M.; Rekesh, A.; Shevchuk, D.; van der Sloot, A.; Gaiński, P.; Bengio, Y.; Liu, C.; Tyers, M.; Batey, R. Rgfn: Synthesizable molecular generation using gflownets. Adv. Neural Inf. Process. Syst. 2024, 37, 46908–46955. [Google Scholar]
- Jin, W.; Yang, K.; Barzilay, R.; Jaakkola, T. Learning multimodal graph-to-graph translation for molecular optimization. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Bajusz, D.; Rácz, A.; Héberger, K. Why is Tanimoto index an appropriate choice for fingerprint-based similarity calculations? J. Cheminform. 2015, 7, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Rogers, D.; Hahn, M. Extended-connectivity fingerprints. J. Chem. Inf. Model. 2010, 50, 742–754. [Google Scholar] [CrossRef] [PubMed]
- Ji, C.; Zheng, Y.; Wang, R.; Cai, Y.; Wu, H. Graph polish: A novel graph generation paradigm for molecular optimization. IEEE Trans. Neural Networks Learn. Syst. 2021, 34, 2323–2337. [Google Scholar] [CrossRef]
- Langevin, M.; Minoux, H.; Levesque, M.; Bianciotto, M. Scaffold-constrained molecular generation. J. Chem. Inf. Model. 2020, 60, 5637–5646. [Google Scholar] [CrossRef] [PubMed]
- Weininger, D. SMILES, a chemical language and information system. 1. Introduction to methodology and encoding rules. J. Chem. Inf. Comput. Sci. 1988, 28, 31–36. [Google Scholar] [CrossRef]
- Krenn, M.; Häse, F.; Nigam, A.; Friederich, P.; Aspuru-Guzik, A. Self-referencing embedded strings (SELFIES): A 100% robust molecular string representation. Mach. Learn. Sci. Technol. 2020, 1, 045024. [Google Scholar] [CrossRef]
- Jensen, J.H. A graph-based genetic algorithm and generative model/Monte Carlo tree search for the exploration of chemical space. Chem. Sci. 2019, 10, 3567–3572. [Google Scholar] [CrossRef]
- Lee, Y.; Choi, K.; Kim, C. Docking-based Multi-objective Molecular optimization Pipeline using Structure-constrained Genetic Algorithm. In Proceedings of the 2022 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), Las Vegas, NV, USA, 6–8 December 2022; pp. 3438–3445. [Google Scholar]
- Nigam, A.; Pollice, R.; Krenn, M.; dos Passos Gomes, G.; Aspuru-Guzik, A. Beyond generative models: Superfast traversal, optimization, novelty, exploration and discovery (STONED) algorithm for molecules using SELFIES. Chem. Sci. 2021, 12, 7079–7090. [Google Scholar] [CrossRef]
- Kwon, Y.; Lee, J. MolFinder: An evolutionary algorithm for the global optimization of molecular properties and the extensive exploration of chemical space using SMILES. J. Cheminform. 2021, 13, 1–14. [Google Scholar] [CrossRef]
- Verhellen, J. Graph-based molecular Pareto optimisation. Chem. Sci. 2022, 13, 7526–7535. [Google Scholar] [CrossRef]
- You, J.; Liu, B.; Ying, Z.; Pande, V.; Leskovec, J. Graph convolutional policy network for goal-directed molecular graph generation. Adv. Neural Inf. Process. Syst. 2018, 31, 6412–6422. [Google Scholar]
- Zhou, Z.; Kearnes, S.; Li, L.; Zare, R.N.; Riley, P. Optimization of molecules via deep reinforcement learning. Sci. Rep. 2019, 9, 1–10. [Google Scholar] [CrossRef]
- Shin, B.; Park, S.; Bak, J.; Ho, J.C. Controlled molecule generator for optimizing multiple chemical properties. In Proceedings of the Conference on Health, Inference, and Learning, Online, 8–9 April 2021; pp. 146–153. [Google Scholar]
- Maziarka, Ł.; Pocha, A.; Kaczmarczyk, J.; Rataj, K.; Danel, T.; Warchoł, M. Mol-CycleGAN: A generative model for molecular optimization. J. Cheminform. 2020, 12, 1–18. [Google Scholar]
- Barshatski, G.; Radinsky, K. Unpaired generative molecule-to-molecule translation for lead optimization. In Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining, Singapore, 14–18 August 2021; pp. 2554–2564. [Google Scholar]
- Barshatski, G.; Nordon, G.; Radinsky, K. Multi-Property Molecular Optimization using an Integrated Poly-Cycle Architecture. In Proceedings of the 30th ACM International Conference on Information & Knowledge Management, Queensland, Australia, 1–5 November 2021; pp. 3727–3736. [Google Scholar]
- Yang, X.; Fu, L.; Deng, Y.; Liu, Y.; Cao, D.; Zeng, X. GPMO: Gradient perturbation-based contrastive learning for molecule optimization. In Proceedings of the Thirty-Second International Joint Conference on Artificial Intelligence, Macao, China, 19–25 August 2023; pp. 4940–4948. [Google Scholar]
- Yu, J.; Xu, T.; Rong, Y.; Huang, J.; He, R. Structure-aware conditional variational auto-encoder for constrained molecule optimization. Pattern Recognit. 2022, 126, 108581. [Google Scholar] [CrossRef]
- Chen, Z.; Min, M.R.; Parthasarathy, S.; Ning, X. A deep generative model for molecule optimization via one fragment modification. Nat. Mach. Intell. 2021, 3, 1040–1049. [Google Scholar] [CrossRef] [PubMed]
- Kaminsky, N.; Singer, U.; Radinsky, K. CFOM: Lead optimization for drug discovery with limited data. In Proceedings of the 32nd ACM International Conference on Information and Knowledge Management, Birmingham, UK, 21–25 October 2023; pp. 1056–1066. [Google Scholar]
- Wu, K.; Xia, Y.; Deng, P.; Liu, R.; Zhang, Y.; Guo, H.; Cui, Y.; Pei, Q.; Wu, L.; Xie, S.; et al. TamGen: Drug design with target-aware molecule generation through a chemical language model. Nat. Commun. 2024, 15, 9360. [Google Scholar] [CrossRef]
- Hoffman, S.C.; Chenthamarakshan, V.; Wadhawan, K.; Chen, P.Y.; Das, P. Optimizing molecules using efficient queries from property evaluations. Nat. Mach. Intell. 2022, 4, 21–31. [Google Scholar] [CrossRef]
- Fu, T.; Gao, W.; Xiao, C.; Yasonik, J.; Coley, C.W.; Sun, J. Differentiable scaffolding tree for molecular optimization. arXiv 2022, arXiv:2109.10469. [Google Scholar]
- Eckmann, P.; Sun, K.; Zhao, B.; Feng, M.; Gilson, M.K.; Yu, R. LIMO: Latent Inceptionism for Targeted Molecule Generation. arXiv 2022, arXiv:2206.09010. [Google Scholar]
- Niu, Y.; Gao, Z.; Xu, T.; Liu, Y.; Bian, Y.; Rong, Y.; Huang, J.; Li, J. InversionGNN: A Dual Path Network for Multi-Property Molecular Optimization. arXiv 2025, arXiv:2503.01488. [Google Scholar]
- Xia, X.; Liu, Y.; Zheng, C.; Zhang, Y.; Wu, Q.; Gao, X.; Zeng, X.; Su, Y. Evolutionary Multiobjective Molecule Optimization in an Implicit Chemical Space. J. Chem. Inf. Model. 2024, 64, 5161–5174. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.; Cheng, X.; Yang, Y.; Bao, Y.; Wang, L.; Gu, Q. Controllable and decomposed diffusion models for structure-based molecular optimization. arXiv 2024, arXiv:2403.13829. [Google Scholar]
- Morehead, A.; Cheng, J. Geometry-complete diffusion for 3D molecule generation and optimization. Commun. Chem. 2024, 7, 150. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Nie, W.; Qiao, Z.; Xiao, C.; Baraniuk, R.; Anandkumar, A. Retrieval-based Controllable Molecule Generation. arXiv 2023, arXiv:2208.11126. [Google Scholar]
- Abeer, A.N.; Urban, N.M.; Weil, M.R.; Alexander, F.J.; Yoon, B.-J. Multi-objective latent space optimization of generative molecular design models. Patterns 2024, 5, 101042. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, O.; Wang, X.; Fu, L.; Zhao, H.; Wang, J.; Du, H.; Jiang, D.; Deng, Y.; Cao, D.; et al. Leveraging language model for advanced multiproperty molecular optimization via prompt engineering. Nat. Mach. Intell. 2024, 6, 1359–1369. [Google Scholar] [CrossRef]
- Ye, G.; Cai, X.; Lai, H.; Wang, X.; Huang, J.; Wang, L.; Liu, W.; Zeng, X. Drugassist: A large language model for molecule optimization. Briefings Bioinform. 2025, 26, bbae693. [Google Scholar] [CrossRef] [PubMed]
- Moerland, T.M.; Broekens, J.; Plaat, A.; Jonker, C.M. Model-based reinforcement learning: A survey. Found. Trends Mach. Learn. 2023, 16, 1–118. [Google Scholar] [CrossRef]
- Pogány, P.; Arad, N.; Genway, S.; Pickett, S.D. De novo molecule design by translating from reduced graphs to SMILES. J. Chem. Inf. Model. 2018, 59, 1136–1146. [Google Scholar] [CrossRef]
- Jin, W.; Barzilay, R.; Jaakkola, T. Junction tree variational autoencoder for molecular graph generation. In Proceedings of the International conference on machine learning. PMLR, Stockholm, Sweden, 10–15 July 2018; pp. 2323–2332. [Google Scholar]
- Lee, S.; Lee, D.B.; Hwang, S.J. Contrastive learning with adversarial perturbations for conditional text generation. arXiv 2021, arXiv:2012.07280. [Google Scholar]
- Grantham, K.; Mukaidaisi, M.; Ooi, H.K.; Ghaemi, M.S.; Tchagang, A.; Li, Y. Deep evolutionary learning for molecular design. IEEE Comput. Intell. Mag. 2022, 17, 14–28. [Google Scholar] [CrossRef]
- Barreto Gomes, D.E.; Galentino, K.; Sisquellas, M.; Monari, L.; Bouysset, C.; Cecchini, M. ChemFlow—From 2D Chemical Libraries to Protein–Ligand Binding Free Energies. J. Chem. Inf. Model. 2023, 63, 407–411. [Google Scholar] [CrossRef] [PubMed]
- Cheng, A.H.; Cai, A.; Miret, S.; Malkomes, G.; Phielipp, M.; Aspuru-Guzik, A. Group SELFIES: A robust fragment-based molecular string representation. Digit. Discov. 2023, 2, 748–758. [Google Scholar] [CrossRef]
- Cheng, Y.; Gong, Y.; Liu, Y.; Song, B.; Zou, Q. Molecular design in drug discovery: A comprehensive review of deep generative models. Briefings Bioinform. 2021, 22, bbab344. [Google Scholar] [CrossRef] [PubMed]
- Zeng, X.; Xiang, H.; Yu, L.; Wang, J.; Li, K.; Nussinov, R.; Cheng, F. Accurate prediction of molecular properties and drug targets using a self-supervised image representation learning framework. Nat. Mach. Intell. 2022, 4, 1004–1016. [Google Scholar] [CrossRef]
- Elton, D.C.; Boukouvalas, Z.; Fuge, M.D.; Chung, P.W. Deep learning for molecular design—A review of the state of the art. Mol. Syst. Des. Eng. 2019, 4, 828–849. [Google Scholar] [CrossRef]
- Kuzminykh, D.; Polykovskiy, D.; Kadurin, A.; Zhebrak, A.; Baskov, I.; Nikolenko, S.; Shayakhmetov, R.; Zhavoronkov, A. 3D molecular representations based on the wave transform for convolutional neural networks. Mol. Pharm. 2018, 15, 4378–4385. [Google Scholar] [CrossRef]
- Kusner, M.J.; Paige, B.; Hernández-Lobato, J.M. Grammar variational autoencoder. In Proceedings of the International conference on machine learning. PMLR, Sydney, Australia, 6–11 August 2017; pp. 1945–1954. [Google Scholar]
- Barthel, S.; Krenn, M.; Ai, Q.; Carson, N.; Frei, A.; Frey, N.C.; Friederich, P.; Gaudin, T.; Gayle, A.A.; Jablonka, K.M.; et al. SELFIES and the future of molecular string representations. Patterns 2022, 3, 100588. [Google Scholar]
- Samanta, B.; De, A.; Jana, G.; Gómez, V.; Chattaraj, P.K.; Ganguly, N.; Gomez-Rodriguez, M. Nevae: A deep generative model for molecular graphs. J. Mach. Learn. Res. 2020, 21, 1–33. [Google Scholar] [CrossRef]
- Kim, S.; Thiessen, P.A.; Bolton, E.E.; Chen, J.; Fu, G.; Gindulyte, A.; Han, L.; He, J.; He, S.; Shoemaker, B.A.; et al. PubChem substance and compound databases. Nucleic Acids Res. 2016, 44, D1202–D1213. [Google Scholar] [CrossRef]
- Polykovskiy, D.; Zhebrak, A.; Sanchez-Lengeling, B.; Golovanov, S.; Tatanov, O.; Belyaev, S.; Kurbanov, R.; Artamonov, A.; Aladinskiy, V.; Veselov, M.; et al. Molecular sets (MOSES): A benchmarking platform for molecular generation models. Front. Pharmacol. 2020, 11, 565644. [Google Scholar] [CrossRef] [PubMed]
- Sterling, T.; Irwin, J.J. ZINC 15–ligand discovery for everyone. J. Chem. Inf. Model. 2015, 55, 2324–2337. [Google Scholar] [CrossRef] [PubMed]
- Gaulton, A.; Bellis, L.J.; Bento, A.P.; Chambers, J.; Davies, M.; Hersey, A.; Light, Y.; McGlinchey, S.; Michalovich, D.; Al-Lazikani, B.; et al. ChEMBL: A large-scale bioactivity database for drug discovery. Nucleic Acids Res. 2012, 40, D1100–D1107. [Google Scholar] [CrossRef]
- Ramakrishnan, R.; Dral, P.O.; Rupp, M.; Von Lilienfeld, O.A. Quantum chemistry structures and properties of 134 kilo molecules. Sci. Data 2014, 1, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Blum, L.C.; Reymond, J.L. 970 million druglike small molecules for virtual screening in the chemical universe database GDB-13. J. Am. Chem. Soc. 2009, 131, 8732–8733. [Google Scholar] [CrossRef]
- Butler, K.T.; Davies, D.W.; Cartwright, H.; Isayev, O.; Walsh, A. Machine learning for molecular and materials science. Nature 2018, 559, 547–555. [Google Scholar] [CrossRef]
- Chen, C.; Yaari, Z.; Apfelbaum, E.; Grodzinski, P.; Shamay, Y.; Heller, D.A. Merging Data Curation and Machine Learning to Improve Nanomedicines. Adv. Drug Deliv. Rev. 2022, 183, 114172. [Google Scholar] [CrossRef]
- Papadatos, G.; Gaulton, A.; Hersey, A.; Overington, J.P. Activity, assay and target data curation and quality in the ChEMBL database. J. Comput. Aided Mol. Des. 2015, 29, 885–896. [Google Scholar] [CrossRef]
- Bowers, E.C.; Hassanin, A.A.; Ramos, K.S. In vitro models of exosome biology and toxicology: New frontiers in biomedical research. Toxicol. Vitr. 2020, 64, 104462. [Google Scholar] [CrossRef]
- Du, H.; Jiang, D.; Zhang, O.; Wu, Z.; Gao, J.; Zhang, X.; Wang, X.; Deng, Y.; Kang, Y.; Li, D.; et al. A flexible data-free framework for structure-based de novo drug design with reinforcement learning. Chem. Sci. 2023, 14, 12166–12181. [Google Scholar] [CrossRef] [PubMed]
- Cubuk, E.D.; Zoph, B.; Shlens, J.; Le, Q.V. Randaugment: Practical automated data augmentation with a reduced search space. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Seattle, WA, USA, 14–19 June 2020; pp. 702–703. [Google Scholar]
- Wang, J.; Zheng, S.; Chen, J.; Yang, Y. Meta learning for low-resource molecular optimization. J. Chem. Inf. Model. 2021, 61, 1627–1636. [Google Scholar] [CrossRef]
- Ma, R.; Li, Y.; Li, C.; Wan, F.; Hu, H.; Xu, W.; Zeng, J. Secure multiparty computation for privacy-preserving drug discovery. Bioinformatics 2020, 36, 2872–2880. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Xue, D.; Chuai, G.; Yang, Q.; Liu, Q. FL-QSAR: A federated learning-based QSAR prototype for collaborative drug discovery. Bioinformatics 2021, 36, 5492–5498. [Google Scholar] [CrossRef] [PubMed]
- Abadi, M.; Chu, A.; Goodfellow, I.; McMahan, H.B.; Mironov, I.; Talwar, K.; Zhang, L. Deep learning with differential privacy. In Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, Vienna, Austria, 24–28 October 2016; pp. 308–318. [Google Scholar]
- Shahverdi, A.; Trieu, N.; Weng, C.; Youmans, W. Privacy-Preserving Prescription Drug Management Using Fully Homomorphic Encryption. In Protecting Privacy through Homomorphic Encryption; Springer: Berlin/Heidelberg, Germany, 2021; pp. 169–176. [Google Scholar]
- Peng, M.; Zhang, Q.; Xing, X.; Gui, T.; Huang, X.; Jiang, Y.G.; Ding, K.; Chen, Z. Trainable undersampling for class-imbalance learning. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 4707–4714. [Google Scholar]
- Mukhoti, J.; Kulharia, V.; Sanyal, A.; Golodetz, S.; Torr, P.; Dokania, P. Calibrating deep neural networks using focal loss. Adv. Neural Inf. Process. Syst. 2020, 33, 15288–15299. [Google Scholar]
- Landrum, G. RDKit: A software suite for cheminformatics, computational chemistry, and predictive modeling. Greg Landrum 2013, 8, 5281. [Google Scholar]
- Huang, K.; Fu, T.; Gao, W.; Zhao, Y.; Roohani, Y.; Leskovec, J.; Coley, C.W.; Xiao, C.; Sun, J.; Zitnik, M. Therapeutics data commons: Machine learning datasets and tasks for drug discovery and development. arXiv 2021, arXiv:2102.09548. [Google Scholar]
- Yang, H.; Lou, C.; Sun, L.; Li, J.; Cai, Y.; Wang, Z.; Li, W.; Liu, G.; Tang, Y. admetSAR 2.0: Web-service for prediction and optimization of chemical ADMET properties. Bioinformatics 2019, 35, 1067–1069. [Google Scholar] [CrossRef]
- Bickerton, G.R.; Paolini, G.V.; Besnard, J.; Muresan, S.; Hopkins, A.L. Quantifying the chemical beauty of drugs. Nat. Chem. 2012, 4, 90–98. [Google Scholar] [CrossRef]
- Daina, A.; Michielin, O.; Zoete, V. iLOGP: A simple, robust, and efficient description of n-octanol/water partition coefficient for drug design using the GB/SA approach. J. Chem. Inf. Model. 2014, 54, 3284–3301. [Google Scholar] [CrossRef]
- Ertl, P.; Schuffenhauer, A. Estimation of synthetic accessibility score of drug-like molecules based on molecular complexity and fragment contributions. J. Cheminform. 2009, 1, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Olivecrona, M.; Blaschke, T.; Engkvist, O.; Chen, H. Molecular de-novo design through deep reinforcement learning. J. Cheminform. 2017, 9, 1–14. [Google Scholar] [CrossRef]
- Jin, W.; Barzilay, R.; Jaakkola, T. Multi-objective molecule generation using interpretable substructures. In Proceedings of the International Conference on Machine Learning. PMLR, Online, 13–18 July 2020; pp. 4849–4859. [Google Scholar]
- Nigam, A.; Pollice, R.; Tom, G.; Jorner, K.; Willes, J.; Thiede, L.A.; Kundaje, A.; Aspuru-Guzik, A. Tartarus: A benchmarking platform for realistic and practical inverse molecular design. arXiv 2022, arXiv:2209.12487. [Google Scholar]
- Trott, O.; Olson, A.J. AutoDock Vina: Improving the speed and accuracy of docking with a new scoring function, efficient optimization, and multithreading. J. Comput. Chem. 2010, 31, 455–461. [Google Scholar] [CrossRef]
- Vogt, M.; Yonchev, D.; Bajorath, J. Computational method to evaluate progress in lead optimization. J. Med. Chem. 2018, 61, 10895–10900. [Google Scholar] [CrossRef] [PubMed]
- Renz, P.; Van Rompaey, D.; Wegner, J.K.; Hochreiter, S.; Klambauer, G. On failure modes in molecule generation and optimization. Drug Discov. Today Technol. 2019, 32, 55–63. [Google Scholar] [CrossRef] [PubMed]
- SV, S.S.; Law, J.N.; Tripp, C.E.; Duplyakin, D.; Skordilis, E.; Biagioni, D.; Paton, R.S.; St. John, P.C. Multi-objective goal-directed optimization of de novo stable organic radicals for aqueous redox flow batteries. Nat. Mach. Intell. 2022, 4, 720–730. [Google Scholar]
- Shin, D.H.; Son, Y.H.; Lee, D.J.; Han, J.W.; Kam, T.E. Dynamic many-objective molecular optimization: Unfolding complexity with objective decomposition and progressive optimization. In Proceedings of the Thirty-Third International Joint Conference on Artificial Intelligence (IJCAI), Jeju, Republic of Korea, 3–9 August 2024; pp. 6026–6034. [Google Scholar]
- Huang, L.; Xu, T.; Yu, Y.; Zhao, P.; Chen, X.; Han, J.; Xie, Z.; Li, H.; Zhong, W.; Wong, K.C.; et al. A dual diffusion model enables 3D molecule generation and lead optimization based on target pockets. Nat. Commun. 2024, 15, 2657. [Google Scholar] [CrossRef]
- Liang, J.; Ban, X.; Yu, K.; Qu, B.; Qiao, K.; Yue, C.; Chen, K.; Tan, K.C. A survey on evolutionary constrained multi-objective optimization. IEEE Trans. Evol. Comput. 2022, 27, 201–221. [Google Scholar] [CrossRef]
- Post, K.L.; Belmadani, M.; Ganguly, P.; Meili, F.; Dingwall, R.; McDiarmid, T.A.; Meyers, W.M.; Herrington, C.; Young, B.P.; Callaghan, D.B.; et al. Multi-model functionalization of disease-associated PTEN missense mutations identifies multiple molecular mechanisms underlying protein dysfunction. Nat. Commun. 2020, 11, 2073. [Google Scholar] [CrossRef]
- Luo, S.; Chen, T.; Xu, Y.; Zheng, S.; Liu, T.Y.; Wang, L.; He, D. One transformer can understand both 2d & 3d molecular data. arXiv 2022, arXiv:2210.01765. [Google Scholar]
- Konstantinidou, M.; Visser, E.J.; Vandenboorn, E.; Chen, S.; Jaishankar, P.; Overmans, M.; Dutta, S.; Neitz, R.J.; Renslo, A.R.; Ottmann, C.; et al. Structure-based optimization of covalent, small-molecule stabilizers of the 14-3-3σ/ERα protein–protein interaction from nonselective fragments. J. Am. Chem. Soc. 2023, 145, 20328–20343. [Google Scholar] [CrossRef] [PubMed]
- Son, Y.H.; Shin, D.H.; Lee, D.J.; Kam, T.E. Molecular Optimization with Mamba-Based GFlowNet. In Proceedings of the 2025 International Conference on Electronics, Information, and Communication (ICEIC), Osaka, Japan, 19–22 January 2025; pp. 1–4. [Google Scholar]
- Gusev, F.; Gutkin, E.; Kurnikova, M.G.; Isayev, O. Active learning guided drug design lead optimization based on relative binding free energy modeling. J. Chem. Inf. Model. 2022, 63, 583–594. [Google Scholar] [CrossRef] [PubMed]
- Cai, C.; Wang, S.; Xu, Y.; Zhang, W.; Tang, K.; Ouyang, Q.; Lai, L.; Pei, J. Transfer learning for drug discovery. J. Med. Chem. 2020, 63, 8683–8694. [Google Scholar] [CrossRef]
- Zhu, J.; Liu, Y.; Zhang, Y.; Chen, Z.; She, K.; Tong, R. DAEM: Deep attributed embedding based multi-task learning for predicting adverse drug–drug interaction. Expert Syst. Appl. 2023, 215, 119312. [Google Scholar] [CrossRef]
- Yu, J.; Zheng, Y.; Koh, H.Y.; Pan, S.; Wang, T.; Wang, H. Collaborative Expert LLMs Guided Multi-Objective Molecular Optimization. arXiv 2025, arXiv:2503.03503. [Google Scholar]

| Dataset | Description | Amount | Website |
|---|---|---|---|
| ZINC | Free database of commercially available compounds for virtual screening | >750,000,000 | https://zinc15.docking.org/ (accessed on 9 April 2025) |
| ChEMBL | A manually curated database of bioactive molecules with drug-like properties | 2,300,000 | https://www.ebi.ac.uk/chembl/ (accessed on 9 April 2025) |
| PubChem | Largest collection of freely accessible chemical information | 119,000,000 | https://pubchem.ncbi.nlm.nih.gov/ (accessed on 9 April 2025) |
| MOSES | Benchmark platform for training process of standardized molecular generation model | 1,940,000 | https://github.com/molecularsets/moses (accessed on 9 April 2025) |
| QM9 | Molecules with up to 9 heavy atoms | 133,885 | http://quantum-machine.org/datasets/ (accessed on 9 April 2025) |
| GDB-13 | Small organic molecules database | 977,468,314 | https://gdb.unibe.ch/downloads/ (accessed on 9 April 2025) |
| GDB-17 | Small organic molecules database | 50,000,000 | https://gdb.unibe.ch/downloads/ (accessed on 9 April 2025) |
| QED Pairs | Similar molecule pairs with low and high QED values | 88,000 | https://github.com/wengong-jin/iclr19-graph2graph (accessed on 9 April 2025) |
| PlogP Pairs | Similar molecule pairs with low and high PlogP values | 99,000 | |
| Drd2 Pairs | Similar molecule pairs with low and high Drd2 values | 34,000 |
| Properties | Descriptions |
|---|---|
| Quantitative estimate of drug-likeness (QED) [92] | A comprehensive index that quantifies the drug-likeness of a molecule as a value between 0 and 1, calculated by combining eight physical descriptors. |
| Octanol–water partition coefficients (LogP) [93] | A metric assessing the dissolution and diffusion of molecules in the human body through their combined water and lipid solubility, reflecting the membrane absorption capacity. |
| Penalized logP (PlogP) [58] | The logarithm of the partition ratio of the solute between octanol and water minus the synthetic accessibility score and the number of long cycles. |
| Synthetic accessibility (SA) [94] | Quantification of the difficulty of synthesizing small molecules in the laboratory on a scale ranging from 1 to 10, where a lower score indicates easier synthesis. |
| Similarity [23] | Similarity between the lead molecule and the optimized molecule. Tanimoto similarity is widely employed in existing molecular optimization studies due to its computational efficiency. |
| DRD2 activity [95] | The predicted biological activity score against the dopamine receptor D2 target. |
| GSK3 inhibition [96] | The estimated inhibition score against the glycogen synthase kinase-3 target. |
| JNK3 inhibition [96] | The estimated inhibition score against the c-Jun N-terminal kinase-3 target. |
| 1SYH [97] | The docking score of a molecule and an ionotropic glutamate receptor that is associated with neurological and psychiatric diseases. |
| 6Y2F [97] | The docking score of a molecule and the main protease of SARS-CoV-2 that is responsible for the translation of the viral RNA of the SARS-CoV-2 virus. |
| 4LDE [97] | The 2-adrenoceptor GPCR receptor that spans the cell membrane and binds adrenaline, a hormone that mediates muscle relaxation and bronchodilation. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, X.; Zhang, Y.; Zeng, X.; Zhang, X.; Zheng, C.; Su, Y. Artificial Intelligence in Molecular Optimization: Current Paradigms and Future Frontiers. Int. J. Mol. Sci. 2025, 26, 4878. https://doi.org/10.3390/ijms26104878
Xia X, Zhang Y, Zeng X, Zhang X, Zheng C, Su Y. Artificial Intelligence in Molecular Optimization: Current Paradigms and Future Frontiers. International Journal of Molecular Sciences. 2025; 26(10):4878. https://doi.org/10.3390/ijms26104878
Chicago/Turabian StyleXia, Xin, Yajie Zhang, Xiangxiang Zeng, Xingyi Zhang, Chunhou Zheng, and Yansen Su. 2025. "Artificial Intelligence in Molecular Optimization: Current Paradigms and Future Frontiers" International Journal of Molecular Sciences 26, no. 10: 4878. https://doi.org/10.3390/ijms26104878
APA StyleXia, X., Zhang, Y., Zeng, X., Zhang, X., Zheng, C., & Su, Y. (2025). Artificial Intelligence in Molecular Optimization: Current Paradigms and Future Frontiers. International Journal of Molecular Sciences, 26(10), 4878. https://doi.org/10.3390/ijms26104878







