Next Article in Journal
Chloroquine Inhibits Contraction Elicited by the Alpha-1 Adrenoceptor Agonist Phenylephrine in the Isolated Rat Aortas
Previous Article in Journal
Renal Apoptosis in Male Rats Induced by Extensive Dietary Exposure to Ochratoxins
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
IJMS
Volume 26
Issue 10
10.3390/ijms26104555
ijms-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Metal-Involving Bifurcated Halogen Bonding with Iodide and Platinum(II) Center

by
Mariya A. Kryukova
,
Margarita B. Kostareva
,
Anna M. Cheranyova
,
Marina A. Khazanova
,
Anton V. Rozhkov
and
Daniil M. Ivanov
*
Institute of Chemistry, Saint Petersburg State University, 7/9 Universitetskaya Nab., Saint Petersburg 199034, Russia
*
Author to whom correspondence should be addressed.
Int. J. Mol. Sci. 2025, 26(10), 4555; https://doi.org/10.3390/ijms26104555
Submission received: 6 April 2025 / Revised: 1 May 2025 / Accepted: 6 May 2025 / Published: 9 May 2025
(This article belongs to the Section Materials Science)
Browse Figures
Versions Notes

Abstract

:
The cocrystallization of trans-[PtI2(NCR)2] (R = NMe2 1, NEt2 2, Ph 3, o-ClC6H4 4) with iodine and iodoform gave the crystalline adducts 1∙4I2, 2∙2CHI3, 3∙2CHI3, and 4∙4I2, whose structures were studied by single-crystal X-ray diffractometry (XRD). In the structures, apart from the rather predictable C–H⋯I hydrogen bonds (HBs) and I–I⋯I or C–I⋯I halogen bonds (XBs) with the iodide ligands, we identified bifurcated I–I⋯(I–Pt) and C–I⋯(I–Pt) metal-involving XBs, where the platinum center and iodide ligands function as simultaneous XB acceptors toward σ-holes of I atoms in I2 or CHI3. Appropriate density functional theory (DFT) calculations (PBE-D3/jorge-DZP-DKH with plane waves in the GAPW method) performed with periodic boundary conditions confirmed the existence of the bifurcated metal-involving I–I⋯(I–Pt) and C–I⋯(I–Pt) interactions and their noncovalent nature.

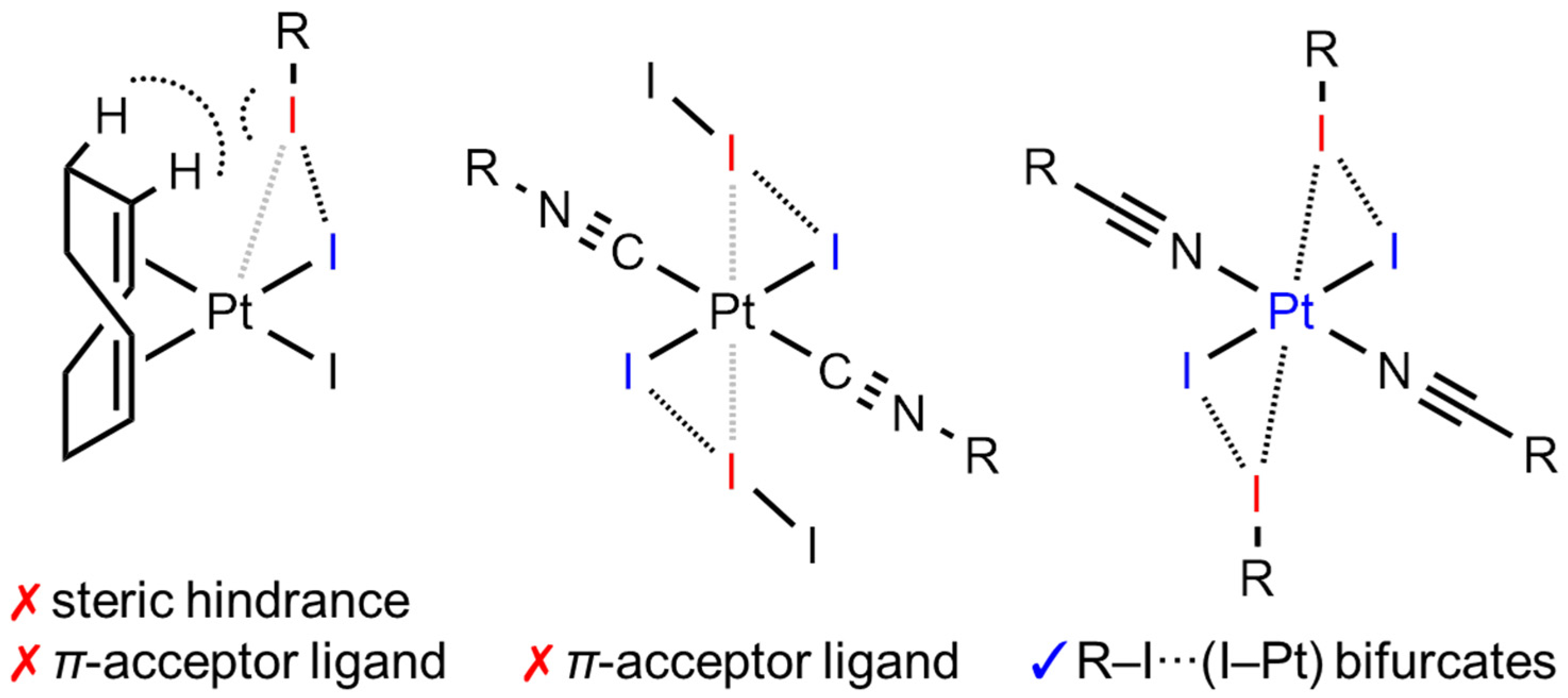
1. Introduction

In recent years, halogen bonding (XB) [1,2], as one of the σ-hole interactions [3], has been actively investigated in the crystal engineering of various supramolecular aggregates [4,5,6], as a tool in synthetic organometallic and coordination chemistry, [7], drug discovery [8,9], polymer science [10], and noncovalent catalysis [11,12,13,14]. XBs can also influence the stability of explosives [15,16], their photophysical properties [17,18], and their solubility [19] and volatility [20].
In a typical XB, the X⋯Nu distance tends to be shorter than the vdW radii sum, and the R–X⋯Nu angle between the covalent R–X bond and the X⋯Nu short contact tends to be linear [1]. When another halogen X’ with one neighbor R’ is a nucleophile in XB, the X⋯X’–R’ angle tends to be different from the R–X⋯Nu angle and close to 90°. This type of XBs is also known as “type II” halogen–halogen contacts [21].
Iodine-centered σ-hole XB donors, including diiodine and iodoform [22], are the most popular since iodine demonstrate the largest σ-hole and the largest polarizability among halogens, and both two properties are important in the formation of XBs [1,2]. In most cases, lone-pair-bearing non-metal atoms or electron-rich π-systems are nucleophiles in the XB formation. However, recent investigations showed that d8- or d10-centers, despite their positive charges, can also be XB acceptors due to the sterically available dz2-orbital [23]. Metal centers can also be parts of joint nucleophilic XB-accepting areas in the formation of bifurcated interactions, including two metal centers in I⋯(Rh,Rh) [24] XB, chlorides in X⋯(Cl–M) (X = Br, I; M = PtII, AuI) [25,26,27], and even in I⋯(Cl2Rh2) interactions [24], and also carbon atoms in cyclometallated ligands in I⋯(C–M) (M = PdII, PtII) [28,29] bonding.
At the same time, the bifurcated metal-involving XBs, which include iodide ligands, seem to be illusive. Previously, we described the I⋯(I–PtII) possible bifurcated XBs in [PtI2(COD)]∙1.5FIB (COD = 1,5-cycloocatadiene; FIB = 1,4-diiodotetrafluorobenzene) [30] and in trans-[PtI2(CN(2,6-MeC6H3))2]∙I2 [31]. In the first case, the C–I⋯PtII components of the bifurcate demonstrate I⋯Pt distances larger than the vdW sum [32] (3.7990(6) and 3.8127(4) vs. 3.73 Å), and the I–I⋯Pt angles deviate from linear (141.13(17) and 142.14(18) vs. 180°). In the second case, the I⋯Pt distances are smaller than the vdW sum (3.4600(6) and 3.4650(6) vs. 3.73 Å), but the angles strongly deviate from linear (128.10(3) and 128.27(3) vs. 180°). We believe these deviations can be explained by steric hindrance for the platinum center in the case of [PtI2(COD)] and the π-accepting properties [33] of both COD and isocyanide ligands, which decrease possible platinum(II) nucleophilicity.
In this work, we continued our systematic investigations of non-electrolyte iodide platinum(II) complexes as XB acceptors [19,30,34,35,36] and found bifurcated I⋯(I–PtII) XBs in four cocrystals of the iodide nitrile or dialkylcyanamide complexes trans-[PtI2(NCR)2] (R = NMe2 1, NEt2 2, Ph 3, o-ClC6H4 4) (Figure 1) with iodine and iodoform (1∙4I2, 2∙2CHI3, 3∙2CHI3, and 4∙4I2), where both components satisfied the geometrical IUPAC criteria for XBs according to X-ray diffraction data. Further theoretical calculations confirmed the existence and noncovalent nature of the interactions.

2. Results and Discussion

2.1. Single-Crystal X-Ray Diffraction Data

Complexes 1 and 4 were cocrystallized with diiodine in a 1:4 molar ratio by slow evaporation of CH2Cl2 solution, whereas 2 and 3 were cocrystallized with iodoform in a molar ratio of 1:2 after slow evaporation of their solutions in CH3NO2 or CH2Cl2/hexane (2:1, v:v), correspondingly, at RT in the dark in all cases. In both cases, the cocrystallizations gave adducts which were studied by single-crystal X-ray diffraction experiments (XRD) (Figure 2 and Figure S16, Table S1).
In all cases, the R–I⋯I–Pt (R = C, I) XBs link the iodide complex molecules with six diiodine (in 1∙4I2 and 4∙4I2), four iodoform (in 3∙2CHI3, see Figure S16 in SI), six iodoform (in 2∙2CHI3), or eight iodoform (in 3∙2CHI3) molecules with I⋯I distances in the range of 3.2362(7)–3.9255(8) Å, R–I⋯I angles ranging from 154.21(13) to 178.450(17)°, and I⋯I–Pt angles ranging from 59.548(13) to 124.317(16)° (for details, see Table 1), which confirmed the XB nature of the contacts, according to the geometric IUPAC criteria [1] and their assignment to “type II” halogen–halogen contacts [21], where the metal-bound iodides act as XB acceptors.
However, among the interactions observed in the different cocrystals, I1S⋯I1–Pt1 interactions showed the largest I⋯I distances (3.7517(5)–3.9255(8) Å), as well as the smallest R–I⋯I (154.21(13)–165.9(3)°) and I⋯I–Pt (59.548(13)–68.795(16)°) angles, which deviate from 180° and 90° for “type II” contacts, respectively. These deviations can be explained by R–I⋯Pt interactions (Table 2), which form joint R–I⋯(I–Pt) bifurcates with the latter (Figure 3), where platinum(II) and coordinated iodide centers compete with each other for the same electrophilic iodine centers in I2 or CHI3. The R–I⋯Pt components of the bifurcates demonstrate 3.4414(6)–3.7362(6) Å distances, which are shorter or close to ΣvdW = 3.73 Å, and 148.77(2)–165.46(14)° angles, which are close to the same values for the R–I⋯I interactions.
Interestingly, in both I2 adducts, most of the intramolecular I–I distances (2.7519(8) and 2.7519(8) Å in 1∙4I2 and 2.7253(5) and 2.7328(4) Å in 4∙4I2) are larger than those in solid I2 (2.7178(1) Å) [37] but longer than those in “coordinated” triiodide (2.774(1) Å for I–I–I–Pd moiety [38]), and the bonding picture can be described as intermediate between these cases. Note that the I4S–I4S bond (2.6940(5) Å) in 4∙4I2 is even shorter than that in solid I2 since this molecule in only involved in two moderate (2.7178(1) Å) I–I⋯I–Pt XBs.
To verify what types of noncovalent forces contribute to the crystal packing in the structures of 1∙4I2, 2∙2CHI3, 3∙2CHI3 and 4∙4I2, we carried out Hirshfeld surface analysis [39,40] using the CrystalExplorer program [41]; for visualization, we used the mapping of the normalized contact distance (dnorm) (Figure 4). The Hirshfeld surface analysis indicated the domination of I⋯H type contacts in all cases (from 34.4 to 46.4%), which was expected as the fraction of the H atoms is large (Table 3). The contribution of I⋯I and Pt⋯I intermolecular contacts to the Hirshfeld surfaces was also significant and comprised 7.4–19.6% (for I⋯I) and 2.0–3.3% (for Pt⋯I), respectively. Although the contacts that involve H atoms mainly contribute to the crystal packing, I⋯I and Pt⋯I interactions are the most fascinating in the context of this work, and therefore, they are consistently discussed further.

2.2. Theoretical Consideration

To obtain more arguments for the existence and noncovalent nature of the interactions, we performed DFT Douglas–Kroll–Hess second-order scalar relativistic (DKH2) calculations with periodic boundary conditions using experimentally obtained atomic coordinates, PBE [42] -D3 [43,44] level of theory with jorge-DZP-DKH [45,46,47,48] basis sets, which were realized in CP2K [49,50,51,52,53,54,55] in Gaussian augmented plane wave (GAPW) [56] formalism.
In all cases, the Bader quantum theory of atoms-in-molecules (QTAIM) topological analysis of electron density ρ was used for periodic wavefunctions for all crystal models under consideration. It showed the bond critical points (BCPs) between iodine in iodoform or diiodine and the platinum atom in 1–4 in all cases, which correspond to the I⋯Pt components of the bifurcate XBs (Table 4). The typically noncovalent nature of the interactions was confirmed by the parameters of the corresponding BCPs, including (i) small values of ρ; (ii) positive and small values of Laplacian ∇2ρ; (iii) positive or close-to-zero values of energy density H; and (iv) the balance of the Lagrangian kinetic energy G and the potential energy density V [57].
For all monofurcated I⋯I interactions, the corresponding BCPs were also found. In the cases of iodoform-involving interactions, the |V|/G relation is also less than 1, and the C–I⋯I XBs can be considered purely noncovalent (Table 5). In most cases, the I–I⋯I monofurcated XBs demonstrate a non-negligible covalent character, since |V|/G > 1.
In the case of the I2S–I1S⋯I1–Pt1 component of bifurcate in 1∙4I2, no BCP was detected (Figure 5, upper left). However, the projection of sign(λ2)ρ function in NCI analysis [58] showed the light blue area with negative λ2 between I1S and I1 atoms. The ρ minimum along the I1S⋯I1 line is not negligible (0.009 e/Bohr3) and is located in the RDG = 0.5 area, indicated by a dotted line. The parameters in this minimum can also be found in Table 5. We suppose the I2S–I1S⋯(I1–Pt1) can also be considered a true bifurcate, since for both the I1S⋯Pt1 and I1S⋯I1 components, blue areas of negative sign(λ2)ρ values were found. In all other cases of I⋯I components of the bifurcates, BCPs were successfully detected, and the BCP parameters are in accordance with longer I⋯I distances, and these interactions can also be treated as purely noncovalent.
In all cases, the nucleophilicity of both iodide and platinum(II) centers toward iodine in iodoform or diiodine was confirmed by electron localization function (ELF) [59,60,61] projections with topological bond paths and critical points for ρ (Figure 5). The I1S⋯Pt1 and I1S⋯I1 bond paths are far from the orange lone pair areas with high ELF values on I1S atoms in all cases. The green low-ELF area, with corresponds to the σ-hole on the I1 atom, is also directed to the yellow high-ELF area on iodide in the case of the I1S⋯I1 interaction in 1∙4I2. Thus, in all cases, the I1 centers are electrophilic partners toward both iodide and platinum(II) centers.
To evaluate the energies of the bifurcate interactions and decompose them into electrostatic, exchange, induction, and dispersion parts, we performed scaled symmetry adapted perturbation theory (sSAPT0) [62,63] calculations with def2-TZVP [64,65] bases for the dissociation of heterotrimeric clusters extracted from crystal structures to isolated iodoform or diiodine molecules and heterodimeric clusters (Figure 6 and Table 6).
According to the sSAPT0 calculations, the energy I⋯(I–Pt) bifurcates are in the range from –8.58 to –9.55 kcal/mol, with diiodine interactions being expectedly stronger. In all cases, the dispersion component is more negative than the electrostatic component, and the Edisp/Eelst ratio is the largest for the 2∙(CHI3)2 cluster, which can be explained by the largest NEt2 substituents and polarizable CHI3 molecules.

3. Materials and Methods

K2[PtCl4], PtI2, KI, I2, CHI3, acetonitrile, N,N-dimethylcyanamide, N,N-diethylcyanamide, benzonitrile, 2-chlorobenzonitrile, and all solvents were obtained from Sigma Aldrich (Merck, Germany) and used as received.
The NMR spectra were recorded on Bruker AVANCE III 400 and Bruker AVANCE 500 spectrometers (Billerica, MA, USA) at ambient temperature in acetone-d6 or CDCl3 (at 500 or 400, 126 or 101, 107 or 86 MHz for 1H, 13C{1H}, and 195Pt NMR spectra, respectively) (Figures S1–S9). K2[PtCl4] in D2O was used as a standard for the 195Pt NMR measurements. IR spectra (Figures S10–S12) were recorded on a Bruker (Billerica, MA, USA) TENSOR 27 FT-IR spectrometer (4000–400 cm–1, KBr or CsI pellets) (Figure S4). TLC was performed on Merck 60 F254 SiO2 plates (Sigma Aldrich, Merck, Germany). The HRESI+-MS data (Figures S13–S15) were obtained on a “MaXis”, Bruker Daltonik GmbH (Billerica, MA, USA), spectrometer equipped with an electrospray ionization (ESI) source; CH2Cl2 was used as a solvent.

3.1. Synthesis of Trans-[PtI2(NCNR2)2] (R = Me 1, Et 2) Dialkylcyanamide Complexes

Complex 1 was synthesized as previously reported [35]. A 2-fold excess of KI (0.4 g, 2.4 mmol) was added to an aqueous solution of K2PtCl4 (0.5 g, 1.2 mmol, 2.5 mL of H2O). The reaction mixture was left for 15 min until the darkening of the solution ceased. After that, a 10-fold excess of N,N-dimethylcyanamide (NCNMe2, 12 mmol, 0.876 mL) was added to the solution and the reaction mixture was left for a week until the solution became clear and an orange precipitate was formed. The resulting precipitate was filtered, washed with three portions of 3 mL of water and diethyl ether, and then dried in air at room temperature. The substance was purified by column chromatography on silica gel (Merck 60 F254, Sigma Aldrich, Merck, Germany), CH2Cl2:EtOAc = 4:1, v/v, first fraction). Yield: 66.7% (473 mg). Analytical data are in accordance with those reported earlier [35].
For 2, the synthetic procedure was based on those previously reported for 1 and trans-[PtI2(NCN(CH2)5)2] [35]. The procedure for 2 was analogous to that described 1, except that N,N-diethylcyanamide (NCNEt2) was used instead of NCNMe2. The purification steps followed the same column chromatography method, affording trans-[PtI₂(NCNEt2)2] at similarly high purity.
Yield: 77.9% (605 mg). TLC (eluent is CH2Cl2:MeOH 50:1, v/v): Rf = 0.79. HRESI+-MS (MeOH, m/z): 667.9313 ([M + Na]+, calcd 667.9317)). IR (CsI, selected bonds, cm−1): 2932 (w), 2853 (w), ν(C–H); 1451 (w), 1284 (m), δ(CH3); 2290 (s), ν(C≡N); 1094 (w), ν(C–N). 1H NMR (acetone-d6, δ): 3.15 (q, J = 7.2 Hz, 2H, NCH2), 1.18 (t, J = 7.4 Hz, 3H, NCH2CH3) ppm. 13C{1H} NMR (acetone-d6, δ): 119.21 (C≡N), 47.01 (NCH2), 13.32 (NCH2CH3) ppm. 195Pt NMR (acetone-d6, δ): −3652.11 ppm.

3.2. Synthesis of Trans-[PtI2(NCR)2] (R = Ph 3, 2-ClC6H4 4) Nitrile Complexes

Complex 3 was synthesized as previously reported [66].
Complex 4 was synthesized from cis/trans-[PtCl2(EtCN)2] [67] in two steps, where all operations were performed under argon atmosphere using standard Schlenk techniques and all solvents were dried by the usual procedures and freshly distilled before use.
I. A solution of [PtCl2(EtCN)2] (211 mg, 0.56 mmol, 1 equiv) in 1.4 mL of dried toluene was prepared, and an excess of o-ClC6H4CN (309 mg, 2.24 mmol, 4 equiv) was added. The resulting mixture was purged with argon and heated under reflux in an oil bath for 5 h with continuous stirring. After completion of the reaction, both the nitrile EtCN and toluene were removed under reduced pressure. The resulting residue was then subjected to column chromatography on silica gel (Merck 60 F254, CH2Cl2:MeOH = 100:1, v/v), which afforded the cis- and trans- isomers of [PtCl2(2-ClC6H4CN)2] as separate fractions. Yield: 47% (142 mg). TLC (eluent is CH2Cl2:MeOH = 100:1, v/v): Rf = 0.52. HRESI+-MS (MeOH, m/z): 562.8972 ([M + Na]+, calcd 562.8938), 578.8686 ([M + K]+, calcd 578.8678). IR (KBr, selected bonds, cm−1): 3063(m) ν(=C–H), 2294(m) ν(C≡N); 1580(m), 1462(m), 1433(m) ν(C=CAr); 1261(m) and 1209(m) in-ring deformations; 1061(s) ν(C–Cl); 776(s), 683(s), 555(s) (C–H oop). 1H NMR (CDCl3, δ): 7.80 (m, 1H, CHAr), 7.69 (m, 1H, CHAr), 7.58 (m, 1H, CHAr), 7.47 (m, 1H, CHAr). 13C{1H} NMR (CDCl3, δ): 139.07, 136.42, 135.62, 130.62, 127.55, 114.17, 110.66. 195Pt NMR (CDCl3, δ): –2348.04.
II. The mixture of [PtCl2(2-ClC6H4CN)2] (100 mg, 0.18 mmol) and NaI (54 mg, 0.36 mmol) was stirred in acetone (2 mL) at 35° in the dark for 24 h. The mixture was cooled to ambient temperature, and the precipitate was filtered off and washed twice with 1 mL of acetone. From the remaining brown solution, the solvent was removed under vacuum. The crystallization of the crude product from acetone gave 4 (89 mg, 68%) as yellow crystals. TLC (eluent is CH2Cl2:hexane = 2:1, v/v): Rf = 0.45. HRESI+-MS (MeOH, m/z): 746.2744 ([M + Na]+, calcd 746.7651). IR (KBr, selected bonds, cm−1): 3445(m) ν(=C–H), 2291(m) ν(C≡N); 1582(m), 1468(m), 1433(m), ν(C=CAr); 1266(s), 1209(s) and 1160(s) in-ring deformations; 1062(s) ν(C–Cl); 761 (s), 686(s), 557(s), 546(s), 464(s) (C–H oop). 1H NMR (500 MHz, Acetone-d6) δ 7.92 (dd, J = 7.8, 1.6 Hz, 1H), 7.79 (ddd, J = 8.2, 7.5, 1.6 Hz, 1H), 7.73 (dd, J = 8.2, 1.2 Hz, 1H), 7.61 (td, J = 7.6, 1.2 Hz, 1H). 13C NMR (126 MHz, Acetone-d6) δ 135.82, 134.76, 134.44, 130.13, 128.02, 115.62, 112.89. 195Pt NMR (107 MHz, Acetone-d6) δ −5050.56 (s).

3.3. Crystallizations of the Adducts

Single crystals of 1·4I2 and 4·4I2 were obtained by slow evaporation of dichloromethane (CH2Cl2) solutions at room temperature. For 1·4I2, 10 mg (0.017 mmol) of the platinum complex was combined with 17.2 mg (0.068 mmol) of iodine (1:4 molar ratio), whereas 4·4I2 was prepared from 10 mg (0.014 mmol) of the corresponding platinum complex and 14.0 mg (0.055 mmol) of iodine, likewise maintaining a 1:4 ratio. In both cases, the solutions were left in loosely covered vials, protected from light, and suitable crystals for X-ray diffraction typically formed within a few days.
For 2·2CHI3, 5 mg (0.008 mmol) of the platinum complex and 6.1 mg (0.015 mmol) of iodoform (1:2 molar ratio) were dissolved in nitromethane (CH3NO2). In the case of 3·2CHI3, 10 mg (0.015 mmol) of the complex was mixed with 12.0 mg (0.031 mmol) of iodoform (1:2 ratio) in a dichloromethane/hexane solvent mixture (2:1 v/v). Both solutions were allowed to evaporate slowly in vials protected from light, yielding single crystals suitable for further structural investigations within several days.

3.4. X-Ray Structure Determination and Refinement

Suitable single crystals of adducts 1∙4I2, 2∙2CHI3, 3∙2CHI3, and 4∙4I2 were studied on an Xcalibur Eos diffractometer (monochromated MoKα radiation, λ = 0.71073, Oxford diffraction, Wrocław, Poland). Crystals were incubated at 100 K during data collection. Using Olex2 [68], the structures were solved with the ShelXT [69] structure solution program using intrinsic phasing and refined with the ShelXL [70] refinement package using least-squares minimization. Hydrogen atoms in all structures were placed in the ideal calculated positions according to neutron diffraction statistical data [71] and refined as colliding atoms with parameters of relative isotropic displacement. The main data of crystallography and details of refinement are given in Table S1 in Supporting Information. CCDC numbers 2441327–2441330 contain all supporting structural and refinement data.

3.5. Computational Details

Hirshfeld surface analysis [39,40] was performed using the CrystalExplorer 21 program [41]. The contact distances (dnorm), based on RvdW [32], were mapped on the Hirshfeld surfaces. In the color scale, the negative values of dnorm were visualized by red color, indicating contacts shorter than ΣvdW. The values represented in white color denote the intermolecular distances close to contacts with dnorm equal to zero. Contacts longer than ΣvdW with positive dnorm values were colored in blue.
Single-point DFT calculations based on experimentally determined coordinates (Tables S2–S5) with periodic boundary conditions for crystal (1 × 1 × 1 cell) 1∙4I2, 2∙2CHI3 (only one disordered Et position preserved), 3∙2CHI3, and 4∙4I2 models were performed in the CP2K-8.1 program [49,50,51,52,53,54,55] with 350 Ry and 50 Ry relative plane-wave cut-offs for the auxiliary grid using the PBE [42]-D3 [43,44] functional, (i) the Gaussian/augmented plane wave (GAPW) [56] with a full-electron jorge-DZP-DKH [45,46,47,48] mixed basis set with the Douglas–Kroll–Hess second-order scalar relativistic calculations requested relativistic core Hamiltonian [72,73]. We achieved 1.0 × 10−6 Hartree convergence for the self-consistent field cycle in the Γ-point approximation. The 0.500 rloc parameter was applied for Pt atoms in full-electron calculations. Electron localization function (ELF) [59,60,61], sign(λ2)ρ+RDG [58] projection analyses, and Bader [57,74,75] atoms-in-molecules topological analysis of electron density (QTAIM) were performed and visualized in Multiwfn 3.8 [76].
Symmetry adapted perturbation theory [62,63] calculations (sSAPT0/def2-TZVP [64,65]) for the 1∙(I2)2, 2∙(CHI3)2, 3∙(CHI3)2, and 4∙(I2)2 models decomposition were performed in Psi4 1.9 [77].

4. Conclusions

In this work, we reported four cocrystals of platinum(II) iodide dialkylcyanamide or nitrile complexes with I2 or CHI3 in a 1:4 or 1:2 ratio, respectively. In all cases, the bifurcated metal-involving C–I⋯(I–Pt) or I–I⋯(I–Pt) XBs were detected by XRD together with conventional C–I⋯I or I–I⋯I XBs. Although I⋯(I–Pt) contacts were previously reported, in this work, the bifurcated interactions with both platinum(II) and iodine centers fulfilled both the distance and angle IUPAC criteria.
The existence and the nature of the interactions were confirmed by further DFT full-electron calculations with periodic boundary conditions (PBE-D3/jorge-DZP-DKH, GAWP). The periodic wavefunctions were investigated by QTAIM topological analysis, sign(λ2)ρ, and ELF projections, which showed the nucleophilicity of both the platinum(II) centers and the iodide ligands toward the same iodine electrophile. Although, in one case, BCP was found only for the I–I⋯Pt component of the bifurcate, the iodide-involving interaction was confirmed by the sign(λ2)ρ+RDG analysis, which demonstrated the area of negative sign(λ2)ρ value along the I⋯I line. This observation is in accordance with previously reported trifurcated C–I⋯(Cl–Pt–Cl) interactions [78], where both I⋯Cl components were also confirmed by sign(λ2)ρ+RDG analysis without corresponding BCPs. Thus, we believe further investigations of polycenter noncovalent interactions require sign(λ2)ρ+RDG analysis, also known as NCI analysis, since one large ρ maximum along the zero-flux surface, i.e., BCP, can interfere with the detection of another, smaller maximum nearby.
In all four cocrystals of platinum(II) iodide dialkylcyanamide or nitrile complexes, “true” R–I⋯(I–Pt) bifurcate XBs were formed, comparing with previously reported [PtI2(COD)]∙1.5FIB (COD = 1,5-cycloocatadiene; FIB = 1,4-diiodotetrafluorobenzene) [30] and trans-[PtI2(CN(2,6-MeC6H3))2]∙I2 [31] (Figure 7).
We suppose that the success of both the nitrile and dialkylcyanamide structures was achieved due to (i) the small steric hindrance for the platinum center compared with [PtI2(COD)] and (ii) the small or even absent [79] π-accepting properties of NCR and NCNR2 compared with both COD and isocyanide ligands [33], which decrease the possible platinum(II) nucleophilicity.

Supplementary Materials

The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/ijms26104555/s1.

Author Contributions

Conceptualization, M.A.K. (Mariya A. Kryukova), A.V.R. and D.M.I.; methodology, M.A.K. (Mariya A. Kryukova), A.V.R. and D.M.I.; investigation, M.A.K. (Mariya A. Kryukova), M.B.K., M.A.K. (Marina A. Khazanova), A.M.C., A.V.R. and D.M.I.; writing—original draft preparation, M.B.K., A.V.R. and D.M.I.; writing—review and editing, D.M.I.; visualization, M.B.K. and D.M.I.; supervision, D.M.I.; project administration, D.M.I. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the Russian Science Foundation (project 22-73-10021).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.

Acknowledgments

The physicochemical measurements were performed at the Center for XRD Studies, Center for Magnetic Resonance, and Center for Chemical Analysis and Materials Research, whereas the theoretical part of this work was performed at the Computing Center (all belonging to St Petersburg State University).

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:
XRDX-ray diffraction
XBhalogen bonding, halogen bond
DFTdensity functional theory
GAPWGaussian augmented plane waves
COD1,5-cycloocatadiene
FIB1,4-diiodotetrafluorobenzene
IUPACInternational Union of Pure and Applied Chemistry
RTroom temperature
DKH2Douglas–Kroll–Hess second-order scalar relativistic
QTAIMquantum theory of atoms-in-molecules
BCPbond critical point
RDGreduced density gradient
NCInoncovalent interaction (analysis)
ELFelectron localization function
sSAPT0scaled symmetry adapted perturbation theory (zero order)
NMRnuclear magnetic resonance
TLCthin-layer chromatography
HRESI+-MShigh-resolution electrospray ionization–mass spectroscopy (positive ions)

References

  1. Desiraju, G.R.; Ho, P.S.; Kloo, L.; Legon, A.C.; Marquardt, R.; Metrangolo, P.; Politzer, P.; Resnati, G.; Rissanen, K. Definition of the halogen bond (IUPAC Recommendations 2013). Pure Appl. Chem. 2013, 85, 1711–1713. [Google Scholar] [CrossRef]
  2. Cavallo, G.; Metrangolo, P.; Milani, R.; Pilati, T.; Priimagi, A.; Resnati, G.; Terraneo, G. The Halogen Bond. Chem. Rev. 2016, 116, 2478–2601. [Google Scholar] [CrossRef] [PubMed]
  3. Politzer, P.; Murray, J. An Overview of Strengths and Directionalities of Noncovalent Interactions: σ-Holes and π-Holes. Crystals 2019, 9, 165. [Google Scholar] [CrossRef]
  4. Wang, H.; Bisoyi, H.K.; Urbas, A.M.; Bunning, T.J.; Li, Q. The Halogen Bond: An Emerging Supramolecular Tool in the Design of Functional Mesomorphic Materials. Chem.-A Eur. J. 2019, 25, 1369–1378. [Google Scholar] [CrossRef] [PubMed]
  5. Mukherjee, A.; Sanz-Matias, A.; Velpula, G.; Waghray, D.; Ivasenko, O.; Bilbao, N.; Harvey, J.N.; Mali, K.S.; De Feyter, S. Halogenated building blocks for 2D crystal engineering on solid surfaces: Lessons from hydrogen bonding. Chem. Sci. 2019, 10, 3881–3891. [Google Scholar] [CrossRef]
  6. Gilday, L.C.; Robinson, S.W.; Barendt, T.A.; Langton, M.J.; Mullaney, B.R.; Beer, P.D. Halogen Bonding in Supramolecular Chemistry. Chem. Rev. 2015, 115, 7118–7195. [Google Scholar] [CrossRef] [PubMed]
  7. Mahmudov, K.T.; Kopylovich, M.N.; Guedes da Silva, M.F.C.; Pombeiro, A.J.L. Non-covalent interactions in the synthesis of coordination compounds: Recent advances. Coord. Chem. Rev. 2017, 345, 54–72. [Google Scholar] [CrossRef]
  8. Dalpiaz, A.; Pavan, B.; Ferretti, V. Can pharmaceutical co-crystals provide an opportunity to modify the biological properties of drugs? Drug Discov. Today 2017, 22, 1134–1138. [Google Scholar] [CrossRef]
  9. Ho, P.S. Halogen bonding in medicinal chemistry: From observation to prediction. Future Med. Chem. 2017, 9, 637–640. [Google Scholar] [CrossRef]
  10. Berger, G.; Soubhye, J.; Meyer, F. Halogen bonding in polymer science: From crystal engineering to functional supramolecular polymers and materials. Polym. Chem. 2015, 6, 3559–3580. [Google Scholar] [CrossRef]
  11. Tepper, R.; Schubert, U.S. Halogen Bonding in Solution: Anion Recognition, Templated Self-Assembly, and Organocatalysis. Angew. Chem. Int. Ed. 2018, 57, 6004–6016. [Google Scholar] [CrossRef] [PubMed]
  12. Bulfield, D.; Huber, S.M. Halogen Bonding in Organic Synthesis and Organocatalysis. Chem.-A Eur. J. 2016, 22, 14434–14450. [Google Scholar] [CrossRef]
  13. Mahmudov, K.T.; Gurbanov, A.V.; Guseinov, F.I.; Guedes da Silva, M.F.C. Noncovalent interactions in metal complex catalysis. Coord. Chem. Rev. 2019, 387, 32–46. [Google Scholar] [CrossRef]
  14. Benz, S.; Poblador-Bahamonde, A.I.; Low-Ders, N.; Matile, S. Catalysis with Pnictogen, Chalcogen, and Halogen Bonds. Angew. Chem. Int. Ed. 2018, 57, 5408–5412. [Google Scholar] [CrossRef] [PubMed]
  15. Bennion, J.C.; Vogt, L.; Tuckerman, M.E.; Matzger, A.J. Isostructural Cocrystals of 1,3,5-Trinitrobenzene Assembled by Halogen Bonding. Cryst. Growth Des. 2016, 16, 4688–4693. [Google Scholar] [CrossRef]
  16. Landenberger, K.B.; Bolton, O.; Matzger, A.J. Energetic-energetic cocrystals of diacetone diperoxide (DADP): Dramatic and divergent sensitivity modifications via cocrystallization. J. Am. Chem. Soc. 2015, 137, 5074–5079. [Google Scholar] [CrossRef]
  17. Sivchik, V.V.; Solomatina, A.I.; Chen, Y.T.; Karttunen, A.J.; Tunik, S.P.; Chou, P.T.; Koshevoy, I.O. Halogen Bonding to Amplify Luminescence: A Case Study Using a Platinum Cyclometalated Complex. Angew. Chem. Int. Ed. 2015, 54, 14057–14060. [Google Scholar] [CrossRef] [PubMed]
  18. Sivchik, V.; Sarker, R.K.; Liu, Z.Y.; Chung, K.Y.; Grachova, E.V.; Karttunen, A.J.; Chou, P.T.; Koshevoy, I.O. Improvement of the photophysical performance of platinum-cyclometalated complexes in halogen-bonded adducts. Chem.-A Eur. J. 2018, 24, 11475–11484. [Google Scholar] [CrossRef]
  19. Kinzhalov, M.A.; Kashina, M.V.; Mikherdov, A.S.; Mozheeva, E.A.; Novikov, A.S.; Smirnov, A.S.; Ivanov, D.M.; Kryukova, M.A.; Ivanov, A.Y.; Smirnov, S.N.; et al. Dramatically Enhanced Solubility of Halide-Containing Organometallic Species in Diiodomethane: The Role of Solvent⋯Complex Halogen Bonding. Angew. Chem. Int. Ed. 2018, 57, 12785–12789. [Google Scholar] [CrossRef]
  20. Mikherdov, A.S.; Novikov, A.S.; Boyarskiy, V.P.; Kukushkin, V.Y. The halogen bond with isocyano carbon reduces isocyanide odor. Nat. Commun. 2020, 11, 2921. [Google Scholar] [CrossRef]
  21. Metrangolo, P.; Resnati, G. Type II halogen···halogen contacts are halogen bonds. IUCrJ 2014, 1, 5–7. [Google Scholar] [CrossRef] [PubMed]
  22. Hassel, O. Structural aspects of interatomic charge-transfer bonding. Science 1970, 170, 497–502. [Google Scholar] [CrossRef] [PubMed]
  23. Ivanov, D.M.; Bokach, N.A.; Kukushkin, V.Y.; Frontera, A. Metal Centers as Nucleophiles: Oxymoron of Halogen Bond-Involving Crystal Engineering. Chem.-A Eur. J. 2022, 28, e202103173. [Google Scholar] [CrossRef] [PubMed]
  24. Eliseeva, A.A.; Ivanov, D.M.; Rozhkov, A.V.; Ananyev, I.V.; Frontera, A.; Kukushkin, V.Y. Bifurcated Halogen Bonding Involving Two Rhodium(I) Centers as an Integrated σ-Hole Acceptor. JACS Au 2021, 1, 354–361. [Google Scholar] [CrossRef]
  25. Ivanov, D.M.; Novikov, A.S.; Ananyev, I.V.; Kirina, Y.V.; Kukushkin, V.Y. Halogen Bonding Between Metal Center and Halocarbon. Chem. Commun. 2016, 52, 5565–5568. [Google Scholar] [CrossRef]
  26. Dabranskaya, U.; Ivanov, D.M.; Novikov, A.S.; Matveychuk, Y.V.; Bokach, N.A.; Kukushkin, V.Y. Metal-Involving Bifurcated Halogen Bonding C–Br···η2(Cl–Pt). Cryst. Growth Des. 2019, 19, 1364–1376. [Google Scholar] [CrossRef]
  27. Aliyarova, I.S.; Tupikina, E.Y.; Ivanov, D.M.; Kukushkin, V.Y. Metal-Involving Halogen Bonding Including Gold(I) as a Nucleophilic Partner. The Case of Isomorphic Dichloroaurate(I)·Halomethane Cocrystals. Inorg. Chem. 2022, 61, 2558–2567. [Google Scholar] [CrossRef]
  28. Katlenok, E.A.; Haukka, M.; Levin, O.V.; Frontera, A.; Kukushkin, V.Y. Supramolecular Assembly of Metal Complexes by (Aryl)I⋯dz2[PtII] Halogen Bond. Chem.-A Eur. J. 2020, 26, 7692–7701. [Google Scholar] [CrossRef]
  29. Katlenok, E.A.; Rozhkov, A.V.; Levin, O.V.; Haukka, M.; Kuznetsov, M.L.; Kukushkin, V.Y. Halogen Bonding Involving Palladium(II) as an XB Acceptor. Cryst. Growth Des. 2021, 21, 1159–1177. [Google Scholar] [CrossRef]
  30. Bulatova, M.; Ivanov, D.M.; Haukka, M. Classics Meet Classics: Theoretical and Experimental Studies of Halogen Bonding in Adducts of Platinum(II) 1,5-Cyclooctadiene Halide Complexes with Diiodine, Iodoform, and 1,4-Diiodotetrafluorobenzene. Cryst. Growth Des. 2021, 21, 974–987. [Google Scholar] [CrossRef]
  31. Bulatova, M.; Ivanov, D.M.; Rautiainen, J.M.; Kinzhalov, M.A.; Truong, K.N.; Lahtinen, M.; Haukka, M. Studies of Nature of Uncommon Bifurcated I-I···(I-M) Metal-Involving Noncovalent Interaction in Palladium(II) and Platinum(II) Isocyanide Cocrystals. Inorg. Chem. 2021, 60, 13200–13211. [Google Scholar] [CrossRef]
  32. Bondi, A. van der Waals Volumes and Radii. J. Phys. Chem. 1964, 68, 441–451. [Google Scholar] [CrossRef]
  33. Comas-Vilà, G.; Salvador, P. Quantification of the Donor-Acceptor Character of Ligands by the Effective Fragment Orbitals. ChemPhysChem 2024, 25, e202400582. [Google Scholar] [CrossRef]
  34. Kashina, M.V.; Kinzhalov, M.A.; Smirnov, A.S.; Ivanov, D.M.; Novikov, A.S.; Kukushkin, V.Y. Dihalomethanes as Bent Bifunctional XB/XB-Donating Building Blocks for Construction of Metal-involving Halogen Bonded Hexagons. Chem.-Asian J. 2019, 14, 3915–3920. [Google Scholar] [CrossRef] [PubMed]
  35. Cheranyova, A.M.; Zelenkov, L.E.; Baykov, S.V.; Izotova, Y.A.; Ivanov, D.M.; Bokach, N.A.; Kukushkin, V.Y. Intermolecular Metal-Involving Pnictogen Bonding: The Case of σ-(SbIII)-Hole···dz[PtII] Interaction. Inorg. Chem. 2024, 63, 14943–14957. [Google Scholar] [CrossRef]
  36. Eliseeva, A.A.; Khazanova, M.A.; Cheranyova, A.M.; Aliyarova, I.S.; Kravchuk, R.I.; Oganesyan, E.S.; Ryabykh, A.V.; Maslova, O.A.; Ivanov, D.M.; Beznosyuk, S.A. Metal-Involving Halogen Bonding Confirmed Using DFT Calculations with Periodic Boundary Conditions. Crystals 2023, 13, 712. [Google Scholar] [CrossRef]
  37. Bertolotti, F.; Shishkina, A.; Forni, A.; Gervasio, G.; Stash, A.; Tsirelson, V. Intermolecular Bonding Features in Solid Iodine. Cryst. Growth Des. 2014, 14, 3587–3595. [Google Scholar] [CrossRef]
  38. Johnson, M.T.; Džolić, Z.; Cetina, M.; Wendt, O.F.; Öhrström, L.; Rissanen, K. Neutral Organometallic Halogen Bond Acceptors: Halogen Bonding in Complexes of PCPPdX (X = Cl, Br, I) with Iodine (I2), 1,4-Diiodotetrafluorobenzene (F4DIBz), and 1,4-Diiodooctafluorobutane (F8DIBu). Cryst. Growth Des. 2012, 12, 362–368. [Google Scholar] [CrossRef] [PubMed]
  39. Spackman, M.A.; Jayatilaka, D. Hirshfeld surface analysis. CrystEngComm 2009, 11, 19–32. [Google Scholar] [CrossRef]
  40. McKinnon, J.J.; Jayatilaka, D.; Spackman, M.A. Towards quantitative analysis of intermolecular interactions with Hirshfeld surfaces. Chem. Commun. 2007, 37, 3814–3816. [Google Scholar] [CrossRef]
  41. Spackman, P.R.; Turner, M.J.; McKinnon, J.J.; Wolff, S.K.; Grimwood, D.J.; Jayatilaka, D.; Spackman, M.A. CrystalExplorer: A program for Hirshfeld surface analysis, visualization and quantitative analysis of molecular crystals. J. Appl. Crystallogr. 2021, 54, 1006–1011. [Google Scholar] [CrossRef] [PubMed]
  42. Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
  43. Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132. [Google Scholar] [CrossRef] [PubMed]
  44. Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef] [PubMed]
  45. Jorge, F.E.; Canal Neto, A.; Camiletti, G.G.; MacHado, S.F. Contracted Gaussian basis sets for Douglas-Kroll-Hess calculations: Estimating scalar relativistic effects of some atomic and molecular properties. J. Chem. Phys. 2009, 130, 064108. [Google Scholar] [CrossRef]
  46. Barros, C.L.; De Oliveira, P.J.P.; Jorge, F.E.; Canal Neto, A.; Campos, M. Gaussian basis set of double zeta quality for atoms Rb through Xe: Application in non-relativistic and relativistic calculations of atomic and molecular properties. Mol. Phys. 2010, 108, 1965–1972. [Google Scholar] [CrossRef]
  47. de Berrêdo, R.C.; Jorge, F.E. All-electron double zeta basis sets for platinum: Estimating scalar relativistic effects on platinum(II) anticancer drugs. J. Mol. Struct. THEOCHEM 2010, 961, 107–112. [Google Scholar] [CrossRef]
  48. Pritchard, B.P.; Altarawy, D.; Didier, B.; Gibson, T.D.; Windus, T.L. New Basis Set Exchange: An Open, Up-to-Date Resource for the Molecular Sciences Community. J. Chem. Inf. Model. 2019, 59, 4814–4820. [Google Scholar] [CrossRef]
  49. Hutter, J.; Iannuzzi, M.; Schiffmann, F.; VandeVondele, J. cp2k atomistic simulations of condensed matter systems. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2014, 4, 15–25. [Google Scholar] [CrossRef]
  50. Kühne, T.D.; Iannuzzi, M.; Del Ben, M.; Rybkin, V.V.; Seewald, P.; Stein, F.; Laino, T.; Khaliullin, R.Z.; Schütt, O.; Schiffmann, F.; et al. CP2K: An electronic structure and molecular dynamics software package -Quickstep: Efficient and accurate electronic structure calculations. J. Chem. Phys. 2020, 152, 194103. [Google Scholar] [CrossRef]
  51. Frigo, M.; Johnson, S.G. The Design and Implementation of FFTW3. Proc. IEEE 2005, 93, 216–231. [Google Scholar] [CrossRef]
  52. Vandevondele, J.; Krack, M.; Mohamed, F.; Parrinello, M.; Chassaing, T.; Hutter, J. Quickstep: Fast and accurate density functional calculations using a mixed Gaussian and plane waves approach. Comput. Phys. Commun. 2005, 167, 103–128. [Google Scholar] [CrossRef]
  53. Borštnik, U.; Vandevondele, J.; Weber, V.; Hutter, J. Sparse matrix multiplication: The distributed block-compressed sparse row library. Parallel Comput. 2014, 40, 47–58. [Google Scholar] [CrossRef]
  54. Schütt, O.; Messmer, P.; Hutter, J.; VandeVondele, J. GPU-Accelerated Sparse Matrix-Matrix Multiplication for Linear Scaling Density Functional Theory. In Electronic Structure Calculations on Graphics Processing Units; John Wiley & Sons, Ltd.: Chichester, UK, 2016; pp. 173–190. [Google Scholar] [CrossRef]
  55. Goerigk, L.; Hansen, A.; Bauer, C.; Ehrlich, S.; Najibi, A.; Grimme, S. A look at the density functional theory zoo with the advanced GMTKN55 database for general main group thermochemistry, kinetics and noncovalent interactions. Phys. Chem. Chem. Phys. 2017, 19, 32184–32215. [Google Scholar] [CrossRef]
  56. Lippert, G.; Hutter, J.; Parrinello, M. The Gaussian and augmented-plane-wave density functional method for ab initio molecular dynamics simulations. Theor. Chem. Acc. 1999, 103, 124–140. [Google Scholar] [CrossRef]
  57. Espinosa, E.; Alkorta, I.; Elguero, J.; Molins, E. From weak to strong interactions: A comprehensive analysis of the topological and energetic properties of the electron density distribution involving X-H⋯F-Y systems. J. Chem. Phys. 2002, 117, 5529–5542. [Google Scholar] [CrossRef]
  58. Johnson, E.R.; Keinan, S.; Mori-Sánchez, P.; Contreras-García, J.; Cohen, A.J.; Yang, W. Revealing noncovalent interactions. J. Am. Chem. Soc. 2010, 132, 6498–6506. [Google Scholar] [CrossRef]
  59. Becke, A.D.; Edgecombe, K.E. A simple measure of electron localization in atomic and molecular systems. J. Chem. Phys. 1990, 92, 5397–5403. [Google Scholar] [CrossRef]
  60. Silvi, B.; Savin, A. Classification of chemical bonds based on topological analysis of electron localization functions. Nature 1994, 371, 683–686. [Google Scholar] [CrossRef]
  61. Savin, A.; Nesper, R.; Wengert, S.; Fässler, T.F. ELF: The Electron Localization Function. Angew. Chemie Int. Ed. Engl. 1997, 36, 1808–1832. [Google Scholar] [CrossRef]
  62. Jeziorski, B.; Moszynski, R.; Szalewicz, K. Perturbation Theory Approach to Intermolecular Potential Energy Surfaces of van der Waals Complexes. Chem. Rev. 1994, 94, 1887–1930. [Google Scholar] [CrossRef]
  63. Parker, T.M.; Burns, L.A.; Parrish, R.M.; Ryno, A.G.; Sherrill, C.D. Levels of symmetry adapted perturbation theory (SAPT). I. Efficiency and performance for interaction energies. J. Chem. Phys. 2014, 140, 94106. [Google Scholar] [CrossRef]
  64. Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef] [PubMed]
  65. Weigend, F. Accurate Coulomb-fitting basis sets for H to Rn. Phys. Chem. Chem. Phys. 2006, 8, 1057–1065. [Google Scholar] [CrossRef]
  66. Sarju, J.; Arbour, J.; Sayer, J.; Rohrmoser, B.; Scherer, W.; Wagner, G. Synthesis and characterisation of mixed ligand Pt(ii) and Pt(iv) oxadiazoline complexes. Dalt. Trans. 2008, 5302–5312. [Google Scholar] [CrossRef] [PubMed]
  67. Hofmann, K.; Bugge, G. Vergleich der Nitrile und Isonitrile im Verhalten gegen Metallsalze, ein Beitrag zur Konstitution der Doppelcyanide. Berichte Der Dtsch. Chem. Ges. 1907, 40, 1772–1778. [Google Scholar] [CrossRef]
  68. Dolomanov, O.V.; Bourhis, L.J.; Gildea, R.J.; Howard, J.A.K.; Puschmann, H. OLEX2: A complete structure solution, refinement and analysis program. J. Appl. Crystallogr. 2009, 42, 339–341. [Google Scholar] [CrossRef]
  69. Sheldrick, G.M. SHELXT-Integrated space-group and crystal-structure determination. Acta Crystallogr. Sect. A Found. Crystallogr. 2015, 71, 3–8. [Google Scholar] [CrossRef]
  70. Sheldrick, G.M. A short history of SHELX. Acta Crystallogr. Sect. A Found. Crystallogr. 2008, 64, 112–122. [Google Scholar] [CrossRef]
  71. Allen, F.H.; Bruno, I.J. Bond lengths in organic and metal-organic compounds revisited: X-H bond lengths from neutron diffraction data. Acta Crystallogr. Sect. B Struct. Sci. 2010, 66, 380–386. [Google Scholar] [CrossRef]
  72. Barysz, M.; Sadlej, A.J. Two-component methods of relativistic quantum chemistry: From the Douglas-Kroll approximation to the exact two-component formalism. J. Mol. Struct. THEOCHEM 2001, 573, 181–200. [Google Scholar] [CrossRef]
  73. Reiher, M. Relativistic Douglas-Kroll-Hess theory. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 139–149. [Google Scholar] [CrossRef]
  74. Bader, R.F.W.; Nguyen-Dang, T.T. Quantum Theory of Atoms in Molecules–Dalton Revisited. Adv. Quantum Chem. 1981, 14, 63–124. [Google Scholar] [CrossRef]
  75. Bader, R.F.W. A Quantum Theory of Molecular Structure and Its Applications. Chem. Rev. 1991, 91, 893–928. [Google Scholar] [CrossRef]
  76. Lu, T.; Chen, F. Multiwfn: A Multifunctional Wavefunction Analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef] [PubMed]
  77. Smith, D.G.A.; Burns, L.A.; Simmonett, A.C.; Parrish, R.M.; Schieber, M.C.; Galvelis, R.; Kraus, P.; Kruse, H.; Di Remigio, R.; Alenaizan, A.; et al. Psi4 1.4: Open-source software for high-throughput quantum chemistry. J. Chem. Phys. 2020, 152, 184108. [Google Scholar] [CrossRef] [PubMed]
  78. Suslonov, V.V.; Soldatova, N.S.; Ivanov, D.M.; Galmés, B.; Frontera, A.; Resnati, G.; Postnikov, P.S.; Kukushkin, V.Y.; Bokach, N.A. Diaryliodonium Tetrachloroplatinates(II): Recognition of a Trifurcated Metal-Involving μ3-I···(Cl,Cl,Pt) Halogen Bond. Cryst. Growth Des. 2021, 21, 5360–5372. [Google Scholar] [CrossRef]
  79. Bokach, N.A.; Kukushkin, V.Y. Coordination chemistry of dialkylcyanamides: Binding properties, synthesis of metal complexes, and ligand reactivity. Coord. Chem. Rev. 2013, 257, 2293–2316. [Google Scholar] [CrossRef]
Ijms 26 04555 g001
Figure 1. Studied XB partners. Nucleophile sites are blue, whereas electrophile sites are red.
Figure 1. Studied XB partners. Nucleophile sites are blue, whereas electrophile sites are red.
Ijms 26 04555 g001
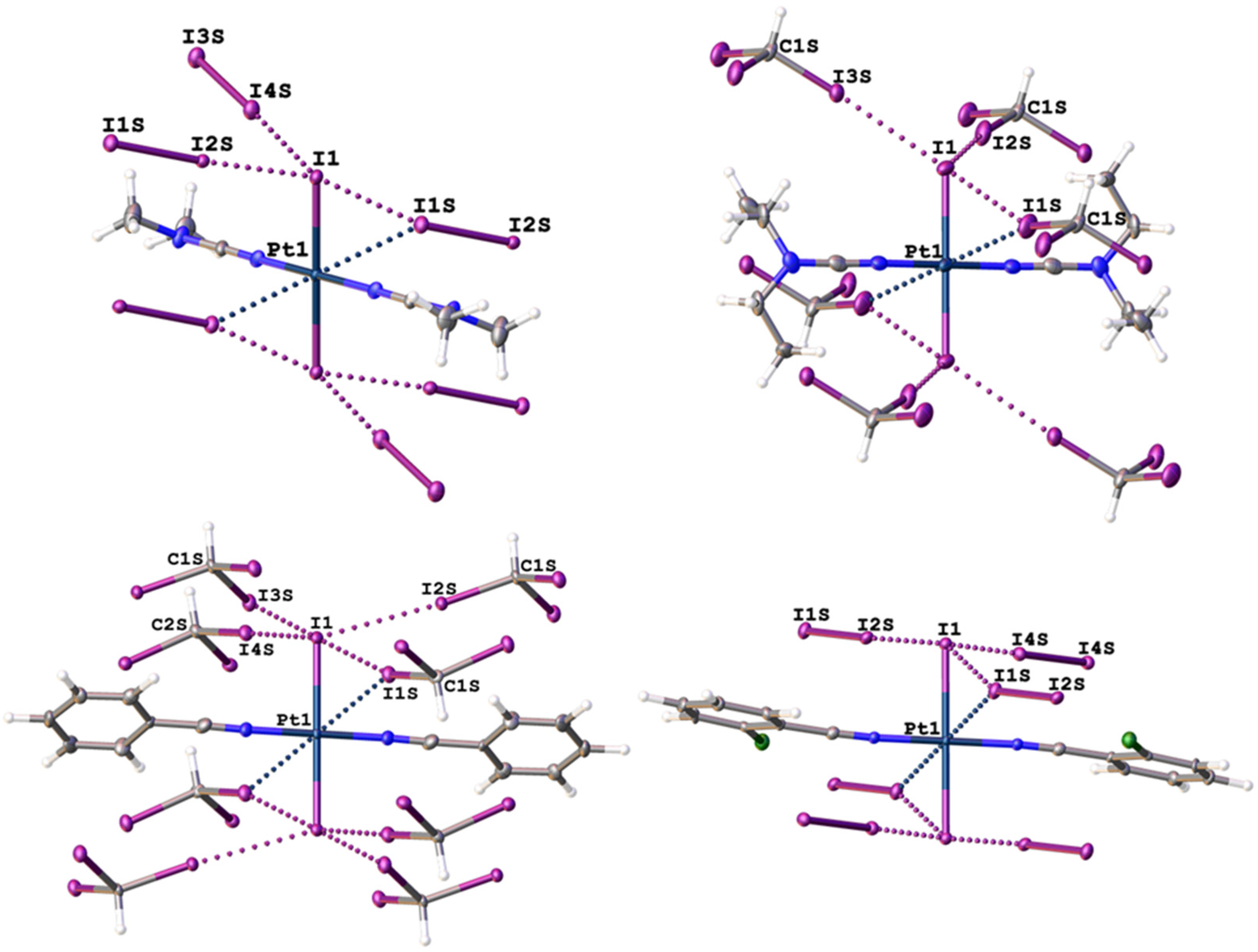
Ijms 26 04555 g002
Figure 2. Environment of complex molecules in 1∙4I2 (upper left), 2∙2CHI3 (upper right), 3∙2CHI3 (lower left), and 4∙4I2 (lower right), where XBs are given by dotted lines. Hereinafter, thermal ellipsoids are shown with 50% probability, whereas H atoms are white, C atoms are grey, N atoms are blue, I atoms are violet, and Pt atoms are dark blue.
Figure 2. Environment of complex molecules in 1∙4I2 (upper left), 2∙2CHI3 (upper right), 3∙2CHI3 (lower left), and 4∙4I2 (lower right), where XBs are given by dotted lines. Hereinafter, thermal ellipsoids are shown with 50% probability, whereas H atoms are white, C atoms are grey, N atoms are blue, I atoms are violet, and Pt atoms are dark blue.
Ijms 26 04555 g002
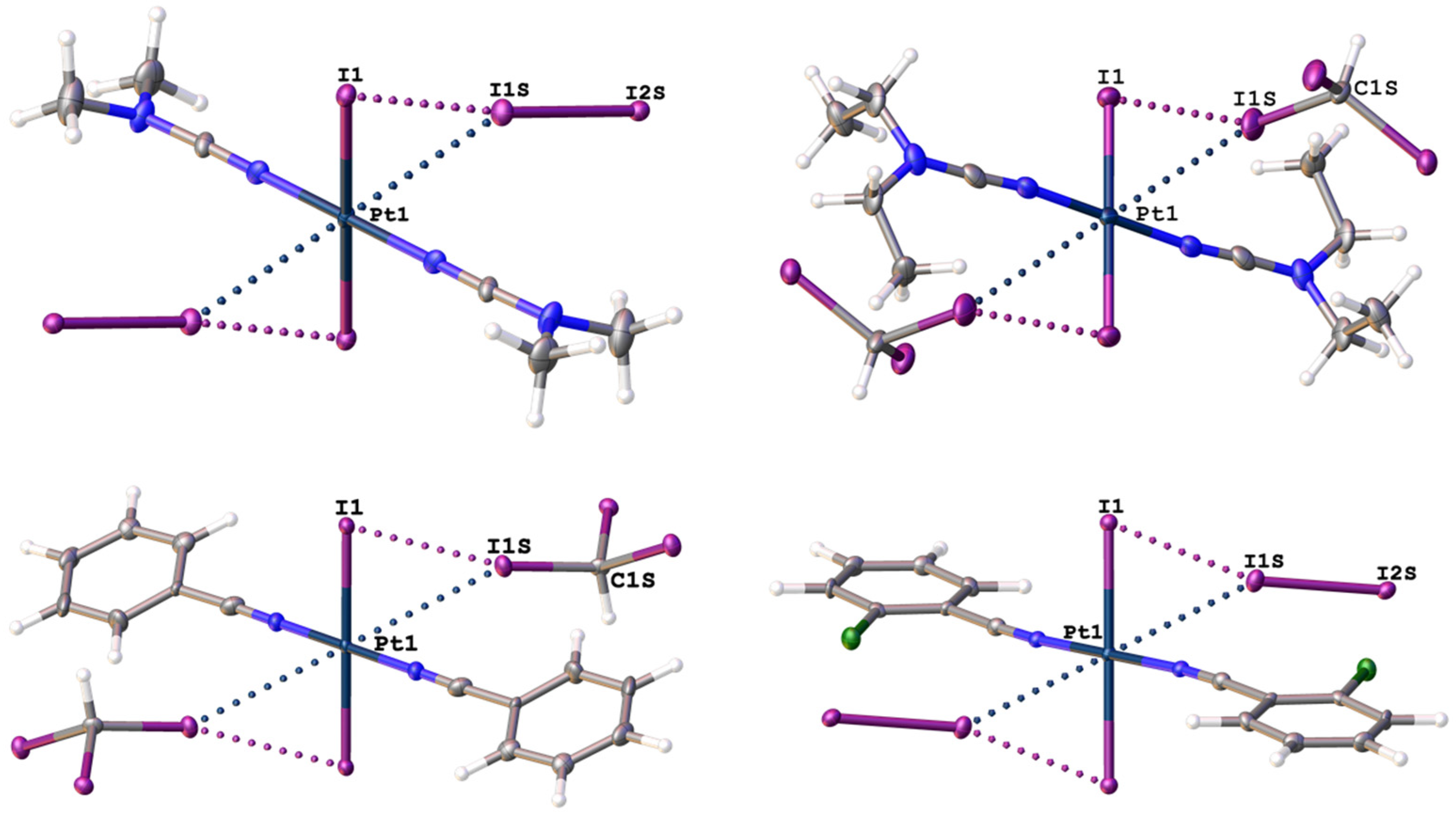
Ijms 26 04555 g003
Figure 3. The bifurcated I⋯(I–PtII) XBs in 1∙4I2 (upper left), 2∙2CHI3 (upper right), 3∙2CHI3 (lower left), and 4∙4I2 (lower right) given by dotted lines.
Figure 3. The bifurcated I⋯(I–PtII) XBs in 1∙4I2 (upper left), 2∙2CHI3 (upper right), 3∙2CHI3 (lower left), and 4∙4I2 (lower right) given by dotted lines.
Ijms 26 04555 g003
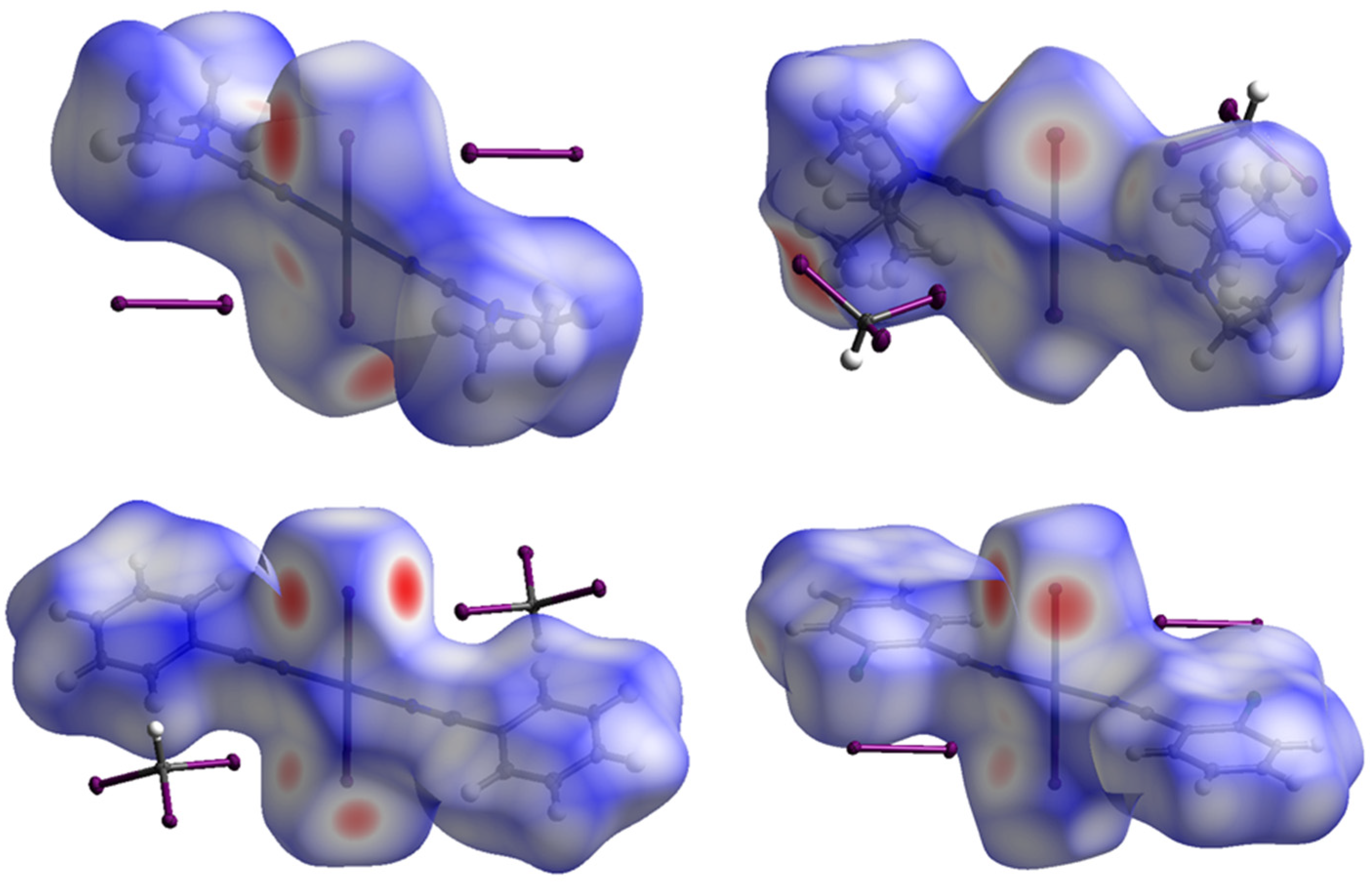
Ijms 26 04555 g004
Figure 4. Hirshfeld surface for 1∙4I2 (upper left), 2∙2CHI3 (upper right), 3∙2CHI3 (lower left), and 4∙4I2 (lower right). Intermolecular contacts closer than the sum of Bondi vdW radii (ΣvdW) are highlighted in red, longer contacts are shown in blue, and contacts with a value of approximately ΣvdW are shown in white.
Figure 4. Hirshfeld surface for 1∙4I2 (upper left), 2∙2CHI3 (upper right), 3∙2CHI3 (lower left), and 4∙4I2 (lower right). Intermolecular contacts closer than the sum of Bondi vdW radii (ΣvdW) are highlighted in red, longer contacts are shown in blue, and contacts with a value of approximately ΣvdW are shown in white.
Ijms 26 04555 g004
Ijms 26 04555 g005
Figure 5. Sign(λ2)ρ with RDG = 0.5 dotted contour lines (upper) and ELF (lower) projections for the bifurcated I⋯(I–Pt) XBs in crystal models of 1∙4I2 (first column), 2∙2CHI3 (second column), 3∙2CHI3 (third column), and 1∙4I2 (fourth column). QTAIM white (for ELF) or black (for sign(λ2)ρ with RDG) bond paths, brown nuclear, blue bond, and orange ring critical points, and black (ELF) interbasin paths.
Figure 5. Sign(λ2)ρ with RDG = 0.5 dotted contour lines (upper) and ELF (lower) projections for the bifurcated I⋯(I–Pt) XBs in crystal models of 1∙4I2 (first column), 2∙2CHI3 (second column), 3∙2CHI3 (third column), and 1∙4I2 (fourth column). QTAIM white (for ELF) or black (for sign(λ2)ρ with RDG) bond paths, brown nuclear, blue bond, and orange ring critical points, and black (ELF) interbasin paths.
Ijms 26 04555 g005
Ijms 26 04555 g006
Figure 6. Scheme of cluster model decomposition for sSAPT0 calculations.
Figure 6. Scheme of cluster model decomposition for sSAPT0 calculations.
Ijms 26 04555 g006
Ijms 26 04555 g007
Figure 7. Differences between previously reported R–I⋯(I–Pt) contacts with [PtI2(COD)] (left) or trans-[PtI2(CN(2,6-MeC6H3))2] (center) and the R–I⋯(I–Pt) bifurcate XBs with trans-[PtI2(NCR)2] (right). Nucleophile sites are blue, whereas electrophile sites are red.
Figure 7. Differences between previously reported R–I⋯(I–Pt) contacts with [PtI2(COD)] (left) or trans-[PtI2(CN(2,6-MeC6H3))2] (center) and the R–I⋯(I–Pt) bifurcate XBs with trans-[PtI2(NCR)2] (right). Nucleophile sites are blue, whereas electrophile sites are red.
Ijms 26 04555 g007
Table 1. Parameters of R–I⋯I–Pt (R = C, I) XBs in cocrystals. For components of bifurcates, italic font is used.
Table 1. Parameters of R–I⋯I–Pt (R = C, I) XBs in cocrystals. For components of bifurcates, italic font is used.
StructureInteractiond(I⋯I), ÅRvdW *∠(R–I⋯I), °∠(I⋯I–X), °
1∙4I2 I1S ⋯I1–Pt1 3.9255(8) 0.99 164.38(2) 59.548(13)
I2S⋯I1–Pt13.2362(7)0.82174.39(2)105.017(18)
I3S⋯I1S–I2S3.4484(8)0.87173.48(2)91.355(18)
I4S⋯I1–Pt13.4568(8)0.87177.88(2)103.462(18)
2∙2CHI3 I1S ⋯I1–Pt1 3.9138(8) 0.99 154.21(13) 63.497(13)
I2S⋯I1–Pt13.5503(9)0.90170.8(2)109.053(18)
I3S⋯I1–Pt13.5687(6)0.90173.6(2)124.317(16)
3∙2CHI3 I1S ⋯I1–Pt1 3.7811(8) 0.95 165.9(3) 68.795(16)
I2S⋯I1–Pt13.5559(8)0.90174.7(3)106.531(19)
I3S⋯I1–Pt13.7176(8)0.94167.6(3)98.484(18)
I4S⋯I1–Pt13.5675(8)0.90173.87(19)98.30(2)
I5S⋯I1A–Pt1A3.5882(8)0.91173.7(3)109.571(18)
I6S⋯I1A–Pt1A3.6094(8)0.91169.6(2)100.947(17)
4∙4I2 I1S ⋯I1–Pt1 3.7517(5) 0.95 158.298(13) 66.909(8)
I2S⋯I1–Pt13.2980(4)0.83177.373(15)95.769(10)
I3S⋯I1S–I2S3.4385(4)0.87178.450(17)99.193(13)
I4S⋯I1–Pt13.4783(4)0.88172.041(17) 88.569(8)
* RvdW = d/ΣvdW; ΣvdW(I + I) = 3.96 Å [32].
Table 2. Parameters of R–I⋯Pt (R = C, I) XBs in cocrystals.
Table 2. Parameters of R–I⋯Pt (R = C, I) XBs in cocrystals.
StructureInteractiond(I⋯Pt), ÅRvdW *∠(R–I⋯Pt), °
1∙4I2I2S–I1S⋯Pt13.4414(6)0.92148.77(2)
2∙2CHI3C1S–I1S⋯Pt13.6065(7)0.97165.46(14)
3∙2CHI3C1S–I1S⋯Pt13.7362(6)1.00152.8(3)
4∙4I2I2S–I1S⋯Pt13.6338(3)0.97150.58(1)
* RvdW = d/ΣvdW; ΣvdW(I + I) = 3.96 Å [32].
Table 3. Results of Hirshfeld surface analysis for the X-ray diffraction structures of all structures.
Table 3. Results of Hirshfeld surface analysis for the X-ray diffraction structures of all structures.
StructureContributions of Different Intermolecular Contacts
to the Molecular Hirshfeld Surface *
1∙4I2Pt⋯I 3.3%, I⋯I 19.6%, I⋯N 9.7%, I⋯C 3.8%, I⋯H 46.4%, C⋯H 1.7%, H⋯H 14.8%
2∙2CHI3Pt⋯I 2.0%, I⋯I 7.4%, I⋯N 1.8%, I⋯H 44.5%, N⋯H 7.8%, C⋯H 2.9%, H⋯H 31.5%
3∙2CHI3Pt⋯I 2.0%, Pt⋯H 1.6%, I⋯I 13.7%, I⋯N 5.3%, I⋯C 6.2%, I⋯H 38.6%, N⋯H 5.1%, C⋯C 3.1%, C⋯H 16.8%, H⋯H 7.0%
4∙4I2Pt⋯I 2.8%, I⋯I 12.8%, I⋯Cl 10.1%, I⋯N 6.1%, I⋯C 2.1%, I⋯H 34.4%, Cl⋯C 8.9%, N⋯H 1.3%, C⋯C 6.9%, C⋯H 11.3%, H⋯H 2.4%
* The contributions of all other intermolecular contacts do not exceed 1%.
Table 4. Electron density ρ (in e/bohr3), Laplacian ∇2ρ (in e/bohr5), potential energy density V, Lagrangian kinetic energy G, and energy density H (in hartree/bohr3) at the bond critical points (3, −1), corresponding to the I⋯Pt interactions with d(I⋯Pt) (in Å) in 1∙4I2, 2∙2CHI3, 3∙2CHI3, and 4∙4I2.
Table 4. Electron density ρ (in e/bohr3), Laplacian ∇2ρ (in e/bohr5), potential energy density V, Lagrangian kinetic energy G, and energy density H (in hartree/bohr3) at the bond critical points (3, −1), corresponding to the I⋯Pt interactions with d(I⋯Pt) (in Å) in 1∙4I2, 2∙2CHI3, 3∙2CHI3, and 4∙4I2.
StructureInteractiond(I···Pt)ρ∇2ρGVH|V|/G
1∙4I2I2S–I1S⋯Pt13.44140.0180.0390.010−0.0100.000°1.003
2∙2CHI3C1S–I1S⋯Pt13.60650.0120.0290.006−0.0060.000°0.872
3∙2CHI3C1S–I1S⋯Pt13.73620.0100.0250.005−0.0040.001°0.798
4∙4I2I2S–I1S⋯Pt13.63380.0120.0300.007−0.0060.001°0.884
Table 5. Electron density ρ (in e/bohr3), Laplacian ∇2ρ (in e/bohr5), potential energy density V(r), Lagrangian kinetic energy G, and energy density H (in hartree/bohr3) at the bond critical points (3, −1), corresponding to the I⋯Pt interactions with d(I⋯I) (in Å) in 1∙4I2, 2∙2CHI3, 3∙2CHI3, and 4∙4I2.
Table 5. Electron density ρ (in e/bohr3), Laplacian ∇2ρ (in e/bohr5), potential energy density V(r), Lagrangian kinetic energy G, and energy density H (in hartree/bohr3) at the bond critical points (3, −1), corresponding to the I⋯Pt interactions with d(I⋯I) (in Å) in 1∙4I2, 2∙2CHI3, 3∙2CHI3, and 4∙4I2.
StructureInteractiond(I⋯I)ρ∇2ρGVH|V|/G
1∙4I2 I1S⋯I1–Pt1 3.9255 0.009 0.024 0.004 −0.003 0.001 0.663
I2S⋯I1–Pt13.23620.0290.0410.014−0.018−0.0041.259
I3S⋯I1S–I2S3.44840.0200.0440.012−0.0120.0001.044
I4S⋯I1–Pt13.45680.0190.0450.012−0.0120.0001.031
2∙2CHI3 I1S⋯I1–Pt1 3.9138 0.008 0.029 0.006 −0.004 0.002 0.768
I2S⋯I1–Pt13.55030.0150.0430.010−0.0100.0000.952
I3S⋯I1–Pt13.56870.0140.0430.010−0.0090.0010.934
3∙2CHI3 I1S⋯I1–Pt1 3.7811 0.010 0.033 0.007 −0.006 0.001 0.815
I2S⋯I1–Pt13.55590.0150.0440.010−0.0100.0000.942
I3S⋯I1–Pt13.71760.0110.0360.008−0.0070.0010.852
I4S⋯I1–Pt13.56750.0150.0420.010−0.0090.0010.932
I5S⋯I1A–Pt1A3.58820.0140.0420.010−0.0090.0010.924
I6S⋯I1A–Pt1A3.60940.0140.0410.009−0.0090.0000.919
4∙4I2 I1S⋯I1–Pt1 3.7517 0.012 0.029 0.006 −0.005 0.001 0.795
I2S⋯I1–Pt13.29800.0260.0410.013−0.015−0.0021.196
I3S⋯I1S–I2S3.43850.0200.0450.012–0.013–0.0011.051
I4S⋯I1–Pt13.47830.0170.0460.011–0.0110.0000.991
Table 6. Scaled symmetry adapted perturbation theory energies of zero-order EsSAPT0 and their electrostatic Eelst, exchange Eexch, induction Eind, and dispersion Edisp components, all in kcal/mol, corresponding to the I⋯(I–Pt) bifurcates in 1∙(I2)2, 2∙(CHI3)2, 3∙(CHI3)2, and 4∙(I2)2 models from 1∙4I2, 2∙2CHI3, 3∙2CHI3, and 4∙4I2, respectively.
Table 6. Scaled symmetry adapted perturbation theory energies of zero-order EsSAPT0 and their electrostatic Eelst, exchange Eexch, induction Eind, and dispersion Edisp components, all in kcal/mol, corresponding to the I⋯(I–Pt) bifurcates in 1∙(I2)2, 2∙(CHI3)2, 3∙(CHI3)2, and 4∙(I2)2 models from 1∙4I2, 2∙2CHI3, 3∙2CHI3, and 4∙4I2, respectively.
ClusterInteractionEsSAPT0EelstEexchEindEdispEdisp/Eelst
1∙(I2)2I2S–I1S⋯(I1–Pt1)–9.55–7.7714.25–4.32–11.721.51
2∙(CHI3)2C1S–I1S⋯(I1–Pt1)–8.58–5.9712.58–2.93–12.272.06
3∙(CHI3)2C1S–I1S⋯(I1–Pt1)–8.80–7.3914.34–3.40–12.351.67
4∙(I2)2I2S–I1S⋯(I1–Pt1)–9.47–7.2614.07–4.17–12.111.67
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Kryukova, M.A.; Kostareva, M.B.; Cheranyova, A.M.; Khazanova, M.A.; Rozhkov, A.V.; Ivanov, D.M. Metal-Involving Bifurcated Halogen Bonding with Iodide and Platinum(II) Center. Int. J. Mol. Sci. 2025, 26, 4555. https://doi.org/10.3390/ijms26104555

AMA Style

Kryukova MA, Kostareva MB, Cheranyova AM, Khazanova MA, Rozhkov AV, Ivanov DM. Metal-Involving Bifurcated Halogen Bonding with Iodide and Platinum(II) Center. International Journal of Molecular Sciences. 2025; 26(10):4555. https://doi.org/10.3390/ijms26104555

Chicago/Turabian Style

Kryukova, Mariya A., Margarita B. Kostareva, Anna M. Cheranyova, Marina A. Khazanova, Anton V. Rozhkov, and Daniil M. Ivanov. 2025. "Metal-Involving Bifurcated Halogen Bonding with Iodide and Platinum(II) Center" International Journal of Molecular Sciences 26, no. 10: 4555. https://doi.org/10.3390/ijms26104555

APA Style

Kryukova, M. A., Kostareva, M. B., Cheranyova, A. M., Khazanova, M. A., Rozhkov, A. V., & Ivanov, D. M. (2025). Metal-Involving Bifurcated Halogen Bonding with Iodide and Platinum(II) Center. International Journal of Molecular Sciences, 26(10), 4555. https://doi.org/10.3390/ijms26104555

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop