Prediction of Composite Clinical Outcomes for Childhood Neuroblastoma Using Multi-Omics Data and Machine Learning
Abstract
1. Introduction
2. Results and Discussion
2.1. Evaluation Metrics
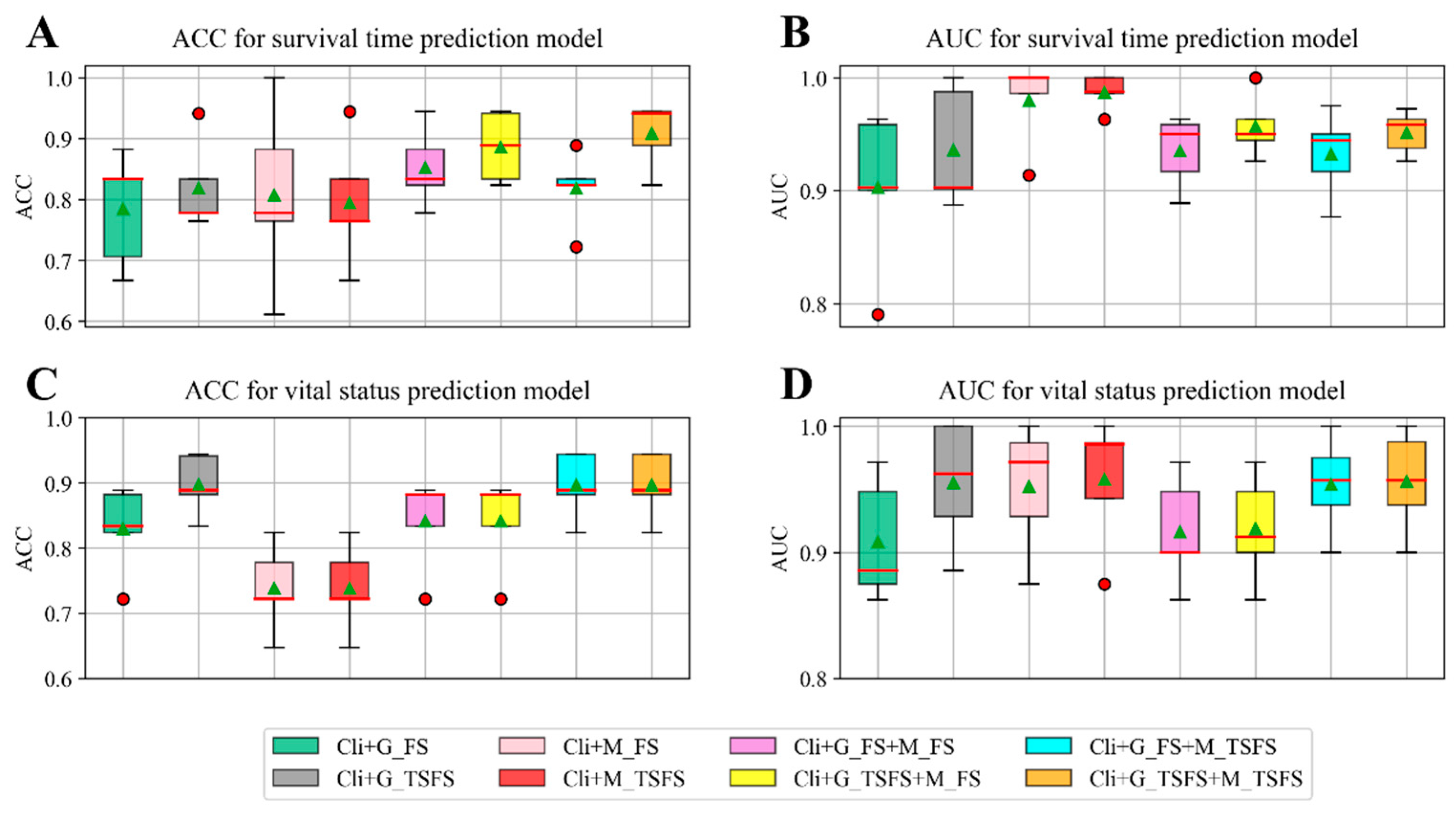
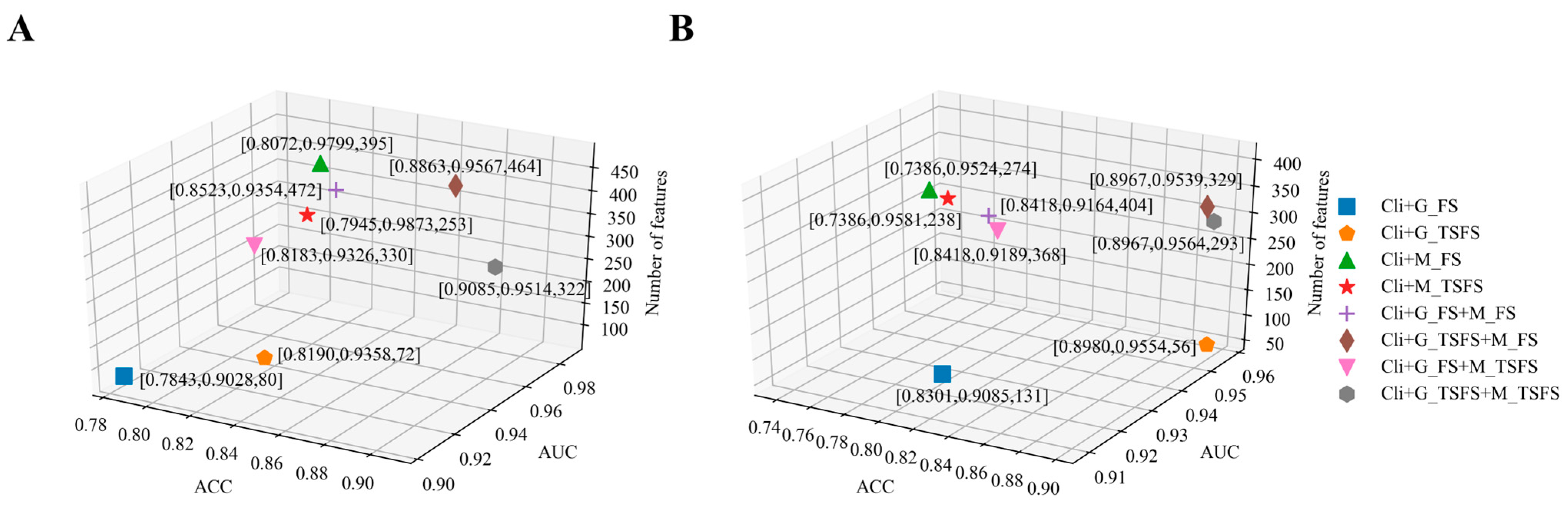
2.2. Single-Task Learning Method for Building Prediction Models
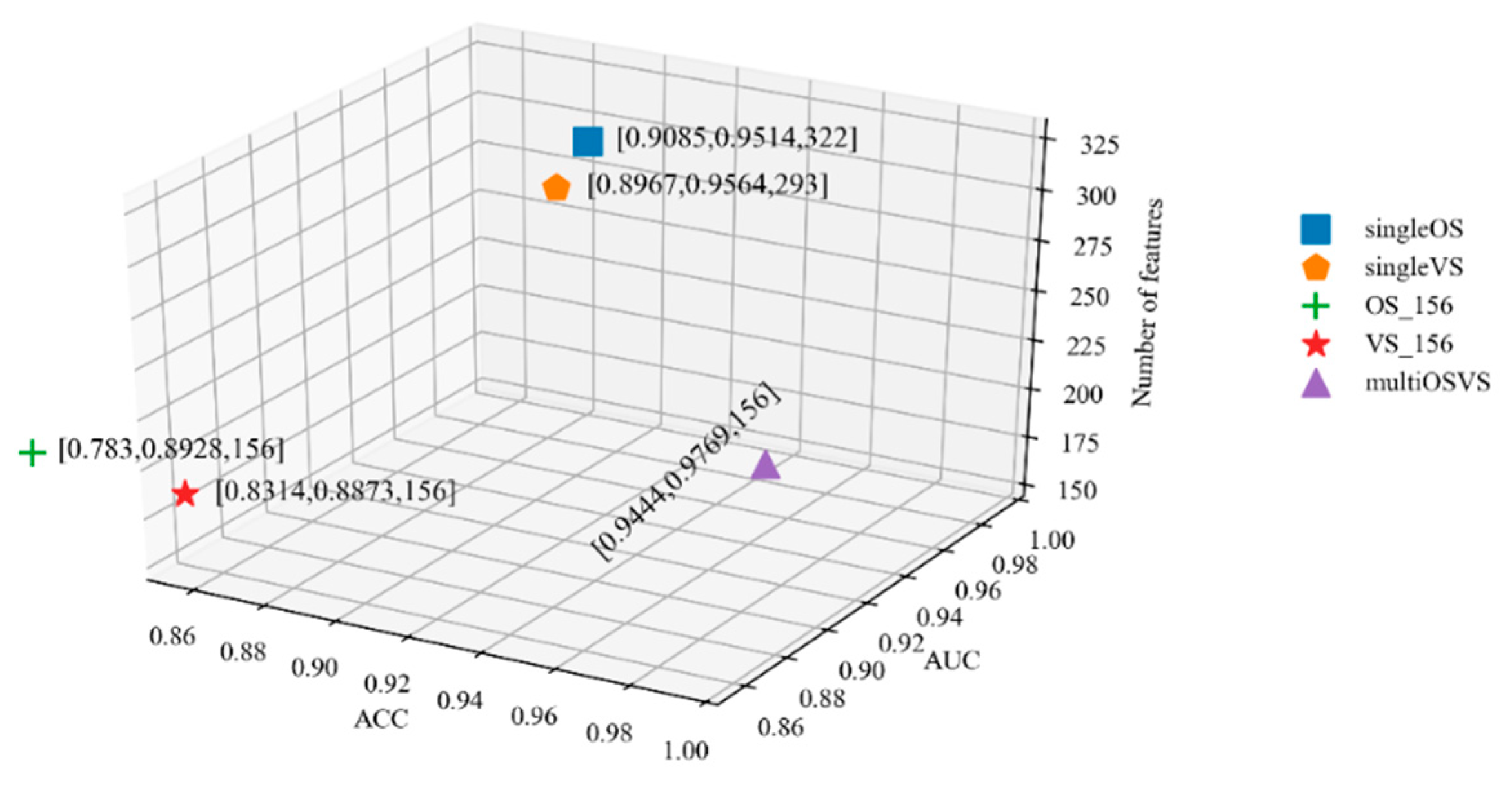
2.3. Multi-Task Learning Method for Building Prediction Models
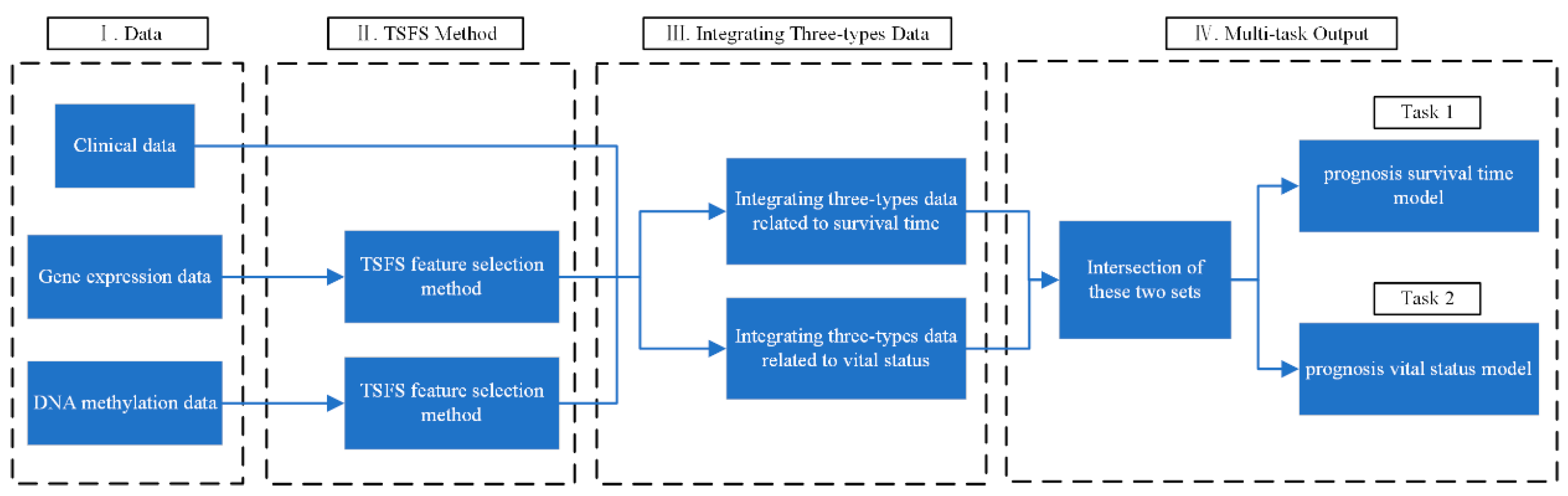
3. Materials and Methods
3.1. Dataset
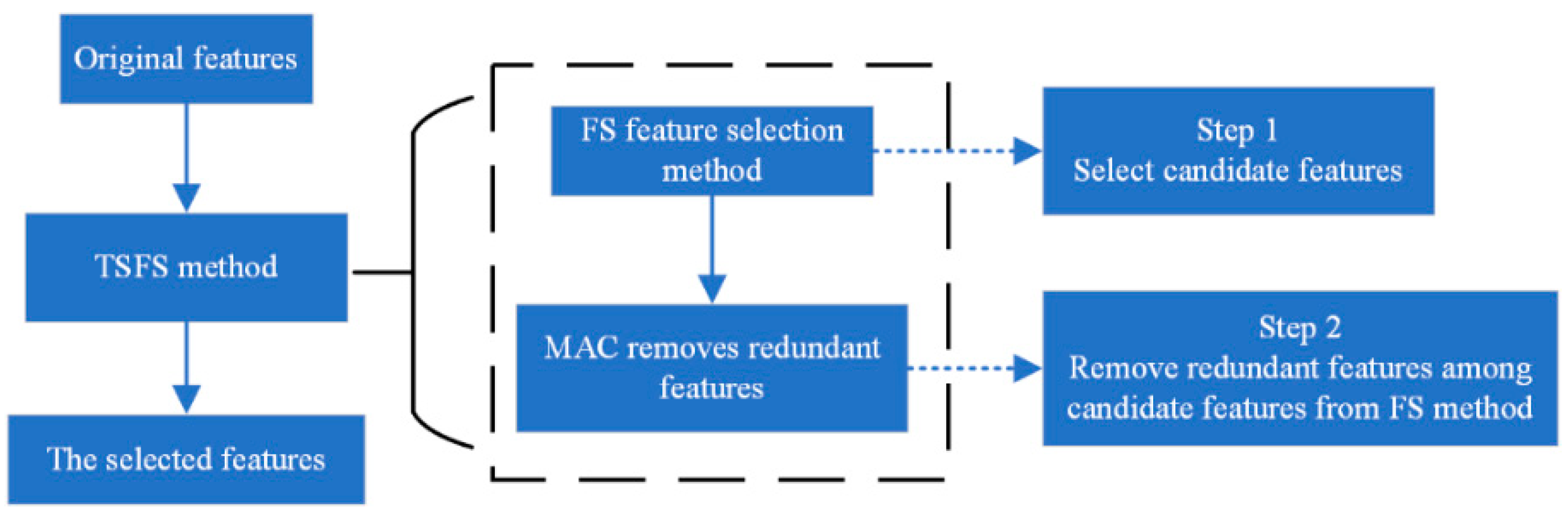
3.2. FS Feature Selection Method
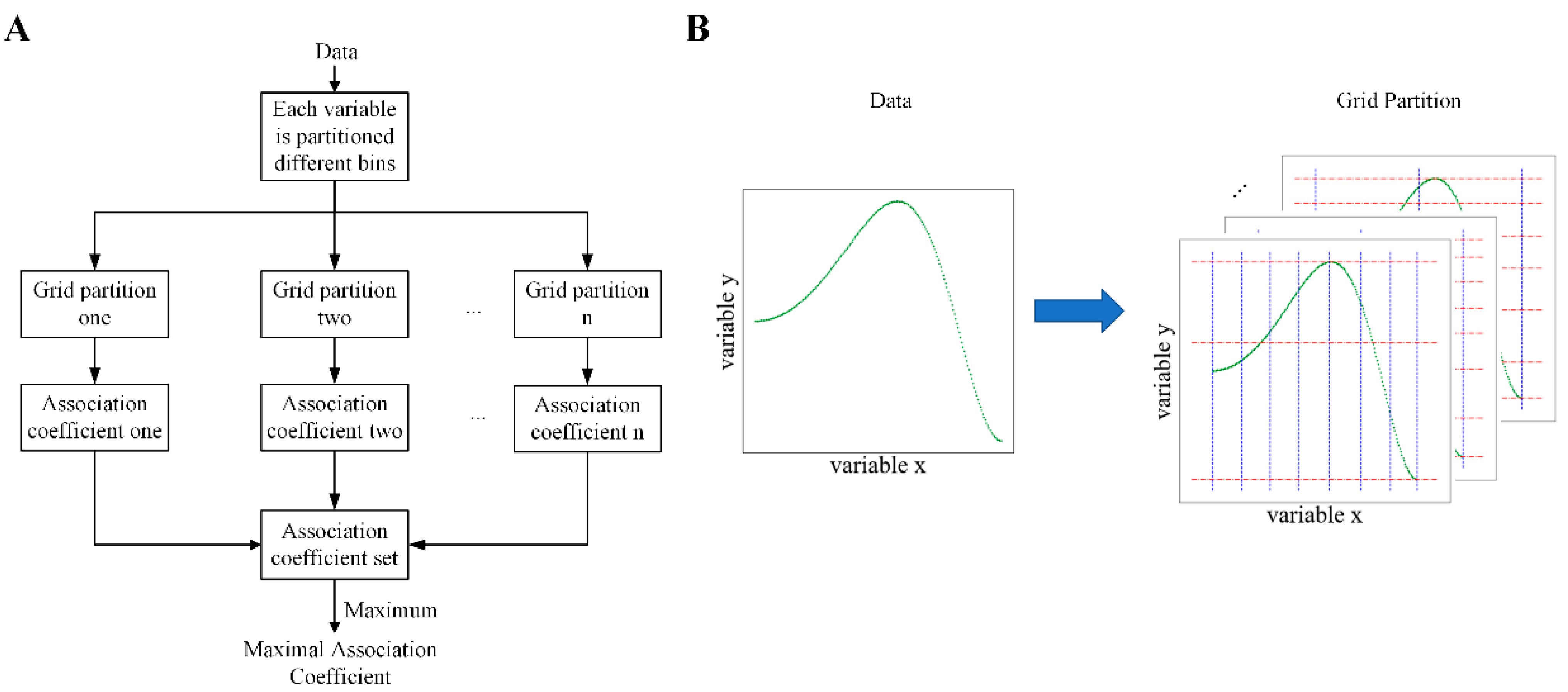
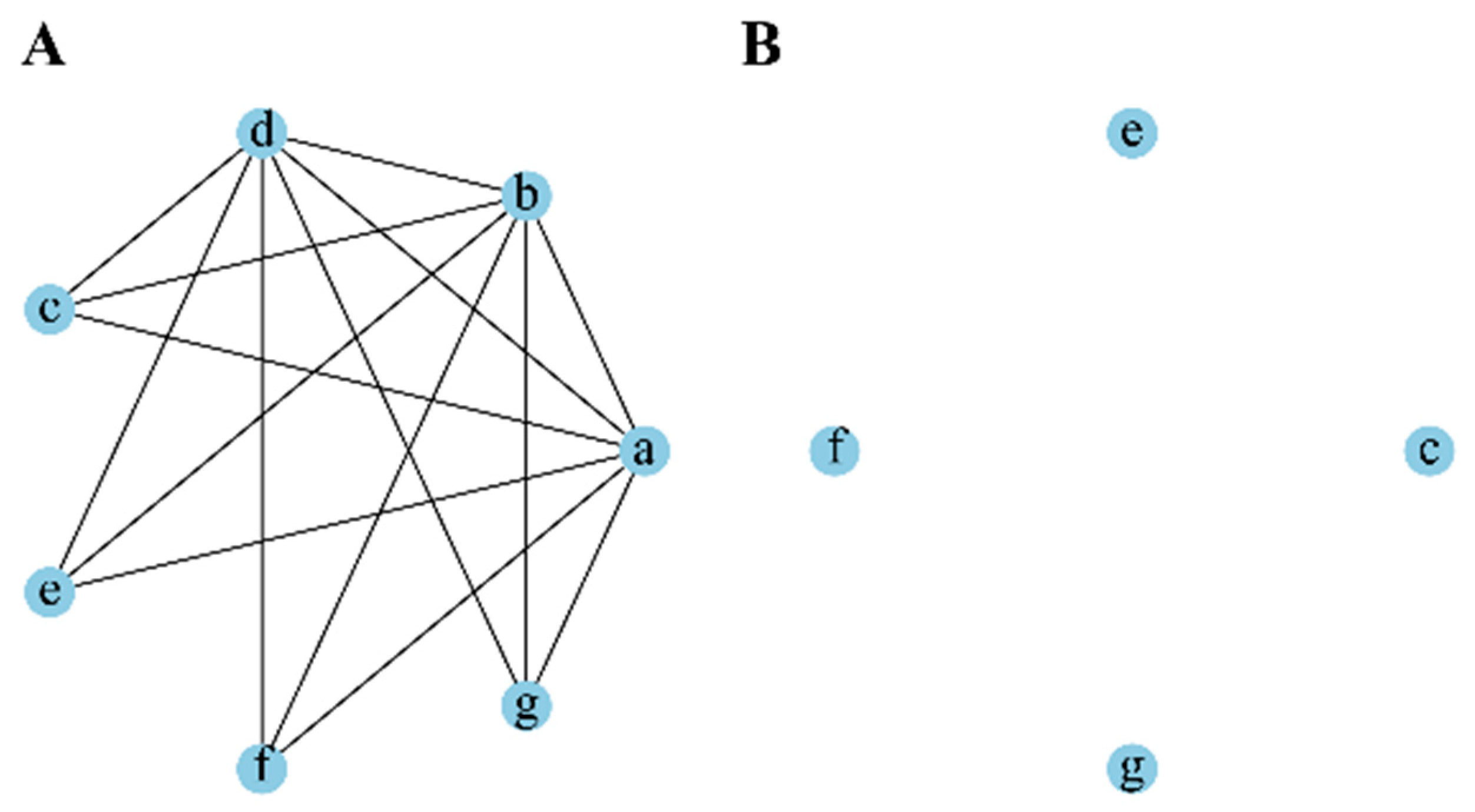
3.3. Maximal Association Coefficient
3.4. TSFS Method
3.5. Multi-Task Learning
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bosse, K.R.; Maris, J.M. Advances in the Translational Genomics of Neuroblastoma: From Improving Risk Stratification and Revealing Novel Biology to Identifying Actionable Genomic Alterations. Cancer 2016. 122, 20–33. [CrossRef]
- Ponzoni, M.; Bachetti, T.; Corrias, M.V.; Brignole, C.; Pastorino, F.; Calarco, E.; Bensa, V.; Giusto, E.; Ceccherini, I.; Perri, P. Recent Advances in the Developmental Origin of Neuroblastoma: An Overview. J. Exp. Clin. Cancer Res. 2022, 41, 92. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.F.; Jia, Y.X.; Hou, C.Z.; Li, N.; Zhang, N.; Yan, X.S.; Yang, L.; Guo, Y.; Chen, H.T.; Li, J.; et al. Pathological Prognosis Classification of Patients with Neuroblastoma Using Computational Pathology Analysis. Comput. Biol. Med. 2022, 149, 105980. [Google Scholar] [CrossRef] [PubMed]
- Jiang, M.R.; Stanke, J.; Lahti, J.M. The Connections between Neural Crest Development and Neuroblastoma. Curr. Top. Dev. Biol. 2011, 94, 77–127. [Google Scholar]
- Salazar, B.M.; Balczewski, E.A.; Ung, C.Y.; Zhu, S.Z. Neuroblastoma, a Paradigm for Big Data Science in Pediatric Oncology. Int. J. Mol. Sci. 2016, 18, 37. [Google Scholar] [CrossRef]
- Rybinski, B.; Wolinsky, T.; Brohl, A.; Moerdler, S.; Reed, D.R.; Ewart, M.; Weiser, D. Multifocal Primary Neuroblastoma Tumor Heterogeneity in Siblings with Co-Occurring PHOX2B and NF1 Genetic Aberrations. Gene. Chromosome. Canc. 2020, 59, 119–124. [Google Scholar] [CrossRef]
- Lundberg, K.I.; Treis, D.; Johnsen, J.I. Neuroblastoma Heterogeneity, Plasticity, and Emerging Therapies. Curr. Oncol. Rep. 2022, 24, 1053–1062. [Google Scholar] [CrossRef]
- Esposito, M.R.; Aveic, S.; Seydel, A.; Tonini, G.P. Neuroblastoma Treatment in the Post-Genomic Era. J. Biomed. Sci. 2017, 24, 14. [Google Scholar] [CrossRef]
- He, X.Y.; Qin, C.; Zhao, Y.D.; Zou, L.; Zhao, H.; Cheng, C. Gene Signatures Associated with Genomic Aberrations Predict Prognosis in Neuroblastoma. Cancer Commun. 2020, 40, 105–118. [Google Scholar] [CrossRef]
- Pugh, T.J.; Morozova, O.; Attiyeh, E.F.; Asgharzadeh, S.; Wei, J.S.; Auclair, D.; Carter, S.L.; Cibulskis, K.; Hanna, M.; Kiezun, A.; et al. The Genetic Landscape of High-Risk Neuroblastoma. Nat. Genet. 2013, 45, 279–284. [Google Scholar] [CrossRef]
- Hidalgo, M.R.; Alicia, A.; Çubuk, C.; Carbonell-Caballero, J.; Dopazo, J. Models of Cell Signaling Uncover Molecular Mechanisms of High-Risk Neuroblastoma and Predict Disease Outcome. Biol. Direct. 2018, 13, 16. [Google Scholar] [CrossRef] [PubMed]
- Applebaum, M.A.; Barr, E.K.; Karpus, J.; Nie, J.; Zhang, Z.; Armstrong, A.E.; Uppal, S.; Sukhanova, M.; Zhang, W.; Chlenski, A.; et al. 5-Hydroxymethylcytosine Profiles are Prognostic of Outcome in Neuroblastoma and Reveal Transcriptional Networks that Correlate with Tumor Phenotype. JCO Precis. Oncol. 2019, 3, PO.18.00402. [Google Scholar] [CrossRef] [PubMed]
- Cangelosi, D.; Morini, M.; Zanardi, N.; Sementa, A.R.; Muselli, M.; Conte, M.; Garaventa, A.; Pfeffer, U.; Bosco, M.C.; Varesio, L.; et al. (2020). Hypoxia Predicts Poor Prognosis in Neuroblastoma Patients and Associates with Biological Mechanisms Involved in Telomerase Activation and Tumor Microenvironment Reprogramming. Cancers 2020, 12, 2343. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.J.; Goodison, S.; Li, J.; Liu, L.; Farmerie, W. Improved Breast Cancer Prognosis Through the Combination of Clinical and Genetic Markers. Bioinformatics 2007, 23, 30–37. [Google Scholar] [CrossRef] [PubMed]
- Sun, D.D.; Wang, M.H.; Li, A. A Multimodal Deep Neural Network for Human Breast Cancer Prognosis Prediction by Integrating Multi-Dimensional Data. IEEE/ACM Trans. Comput. Biol. Bioinform. 2018, 16, 841–850. [Google Scholar] [CrossRef]
- Zafar, A.; Wang, W.; Liu, G.; Wang, X.J.; Xian, W.; McKeon, F.; Foster, J.; Zhou, J.; Zhang, R.W. Molecular Targeting Therapies for Neuroblastoma: Progress and Challenges. Med. Res. Rev. 2021, 41, 961–1021. [Google Scholar] [CrossRef]
- Bagatell, R.; DuBois, S.G.; Naranjo, A.; Belle, J.; Coldsmith, K.C.; Park, J.R.; Irwin, M.S.; COG Neuroblastoma Committee. Children’s Oncology Group’s 2023 Blueprint for Research: Neuroblastoma. Pediatr. Blood Cancer. 2023, 70, e30572. [Google Scholar] [CrossRef]
- Olsson, M.; Beck, S.; Kogner, P.; Martinsson, T.; Carén, H. Genome-Wide Methylation Profiling Identifies Novel Methylated Genes in Neuroblastoma Tumors. Epigenetics 2016, 11, 74–84. [Google Scholar] [CrossRef] [PubMed]
- Yang, Q.W.; Tian, Y.F.; Ostler, K.R.; Chlenski, A.; Guerrero, L.J.; Salwen, H.R.; Godley, L.A.; Cohn, S.L. Epigenetic Alterations Differ in Phenotypically Distinct Human Neuroblastoma Cell Lines. BMC Cancer 2010, 10, 286. [Google Scholar] [CrossRef] [PubMed]
- Domingo-Fernandez, R.; Watters, K.; Piskareva, O.; Stallings, R.L.; Bray, I. The Role of Genetic and Epigenetic Alterations in Neuroblastoma Disease Pathogenesis. Pediatr. Surg. Int. 2013, 29, 101–119. [Google Scholar] [CrossRef]
- Gómez, S.; Castellano, G.; Mayol, G.; Suñol, M.; Queiros, A.; Bibikova, M.; Nazor, K.L.; Loring, J.F.; Lemos, I.; Rodríguez, E.; et al. DNA Methylation Fingerprint of Neuroblastoma Reveals new Biological and Clinical Insights. Epigenomics 2015, 5, 1137–1153. [Google Scholar] [CrossRef] [PubMed]
- Charlet, J.; Tomari, A.; Dallosso, A.R.; Szemes, M.; Kaselova, M.; Curry, T.J.; Almutairi, B.; Etchevers, H.C.; McConville, C.; Malik, K.T.; et al. Genome-Wide DNA Methylation Analysis Identifies MEGF10 as a Novel Epigenetically Repressed Candidate Tumor Suppressor Gene in Neuroblastoma. Mol. Carcinog. 2017, 56, 1290–1301. [Google Scholar] [CrossRef] [PubMed]
- Durinck, K.; Speleman, F. Epigenetic Regulation of Neuroblastoma Development. Cell Tissue. Res. 2018, 372, 309–324. [Google Scholar] [CrossRef]
- Abe, M.; Ohira, M.; Kaneda, A.; Yagi, Y.; Yamamoto, S.; Kitano, Y.; Takato, T.; Nakagawara, A.; Ushijima, T. CpG Island Methylator Phenotype is a Strong Determinant of Poor Prognosis in Neuroblastomas. Cancer Res. 2005, 65, 828–834. [Google Scholar] [CrossRef] [PubMed]
- Gumy-Pause, F.; Pardo, B.; Khoshbeen-Boudal, M.; Ansari, M.; Gayet-Ageron, A.; Sappino, A.P.; Attiyeh, E.F.; Ozsahin, H. GSTP1 Hypermethylation is Associated with Reduced Protein Expression, Aggressive Disease and Prognosis in Neuroblastoma. Gene. Chromosome. Canc. 2012, 51, 174–185. [Google Scholar] [CrossRef]
- Fetahu, I.S.; Taschner-Mandl, S. Neuroblastoma and the Epigenome. Cancer Metast. Rev. 2021, 40, 173–189. [Google Scholar] [CrossRef] [PubMed]
- Watanabe, K.; Kimura, S.; Seki, M.; Isobe, T.; Kubota, Y.; Sekiguchi, M.; Sato-Otsubo, A.; Hiwatari, M.; Kato, M.; Oka, A.; et al. Identification of the Ultrahigh-Risk Subgroup in Neuroblastoma Cases through DNA Methylation Analysis and Its Treatment Exploiting Cancer Metabolism. Oncogene 2022, 41, 4994–5007. [Google Scholar] [CrossRef] [PubMed]
- Lalchungnunga, H.; Hao, W.; Maris, J.M.; Asgharzadeh, S.; Henrich, K.O.; Westermann, F.; Tweddle, D.A.; Schwalbe, E.C.; Strathdee, G. Genome Wide DNA Methylation Analysis Identifies Novel Molecular Subgroups and Predicts Survival in Neuroblastoma. Brit. J. Cancer. 2022, 127, 2006–2015. [Google Scholar] [CrossRef]
- Yang, Q.W.; Zage, P.; Kagan, D.; Tian, Y.F.; Seshadri, R.; Salwen, H.R.; Liu, S.Q.; Chlenski, A.; Cohn, S.L. Association of Epigenetic Inactivation of RASSF1A with Poor Outcome in Human Neuroblastoma. Clin. Cancer Res. 2004, 10, 8493–8500. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Banelli, B.; Gelvi, I.; Di Vinci, A.; Scaruffi, P.; Casciano, I.; Allemanni, G.; Bonassi, S.; Tonini, G.P.; Romani, M. Distinct CpG Methylation Profiles Characterize Different Clinical Groups of Neuroblastic Tumors. Oncogene 2005, 24, 5619–5628. [Google Scholar] [CrossRef][Green Version]
- Abe, M.; Westermann, F.; Nakagawara, A.; Takato, T.; Schwab, M.; Ushijima, T. Marked and Independent Prognostic Significance of the CpG Island Methylator Phenotype in Neuroblastomas. Cancer Lett. 2007, 247, 253–258. [Google Scholar] [CrossRef] [PubMed]
- Jones, P.A. Functions of DNA Methylation: Islands, Start Sites, Gene Bodies and Beyond. Nat. Rev. Genet. 2012, 13, 484–492. [Google Scholar] [CrossRef] [PubMed]
- Moore, L.D.; Le, T.; Fan, G.P. DNA Methylation and Its Basic Function. Neuropsychopharmacol. 2013, 38, 23–38. [Google Scholar] [CrossRef]
- Pickles, J.C.; Stone, T.J.; Jacques, T.S. Methylation-Based Algorithms for Diagnosis: Experience from Neuro-Oncology. J. Pathol. 2020, 250, 510–517. [Google Scholar] [CrossRef]
- Zitnik, M.; Nguyen, F.; Wang, B.; Leskovec, J.; Goldenberg, A.; Hoffman, M.M. Machine Learning for Integrating Data in Biology and Medicine: Principles, Practice, and Opportunities. Inform. Fusion. 2019, 50, 71–91. [Google Scholar] [CrossRef] [PubMed]
- Kasemeier-Kulesa, J.C.; Schnell, S.; Woolley, T.; Spengler, J.A.; Morrison, J.A.; McKinney, M.C.; Pushel, I.; Wolfe, L.A.; Kulesa, P.M. Predicting Neuroblastoma Using Developmental Signals and a Logic-Based Model. Biophys. Chem. 2018, 238, 30–38. [Google Scholar] [CrossRef] [PubMed]
- Tranchevent, L.C.; Azuaje, F.; Rajapakse, J.C. A Deep Neural Network Approach to Predicting Clinical Outcomes of Neuroblastoma Patients. BMC Med. Genomics. 2019, 12, 178. [Google Scholar] [CrossRef]
- Masecchia, S.; Coco, S.; Barla, A.; Verri, A.; Tonini, G.P. Genome Instability Model of Metastatic Neuroblastoma Tumorigenesis by a Dictionary Learning Algorithm. BMC Med. Genomics. 2015, 8, 57. [Google Scholar] [CrossRef]
- Mihaylov, I.; Kańduła, M.; Krachunov, M.; Vassilev, D. A Novel Framework for Horizontal and Vertical Data Integration in Cancer Studies with Application to Survival Time Prediction Models. Biol. Direct. 2019, 14, 22. [Google Scholar] [CrossRef]
- Polewko-Klim, A.; Lesiński, W.; Mnich, K.; Piliszek, R.; Rudnicki, W.R. Integration of Multiple Types of Genetic Markers for Neuroblastoma May Contribute to Improved Prediction of the Overall Survival. Biol. Direct. 2018, 13, 17. [Google Scholar] [CrossRef]
- Tranchevent, L.C.; Nazarov, P.V.; Kaoma, T.; Schmartz, G.P.; Muller, A.; Kim, S.Y.; Rajapakse, J.C.; Azuaje, F. Predicting Clinical Outcome of Neuroblastoma Patients Using an Integrative Network-Based Approach. Biol. Direct. 2018, 13, 12. [Google Scholar] [CrossRef]
- Baali, I.; Acar, D.A.E.; Aderinwale, T.W.; HafezQorani, S.; Kazan, H. Predicting Clinical Outcomes in Neuroblastoma with Genomic Data Integration. Biol. Direct. 2018, 13, 20. [Google Scholar] [CrossRef]
- Körber, V.; Stainczyk, S.A.; Kurilov, R.; Henrich, K.O.; Hero, B.; Brors, B.; Westermann, F.; Höfer, H. Neuroblastoma Arises in Early Fetal Development and Its Evolutionary Duration Predicts Outcome. Nat. Genet. 2023, 55, 619–630. [Google Scholar] [CrossRef] [PubMed]
- Cangelosi, D.; Muselli, M.; Parodi, S.; Blengio, F.; Becherini, P.; Versteeg, R.; Conte, M.; Varesio, L. Use of Attribute Driven Incremental Discretization and Logic Learning Machine to Build a Prognostic Classifier for Neuroblastoma Patients. BMC Bioinformatics 2014, 15, S4. [Google Scholar] [CrossRef]
- Maggio, V.; Chierici, M.; Jurman, G.; Furlanello, C. Distillation of the Clinical Algorithm Improves Prognosis by Multi-Task Deep Learning in High-Risk Neuroblastoma. PLoS ONE 2018, 13, e0208924. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Gao, J. A Novel Online Nomogram Established with Five Features before Surgical Resection for Predicating Prognosis of Neuroblastoma Children: A Population-Based Study. Technol. Cancer Res. Treat. 2023, 22, 15330338221145141. [Google Scholar] [CrossRef]
- Oberthuer, A.; Kaderali, L.; Kahlert, Y.; Hero, B.; Westermann, F.; Berthold, F.; Brors, B.; Eils, R.; Fischer, M. Subclassification and Individual Survival Time Prediction from Gene Expression Data of Neuroblastoma Patients by Using CASPAR. Clin. Cancer Res. 2008, 14, 6590–6601. [Google Scholar] [CrossRef]
- Stigliani, S.; Coco, S.; Moretti, S.; Oberthuer, A.; Fischer, M.; Theissen, J.; Gallo, F.; Garavent, A.; Berthold, F.; Bonassi, S.; et al. High Genomic Instability Predicts Survival in Metastatic High-Risk Neuroblastoma. Neoplasia 2012, 14, 823–832. [Google Scholar] [CrossRef]
- Kang, Z.L.; Grauman, K.; Sha, F. Learning with Whom to Share in Multi-Task Feature Learning. In ICML’11: Proceedings of the 28th International Conference on International Conference on Machine Learning; Bellevue, WA, USA, 28 June–2 July 2011; Getoor, L., Scheffer, T., Eds.; Omnipress: Madison, WI, USA, 2011; pp. 521–528. [Google Scholar]
- Ma, J.Q.; Zhao, Z.; Yi, X.Y.; Chen, J.L.; Hong, L.C.; Chi, E.H. Modeling Task Relationships in Multi-Task Learning with Multi-Gate Mixture-of-Experts. In KDD ‘18: Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, KDD ‘18: The 24th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, London, UK, 19–23 August 2018; Association for Computing Machinery: New York, NY, USA, 2018; pp. 1930–1939. [Google Scholar]
- Wang, X.; Zhang, Y.; Ren, X.; Zhang, Y.H.; Zitnik, M.; Shang, J.B.; Langlotz, C.; Han, J.W. Cross-Type Biomedical Named Entity Recognition with Deep Multi-Task Learning. Bioinformatics 2019, 35, 1745–1752. [Google Scholar] [CrossRef]
- Liang, W.; Zhang, K.; Cao, P.; Liu, X.L.; Yang, J.Z.; Zaiane, O. Rethinking Modeling Alzheimer’s Disease Progression from a Multi-Task Learning Perspective with Deep Recurrent Neural Network. Comput. Biol. Med. 2021, 138, 104935. [Google Scholar] [CrossRef] [PubMed]
- Tu, G.; Wen, J.T.; Liu, H.; Chen, S.T.; Zheng, L.; Jiang, D.Z. Exploration Meets Exploitation: Multitask Learning for Emotion Recognition Based on Discrete and Dimensional Models. Knowl.-Based Syst. 2022, 235, 107598. [Google Scholar] [CrossRef]
- Castro, D.M.; de Veaux, N.R.; Miraldi, E.R.; Bonneau, R. Multi-Study Inference of Regulatory Networks for More Accurate Models of Gene Regulation. PLoS Comput. Biol. 2019, 15, e1006591. [Google Scholar] [CrossRef] [PubMed]
- Shao, W.; Wang, T.X.; Sun, L.; Dong, T.H.; Han, T.; Huang, Z.; Zhang, J.; Zhang, D.Q.; Huang, K. Multi-Task Multi-Modal Learning for Joint Diagnosis and Prognosis of Human Cancers. Med. Image Anal. 2020, 65, 101795. [Google Scholar] [CrossRef] [PubMed]
- Stetson, L.C.; Pearl, T.; Chen, Y.W.; Barnholtz-Sloan, J.S. Computational Identification of Multi-Omic Correlates of Anticancer Therapeutic Response. BMC Genom. 2014, 15, S2. [Google Scholar] [CrossRef]
- Auslander, N.; Yizhak, K.; Weinstock, A.; Budhu, A.; Tang, W.; Wang, X.W.; Ambs, S.; Ruppin, E. A Joint Analysis of Transcriptomic and Metabolomic Data Uncovers Enhanced Enzyme-Metabolite Coupling in Breast Cancer. Sci. Rep. 2016, 6, 29662. [Google Scholar] [CrossRef]
- Giang, T.T.; Nguyen, T.P.; Tran, D.H. Stratifying Patients Using Fast Multiple Kernel Learning Framework: Case Studies of Alzheimer’s Disease and Cancers. BMC Med. Inform. Decis. Mak. 2020, 20, 108. [Google Scholar] [CrossRef] [PubMed]
- Crawford, S.E.; Stellmach, V.; Ranalli, M.; Huang, X.; Huang, L.; Volpert, O.; De Vries, G.H.; Abramson, L.P.; Bouck, N. Pigment Epithelium-Derived Factor (PEDF) in Neuroblastoma: A Multifunctional Mediator of Schwann Cell Antitumor Activity. J. Cell. Sci. 2001, 114, 4421–4428. [Google Scholar] [CrossRef]
- Cheng, G.; Zhong, M.; Kawaguchi, R.; Kassai, M.; Al-Ubaidi, M.; Deng, J.; Ter-Stepanian, M.; Sun, H. Identification of PLXDC1 and PLXDC2 as the Transmembrane Receptors for the Multifunctional Factor PEDF. eLife 2014, 3, e05401. [Google Scholar] [CrossRef] [PubMed]
- Sheikh, A.; Takatori, A.; Hossain, M.S.; Hasan, M.K.; Tagawa, M.; Nagase, H.; Nakagawara, A. Unfavorable Neuroblastoma Prognostic Factor NLRR2 Inhibits Cell Differentiation by Transcriptional Induction through JNK Pathway. Cancer Sci. 2016, 107, 1223–1232. [Google Scholar] [CrossRef] [PubMed]
- Banelli, B.; Bonassi, S.; Casciano, I.; Mazzocco, K.; Di Vinic, A.; Scaruffi, P.; Brigati, C.; Allemanni, G.; Borzì, L.; Tonini, G.P.; et al. Outcome Prediction and Risk Assessment by Quantitative Pyrosequencing Methylation Analysis of the SFN Gene in Advanced Stage, High-Risk, Neuroblastic Tumor Patients. Int. J. Cancer 2010, 126, 656–668. [Google Scholar] [CrossRef] [PubMed]
- Whittle, S.B.; Reyes, S.; Du, M.; Gireud, M.; Zhang, L.N.; Woodfield, S.E.; Ittmann, M.; Scheurer, M.E.; Bean, A.J.; Zage, P.E. A Polymorphism in the FGFR4 Gene is Associated with Risk of Neuroblastoma and Altered Receptor Degradation. J. Pediatr. Hematol. Oncol. 2016, 38, 131–138. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Wagner, L.M.; McLendon, R.E.; Yoon, K.J.; Weiss, B.D.; Billups, C.A.; Danks, M.K. Targeting Methylguanine-DNA Methyltransferase in the Treatment of Neuroblastoma. Clin. Cancer Res. 2007, 13, 5418–5425. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.Y.; Ding, Z.Z.; Luo, H. The Prognostic Role of m6A-Related Genes in Paediatric Neuroblastoma Patients. Comput. Math. Method. M. 2022, 8354932. [Google Scholar] [CrossRef] [PubMed]
- Zhu, K.; Gao, T.Y.; Wang, Z.R.; Zhang, L.R.; Tan, K.Z.; Lv, Z.B. RNA N6-Methyladenosine Reader IGF2BP3 Interacts with MYCN and Facilitates Neuroblastoma Cell Proliferation. Cell Death Discov. 2023, 9, 151. [Google Scholar] [CrossRef]
- Romani, M.; Scaruffi, P.; Casciano, I.; Mazzocco, K.; Lo Cunsolo, C.; Cavazzana, A.; Gambini, C.; Boni, L.; De Bernardi, B.; Tonini, G.P. Stage-Independent Expression and Genetic Analysis of TP73 in Neuroblastoma. Int. J. Cancer 1999, 84, 365–369. [Google Scholar] [CrossRef]
- Kaghad, M.; Bonnet, H.; Yang, A.; Creancier, L.; Biscan, J.C.; Valent, A.; Minty, A.; Chalon, P.; Lelias, J.M.; Dumont, X.; et al. Monoallelically Expressed Gene Related to p53 at 1p36, a Region Frequently Deleted in Neuroblastoma and Other Human Cancers. Cell 1997, 90, 809–819. [Google Scholar] [CrossRef]
- Rossi, M.; Sayan, E.A.; Terrinoni, A.; Melino, G.; Knight, R.A. Mechanism of Induction of Apoptosis by p73 and Its Relevance to Neuroblastoma Biology. Ann. N. Y. Acad. Sci. 2004, 1028, 143–149. [Google Scholar] [CrossRef] [PubMed]
- Sobhan, P.K.; Zhai, Q.W.; Green, L.C.; Hansford, L.M.; Funa, K. ASK1 Regulates the Survival of Neuroblastoma Cells by Interacting with TLX and Stabilizing HIF-1α. Cell. Signal. 2017, 30, 104–117. [Google Scholar] [CrossRef]
- Khademi, M.; Nedialkov, N.S. Probabilistic Graphical Models and Deep Belief Networks for Prognosis of Breast Cancer. ICMLA 2015: 14th IEEE International Conference on Machine Learning and Applications, Miami, FL, USA, 9–11 December 2015; pp. 727–732. [Google Scholar]
- Lundin, M.; Lundin, J.; Burke, H.B.; Toikkanen, S.; Pylkkänen, L.; Joensuu, H. Artificial Neural Networks Applied to Survival Prediction in Breast Cancer. Oncology 1999, 57, 281–286. [Google Scholar] [CrossRef]
- Duda, R.O.; Hart, P.E.; Stork, D.G. Pattern Classification, 2nd ed.; Wiley-interscience: Hoboken, NJ, USA, 2000; Volume 4, pp. 44–47. [Google Scholar]
- Gu, Q.Q.; Li, H.; Han, J.W. Generalized Fisher Score for Feature Selection. In UAI’11: Proceedings of the Twenty-Seventh Conference on Uncertainty in Artificial Intelligence; Barcelona, Spain, 14–17 July 2011; Cozman, F., Pfeffer, A., Eds.; AUAI Press: Arlington, VA, USA, 2011; pp. 266–273. [Google Scholar]
- Dudoit, S.; Fridlyand, J.; Speed, T.P. Comparison of Discrimination Methods for the Classification of Tumors Using Gene Expression Data. J. Am. Stat. Assoc. 2002, 97, 77–87. [Google Scholar] [CrossRef]
- Wang, P.R.; Zhang, J.Y. A Novel Piecewise-Linear Method for Detecting Associations between Variables. PLoS ONE 2023, 18, e0290280. [Google Scholar] [CrossRef]
- Lu, Y.X.; Kumar, A.; Zhai, S.F.; Cheng, Y.; Javidi, T.; Feris, R. Fully-Adaptive Feature Sharing in Multi-Task Networks with Applications in Person Attribute Classification. CVPR 2017: 2017 IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1131–1140. [Google Scholar]
- Silva, A.G.D.A.E.; Gomes, H.M.; Batista, L.V. A Collaborative Deep Multitask Learning Network for Face Image Compliance to ISO/IEC19794-5 Standard. Expert Syst. Appl. 2022, 198, 116756. [Google Scholar] [CrossRef]
- Zhang, J.W.; Zhang, P.; Guo, D.Y.; Zhou, Y.; Wu, Y.K.; Yang, B.; Lin, L. Automatic Repetition Instruction Generation for Air Traffic Control Training Using Multi-Task Learning with an Improved Copy Network. Knowl.-Based Syst. 2022, 241, 108232. [Google Scholar] [CrossRef]


| Confusion Matrix | Real | ||
|---|---|---|---|
| Predicted | Positive | Negative | |
| Positive | TP | FP | |
| Negative | FN | TN | |
| Hyperparameter | Survival Time Prediction Problem | Vital Status Prediction Problem | ||
|---|---|---|---|---|
| Gene data | methylation data | Gene data | methylation data | |
| α | 0.7 | 0.55 | 0.35 | 0.6 |
| Rth | 0.65 | 0.9 | 0.2 | 0.9 |
| Feature | SingleOS | SingleVS | MultiOSVS |
|---|---|---|---|
| Clinical | 3 | 1 | 1 |
| Gene | 69 | 55 | 4 |
| Methylation | 250 | 237 | 151 |
| Name | Category | Description | References |
|---|---|---|---|
| Age | Clinical | Age at diagnosis. | [44] |
| PLXDC2 | Gene expression data | PLXDC2 is the surface receptor of pigment epithelium-derived factor (PEDF); PEDF effects induces cell differentiation and neurite outgrowth. | [59,60] |
| LRRN2 | DNA methylation data | LRRN2 serves as a prognostic marker of NB. | [61] |
| SFN | DNA methylation data | The methylation of the SFN gene above a defined threshold is a strong and reliable predictor of adverse outcome independently from other prognostic factors. | [62] |
| FGFR4 | DNA methylation data | The FGFR4 is associated with an increased prevalence of neuroblastoma in children. | [63] |
| MGMT | DNA methylation data | MGMT methylation is a relevant therapeutic target in neuroblastoma. | [64] |
| IGF2BP3 | DNA methylation data | An IGF2BP3 positive coefficient was a risk factor for poor prognosis and the levels of IGF2BP3 and N-myc are positively correlated in NB. | [65,66] |
| TP73 | DNA methylation data | The TP73 gene, also called p73, banded at 1p36.3, is homologue of the TP53 tumor suppressor. TP73 can inhibit cell proliferation and induce apoptosis; a role for TP73 in the development of neuroblastoma could not be completely ruled out. TP73 has been proposed as a candidate tumor suppressor gene involved in neuroblastoma development. | [67,68,69] |
| NR2E1 | DNA methylation data | Elevated expression of NR2E1, also called TLX, in neuroblastoma (NB) correlates with unfavorable prognosis. | [70] |
| DNA methylation regulates gene expression. | [32,33,34] | ||
| Variables | Categories | Frequency | Percentage (%) |
|---|---|---|---|
| Average age at diagnosis in years: Mean (SD *) | Male | 3.01 (2.80) | |
| Female | 3.03 (1.55) | ||
| All patients | 3.02 (2.36) | ||
| Gender | Male | 51 | 57.95 |
| Female | 37 | 42.05 | |
| Race | White | 69 | 78.41 |
| Black or African American | 9 | 10.23 | |
| Unknown | 7 | 7.95 | |
| Native Hawaiian or other Pacific Islander | 2 | 2.27 | |
| Asian | 1 | 1.14 | |
| INSS stage | Stage 1 | 12 | 13.64 |
| Stage 3 | 1 | 1.14 | |
| Stage 4 | 75 | 85.23 | |
| COG risk group | Low risk | 12 | 13.64 |
| High risk | 76 | 86.36 | |
| Vital status at the last follow-up | Dead | 51 | 57.95 |
| Alive | 37 | 42.05 | |
| Overall survival time of all patients in years: Mean (SD *) | Median survival time | 4.58 (3.43) | |
| Average survival time | 5.02 (3.43) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, P.; Zhang, J. Prediction of Composite Clinical Outcomes for Childhood Neuroblastoma Using Multi-Omics Data and Machine Learning. Int. J. Mol. Sci. 2025, 26, 136. https://doi.org/10.3390/ijms26010136
Wang P, Zhang J. Prediction of Composite Clinical Outcomes for Childhood Neuroblastoma Using Multi-Omics Data and Machine Learning. International Journal of Molecular Sciences. 2025; 26(1):136. https://doi.org/10.3390/ijms26010136
Chicago/Turabian StyleWang, Panru, and Junying Zhang. 2025. "Prediction of Composite Clinical Outcomes for Childhood Neuroblastoma Using Multi-Omics Data and Machine Learning" International Journal of Molecular Sciences 26, no. 1: 136. https://doi.org/10.3390/ijms26010136
APA StyleWang, P., & Zhang, J. (2025). Prediction of Composite Clinical Outcomes for Childhood Neuroblastoma Using Multi-Omics Data and Machine Learning. International Journal of Molecular Sciences, 26(1), 136. https://doi.org/10.3390/ijms26010136





