An Explainable Deep Learning Classifier of Bovine Mastitis Based on Whole-Genome Sequence Data—Circumventing the p >> n Problem
Abstract
1. Introduction
2. Results
2.1. Data Processing
2.2. The Optimal DL Architecture
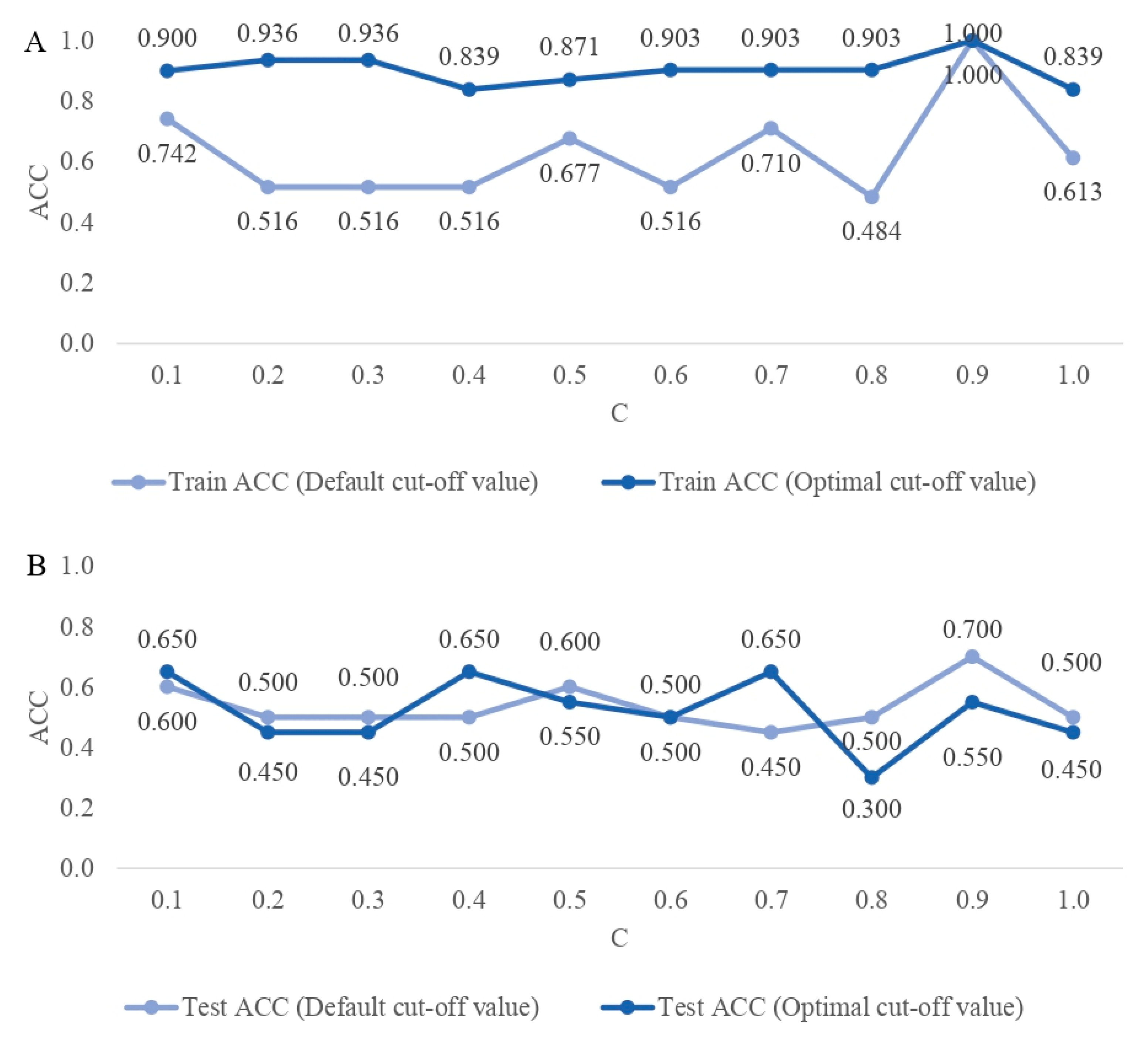
2.3. The Classification Quality
2.4. Selection of the Best DL Architecture
2.5. Genomic and Functional Annotation
2.6. GWAS for Clinical Mastitis in Polish Holstein–Friesian Cows
3. Discussion
3.1. Data Processing
3.2. Functional Interpretation of Significant SNPs
4. Materials and Methods
4.1. Sequenced Animals
4.2. Genotyped Animals
4.3. Data Processing
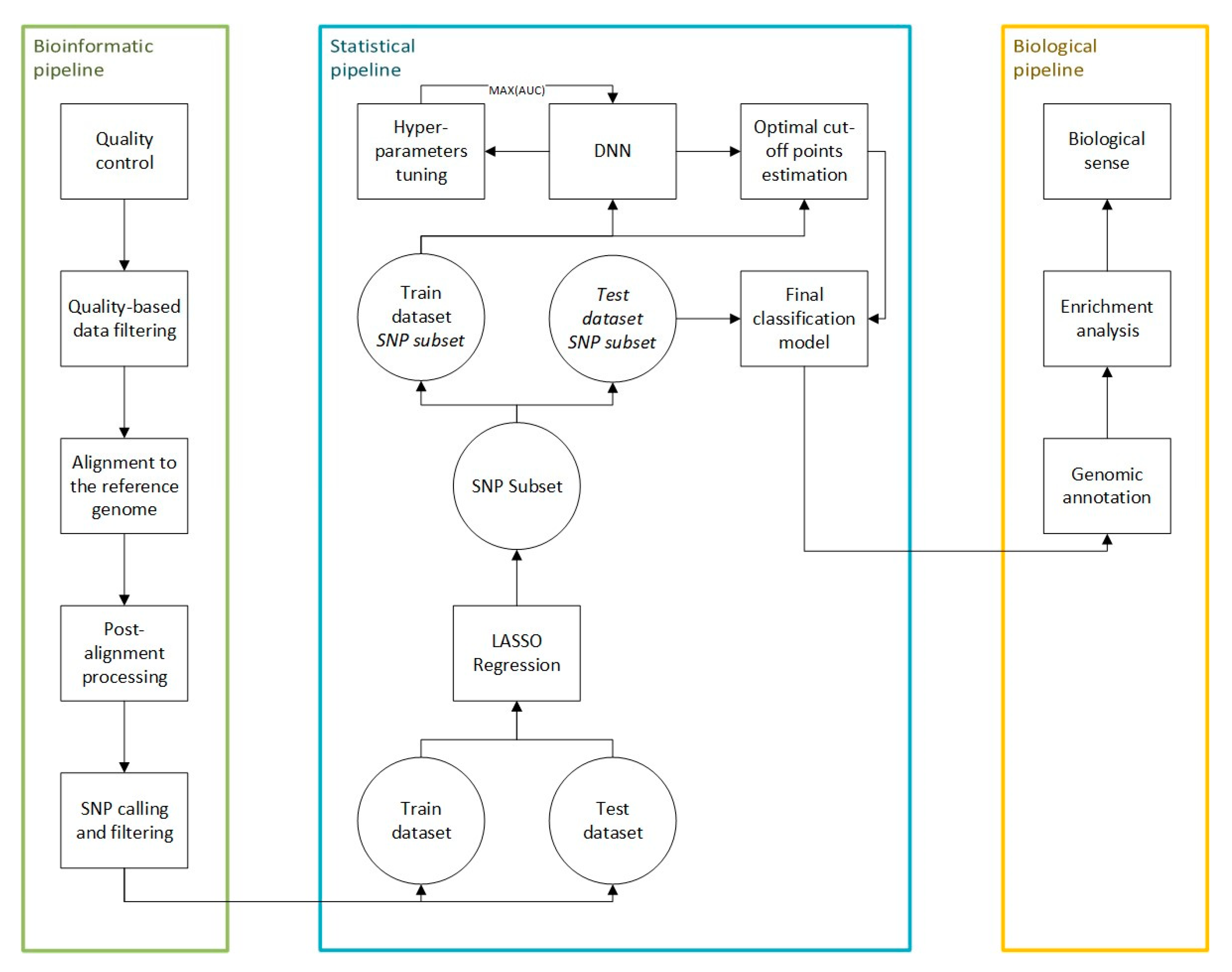
4.4. Bioinformatic Pipeline
4.5. Statistical Pipeline
4.5.1. Logistic LASSO Regression
4.5.2. The Deep Learning Algorithm
4.5.3. Hyperparameter Tuning and Validation
4.5.4. The Estimation of the Optimal Cut-Off Point
4.5.5. The Selection of Significant SNPs
4.5.6. The Evaluation of DL Classifiers
- True positive (TP), defined as the scenario in which a mastitis-susceptible individual was classified as mastitis-susceptible.
- False positive (FP), defined as the scenario in which a mastitis-resistant individual was classified as mastitis-susceptible.
- True negative (TN), defined as the scenario in which a mastitis-resistant individual was classified as mastitis-resistant.
- False negative (FN), defined as the scenario in which a mastitis-susceptible individual was classified as mastitis-resistant.
4.6. Biological Pipeline
4.7. Genome-Wide Association Study for Clinical Mastitis in Genotyped Cows
- , with I being an identity matrix, representing the additive genetic variance component, and being equal to the number of SNPs (53,557);
- , where is the numerator relationship matrix calculated based on the pedigree relationship and is the rest of additive genetic variance that was not explained by SNPs ;
- where is an identity matrix and representing the residual variance.
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cao, C.; Liu, F.; Tan, H.; Song, D.; Shu, W.; Li, W.; Zhou, Y.; Bo, X.; Xie, Z. Deep Learning and Its Applications in Biomedicine. Genom. Proteom. Bioinform. 2018, 16, 17–32. [Google Scholar] [CrossRef] [PubMed]
- Routhier, E.; Mozziconacci, J. Genomics Enters the Deep Learning Era. PeerJ 2022, 10, e13613. [Google Scholar] [CrossRef]
- Hayes, B.J.; Daetwyler, H.D. 1000 Bull Genomes Project to Map Simple and Complex Genetic Traits in Cattle: Applications and Outcomes. Annu. Rev. Anim. Biosci. 2019, 7, 89–102. [Google Scholar] [CrossRef]
- Asgari, E.; Mofrad, M.R.K. Continuous Distributed Representation of Biological Sequences for Deep Proteomics and Genomics. PLoS ONE 2015, 10, e0141287. [Google Scholar] [CrossRef]
- Cios, K.J.; Mamitsuka, H.; Nagashima, T.; Tadeusiewicz, R. Computational Intelligence in Solving Bioinformatics Problems. Artif. Intell. Med. 2005, 35, 1–8. [Google Scholar] [CrossRef]
- Liao, J.G.; Chin, K.-V. Logistic Regression for Disease Classification Using Microarray Data: Model Selection in a Large p and Small n Case. Bioinformatics 2007, 23, 1945–1951. [Google Scholar] [CrossRef]
- Severe COVID-19 GWAS Group; Ellinghaus, D.; Degenhardt, F.; Bujanda, L.; Buti, M.; Albillos, A.; Invernizzi, P.; Fernández, J.; Prati, D.; Baselli, G.; et al. Genomewide Association Study of Severe COVID-19 with Respiratory Failure. N. Engl. J. Med. 2020, 383, 1522–1534. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.; Qiao, D.; Yang, C.; Kasela, S.; Kim, W.; Ma, Y.; Shrine, N.; Batini, C.; Sofer, T.; Taliun, S.A.G.; et al. Whole Genome Sequence Analysis of Pulmonary Function and COPD in 19,996 Multi-Ethnic Participants. Nat. Commun. 2020, 11, 5182. [Google Scholar] [CrossRef]
- Wesolowska-Andersen, A.; Zhuo Yu, G.; Nylander, V.; Abaitua, F.; Thurner, M.; Torres, J.M.; Mahajan, A.; Gloyn, A.L.; McCarthy, M.I. Deep Learning Models Predict Regulatory Variants in Pancreatic Islets and Refine Type 2 Diabetes Association Signals. eLife 2020, 9, e51503. [Google Scholar] [CrossRef] [PubMed]
- Sundaram, L.; Gao, H.; Padigepati, S.R.; McRae, J.F.; Li, Y.; Kosmicki, J.A.; Fritzilas, N.; Hakenberg, J.; Dutta, A.; Shon, J.; et al. Predicting the Clinical Impact of Human Mutation with Deep Neural Networks. Nat. Genet. 2018, 50, 1161–1170. [Google Scholar] [CrossRef]
- Cheng, L.; Karkhanis, P.; Gokbag, B.; Liu, Y.; Li, L. DGCyTOF: Deep Learning with Graphic Cluster Visualization to Predict Cell Types of Single Cell Mass Cytometry Data. PLoS Comput. Biol. 2022, 18, e1008885. [Google Scholar] [CrossRef]
- Bychkov, D.; Linder, N.; Turkki, R.; Nordling, S.; Kovanen, P.E.; Verrill, C.; Walliander, M.; Lundin, M.; Haglund, C.; Lundin, J. Deep Learning Based Tissue Analysis Predicts Outcome in Colorectal Cancer. Sci. Rep. 2018, 8, 3395. [Google Scholar] [CrossRef]
- Halasa, T.; Huijps, K.; Østerås, O.; Hogeveen, H. Economic Effects of Bovine Mastitis and Mastitis Management: A Review. Vet. Q. 2007, 29, 18–31. [Google Scholar] [CrossRef]
- Jamali, H.; Barkema, H.W.; Jacques, M.; Lavallée-Bourget, E.-M.; Malouin, F.; Saini, V.; Stryhn, H.; Dufour, S. Invited Review: Incidence, Risk Factors, and Effects of Clinical Mastitis Recurrence in Dairy Cows. J. Dairy. Sci. 2018, 101, 4729–4746. [Google Scholar] [CrossRef] [PubMed]
- Ruegg, P.L. Investigation of Mastitis Problems on Farms. Vet. Clin. N. Am. Food Anim. Pract. 2003, 19, 47–73. [Google Scholar] [CrossRef]
- Zhao, X.; Lacasse, P. Mammary Tissue Damage during Bovine Mastitis: Causes and Control. J. Anim. Sci. 2008, 86, 57–65. [Google Scholar] [CrossRef] [PubMed]
- Kossaibati, M.A.; Esslemont, R.J. The Costs of Production Diseases in Dairy Herds in England. Vet. J. 1997, 154, 41–51. [Google Scholar] [CrossRef] [PubMed]
- Lundberg, S.M.; Lee, S.-I. A Unified Approach to Interpreting Model Predictions. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Curran Associates Inc.: Red Hook, NY, USA, 2017; pp. 4768–4777. [Google Scholar]
- Lakew, B.T.; Fayera, T.; Ali, Y.M. Risk Factors for Bovine Mastitis with the Isolation and Identification of Streptococcus Agalactiae from Farms in and around Haramaya District, Eastern Ethiopia. Trop. Anim. Health Prod. 2019, 51, 1507–1513. [Google Scholar] [CrossRef]
- Smith, K.L.; Hogan, J.S. Environmental Mastitis. Vet. Clin. N. Am. Food Anim. Pract. 1993, 9, 489–498. [Google Scholar] [CrossRef] [PubMed]
- Nash, D.L.; Rogers, G.W.; Cooper, J.B.; Hargrove, G.L.; Keown, J.F.; Hansen, L.B. Heritability of Clinical Mastitis Incidence and Relationships with Sire Transmitting Abilities for Somatic Cell Score, Udder Type Traits, Productive Life, and Protein Yield. J. Dairy Sci. 2000, 83, 2350–2360. [Google Scholar] [CrossRef]
- Kour, S.; Sharma, N.; Balaji, N.; Kumar, P.; Soodan, J.S.; Santos, M.V.d.; Son, Y.-O. Advances in Diagnostic Approaches and Therapeutic Management in Bovine Mastitis. Vet. Sci. 2023, 10, 449. [Google Scholar] [CrossRef] [PubMed]
- Asir, D.; Appavu, S.; Jebamalar, E. Literature Review on Feature Selection Methods for High-Dimensional Data. Int. J. Comput. Appl. 2016, 136, 9–17. [Google Scholar] [CrossRef]
- Simon, R.; Radmacher, M.D.; Dobbin, K.; McShane, L.M. Pitfalls in the Use of DNA Microarray Data for Diagnostic and Prognostic Classification. JNCI J. Natl. Cancer Inst. 2003, 95, 14–18. [Google Scholar] [CrossRef]
- Fallerini, C.; Picchiotti, N.; Baldassarri, M.; Zguro, K.; Daga, S.; Fava, F.; Benetti, E.; Amitrano, S.; Bruttini, M.; Palmieri, M.; et al. Common, Low-Frequency, Rare, and Ultra-Rare Coding Variants Contribute to COVID-19 Severity. Hum. Genet. 2022, 141, 147–173. [Google Scholar] [CrossRef] [PubMed]
- Guyon, I.; Elisseeff, A. An Introduction to Variable and Feature Selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar]
- Hasan, K.M.A.; Siddique, M.S.; Rahman, M.A. Selectivity Estimation of Large Multidimensional Data Warehouses Using Logical Grid Directory. In Proceedings of the 2014 9th International Forum on Strategic Technology (IFOST), Cox’s Bazar, Bangladesh, 21–23 October 2014; pp. 9–13. [Google Scholar]
- Hicks, S.A.; Strümke, I.; Thambawita, V.; Hammou, M.; Riegler, M.A.; Halvorsen, P.; Parasa, S. On Evaluation Metrics for Medical Applications of Artificial Intelligence. Sci. Rep. 2022, 12, 5979. [Google Scholar] [CrossRef] [PubMed]
- Hand, D.J. Measuring Classifier Performance: A Coherent Alternative to the Area under the ROC Curve. Mach. Learn. 2009, 77, 103–123. [Google Scholar] [CrossRef]
- Parikh, R.; Mathai, A.; Parikh, S.; Chandra Sekhar, G.; Thomas, R. Understanding and Using Sensitivity, Specificity and Predictive Values. Indian J. Ophthalmol. 2008, 56, 45. [Google Scholar] [CrossRef] [PubMed]
- Neculai-Valeanu, A.-S.; Ariton, A.-M. Udder Health Monitoring for Prevention of Bovine Mastitis and Improvement of Milk Quality. Bioengineering 2022, 9, 608. [Google Scholar] [CrossRef]
- Kabelitz, T.; Aubry, E.; van Vorst, K.; Amon, T.; Fulde, M. The Role of Streptococcus spp. in Bovine Mastitis. Microorganisms 2021, 9, 1497. [Google Scholar] [CrossRef]
- Carbon, S.; Ireland, A.; Mungall, C.J.; Shu, S.; Marshall, B.; Lewis, S. AmiGO: Online Access to Ontology and Annotation Data. Bioinformatics 2009, 25, 288–289. [Google Scholar] [CrossRef] [PubMed]
- Younis, S.; Javed, Q.; Blumenberg, M. Meta-Analysis of Transcriptional Responses to Mastitis-Causing Escherichia coli. PLoS ONE 2016, 11, e0148562. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Hao, H.; Zhao, P.; Ji, W.; Li, M.; Liu, Y.; Chu, Y. Differential Immunoreactivity to Bovine Convalescent Serum between Mycoplasma Bovis Biofilms and Planktonic Cells Revealed by Comparative Immunoproteomic Analysis. Front. Microbiol. 2018, 9, 379. [Google Scholar] [CrossRef] [PubMed]
- Tong, J.; Ji, X.; Zhang, H.; Xiong, B.; Cui, D.; Jiang, L. The Analysis of the Ubiquitylomic Responses to Streptococcus Agalactiae Infection in Bovine Mammary Gland Epithelial Cells. J. Inflamm. Res. 2022, 15, 4331–4343. [Google Scholar] [CrossRef] [PubMed]
- Enany, S.; Tartor, Y.H.; Kishk, R.M.; Gadallah, A.M.; Ahmed, E.; Magdeldin, S. Proteomics and Metabolomics Analyses of Streptococcus Agalactiae Isolates from Human and Animal Sources. Sci. Rep. 2023, 13, 20980. [Google Scholar] [CrossRef] [PubMed]
- Günther, J.; Petzl, W.; Bauer, I.; Ponsuksili, S.; Zerbe, H.; Schuberth, H.-J.; Brunner, R.M.; Seyfert, H.-M. Differentiating Staphylococcus aureus from Escherichia coli Mastitis: S. Aureus Triggers Unbalanced Immune-Dampening and Host Cell Invasion Immediately after Udder Infection. Sci. Rep. 2017, 7, 4811. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Yang, J.; Huang, Z.; Yin, B.; Umar, T.; Yang, C.; Zhang, X.; Jing, H.; Guo, S.; Guo, M.; et al. Vitexin Mitigates Staphylococcus Aureus-Induced Mastitis via Regulation of ROS/ER Stress/NF-ΚB/MAPK Pathway. Oxid. Med. Cell Longev. 2022, 2022, 7977433. [Google Scholar] [CrossRef]
- Hughes, K.; Watson, C.J. The Mammary Microenvironment in Mastitis in Humans, Dairy Ruminants, Rabbits and Rodents: A One Health Focus. J. Mammary Gland. Biol. Neoplasia 2018, 23, 27–41. [Google Scholar] [CrossRef]
- Logan, M.R.; Odemuyiwa, S.O.; Moqbel, R. Understanding Exocytosis in Immune and Inflammatory Cells: The Molecular Basis of Mediator Secretion. J. Allergy Clin. Immunol. 2003, 111, 923–932, quiz 933. [Google Scholar] [CrossRef]
- Jaeger, A.; Hadlich, F.; Kemper, N.; Lübke-Becker, A.; Muráni, E.; Wimmers, K.; Ponsuksili, S. MicroRNA Expression Profiling of Porcine Mammary Epithelial Cells after Challenge with Escherichia Coli in Vitro. BMC Genom. 2017, 18, 660. [Google Scholar] [CrossRef]
- Wu, J.; Li, L.; Sun, Y.; Huang, S.; Tang, J.; Yu, P.; Wang, G. Altered Molecular Expression of the TLR4/NF-ΚB Signaling Pathway in Mammary Tissue of Chinese Holstein Cattle with Mastitis. PLoS ONE 2015, 10, e0118458. [Google Scholar] [CrossRef] [PubMed]
- Pavlov, V.A.; Chavan, S.S.; Tracey, K.J. Molecular and Functional Neuroscience in Immunity. Annu. Rev. Immunol. 2018, 36, 783–812. [Google Scholar] [CrossRef] [PubMed]
- El Kouni, M.H. Purine Metabolism in Parasites: Potential Targets for Chemotherapy. In Recent Advances in Nucleosides: Chemistry and Chemotherapy; Elsevier: Amsterdam, The Netherlands, 2002; pp. 377–416. [Google Scholar]
- Goncheva, M.I.; Chin, D.; Heinrichs, D.E. Nucleotide Biosynthesis: The Base of Bacterial Pathogenesis. Trends Microbiol. 2022, 30, 793–804. [Google Scholar] [CrossRef]
- Usman, T.; Ali, N.; Wang, Y.; Yu, Y. Association of Aberrant DNA Methylation Level in the CD4 and JAK-STAT-Pathway-Related Genes with Mastitis Indicator Traits in Chinese Holstein Dairy Cattle. Animals 2021, 12, 65. [Google Scholar] [CrossRef]
- Szyda, J.; Frąszczak, M.; Mielczarek, M.; Giannico, R.; Minozzi, G.; Nicolazzi, E.L.; Kamiński, S.; Wojdak-Maksymiec, K. The Assessment of Inter-Individual Variation of Whole-Genome DNA Sequence in 32 Cows. Mamm. Genome 2015, 26, 658–665. [Google Scholar] [CrossRef]
- Sargolzaei, M.; Chesnais, J.P.; Schenkel, F.S. A New Approach for Efficient Genotype Imputation Using Information from Relatives. BMC Genom. 2014, 15, 478. [Google Scholar] [CrossRef] [PubMed]
- Andrews, S. FastQC: A Quality Control Tool for High Throughput Sequence Data 2010. Available online: https://www.bioinformatics.babraham.ac.uk/projects/fastqc/ (accessed on 22 April 2024).
- Bolger, A.M.; Lohse, M.; Usadel, B. Trimmomatic: A Flexible Trimmer for Illumina Sequence Data. Bioinformatics 2014, 30, 2114–2120. [Google Scholar] [CrossRef]
- Li, H.; Durbin, R. Fast and Accurate Short Read Alignment with Burrows–Wheeler Transform. Bioinformatics 2009, 25, 1754–1760. [Google Scholar] [CrossRef]
- Li, H.; Handsaker, B.; Wysoker, A.; Fennell, T.; Ruan, J.; Homer, N.; Marth, G.; Abecasis, G.; Durbin, R. The Sequence Alignment/Map Format and SAMtools. Bioinformatics 2009, 25, 2078–2079. [Google Scholar] [CrossRef]
- Quinlan, A.R.; Hall, I.M. BEDTools: A Flexible Suite of Utilities for Comparing Genomic Features. Bioinformatics 2010, 26, 841–842. [Google Scholar] [CrossRef]
- McKenna, A.; Hanna, M.; Banks, E.; Sivachenko, A.; Cibulskis, K.; Kernytsky, A.; Garimella, K.; Altshuler, D.; Gabriel, S.; Daly, M.; et al. The Genome Analysis Toolkit: A MapReduce Framework for Analyzing next-Generation DNA Sequencing Data. Genome Res. 2010, 20, 1297–1303. [Google Scholar] [CrossRef]
- Danecek, P.; Auton, A.; Abecasis, G.; Albers, C.A.; Banks, E.; DePristo, M.A.; Handsaker, R.E.; Lunter, G.; Marth, G.T.; Sherry, S.T.; et al. The Variant Call Format and VCFtools. Bioinformatics 2011, 27, 2156–2158. [Google Scholar] [CrossRef] [PubMed]
- der Auwera, G.A.; O’Connor, B.D. Genomics in the Cloud: Using Docker, GATK, and WDL in Terra; O’Reilly Media: Sebastopol, CA, USA, 2020. [Google Scholar]
- Tibshirani, R. Regression Shrinkage and Selection Via the Lasso. J. R. Stat. Soc. Ser. B (Methodol.) 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-Learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Defazio, A.; Bach, F.; Lacoste-Julien, S. SAGA: A Fast Incremental Gradient Method With Support for Non-Strongly Convex Composite Objectives. Adv. Neural Inf. Process. Syst. 2014, 27. [Google Scholar]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. Tensorflow: A System for Large-Scale Machine Learning. In Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation (OSDI 16), Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A Next-Generation Hyperparameter Optimization Framework. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019. [Google Scholar] [CrossRef]
- Thiele, C.; Hirschfeld, G. Cutpointr : Improved Estimation and Validation of Optimal Cutpoints in R. J. Stat. Softw. 2021, 98, 1–27. [Google Scholar] [CrossRef]
- Shrikumar, A.; Greenside, P.; Kundaje, A. Learning Important Features through Propagating Activation Differences. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; Volume 70, pp. 3145–3153. [Google Scholar]
- Benjamini, Y.; Hochberg, Y. Controlling The False Discovery Rate—A Practical And Powerful Approach To Multiple Testing. J. R. Statist. Soc. Ser. B 1995, 57, 289–300. [Google Scholar]
- Wu, S.; Flach, P. A Scored AUC Metric for Classifier Evaluation and Selection. In Proceedings of the Second Workshop on ROC Analysis in ML, Bonn, Germany, 11 August 2005. [Google Scholar]
- Hanley, J.A.; McNeil, B.J. The Meaning and Use of the Area under a Receiver Operating Characteristic (ROC) Curve. Radiology 1982, 143, 29–36. [Google Scholar] [CrossRef]
- McLaren, W.; Gil, L.; Hunt, S.E.; Riat, H.S.; Ritchie, G.R.S.; Thormann, A.; Flicek, P.; Cunningham, F. The Ensembl Variant Effect Predictor. Genome Biol. 2016, 17, 122. [Google Scholar] [CrossRef]
- Sherman, B.T.; Hao, M.; Qiu, J.; Jiao, X.; Baseler, M.W.; Lane, H.C.; Imamichi, T.; Chang, W. DAVID: A Web Server for Functional Enrichment Analysis and Functional Annotation of Gene Lists (2021 Update). Nucleic Acids Res. 2022, 50, W216–W221. [Google Scholar] [CrossRef] [PubMed]
- Ashburner, M.; Ball, C.A.; Blake, J.A.; Botstein, D.; Butler, H.; Cherry, J.M.; Davis, A.P.; Dolinski, K.; Dwight, S.S.; Eppig, J.T.; et al. Gene Ontology: Tool for the Unification of Biology. Nat. Genet. 2000, 25, 25–29. [Google Scholar] [CrossRef] [PubMed]
- Kanehisa, M. KEGG: Kyoto Encyclopedia of Genes and Genomes. Nucleic Acids Res. 2000, 28, 27–30. [Google Scholar] [CrossRef] [PubMed]
- Gillespie, M.; Jassal, B.; Stephan, R.; Milacic, M.; Rothfels, K.; Senff-Ribeiro, A.; Griss, J.; Sevilla, C.; Matthews, L.; Gong, C.; et al. The Reactome Pathway Knowledgebase 2022. Nucleic Acids Res. 2022, 50, D687–D692. [Google Scholar] [CrossRef]
- Henderson, C.R. Applications of Linear Models in Animal Breeding; University of Guelph: Guelph, ON, Canada, 1984. [Google Scholar]
- Sayers, E.W.; Bolton, E.E.; Brister, J.R.; Canese, K.; Chan, J.; Comeau, D.C.; Connor, R.; Funk, K.; Kelly, C.; Kim, S.; et al. Database Resources of the National Center for Biotechnology Information. Nucleic Acids Res. 2022, 50, D20–D26. [Google Scholar] [CrossRef]





| N Layers | N Units Inside Each Layer | Dropout Rate within Each Layer | Learning Rate | |
|---|---|---|---|---|
| 0.1 | 1 | [31] | [0.285] | 3.026 × 10−09 |
| 0.2 | 3 | [32; 36; 37] | [0.302; 0.218; 0.311] | 4.263 × 10−10 |
| 0.3 | 3 | [11; 16; 12] | [0.323; 0.242; 0.243] | 7.147 × 10−09 |
| 0.4 | 2 | [7; 46] | [0.210; 0.358] | 2.328 × 10−11 |
| 0.5 | 2 | [48; 45] | [0.312; 0.250] | 6.700 × 10−12 |
| 0.6 | 3 | [47; 37; 28] | [0.398; 0.278, 0.300] | 6.900 × 10−09 |
| 0.7 | 2 | [10; 18] | [0.215; 0.222] | 7.896 × 10−09 |
| 0.8 | 4 | [35; 35; 26; 13] | [0.323; 0.261, 0.257; 0.327] | 4.268 × 10−10 |
| 0.9 | 1 | [50] | [0.250] | 6.829 × 10−09 |
| 1.0 | 3 | [23; 49; 9] | [0.297; 0.362, 0.365] | 1.698 × 10−09 |
| Sampled Hyperparameters | Range |
|---|---|
| Number of layers | [1, 6] |
| Number of units per layer | [4, 50] |
| Dropout rate | [0.2, 0.4] |
| Learning rate | [1.0 × 10−12, 1.0 × 10−8] |
| Fixed hyperparameters | |
| Number of epochs | 300 |
| Label smoothing | 0.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kotlarz, K.; Mielczarek, M.; Biecek, P.; Wojdak-Maksymiec, K.; Suchocki, T.; Topolski, P.; Jagusiak, W.; Szyda, J. An Explainable Deep Learning Classifier of Bovine Mastitis Based on Whole-Genome Sequence Data—Circumventing the p >> n Problem. Int. J. Mol. Sci. 2024, 25, 4715. https://doi.org/10.3390/ijms25094715
Kotlarz K, Mielczarek M, Biecek P, Wojdak-Maksymiec K, Suchocki T, Topolski P, Jagusiak W, Szyda J. An Explainable Deep Learning Classifier of Bovine Mastitis Based on Whole-Genome Sequence Data—Circumventing the p >> n Problem. International Journal of Molecular Sciences. 2024; 25(9):4715. https://doi.org/10.3390/ijms25094715
Chicago/Turabian StyleKotlarz, Krzysztof, Magda Mielczarek, Przemysław Biecek, Katarzyna Wojdak-Maksymiec, Tomasz Suchocki, Piotr Topolski, Wojciech Jagusiak, and Joanna Szyda. 2024. "An Explainable Deep Learning Classifier of Bovine Mastitis Based on Whole-Genome Sequence Data—Circumventing the p >> n Problem" International Journal of Molecular Sciences 25, no. 9: 4715. https://doi.org/10.3390/ijms25094715
APA StyleKotlarz, K., Mielczarek, M., Biecek, P., Wojdak-Maksymiec, K., Suchocki, T., Topolski, P., Jagusiak, W., & Szyda, J. (2024). An Explainable Deep Learning Classifier of Bovine Mastitis Based on Whole-Genome Sequence Data—Circumventing the p >> n Problem. International Journal of Molecular Sciences, 25(9), 4715. https://doi.org/10.3390/ijms25094715






