Modelling Annihilation Properties of Positronium Confined in Nanoporous Materials: A Review
Abstract
1. Introduction
2. General Description of Ps Annihilation in Nanocavities
3. One-Particle Theoretical Models
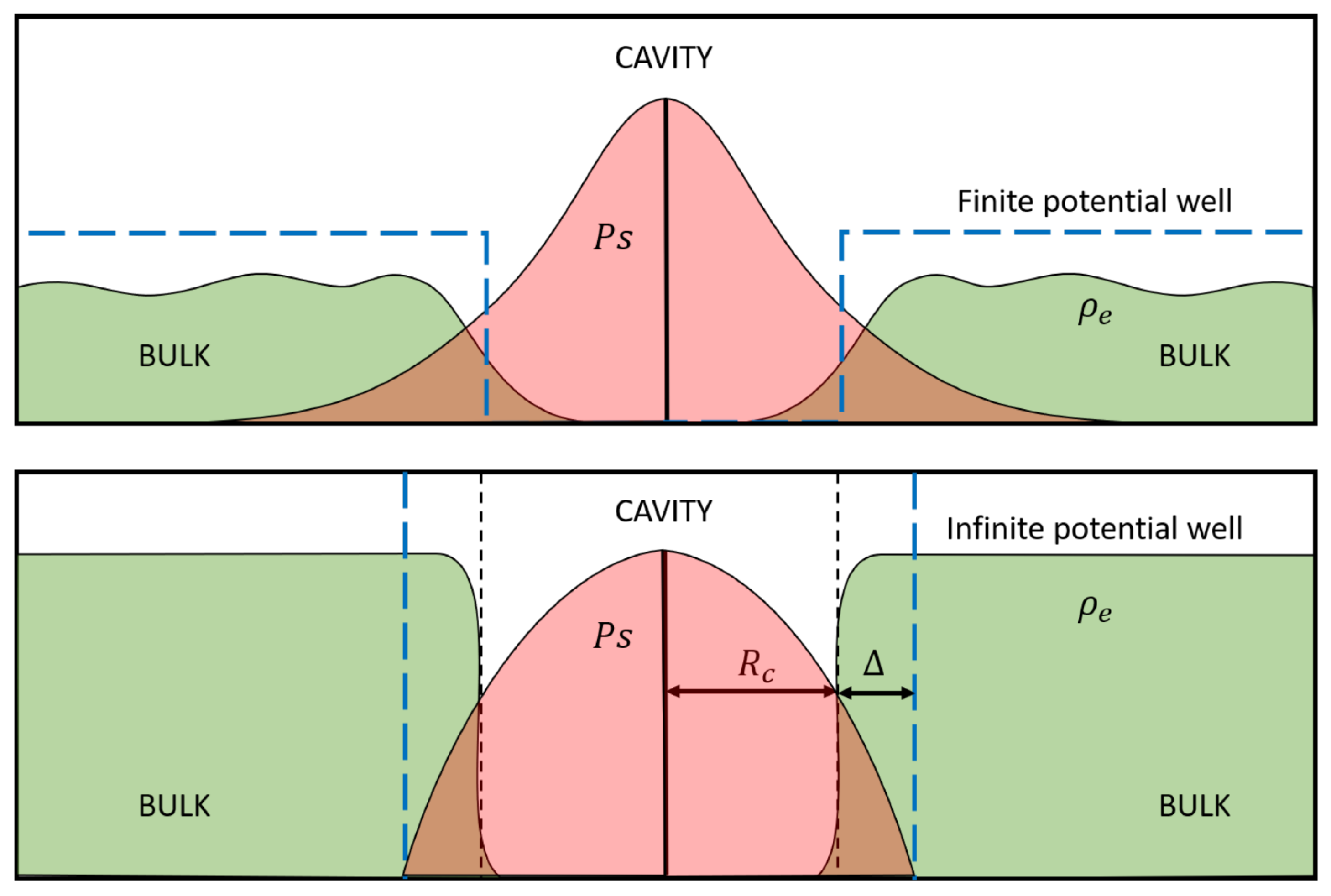
3.1. The Tao–Eldrup (TE) Model
3.2. Some Extensions of the TE Model
3.3. A Classical Modellization
4. Two-Particle Theoretical Models
4.1. The Compressed Ps Model
4.2. The Springs Model
4.3. The Bubble Model
4.4. A Formal Two-Particle Model for Ps Confinement in Nanoporous Materials
5. Electron Exchange Correlation Effects
5.1. Pick-Off and Over-Counting
5.2. Elements of the Theoretical Treatment for the Ps Environment System
5.3. Perturbative Approach to Annihilation Rates
5.4. Calculation of Pick-Off Annihilation Rate
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Charlton, M.; Humberston, J.W. Positron Physics; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Nakanishi, H.; Ujihira, Y. Application of positron annihilation to the characterization of zeolites. J. Phys. Chem 1982, 86, 4446. [Google Scholar] [CrossRef]
- Consolati, G.; Quasso, F. The experimental determination of the Ps contact density in matter. Appl. Phys. A 1991, 52, 295. [Google Scholar] [CrossRef]
- Gidley, D.W.; Frieze, W.E.; Dull, T.L.; Yee, A.F.; Ryan, E.T.; Ho, H.-M. Positronium annihilation in mesoporous thin films. Phys. Rev. B 1999, 60, R5157. [Google Scholar] [CrossRef]
- Consolati, G.; Nichetti, D.; Quasso, F. Probing the Free Volume in Polymers by Means of Positron Annihilation Lifetime Spectroscopy. Polymers 2023, 15, 3128. [Google Scholar] [CrossRef] [PubMed]
- Shpotyuk, O.; Ingram, A.; Shpotyuk, Y. Free-volume characterization of nanostructurized substances by positron annihilation lifetime spectroscopy. Nucl. Instrum. Methods Phys. Res. B 2018, 416, 102. [Google Scholar] [CrossRef]
- Jean, C.; Mallon, P.E.; Schrader, D.M. Principles and Applications of Positron and Positronium Chemistry; World Scientific: Singapore, 2003. [Google Scholar]
- Goldanskii, V.I. Physical chemistry of the positron and positronium. At. Energy Rev. 1968, 6, 3. [Google Scholar]
- Rich, A. Recent experimental advances in positronium research. Rev. Mod. Phys. 1981, 53, 127. [Google Scholar] [CrossRef]
- Dupasquier, A. Positron Solid State Physics, Proceedings of the International School of Physics Enrico Fermi, Course 83, Varenna, Italy; Brandt, W., Dupasquier, A., Eds.; North-Holland: Amsterdam, The Netherlands, 1983. [Google Scholar]
- Marlotti, G.T.; Castelli, F.; Consolati, G. Positronium confinement in small cavities: A two-particle model for the lowering of contact density. Phys. Rev. Lett. 2016, 116, 033401. [Google Scholar] [CrossRef] [PubMed]
- Marlotti, G.T.; Castelli, F.; Consolati, G. Numerical solution of a two-particle model of positronium cofined in small cavities. Acta Phys. Pol. A 2017, 132, 1575. [Google Scholar] [CrossRef]
- Dupasquier, A.; de Natale, P.; Rolando, A. Formal calculation of the pick-off annihilation rate for ortho- and para-positronium. Phys. Rev. B 1991, 43, 10036. [Google Scholar] [CrossRef]
- Goworek, T.; Ciesielski, K.; Jasinska, B.; Wawryszczuk, J. Positronium states in the pores of silica gel. Chem. Phys. 1998, 230, 305. [Google Scholar] [CrossRef]
- Ito, K.; Nakanishi, H.; Ujihira, Y.J. Extension of the equation for the annihilation lifetime of ortho-positronium at a cavity larger than 1 nm in radius. Phys. Chem. B 1999, 103, 4555. [Google Scholar] [CrossRef]
- Jean, Y.C.; van Horn, J.D.; Hung, W.-S.; Lee, K.-R. Perspective of positron annihilation spectroscopy in polymers. Macromolecules 2013, 46, 7133. [Google Scholar] [CrossRef]
- Goworek, T. Comments on the relation: Positronium lifetime–free volume size parameters of the Tao–Eldrup model. Chem. Phys. Lett. 2002, 366, 184. [Google Scholar] [CrossRef]
- Zaleski, R.; Wawryszczuk, J.; Goworek, T. Electron density at positrons site in mcm-41 ordered silica. Chem. Phys. Lett. 2003, 372, 800. [Google Scholar] [CrossRef]
- Ferrel, R.A. Positronium annihilation in solids. Rev. Mod. Phys. 1956, 28, 308. [Google Scholar] [CrossRef]
- Tao, S.J. Positronium annihilation in molecular substances. J. Chem. Phys. 1972, 56, 5499. [Google Scholar] [CrossRef]
- Eldrup, M.; Lightbody, D.; Sherwood, J.N. The temperature dependence of positron lifetimes in solid pivalic acid. Chem. Phys. 1981, 63, 51. [Google Scholar] [CrossRef]
- Zgardzińska, B. Can Tao–Eldrup Model Be Used at Short o-Ps Lifetime? Acta Phys. Pol. A 2014, 125, 700. [Google Scholar] [CrossRef]
- Dutta, D.; Ganguly, B.N.; Gangopadhyay, D.; Mukherjee, T.; Dutta-Roy, B. General trends of positronium pick-off annihilation in molecular substances. J. Phys. Condens. Matter 2002, 14, 7539. [Google Scholar] [CrossRef]
- Wada, K.; Hiodo, T. A simple shape-free model for pore-size estimation with positron annihilation lifetime spectroscopy. J. Phys. Conf. Ser. 2013, 443, 012003. [Google Scholar] [CrossRef]
- Stepanov, S.V.; Zvezhinskiy, D.S.; Byakov, V.M. Beyond the Point Ps Approximation. Mater. Sci. Forum 2013, 733, 7. [Google Scholar] [CrossRef]
- Bug, A.L.R.; Muluneh, M.; Waldman, J.; Sterne, P.A. Computer simulation of pick-off and selfannihilation. Mater. Sci. Forum 2004, 445, 375. [Google Scholar] [CrossRef]
- Zubiaga, A.; Ervasti, M.M.; Makkonen, I.; Harju, A.; Tuomisto, F.; Puska, M.J. Modelling positronium beyond the single particle approximation. J. Phys. B At. Mol. Opt. Phys. 2016, 49, 064005. [Google Scholar] [CrossRef]
- Consolati, G.; Quasso, F.; Trezzi, D. Swelling of Positronium Confined in a Small Cavity. PLoS ONE 2014, 9, e109937. [Google Scholar] [CrossRef] [PubMed]
- McMullen, T.; Stott, M.J. Dependence of the positronium hyperfine interaction on the environment: A simple model. Can. J. Phys. 1983, 61, 504. [Google Scholar] [CrossRef]
- Stepanov, S.V.; Byakov, V.M.; Zvezhinskiy, D.S.; Duplâtre, G.; Nurmukhametov, R.R.; Stepanov, P.S. Positronium in a liquid phase: Formation, bubble state and chemical reactions. Adv. Phys. Chem. 2012, 2012, 431962. [Google Scholar] [CrossRef]
- Puska, J.; Nieminen, R.M. Theory of positrons in solids and on solid surfaces. Rev. Mod. Phys. 1994, 66, 841. [Google Scholar] [CrossRef]
- Bouarissa, N.; Aourag, H. Positron energy levels in narrow gap semiconductors. Mater. Sci. Eng. 1995, B34, 58. [Google Scholar] [CrossRef]
- Rubaszek, A. Positron Spectroscopy of Solids, Proceedings of the International School of Physics Enrico Fermi, Course 125, Varenna, Italy; Dupasquier, A., Mills, A.P., Eds.; IOS Press: Amsterdam, The Netherlands, 1995. [Google Scholar]
- Nagashima, Y.; Morinaka, Y.; Kurihara, T.; Nagai, Y.; Hyodo, T.; Shidara, T.; Nakahara, K. Origins of positronium emitted from SiO2. Phys. Rev. B 1998, 58, 12676. [Google Scholar]
- Fulop, T.; Farkas, Z.; Seeger, A.; Major, J. On the inner structure of confined positronium. arXiv 2003, arXiv:condmat/0304442v1. [Google Scholar]
- Brawley, S.J.; Armitage, S.; Beale, J.; Leslie, D.E.; Williams, A.J.; Laricchia, G. Electron-Like Scattering of Positronium. Science 2010, 330, 789. [Google Scholar] [CrossRef]
- Shipman, M.; Brawley, S.J.; Sarkadi, L.; Laricchia, G. Resonant scattering of Positronium as a quasifree electron. Phys. Rev. A 2017, 95, 032704. [Google Scholar] [CrossRef]
- Marlotti, G.T.; Consolati, G.; Castelli, F. Formal calculation of exchange correlation effects on annihilation lifetimes of positronium confined in small cavities. J. Phys. Condens. Matter 2020, 32, 025602. [Google Scholar] [CrossRef] [PubMed]
- Castelli, F.; Consolati, G.; Tanzi Marlotti, G. Positronium Confined in Nanocavities: The Role of Electron Exchange Correlations. Nanomaterials 2021, 11, 2350. [Google Scholar] [CrossRef] [PubMed]
- Szalewicz, K.; Patkowski, K.; Jeziorski, B. Intermolecular interactions via perturbation theory: From diatoms to biomolecules. In Intermolecular Forces and Clusters II; Springer: Berlin/Heidelberg, Germany, 2005; pp. 43–117. [Google Scholar]
- Mogensen, O.E.; Eldrup, M. Positronium bloch function, and trapping of positronium in vacancies. In Ice, Technical Report; Risø National Laboratory: Roskilde, Denmark, 1977. [Google Scholar]
- Mogensen, O.E. Spur reaction model of positronium formation. J. Chem. Phys. 1974, 60, 998. [Google Scholar] [CrossRef]
- Klein, D.J. Exchange Perturbation Theories. Int. J. Quantum Chem. 1987, 32, 377. [Google Scholar] [CrossRef]
- Klein, D.J.; Oliva, J.M. Composite–system models. Int. J. Quantum Chem. 2010, 110, 2784. [Google Scholar] [CrossRef]
- Igarashi, A.; Kimura, M.; Shimamura, I.; Toshima, N. Inseparable positron annihilation and positronium formation in positron-atom collisions: Description in terms of an absorption potential. Phys. Rev. A 2003, 68, 042716. [Google Scholar] [CrossRef]
- Maruhn, J.A.; Reinhard, P.-G.; Suraud, E. Simple Models of Many-Fermion Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Mitroy, J.A.; Bubin, S.; Horiuchi, W.; Suzuki, Y.; Adamowicz, L.; Cencek, W.; Szalewicz, K.; Komasa, J.; Blume, D.; Varga, K. Theory and application of explicitly correlated Gaussians. Rev. Mod. Phys. 2013, 85, 693. [Google Scholar] [CrossRef]
- Kuriplach, J.; Barbiellini, B. Improved generalized gradient approximation for positron states in solids. Phys. Rev. B 2014, 89, 155111. [Google Scholar] [CrossRef]
- Frolov, A.M. Positron annihilation in the positronium negative ion Ps−. Phys. Lett. A 2005, 342, 430. [Google Scholar] [CrossRef]
- Drachman, R.J. The interaction of positrons and positronium with small atoms. Can. J. Phys. 1982, 60, 494. [Google Scholar] [CrossRef]
- Zanatta, M.; Brusa, R.S.; Egger, W.; Fontana, A.; Gilioli, E.; Mariazzi, S.; Monaco, G.; Ravelli, L.; Sacchetti, F. Structural Evolution and Medium Range Order in Permanently Densified Vitreous SiO2. Phys. Rev. Lett. 2014, 112, 045501. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Castelli, F.; Consolati, G. Modelling Annihilation Properties of Positronium Confined in Nanoporous Materials: A Review. Int. J. Mol. Sci. 2024, 25, 3692. https://doi.org/10.3390/ijms25073692
Castelli F, Consolati G. Modelling Annihilation Properties of Positronium Confined in Nanoporous Materials: A Review. International Journal of Molecular Sciences. 2024; 25(7):3692. https://doi.org/10.3390/ijms25073692
Chicago/Turabian StyleCastelli, Fabrizio, and Giovanni Consolati. 2024. "Modelling Annihilation Properties of Positronium Confined in Nanoporous Materials: A Review" International Journal of Molecular Sciences 25, no. 7: 3692. https://doi.org/10.3390/ijms25073692
APA StyleCastelli, F., & Consolati, G. (2024). Modelling Annihilation Properties of Positronium Confined in Nanoporous Materials: A Review. International Journal of Molecular Sciences, 25(7), 3692. https://doi.org/10.3390/ijms25073692






