Influence of Ethanol Parametrization on Diffusion Coefficients Using OPLS-AA Force Field
Abstract
1. Introduction
2. Results and Discussion
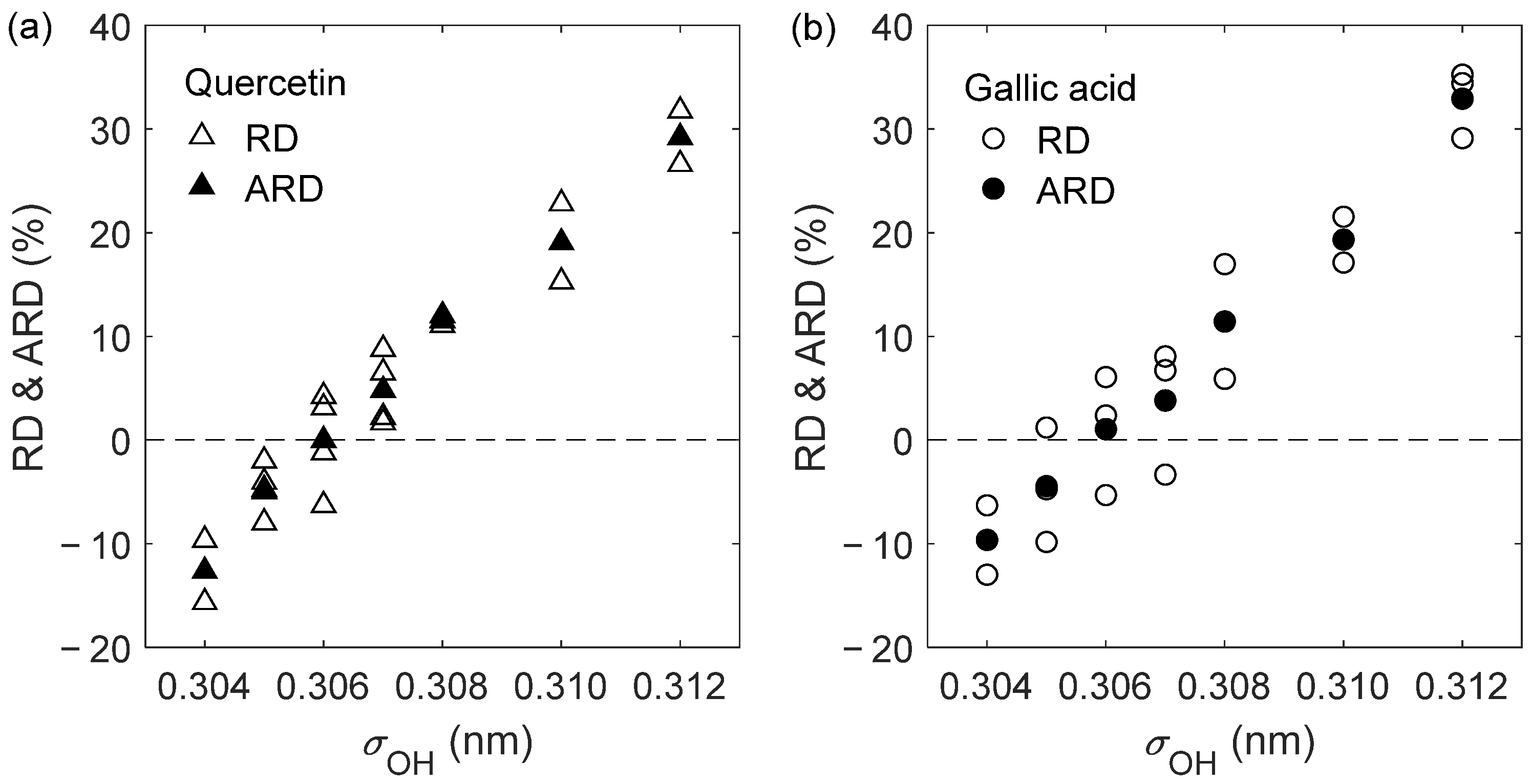
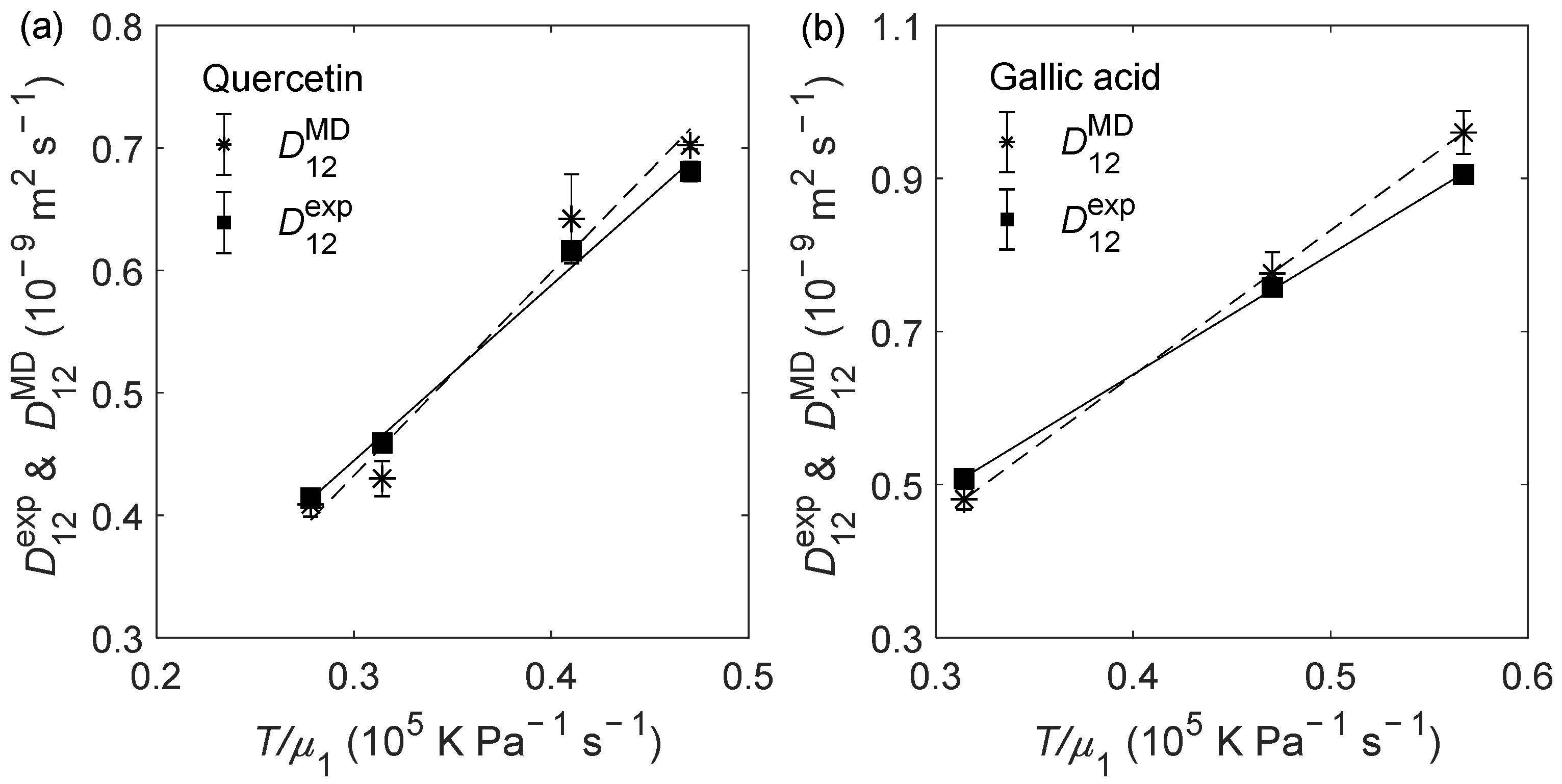
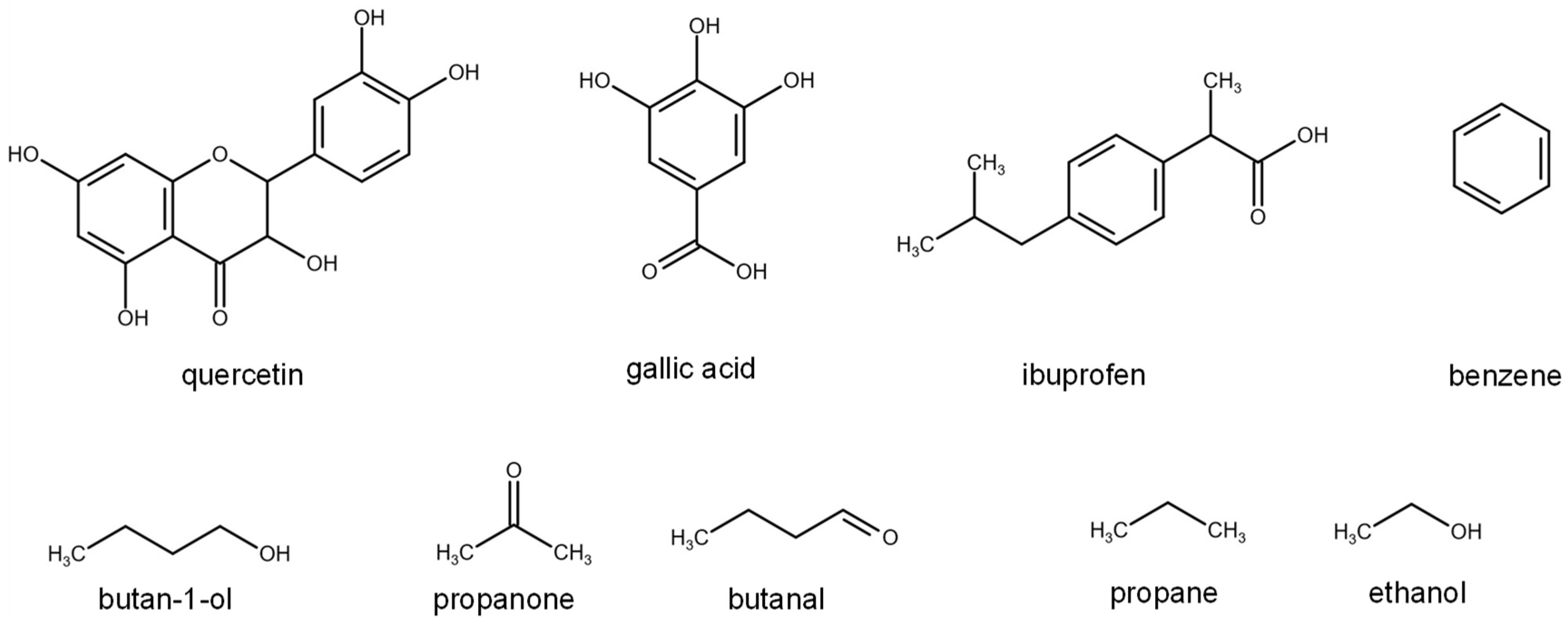
2.1. D12 of Quercetin and Gallic Acid in Liquid Ethanol: Optimization of the Oxygen’s Radius
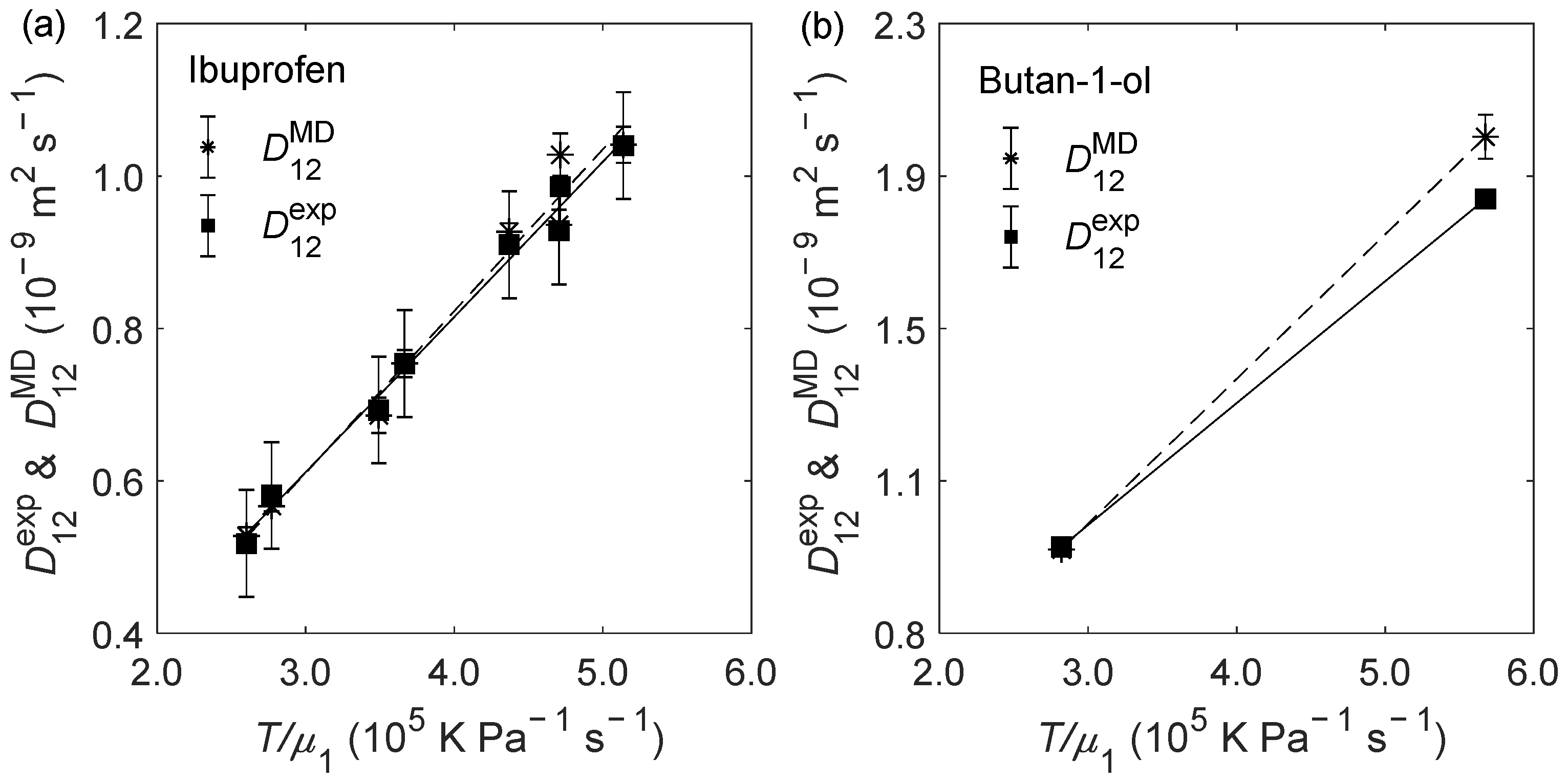
2.2. D12 of Organic Solutes in Liquid Ethanol: Oxygen’s Radius Validation and Cases of Applicability
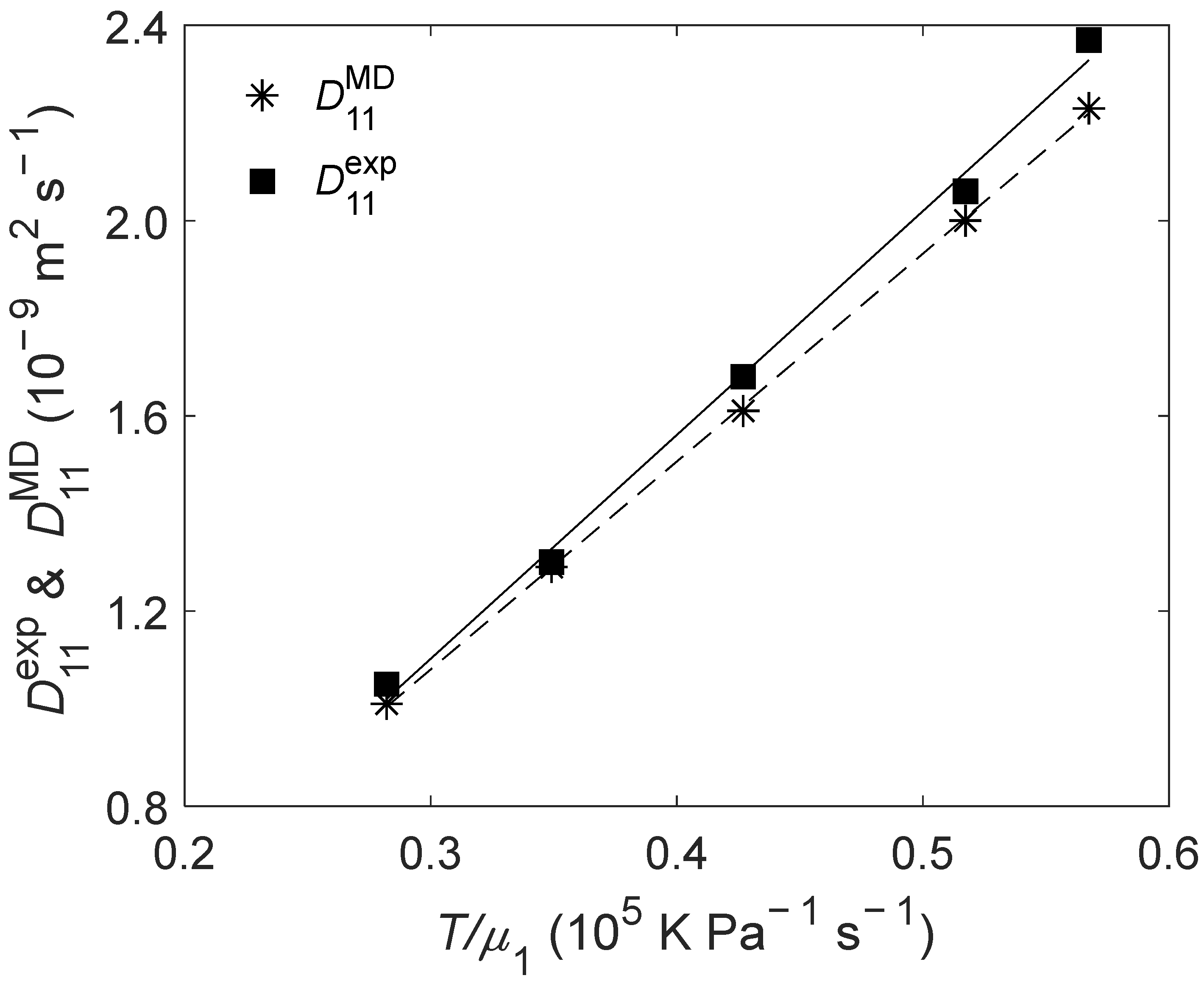
2.3. of Liquid Ethanol
2.4. Influence of the Oxygen’s Energy Parameter
2.5. Equilibrium Properties of Ethanol
3. Materials and Methods
3.1. Database
3.2. Molecular Dynamics Simulation Procedure
3.3. Self-Diffusion and Binary Diffusion Coefficients
3.4. Calculation of Equilibrium Properties
3.4.1. Enthalpy of Vaporization
3.4.2. Density
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Taylor, R.; Krishna, R. Multicomponent Mass Transfer. In Wiley Series in Chemical Engineering; John Wiley & Sons, Inc.: New York, NY, USA, 1993. [Google Scholar]
- Oliveira, E.L.G.; Silvestre, A.J.D.; Silva, C.M. Review of kinetic models for supercritical fluid extraction. Chem. Eng. Res. Des. 2011, 89, 1104–1117. [Google Scholar] [CrossRef]
- Zêzere, B.; Portugal, I.; Gomes, J.R.B.; Silva, C.M. Modeling Tracer Diffusion Coefficients of Any Type of Solutes in Polar and Non-Polar Dense Solvents. Materials 2022, 15, 6416. [Google Scholar] [CrossRef] [PubMed]
- Kong, C.Y.; Sugiura, K.; Natsume, S.; Sakabe, J.; Funazukuri, T.; Miyake, K.; Okajima, I.; Badhulika, S.; Sako, T. Measurements and correlation of diffusion coefficients of ibuprofen in both liquid and supercritical fluids. J. Supercrit. Fluids 2020, 159, 104776. [Google Scholar] [CrossRef]
- Leite, J.; Magalhães, A.L.; Valente, A.A.; Silva, C.M. Measurement and modelling of tracer diffusivities of gallic acid in liquid ethanol and in supercritical CO2 modified with ethanol. J. Supercrit. Fluids 2018, 131, 130–139. [Google Scholar] [CrossRef]
- Cai, G.; Katsumata, W.; Okajima, I.; Sako, T.; Funazukuri, T.; Kong, C.Y. Determination of diffusivities of triolein in pressurized liquids and in supercritical CO2. J. Mol. Liq. 2022, 354, 118860. [Google Scholar] [CrossRef]
- Taylor, G. Dispersion of soluble matter in solvent flowing slowly through a tube. Proc. R. Soc. A Math. Phys. Eng. Sci. 1953, 219, 186–203. [Google Scholar] [CrossRef]
- Taylor, G. Diffusion and mass transport in tubes. Proc. Phys. Soc. Sect. B 1954, 67, 857–869. [Google Scholar] [CrossRef]
- Taylor, G. The dispersion of matter in turbulent flow through a pipe. Proc. R. Soc. A Math. Phys. Eng. Sci. 1954, 223, 446–468. [Google Scholar] [CrossRef]
- Aris, R. On the dispersion of a solute by diffusion, convection and exchange between phases. Proc. R. Soc. A Math. Phys. Eng. Sci. 1959, 252, 538–550. [Google Scholar] [CrossRef]
- Wilke, C.R.; Chang, P. Correlation of diffusion coefficients in dilute solutions. AIChE J. 1955, 1, 264–270. [Google Scholar] [CrossRef]
- Poling, B.E.; Prausnitz, J.M.; O’Connell, J.P. The Properties of Gases and Liquids, 5th ed.; Company, M.-H.B., Ed.; The McGraw-Hill Companies, Inc.: New York, NY, USA, 2001; ISBN 0071499997. [Google Scholar]
- Aniceto, J.P.S.; Zêzere, B.; Silva, C.M. Predictive Models for the Binary Diffusion Coefficient at Infinite Dilution in Polar and Nonpolar Fluids. Materials 2021, 14, 542. [Google Scholar] [CrossRef] [PubMed]
- Silva, C.M.; Liu, H. Modelling of Transport Properties of Hard Sphere Fluids and Related Systems, and its Applications. In Theory and Simulation of Hard-Sphere Fluids and Related Systems; Mulero, A., Ed.; Springer: Berlin/Heidelberg, Germany, 2008; Volume 753, pp. 383–492. ISBN 978-3-540-78766-2. [Google Scholar]
- Dymond, J.H. Corrected Enskog theory and the transport coefficients of liquids. J. Chem. Phys. 1974, 60, 969–973. [Google Scholar] [CrossRef]
- Dymond, J.H.; Bich, E.; Vogel, E.; Wakeham, W.A.; Vesovic, V.; Assael, M.J. Dense fluids. In Transport Properties of Fluids—Their Correlation, Prediction and Estimation; Millat, J., Dymond, J.H., Nieto de Castro, C.A., Eds.; Cambridge University Press: Cambridge, UK, 1996; pp. 66–112. [Google Scholar]
- Aniceto, J.P.S.; Zêzere, B.; Silva, C.M. Machine learning models for the prediction of diffusivities in supercritical CO2 systems. J. Mol. Liq. 2021, 326, 115281. [Google Scholar] [CrossRef]
- Allers, J.P.; Priest, C.W.; Greathouse, J.A.; Alam, T.M. Using Computationally-Determined Properties for Machine Learning Prediction of Self-Diffusion Coefficients in Pure Liquids. J. Phys. Chem. B 2021, 125, 12990–13002. [Google Scholar] [CrossRef] [PubMed]
- Allers, J.P.; Keth, J.; Alam, T.M. Prediction of Self-Diffusion in Binary Fluid Mixtures Using Artificial Neural Networks. J. Phys. Chem. B 2022, 126, 4555–4564. [Google Scholar] [CrossRef] [PubMed]
- Zêzere, B.; Portugal, I.; Silva, C.M.; Gomes, J.R.B. Diffusivities of ketones and aldehydes in liquid ethanol by molecular dynamics simulations. J. Mol. Liq. 2023, 371, 121068. [Google Scholar] [CrossRef]
- Vaz, R.V.; Gomes, J.R.B.; Silva, C.M. Molecular dynamics simulation of diffusion coefficients and structural properties of ketones in supercritical CO2 at infinite dilution. J. Supercrit. Fluids 2016, 107, 630–638. [Google Scholar] [CrossRef]
- Baba, H.; Urano, R.; Nagai, T.; Okazaki, S. Prediction of self-diffusion coefficients of chemically diverse pure liquids by all-atom molecular dynamics simulations. J. Comput. Chem. 2022, 43, 1892–1900. [Google Scholar] [CrossRef]
- Barrera, M.C.; Jorge, M. A Polarization-Consistent Model for Alcohols to Predict Solvation Free Energies. J. Chem. Inf. Model. 2020, 60, 1352–1367. [Google Scholar] [CrossRef]
- Bordonhos, M.; Galvão, T.L.P.; Gomes, J.R.B.; Gouveia, J.D.; Jorge, M.; Lourenço, M.A.O.; Pereira, J.M.; Pérez-Sánchez, G.; Pinto, M.L.; Silva, C.M.; et al. Multiscale Computational Approaches toward the Understanding of Materials. Adv. Theory Simul. 2022, 2200628. [Google Scholar] [CrossRef]
- Marrink, S.J.; de Vries, A.H.; Mark, A.E. Coarse Grained Model for Semiquantitative Lipid Simulations. J. Phys. Chem. B 2004, 108, 750–760. [Google Scholar] [CrossRef]
- Eggimann, B.L.; Sun, Y.; DeJaco, R.F.; Singh, R.; Ahsan, M.; Josephson, T.R.; Siepmann, J.I. Assessing the Quality of Molecular Simulations for Vapor–Liquid Equilibria: An Analysis of the TraPPE Database. J. Chem. Eng. Data 2020, 65, 1330–1344. [Google Scholar] [CrossRef]
- Wang, J.; Wang, W.; Kollman, P.A.; Case, D.A. Automatic atom type and bond type perception in molecular mechanical calculations. J. Mol. Graph. Model. 2006, 25, 247–260. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W.L.; Maxwell, D.S.; Tirado-Rives, J. Development and Testing of the OPLS All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids. J. Am. Chem. Soc. 1996, 118, 11225–11236. [Google Scholar] [CrossRef]
- Siu, S.W.I.; Pluhackova, K.; Böckmann, R.A. Optimization of the OPLS-AA Force Field for Long Hydrocarbons. J. Chem. Theory Comput. 2012, 8, 1459–1470. [Google Scholar] [CrossRef]
- Pluhackova, K.; Morhenn, H.; Lautner, L.; Lohstroh, W.; Nemkovski, K.S.; Unruh, T.; Böckmann, R.A. Extension of the LOPLS-AA Force Field for Alcohols, Esters, and Monoolein Bilayers and its Validation by Neutron Scattering Experiments. J. Phys. Chem. B 2015, 119, 15287–15299. [Google Scholar] [CrossRef]
- Robertson, M.J.; Tirado-Rives, J.; Jorgensen, W.L. Improved Peptide and Protein Torsional Energetics with the OPLS-AA Force Field. J. Chem. Theory Comput. 2015, 11, 3499–3509. [Google Scholar] [CrossRef]
- Lu, C.; Wu, C.; Ghoreishi, D.; Chen, W.; Wang, L.; Damm, W.; Ross, G.A.; Dahlgren, M.K.; Russell, E.; Von Bargen, C.D.; et al. OPLS4: Improving Force Field Accuracy on Challenging Regimes of Chemical Space. J. Chem. Theory Comput. 2021, 17, 4291–4300. [Google Scholar] [CrossRef]
- Zangi, R. Refinement of the OPLSAA Force-Field for Liquid Alcohols. ACS Omega 2018, 3, 18089–18099. [Google Scholar] [CrossRef]
- Kulschewski, T.; Pleiss, J. A molecular dynamics study of liquid aliphatic alcohols: Simulation of density and self-diffusion coefficient using a modified OPLS force field. Mol. Simul. 2013, 39, 754–767. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Y.; Yao, J.; Li, H.; Mochizuki, K. A tiny charge-scaling in the OPLS-AA + L-OPLS force field delivers the realistic dynamics and structure of liquid primary alcohols. J. Comput. Chem. 2022, 43, 421–430. [Google Scholar] [CrossRef] [PubMed]
- Petravic, J.; Delhommelle, J. Influence of temperature, pressure and internal degrees of freedom on hydrogen bonding and diffusion in liquid ethanol. Chem. Phys. 2003, 286, 303–314. [Google Scholar] [CrossRef]
- Cardona, J.; Fartaria, R.; Sweatman, M.B.; Lue, L. Molecular dynamics simulations for the prediction of the dielectric spectra of alcohols, glycols and monoethanolamine. Mol. Simul. 2016, 42, 370–390. [Google Scholar] [CrossRef]
- Schnabel, T.; Vrabec, J.; Hasse, H. Henry’s law constants of methane, nitrogen, oxygen and carbon dioxide in ethanol from 273 to 498 K: Prediction from molecular simulation. Fluid Phase Equilib. 2005, 233, 134–143. [Google Scholar] [CrossRef]
- Guevara-Carrion, G.; Nieto-Draghi, C.; Vrabec, J.; Hasse, H. Prediction of Transport Properties by Molecular Simulation: Methanol and Ethanol and Their Mixture. J. Phys. Chem. B 2008, 112, 16664–16674. [Google Scholar] [CrossRef]
- Hirschfelder, J.O.; Curtiss, C.F.; Bird, R.B. The Molecular Theory of Gases and Liquids; John Wiley & Sons Inc: New York, NY, USA, 1964; ISBN 9780471400653. [Google Scholar]
- Liu, H.; Silva, C.M.; Macedo, E.A. Unified approach to the self-diffusion coefficients of dense fluids over wide ranges of temperature and pressure—Hard-sphere, square-well, Lennard-Jones and real substances. Chem. Eng. Sci. 1998, 53, 2403–2422. [Google Scholar] [CrossRef]
- Silva, C.M.; Liu, H.; Macedo, E.A. Models for self-diffusion coefficients of dense fluids, including hydrogen-bonding substances. Chem. Eng. Sci. 1998, 53, 2423–2429. [Google Scholar] [CrossRef]
- Liu, H.; Silva, C.M.; Macedo, E.A. Generalised free-volume theory for transport properties and new trends about the relationship between free volume and equations of state. Fluid Phase Equilib. 2002, 202, 89–107. [Google Scholar] [CrossRef]
- Cano-Gómez, J.J.; Iglesias-Silva, G.A.; Ramos-Estrada, M. Correlations for the prediction of the density and viscosity of 1-alcohols at high pressures. Fluid Phase Equilib. 2015, 404, 109–117. [Google Scholar] [CrossRef]
- National Institute of Standards and Technology NIST Chemistry WebBook—Ethanol. Available online: https://webbook.nist.gov/cgi/cbook.cgi?ID=C64175&Mask=4 (accessed on 11 December 2022).
- Zêzere, B.; Iglésias, J.; Portugal, I.; Gomes, J.R.B.; Silva, C.M. Diffusion of quercetin in compressed liquid ethyl acetate and ethanol. J. Mol. Liq. 2020, 324, 114714. [Google Scholar] [CrossRef]
- Tominaga, T.; Matsumoto, S. Diffusion of polar and nonpolar molecules in water and ethanol. Bull. Chem. Soc. Jpn. 1990, 63, 533–537. [Google Scholar] [CrossRef]
- Zêzere, B.; Buchgeister, S.; Faria, S.; Portugal, I.; Gomes, J.R.B.; Silva, C.M. Diffusivities of linear unsaturated ketones and aldehydes in compressed liquid ethanol. J. Mol. Liq. 2022, 367, 120480. [Google Scholar] [CrossRef]
- Sun, C.K.J.; Chen, S.H. Tracer diffusion in dense ethanol: A generalized correlation for nonpolar and hydrogen-bonded solvents. AIChE J. 1986, 32, 1367–1371. [Google Scholar] [CrossRef]
- Cooper, E. Diffusion Coefficients at Infinite Dilution in Alcohol Solvents at Temperatures to 348 K and Pressures to 17 MPa; University of Ottawa: Ottawa, ON, Canada, 1992. [Google Scholar]
- Meckl, S.; Zeidler, M.D. Self-diffusion measurements of ethanol and propanol. Mol. Phys. 1988, 63, 85–95. [Google Scholar] [CrossRef]
- Hardt, A.P.; Anderson, D.K.; Rathbun, R.; Mar, B.W.; Babb, A.L. Self-Diffusion in Liquids. II. Comparison between Mutual and Self-Diffusion Coefficients. J. Phys. Chem. 1959, 63, 2059–2061. [Google Scholar] [CrossRef]
- Rathbun, R.E.; Babb, A.L. Self-diffusion in liquids. III. Tempretaure dependence in pure liquids. J. Phys. Chem. 1961, 65, 1072–1074. [Google Scholar] [CrossRef]
- Hurle, R.L.; Easteal, A.J.; Woolf, L.A. Self-diffusion in monohydric alcohols under pressure. Methanol, methan(2H)ol and ethanol. J. Chem. Soc. Faraday Trans. 1 Phys. Chem. Condens. Phases 1985, 81, 769. [Google Scholar] [CrossRef]
- Johnson, P.A.; Babb, A.L. Self-diffusion in.Liquids. 1. Concentration Dependence in Ideal and Non-ideal Binary Solutions. J. Phys. Chem. 1956, 60, 14–19. [Google Scholar] [CrossRef]
- Partington, J.R.; Hudson, R.F.; Bagnall, K.W. Self-diffusion of Aliphatic Alcohols. Nature 1952, 169, 583–584. [Google Scholar] [CrossRef]
- Graupner, K.; Winter, E.R.S. 201. Some measurements of the self-diffusion coefficients of liquids. J. Chem. Soc. 1952, 1145–1150. [Google Scholar] [CrossRef]
- Holz, M.; Weingartner, H. Calibration in accurate spin-echo self-diffusion measurements using 1H and less-common nuclei. J. Magn. Reson. 1991, 92, 115–125. [Google Scholar] [CrossRef]
- Zéberg-Mikkelsen, C.K.; Lugo, L.; Fernández, J. Density measurements under pressure for the binary system (ethanol+methylcyclohexane). J. Chem. Thermodyn. 2005, 37, 1294–1304. [Google Scholar] [CrossRef]
- Mokhtarani, B.; Sharifi, A.; Mortaheb, H.R.; Mirzaei, M.; Mafi, M.; Sadeghian, F. Density and viscosity of 1-butyl-3-methylimidazolium nitrate with ethanol, 1-propanol, or 1-butanol at several temperatures. J. Chem. Thermodyn. 2009, 41, 1432–1438. [Google Scholar] [CrossRef]
- Zhu, T.; Gong, H.; Dong, M. Density and viscosity of CO2 + ethanol binary systems measured by a capillary viscometer from 308.15 to 338.15 K and 15 to 45 MPa. J. Chem. Eng. Data 2020, 65, 3820–3833. [Google Scholar] [CrossRef]
- Watson, G.; Zéberg-Mikkelsen, C.K.; Baylaucq, A.; Boned, C. High-Pressure Density Measurements for the Binary System Ethanol + Heptane. J. Chem. Eng. Data 2006, 51, 112–118. [Google Scholar] [CrossRef]
- Lindahl, E.; Abraham, M.J.; Hess, B.; van der Spoel, D. GROMACS 2019.3 Manual; 2019. [CrossRef]
- Lindahl, E.; Abraham, M.J.; Hess, B.; Van Der Spoel, D. GROMACS 2019.3 Source Code 2019. [CrossRef]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1–2, 19–25. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Postma, J.P.M.; van Gunsteren, W.F.; DiNola, A.; Haak, J.R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar] [CrossRef]
- Hockney, R.W.; Goel, S.P.; Eastwood, J.W. Quiet high-resolution computer models of a plasma. J. Comput. Phys. 1974, 14, 148–158. [Google Scholar] [CrossRef]
- Bussi, G.; Donadio, D.; Parrinello, M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007, 126, 014101. [Google Scholar] [CrossRef]
- Parrinello, M.; Rahman, A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar] [CrossRef]
- Essmann, U.; Perera, L.; Berkowitz, M.L.; Darden, T.; Lee, H.; Pedersen, L.G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577–8593. [Google Scholar] [CrossRef]
- DDBST GmbH Compressibility (Isothermal) of Ethanol. Available online: http://www.ddbst.com/en/EED/PCP/CMPT_C11.php (accessed on 18 March 2022).
- Hoheisel, C. Computer Calculation. In Transport Properties of Fluids. Their Correlation, Prediction and Estimation; Millat, J., Dymond, J.H., Nieto de Castro, C.A., Eds.; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Yeh, I.-C.; Hummer, G. System-Size Dependence of Diffusion Coefficients and Viscosities from Molecular Dynamics Simulations with Periodic Boundary Conditions. J. Phys. Chem. B 2004, 108, 15873–15879. [Google Scholar] [CrossRef]
- Caleman, C.; van Maaren, P.J.; Hong, M.; Hub, J.S.; Costa, L.T.; van der Spoel, D. Force Field Benchmark of Organic Liquids: Density, Enthalpy of Vaporization, Heat Capacities, Surface Tension, Isothermal Compressibility, Volumetric Expansion Coefficient, and Dielectric Constant. J. Chem. Theory Comput. 2012, 8, 61–74. [Google Scholar] [CrossRef] [PubMed]
| Solute | (K) | (bar) | (10−9 m2 s−1) | (10−9 m2 s−1) | RD (%) |
|---|---|---|---|---|---|
| Quercetin | 303.15 | 1 | 0.459 ± 0.003 | 0.430 ± 0.014 | −6.30 |
| 303.15 | 150 | 0.414 ± 0.002 | 0.409 ± 0.010 | −1.21 | |
| 323.15 | 1 | 0.681 ± 0.002 | 0.702 ± 0.003 | 3.13 | |
| 323.15 | 150 | 0.616 ± 0.003 | 0.642 ± 0.036 | 4.22 | |
| ARD = −0.04% | |||||
| AARD = 3.71% | |||||
| Gallic acid | 303.15 | 1 | 0.508 ± 0.009 | 0.481 ± 0.014 | −5.31 |
| 323.15 | 1 | 0.758 ± 0.006 | 0.776 ± 0.028 | 2.37 | |
| 333.15 | 1 | 0.905 ± 0.011 | 0.960 ± 0.028 | 6.08 | |
| ARD = 1.05% | |||||
| AARD = 4.59% | |||||
| Solute | (K) | (bar) | (10−9 m2 s−1) | (10−9 m2 s−1) | RD (%) |
|---|---|---|---|---|---|
| ibuprofen | 298.15 | 100 | 0.518 ± 0.070 | 0.528 ± 0.011 | 1.93 |
| 308.15 | 1 | 0.693 ± 0.070 | 0.686 ± 0.023 | −1.01 | |
| 308.15 | 300 | 0.581 ± 0.070 | 0.567 ± 0.007 | −2.41 | |
| 323.15 | 1 | 0.928 ± 0.070 | 0.936 ± 0.020 | 0.86 | |
| 323.15 | 300 | 0.754 ± 0.070 | 0.754 ± 0.018 | 0.00 | |
| 333.15 | 100 | 1.04 ± 0.07 | 1.04 ± 0.02 | 0.10 | |
| 333.15 | 200 | 0.986 ± 0.070 | 1.03 ± 0.03 | 4.26 | |
| 333.15 | 300 | 0.910 ± 0.070 | 0.927 ± 0.011 | 1.87 | |
| ARD = 0.70% | |||||
| AARD = 1.55% | |||||
| butan-1-ol | 298.15 | 1 | 0.927 | 0.920 ± 0.011 | −0.76 |
| 333.15 | 1 | 1.84 | 2.00 ± 0.06 | 8.86 | |
| ARD = 4.05% | |||||
| AARD = 4.81% | |||||
(K) | (bar) | (10−9 m2 s−1) | (10−9 m2 s−1) | RD (%) |
|---|---|---|---|---|
| 298.15 | 1 | 1.05 | 1.01 | −3.81 |
| 308.15 | 1 | 1.30 | 1.29 | −0.77 |
| 318.15 | 1 | 1.68 | 1.61 | −4.17 |
| 328.15 | 1 | 2.06 | 2.00 | −2.91 |
| 333.15 | 1 | 2.37 | 2.23 | −5.91 |
| ARD = −3.51% | ||||
| AARD = 3.51% | ||||
(K) | (bar) | (kg m−3) | (kg m−3) | RD (%) |
|---|---|---|---|---|
| 298.15 | 1 | 786 | 806 | 2.54 |
| 308.15 | 1 | 776 | 796 | 2.58 |
| 308.15 | 300 | 795 | 817 | 2.77 |
| 318.15 | 1 | 767 | 785 | 2.08 |
| 328.15 | 1 | 759 | 773 | 1.84 |
| 333.15 | 1 | 754 | 768 | 1.59 |
| 333.15 | 300 | 782 | 793 | 1.41 |
| ARD = 2.12% | ||||
| AARD = 2.12% | ||||
| System | Property | NDP | (K) | (bar) | Source |
|---|---|---|---|---|---|
| EtOH/quercetin | 4 | 303.15–323.15 | 1–150 | [46] | |
| EtOH/gallic acid | 3 | 303.15–333.15 | 1 | [5] | |
| EtOH/ibuprofen | 8 | 298.15–333.15 | 1–300 | [4] | |
| EtOH/butan-1-ol | 2 | 298.15–333.15 | 1 | [47] | |
| EtOH/propanone | 2 | 298.15–333.15 | 1 | [48] | |
| EtOH/butanal | 2 | 298.15–333.15 | 1 | [48] | |
| EtOH/benzene | 1 | 313.15 | 1 | [47,49] | |
| EtOH/propane | 1 | 323.15 | 103 | [50] | |
| EtOH | 5 | 298.15–333.15 | 1 | [51,52,53,54,55,56,57,58] | |
| EtOH | 8 | 298.15–333.15 | 1–300 | [59,60,61,62] | |
| EtOH | 1 | 298.15 | 1 | [45] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zêzere, B.; Fonseca, T.V.B.; Portugal, I.; Simões, M.M.Q.; Silva, C.M.; Gomes, J.R.B. Influence of Ethanol Parametrization on Diffusion Coefficients Using OPLS-AA Force Field. Int. J. Mol. Sci. 2023, 24, 7316. https://doi.org/10.3390/ijms24087316
Zêzere B, Fonseca TVB, Portugal I, Simões MMQ, Silva CM, Gomes JRB. Influence of Ethanol Parametrization on Diffusion Coefficients Using OPLS-AA Force Field. International Journal of Molecular Sciences. 2023; 24(8):7316. https://doi.org/10.3390/ijms24087316
Chicago/Turabian StyleZêzere, Bruno, Tiago V. B. Fonseca, Inês Portugal, Mário M. Q. Simões, Carlos M. Silva, and José R. B. Gomes. 2023. "Influence of Ethanol Parametrization on Diffusion Coefficients Using OPLS-AA Force Field" International Journal of Molecular Sciences 24, no. 8: 7316. https://doi.org/10.3390/ijms24087316
APA StyleZêzere, B., Fonseca, T. V. B., Portugal, I., Simões, M. M. Q., Silva, C. M., & Gomes, J. R. B. (2023). Influence of Ethanol Parametrization on Diffusion Coefficients Using OPLS-AA Force Field. International Journal of Molecular Sciences, 24(8), 7316. https://doi.org/10.3390/ijms24087316










