Mott Transition in the Hubbard Model on Anisotropic Honeycomb Lattice with Implications for Strained Graphene: Gutzwiller Variational Study
Abstract
1. Introduction
2. Model and Methods
2.1. The Anisotropic Hubbard Model
2.2. Hartree–Fock Approximation
2.3. Gutzwiller Wavefunction
2.4. Gutzwiller Approximation and Its Variants
3. Results and Discussion
3.1. Phase Diagram
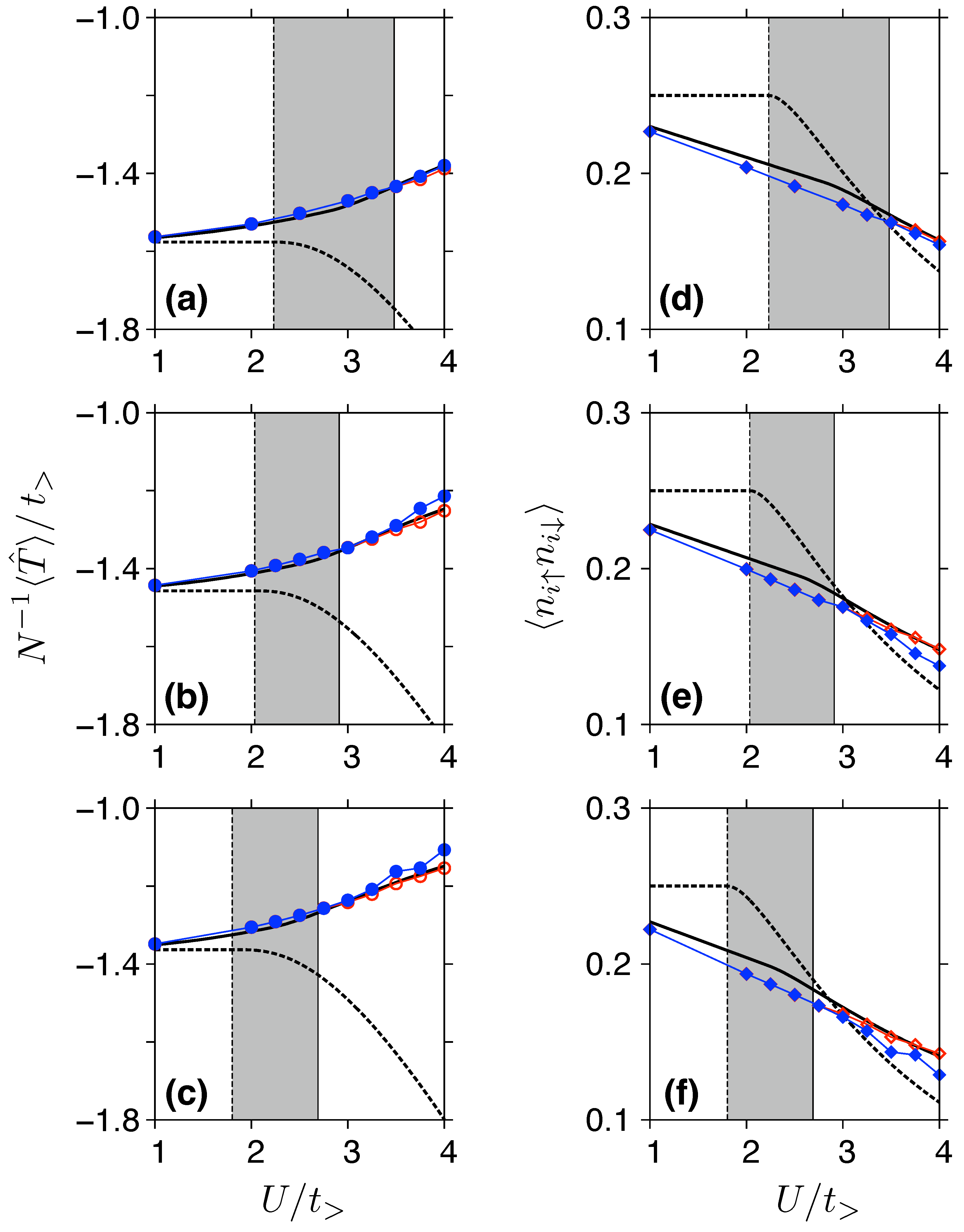
3.2. Effects of Strain on Measurable Quantities
4. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Coherent Potential Approximation
Appendix B. Su–Schrieffer–Heeger Model for Graphene
References and Notes
- Gutzwiller, M. Effect of Correlation on the Ferromagnetism of Transition Metals. Phys. Rev. Lett. 1963, 10, 159. [Google Scholar] [CrossRef]
- Hubbard, J. Electron Correlations in Narrow Energy Bands. Proc. R. Soc. A 1963, 276, 238. [Google Scholar] [CrossRef]
- Lieb, E.H.; Wu, F.Y. Absence of Mott transition in an exact solution of the short-range one-band model in one dimension. Phys. Rev. Lett. 1968, 20, 1445, Erratum in Phys. Rev. Lett. 1968, 21, 192. [Google Scholar] [CrossRef]
- Lieb, E.H.; Wu, F.Y. The one-dimensional Hubbard model: A reminiscence. Phys. A 2003, 321, 1. [Google Scholar] [CrossRef]
- Hirsch, J.E. Two-dimensional Hubbard model: Numerical simulation study. Phys. Rev. B 1985, 31, 4403. [Google Scholar] [CrossRef]
- Acquarone, M.; Ray, D.K.; Spałek, J. The Hubbard sub-band structure and the cohesive energy of narrow band systems. J. Phys. C Solid State Phys. 1982, 15, 959. [Google Scholar] [CrossRef]
- Yokoyama, H.; Shiba, H. Variational Monte-Carlo Studies of Hubbard Model. II. J. Phys. Soc. Jpn. 1987, 56, 3582. [Google Scholar] [CrossRef]
- Li, Y.M.; d’Ambrumenil, N. Sum rule and symmetry-controlled expansion for generalized Gutzwiller wave functions. Phys. Rev. B 1992, 46, 13928. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.M.; d’Ambrumenil, N. A new expansion for generalized Gutzwiller wave functions: Antiferromagnetic case. J. Appl. Phys. 1993, 73, 6537. [Google Scholar] [CrossRef]
- Koch, E.; Gunnarsson, O.; Martin, R.M. Optimization of Gutzwiller wave functions in quantum Monte Carlo. Phys. Rev. B 1999, 59, 15632. [Google Scholar] [CrossRef]
- Becca, F.; Sorella, S. Quantum Monte Carlo Approaches for Correlated Systems; For a Comprehensive Review of the Topic; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar] [CrossRef]
- Czarnik, P.; Rams, M.M.; Dziarmaga, J. Variational tensor network renormalization in imaginary time: Benchmark results in the Hubbard model at finite temperature. Phys. Rev. B 2016, 94, 235142. [Google Scholar] [CrossRef]
- Schneider, M.; Ostmeyer, J.; Jansen, K.; Luu, T.; Urbach, C. The Hubbard model with fermionic tensor networks. arXiv 2021, arXiv:2110.15340. [Google Scholar]
- Fishman, M.; White, S.R.; Stoudenmire, E.M. The ITensor Software Library for Tensor Network Calculations. SciPost Phys. Codebases 2022, 4. [Google Scholar] [CrossRef]
- Martelo, L.M.; Dzierzawa, M.; Siffert, L.; Baeriswyl, D. Mott-Hubbard transition and antiferromagnetism on the honeycomb lattice. Z. Phys. B 1997, 103, 335. [Google Scholar] [CrossRef]
- Le, D.A. Mott transition in the half-filled Hubbard model on the honeycomb lattice within coherent potential approximation. Mod. Phys. Lett. B 2013, 27, 1350046. [Google Scholar] [CrossRef]
- Rowlands, D.A.; Zhang, Y.-Z. Disappearance of the Dirac cone in silicene due to the presence of an electric field. Chin. Phys. B 2014, 23, 037101. [Google Scholar] [CrossRef][Green Version]
- Sorella, S.; Otsuka, Y.; Yunoki, S. Absence of a Spin Liquid Phase in the Hubbard Model on the Honeycomb Lattice. Sci. Rep. 2012, 2, 992. [Google Scholar] [CrossRef]
- Sorella, S.; Tosatti, E. Semi-Metal-Insulator Transition of the Hubbard Model in the Honeycomb Lattice. Eur. Lett. 1992, 19, 699. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Katsnelson, M.I.; Grigorieva, I.V.; Dubonos, S.V.; Firsov, A.A. Two-dimensional gas of massless Dirac fermions in graphene. Nature 2005, 438, 197. [Google Scholar] [CrossRef]
- Zhang, Y.; Tan, Y.-W.; Stormer, H.L.; Kim, P. Experimental observation of the quantum Hall effect and Berry’s phase in graphene. Nature 2005, 438, 201. [Google Scholar] [CrossRef]
- Katsnelson, M.I. The Physics of Graphene, 2nd ed.; Cambridge University Press: Cambridge, UK, 2020. [Google Scholar] [CrossRef]
- Schüler, M.; Rösner, M.; Wehling, T.O.; Lichtenstein, A.I.; Katsnelson, M.I. Optimal Hubbard models for materials with nonlocal Coulomb interactions: Graphene, silicene and benzene. Phys. Rev. Lett. 2013, 111, 036601. [Google Scholar] [CrossRef] [PubMed]
- Tang, H.-K.; Laksono, E.; Rodrigues, J.N.B.; Sengupta, P.; Assaad, F.F.; Adam, S. Interaction-Driven Metal-Insulator Transition in Strained Graphene. Phys. Rev. Lett. 2015, 115, 186602. [Google Scholar] [CrossRef]
- Zhang, L.; Ma, C.; Ma, T. Metal-Insulator Transition in Strained Graphene: A Quantum Monte Carlo Study. Phys. Status Solidi RRL 2021, 15, 2100287. [Google Scholar] [CrossRef]
- Pasternak, M.P.; Nasu, S.; Wada, K.; Endo, S. High-pressure phase of magnetite. Phys. Rev. B 1994, 50, 6446. [Google Scholar] [CrossRef]
- Goncharenko, I.N. Evidence for a Magnetic Collapse in the Epsilon Phase of Solid Oxygen. Phys. Rev. Lett. 2005, 94, 205701. [Google Scholar] [CrossRef] [PubMed]
- Drozdov, A.P.; Eremets, M.I.; Troyan, I.A.; Ksenofontov, V.; Shylin, S.I. Conventional superconductivity at 203 kelvin at high pressures in the sulfur hydride system. Nature 2015, 525, 73. [Google Scholar] [CrossRef]
- Somayazulu, M.; Ahart, M.; Mishra, A.K.; Geballe, Z.M.; Baldini, M.; Meng, Y.; Struzhkin, V.V.; Hemley, R.J. Evidence for Superconductivity above 260 K in Lanthanum Superhydride at Megabar Pressures. Phys. Rev. Lett. 2019, 122, 027001. [Google Scholar] [CrossRef]
- Celliers, P.M.; Millot, M.; Brygoo, S.; McWilliams, R.S.; Fratanduono, D.E.; Rygg, J.R.; Goncharov, A.F.; Loubeyre, P.; Eggert, J.H.; Peterson, J.L.; et al. Insul.-Met. Transit. Dense Fluid Deuterium. Science 2018, 361, 677. [Google Scholar] [CrossRef]
- Feldner, H.; Meng, Z.Y.; Honecker, A.; Cabra, D.; Wessel, S.; Assaad, F.F. Magnetism of finite graphene samples: Mean-field theory compared with exact diagonalization and quantum Monte Carlo simulations. Phys. Rev. B 2010, 81, 115416. [Google Scholar] [CrossRef]
- Potasz, P.; Güçlü, A.D.; Wójs, A.; Hawrylak, P. Electronic properties of gated triangular graphene quantum dots: Magnetism, correlations, and geometrical effects. Phys. Rev. B 2012, 85, 075431. [Google Scholar] [CrossRef]
- Brito, F.M.O.; Li, L.; Lopes, J.M.V.P.; Castro, E.V. Edge magnetism in transition metal dichalcogenide nanoribbons: Mean field theory and determinant quantum Monte Carlo. Phys. Rev. B 2022, 105, 195130. [Google Scholar] [CrossRef]
- Rycerz, A.; Spałek, J. Exact Diagonalization of Many-Fermion Hamiltonian with Wave-Function Renormalization. Phys. Rev. B 2001, 63, 073101. [Google Scholar] [CrossRef]
- Spałek, J.; Rycerz, A. Electron localization in one-dimensional nanoscopic system: A combined exact diagonalization-an ab initio approach. Phys. Rev. B 2001, 64, 161105. [Google Scholar] [CrossRef]
- Singha, A.; Gibertini, M.; Karmakar, B.; Yuan, S.; Polini, M.; Vignale, G.; Katsnelson, M.I.; Pinczuk, A.; Pfeiffer, L.N.; West, K.W.; et al. Two-dimensional Mott-Hubbard electrons in an artificial honeycomb lattice. Science 2011, 332, 1176. [Google Scholar] [CrossRef] [PubMed]
- Polini, M.; Guinea, F.; Lewenstein, M.; Manoharan, H.C.; Pellegrini, V. Artificial honeycomb lattices for electrons, atoms and photons. Nat. Nanotechnol. 2013, 8, 625. [Google Scholar] [CrossRef]
- Gardenier, T.S.; van den Broeke, J.J.; Moes, J.R.; Swart, I.; Delerue, C.; Slot, M.R.; Smith, C.M.; Vanmaekelbergh, D. p Orbital Flat Band and Dirac Cone in the Electronic Honeycomb Lattice. ACS Nano 2020, 14, 13638. [Google Scholar] [CrossRef]
- Trainer, D.J.; Srinivasan, S.; Fisher, B.L.; Zhang, Y.; Pfeiffer, C.R.; Hla, S.-W.; Darancet, P.; Guisinger, N.P. Manipulating topology in tailored artificial graphene nanoribbons. arXiv 2021, arXiv:2104.11334. [Google Scholar]
- Cao, Y.; Fatemi, V.; Demir, A.; Fang, S.; Tomarken, S.L.; Luo, J.Y.; Sanchez-Yamagishi, J.D.; Watanabe, K.; Taniguchi, T.; Kaxiras, E.; et al. Correlated insulator behaviour at half-filling in magic-angle graphene superlattices. Nature 2018, 556, 80. [Google Scholar] [CrossRef] [PubMed]
- Fidrysiak, M.; Zegrodnik, M.; Spałek, J. Unconventional topological superconductivity and phase diagram for an effective two-orbital model as applied to twisted bilayer graphene. Phys. Rev. B 2018, 98, 085436. [Google Scholar] [CrossRef]
- Lee, S.-H.; Chung, H.-J.; Heo, J.; Yang, H.; Shin, J.; Chung, U.-I.; Seo, S. Band Gap Opening by Two-Dimensional Manifestation of Peierls Instability in Graphene. ACS Nano 2011, 5, 2964. [Google Scholar] [CrossRef]
- Lee, S.-H.; Kim, S.; Kim, K. Semimetal-antiferromagnetic insulator transition in graphene induced by biaxial strain. Phys. Rev. B 2012, 86, 155436. [Google Scholar] [CrossRef]
- Sorella, S.; Seki, K.; Brovko, O.O.; Shirakawa, T.; Miyakoshi, S.; Yunoki, S.; Tosatti, E. Correlation-Driven Dimerization and Topological Gap Opening in Isotropically Strained Graphene. Phys. Rev. Lett. 2018, 121, 066402. [Google Scholar] [CrossRef] [PubMed]
- Eom, D.; Koo, J.-Y. Direct measurement of strain-driven Kekulé distortion in graphene and its electronic properties. Nanoscale 2020, 12, 19604. [Google Scholar] [CrossRef] [PubMed]
- Bao, C.; Zhang, H.; Zhang, T.; Wu, X.; Luo, L.; Zhou, S.; Li, Q.; Hou, Y.; Yao, W.; Liu, L.; et al. Exp. Evid. Chiral Symmetry Break. Kekulé-Ordered Graphene. Phys. Rev. Lett. 2021, 126, 206804. [Google Scholar] [CrossRef]
- Costa, N.C.; Seki, K.; Sorella, S. Magnetism and Charge Order in the Honeycomb Lattice. Phys. Rev. Lett. 2021, 126, 107205. [Google Scholar] [CrossRef]
- Dresselhaus, G.; Dresselhaus, M.S.; Saito, R. Physical Properties of Carbon Nanotubes; World Scientific: Singapore, 1998; Chapter 11. [Google Scholar] [CrossRef]
- Tsai, J.-L.; Tu, J.-F. Characterizing mechanical properties of graphite using molecular dynamics simulation. Mater. Des. 2010, 31, 194. [Google Scholar] [CrossRef]
- Hur, K.L. Weakly coupled Hubbard chains at half-filling and confinement. Phys. Rev. B 2001, 63, 165110. [Google Scholar] [CrossRef]
- Spałek, J.; Görlich, E.M.; Rycerz, A.; Zahorbeński, R. The combined exact diagonalization-ab initio approach and its application to correlated electronic states and Mott-Hubbard localization in nanoscopic systems. J. Phys. Condens. Matter 2007, 19, 255212. [Google Scholar] [CrossRef]
- Lenz, B.; Manmana, S.R.; Pruschke, T.; Assaad, F.F.; Raczkowski, M. Mott Quantum Criticality in the Anisotropic 2D Hubbard Model. Phys. Rev. Lett. 2016, 116, 086403. [Google Scholar] [CrossRef]
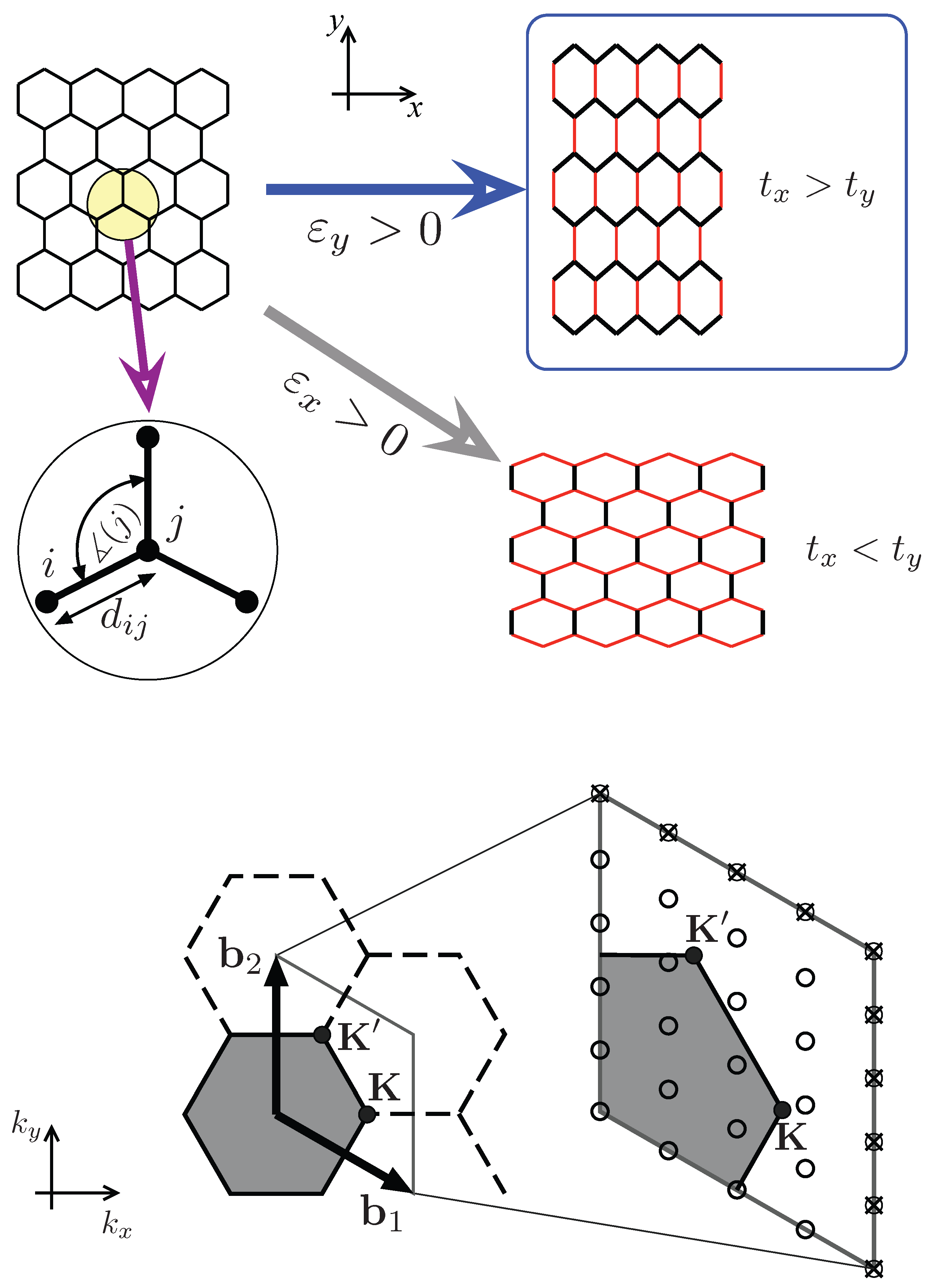
- Due to mirror symmetries, it sufficient to sum over first quarter of the hexagonal Brilloun zone, namely, for 0 ⩽ ky < 2π/ and 0 ⩽ kx < 4π/3−|ky|/.
- Castro Neto, A.H.; Guinea, F.; Peres, N.M.R.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109. [Google Scholar] [CrossRef]
- Typically, for each combination of ty/tx, U/tx and Δ/tx, we took 15÷20 values of the parameter g = e−η separated by the steps of 0.01, in the vicinity of a predicted energy minimum. For each g, the averages over distributions of electrons in real space were calculated by performing 105 iterations per lattice, according to the Glauber’s algorithm [see, e.g.: M. Lewerenz, Monte Carlo Methods: Overview and Basics. In: Grotendorst, J.; Marx, D.; Muramatsu, A. (eds) Quantum simulations of complex many-body systems: From theory to algorithms, lecture notes; winter school, 25 February–1 March 2002, Rolduc Conference Centre, Kerkrade, The Netherlands. John von Neumann Institute for Computing Jülich, 2002. http://hdl.handle.net/2128/2921]. Initial 104 iterations per site was neglected for each simulation, to avoid the effects of initial configuration. The variational energy together with the corresponding optimal value of the parameter g were then determined via the least-squares fitting of a quadratic function.
- Takano, F.; Uchinami, M. Application of the Gutzwiller Method to Antiferromagnetism. Prog. Theor. Phys. 1975, 53, 1267. [Google Scholar] [CrossRef][Green Version]
- Vollhardt, D. Normal 3He: An almost localized Fermi liquid. Rev. Mod. Phys. 1984, 56, 99. [Google Scholar] [CrossRef]
- Jędrak, J.; Kaczmarczyk, J.; Spałek, J. Statistically-consistent Gutzwiller approach and its equivalence with the mean-field slave-boson method for correlated systems. arXiv 2010, arXiv:1008.0021. [Google Scholar]
- Lanatà, N.; Strand, H.U.R.; Dai, X.; Hellsing, B. Efficient implementation of the Gutzwiller variational method. Phys. Rev. B 2012, 85, 035133. [Google Scholar] [CrossRef]
- Wysokiński, M.M.; Spałek, J. Properties of an almost localized Fermi liquid in an applied magnetic field revisited: A statistically consistent Gutzwiller approach. J. Phys. Condens. Matter 2014, 26, 055601. [Google Scholar] [CrossRef] [PubMed]
- Chern, G.-W.; Barros, K.; Batista, C.D.; Kress, J.D.; Kotliar, G. Mott Transition in a Metallic Liquid: Gutzwiller Molecular Dynamics Simulations. Phys. Rev. Lett. 2017, 118, 226401. [Google Scholar] [CrossRef] [PubMed]
- Fidrysiak, M.; Zegrodnik, M.; Spałek, J. Realistic estimates of superconducting properties for the cuprates: Reciprocal-space diagrammatic expansion combined with variational approach. J. Phys. Condens. Matter 2018, 30, 475602. [Google Scholar] [CrossRef] [PubMed]
- Gutzwiller, M.C. Effect of Correlation on the Ferromagnetism of Transition Metals. Phys. Rev. 1964, 134, A923. [Google Scholar] [CrossRef]
- Gutzwiller, M.C. Correlation of Electrons in a Narrow s Band. Phys. Rev. 1965, 137, A1726. [Google Scholar] [CrossRef]
- Kennedy, T.; Lieb, E.H.; Shastry, B.S. The XY Model Has Long-Range Order for All Spins and All Dimensions Greater than One. Phys. Rev. Lett. 1988, 61, 2582. [Google Scholar] [CrossRef]
- Pereira, V.M.; Castro Neto, A.H.; Peres, N.M.R. Tight-binding approach to uniaxial strain in graphene. Phys. Rev. B 2009, 80, 045401. [Google Scholar] [CrossRef]
- Tran, M.-T.; Kuroki, K. Finite temperature semimetal insulator transition on the honeycomb lattice. Phys. Rev. B 2009, 79, 125125. [Google Scholar] [CrossRef]
- Capello, M.; Becca, F.; Fabrizio, M.; Sorella, S.; Tosatti, E. Variational Description of Mott Insulators. Phys. Rev. Lett. 2005, 94, 026406. [Google Scholar] [CrossRef] [PubMed]
- Biborski, A.; Kądzielawa, A.P.; Spałek, J. Atomization of correlated molecular-hydrogen chain: A fully microscopic variational Monte Carlo solution. Phys. Rev. B 2018, 98, 085112. [Google Scholar] [CrossRef]
- Gröning, O.; Wang, S.; Yao, X.; Pignedoli, C.A.; Barin, G.B.; Daniels, C.; Cupo, A.; Meunier, V.; Feng, X.; Narita, A.; et al. Eng. Robust Topol. Quantum Phases Graphene Nanoribbons. Nature 2018, 560, 209. [Google Scholar] [CrossRef]
- Rycerz, A. Strain-induced transitions to quantum chaos and effective time-reversal symmetry breaking in triangular graphene nanoflakes. Phys. Rev. B 2013, 87, 195431. [Google Scholar] [CrossRef]
- Rostami, H.; Asgari, R. Electronic ground-state properties of strained graphene. Phys. Rev. B 2012, 86, 155435. [Google Scholar] [CrossRef]
- Oliva-Leyva, M.; Naumis, G.G. Generalizing the Fermi velocity of strained graphene from uniform to nonuniform strain. Phys. Lett. A 2015, 379, 2645. [Google Scholar] [CrossRef]
- Singh, J.; Jamdagni, P.; Jakhara, M.; Kumar, A. Stability, electronic and mechanical properties of chalcogen (Se and Te) monolayers. Phys. Chem. Chem. Phys. 2020, 22, 5749. [Google Scholar] [CrossRef]
- Zhang, G.; Lu, K.; Wang, Y.; Wang, H.; Chen, Q. Mechanical and electronic properties of α−M2X3 (M = Ga, In; X = S, Se) monolayers. Phys. Rev. B 2022, 105, 235303. [Google Scholar] [CrossRef]
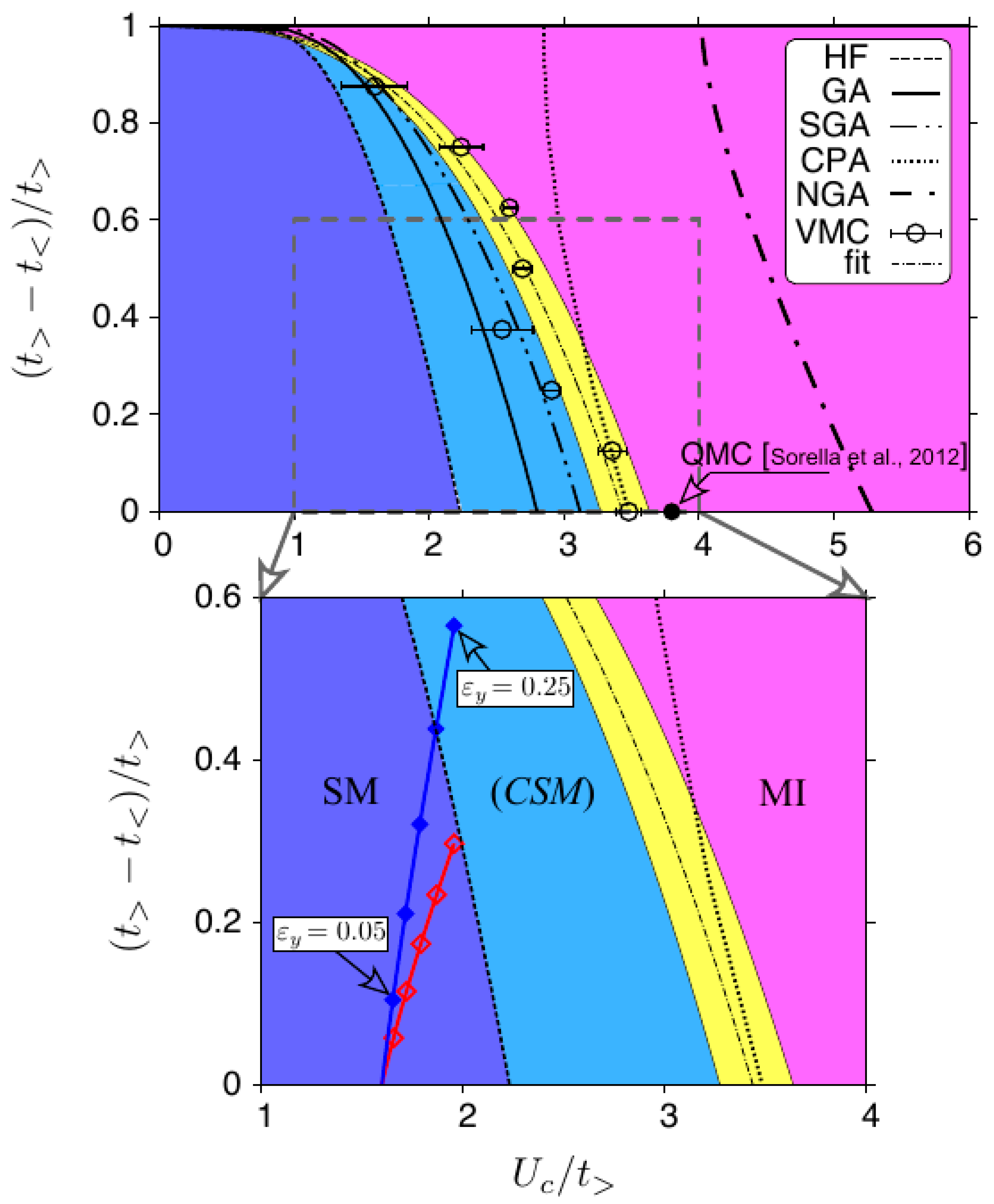
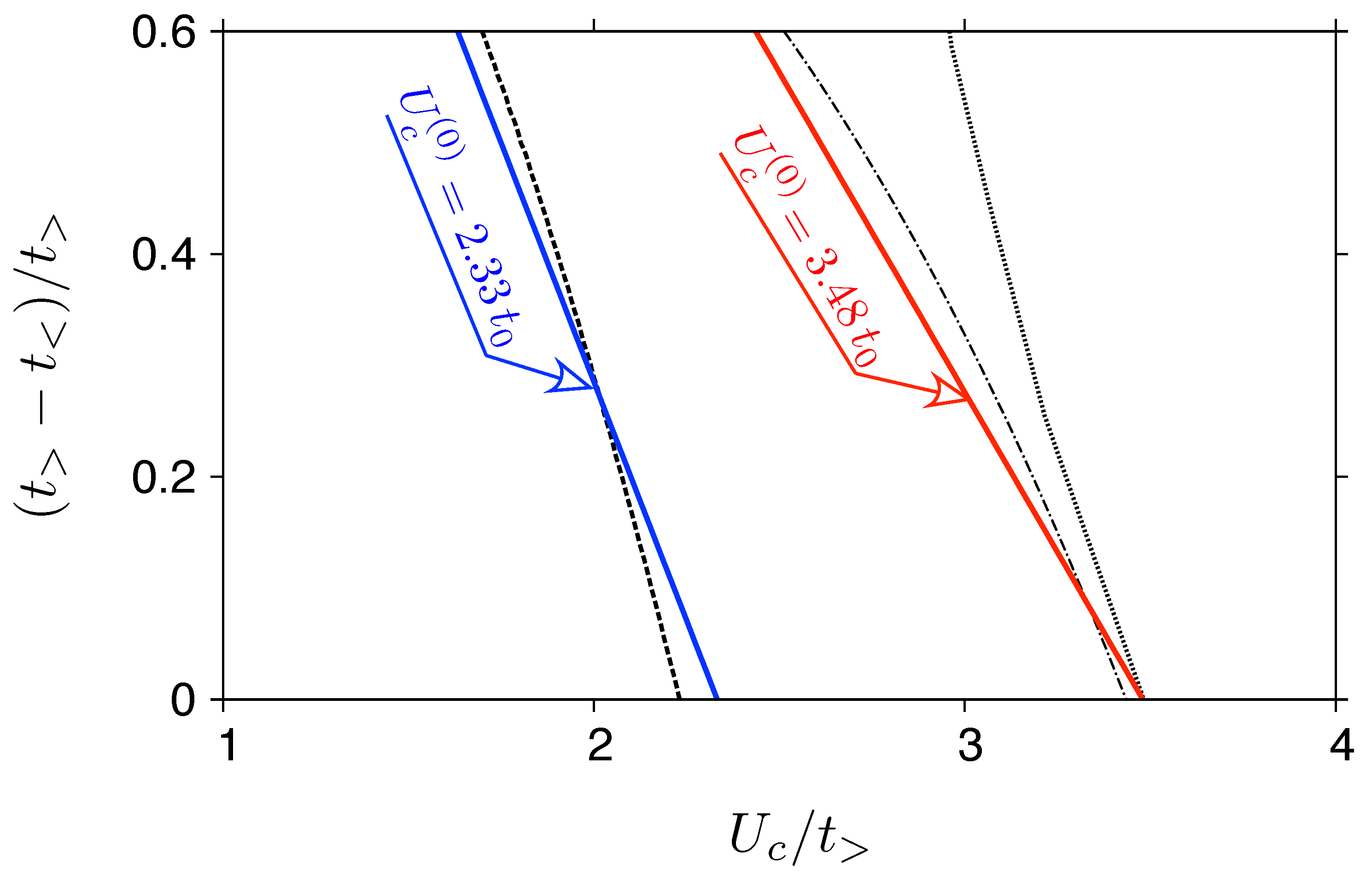
| 1.00 | 3.48(1) | 2.804 | 3.12 | 5.281 |
| 0.75 | 2.91(1) | 2.550 | 2.83 | 4.871 |
| 0.50 | 2.69(3) | 2.241 | 2.47 | 4.508 |
| 0.25 | 2.24(1) | 1.830 | 1.98 | 4.199 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rut, G.; Fidrysiak, M.; Goc-Jagło, D.; Rycerz, A. Mott Transition in the Hubbard Model on Anisotropic Honeycomb Lattice with Implications for Strained Graphene: Gutzwiller Variational Study. Int. J. Mol. Sci. 2023, 24, 1509. https://doi.org/10.3390/ijms24021509
Rut G, Fidrysiak M, Goc-Jagło D, Rycerz A. Mott Transition in the Hubbard Model on Anisotropic Honeycomb Lattice with Implications for Strained Graphene: Gutzwiller Variational Study. International Journal of Molecular Sciences. 2023; 24(2):1509. https://doi.org/10.3390/ijms24021509
Chicago/Turabian StyleRut, Grzegorz, Maciej Fidrysiak, Danuta Goc-Jagło, and Adam Rycerz. 2023. "Mott Transition in the Hubbard Model on Anisotropic Honeycomb Lattice with Implications for Strained Graphene: Gutzwiller Variational Study" International Journal of Molecular Sciences 24, no. 2: 1509. https://doi.org/10.3390/ijms24021509
APA StyleRut, G., Fidrysiak, M., Goc-Jagło, D., & Rycerz, A. (2023). Mott Transition in the Hubbard Model on Anisotropic Honeycomb Lattice with Implications for Strained Graphene: Gutzwiller Variational Study. International Journal of Molecular Sciences, 24(2), 1509. https://doi.org/10.3390/ijms24021509








