Spectral Relaxation Imaging Microscopy II: Complex Dynamics
Abstract
1. Introduction
2. Results and Materials and Methods
2.1. Theory of the Red-Fluorescence-Edge Phasor Ellipse Approach
2.1.1. Derivation of Initial and Relaxed States for Single-Spectral-Relaxation/Single-Lifetime Model
2.2. Complex Models of Spectral Relaxation (Two Spectral Relaxation Times and One Lifetime)
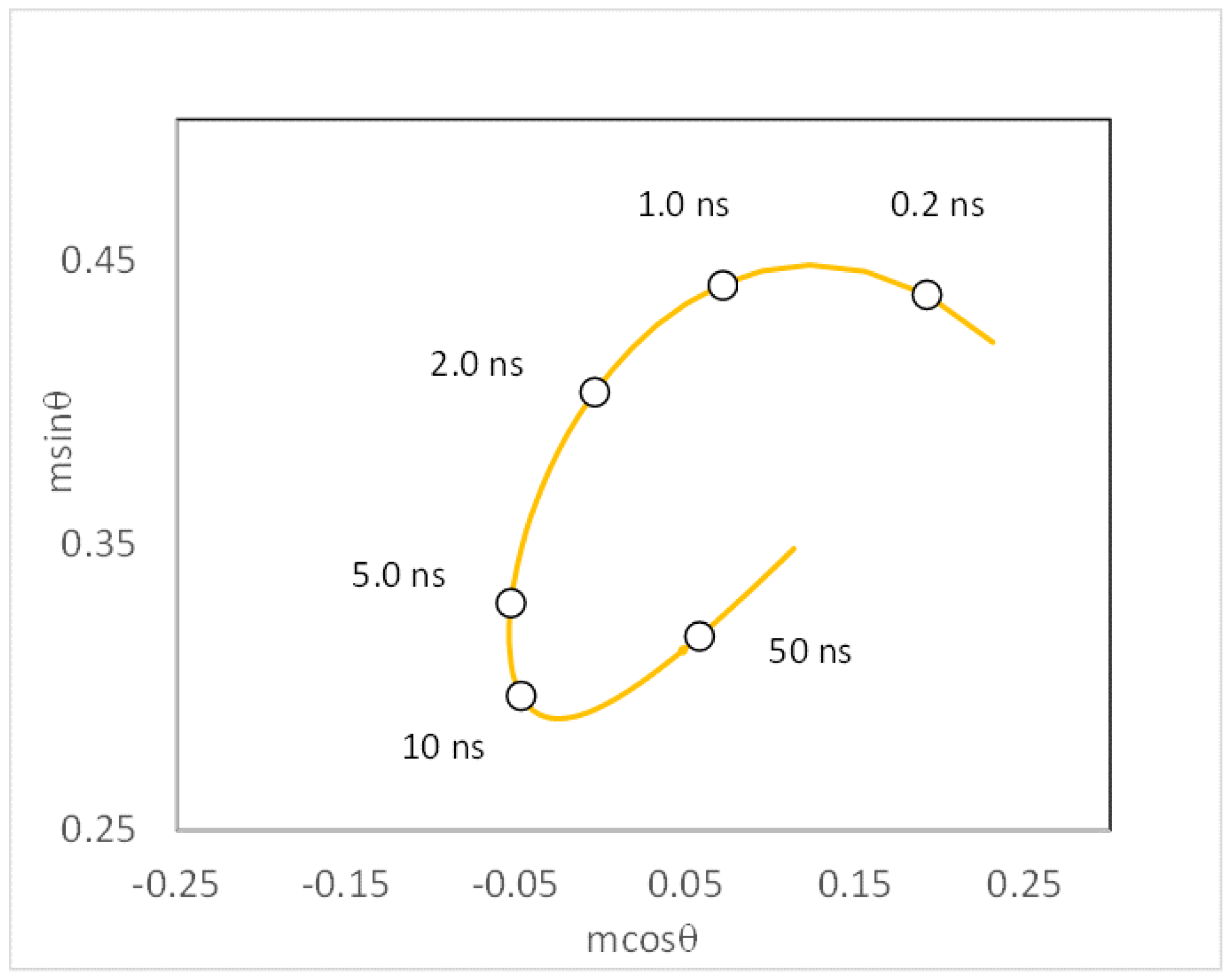
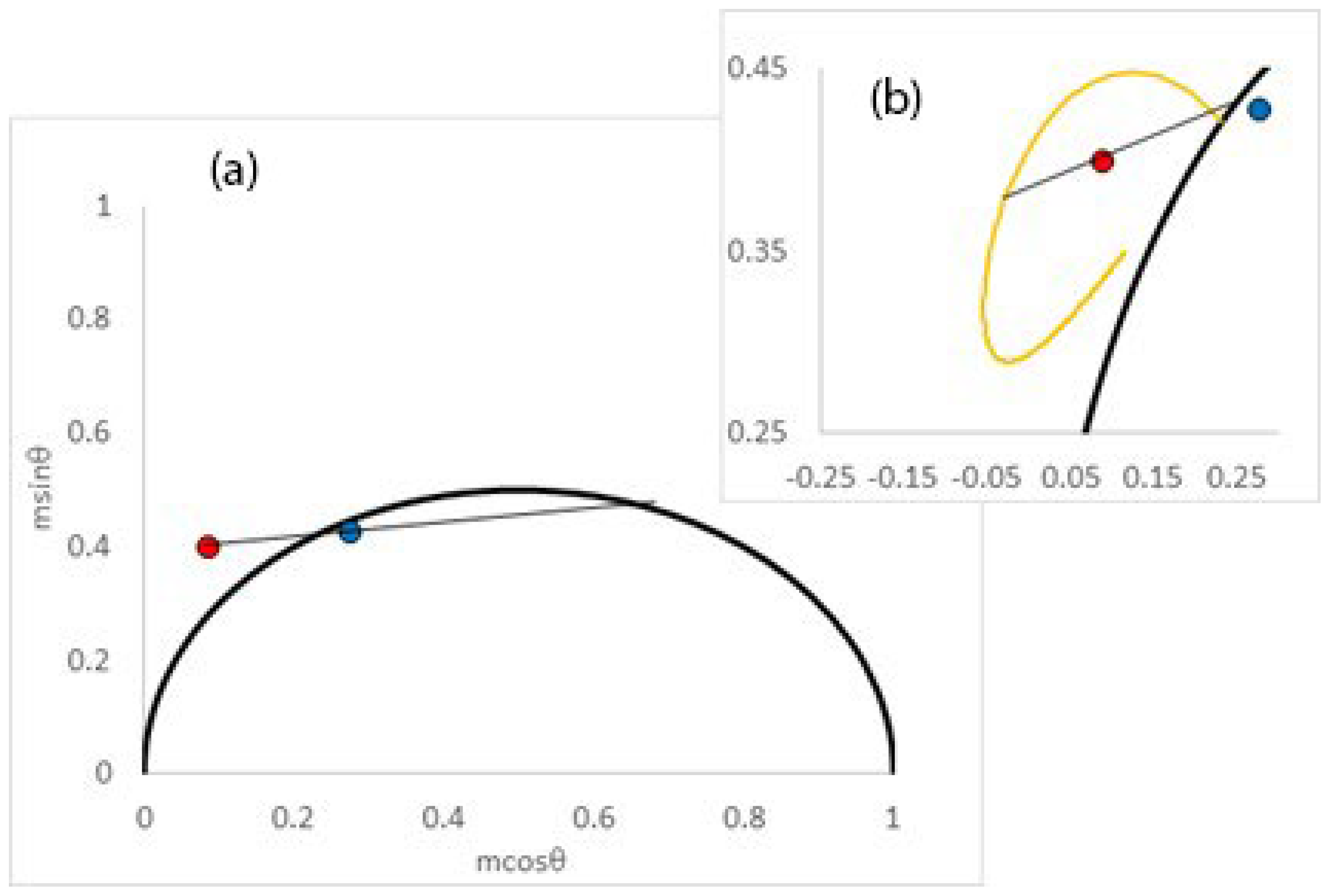
2.3. Interpretation of Motions by Projection onto Sub-Nanosecond–Super-Nanosecond Spectral Relaxation Correlation Times (IMPOSSE)
3. Discussion
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Maroncelli, M.; MacInnis, J.; Fleming, G.R. Polar Solvent Dynamics and Electron-Transfer Reactions. Science 1989, 243, 1674–1681. [Google Scholar] [CrossRef] [PubMed]
- Maroncelli, M.; Fleming, G.R. Picosecond solvation dynamics of coumarin 153: The importance of molecular aspects of solvation. J. Chem. Phys. 1987, 86, 6221–6239. [Google Scholar] [CrossRef]
- Jurkiewicz, P.; Sýkora, J.; Żyńska, A.O.; Humpolíčková, J.; Hof, M. Solvent Relaxation in Phospholipid Bilayers: Principles and Recent Applications. J. Fluoresc. 2005, 15, 883–894. [Google Scholar] [CrossRef] [PubMed]
- Amaro, M.; Reina, F.; Hof, M.; Eggeling, C.; Sezgin, E. Laurdan and Di−4-ANEPPDHQ probe different properties of the membrane. J. Phys. D Appl. Phys. 2017, 50, 134004. [Google Scholar] [CrossRef] [PubMed]
- Scollo, F.; Evci, H.; Amaro, M.; Jurkiewicz, P.; Sykora, J.; Hof, M. What Does Time-Dependent Fluorescence Shift (TDFS) in Biomembranes (and Proteins) Report on? Front Chem. 2021, 9, 738350. [Google Scholar] [CrossRef] [PubMed]
- Parasassi, T.; Gratton, E.; Yu, W.; Wilson, P.; Levi, M. Two-photon fluorescence microscopy of laurdan generalized polarization domains in model and natural membranes. Biophys. J. 1997, 72, 2413–2429. [Google Scholar] [CrossRef] [PubMed]
- Parasassi, T.; Conti, F.; Gratton, E. Time-resolved fluorescence emission spectra of Laurdan in phospholipid vesicles by multifrequency phase and modulation fluorometry. Cell. Mol. Biol. 1986, 32, 103–108. [Google Scholar] [PubMed]
- Owen, D.M.; Gaus, K. Optimized time-gated generalized polarization imaging of Laurdan and di−4-ANEPPDHQ for membrane order image contrast enhancement. Microsc. Res. Tech. 2010, 73, 618–622. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Benda, A.; Kwiatek, J.; Owen, D.M.; Gaus, K. Time-Resolved Laurdan Fluorescence Reveals Insights into Membrane Viscosity and Hydration Levels. Biophys. J. 2018, 115, 1498–1508. [Google Scholar] [CrossRef] [PubMed]
- Golfetto, O.; Hinde, E.; Gratton, E. Laurdan Fluorescence Lifetime Discriminates Cholesterol Content from Changes in Fluidity in Living Cell Membranes. Biophys. J. 2013, 104, 1238–1247. [Google Scholar] [CrossRef] [PubMed]
- Lajevardipour, A.; Chon, J.W.M.; Chattopadhyay, A.; Clayton, A.H.A. Imaging Cellular Dynamics with Spectral Relaxation Imaging Microscopy: Distinct Spectral Dynamics in Golgi Membranes of Living Cells. Sci. Rep. 2016, 6, 37038. [Google Scholar] [CrossRef] [PubMed]
- Amaro, M.; Filipe, H.A.L.; Ramalho, J.P.P.; Hof, M.; Loura, L.M.S. Fluorescence of nitrobenzoxadiazole (NBD)-labeled lipids in model membranes is connected not to lipid mobility but to probe location. Phys. Chem. Chem. Phys. 2016, 18, 7042–7054. [Google Scholar] [CrossRef] [PubMed]
- Lakowicz, J.R.; Balter, A. Analysis of excited-state processes by phase-modulation fluorescence spectroscopy. Biophys. Chem. 1982, 16, 117–132. [Google Scholar] [CrossRef] [PubMed]
- Weber, G. Resolution of the fluorescence lifetimes in a heterogeneous system by phase and modulation measurements. J. Phys. Chem. 1981, 85, 949–953. [Google Scholar] [CrossRef]
- Weber, G.; Farris, F.J. Synthesis and spectral properties of a hydrophobic fluorescent probe: 6-propionyl−2-(dimethylamino)naphthalene. Biochemistry 1979, 18, 3075–3078. [Google Scholar] [CrossRef] [PubMed]
- Kozer, N.; Clayton, A.H.A. In-cell structural dynamics of an EGF receptor during ligand-induced dimer–oligomer transition. Eur. Biophys. J. 2020, 49, 21–37. [Google Scholar] [CrossRef] [PubMed]
- Kozer, N.; Clayton, A.H.A. Analysis of complex anisotropy decays from single-frequency polarized-phasor ellipse plots. Methods Appl. Fluoresc. 2016, 4, 24005. [Google Scholar] [CrossRef] [PubMed]
- Khan, S.N.; Charlier, C.; Augustyniak, R.; Salvi, N.; Déjean, V.; Bodenhausen, G.; Lequin, O.; Pelupessy, P.; Ferrage, F. Distribution of Pico- and Nanosecond Motions in Disordered Proteins from Nuclear Spin Relaxation. Biophys. J. 2015, 109, 988–999. [Google Scholar] [CrossRef] [PubMed]
- Demchenko, A.P.; Shcherbatska, N.V. Nanosecond dynamics of charged fluorescent probes at the polar interface of a membrane phospholipid bilayer. Biophys. Chem. 1985, 22, 131–143. [Google Scholar] [CrossRef] [PubMed]


| Model | Input τs | Input GPi | Input GPf | Output Parameters |
|---|---|---|---|---|
| 1 | 0.1 | 0.6 | −0.6 | 0.1, 0.6, −0.6 |
| 2 | 1 | 0.0 | −0.6 | 1, 0.0, −0.6 |
| 3 | 3 | −0.2 | −0.6 | 3, −0.2, −0.6 |
| 4 | 10 | 0.3 | −0.3 | 10, 0.3, −0.3 |
| Input GPi; GPf | Input τ1; τ2 | Input A1; A2 | Ouput GPi; GPf | Output τs |
|---|---|---|---|---|
| 0.6; −0.6 | 0.1; 3 | 0.2; 0.8 | 0.385; −0.598 | 2.91 |
| 0.6; −0.6 | 0.1; 3 | 0.4; 0.6 | 0.172; −0.596 | 2.78 |
| 0.6; −0.6 | 0.1; 3 | 0.6; 0.4 | −0.05; −0.594 | 2.56 |
| 0.6; −0.6 | 0.1; 3 | 0.8; 0.2 | −0.25; −0.594 | 2.06 |
| 0.6; −0.6 | 1; 3 | 0.2; 0.8 | 0.536; −0.594 | 2.67 |
| 0.6; −0.6 | 1; 3 | 0.4; 0.6 | 0.484; −0.590 | 2.31 |
| 0.6; −0.6 | 1; 3 | 0.6; 0.4 | 0.453; −0.590 | 1.91 |
| 0.6; −0.6 | 1; 3 | 0.8; 0.2 | 0.467; −0.593 | 1.48 |
| 0.6; −0.6 | 100; 3 | 0.2; 0.8 | 0.582; −0.397 | 3.22 |
| 0.6; −0.6 | 100; 3 | 0.4; 0.6 | 0.568; −0.195 | 3.61 |
| 0.6; −0.6 | 100; 3 | 0.6; 0.4 | 0.561; 0.003 | 4.35 |
| 0.6; −0.6 | 100; 3 | 0.8; 0.2 | 0.566; 0.185 | 6.53 |
| Guess τs1 | τs2 | A1/A2 | Calculated GP | True GP |
|---|---|---|---|---|
| 0.50 | 3.49 | 0.55/0.45 | −0.378 | −0.329 |
| 0.80 | 6.25 | 0.72/0.28 | −0.352 | −0.329 |
| 0.89 | 8.62 | 0.748/0.252 | −0.332 | −0.329 |
| 0.90 | 9.00 | 0.750/0.250 | −0.329 | −0.329 |
| 0.91 | 9.41 | 0.752/0.248 | −0.325 | −0.329 |
| 1.0 | 15.27 | 0.75/0.25 | −0.282 | −0.329 |
| 1.2 | 47.83 | 0.635/0.365 | −0.106 | −0.329 |
| Phasor | Phasor | Model | GPi | GPf | τs1 | τs2 | A1 | τ | |
|---|---|---|---|---|---|---|---|---|---|
| interior | (0.276, 0.428) | (0.087, 0.4) | single | 0.76 | 0.35 | 2.55 | 0 | 0 | 3.63 |
| interior | (0.087, 0.4) | single | 0.73 | 0.25(f) | 2.20 | 0 | 0 | 3.63(f) | |
| interior | (0.087, 0.4) | double | 0.95(f) | 0.25(f) | 2.70 | 0.03 | 0.66 | 3.63(f) | |
| plasma | (0.190, 0.389) | (0.035, 0.350) | single | 0.960 | 0.880 | 2.70 | 0 | 0 | 4.19 |
| plasma | (0.035, 0.350) | single | 0.76 | 0.25(f) | 2.80 | 0 | 0 | 4.19(f) | |
| plasma | (0.035, 0.350) | double | 0.95(f) | 0.25(f) | 13 | 0.65 | 0.59 | 4.19(f) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Clayton, A.H.A. Spectral Relaxation Imaging Microscopy II: Complex Dynamics. Int. J. Mol. Sci. 2023, 24, 12271. https://doi.org/10.3390/ijms241512271
Clayton AHA. Spectral Relaxation Imaging Microscopy II: Complex Dynamics. International Journal of Molecular Sciences. 2023; 24(15):12271. https://doi.org/10.3390/ijms241512271
Chicago/Turabian StyleClayton, Andrew H. A. 2023. "Spectral Relaxation Imaging Microscopy II: Complex Dynamics" International Journal of Molecular Sciences 24, no. 15: 12271. https://doi.org/10.3390/ijms241512271
APA StyleClayton, A. H. A. (2023). Spectral Relaxation Imaging Microscopy II: Complex Dynamics. International Journal of Molecular Sciences, 24(15), 12271. https://doi.org/10.3390/ijms241512271





