Search for Dispersed Repeats in Bacterial Genomes Using an Iterative Procedure
Abstract
1. Introduction
2. Results
2.1. Using Model Sequences for the IP Method
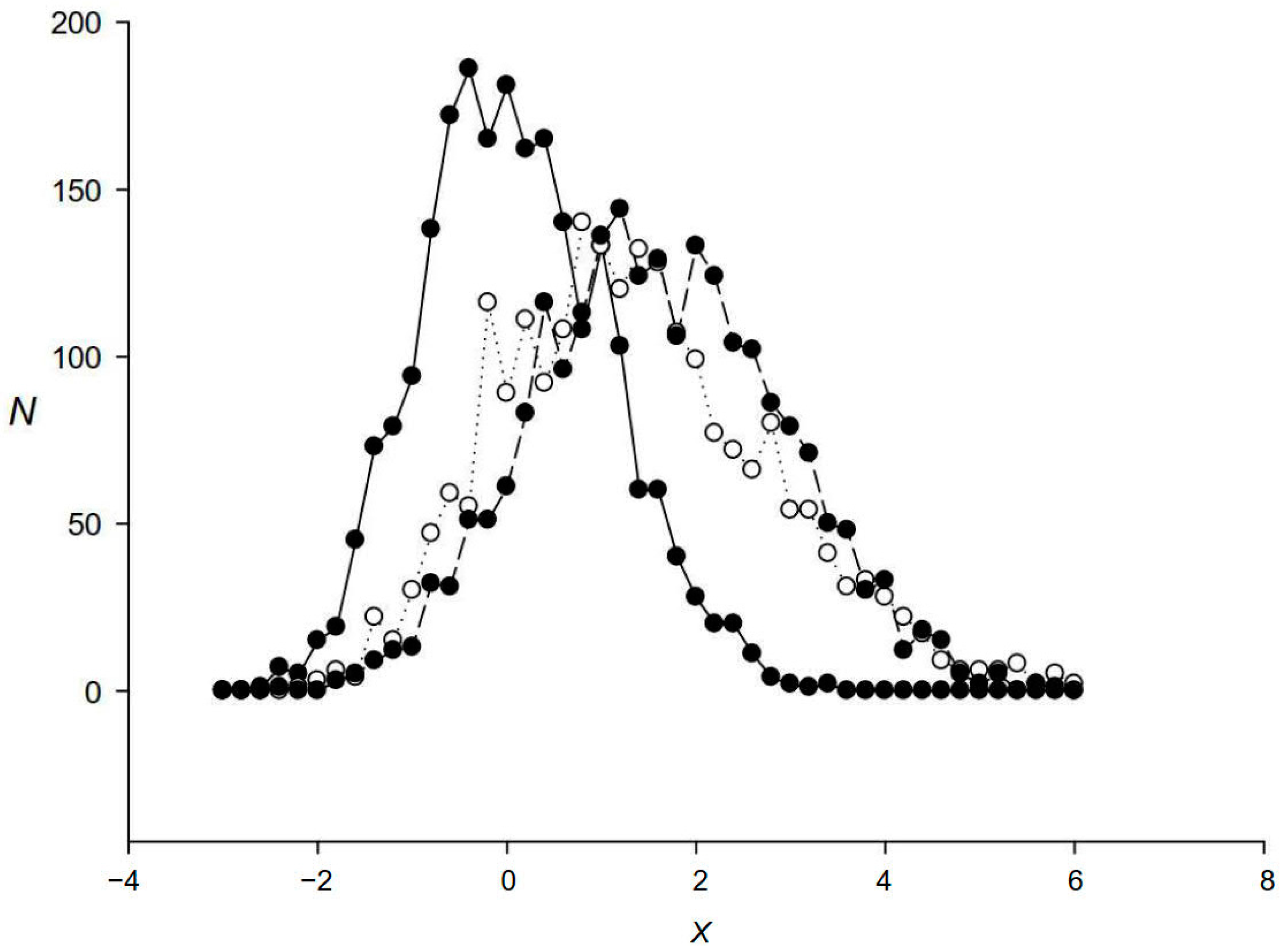
2.2. Comparison of the IP Method with RED, RECON, RepeatMasker, BLAST, and nHMMER
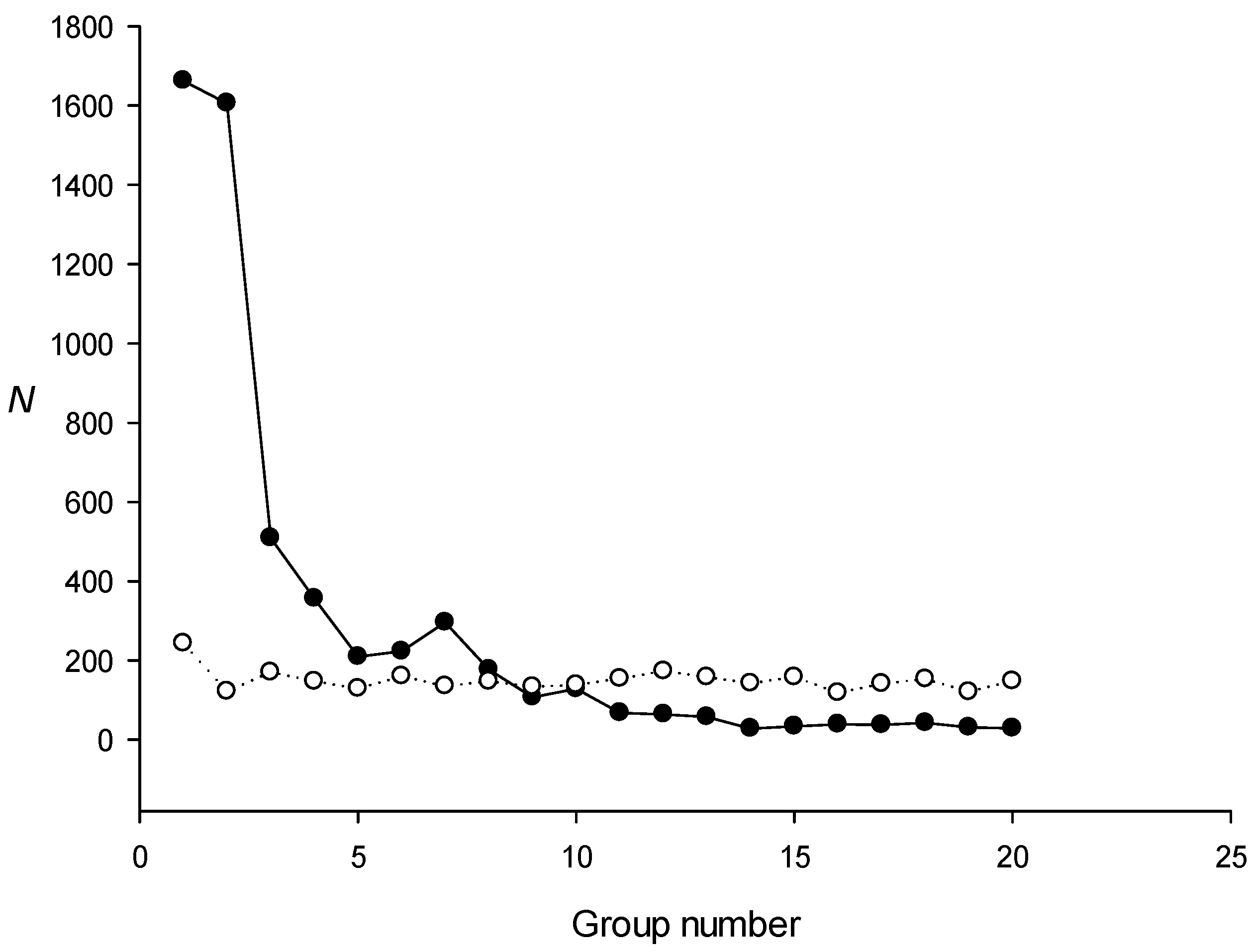
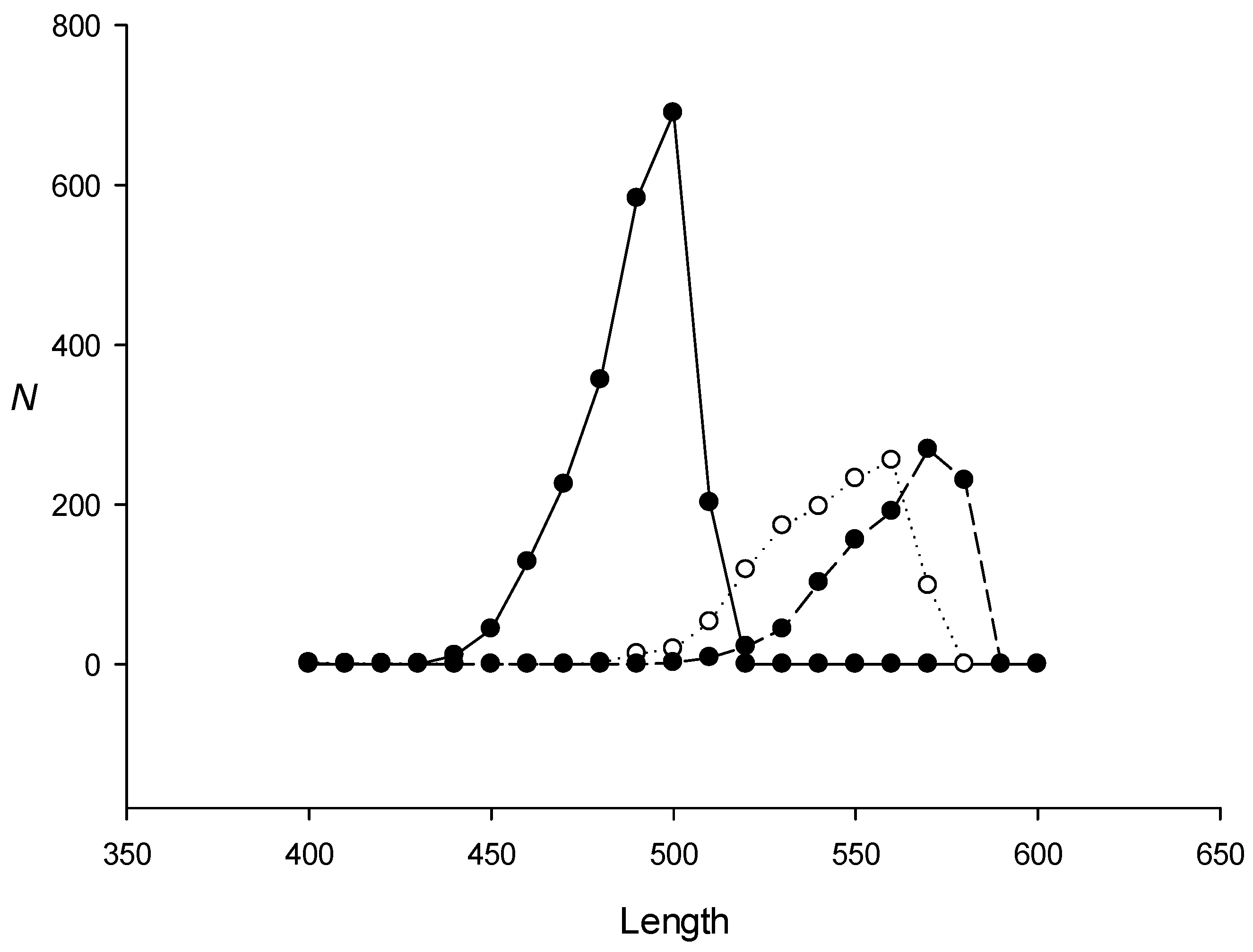
2.3. Search for Dispersed Repeats in the E. coli Genome Using the IP Method
2.4. Triplet Periodicity of Dispersed Repeat Families in the E. coli Genome
2.5. Comparison with Nucleoid-Associated Protein-Binding Sites
2.6. Search for the Families of Dispersed Repeats in the Genomes of Other Bacteria
3. Discussion
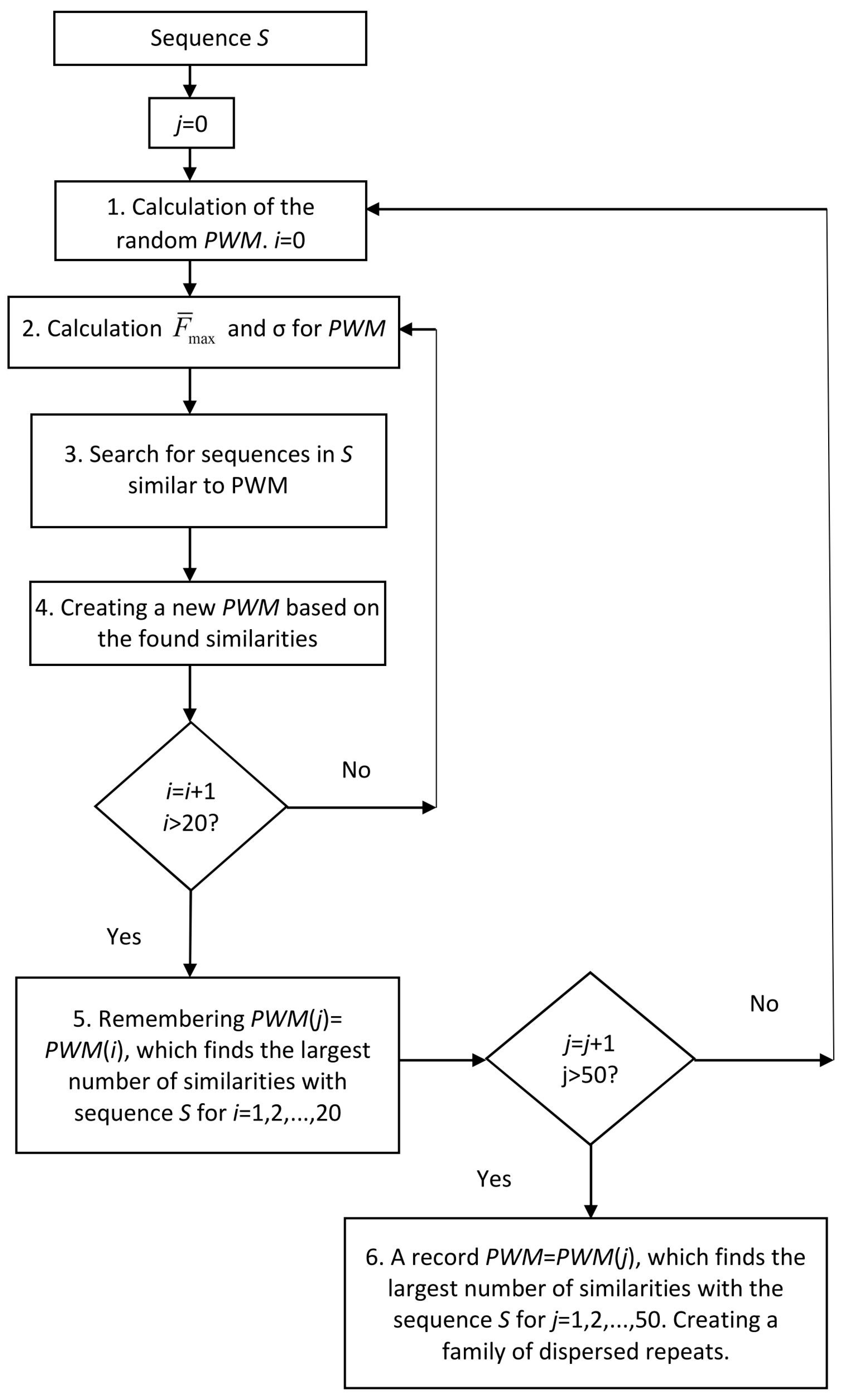
4. Materials and Methods
4.1. Calculation of the Random Matrix
4.2. Calculation of and σ for the PWM
4.3. Search for Similarities to the PWM in Sequence S
4.4. Creating a New PWM Based on the Found Similarities
4.5. Selection of the PWM to Find the Greatest Number of Similarities with Sequence S
4.6. Creating a Family of Dispersed Repeats
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Smit, A.F.A. The origin of interspersed repeats in the human genome. Curr. Opin. Genet. Dev. 1996, 6, 743–748. [Google Scholar] [CrossRef]
- Mayer, K.F.X.; Waugh, R.; Langridge, P.; Close, T.J.; Wise, R.P.; Graner, A.; Matsumoto, T.; Sato, K.; Schulman, A.; Ariyadasa, R.; et al. A physical, genetic and functional sequence assembly of the barley genome. Nature 2012, 491, 711–716. [Google Scholar] [CrossRef]
- Meyer, A.; Schloissnig, S.; Franchini, P.; Du, K.; Woltering, J.M.; Irisarri, I.; Wong, W.Y.; Nowoshilow, S.; Kneitz, S.; Kawaguchi, A.; et al. Giant lungfish genome elucidates the conquest of land by vertebrates. Nature 2021, 590, 284–289. [Google Scholar] [CrossRef]
- Gupta, P.K. Earth Biogenome Project: Present status and future plans: (Trends in Genetics 38:8 p: 811-820, 2022). Trends Genet. 2023, 39, 167. [Google Scholar] [CrossRef] [PubMed]
- Storer, J.M.; Hubley, R.; Rosen, J.; Smit, A.F.A. Methodologies for the De novo Discovery of Transposable Element Families. Genes 2022, 13, 709. [Google Scholar] [CrossRef] [PubMed]
- Tempel, S. Using and understanding repeatMasker. Methods Mol. Biol. 2012, 859, 29–51. [Google Scholar] [CrossRef] [PubMed]
- Jurka, J.; Klonowski, P.; Dagman, V.; Pelton, P. CENSOR—A program for identification and elimination of repetitive elements from DNA sequences. Comput. Chem. 1996, 20, 119–121. [Google Scholar] [CrossRef]
- Bedell, J.A.; Korf, I.; Gish, W. MaskerAid: A performance enhancement to RepeatMasker. Bioinformatics 2000, 16, 1040–1041. [Google Scholar] [CrossRef]
- Bao, W.; Kojima, K.K.; Kohany, O. Repbase Update, a database of repetitive elements in eukaryotic genomes. Mob. DNA 2015, 6, 11. [Google Scholar] [CrossRef]
- Girgis, H.Z. Red: An intelligent, rapid, accurate tool for detecting repeats de-novo on the genomic scale. BMC Bioinform. 2015, 16, 227. [Google Scholar] [CrossRef]
- Bao, Z.; Eddy, S.R. Automated de novo identification of repeat sequence families in sequenced genomes. Genome Res. 2002, 12, 1269–1276. [Google Scholar] [CrossRef]
- Edgar, R.C.; Myers, E.W. PILER: Identification and classification of genomic repeats. Bioinformatics 2005, 21 (Suppl. S1), i152–i158. [Google Scholar] [CrossRef]
- Price, A.L.; Jones, N.C.; Pevzner, P.A. De novo identification of repeat families in large genomes. Bioinformatics 2005, 21 (Suppl. S1), i351–i358. [Google Scholar] [CrossRef]
- Volfovsky, N.; Haas, B.J.; Salzberg, S.L. A clustering method for repeat analysis in DNA sequences. Genome Biol. 2001, 2, 0027.1. [Google Scholar] [CrossRef]
- Altschul, S.F.; Madden, T.L.; Schäffer, A.A.; Zhang, J.; Zhang, Z.; Miller, W.; Lipman, D.J. Gapped BLAST and PSI-BLAST: A new generation of protein database search programs. Nucleic Acids Res. 1997, 25, 3389–3402. [Google Scholar] [CrossRef] [PubMed]
- Mount, D.W. Using a FASTA Sequence Database Similarity Search. CSH Protoc. 2007, 2007, pdb.top16. [Google Scholar] [CrossRef] [PubMed]
- Tamura, K.; Peterson, D.; Peterson, N.; Stecher, G.; Nei, M.; Kumar, S. MEGA5: Molecular evolutionary genetics analysis using maximum likelihood, evolutionary distance, and maximum parsimony methods. Mol. Biol. Evol. 2011, 28, 2731–2739. [Google Scholar] [CrossRef] [PubMed]
- Wheeler, T.J.; Eddy, S.R. Nhmmer: DNA homology search with profile HMMs. Bioinformatics 2013, 29, 2487–2489. [Google Scholar] [CrossRef]
- Notredame, C.; Higgins, D.G.; Heringa, J. T-coffee: A novel method for fast and accurate multiple sequence alignment. J. Mol. Biol. 2000, 302, 205–217. [Google Scholar] [CrossRef]
- Edgar, R.C. MUSCLE: Multiple sequence alignment with high accuracy and high throughput. Nucleic Acids Res. 2004, 32, 1792–1797. [Google Scholar] [CrossRef]
- Korotkov, E.V.; Suvorova, Y.M.; Kostenko, D.O.; Korotkova, M.A. Multiple alignment of promoter sequences from the arabidopsis thaliana l. Genome. Genes 2021, 12, 135. [Google Scholar] [CrossRef]
- Blattner, F.R.; Plunkett, G.; Bloch, C.A.; Perna, N.T.; Burland, V.; Riley, M.; Collado-Vides, J.; Glasner, J.D.; Rode, C.K.; Mayhew, G.F.; et al. The complete genome sequence of Escherichia coli K-12. Science 1997, 277, 1453–1462. [Google Scholar] [CrossRef] [PubMed]
- Kostenko, D.O.; Korotkov, E.V.; Kostenko, D.O.; Korotkov, E.V. Application of the MAHDS Method for Multiple Alignment of Highly Diverged Amino Acid Sequences. Int. J. Mol. Sci. 2022, 23, 3764. [Google Scholar] [CrossRef] [PubMed]
- Verma, S.C.; Qian, Z.; Adhya, S.L. Architecture of the Escherichia coli nucleoid. PLoS Genet. 2019, 15, e1008456. [Google Scholar] [CrossRef] [PubMed]
- Suvorova, Y.M.; Kamionskaya, A.M.; Korotkov, E.V. Search for SINE repeats in the rice genome using correlation-based position weight matrices. BMC Bioinform. 2021, 22, 42. [Google Scholar] [CrossRef]
- Frenkel, F.E.E.; Korotkov, E.V. V Classification analysis of triplet periodicity in protein-coding regions of genes. Gene 2008, 421, 52–60. [Google Scholar] [CrossRef]
- Suvorova, Y.M.; Korotkov, E.V. Study of triplet periodicity differences inside and between genomes. Stat. Appl. Genet. Mol. Biol. 2015, 14, 113–123. [Google Scholar] [CrossRef]
- Kahramanoglou, C.; Seshasayee, A.S.N.; Prieto, A.I.; Ibberson, D.; Schmidt, S.; Zimmermann, J.; Benes, V.; Fraser, G.M.; Luscombe, N.M. Direct and indirect effects of H-NS and Fis on global gene expression control in Escherichia coli. Nucleic Acids Res. 2011, 39, 2073–2091. [Google Scholar] [CrossRef]
- Prieto, A.I.; Kahramanoglou, C.; Ali, R.M.; Fraser, G.M.; Seshasayee, A.S.N.; Luscombe, N.M. Genomic analysis of DNA binding and gene regulation by homologous nucleoid-associated proteins IHF and HU in Escherichia coli K12. Nucleic Acids Res. 2012, 40, 3524–3537. [Google Scholar] [CrossRef]
- Quinlan, A.R.; Hall, I.M. BEDTools: A flexible suite of utilities for comparing genomic features. Bioinformatics 2010, 26, 841–842. [Google Scholar] [CrossRef]
- Trotta, E. The 3-Base Periodicity and Codon Usage of Coding Sequences Are Correlated with Gene Expression at the Level of Transcription Elongation. PLoS ONE 2011, 6, e21590. [Google Scholar] [CrossRef] [PubMed]
- Sánchez, J.; López-Villaseñor, I. A simple model to explain three-base periodicity in coding DNA. FEBS Lett. 2006, 580, 6413–6422. [Google Scholar] [CrossRef] [PubMed]
- Großmann, P.; Lück, A.; Kaleta, C. Model-based genome-wide determination of RNA chain elongation rates in Escherichia coli. Sci. Rep. 2017, 7, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Yevdokimov, Y.M.; Salyanov, V.I.; Nechipurenko, Y.D.; Skuridin, S.G.; Zakharov, M.A.; Spener, F.; Palumbo, M. Molecular Constructions (Superstructures) with Adjustable Properties Based on Double-Stranded Nucleic Acids. Mol. Biol. 2003, 37, 293–306. [Google Scholar] [CrossRef]
- Yevdokimov, Y.M.; Salyanov, V.I.; Skuridin, S.G. From liquid crystals to DNA nanoconstructions. Mol. Biol. 2009, 43, 284–300. [Google Scholar] [CrossRef]
- Skuridin, S.G.; Vereshchagin, F.V.; Salyanov, V.I.; Chulkov, D.P.; Kompanets, O.N.; Yevdokimov, Y.M. Ordering of double-stranded DNA molecules in a cholesteric liquid-crystalline phase and in dispersion particles of this phase. Mol. Biol. 2016, 50, 783–790. [Google Scholar] [CrossRef]
- Pugacheva, V.; Korotkov, A.; Korotkov, E. Search of latent periodicity in amino acid sequences by means of genetic algorithm and dynamic programming. Stat. Appl. Genet. Mol. Biol. 2016, 15, 381–400. [Google Scholar] [CrossRef]
- Korotkov, E.V.; Suvorova, Y.M.; Nezhdanova, A.V.; Gaidukova, S.E.; Yakovleva, I.V.; Kamionskaya, A.M.; Korotkova, M.A. Mathematical Algorithm for Identification of Eukaryotic Promoter Sequences. Symmetry 2021, 13, 917. [Google Scholar] [CrossRef]
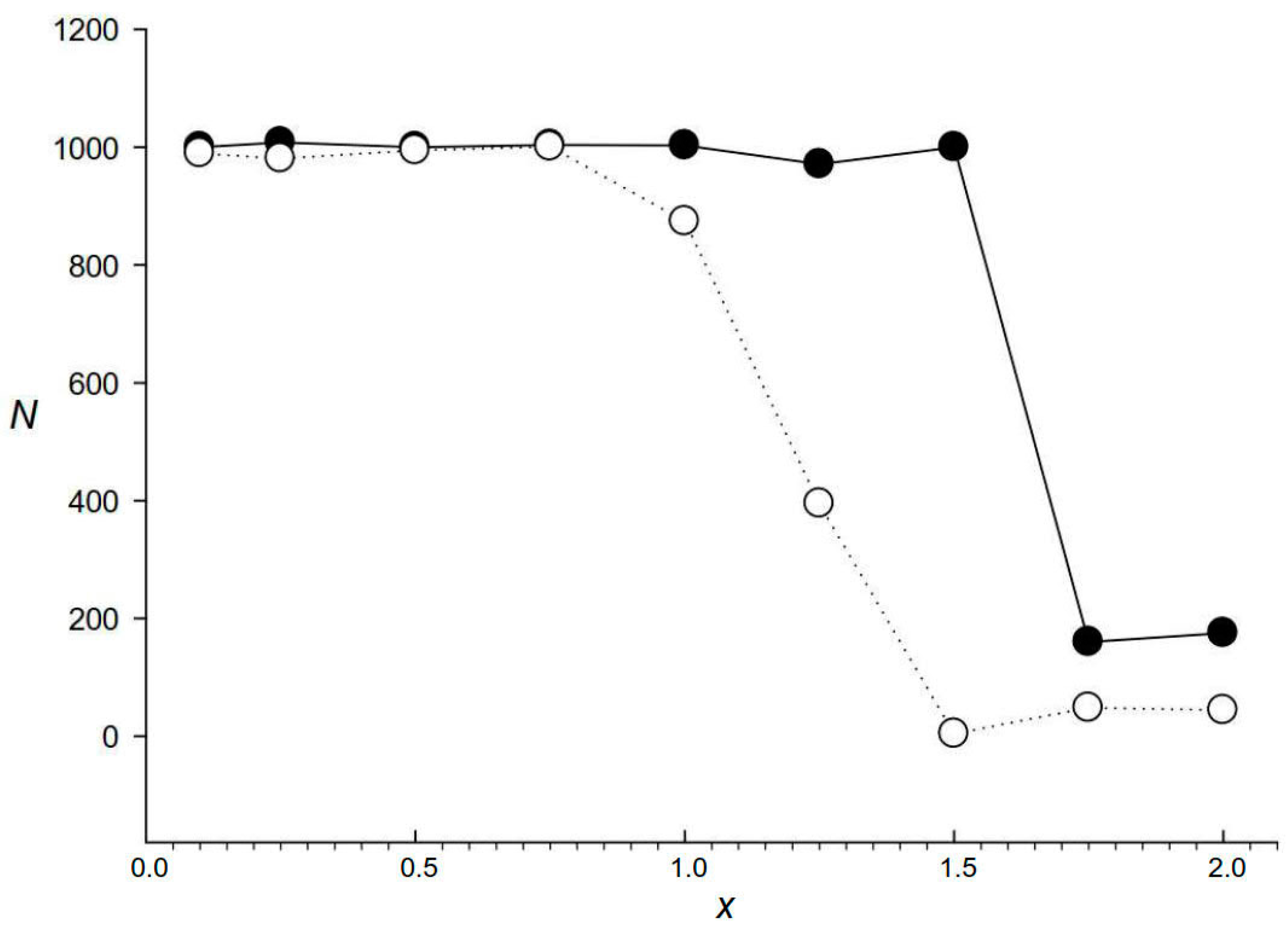

| x | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 0 | 508 | 490 | 51 | 71 |
| 0.5 | 503 | 502 | 55 | 62 |
| 0.75 | 507 | 496 | 95 | 75 |
| 1.0 | 505 | 502 | 102 | 113 |
| 1.25 | 506 | 501 | 85 | 92 |
| 1.5 | 501 | 483 | 112 | 101 |
| 1.75 | 166 | 152 | 139 | 124 |
| 2.0 | 125 | 144 | 138 | 132 |
| 4.0 | 114 | 127 | 132 | 90 |
| x | 0.1 | 0.25 | 0.5 | 0.75 | 1.0 | 1.25 | 1.5 | 2.0 | 2.5 | 3.0 | 4.0 | 20.0 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| BLAST | 1000 | 1000 | 1001 | 1000 | 1000 | 2.9 | 1.4 | 1.1 | 2.0 | 0.2 | 1.1 | 1.2 |
| nHMMER | 1004 | 1002 | 1004 | 1006 | 1002 | 1002 | 1004 | 1003 | 992 | 668 | 21 | 0 |
| IP | 1068 | 1006 | 1003 | 1002 | 1005 | 1002 | 1004 | 1003 | 1065 | 907 | 221 | 80 |
| Families | Proportion of Non-Coding Sequences | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0.0–0.1 | 0.1–0.2 | 0.2–0.3 | 0.3–0.4 | 0.4–0.5 | 0.5–0.6 | 0.6–0.7 | 0.7–0.8 | 0.8–0.9 | 0.9–1.0 | |
| 1 | 1956 | 129 | 58 | 36 | 22 | 7 | 3 | 2 | 1 | 25 |
| 2 | 918 | 97 | 60 | 32 | 13 | 11 | 4 | 4 | 3 | 28 |
| 3 | 709 | 116 | 72 | 43 | 29 | 15 | 8 | 2 | 3 | 27 |
| DNA Bases | A | B | C | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | |
| A | −48.7 | −3.5 | 52.2 | 9.2 | 22.8 | −32.0 | 24.7 | 3.9 | −28.6 |
| T | −9.8 | −27.4 | 37.3 | −40.4 | 7.7 | 32.7 | −19.1 | 28.0 | −8.8 |
| C | 17.2 | 37.1 | −54.4 | −20.4 | −22.1 | 42.6 | −6.8 | −18.7 | 25.6 |
| G | 37.2 | −8.6 | −28.5 | 49.3 | −7.13 | −42.2 | 1.4 | −12.1 | 10.7 |
| Bacteria | 1 | 2 | 3 | 4 | Genome Size |
|---|---|---|---|---|---|
| Azotobacter vinelandii | 4565 | 1357 | 322 | 178 | 5.3 × 106 |
| Bacillus subtilis | 2563 | 768 | 340 | 305 | 4.2 × 106 |
| Clostridium tetani | 1605 | 640 | 168 | 111 | 2.8 × 106 |
| Methylococcus capsulatus | 2489 | 375 | 280 | 95 | 3.3 × 106 |
| Mycobacterium tuberculosis | 3343 | 1152 | 299 | 103 | 4.4 × 106 |
| Shigella sonnei | 2606 | 645 | 519 | 358 | 5.0 × 106 |
| Treponema pallidum | 590 | 273 | 83 | 46 | 1.1 × 106 |
| Xanthomonas campestris | 4622 | 1348 | 359 | 75 | 5.1 × 106 |
| Yersinia pestis | 1953 | 43 | 35 | 43 | 4.8 × 106 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Korotkov, E.; Suvorova, Y.; Kostenko, D.; Korotkova, M. Search for Dispersed Repeats in Bacterial Genomes Using an Iterative Procedure. Int. J. Mol. Sci. 2023, 24, 10964. https://doi.org/10.3390/ijms241310964
Korotkov E, Suvorova Y, Kostenko D, Korotkova M. Search for Dispersed Repeats in Bacterial Genomes Using an Iterative Procedure. International Journal of Molecular Sciences. 2023; 24(13):10964. https://doi.org/10.3390/ijms241310964
Chicago/Turabian StyleKorotkov, Eugene, Yulia Suvorova, Dimitry Kostenko, and Maria Korotkova. 2023. "Search for Dispersed Repeats in Bacterial Genomes Using an Iterative Procedure" International Journal of Molecular Sciences 24, no. 13: 10964. https://doi.org/10.3390/ijms241310964
APA StyleKorotkov, E., Suvorova, Y., Kostenko, D., & Korotkova, M. (2023). Search for Dispersed Repeats in Bacterial Genomes Using an Iterative Procedure. International Journal of Molecular Sciences, 24(13), 10964. https://doi.org/10.3390/ijms241310964





