Application of Multivariate Adaptive Regression Splines (MARSplines) for Predicting Antitumor Activity of Anthrapyrazole Derivatives
Abstract
:1. Introduction
2. Results
2.1. Geometry Optimization
2.2. Statistical Analysis
2.2.1. Model Construction and Prediction of pIC50 Values
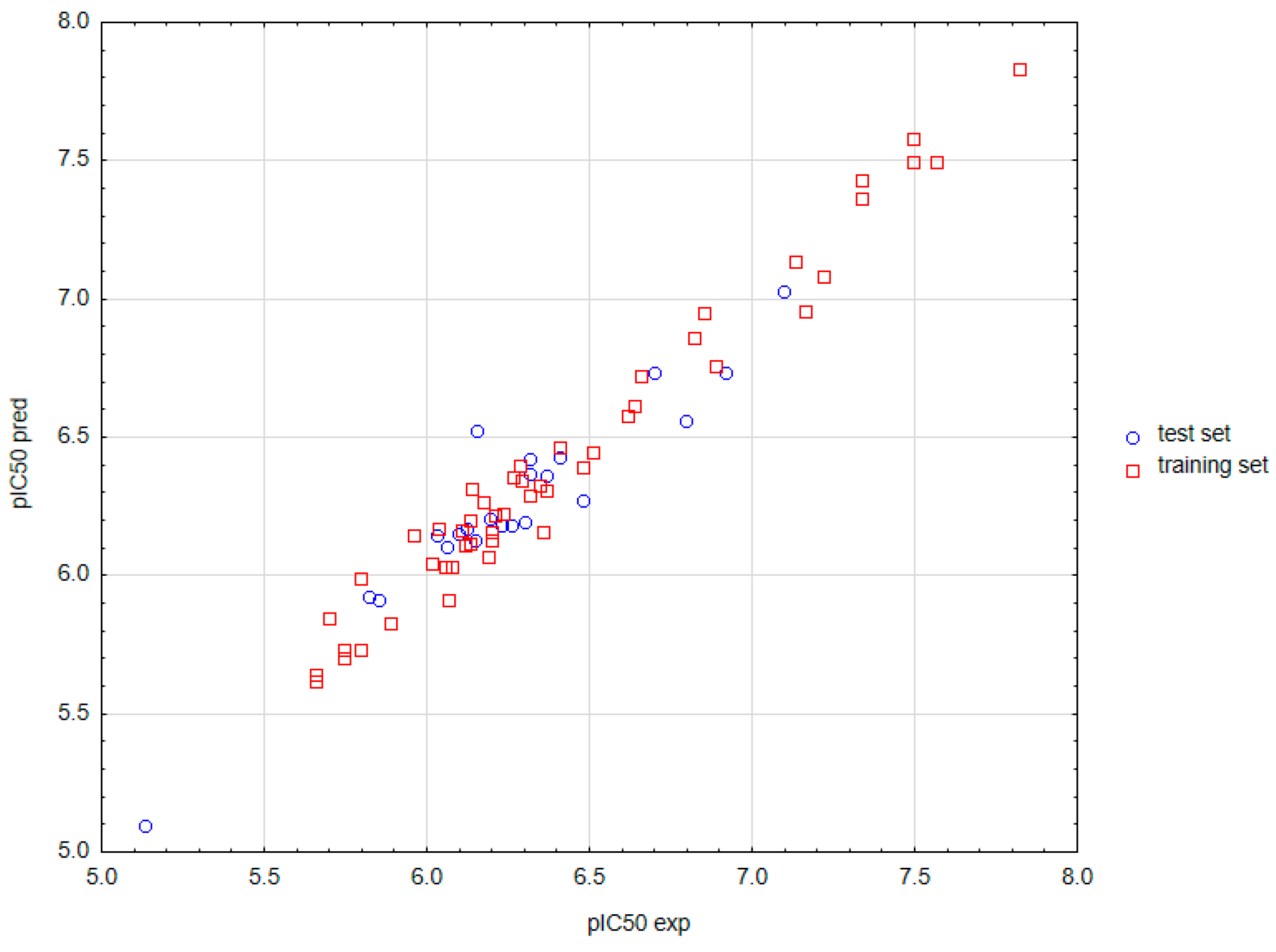
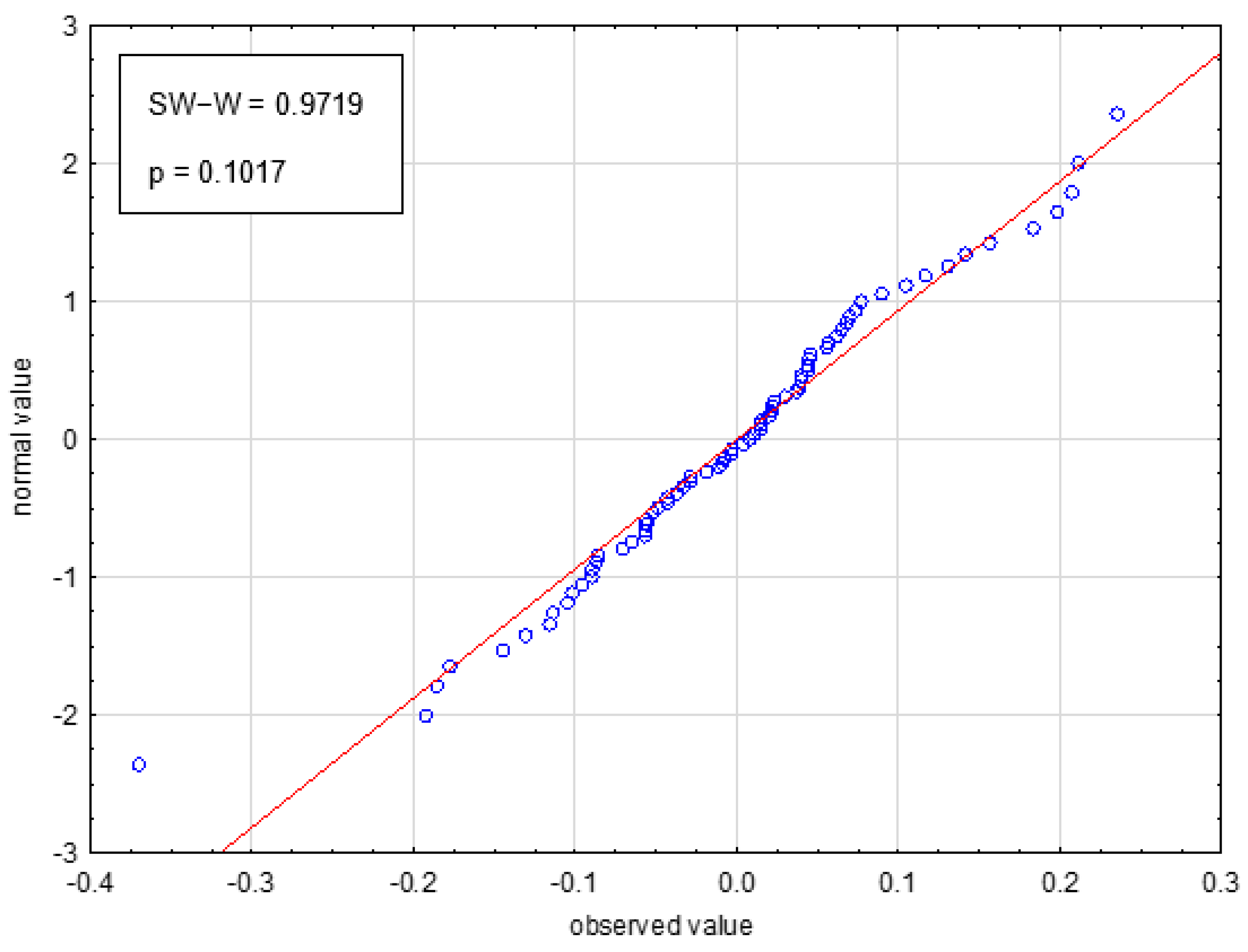
2.2.2. Validation of Models and Selection of the Optimal One for Prediction
2.3. Values of Predicted Data
3. Discussion
4. Materials and Methods
4.1. Anthrapyrazole Derivatives
4.2. Geometry Optimization and Structural Descriptors
4.3. Statistical Analysis
4.4. MARSplines Analysis
4.5. Model Validation
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Nelson, J.M.; Plowman, J.; Jackson, R.C.; Leopold, W.R. Anthrapyrazoles, a new class of intercalating agents with high-level, broad spectrum activity against murine tumors. Cancer Res. 1985, 45, 5532–5539. [Google Scholar]
- Fry, D.W.; Boritzki, T.J.; Besserer, J.A.; Jackson, R.C. In vitro DNA strand scission and inhibition of nucleic acid synthesis in L1210 leukemia cells by a new class of DNA complexers, the anthra[1,9-cd]pyrazol-6(2H)-ones (anthrapyrazoles). Biochem. Pharmacol. 1985, 34, 3499–3508. [Google Scholar] [CrossRef]
- Begleiter, A.; Lin, D.; Larson, K.K.; Lang, J.; Wu, X.; Cabral, T.; Taylor, H.; Guziec, L.J.; Kerr, P.D.; Hasinoff, B.B.; et al. Structure-activity studies with cytotoxic anthrapyrazoles. Oncol. Rep. 2006, 15, 1575–1580. [Google Scholar] [CrossRef] [Green Version]
- Klohs, W.D.; Steinkampf, R.W.; Havlick, M.J.; Jackson, R.C. Resistance to anthrapyrazoles and anthracyclines in multidrug-resistant P388 murine leukemia cells: Reversal by calcium blockers and calmodulin antagonists. Cancer Res. 1986, 46, 4352–4356. [Google Scholar] [PubMed]
- Talbot, D.C.; Smith, I.E.; Mansi, J.L.; Judson, I.; Calvert, A.H.; Ashley, S.E. Anthrapyrazole CI941: A highly active new agent in the treatment of advanced breast cancer. J. Clin. Oncol. 1991, 9, 2141–2147. [Google Scholar] [CrossRef] [PubMed]
- Friedman, J.H. Multivariate adaptive regression splines. Ann. Stat. 1991, 19, 1–141. [Google Scholar] [CrossRef]
- Kryshchyshyn, A.; Devinyak, O.; Kaminskyy, D.; Grellier, P.; Lesyk, R. Development of predictive QSAR models of 4-thiazolidinones antitrypanosomal activity using modern machine learning algorithms. Mol. Inform. 2018, 37, 1700078. [Google Scholar] [CrossRef] [PubMed]
- Nguyen-Cong, V.; Van Dang, G.; Rode, B.M. Using multivariate adaptive regression splines to QSAR studies of dihydroartemisinin derivatives. Eur. J. Med. Chem. 1996, 31, 797–803. [Google Scholar] [CrossRef]
- Jalali-Heravi, M.; Asadollahi-Baboli, M.; Mani-Varnosfaderani, A. Shuffling multivariate adaptive regression splines and adaptive neuro-fuzzy inference system as tools for QSAR study of SARS inhibitors. J. Pharm. Biomed. Anal. 2009, 50, 853–860. [Google Scholar] [CrossRef] [PubMed]
- Koba, M.; Bączek, T. The evaluation of multivariate adaptive regression splines for the prediction of antitumor activity of acridinone derivatives. Med. Chem. 2013, 9, 1041–1050. [Google Scholar] [CrossRef] [PubMed]
- Hollis Showalter, H.D.; Johnson, J.L.; Hoftiezer, J.M.; Turner, W.R.; Werbel, L.M.; Leopold, W.R.; Shillis, J.L.; Jackson, R.C.; Elslager, E.F. Anthrapyrazole anticancer agents. synthesis and structure-activity relationships against murine leukemias. J. Med. Chem. 1987, 30, 121–131. [Google Scholar] [CrossRef] [PubMed]
- Liang, H.; Wu, X.; Guziec, L.J.; Guziec, F.S.; Larson, K.K.; Lang, J.; Yalowich, J.C.; Hasinoff, B.B. A structure-based 3D-QSAR study of anthrapyrazole analogues of the anticancer agents losoxantrone and piroxantrone. J. Chem. Inf. Model. 2006, 46, 1827–1835. [Google Scholar] [CrossRef] [PubMed]
- Roy, K.; Ambure, P.; Kar, S.; Ojha, P.K. Is it possible to improve the quality of predictions from an “intelligent” use of multiple QSAR/QSPR/QSTR models? J. Chemom. 2018, 32, e2992. [Google Scholar] [CrossRef]
- Devinyak, O.; Havrylyuk, D.; Lesyk, R. 3D-MoRSE descriptors explained. J. Mol. Graph. Model. 2014, 54, 194–203. [Google Scholar] [CrossRef] [PubMed]
- Todeschini, R.; Consonni, V. Molecular Descriptors for Chemoinformatics; Wiley-VCH: Weinheim, Germany, 2009. [Google Scholar]
- Hollas, B. An analysis of the autocorrelation descriptor for molecules. J. Math. Chem. 2003, 33, 91–101. [Google Scholar] [CrossRef]
- Wong, K.Y.; Mercader, A.G.; Saavedra, L.M.; Honarparvar, B.; Romanelli, G.P.; Duchowicz, P.R. QSAR analysis on tacrine-related acetylcholinesterase inhibitors. J. Biomed. Sci. 2014, 21, 84. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hartley, J.A.; Reszka, K.; Zuo, E.T.; Wilson, W.D.; Morgan, A.R.; Lown, J.W. Characteristics of the interaction of anthrapyrazole anticancer agents with deoxyribonucleic acids: Structural requirements for DNA binding, intercalation, and photosensitization. Mol. Pharmacol. 1988, 33, 265–271. [Google Scholar] [PubMed]
- Alamdari, R.F.; Mani-Varnosfaderani, A.; Asadollahi-Baboli, M.; Khalafi-Nezhad, A. Monte Carlo sampling and multivariate adaptive regression splines as tools for QSAR modelling of HIV-1 reverse transcriptase inhibitors. SAR QSAR Environ. Res. 2012, 23, 665–682. [Google Scholar] [CrossRef] [PubMed]
- Talete SRL List of Molecular Descriptors Calculated by Dragon. Available online: http://www.talete.mi.it/products/dragon_molecular_descriptor_list.pdf (accessed on 25 February 2022).
- Tropsha, A. Best practices for QSAR model development, validation, and exploitation. Mol. Inform. 2010, 29, 476–488. [Google Scholar] [CrossRef] [PubMed]
- Hastie, T.; Tibshirani, R.; Friedman, J. Additive models, trees, and related methods. In The Elements of Statistical Learning Data Mining, Inference, and Prediction; Springer Series in Statistics; Springer: Stanford, CA, USA, 2001. [Google Scholar]
| Compound | Set | Descriptors | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mor05s | Mor19m | MATS8e | H1e | ATSC7v | ATSC1e | SpMax8_Bh(s) | Mor21e | Mor13s | R5p | ATSC1s | ATSC8s | RDF135e | HATS5s | ||
| a-01 | training | −23.248 | 0.14 | 0.071 | 1.868 | 8.747 | 0.089 | 3.701 | −1.038 | −3.106 | 0.355 | 10.915 | 24.843 | 3.716 | 0.885 |
| a-02 | test | −24.151 | 0.35 | 0.086 | 2.449 | 10.376 | 0.063 | 3.729 | −1.668 | −2.011 | 0.431 | 7.562 | 17.708 | 2.312 | 0.888 |
| a-03 | test | −25.044 | 0.312 | 0.088 | 1.887 | 10.229 | 0.072 | 3.805 | −1.273 | −3.232 | 0.352 | 9.636 | 26.817 | 4.833 | 0.696 |
| a-04 | training | −26.013 | 0.527 | 0.093 | 2.415 | 11.909 | 0.062 | 3.826 | −1.909 | −1.983 | 0.42 | 7.486 | 19.947 | 2.33 | 0.731 |
| a-07 | training | −28.355 | 0.374 | 0.136 | 2.266 | 12.334 | 0.108 | 3.868 | −1.422 | −3.935 | 0.34 | 14.861 | 70.152 | 8.044 | 0.59 |
| a-08 | training | −29.427 | 0.556 | 0.173 | 2.494 | 14.042 | 0.067 | 3.892 | −1.992 | −2.491 | 0.393 | 9.462 | 63.182 | 6.066 | 0.623 |
| a-14 | test | −27.108 | 0.38 | 0.081 | 2.352 | 13.021 | 0.09 | 3.868 | −1.49 | −4.166 | 0.356 | 12.928 | 53.706 | 7.109 | 0.56 |
| a-15 | training | −24.585 | 0.405 | 0.087 | 2.499 | 10.664 | 0.072 | 3.731 | −0.942 | −2.711 | 0.462 | 9.69 | 34.523 | 0 | 1.068 |
| a-16 | test | −27.47 | 0.41 | 0.104 | 2.485 | 12.554 | 0.108 | 3.93 | −1.01 | −5.516 | 0.43 | 14.861 | 50.769 | 2.714 | 0.979 |
| a-17 | training | −26.332 | 0.399 | 0.045 | 2.651 | 13.246 | 0.09 | 3.91 | −0.998 | −4.039 | 0.463 | 12.928 | 48.529 | 2.581 | 0.748 |
| a-18 | training | −27.16 | 0.354 | 0.051 | 2.486 | 14.206 | 0.117 | 4.11 | −1.333 | −4.656 | 0.372 | 15.025 | 49.723 | 9.628 | 0.857 |
| a-19 | training | −27.182 | 0.593 | 0.084 | 2.453 | 15.132 | 0.071 | 3.913 | −1.856 | −4.49 | 0.397 | 10.351 | 43.961 | 5.776 | 0.78 |
| a-20 | training | −30.264 | 0.711 | 0.074 | 2.685 | 16.896 | 0.084 | 3.943 | −2.188 | −2.689 | 0.513 | 10.256 | 41.257 | 8.767 | 0.675 |
| a-21 | training | −30.336 | 0.887 | −0.015 | 2.454 | 18.916 | 0.093 | 3.892 | −2.927 | −1.602 | 0.439 | 9.089 | 37.67 | 14.127 | 0.535 |
| a-23 | training | −28.063 | 0.473 | 0.052 | 2.395 | 15.141 | 0.079 | 3.892 | −1.916 | −3.363 | 0.473 | 9.555 | 42.176 | 3.359 | 0.664 |
| a-24 | training | −28.566 | 0.547 | 0.075 | 2.397 | 16.123 | 0.079 | 3.892 | −2.428 | −2.117 | 0.456 | 8.749 | 39.386 | 6.171 | 0.6 |
| a-25 | training | −28.039 | 0.772 | 0.062 | 2.431 | 17.093 | 0.084 | 3.892 | −1.927 | −3.76 | 0.447 | 10.256 | 40.357 | 5.936 | 0.665 |
| a-26 | test | −28.873 | 0.779 | 0.086 | 2.44 | 18.887 | 0.093 | 3.892 | −2.847 | −1.14 | 0.526 | 9.581 | 35.763 | 10.198 | 0.721 |
| a-27 | training | −32.526 | 0.886 | 0.054 | 2.46 | 20.027 | 0.099 | 3.892 | −3.152 | −2.312 | 0.496 | 10.073 | 41.721 | 15.563 | 0.608 |
| a-28 | training | −31.513 | 0.772 | −0.034 | 2.59 | 21.69 | 0.105 | 3.892 | −3.454 | −0.694 | 0.575 | 10.551 | 43.578 | 19.845 | 0.613 |
| a-29 | training | −35.189 | 1.108 | 0.022 | 2.504 | 25.218 | 0.122 | 3.941 | −4.494 | 0.073 | 0.54 | 11.901 | 44.571 | 23.851 | 0.586 |
| a-30 | test | −29.895 | 0.984 | 0.074 | 2.711 | 18.211 | 0.069 | 3.892 | −2.825 | −3.798 | 0.571 | 7.221 | 34.729 | 4.623 | 0.685 |
| a-31 | test | −32.648 | 1.182 | 0.088 | 2.692 | 18.629 | 0.09 | 3.892 | −2.855 | −1.78 | 0.566 | 8.368 | 34.604 | 4.618 | 0.639 |
| a-32 | training | −37.679 | 0.603 | 0.07 | 2.84 | 23.509 | 0.063 | 4.302 | −3.52 | −2.193 | 0.555 | 10.118 | 61.697 | 2.066 | 0.602 |
| a-33 | training | −31.756 | 0.295 | −0.15 | 1.854 | 7.964 | 0.15 | 3.907 | −0.585 | −6.758 | 0.325 | 19.422 | 68.778 | 0 | 0.778 |
| a-34 | training | −32.952 | 0.272 | −0.084 | 1.962 | 9.944 | 0.173 | 4.222 | −0.896 | −7.17 | 0.355 | 21.396 | 65.841 | 4.312 | 0.899 |
| a-35 | training | −34.132 | 0.496 | −0.082 | 2.486 | 11.745 | 0.09 | 3.942 | −1.561 | −5.943 | 0.429 | 12.554 | 50.107 | 5.362 | 0.949 |
| a-36 | training | −36.292 | 0.493 | −0.047 | 2.613 | 14.261 | 0.089 | 4.279 | −1.313 | −5.809 | 0.423 | 13.378 | 57.153 | 3.503 | 0.845 |
| a-38 | training | −35.884 | 0.327 | 0.03 | 2.49 | 13.45 | 0.186 | 4.35 | −1.215 | −7.443 | 0.375 | 21.7 | 96.608 | 7.612 | 0.876 |
| a-40 | training | −35.247 | 0.336 | −0.005 | 2.396 | 10.119 | 0.194 | 4.342 | −0.67 | −7.823 | 0.364 | 27.496 | 130.412 | 0 | 0.885 |
| a-41 | training | −36.566 | 0.293 | 0.019 | 2.379 | 12.094 | 0.218 | 4.352 | −1.021 | −7.791 | 0.354 | 29.098 | 127.386 | 7.555 | 0.807 |
| a-42 | training | −36.299 | 0.373 | 0.052 | 2.445 | 12.008 | 0.152 | 4.281 | −1.172 | −7.005 | 0.324 | 19.476 | 115.944 | 1.162 | 0.692 |
| a-43 | training | −37.466 | 0.485 | 0.052 | 2.58 | 13.9 | 0.128 | 4.279 | −1.574 | −6.836 | 0.419 | 18.037 | 111.512 | 4.311 | 0.833 |
| a-44 | training | −38.067 | 0.711 | 0.036 | 2.823 | 13.123 | 0.178 | 4.346 | −1.597 | −7.37 | 0.535 | 20.604 | 115.411 | 0 | 1.067 |
| a-46 | training | −40.983 | 0.422 | 0.034 | 2.466 | 16.838 | 0.191 | 4.376 | −1.732 | −7.572 | 0.369 | 26.156 | 131.348 | 11.288 | 0.83 |
| a-47 | test | −34.614 | 0.389 | −0.101 | 2.466 | 10.872 | 0.166 | 4.339 | −0.836 | −7.493 | 0.38 | 24.127 | 106.027 | 0 | 0.873 |
| a-48 | training | −34.595 | 0.45 | −0.09 | 2.484 | 12.098 | 0.155 | 4.343 | −1.003 | −7.772 | 0.37 | 23.038 | 115.094 | 0 | 0.866 |
| a-49 | test | −34.259 | 0.372 | −0.064 | 2.438 | 11.805 | 0.147 | 4.281 | −1.068 | −7.085 | 0.368 | 18.738 | 96.646 | 0.712 | 0.82 |
| a-50 | training | −37.076 | 0.338 | −0.056 | 2.383 | 12.827 | 0.189 | 4.351 | −0.811 | −7.866 | 0.355 | 25.724 | 102.909 | 8.225 | 0.782 |
| a-51 | test | −38.93 | 0.529 | −0.085 | 2.593 | 14.213 | 0.177 | 4.35 | −0.971 | −7.42 | 0.451 | 24.541 | 110.401 | 2.928 | 1.43 |
| a-52 | test | −39.941 | 0.441 | −0.064 | 2.404 | 15.776 | 0.126 | 4.331 | −1.487 | −6.097 | 0.372 | 16.891 | 97.497 | 10.951 | 0.628 |
| a-53 | test | −36.787 | 0.433 | −0.133 | 2.481 | 14.405 | 0.177 | 4.354 | −1.006 | −8.223 | 0.363 | 24.541 | 84.423 | 7.287 | 0.858 |
| a-54 | test | −39.871 | 0.503 | −0.151 | 2.419 | 17.328 | 0.116 | 4.336 | −1.735 | −6.213 | 0.358 | 16.214 | 74.598 | 13.241 | 0.756 |
| a-55 | training | −36.81 | 0.361 | −0.043 | 2.5 | 14.185 | 0.169 | 4.308 | −1.119 | −7.462 | 0.376 | 20.409 | 83.802 | 6.619 | 0.863 |
| a-56 | training | −34.217 | 0.218 | −0.08 | 2.735 | 13.043 | 0.189 | 4.354 | −0.752 | −9.059 | 0.476 | 25.724 | 93.711 | 2.594 | 0.994 |
| a-57 | training | −36.624 | 0.562 | −0.074 | 2.586 | 14.298 | 0.177 | 4.356 | −0.99 | −10.128 | 0.414 | 24.541 | 102.629 | 3.705 | 1.362 |
| a-60 | training | −33.756 | 0.421 | −0.054 | 2.572 | 14.011 | 0.169 | 4.302 | −0.952 | −8.742 | 0.416 | 20.409 | 84.468 | 4.29 | 1.368 |
| a-62 | training | −37.503 | 0.552 | −0.048 | 2.772 | 15.019 | 0.212 | 4.359 | −1.275 | −8.56 | 0.43 | 27.21 | 90.663 | 3.006 | 0.789 |
| a-63 | training | −41.791 | 0.386 | −0.072 | 2.813 | 16.385 | 0.199 | 4.358 | −1.074 | −9.141 | 0.5 | 25.97 | 97.975 | 2.933 | 0.898 |
| a-64 | test | −41.408 | 0.429 | −0.024 | 2.67 | 17.542 | 0.234 | 4.447 | −1.311 | −9.127 | 0.436 | 32.045 | 92.108 | 8.337 | 1.114 |
| a-65 | training | −42.394 | 0.647 | −0.069 | 2.737 | 18.936 | 0.22 | 4.445 | −1.996 | −8.813 | 0.484 | 30.676 | 102.443 | 9.966 | 0.994 |
| a-66 | training | −35.171 | 0.471 | −0.031 | 2.571 | 14.998 | 0.149 | 4.297 | −1.291 | −8.145 | 0.405 | 18.91 | 79.856 | 7.264 | 1.18 |
| a-67 | training | −37.34 | 0.443 | −0.033 | 2.746 | 16.838 | 0.126 | 4.296 | −2.132 | −8.091 | 0.507 | 17.382 | 73.971 | 5.859 | 0.842 |
| a-68 | training | −37.247 | 0.848 | −0.033 | 2.849 | 16.092 | 0.172 | 4.356 | −1.65 | −8.684 | 0.512 | 19.233 | 77.96 | 2.225 | 0.842 |
| a-69 | training | −35.64 | 0.589 | −0.089 | 2.618 | 15.742 | 0.14 | 4.267 | −1.564 | −7.446 | 0.426 | 17.569 | 78.636 | 7.216 | 0.946 |
| a-70 | test | −36.907 | 0.519 | −0.048 | 2.682 | 15.457 | 0.186 | 4.358 | −1.247 | −8.227 | 0.395 | 24.211 | 85.133 | 10.285 | 0.744 |
| a-71 | training | −39.599 | 0.429 | −0.055 | 2.558 | 17.935 | 0.146 | 4.348 | −1.844 | −6.618 | 0.381 | 18.312 | 84.952 | 13.548 | 0.808 |
| a-73 | training | −39.446 | 0.471 | −0.062 | 2.605 | 18.474 | 0.129 | 4.297 | −1.592 | −7.497 | 0.415 | 17.763 | 82.352 | 4.101 | 0.769 |
| a-74 | training | −38.284 | 0.554 | −0.131 | 2.505 | 15.558 | 0.165 | 4.353 | −1.035 | −8.24 | 0.401 | 23.364 | 100.733 | 11.198 | 0.861 |
| a-76 | training | −38.074 | 0.387 | −0.038 | 2.597 | 16.406 | 0.191 | 4.357 | −1.39 | −6.331 | 0.411 | 25.148 | 83.897 | 8.133 | 0.984 |
| a-77 | training | −35.23 | 0.447 | −0.064 | 2.558 | 13.577 | 0.128 | 4.285 | −0.952 | −6.533 | 0.464 | 17.289 | 79.755 | 0 | 0.918 |
| a-78 | training | −36.941 | 0.529 | −0.06 | 2.475 | 14.84 | 0.117 | 4.289 | −1.303 | −7.397 | 0.416 | 16.659 | 88.64 | 2.311 | 1.377 |
| a-79 | test | −32.38 | 0.413 | −0.033 | 2.727 | 15.563 | 0.149 | 4.303 | −1.113 | −7.931 | 0.463 | 18.91 | 77.174 | 7.047 | 0.88 |
| a-80 | test | −35.172 | 0.604 | −0.18 | 2.487 | 13.832 | 0.117 | 4.312 | −1.267 | −7.558 | 0.463 | 16.659 | 74.551 | 2.789 | 1.292 |
| a-81 | test | −38.719 | 0.681 | −0.169 | 2.511 | 15.108 | 0.108 | 4.315 | −1.611 | −7.898 | 0.415 | 15.991 | 82.931 | 4.808 | 1.146 |
| a-82 | test | −35.243 | 0.672 | −0.127 | 2.766 | 15.826 | 0.137 | 4.323 | −1.786 | −8.211 | 0.488 | 18.164 | 72.004 | 0.053 | 0.897 |
| a-83 | training | −36.32 | 0.495 | −0.062 | 2.546 | 15.014 | 0.108 | 4.286 | −1.608 | −8.139 | 0.532 | 15.974 | 73.76 | 0.419 | 0.896 |
| a-84 | test | −36.382 | 0.473 | −0.039 | 2.465 | 16.024 | 0.089 | 4.26 | −1.908 | −6.312 | 0.465 | 12.755 | 67.073 | 5.692 | 0.813 |
| a-86 | training | −38.16 | 0.486 | −0.034 | 2.499 | 17.02 | 0.126 | 4.301 | −1.772 | −7.501 | 0.447 | 17.382 | 71.601 | 6.725 | 0.797 |
| a-87 | test | −38.523 | 0.577 | −0.021 | 2.535 | 18.877 | 0.089 | 4.257 | −2.65 | −5.673 | 0.481 | 13.34 | 61.78 | 18.608 | 0.73 |
| a-88 | test | −39.825 | 0.429 | −0.048 | 2.644 | 17.927 | 0.146 | 4.353 | −2.036 | −7.398 | 0.406 | 18.312 | 82.663 | 18.698 | 0.771 |
| a-90 | training | −39.406 | 0.784 | 0.02 | 2.675 | 18.546 | 0.166 | 4.352 | −1.824 | −6.002 | 0.486 | 24.308 | 118.33 | 17.894 | 0.78 |
| a-91 | training | −40.792 | 1.003 | 0.048 | 2.645 | 20.3 | 0.095 | 4.302 | −2.484 | −5.435 | 0.529 | 17.575 | 106.766 | 18.072 | 0.75 |
| Symbol | Definition | Block | Dimensionality | Number in the Basis Function |
|---|---|---|---|---|
| Mor05s | signal 05/weighted by I-state | 3D-MoRSE descriptors | 3D | 9 |
| Mor19m | signal 19/weighted by mass | 3D-MoRSE descriptors | 3D | 6 |
| MATS8e | Moran autocorrelation of lag 8 weighted by Sanderson electronegativity | 2D autocorrelations | 2D | 4 |
| H1e | H autocorrelation of lag 1/weighted by Sanderson electronegativity | GETAWAY descriptors | 3D | 3 |
| ATSC7v | Centred Broto–Moreau autocorrelation of lag 7 weighted by van der Waals volume | 2D autocorrelations | 2D | 2 |
| ATSC1e | Centred Broto–Moreau autocorrelation of lag 1 weighted by Sanderson electronegativity | 2D autocorrelations | 2D | 2 |
| SpMax8_Bh(s) | largest eigenvalue n. 8 of Burden matrix weighted by I-state | Burden eigenvalues | 2D | 2 |
| Mor21e | signal 21/weighted by Sanderson electronegativity | 3D-MoRSE descriptors | 3D | 2 |
| Mor13s | signal 13/weighted by I-state | 3D-MoRSE descriptors | 3D | 2 |
| R5p | R autocorrelation of lag 5/weighted by polarizability | GETAWAY descriptors | 3D | 2 |
| ATSC1s | Centred Broto–Moreau autocorrelation of lag 1 weighted by I-state | 2D autocorrelations | 2D | 1 |
| ATSC8s | Centred Broto–Moreau autocorrelation of lag 8 weighted by I-state | 2D autocorrelations | 2D | 1 |
| RDF135e | Radial Distribution Function—135/weighted by Sanderson electronegativity | RDF descriptors | 3D | 1 |
| HATS5s | leverage-weighted autocorrelation of lag 5/weighted by I-state | GETAWAY descriptors | 3D | 1 |
| Bm | Definition | am |
|---|---|---|
| B1 | 1 | 7.00228 |
| B2 | (Mor05s + 28.56600)+ | −0.41345 |
| B3 | (−28.56600 − Mor05s)+ | −0.10460 |
| B4 | (ATSC7v − 12.33400) + (Mor05s + 28.56600)+ | 0.29808 |
| B5 | (12.33400 − ATSC7v) + (Mor05s + 28.56600)+ | 0.11583 |
| B6 | (−28.56600 − Mor05s) + (R5p − 0.37500)+ | 0.98096 |
| B7 | (−28.56600 − Mor05s) +(0.37500 − R5p) + | 3.57380 |
| B8 | (Mor19m − 0.42100) + | −1.63111 |
| B9 | (0.42100 − Mor19m)+ | −5.67335 |
| B10 | (MATS8e − 0.07400)+ | −14.65355 |
| B11 | (15.99100 − ATSC1s)+ (0.07400 − MATS8e)+ | −6.03111 |
| B12 | (70.15200 − ATSC8s)+ (0.07400 − MATS8e)+ | 0.92668 |
| B13 | (−28.56600 − Mor05s)+ (H1e − 2.54600)+ | −0.53694 |
| B14 | (MATS8e − 0.07400)+ (RDF135e − 7.04700)+ | −8.31766 |
| B15 | (SpMax8_Bh(s) − 4.32300)+ (−28.56600 − Mor05s)+ (0; 2.54600 − H1e)+ | −16.59500 |
| B16 | (4.32300 − SpMax8_Bh(s))+ (−28.56600 − Mor05s)+ (2.54600 − H1e)+ | −0.64411 |
| B17 | (Mor19m − 0.42100)+ (Mor21e + 1.26700)+ | −19.90208 |
| B18 | (Mor19m − 0.42100)+ (−1.26700 − Mor21e)+ | −0.88179 |
| B19 | (Mor19m − 0.42100)+ (Mor13s + 6.31200)+ | 0.33453 |
| B20 | (Mor19m − 0.42100)+ (−6.31200 − Mor13s)+ | 0.65372 |
| B21 | (0.85700 − HATS5s)+ | 1.71725 |
| B22 | (ATSC1e − 0.11600)+ | 6.68741 |
| B23 | (0.11600 − ATSC1e)+ | 6.15634 |
| Degree of Interaction | Number of Basis Functions | R2 | Q2 | MAE |
|---|---|---|---|---|
| 1 | 6 | 0.5291 | −0.1525 | 0.2622 |
| 16 | 0.8288 | 0.5787 | 0.1709 | |
| 21 | 0.9277 | 0.8706 | 0.1133 | |
| 21 | 0.9185 | 0.8807 | 0.1230 | |
| 2 | 6 | 0.4691 | 0.1343 | 0.2819 |
| 16 | 0.8649 | 0.7480 | 0.1616 | |
| 33 | 0.9328 | 0.9311 | 0.1096 | |
| 3 | 6 | 0.4691 | 0.1343 | 0.2819 |
| 26 | 0.8649 | 0.7480 | 0.1616 | |
| 38 | 0.9617 | 0.9016 | 0.0772 | |
| 40 | 0.9532 | 0.9033 | 0.0897 |
| Parameter [13] | Value | Threshold [13] | Meaning [13] |
|---|---|---|---|
| 0.9617 | ~1 (1 means perfect correlation) | It measures the variation of observed data with the predicted ones. | |
| 0.9016 | ≥0.5 | Cross-validated R2 (Q2) checked for internal validation. | |
| 0.9119 | ≥0.5 | A measure of correlation between the observed and predicted data of the test set. | |
| 0.90163 | ≥0.5 | Almost equal or closer values of Q2(F2) and Q2(F1) infer that the training set mean lies in the close propinquity to that of the test set. | |
| 0.7959 | ≥0.5 | It measures the model predictability. | |
| 0.9496 | ~1 | Concordance correlation coefficient (CCC) measures both precision and accuracy, detecting the distance of the observations from the fitting line and the degree of deviation of the regression line from that passing through the origin, respectively. | |
| , are denoted as follows: and The terms k and k′ are explained as follows: | 0.0173 and 0.9181 | 2 > 0.5 | They reflect the overall predictability of the model for the entire data set. |
| 0.3446 | It evaluates the model using the predicted residual sum of squares. | ||
| 0.1252 | Standard deviation of error of prediction (SDEP) is calculated from PRESS. | ||
| 0.0772 | Index of errors in the context of predictive modeling studies. |
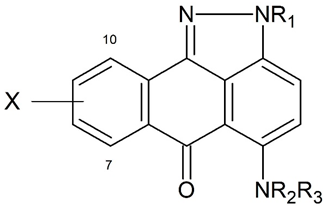
| Compound | Set | X | R1 | NR2R3 | L1210 Leukemia In Vitro: IC50,M |
|---|---|---|---|---|---|
| a-01 | training | H | H | NHCH2CH2NHCH2CH2OH | 2.2 × 10−6 |
| a-02 | test | H | H | NHCH2CH2NEt2 | 1.5 × 10−6 |
| a-03 | test | H | CH3 | NHCH2CH2NHCH2CH2OH | 7.1 × 10−7 |
| a-04 | training | H | CH3 | NHCH2CH2NEt2 | 6.7 × 10−7 |
| a-07 | training | H | CH2CH2OH | NHCH2CH2NHCH2CH2OH | 1.8 × 10−6 |
| a-08 | training | H | CH2CH2OH | NHCH2CH2NEt2 | 8.8 × 10−6 |
| a-14 | test | H | CH2CH2NH2 | NHCH2CH2NHCH2CH2OH | 8.0 × 10−8 |
| a-15 | training | H | CH2CH2NHCH2CH2OH | NHCH3 | 7.4 × 10−7 |
| a-16 | test | H | CH2CH2NHCH2CH2OH | NHCH2CH2OH | 7.5 × 10−7 |
| a-17 | training | H | CH2CH2NHCH2CH2OH | NHCH2CH2NH2 | 6.9 × 10−8 |
| a-18 | training | H | CH2CH2NHCH2OH | NHCH2CH2NHCH2CH2OH | 7.4 × 10−8 |
| a-19 | training | H | CH2CH2NHCH2CH2OH | NHCH2CH2NMe2 | 3.2 × 10−8 |
| a-20 | training | H | CH2CH2NHCH2CH2OH | NHCH2CH2NEt2 | 6.0 × 10−8 |
| a-21 | training | H | CH2CH2NEt2 | NH(CH2)5CH3 | 2.0 × 10−6 |
| a-23 | training | H | CH2CH2NEt2 | NHCH2CH2NH2 | 4.6 × 10−8 |
| a-24 | training | H | CH2CH2NEt2 | NHCH2CH2NHMe | 2.7 × 10−8 |
| a-25 | training | H | CH2CH2NEt2 | NHCH2CH2NHCH2CH2OH | 3.2 × 10−8 |
| a-26 | test | H | CH2CH2NEt2 | NHCH2CH2NEt2 | 3.9 × 10−7 |
| a-27 | training | H | CH2CH2NEt2 | NH(CH2)3NEt2 | 5.2 × 10−7 |
| a-28 | training | H | CH2CH2NEt2 | NH(CH2)4NEt2 | 6.2 × 10−7 |
| a-29 | training | H | CH2CH2NEt2 | NH(CH2)7NEt2 | 6.3 × 10−7 |
| a-30 | test | H | CH2CH2NEt2 | NHCH2CH2N(CH2CH2)2O | 4.8 × 10−7 |
| a-31 | test | H | CH2CH2NEt2 | NHCH2CH2N(CH2CH2)2NH | 5.0 × 10−7 |
| a-32 | training | H | CH2CH2NEt2 | NHCH2CH2N(CH2CH2)2NCOOCH2Ph | 3.9 × 10−7 |
| a-33 | training | 7,10-(OH)2 | CH3 | NHCH2CH2NH2 | 2.4 × 10−7 |
| a-34 | training | 7,10-(OH)2 | CH3 | NHCH2CH2NHCH2CH2OH | 1.5 × 10−7 |
| a-35 | training | 7,10-(OH)2 | CH3 | NHCH2CH2NEt2 | 4.5 × 10−7 |
| a-36 | training | 7,10-(OH)2 | CH2Ph | NHCH2CH2NMe2 | 8.6 × 10−7 |
| a-38 | training | 7,10-(OH)2 | CH2CH2OMe | NHCH2CH2NHCH2CH2OH | 1.6 × 10−6 |
| a-40 | training | 7,10-(OH)2 | CH2CH2OH | NHCH2CH2NH2 | 4.8 × 10−7 |
| a-41 | training | 7,10-(OH)2 | CH2CH2OH | NHCH2CH2NHCH2CH2OH | 7.8 × 10−7 |
| a-42 | training | 7,10-(OH)2 | CH2CH2OH | NHCH2CH2NMe2 | 1.5 × 10−8 |
| a-43 | training | 7,10-(OH)2 | CH2CH2OH | NHCH2CH2NEt2 | 7.3 × 10−7 |
| a-44 | training | 7,10-(OH)2 | CH2CH2OH | NHCH2CH2N(CH2CH2)2O | 1.1 × 10−6 |
| a-46 | training | 7,10-(OH)2 | CH2CH(OH)CH2OH | NHCH2CH2NHCH2CH2NMe2 | 2.2 × 10−6 |
| a-47 | test | 7,10-(OH)2 | CH2CH2NH2 | NHCH2CH2NH2 | 4.8 × 10−7 |
| a-48 | training | 7,10-(OH)2 | CH2CH2NH2 | NH(CH2)3NH2 | 3.1 × 10−7 |
| a-49 | test | 7,10-(OH)2 | CH2CH2NH2 | NHCH2CH2NHMe | 7.0 × 10−7 |
| a-50 | training | 7,10-(OH)2 | CH2CH2NH2 | NHCH2CH2NHCH2CH2OH | 5.8 × 10−7 |
| a-51 | test | 7,10-(OH)2 | CH2CH2NH2 | NH(CH2)3NHCH2CH2OH | 8.7 × 10−7 |
| a-52 | test | 7,10-(OH)2 | CH2CH2NH2 | NHCH2CH2NHCH2CH2NMe2 | 9.3 × 10−7 |
| a-53 | test | 7,10-(OH)2 | (CH2)3NH2 | NHCH2CH2NHCH2CH2OH | 1.6 × 10−7 |
| a-54 | test | 7,10-(OH)2 | (CH2)3NH2 | NHCH2CH2NHCH2CH2NMe2 | 6.4 × 10−7 |
| a-55 | training | 7,10-(OH)2 | CH2CH2NHMe | NHCH2CH2NHCH2CH2OH | 4.4 × 10−7 |
| a-56 | training | 7,10-(OH)2 | CH2CH2NHCH2CH2OH | NHCH2CH2NH2 | 1.6 × 10−6 |
| a-57 | training | 7,10-(OH)2 | CH2CH2NHCH2CH2OH | NH(CH2)3NH2 | 9.6 × 10−7 |
| a-60 | training | 7,10-(OH)2 | CH2CH2NHCH2CH2OH | NHCH2CH2NHMe | 1.4 × 10−7 |
| a-62 | training | 7,10-(OH)2 | CH2CH2NHCH2CH2OH | NHCH2CH2NHCH2CH2OH | 7.4 × 10−7 |
| a-63 | training | 7,10-(OH)2 | CH2CH2NHCH2CH2OH | NH(CH2)3NHCH2CH2OH | 1.8 × 10−6 |
| a-64 | test | 7,10-(OH)2 | CH2CH2NHCH2CH2OH | NHCH2CH2N(CH2CH2OH)2 | 4.3 × 10−7 |
| a-65 | training | 7,10-(OH)2 | CH2CH2NHCH2CH2OH | NH(CH2)3N(CH2CH2OH)2 | 9.2 × 10−7 |
| a-66 | training | 7,10-(OH)2 | CH2CH2NHCH2CH2OH | NHCH2CH2NMe2 | 2.3 × 10−7 |
| a-67 | training | 7,10-(OH)2 | CH2CH2NHCH2CH2OH | NHCH2CH2NEt2 | 5.1 × 10−7 |
| a-68 | training | 7,10-(OH)2 | CH2CH2NHCH2CH2OH | NHCH2CH2N(CH2CH2)2O | 6.5 × 10−7 |
| a-69 | training | 7,10-(OH)2 | CH2CH2NHCH2CH2OH | N(CH2CH2)2NMe | 4.3 × 10−7 |
| a-70 | test | 7,10-(OH)2 | CH2CH2NHCH2CH2OH | NHCH2CH2NHCH2CH2NH2 | 3.3 × 10−7 |
| a-71 | training | 7,10-(OH)2 | CH2CH2NHCH2CH2OH | NHCH2CH2NHCH2CH2NMe2 | 7.6 × 10−7 |
| a-73 | training | 7,10-(OH)2 | CH2CH2NHCH2CH2OH | N(Me)CH2CH2NMe2 | 6.3 × 10−7 |
| a-74 | training | 7,10-(OH)2 | CH2CH2NHCH2CH2OH | NH(CH2)3NH2 | 1.8 × 10−6 |
| a-76 | training | 7,10-(OH)2 | CH2CH2NMeCH2CH2OH | NHCH2CH2NHCH2CH2OH | 3.3 × 10−7 |
| a-77 | training | 7,10-(OH)2 | CH2CH2NMe2 | NHCH2CH2NH2 | 2.2 × 10−7 |
| a-78 | training | 7,10-(OH)2 | CH2CH2NMe2 | NH(CH2)3NH2 | 5.4 × 10−7 |
| a-79 | test | 7,10-(OH)2 | CH2CH2NMe2 | NHCH2CH2NHCH2CH2OH | 1.2 × 10−7 |
| a-80 | test | 7,10-(OH)2 | (CH2)3NMe2 | NHCH2CH2NH2 | 2.2 × 10−6 |
| a-81 | test | 7,10-(OH)2 | (CH2)3NMe2 | NH(CH2)3NH2 | 8.0 × 10−7 |
| a-82 | test | 7,10-(OH)2 | (CH2)3NMe2 | NHCH2CH2NHCH2CH2OH | 5.9 × 10−7 |
| a-83 | training | 7,10-(OH)2 | CH2CH2NEt2 | NHCH2CH2NH2 | 4.6 × 10−8 |
| a-84 | test | 7,10-(OH)2 | CH2CH2NEt2 | NHCH2CH2NHMe | 7.4 × 10−6 |
| a-86 | training | 7,10-(OH)2 | CH2CH2NEt2 | NHCH2CH2NHCH2CH2OH | 1.3 × 10−7 |
| a-87 | test | 7,10-(OH)2 | CH2CH2NEt2 | NHCH2CH2NEt2 | 5.5 × 10−7 |
| a-88 | test | 7,10-(OH)2 | CH2CH2NHCH2CH2NMe2 | NHCH2CH2NHCH2CH2OH | 1.4 × 10−6 |
| a-90 | training | 7,10-(OH)2 | CH2CH(OH)CH2NEt2 | NHCH2CH2NHCH2CH2OH | 8.4 × 10−7 |
| a-91 | training | 7,10-(OH)2 | CH2CH(OH)CH2NEt2 | NHCH2CH2NEt2 | 1.3 × 10−6 |
| Options | Values |
|---|---|
| Maximum number of basis functions | 40 |
| Degree of interactions | 3 |
| Penalty | 2 |
| Threshold | 0.0005 |
| Apply pruning | YES |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gackowski, M.; Szewczyk-Golec, K.; Pluskota, R.; Koba, M.; Mądra-Gackowska, K.; Woźniak, A. Application of Multivariate Adaptive Regression Splines (MARSplines) for Predicting Antitumor Activity of Anthrapyrazole Derivatives. Int. J. Mol. Sci. 2022, 23, 5132. https://doi.org/10.3390/ijms23095132
Gackowski M, Szewczyk-Golec K, Pluskota R, Koba M, Mądra-Gackowska K, Woźniak A. Application of Multivariate Adaptive Regression Splines (MARSplines) for Predicting Antitumor Activity of Anthrapyrazole Derivatives. International Journal of Molecular Sciences. 2022; 23(9):5132. https://doi.org/10.3390/ijms23095132
Chicago/Turabian StyleGackowski, Marcin, Karolina Szewczyk-Golec, Robert Pluskota, Marcin Koba, Katarzyna Mądra-Gackowska, and Alina Woźniak. 2022. "Application of Multivariate Adaptive Regression Splines (MARSplines) for Predicting Antitumor Activity of Anthrapyrazole Derivatives" International Journal of Molecular Sciences 23, no. 9: 5132. https://doi.org/10.3390/ijms23095132
APA StyleGackowski, M., Szewczyk-Golec, K., Pluskota, R., Koba, M., Mądra-Gackowska, K., & Woźniak, A. (2022). Application of Multivariate Adaptive Regression Splines (MARSplines) for Predicting Antitumor Activity of Anthrapyrazole Derivatives. International Journal of Molecular Sciences, 23(9), 5132. https://doi.org/10.3390/ijms23095132









