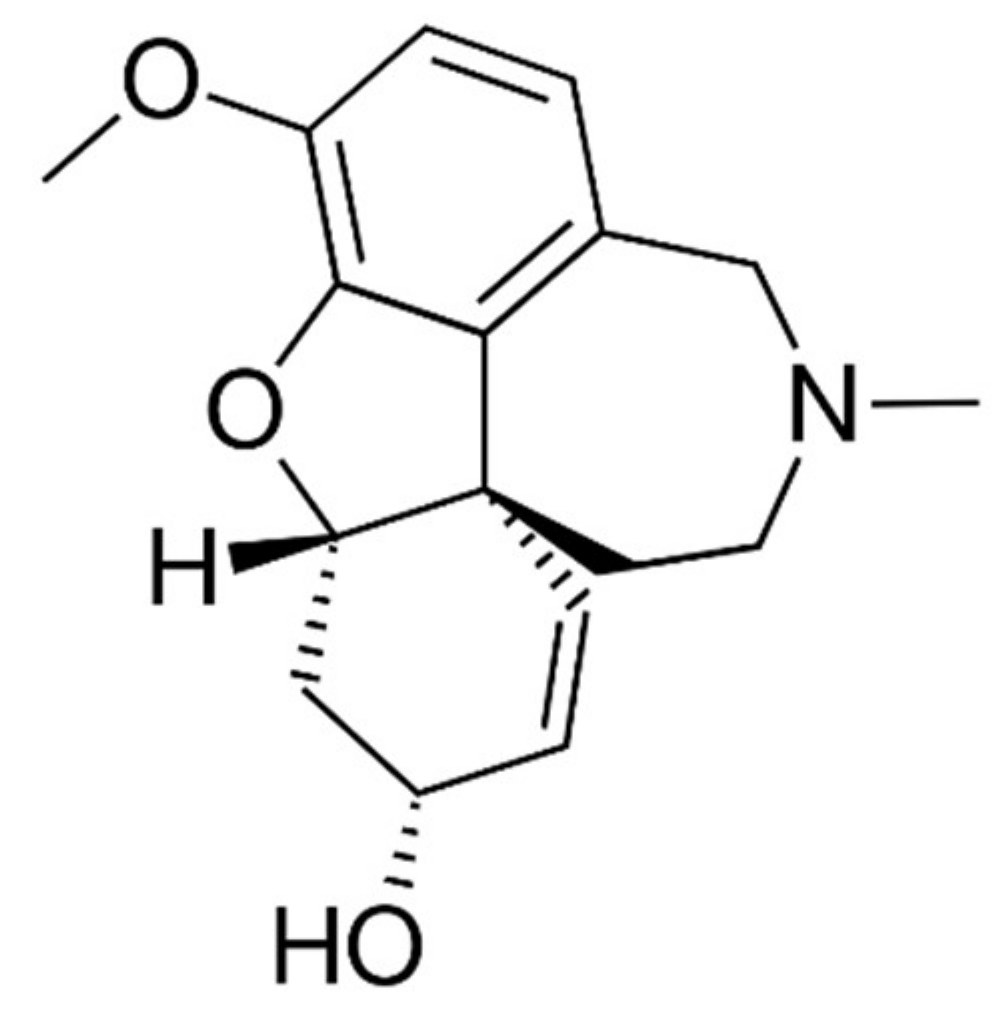
Kinetic Modeling of Time-Dependent Enzyme Inhibition by Pre-Steady-State Analysis of Progress Curves: The Case Study of the Anti-Alzheimer’s Drug Galantamine
Abstract
1. Introduction
2. Results
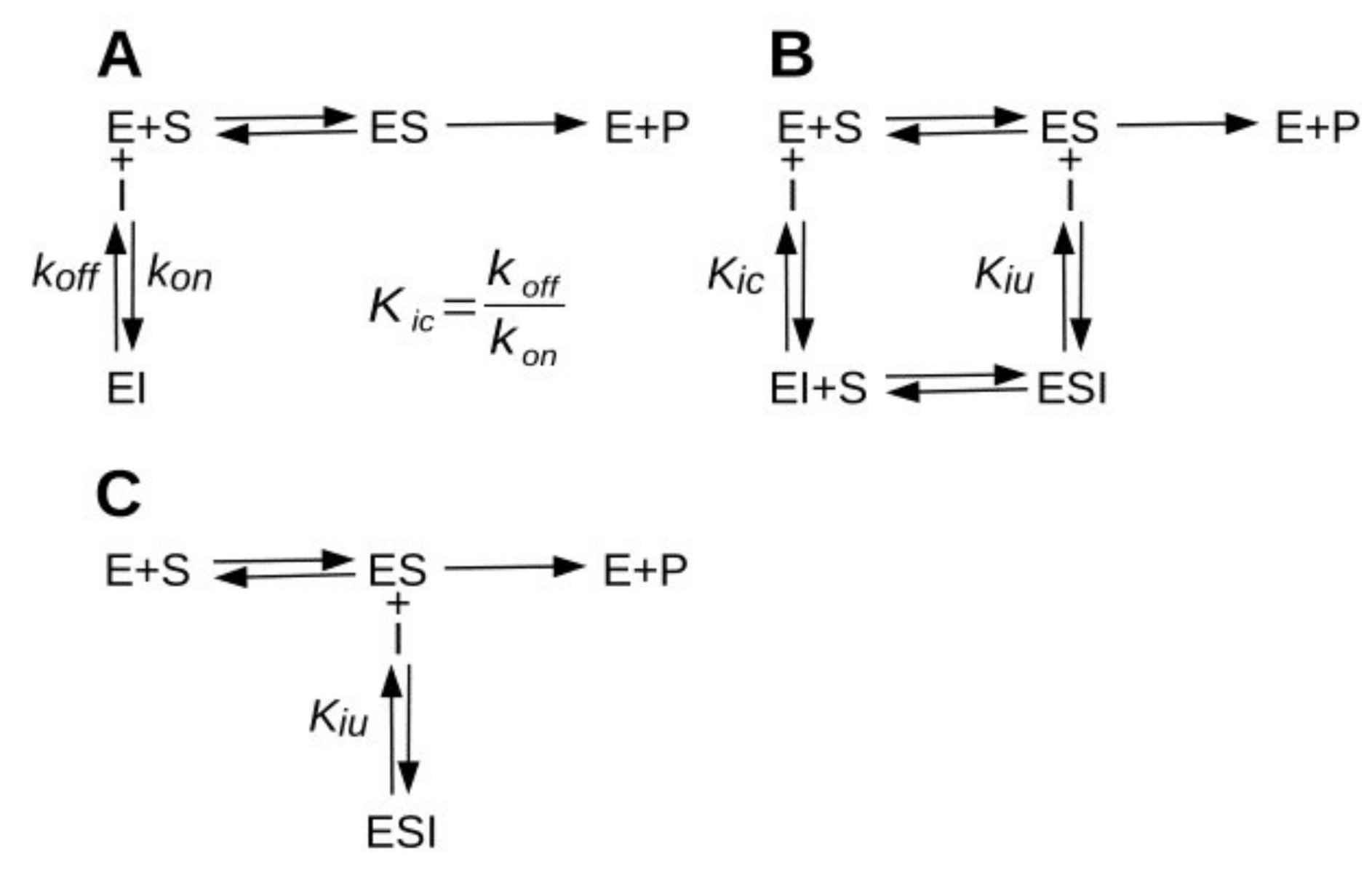
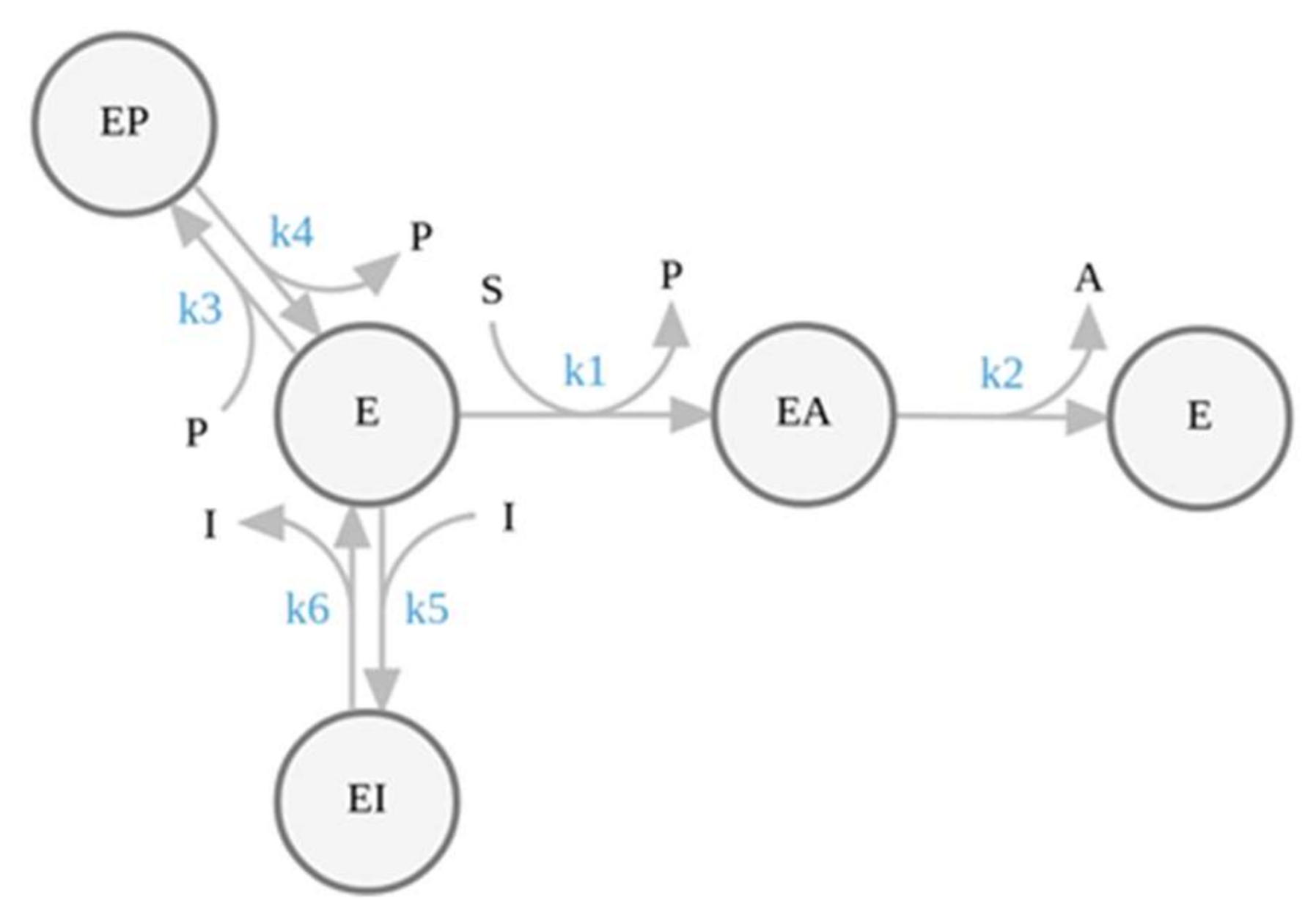
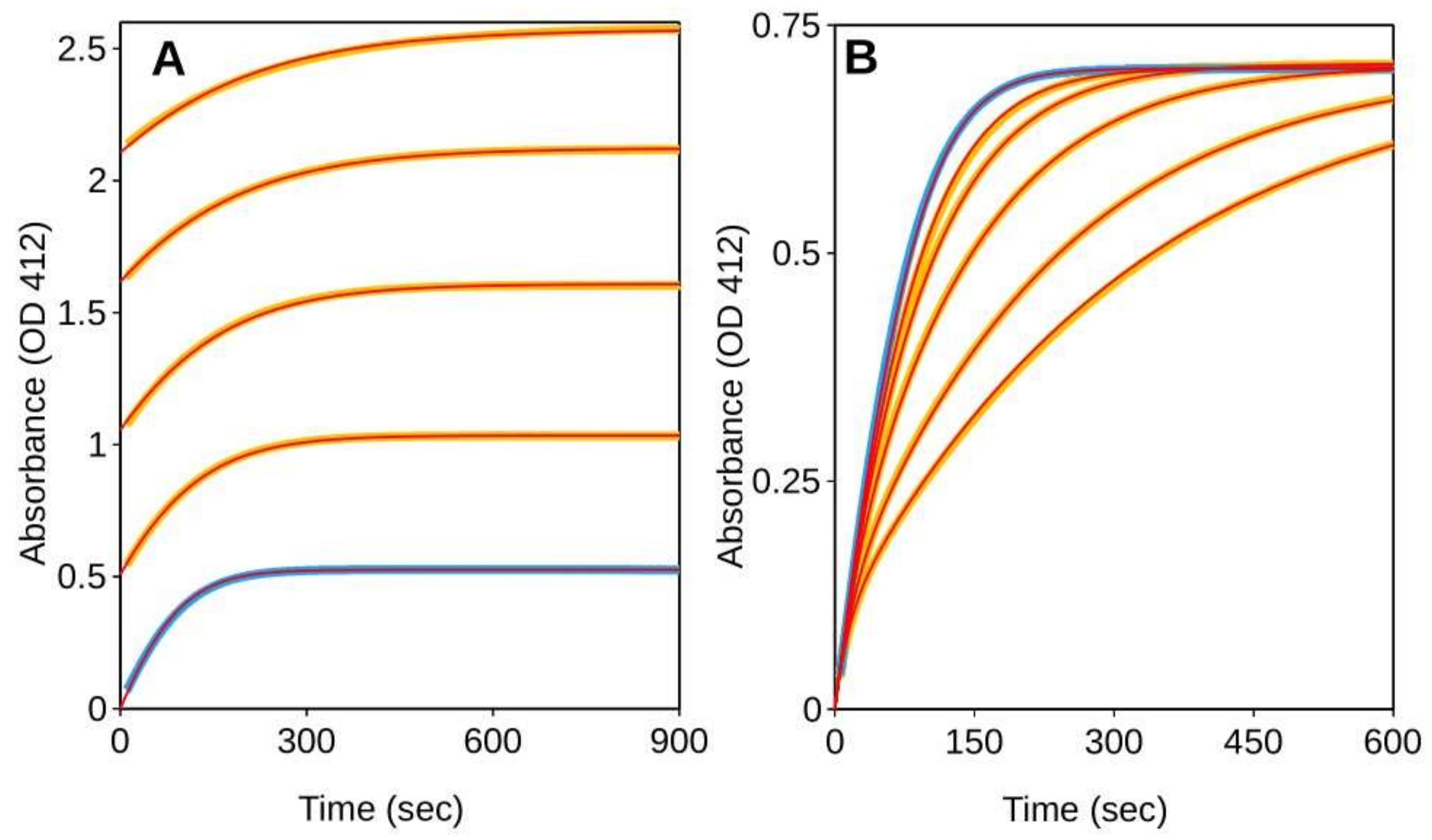
2.1. Simulation of Enzyme Inhibition by Slow-Dissociating Inhibitors
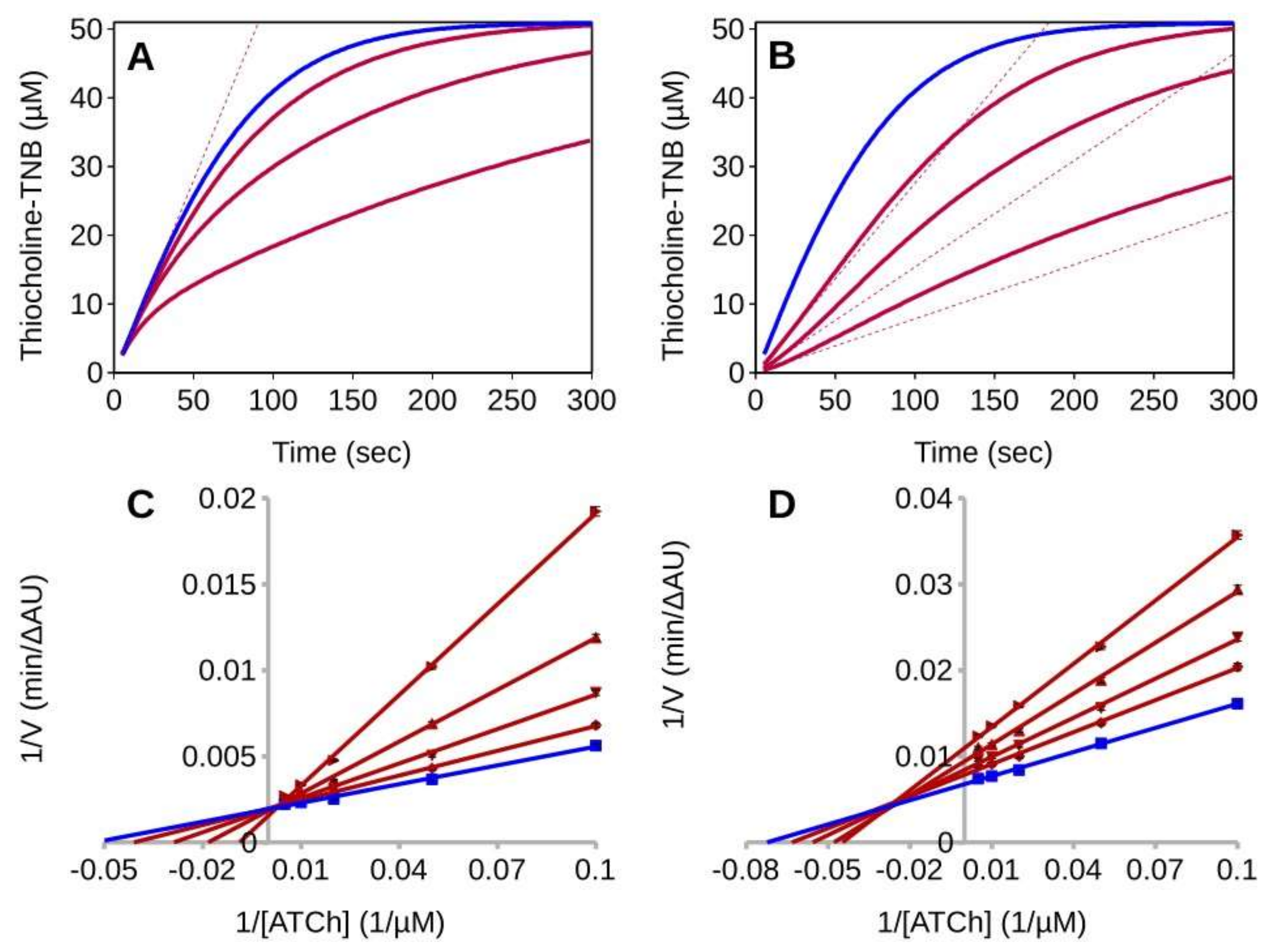
2.2. Steady-State Analysis of AChE Inhibition by GAL
2.3. Pre-Steady-State Analysis of AChE Inhibition by Fitting of the Full Progress Curves
3. Discussion
4. Material and Methods
4.1. Generation and Analysis of Synthetic Kinetic Data
4.2. Chemicals
4.3. Measure of Enzymatic Activity
4.4. Steady-State Inhibition Analysis
4.5. Kinetic Analysis of Reaction Progress Curves
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Alam, M.T.; Olin-Sandoval, V.; Stincone, A.; Keller, M.A.; Zelezniak, A.; Luisi, B.F.; Ralser, M. The self-inhibitory nature of metabolic networks and its alleviation through compartmentalization. Nat. Commun. 2017, 10, 16018. [Google Scholar] [CrossRef] [PubMed]
- Koch, G.; Schropp, J.; Jusko, W.J. Assessment of non-linear combination effect terms for drug-drug interactions. J. Pharmacokinet. Pharmacodyn. 2016, 43, 461–479. [Google Scholar] [CrossRef] [PubMed]
- Deodhar, M.; Al Rihani, S.B.; Arwood, M.J.; Darakjian, L.; Dow, P.; Turgeon, J.; Michaud, V. Mechanisms of CYP450 Inhibition: Understanding Drug-Drug Interactions Due to Mechanism-Based Inhibition in Clinical Practice. Pharmaceutics 2020, 4, 846. [Google Scholar] [CrossRef] [PubMed]
- Upton, R.N.; Mould, D.R. Basic concepts in population modeling, simulation, and model-based drug development: Part 3-introduction to pharmacodynamic modeling methods. CPT Pharmacomet. Syst. Pharmacol. 2014, 3, e88. [Google Scholar] [CrossRef] [PubMed]
- Holdgate, G.A.; Meek, T.D.; Grimley, R.L. Mechanistic enzymology in drug discovery: A fresh perspective. Nat. Rev. Drug Discov. 2018, 17, 115–132. [Google Scholar] [CrossRef] [PubMed]
- Copeland, R.A.; Pompliano, D.L.; Meek, T.D. Drug-target residence time and its implications for lead optimization. Nat. Rev. Drug Discov. 2006, 5, 730–739. [Google Scholar] [CrossRef] [PubMed]
- Copeland, R.A. The drug-target residence time model: A 10-year retrospective. Nat. Rev. Drug Discov. 2016, 15, 87–95. [Google Scholar] [CrossRef] [PubMed]
- Contestabile, A. The history of the cholinergic hypothesis. Behav. Brain Res. 2011, 221, 334–340. [Google Scholar] [CrossRef]
- Ueda, M.; Matsumura, S.; Kimoto, S.; Matsuda, S. Studies on the anticholinesterase and twitch potentiation activities of galanthamine. Jpn. J. Pharmacol. 1962, 12, 111–119. [Google Scholar] [CrossRef]
- Olin, J.; Schneider, L. Galantamine for Alzheimer’s disease. Cochrane Database Syst. Rev. 2002, 3, CD001747, Update in: Cochrane Database Syst. Rev. 2004, 4, CD001747. [Google Scholar] [CrossRef]
- Przybyłowska, M.; Dzierzbicka, K.; Kowalski, S.; Chmielewska, K.; Inkielewicz-Stepniak, I. Therapeutic Potential of Multifunctional Derivatives of Cholinesterase Inhibitors. Curr. Neuropharmacol. 2021, 19, 1323–1344. [Google Scholar] [CrossRef]
- Lazarova, M.I.; Tsekova, D.S.; Tancheva, L.P.; Kirilov, K.T.; Uzunova, D.N.; Vezenkov, L.T.; Tsvetanova, E.R.; Alexandrova, A.V.; Georgieva, A.P.; Gavrilova, P.T.; et al. New Galantamine Derivatives with Inhibitory Effect on Acetylcholinesterase Activity. J. Alzheimers Dis. 2021, 83, 1211–1220. [Google Scholar] [CrossRef]
- Lazarova, M.; Tancheva, L.; Alexandrova, A.; Tsvetanova, E.; Georgieva, A.; Stefanova, M.; Tsekova, D.; Vezenkov, L.; Kalfin, R.; Uzunova, D.; et al. Effects of New Galantamine Derivatives in a Scopolamine Model of Dementia in Mice. J. Alzheimers Dis. 2021, 84, 671–690. [Google Scholar] [CrossRef]
- Colović, M.B.; Krstić, D.Z.; Lazarević-Pašti, T.D.; Bondžić, A.M.; Vasić, V.M. Acetylcholinesterase inhibitors: Pharmacology and toxicology. Curr. Neuropharmacol. 2013, 11, 315–335. [Google Scholar] [CrossRef]
- Caliandro, R.; Pesaresi, A.; Cariati, L.; Procopio, A.; Oliverio, M.; Lamba, D. Kinetic and structural studies on the interactions of Torpedo californica acetylcholinesterase with two donepezil-like rigid analogues. J. Enzym. Inhib. Med. Chem. 2018, 33, 794–803. [Google Scholar] [CrossRef]
- Sugimoto, H.; Yamanishi, Y.; Iimura, Y.; Kawakami, Y. Donepezil hydrochloride (E2020) and other acetylcholinesterase inhibitors. Curr. Med. Chem. 2000, 7, 303–339. [Google Scholar] [CrossRef]
- Chang, A.; Jeske, L.; Ulbrich, S.; Hofmann, J.; Koblitz, J.; Schomburg, I.; Neumann-Schaal, M.; Jahn, D.; Schomburg, D. BRENDA, the ELIXIR core data resource in 2021: New developments and updates. Nucleic Acids Res. 2021, 49, D498–D508. [Google Scholar] [CrossRef]
- Jukic, M.; Politeo, O.; Maksimovic, M.; Milos, M. In vitro acetylcholinesterase inhibitory properties of thymol, carvacrol and their derivatives thymoquinone and thymohydroquinone. Phytother. Res. 2007, 21, 259–261. [Google Scholar] [CrossRef]
- Alarcón, J.; Astudillo, L.; Gutierrez, M. Inhibition of acetylcholinesterase activity by dihydro-beta-agarofuran sesquiterpenes isolated from Chilean Celastraceae. Z. Naturforsch. C J. Biosci. 2008, 63, 853–856. [Google Scholar] [CrossRef]
- Schuh, F.T. Zum molekularen Wirkungsmechanismus von Galathamin, einem Curare-Antagonisten (On the molecular mechanism of action of galanthamine, an antagonist of nondepolarizing muscle relaxants (author’s transl)). Anaesthesist 1976, 25, 444–448. [Google Scholar]
- Darvesh, S.; Walsh, R.; Kumar, R.; Caines, A.; Roberts, S.; Magee, D.; Rockwood, K.; Martin, E. Inhibition of human cholinesterases by drugs used to treat Alzheimer disease. Alzheimer Dis. Assoc. Disord. 2003, 17, 117–126. [Google Scholar] [CrossRef]
- Han, S.Y.; Sweeney, J.E.; Bachman, E.S.; Schweiger, E.J.; Forloni, G.; Coyle, J.T.; Davis, B.M.; Joullié, M.M. Chemical and pharmacological characterization of galanthamine, an acetylcholinesterase inhibitor, and its derivatives. A potential application in Alzheimer’s disease? Eur. J. Med. Chem. 1992, 27, 673–687. [Google Scholar] [CrossRef]
- Bores, G.M.; Huger, F.P.; Petko, W.; Mutlib, A.E.; Camacho, F.; Rush, D.K.; Selk, D.E.; Wolf, V.; Kosley, R.W.; Davis, L.; et al. Pharmacological evaluation of novel Alzheimer’s disease therapeutics: Acetylcholinesterase inhibitors related to galanthamine. J. Pharmacol. Exp. Ther. 1996, 277, 728–738. [Google Scholar]
- Sussman, J.L.; Harel, M.; Frolow, F.; Oefner, C.; Goldman, A.; Toker, L.; Silman, I. Atomic structure of acetylcholinesterase from Torpedo californica: A prototypic acetylcholine-binding protein. Science 1991, 253, 872–879. [Google Scholar] [CrossRef]
- Khalid, A.; Azim, M.K.; Parveen, S.; Atta-ur-Rahman; Choudhary, M.I. Structural basis of acetylcholinesterase inhibition by triterpenoidal alkaloids. Biochem. Biophys. Res. Commun. 2005, 331, 1528–1532. [Google Scholar] [CrossRef] [PubMed]
- Geerts, H.; Guillaumat, P.O.; Grantham, C.; Bode, W.; Anciaux, K.; Sachak, S. Brain levels and acetylcholinesterase inhibition with galantamine and donepezil in rats, mice, and rabbits. Brain Res. 2005, 1033, 186–193. [Google Scholar] [CrossRef] [PubMed]
- Wiesner, J.; Kriz, Z.; Kuca, K.; Jun, D.; Koca, J. Acetylcholinesterases—The structural similarities and differences. J. Enzym. Inhib. Med. Chem. 2007, 22, 417–424. [Google Scholar] [CrossRef]
- Masson, P.; Lushchekina, S.V. Slow-binding inhibition of cholinesterases, pharmacological and toxicological relevance. Arch. Biochem. Biophys. 2016, 593, 60–68. [Google Scholar] [CrossRef]
- Lushchekina, S.V.; Masson, P. Slow-binding inhibitors of acetylcholinesterase of medical interest. Neuropharmacology 2020, 177, 108236. [Google Scholar] [CrossRef]
- Waley, S.G. The kinetics of slow-binding and slow, tight-binding inhibition: The effects of substrate depletion. Biochem. J. 1993, 15, 195–200. [Google Scholar] [CrossRef] [PubMed]
- Morrison, J.F.; Walsh, C.T. The behavior and significance of slow-binding enzyme inhibitors. In Advances in Enzymology and Related Areas of Molecular Biology; Meister, A., Ed.; John Wyley & Sons, Inc.: Hoboken, NJ, USA, 2007; Volume 61, pp. 201–301. [Google Scholar] [CrossRef]
- Johnson, K.A. Slow-onset Inhibition. In Kinetic Analysis for the New Enzymology; Johnson, K.A., Ed.; Kintek Corporation: Austin, TX, USA, 2019; pp. 361–383. [Google Scholar]
- Cornish-Bowden, A. Tight-binding and irreversible inhibitors. In Fundamentals of Enzyme Kinetic, 3rd ed.; Portland Press Ltd.: London, UK, 2004; pp. 145–155. [Google Scholar]
- Turner, P.M.; Lerea, K.M.; Kull, F.J. The ribonuclease inhibitors from porcine thyroid and liver are slow, tight-binding inhibitors of bovine pancreatic ribonuclease A. Biochem. Biophys. Res. Commun. 1983, 114, 1154–1160. [Google Scholar] [CrossRef]
- Kuzmic, P. Optimal Duration of the Pre-incubation Phase in Enzyme Inhibition Experiments. ChemRxiv 2020. [Google Scholar] [CrossRef]
- Duggleby, R.G. Quantitative analysis of the time courses of enzyme-catalyzed reactions. Methods 2001, 24, 168–174. [Google Scholar] [CrossRef]
- Johnson, K.A.; Simpson, Z.B.; Blom, T. Global kinetic explorer: A new computer program for dynamic simulation and fitting of kinetic data. Anal. Biochem. 2009, 387, 20–29. [Google Scholar] [CrossRef]
- Zimmerle, C.T.; Frieden, C. Analysis of progress curves by simulations generated by numerical integration. Biochem. J. 1989, 258, 381–387. [Google Scholar] [CrossRef]
- Bevc, S.; Konc, J.; Stojan, J.; Hodošček, M.; Penca, M.; Praprotnik, M.; Janežič, D. ENZO: A web tool for derivation and evaluation of kinetic models of enzyme catalyzed reactions. PLoS ONE 2011, 6, e22265. [Google Scholar] [CrossRef]
- Bäuerle, F.; Zotter, A.; Schreiber, G. Direct determination of enzyme kinetic parameters from single reactions using a new progress curve analysis tool. Protein Eng. Des. Sel. 2017, 30, 149–156. [Google Scholar] [CrossRef][Green Version]
- Stojan, J. The mechanism and benefit of human butyrylcholinesterase activation by what would otherwise be inhibitors. Chem. Biol. Interact. 2019, 308, 350–356. [Google Scholar] [CrossRef]
- Kuzmic, P. Application of the Van Slyke-Cullen irreversible mechanism in the analysis of enzymatic progress curves. Anal. Biochem. 2009, 394, 287–289. [Google Scholar] [CrossRef]
- Berkov, S.; Codina, C.; Viladomat, F.; Bastida, J. N-Alkylated galanthamine derivatives: Potent acetylcholinesterase inhibitors from Leucojum aestivum. Bioorg. Med. Chem. Lett. 2008, 18, 2263–2266. [Google Scholar] [CrossRef]
- Tonge, P.J. Drug-Target Kinetics in Drug Discovery. ACS Chem. Neurosci. 2018, 9, 29–39. [Google Scholar] [CrossRef]
- Damborsky, J.; Kozlikova, B. CAVER Analyst 2.0: Analysis and visualization of channels and tunnels in protein structures and molecular dynamics trajectories. BioinformaticS 2018, 34, 3586–3588. [Google Scholar] [CrossRef]
- Dvir, H.; Jiang, H.L.; Wong, D.M.; Harel, M.; Chetrit, M.; He, X.C.; Jin, G.Y.; Yu, G.L.; Tang, X.C.; Silman, I.; et al. X-ray structures of Torpedo californica acetylcholinesterase complexed with (+)-huperzine A and (−)-huperzine B: Structural evidence for an active site rearrangement. Biochemistry 2002, 41, 10810–10818. [Google Scholar] [CrossRef]
- Greenblatt, H.M.; Kryger, G.; Lewis, T.; Silman, I.; Sussman, J.L. Structure of acetylcholinesterase complexed with (−)-galanthamine at 2.3 A resolution. FEBS Lett. 1999, 463, 321–326. [Google Scholar] [CrossRef]
- Cheung, J.; Rudolph, M.J.; Burshteyn, F.; Cassidy, M.S.; Gary, E.N.; Love, J.; Franklin, M.C.; Height, J.J. Structures of human acetylcholinesterase in complex with pharmacologically important ligands. J. Med. Chem. 2012, 55, 10282–10286. [Google Scholar] [CrossRef]
- DeLano, W.L. PyMOL: An open-source molecular graphics tool. CCP4 Newsl. Protein Crystallogr. 2002, 40, 82–92. [Google Scholar]
- Henzler-Wildman, K.; Kern, D. Dynamic personalities of proteins. Nature 2007, 450, 964–972. [Google Scholar] [CrossRef]
- Fabini, E.; Tramarin, A.; Bartolini, M. Combination of human acetylcholinesterase and serum albumin sensing surfaces as highly informative analytical tool for inhibitor screening. J. Pharm. Biomed. Anal. 2018, 155, 177–184. [Google Scholar] [CrossRef]
- Sundberg, E.J.; Andersen, P.S.; Gorshkova, I.I.; Schuck, P. Surface Plasmon Resonance Biosensing in the Study of Ternary Systems of Interacting Proteins. In Protein Interactions—Biophysical Approaches for the Study of Complex Reversible Systems; Schuck, P., Ed.; Springer: Boston, MA, USA, 2007; pp. 97–141. [Google Scholar] [CrossRef]
- Rich, R.L.; Myszka, D.G. Survey of the year 2007 commercial optical biosensor literature. J. Mol. Recognit. 2008, 21, 355–400. [Google Scholar] [CrossRef] [PubMed]
- Mehta, M.; Adem, A.; Sabbagh, M. New Acetylcholinesterase Inhibitors for Alzheimer’s Disease. Int. J. Alzheimer Dis. 2012, 2012, 728983. [Google Scholar] [CrossRef]
- Sussman, J.L.; Harel, M.; Frolow, F.; Varon, L.; Toker, L.; Futerman, A.H.; Silman, I. Purification and crystallization of a dimeric form of acetylcholinesterase from Torpedo californica subsequent to solubilization with phosphatidylinositol-specific phospholipase C. J. Mol. Biol. 1988, 203, 821–823. [Google Scholar] [CrossRef]
- Ellman, G.L.; Courtney, K.D.; Andres, V.; Feather-Stone, R.M. A new and rapid colorimetric determination of acetylcholinesterase activity. Biochem. Pharmacol. 1961, 7, 88–95. [Google Scholar] [CrossRef]
- Pinto, M.F.; Baici, A.; Pereira, P.J.B.; Macedo-Ribeiro, S.; Pastore, A.; Rocha, F.; Martins, P.M. interferENZY: A Web-Based Tool for Enzymatic Assay Validation and Standardized Kinetic Analysis. J. Mol. Biol. 2021, 433, 166613. [Google Scholar] [CrossRef] [PubMed]
- Swainston, N.; Baici, A.; Bakker, B.M.; Cornish-Bowden, A.; Fitzpatrick, P.F.; Halling, P.; Leyh, T.S.; O’Donovan, C.; Raushel, F.M.; Reschel, U.; et al. STRENDA DB: Enabling the validation and sharing of enzyme kinetics data. FEBS J. 2018, 285, 2193–2204. [Google Scholar] [CrossRef]
- Haupt, L.J.; Kazmi, F.; Ogilvie, B.W.; Buckley, D.B.; Smith, B.D.; Leatherman, S.; Paris, B.; Parkinson, O.; Parkinson, A. The Reliability of Estimating Ki Values for Direct, Reversible Inhibition of Cytochrome P450 Enzymes from Corresponding IC50 Values: A Retrospective Analysis of 343 Experiments. Drug Metab. Dispos. 2015, 43, 1744–1750. [Google Scholar] [CrossRef]
- Ramsay, R.R.; Tipton, K.F. Assessment of Enzyme Inhibition: A Review with Examples from the Development of Monoamine Oxidase and Cholinesterase Inhibitory Drugs. Molecules 2017, 22, 1192. [Google Scholar] [CrossRef]
- Lloyd, M.D. High-Throughput Screening for the Discovery of Enzyme Inhibitors. J. Med. Chem. 2020, 63, 10742–10772. [Google Scholar] [CrossRef]
- Swinney, D.C. Biochemical mechanisms of drug action: What does it take for success? Nat. Rev. Drug Discov. 2004, 3, 801–808. [Google Scholar] [CrossRef]
- Daryaee, F.; Tonge, P.J. Pharmacokinetic-pharmacodynamic models that incorporate drug-target binding kinetics. Curr. Opin. Chem. Biol. 2019, 50, 120–127. [Google Scholar] [CrossRef]
- Johnson, K.A. A century of enzyme kinetic analysis, 1913 to 2013. FEBS Lett. 2013, 587, 2753–2766. [Google Scholar] [CrossRef]
- Stojan, J. Rapid Mechanistic Evaluation and Parameter Estimation of Putative Inhibitors in a Single-Step Progress-Curve Analysis: The Case of Horse Butyrylcholinesterase. Molecules 2017, 22, 1248. [Google Scholar] [CrossRef]
- Cook, D.; Brown, D.; Alexander, R.; March, R.; Morgan, P.; Satterthwaite, G.; Pangalos, M.N. Lessons learned from the fate of AstraZeneca’s drug pipeline: A five-dimensional framework. Nat. Rev. Drug Discov. 2014, 13, 419–431. [Google Scholar] [CrossRef]
- Schuetz, D.A.; de Witte, W.E.A.; Wong, Y.C.; Knasmueller, B.; Richter, L.; Kokh, D.B.; Sadiq, S.K.; Bosma., R.; Nederpelt, I.; Heitman, L.H.; et al. Kinetics for Drug Discovery: An industry-driven effort to target drug residence time. Drug Discov. Today 2017, 22, 896–911. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lamba, D.; Pesaresi, A. Kinetic Modeling of Time-Dependent Enzyme Inhibition by Pre-Steady-State Analysis of Progress Curves: The Case Study of the Anti-Alzheimer’s Drug Galantamine. Int. J. Mol. Sci. 2022, 23, 5072. https://doi.org/10.3390/ijms23095072
Lamba D, Pesaresi A. Kinetic Modeling of Time-Dependent Enzyme Inhibition by Pre-Steady-State Analysis of Progress Curves: The Case Study of the Anti-Alzheimer’s Drug Galantamine. International Journal of Molecular Sciences. 2022; 23(9):5072. https://doi.org/10.3390/ijms23095072
Chicago/Turabian StyleLamba, Doriano, and Alessandro Pesaresi. 2022. "Kinetic Modeling of Time-Dependent Enzyme Inhibition by Pre-Steady-State Analysis of Progress Curves: The Case Study of the Anti-Alzheimer’s Drug Galantamine" International Journal of Molecular Sciences 23, no. 9: 5072. https://doi.org/10.3390/ijms23095072
APA StyleLamba, D., & Pesaresi, A. (2022). Kinetic Modeling of Time-Dependent Enzyme Inhibition by Pre-Steady-State Analysis of Progress Curves: The Case Study of the Anti-Alzheimer’s Drug Galantamine. International Journal of Molecular Sciences, 23(9), 5072. https://doi.org/10.3390/ijms23095072







