Comparing Microscopic and Macroscopic Dynamics in a Paradigmatic Model of Glass-Forming Molecular Liquid
Abstract
1. Introduction
2. Materials and Methods
2.1. Simulations
2.2. Cage-Jump Algorithm and Microscopic Observables
2.3. Macroscopic Observables
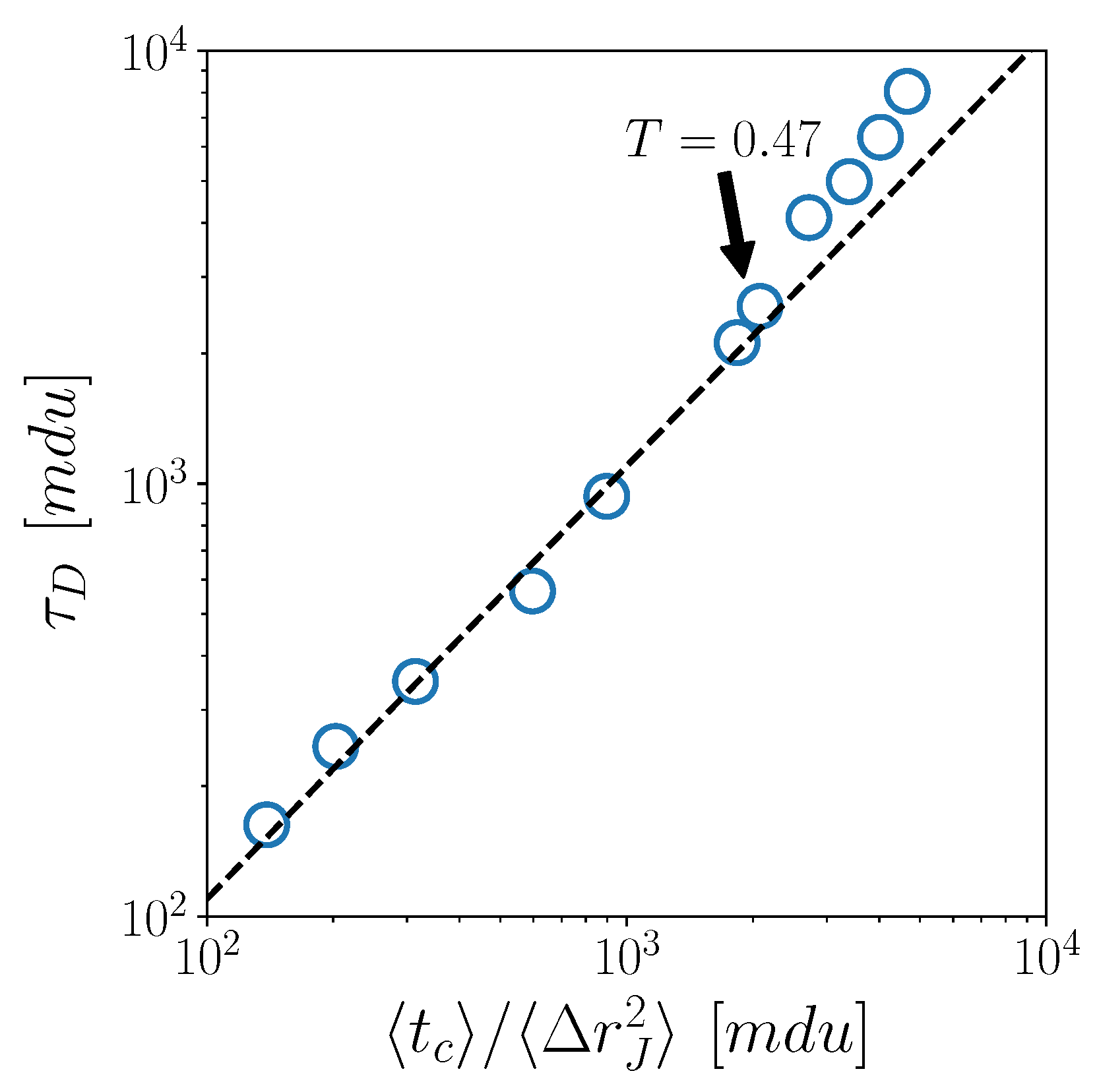
3. Results
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| KALJ | Kob and Andersen Lennard–Jones 80:20 binary mixture |
| CJ | Cage-Jump algorithm |
| CTRW | Continuous Time Random Walk |
| MCT | Mode-Coupling Theory |
| SEB | Stokes–Einstein Breakdown |
| MD | Molecular Dynamics |
References
- Debenedetti, P.G.; Stillinger, F.H. Supercooled liquids and the glass transition. Nature 2001, 410, 259–267. [Google Scholar] [CrossRef] [PubMed]
- Cavagna, A. Supercooled liquids for pedestrians. Phys. Rep. 2009, 476, 51–124. [Google Scholar] [CrossRef]
- Kob, W.; Andersen, H.C. Testing mode-coupling theory for a supercooled binary Lennard-Jones mixture I: The van Hove correlation function. Phys. Rev. E 1995, 51, 4626. [Google Scholar] [CrossRef] [PubMed]
- Royall, C.P.; Williams, S.R. The role of local structure in dynamical arrest. Phys. Rep. 2015, 560, 1–75. [Google Scholar] [CrossRef]
- Pastore, R.; Pica Ciamarra, M.; Coniglio, A. Pacman Percolation and the Glass Transition. Fractals 2013, 21, 1350021. [Google Scholar] [CrossRef]
- Ojovan, M.I.; Louzguine-Luzgin, D.V. Revealing structural changes at glass transition via radial distribution functions. J. Phys. Chem. B 2020, 124, 3186–3194. [Google Scholar] [CrossRef]
- Hecksher, T.; Nielsen, A.I.; Olsen, N.B.; Dyre, J.C. Little evidence for dynamic divergences in ultraviscous molecular liquids. Nat. Phys. 2008, 4, 737–741. [Google Scholar] [CrossRef]
- Götze, W. Complex Dynamics of Glass-Forming Liquids: A Mode-Coupling Theory; OUP Oxford: Oxford, UK, 2008; Volume 143. [Google Scholar]
- Candelier, R.; Widmer-Cooper, A.; Kummerfeld, J.K.; Dauchot, O.; Biroli, G.; Harrowell, P.; Reichman, D.R. Spatiotemporal hierarchy of relaxation events, dynamical heterogeneities, and structural reorganization in a supercooled liquid. Phys. Rev. Lett. 2010, 105, 135702. [Google Scholar] [CrossRef]
- Keys, A.S.; Hedges, L.O.; Garrahan, J.P.; Glotzer, S.C.; Chandler, D. Excitations are localized and relaxation is hierarchical in glass-forming liquids. Phys. Rev. X 2011, 1, 029901. [Google Scholar] [CrossRef]
- Ciamarra, M.P.; Pastore, R.; Coniglio, A. Particle jumps in structural glasses. Soft Matter 2016, 12, 358–366. [Google Scholar] [CrossRef]
- Perakis, F.; Camisasca, G.; Lane, T.J.; Späh, A.; Wikfeldt, K.T.; Sellberg, J.A.; Lehmkühler, F.; Pathak, H.; Kim, K.H.; Amann-Winkel, K.; et al. Coherent X-rays reveal the influence of cage effects on ultrafast water dynamics. Nat. Commun. 2018, 9, 1917. [Google Scholar] [CrossRef] [PubMed]
- Weeks, E.R.; Crocker, J.C.; Levitt, A.C.; Schofield, A.; Weitz, D.A. Three-dimensional direct imaging of structural relaxation near the colloidal glass transition. Science 2000, 287, 627–631. [Google Scholar] [CrossRef] [PubMed]
- Pastore, R.; Coniglio, A.; Ciamarra, M.P. From cage-jump motion to macroscopic diffusion in supercooled liquids. Soft Matter 2014, 10, 5724–5728. [Google Scholar] [CrossRef]
- Vollmayr-Lee, K. Single particle jumps in a binary Lennard-Jones system below the glass transition. J. Chem. Phys. 2004, 121, 4781–4794. [Google Scholar] [CrossRef] [PubMed]
- Helfferich, J.; Ziebert, F.; Frey, S.; Meyer, H.; Farago, J.; Blumen, A.; Baschnagel, J. Continuous-time random-walk approach to supercooled liquids. I. Different definitions of particle jumps and their consequences. Phys. Rev. E 2014, 89, 042603. [Google Scholar] [CrossRef]
- Shiba, H.; Kawasaki, T.; Onuki, A. Relationship between bond-breakage correlations and four-point correlations in heterogeneous glassy dynamics: Configuration changes and vibration modes. Phys. Rev. E 2012, 86, 041504. [Google Scholar] [CrossRef]
- Kikutsuji, T.; Kim, K.; Matubayasi, N. Diffusion dynamics of supercooled water modeled with the cage-jump motion and hydrogen-bond rearrangement. J. Chem. Phys. 2019, 150, 204502. [Google Scholar] [CrossRef]
- Mahanta, D.D.; Mitra, R.K. Connection of large amplitude angular jump motions with temporal heterogeneity in aqueous solutions. Phys. Chem. Chem. Phys. 2020, 22, 9339–9348. [Google Scholar] [CrossRef]
- Doliwa, B.; Heuer, A. Hopping in a supercooled Lennard-Jones liquid: Metabasins, waiting time distribution, and diffusion. Phys. Rev. E 2003, 67, 030501. [Google Scholar] [CrossRef]
- De Souza, V.K.; Wales, D.J. Energy landscapes for diffusion: Analysis of cage-breaking processes. J. Chem. Phys. 2008, 129, 164507. [Google Scholar] [CrossRef]
- Montroll, E.W.; Weiss, G.H. Random walks on lattices. II. J. Math. Phys. 1965, 6, 167–181. [Google Scholar] [CrossRef]
- Klafter, J.; Sokolov, I.M. First Steps in Random Walks: From Tools to Applications; Oxford University Press: Oxford, UK, 2011. [Google Scholar]
- Charbonneau, P.; Jin, Y.; Parisi, G.; Zamponi, F. Hopping and the Stokes–Einstein relation breakdown in simple glass formers. Proc. Natl. Acad. Sci. USA 2014, 111, 15025–15030. [Google Scholar] [CrossRef] [PubMed]
- Tarjus, G.; Kivelson, D. Breakdown of the Stokes–Einstein relation in supercooled liquids. J. Chem. Phys. 1995, 103, 3071–3073. [Google Scholar] [CrossRef]
- Shi, Z.; Debenedetti, P.G.; Stillinger, F.H. Relaxation processes in liquids: Variations on a theme by Stokes and Einstein. J. Chem. Phys. 2013, 138, 12A526. [Google Scholar] [CrossRef] [PubMed]
- Berthier, L.; Chandler, D.; Garrahan, J.P. Length scale for the onset of Fickian diffusion in supercooled liquids. EPL (Europhys. Lett.) 2004, 69, 320. [Google Scholar] [CrossRef]
- Hedges, L.O.; Maibaum, L.; Chandler, D.; Garrahan, J.P. Decoupling of exchange and persistence times in atomistic models of glass formers. J. Chem. Phys. 2007, 127, 211101. [Google Scholar] [CrossRef]
- Pastore, R.; Coniglio, A.; de Candia, A.; Fierro, A.; Ciamarra, M.P. Cage-jump motion reveals universal dynamics and non-universal structural features in glass forming liquids. J. Stat. Mech. Theory Exp. 2016, 2016, 054050. [Google Scholar] [CrossRef][Green Version]
- Mackowiak, S.A.; Herman, T.K.; Kaufman, L.J. Spatial and temporal heterogeneity in supercooled glycerol: Evidence from wide field single molecule imaging. J. Chem. Phys. 2009, 131, 244513. [Google Scholar] [CrossRef]
- Mackowiak, S.A.; Leone, L.M.; Kaufman, L.J. Probe dependence of spatially heterogeneous dynamics in supercooled glycerol as revealed by single molecule microscopy. Phys. Chem. Chem. Phys. 2011, 13, 1786–1799. [Google Scholar] [CrossRef]
- Yu, C.; Granick, S. Revisiting polymer surface diffusion in the extreme case of strong adsorption. Langmuir 2014, 30, 14538–14544. [Google Scholar] [CrossRef]
- Mackowiak, S.A.; Kaufman, L.J. When the heterogeneous appears homogeneous: Discrepant measures of heterogeneity in single-molecule observables. J. Phys. Chem. Lett. 2011, 2, 438–442. [Google Scholar] [CrossRef] [PubMed]
- Yukimoto, N.; Tsutsui, M.; He, Y.; Shintaku, H.; Tanaka, S.; Kawano, S.; Kawai, T.; Taniguchi, M. Tracking single-particle dynamics via combined optical and electrical sensing. Sci. Rep. 2013, 3, 1855. [Google Scholar] [CrossRef] [PubMed]
- Wei, C.Y.J.; Kim, Y.H.; Darst, R.K.; Rossky, P.J.; Bout, D.A.V. Origins of nonexponential decay in single molecule measurements of rotational dynamics. Phys. Rev. Lett. 2005, 95, 173001. [Google Scholar] [CrossRef] [PubMed]
- Jung, Y.; Garrahan, J.P.; Chandler, D. Excitation lines and the breakdown of Stokes–Einstein relations in supercooled liquids. Phys. Rev. E 2004, 69, 061205. [Google Scholar] [CrossRef] [PubMed]
- Ritort, F.; Sollich, P. Glassy dynamics of kinetically constrained models. Adv. Phys. 2003, 52, 219–342. [Google Scholar] [CrossRef]
- Pastore, R.; Kikutsuji, T.; Rusciano, F.; Matubayasi, N.; Kim, K.; Greco, F. Breakdown of the Stokes–Einstein relation in supercooled liquids: A cage-jump perspective. J. Chem. Phys. 2021, 155, 114503. [Google Scholar] [CrossRef] [PubMed]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Coslovich, D.; Ozawa, M.; Kob, W. Dynamic and thermodynamic crossover scenarios in the Kob-Andersen mixture: Insights from multi-CPU and multi-GPU simulations. Eur. Phys. J. E 2018, 41, 62. [Google Scholar] [CrossRef]
- Kob, W.; Andersen, H.C. Scaling behavior in the β-relaxation regime of a supercooled Lennard-Jones mixture. Phys. Rev. Lett. 1994, 73, 1376. [Google Scholar] [CrossRef]
- Hukushima, K.; Nemoto, K. Exchange Monte Carlo method and application to spin glass simulations. J. Phys. Soc. Jpn. 1996, 65, 1604–1608. [Google Scholar] [CrossRef]
- Larini, L.; Ottochian, A.; De Michele, C.; Leporini, D. Universal scaling between structural relaxation and vibrational dynamics in glass-forming liquids and polymers. Nat. Phys. 2008, 4, 42–45. [Google Scholar] [CrossRef]
- Kob, W.; Andersen, H.C. Testing mode-coupling theory for a supercooled binary Lennard-Jones mixture. II. Intermediate scattering function and dynamic susceptibility. Phys. Rev. E 1995, 52, 4134. [Google Scholar] [CrossRef] [PubMed]
- Flenner, E.; Szamel, G. Relaxation in a glassy binary mixture: Mode-coupling-like power laws, dynamic heterogeneity, and a new non-Gaussian parameter. Phys. Rev. E 2005, 72, 011205. [Google Scholar] [CrossRef] [PubMed]
- Ashwin, S.; Sastry, S. Low-temperature behaviour of the Kob–Andersen binary mixture. J. Phys. Condens. Matter 2003, 15, S1253. [Google Scholar]
- Berthier, L.; Tarjus, G. Critical test of the mode-coupling theory of the glass transition. Phys. Rev. E 2010, 82, 031502. [Google Scholar] [CrossRef]
- Kumar, S.K.; Szamel, G.; Douglas, J.F. Nature of the breakdown in the Stokes–Einstein relationship in a hard sphere fluid. J. Chem. Phys. 2006, 124, 214501. [Google Scholar] [CrossRef]
- Pastore, R.; Coniglio, A.; Ciamarra, M.P. Spatial correlations of elementary relaxation events in glass-forming liquids. Soft Matter 2015, 11, 7214–7218. [Google Scholar] [CrossRef]
- Pastore, R.; Coniglio, A.; Ciamarra, M.P. Dynamic phase coexistence in glass–forming liquids. Sci. Rep. 2015, 5, 11770. [Google Scholar] [CrossRef]
- Dubey, V.; Dueby, S.; Daschakraborty, S. Breakdown of the Stokes–Einstein relation in supercooled water: The jump-diffusion perspective. Phys. Chem. Chem. Phys. 2021, 23, 19964–19986. [Google Scholar] [CrossRef]


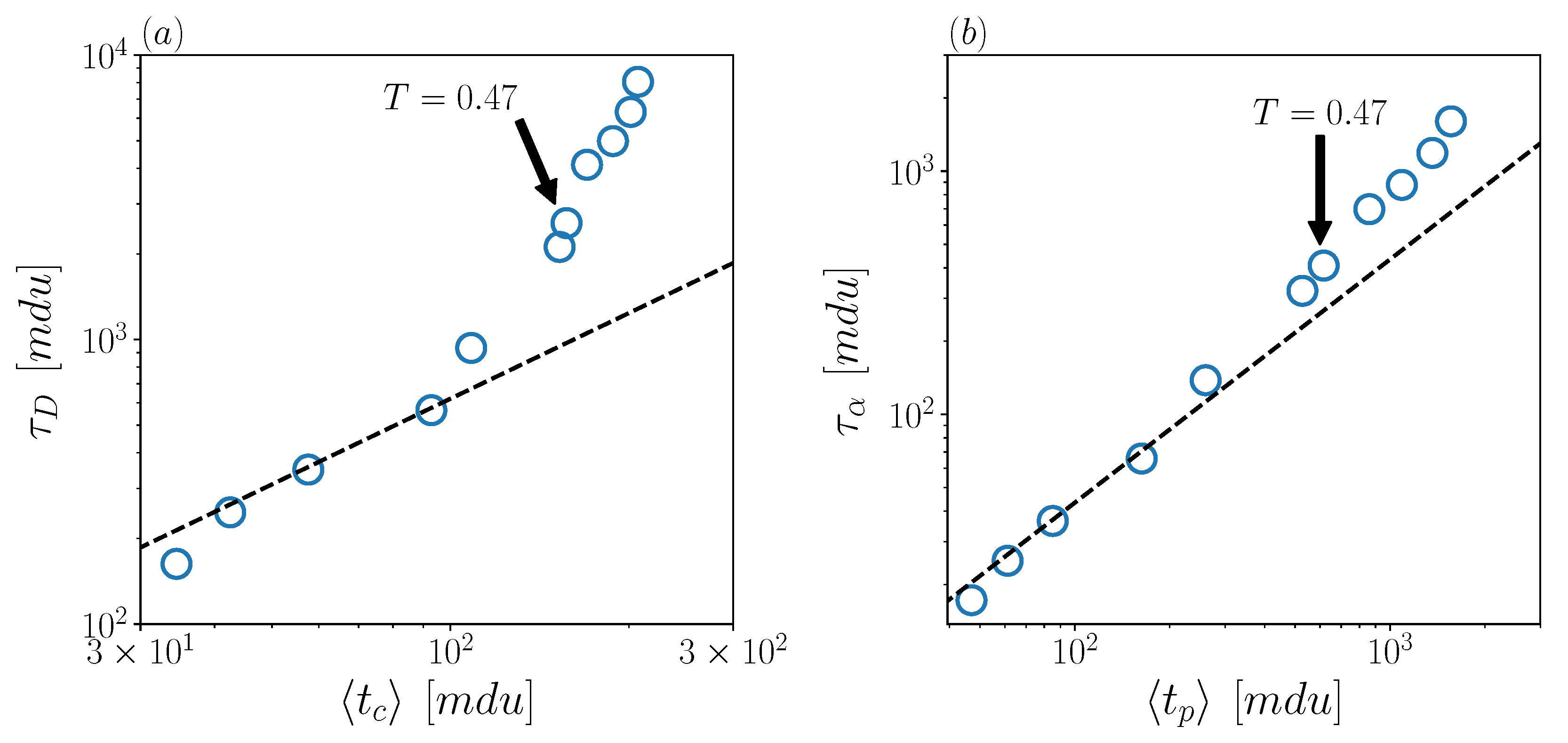
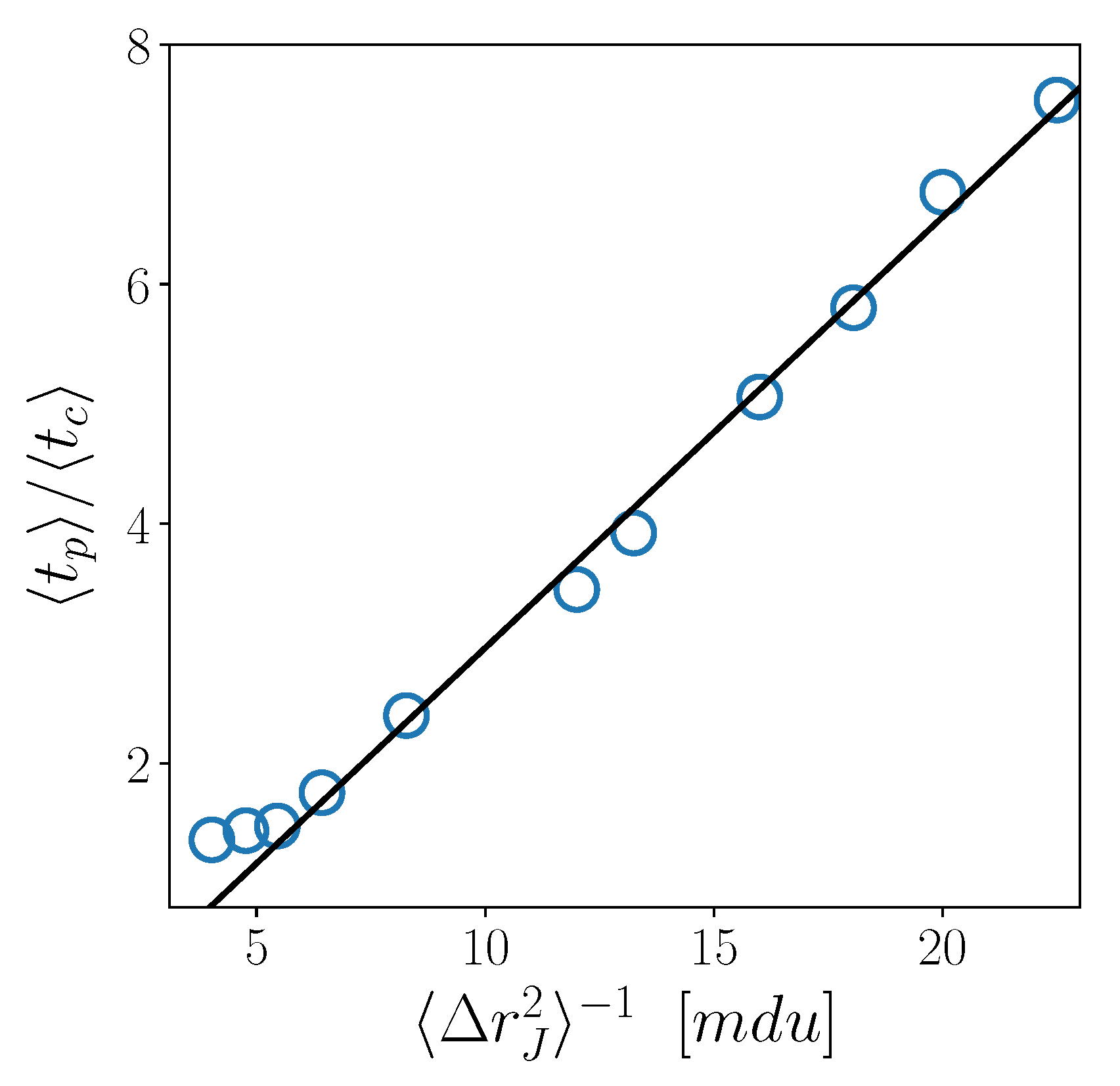
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Porpora, G.; Rusciano, F.; Pastore, R.; Greco, F. Comparing Microscopic and Macroscopic Dynamics in a Paradigmatic Model of Glass-Forming Molecular Liquid. Int. J. Mol. Sci. 2022, 23, 3556. https://doi.org/10.3390/ijms23073556
Porpora G, Rusciano F, Pastore R, Greco F. Comparing Microscopic and Macroscopic Dynamics in a Paradigmatic Model of Glass-Forming Molecular Liquid. International Journal of Molecular Sciences. 2022; 23(7):3556. https://doi.org/10.3390/ijms23073556
Chicago/Turabian StylePorpora, Giuseppe, Francesco Rusciano, Raffaele Pastore, and Francesco Greco. 2022. "Comparing Microscopic and Macroscopic Dynamics in a Paradigmatic Model of Glass-Forming Molecular Liquid" International Journal of Molecular Sciences 23, no. 7: 3556. https://doi.org/10.3390/ijms23073556
APA StylePorpora, G., Rusciano, F., Pastore, R., & Greco, F. (2022). Comparing Microscopic and Macroscopic Dynamics in a Paradigmatic Model of Glass-Forming Molecular Liquid. International Journal of Molecular Sciences, 23(7), 3556. https://doi.org/10.3390/ijms23073556






