Mathematical Description of the Increase in Selectivity of an Anion-Exchange Membrane Due to Its Modification with a Perfluorosulfonated Ionomer
Abstract
:1. Introduction
2. Results and Discussion
2.1. Model Formulation
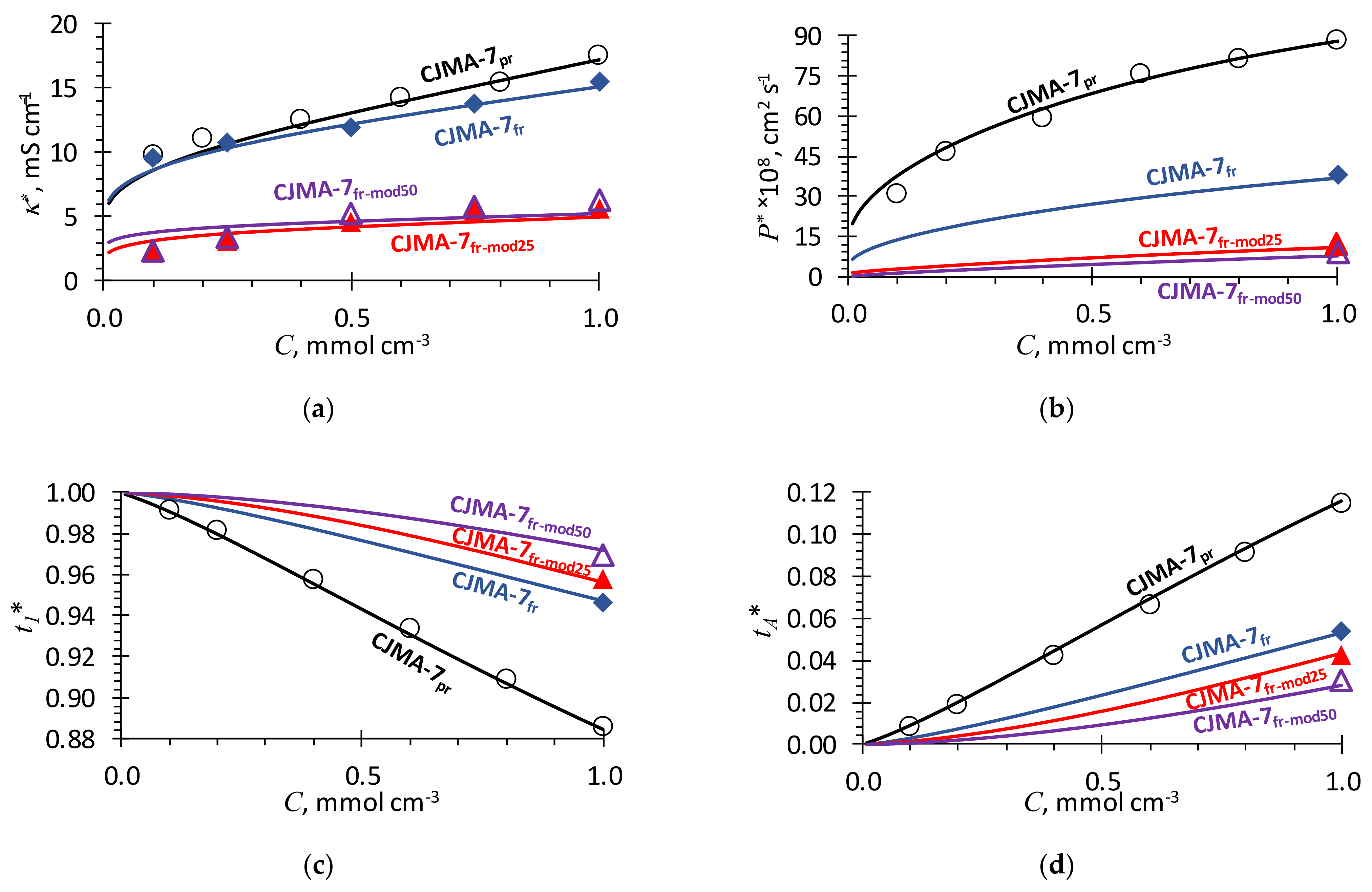
2.2. Comparison of Simulation and Experiment
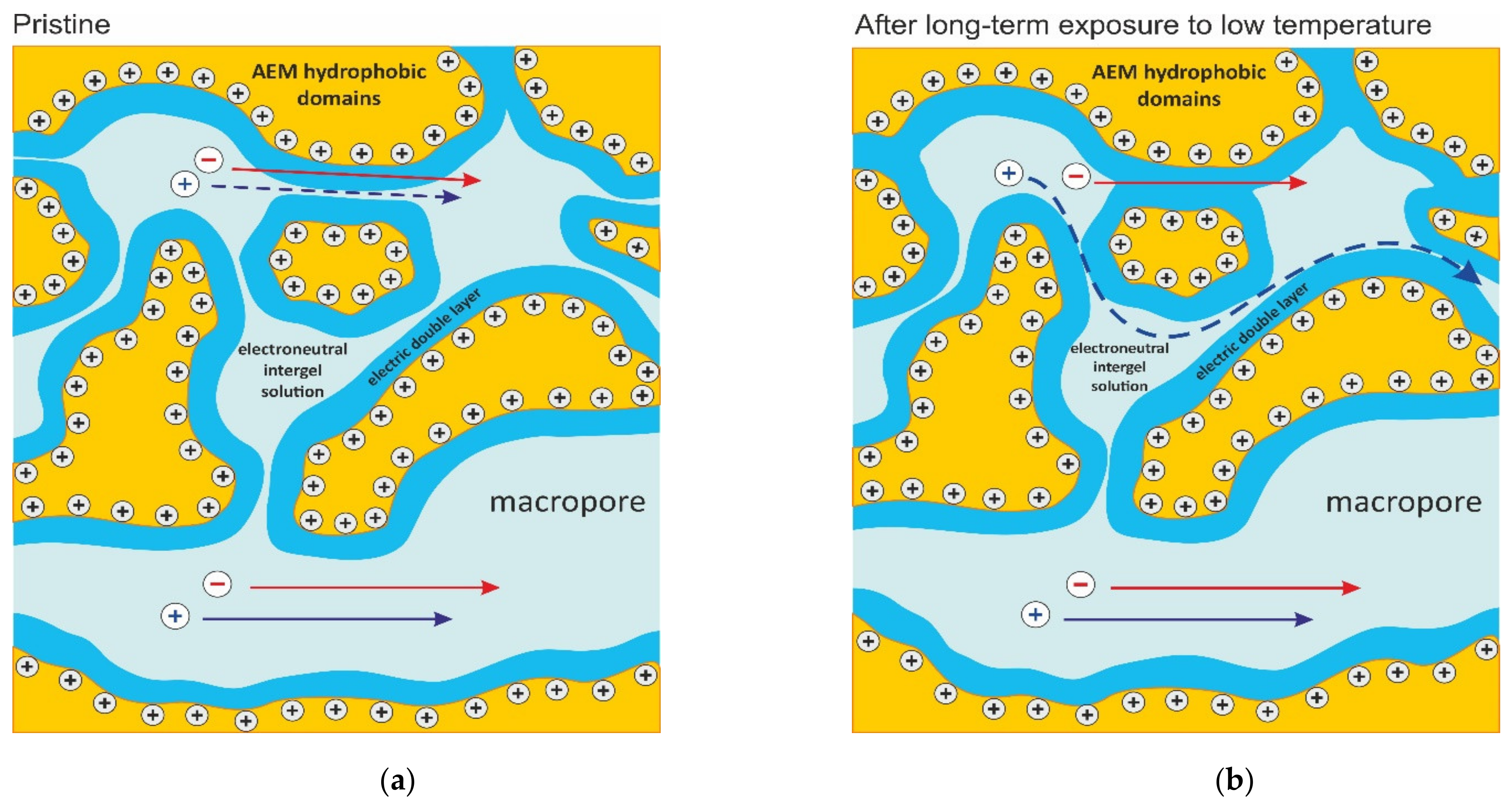
2.3. Exposure to a Low Temperature
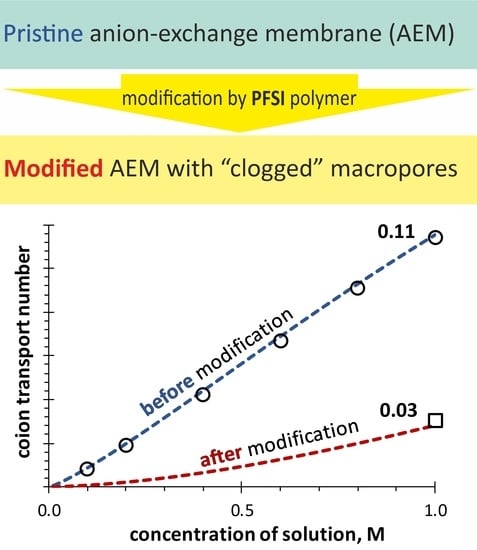
2.4. Effect of Membrane Modification with PFSI Solution
| Membrane | Fixed Groups | Thickness in 0.02 M NaCl, µm | Ion Exchange Capacity in Swollen State, mmol·gwet−1 | Water Content, mol H2O/mol Fixed Groups | Density in Swollen State, g·cm−3 |
|---|---|---|---|---|---|
| CJMA-7 | Mainly | 174 ± 10 | 0.75 ± 0.05 | 21.7 ± 1.0 | 1.13 ± 0.05 |
| PFSI | - | 0.87 ± 0.05 [71] | 36.5 ± 1.0 [71] | a 1.40 ± 0.15 [72] |
3. Experimental
3.1. Membrane and Modifier
3.2. Membrane Modification
3.3. Membrane Characterization
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Helfferich, F. Ion Exchange; McGraw-Hill: New York, NY, USA, 1962. [Google Scholar]
- Strathmann, H. Applications of Ion-Exchange Membrane Separation Processes. Membr. Sci. Technol. 2004, 9, 287–330. [Google Scholar] [CrossRef]
- Strathmann, H. Electrodialysis, a mature technology with a multitude of new applications. Desalination 2010, 264, 268–288. [Google Scholar] [CrossRef]
- Ran, J.; Wu, L.; He, Y.; Yang, Z.; Wang, Y.; Jiang, C.; Ge, L.; Bakangura, E.; Xu, T. Ion exchange membranes: New developments and applications. J. Memb. Sci. 2017, 522, 267–291. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, Y. Circular economy-driven ammonium recovery from municipal wastewater: State of the art, challenges and solutions forward. Bioresour. Technol. 2021, 334, 125231. [Google Scholar] [CrossRef]
- Merle, G.; Wessling, M.; Nijmeijer, K. Anion exchange membranes for alkaline fuel cells: A review. J. Memb. Sci. 2011, 377, 1–35. [Google Scholar] [CrossRef]
- Yaroslavtsev, A.B.; Dobrovolsky, Y.A.; Shaglaeva, N.S.; Frolova, L.A.; Gerasimova, E.V.; Sanginov, E.A. Nanostructured materials for low-temperature fuel cells. Russ. Chem. Rev. 2012, 81, 191–220. [Google Scholar] [CrossRef]
- Wang, J.; Zhao, Y. Poly(aryl piperidinium) membranes and ionomers for hydroxide exchange membrane fuel cells. Nat. Energy 2019, 4, 392–398. [Google Scholar] [CrossRef]
- Thangarasu, S.; Oh, T.H. Progress in poly(phenylene oxide) based cation exchange membranes for fuel cells and redox flow batteries applications. Int. J. Hydrog. Energy 2021, 46, 38381–38415. [Google Scholar] [CrossRef]
- Ye, J.; Cheng, Y.; Sun, L.; Ding, M.; Wu, C.; Yuan, D.; Zhao, X.; Xiang, C.; Jia, C. A green SPEEK/lignin composite membrane with high ion selectivity for vanadium redox flow battery. J. Memb. Sci. 2019, 572, 110–118. [Google Scholar] [CrossRef]
- Jiang, S.; Sun, H.; Wang, H.; Ladewig, B.P.; Yao, Z. A comprehensive review on the synthesis and applications of ion exchange membranes. Chemosphere 2021, 282, 130817. [Google Scholar] [CrossRef]
- Luo, T.; Abdu, S.; Wessling, M. Selectivity of ion exchange membranes: A review. J. Memb. Sci. 2018, 555, 429–454. [Google Scholar] [CrossRef]
- Xu, S.; Song, J.; Bi, Q.; Chen, Q.; Zhang, W.M.; Qian, Z.; Zhang, L.; Xu, S.; Tang, N.; He, T. Extraction of lithium from Chinese salt-lake brines by membranes: Design and practice. J. Memb. Sci. 2021, 635, 119441. [Google Scholar] [CrossRef]
- Merino-Garcia, I.; Velizarov, S. New insights into the definition of membrane cleaning strategies to diminish the fouling impact in ion exchange membrane separation processes. Sep. Purif. Technol. 2021, 277, 119445. [Google Scholar] [CrossRef]
- Sharma, M.; Das, P.P.; Chakraborty, A.; Purkait, M.K. Clean energy from salinity gradients using pressure retarded osmosis and reverse electrodialysis: A review. Sustain. Energy Technol. Assess. 2022, 49, 101687. [Google Scholar] [CrossRef]
- Uliana, A.A.; Bui, N.T.; Kamcev, J.; Taylor, M.K.; Urban, J.J.; Long, J.R. Ion-capture electrodialysis using multifunctional adsorptive membranes. Science 2021, 372, 296–299. [Google Scholar] [CrossRef]
- Rathi, B.S.; Kumar, P.S.; Parthiban, R. A review on recent advances in electrodeionization for various environmental applications. Chemosphere 2022, 289, 133223. [Google Scholar] [CrossRef]
- Akhtar, N.; Ishak, M.I.S.; Ahmad, M.I.; Umar, K.; Md Yusuff, M.S.; Anees, M.T.; Qadir, A.; Ali Almanasir, Y.K. Modification of the Water Quality Index (WQI) Process for Simple Calculation Using the Multi-Criteria Decision-Making (MCDM) Method: A Review. Water 2021, 13, 905. [Google Scholar] [CrossRef]
- Akhtar, N.; Syakir Ishak, M.I.; Bhawani, S.A.; Umar, K. Various Natural and Anthropogenic Factors Responsible for Water Quality Degradation: A Review. Water 2021, 13, 2660. [Google Scholar] [CrossRef]
- Wenten, I.G.; Khoiruddin. Recent developments in heterogeneous ion-exchange membrane: Preparation, modification, characterization and performance evaluation. J. Eng. Sci. Technol. 2016, 11, 916–934. [Google Scholar]
- Ariono, D.; Khoiruddin; Subagjo; Wenten, I.G. Heterogeneous structure and its effect on properties and electrochemical behavior of ion-exchange membrane. Mater. Res. Express 2017, 4, 024006. [Google Scholar] [CrossRef]
- Kotoka, F.; Merino-Garcia, I.; Velizarov, S. Surface modifications of anion exchange membranes for an improved reverse electrodialysis process performance: A review. Membranes 2020, 10, 160. [Google Scholar] [CrossRef]
- Kucera, J. Reverse Osmosis; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2010; ISBN 9780470882634. [Google Scholar]
- Kedem, O.; Schechtmann, L.; Mirsky, Y.; Saveliev, G.; Daltrophe, N. Low-polarisation electrodialysis membranes. Desalination 1998, 118, 305–314. [Google Scholar] [CrossRef]
- Andreeva, M.A.; Gil, V.V.; Pismenskaya, N.D.; Nikonenko, V.V.; Dammak, L.; Larchet, C.; Grande, D.; Kononenko, N.A. Effect of homogenization and hydrophobization of a cation-exchange membrane surface on its scaling in the presence of calcium and magnesium chlorides during electrodialysis. J. Memb. Sci. 2017, 540, 183–191. [Google Scholar] [CrossRef]
- Sharafan, M.V.; Zabolotskii, V.I.; Bugakov, V.V. Electric mass transport through homogeneous and surface-modified heterogeneous ion-exchange membranes at a rotating membrane disk. Russ. J. Electrochem. 2009, 45, 1162–1169. [Google Scholar] [CrossRef]
- Andreeva, M.A.; Gil, V.V.; Pismenskaya, N.D.; Dammak, L.; Kononenko, N.A.; Larchet, C.; Grande, D.; Nikonenko, V.V. Mitigation of membrane scaling in electrodialysis by electroconvection enhancement, pH adjustment and pulsed electric field application. J. Memb. Sci. 2018, 549, 129–140. [Google Scholar] [CrossRef]
- Sata, T. Studies on anion exchange membranes having permselectivity for specific anions in electrodialysis—Effect of hydrophilicity of anion exchange membranes on permselectivity of anions. J. Memb. Sci. 2000, 167, 1–31. [Google Scholar] [CrossRef]
- Zhu, Y.; Ahmad, M.; Yang, L.; Misovich, M.; Yaroshchuk, A.; Bruening, M.L. Adsorption of polyelectrolyte multilayers imparts high monovalent/divalent cation selectivity to aliphatic polyamide cation-exchange membranes. J. Memb. Sci. 2017, 537, 177–185. [Google Scholar] [CrossRef]
- Wang, Z.; Liang, S.; Kang, Y.; Zhao, W.; Xia, Y.; Yang, J.; Wang, H.; Zhang, X. Manipulating interfacial polymerization for polymeric nanofilms of composite separation membranes. Prog. Polym. Sci. 2021, 122, 101450. [Google Scholar] [CrossRef]
- Zabolotskii, V.I.; Melnikov, S.S.; Achoh, A.R. Nitrate selective anion exchange membrane. J. Membr. Sci. 1988, 38, 101–111. [Google Scholar]
- Chen, J.; Cao, J.; Zhang, R.; Zhou, J.; Wang, S.; Liu, X.; Zhang, T.; Tao, X.; Zhang, Y. Modifications on Promoting the Proton Conductivity of Polybenzimidazole-Based Polymer Electrolyte Membranes in Fuel Cells. Membranes 2021, 11, 826. [Google Scholar] [CrossRef]
- Agel, E.; Bouet, J.; Fauvarque, J. Characterization and use of anionic membranes for alkaline fuel cells. J. Power Sources 2001, 101, 267–274. [Google Scholar] [CrossRef]
- Wilhelm, F.G.; Pünt, I.; van der Vegt, N.F.A.; Strathmann, H.; Wessling, M. Asymmetric Bipolar Membranes in Acid−Base Electrodialysis. Ind. Eng. Chem. Res. 2002, 41, 579–586. [Google Scholar] [CrossRef]
- Pärnamäe, R.; Mareev, S.; Nikonenko, V.; Melnikov, S.; Sheldeshov, N.; Zabolotskii, V.; Hamelers, H.V.M.; Tedesco, M. Bipolar membranes: A review on principles, latest developments, and applications. J. Memb. Sci. 2021, 617, 118538. [Google Scholar] [CrossRef]
- Melnikov, S.; Zabolotskii, V.; Sheldeshov, N.; Achoh, A.; Bondarev, D. Catalysis of water splitting reaction in asymmetric bipolar membranes with different chemical composition of cation-exchange layer. Desalin. Water Treat. 2018, 124, 30–36. [Google Scholar] [CrossRef]
- Park, H.B.; Kamcev, J.; Robeson, L.M.; Elimelech, M.; Freeman, B.D. Maximizing the right stuff: The trade-off between membrane permeability and selectivity. Science 2017, 356, 1138–1148. [Google Scholar] [CrossRef] [Green Version]
- Epsztein, R.; DuChanois, R.M.; Ritt, C.L.; Noy, A.; Elimelech, M. Towards single-species selectivity of membranes with subnanometre pores. Nat. Nanotechnol. 2020, 15, 426–436. [Google Scholar] [CrossRef]
- Reig, M.; Farrokhzad, H.; Van der Bruggen, B.; Gibert, O.; Cortina, J.L. Synthesis of a monovalent selective cation exchange membrane to concentrate reverse osmosis brines by electrodialysis. Desalination 2015, 375, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Ounissi, T.; Dammak, L.; Fauvarque, J.-F.; Selmane Bel Hadj Hmida, E. Ecofriendly lithium-sodium separation by diffusion processes using lithium composite membrane. Sep. Purif. Technol. 2021, 275, 119134. [Google Scholar] [CrossRef]
- Golubenko, D.V.; Karavanova, Y.A.; Melnikov, S.S.; Achoh, A.R.; Pourcelly, G.; Yaroslavtsev, A.B. An approach to increase the permselectivity and mono-valent ion selectivity of cation-exchange membranes by introduction of amorphous zirconium phosphate nanoparticles. J. Memb. Sci. 2018, 563, 777–784. [Google Scholar] [CrossRef]
- Stenina, I.; Golubenko, D.; Nikonenko, V.; Yaroslavtsev, A. Selectivity of Transport Processes in Ion-Exchange Membranes: Relationship with the Structure and Methods for Its Improvement. Int. J. Mol. Sci. 2020, 21, 5517. [Google Scholar] [CrossRef]
- Falina, I.; Loza, N.; Loza, S.; Titskaya, E.; Romanyuk, N. Permselectivity of Cation Exchange Membranes Modified by Polyaniline. Membranes 2021, 11, 227. [Google Scholar] [CrossRef] [PubMed]
- Sarapulova, V.; Pismenskaya, N.; Titorova, V.; Sharafan, M.; Wang, Y.; Xu, T.; Zhang, Y.; Nikonenko, V. Transport characteristics of CJMAEDTM homogeneous anion exchange membranes in sodium chloride and sodium sulfate solutions. Int. J. Mol. Sci. 2021, 22, 1415. [Google Scholar] [CrossRef] [PubMed]
- Kingsbury, R.S.; Coronell, O. Modeling and validation of concentration dependence of ion exchange membrane permselectivity: Significance of convection and Manning’s counter-ion condensation theory. J. Memb. Sci. 2021, 620, 118411. [Google Scholar] [CrossRef]
- Luo, T.; Roghmans, F.; Wessling, M. Ion mobility and partition determine the counter-ion selectivity of ion exchange membranes. J. Memb. Sci. 2020, 597, 117645. [Google Scholar] [CrossRef] [Green Version]
- Akberova, E.M.; Vasil’eva, V.I.; Zabolotsky, V.I.; Novak, L. A Study of Ralex Membrane Morphology by SEM. Membranes 2019, 9, 169. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sarapulova, V.; Shkorkina, I.; Mareev, S.; Pismenskaya, N.; Kononenko, N.; Larchet, C.; Dammak, L.; Nikonenko, V. Transport characteristics of fujifilm ion-exchange membranes as compared to homogeneous membranes АМХ and СМХ and to heterogeneous membranes MK-40 and MA-41. Membranes 2019, 9, 84. [Google Scholar] [CrossRef] [Green Version]
- Kamcev, J.; Sujanani, R.; Jang, E.S.; Yan, N.; Moe, N.; Paul, D.R.; Freeman, B.D. Salt concentration dependence of ionic conductivity in ion exchange membranes. J. Memb. Sci. 2018, 547, 123–133. [Google Scholar] [CrossRef]
- Filippov, A.N.; Koroleva, Y.O.; Verma, A.K. Cell Model of a Fibrous Medium (Membrane). Comparison between Two Different Approaches to Varying Liquid Viscosity. Membr. Membr. Technol. 2020, 2, 230–243. [Google Scholar] [CrossRef]
- Filippov, A.; Afonin, D.; Kononenko, N.; Lvov, Y.; Vinokurov, V. New approach to characterization of hybrid nanocomposites. Colloids Surf. A Physicochem. Eng. Asp. 2017, 521, 251–259. [Google Scholar] [CrossRef]
- Nikonenko, V.; Nebavsky, A.; Mareev, S.; Kovalenko, A.; Urtenov, M.; Pourcelly, G. Modelling of ion transport in electromembrane systems: Impacts of membrane bulk and surface heterogeneity. Appl. Sci. 2018, 9, 25. [Google Scholar] [CrossRef] [Green Version]
- Guzmán-Garcia, A.G.; Pintauro, P.N.; Verbrugge, M.W.; Hill, R.F. Development of a space-charge transport model for ion-exchange membranes. AIChE J. 1990, 36, 1061–1074. [Google Scholar] [CrossRef]
- Peters, P.B.; van Roij, R.; Bazant, M.Z.; Biesheuvel, P.M. Analysis of electrolyte transport through charged nanopores. Phys. Rev. E 2016, 93, 053108. [Google Scholar] [CrossRef] [Green Version]
- Choy, T.C. Effective Medium Theory; Oxford University Press: Oxford, UK, 2015; ISBN 9780198705093. [Google Scholar]
- Mackie, J.S.; Meares, P. The diffusion of electrolytes in a cation-exchange resin membrane I. Theoretical. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1955, 232, 498–509. [Google Scholar] [CrossRef]
- Prager, S. Diffusion in Inhomogeneous Media. J. Chem. Phys. 1960, 33, 122–127. [Google Scholar] [CrossRef]
- Glueckauf, E.; A, P.R.S.L. A new approach to ion exchange polymers. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1962, 268, 350–370. [Google Scholar] [CrossRef]
- Zabolotsky, V.I.; Nikonenko, V.V. Effect of structural membrane inhomogeneity on transport properties. J. Memb. Sci. 1993, 79, 181–198. [Google Scholar] [CrossRef]
- Nikonenko, V.V.; Yaroslavtsev, A.B.; Pourcelly, G. Ion Transfer in and Through Charged Membranes: Structure, Properties, and Theory. In Ionic Interactions in Natural and Synthetic Macromolecules; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012; pp. 267–335. ISBN 9780470529270. [Google Scholar]
- Löwemark, L.; Liao, A.C.-Y.; Liou, Y.-H.; Godad, S.; Chang, T.-Y.; Kunz, A. Potential and pitfalls of XRF-CS analysis of ion-exchange resins in environmental studies. Sci. Rep. 2021, 11, 20941. [Google Scholar] [CrossRef]
- Aittola, J.-P.; Chyssler, J.; Ringberg, H. Thermal Stability of Ion-Exchange Resins; Studsvik Energiteknik AB: Nykoeping, Sweden, 1982. [Google Scholar]
- Perepechko, I. Viscoelastic parameters of polymers at low temperatures. In Low-Temperature Properties of Polymers; Elsevier: Amsterdam, The Netherlands, 1980; pp. 241–254. ISBN 978-0-08-025301-5. [Google Scholar]
- Alberti, G.; Narducci, R.; Sganappa, M. Effects of hydrothermal/thermal treatments on the water-uptake of Nafion membranes and relations with changes of conformation, counter-elastic force and tensile modulus of the matrix. J. Power Sources 2008, 178, 575–583. [Google Scholar] [CrossRef]
- Gierke, T.D.; Munn, G.E.; Wilson, F.C. The morphology in nafion perfluorinated membrane products, as determined by wide- and small-angle x-ray studies. J. Polym. Sci. Polym. Phys. Ed. 1981, 19, 1687–1704. [Google Scholar] [CrossRef]
- Kreuer, K.-D.; Paddison, S.J.; Spohr, E.; Schuster, M. Transport in Proton Conductors for Fuel-Cell Applications: Simulations, Elementary Reactions, and Phenomenology. Chem. Rev. 2004, 104, 4637–4678. [Google Scholar] [CrossRef] [Green Version]
- Mauritz, K.A.; Moore, R.B. State of Understanding of Nafion. Chem. Rev. 2004, 104, 4535–4586. [Google Scholar] [CrossRef] [PubMed]
- Tsehaye, M.T.; Gebreslassie, G.T.; Choi, N.H.; Milian, D.; Martin, V.; Fischer, P.; Tübke, J.; Kissi, N.E.; Donten, M.L.; Alloin, F.; et al. Pristine and modified porous membranes for zinc slurry–air flow battery. Molecules 2021, 26, 4062. [Google Scholar] [CrossRef] [PubMed]
- Larchet, C.; Dammak, L.; Auclair, B.; Parchikov, S.; Nikonenko, V. A simplified procedure for ion-exchange membrane characterisation. New J. Chem. 2004, 28, 1260–1267. [Google Scholar] [CrossRef]
- Rollins, C.; Jensen, L.; Schwartz, A.N. Desalting of Amino Acid Solutions by an Ion Retardation Resin. Anal. Chem. 1962, 34, 711–712. [Google Scholar] [CrossRef]
- Berezina, N.P.; Kubaisi, A.A.R.; Alpatova, N.M.; Andreev, V.N.; Griga, E.I. Composite Polyaniline/MF-4SK Membranes: A Chemical Template Synthesis and the Sorption and Conduction Properties. Russ. J. Electrochem. 2004, 40, 286–293. [Google Scholar] [CrossRef]
- Zook, L.A.; Leddy, J. Density and Solubility of Nafion: Recast, Annealed, and Commercial Films. Anal. Chem. 1996, 68, 3793–3796. [Google Scholar] [CrossRef]
- Shin, M.G.; Seo, J.Y.; Park, H.; Park, Y.-I.; Lee, J.-H. Overcoming the permeability-selectivity trade-off of desalination membranes via controlled solvent activation. J. Memb. Sci. 2021, 620, 118870. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Z.; Jiang, C.; Xu, T. Recovery of gamma-aminobutyric acid (GABA) from reaction mixtures containing salt by electrodialysis. Sep. Purif. Technol. 2016, 170, 353–359. [Google Scholar] [CrossRef]
- Yan, H.; Wang, Y.; Xu, T. Developing Ion Exchange Membrane for Treating High Salinity Water Using Electrodialysis. In Proceedings of the 5th International Conferences on Sustainable Chemical Product and Process Engineering (SCPPE), Tianjin, China, 30 June–3 July 2019; pp. 65–67. [Google Scholar]
- Berezina, N.P.; Timofeev, S.V.; Kononenko, N.A. Effect of conditioning techniques of perfluorinated sulphocationic membranes on their hydrophylic and electrotransport properties. J. Memb. Sci. 2002, 209, 509–518. [Google Scholar] [CrossRef]
- Lteif, R.; Dammak, L.; Larchet, C.; Auclair, B. Conductivité électrique membranaire: Étude de l’effet de la concentration, de la nature de l’électrolyte et de la structure membranaire. Eur. Polym. J. 1999, 35, 1187–1195. [Google Scholar] [CrossRef]
- Pismenskaya, N.D.; Nevakshenova, E.E.; Nikonenko, V. V Using a Single Set of Structural and Kinetic Parameters of the Microheterogeneous Model to Describe the Sorption and Kinetic Properties of Ion-Exchange Membranes. Pet. Chem. 2018, 58, 147–156. [Google Scholar] [CrossRef]
- Gnusin, N.P.; Berezina, N.P.; Shudrenko, A.A.; Ivina, A.P. Electrolyte diffusion across ion-exchange membranes. Russ. J. Phys. Chem. A 1994, 68, 506–510. [Google Scholar]
- Auclair, B.; Nikonenko, V.; Larchet, C.; Métayer, M.; Dammak, L. Correlation between transport parameters of ion-exchange membranes. J. Memb. Sci. 2002, 195, 89–102. [Google Scholar] [CrossRef]


| f1 | f2 | × 106, cm2 s−1 | × 106, cm2 s−1 | × 106, cm2 s−1 | × 106, cm2 s−1 | , mmol cm−3 | |||
|---|---|---|---|---|---|---|---|---|---|
| CJMA-7pr | 0.82 | 0.18 | 2.30 | 1.50 | 20.3 | 13.4 | 0.30 | 0.07 | 0.92 |
| CJMA-7fr | 0.84 | 0.16 | 2.25 | 0.65 | 0.25 | 0.05 | 0.94 | ||
| CJMA-7fr-mod25 | 0.85 | 0.15 | 1.50 | 0.55 | 4.5 | 5.5 | 0.12 | 0.05 | 0.95 |
| CJMA-7fr-mod50 | 0.90 | 0.10 | 1.45 | 0.50 | 4.3 | 5.2 | 0.10 | 0.05 | 1.0 |
| PFSI-25 | - | - | - | - | 4.5 | 5.5 | - | 0.1 | 0.13 |
| PFSI-50 | - | - | - | - | 4.3 | 5.2 | - | 0.1 | 0.18 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kozmai, A.; Pismenskaya, N.; Nikonenko, V. Mathematical Description of the Increase in Selectivity of an Anion-Exchange Membrane Due to Its Modification with a Perfluorosulfonated Ionomer. Int. J. Mol. Sci. 2022, 23, 2238. https://doi.org/10.3390/ijms23042238
Kozmai A, Pismenskaya N, Nikonenko V. Mathematical Description of the Increase in Selectivity of an Anion-Exchange Membrane Due to Its Modification with a Perfluorosulfonated Ionomer. International Journal of Molecular Sciences. 2022; 23(4):2238. https://doi.org/10.3390/ijms23042238
Chicago/Turabian StyleKozmai, Anton, Natalia Pismenskaya, and Victor Nikonenko. 2022. "Mathematical Description of the Increase in Selectivity of an Anion-Exchange Membrane Due to Its Modification with a Perfluorosulfonated Ionomer" International Journal of Molecular Sciences 23, no. 4: 2238. https://doi.org/10.3390/ijms23042238
APA StyleKozmai, A., Pismenskaya, N., & Nikonenko, V. (2022). Mathematical Description of the Increase in Selectivity of an Anion-Exchange Membrane Due to Its Modification with a Perfluorosulfonated Ionomer. International Journal of Molecular Sciences, 23(4), 2238. https://doi.org/10.3390/ijms23042238