Secondary Structures of Proteins Follow Menzerath–Altmann Law
Abstract
:1. Introduction
2. Results
2.1. Verifying the x-y Dependence and ML
2.2. MAL Formula Fitting and Assessment
2.3. Assessment of MAL Model Outliers
3. Discussion
3.1. Presence of Menzerath’s Law, Menzerath–Altmann’s Law and the Formulae
3.2. Outliers of Menzerath–Altmann’s Law
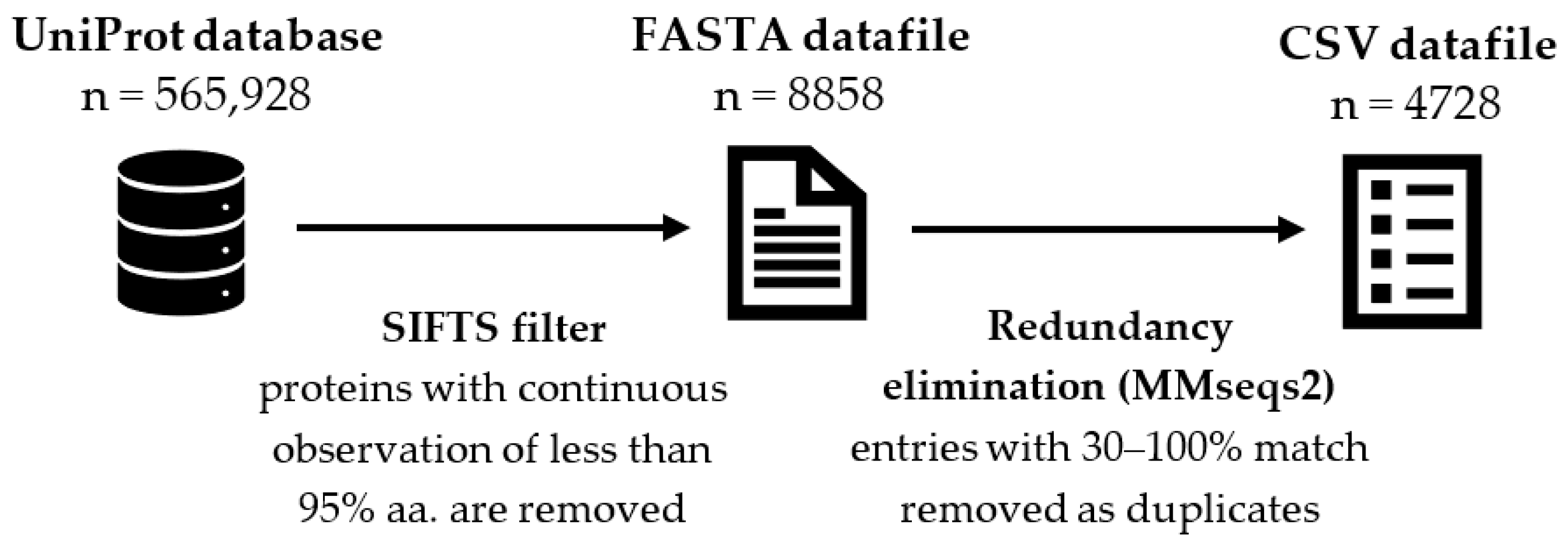
4. Materials and Methods
4.1. Materials
4.2. Methods of Testing ML and MAL
5. Conclusions
5.1. The Average Secondary Structures Length of a Protein Is Dependent on Their Number
5.2. The Formula Describes a Possible OPTIMAL Relation
5.3. Proteins Can Outlie the Described Relation
5.4. The Relation Can Be Connected to Evolution
5.5. Implications and Possible Applications
5.6. Further Research
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AA | Amino acid(s). |
| AIC | Akaike Information Criterion. |
| CI | Confidence Interval, 95%. |
| MAL | Menzerath–Altmann Law. |
| ML | Menzerath’s Law. |
| MSE | Mean-Squared error. |
| NLS | Non-linear Least Squares. |
| NWLS | Non-linear Weighted Least Squares. |
| OLS | Ordinary Linear Squares. |
| r | Pearson’s correlation coefficient. |
| s | Standard error. |
| st. res. | Studentized residuals. |
| ρ | Spearman’s rank correlation coefficient. |
| Correlation coefficient eta. | |
| The number of secondary structures in a given protein. | |
| The average length of the secondary structures in a given protein, measured in number of amino acids (AA). | |
| The average of multiple y values in a bin (i.e., a group of proteins with the same number of secondary structures x). |
Appendix A
| Model | a | b | c | d | s | AIC |
|---|---|---|---|---|---|---|
| 1 | 11.252 (±1.42) | −0.132 (±0.042) | 0.001 (±0.001) | 5.325 | −39,821.1 | |
| 2 | 9.429 (±0.671) | −0.069 (±0.017) | 5.361 | −39,822.6 | ||
| 3 | 150.149 (±18.233) | 41.601 | −39,433.5 | |||
| 4 | 12.493 (±2.891) | 6.825 (±0.086) | 5.286 | −39,822.8 | ||
| 5 | 229.332 (±58.361) | 45.681 (±1.360) | 5.258 | −39,823.2 |
Appendix B
References
- Menzerath, P. Über Einige Phonetische Probleme. In Actes du Premier Congres International de Linguistes; Sijthoff: Leiden, The Netherlands, 1928; pp. 104–105. [Google Scholar]
- Altmann, G. Prolegomena to Menzerath’s Law. Glottometrika 1980, 2, 124–129. [Google Scholar]
- Ferrer-I-Cancho, R.; Forns, N. The self-organization of genomes. Complexity 2009, 15, 34–36. [Google Scholar] [CrossRef] [Green Version]
- Solé, R.V. Genome size, self-organization and DNA’s dark matter. Complexity 2010, 16, 20–23. [Google Scholar] [CrossRef]
- Hernández-Fernández, A.; Baixeries, J.; Forns, N.; Ferrer-I-Cancho, R. Size of the Whole versus Number of Parts in Genomes. Entropy 2011, 13, 1465–1480. [Google Scholar] [CrossRef] [Green Version]
- Baixeries, J.; Hernández-Fernández, A.; Forns, N.; Ferrer-I-Cancho, R. The Parameters of the Menzerath-Altmann Law in Genomes. J. Quant. Linguist. 2013, 20, 94–104. [Google Scholar] [CrossRef]
- Ferrer-I-Cancho, R.; Forns, N.; Hernández-Fernández, A.; Bel-Enguix, G.; Baixeries, J. The challenges of statistical patterns of language: The case of Menzerath’s law in genomes. Complexity 2012, 18, 11–17. [Google Scholar] [CrossRef] [Green Version]
- Li, W. Menzerath’s law at the gene-exon level in the human genome. Complexity 2011, 17, 49–53. [Google Scholar] [CrossRef]
- Eroglu, S. Language-like behavior of protein length distribution in proteomes. Complexity 2014, 20, 12–21. [Google Scholar] [CrossRef]
- Shahzad, K.; Mittenthal, J.E.; Caetano-Anollés, G. The organization of domains in proteins obeys Menzerath-Altmann’s law of language. BMC Syst. Biol. 2015, 9, 44. [Google Scholar] [CrossRef] [Green Version]
- Baixeries, J.; Hernández-Fernández, A.; Ferrer-I-Cancho, R. Random models of Menzerath–Altmann law in genomes. Biosystems 2012, 107, 167–173. [Google Scholar] [CrossRef] [Green Version]
- Torre, I.G.; Dębowski, Ł.; Hernández-Fernández, A. Can Menzerath’s Law Be a Criterion of Complexity in Communication? PLoS ONE 2021, 16, e0256133. [Google Scholar] [CrossRef]
- Milička, J. Menzerath’s Law: The Whole is Greater than the Sum of its Parts. J. Quant. Linguist. 2014, 21, 85–99. [Google Scholar] [CrossRef]
- Ferrer-I-Cancho, R.; Hernández-Fernández, A.; Baixeries, J.; Dębowski, L.; Mačutek, J. When is Menzerath-Altmann law mathematically trivial? A new approach. Stat. Appl. Genet. Mol. Biol. 2014, 13, 633–644. [Google Scholar] [CrossRef] [Green Version]
- Bowie, J.U. Helix packing in membrane proteins. J. Mol. Biol. 1997, 272, 780–789. [Google Scholar] [CrossRef]
- Sjöblom, B.; Salmazo, A.; Djinović-Carugo, K. α-Actinin Structure and Regulation. Cell. Mol. Life Sci. 2008, 65, 2688. [Google Scholar] [CrossRef]
- The UniProt Consortium. UniProt: The Universal Protein Knowledgebase in 2021. Nucleic Acids Res. 2021, 49, D480–D489. [Google Scholar] [CrossRef]
- Dana, J.M.; Gutmanas, A.; Tyagi, N.; Qi, G.; O’Donovan, C.; Martin, M.-J.; Velankar, S. SIFTS: Updated Structure Integration with Function, Taxonomy and Sequences resource allows 40-fold increase in coverage of structure-based annotations for proteins. Nucleic Acids Res. 2018, 47, D482–D489. [Google Scholar] [CrossRef]
- Gutmanas, A.; Alhroub, Y.; Battle, G.M.; Berrisford, J.M.; Bochet, E.; Conroy, M.J.; Dana, J.M.; Montecelo, M.A.F.; van Ginkel, G.; Gore, S.P.; et al. PDBe: Protein Data Bank in Europe. Nucleic Acids Res. 2013, 42, D285–D291. [Google Scholar] [CrossRef] [Green Version]
- Steinegger, M.; Söding, J. MMseqs2 enables sensitive protein sequence searching for the analysis of massive data sets. Nat. Biotechnol. 2017, 35, 1026–1028. [Google Scholar] [CrossRef] [Green Version]
- Jumper, J.; Evans, R.; Pritzel, A.; Green, T.; Figurnov, M.; Ronneberger, O.; Tunyasuvunakool, K.; Bates, R.; Žídek, A.; Potapenko, A.; et al. Highly accurate protein structure prediction with AlphaFold. Nature 2021, 596, 583–589. [Google Scholar] [CrossRef]
- Gao, Y.; Wang, S.; Deng, M.; Xu, J. RaptorX-Angle: Real-Value Prediction of Protein Backbone Dihedral Angles through a Hybrid Method of Clustering and Deep Learning. BMC Bioinform. 2018, 19, 100. [Google Scholar] [CrossRef] [Green Version]
- Mistry, J.; Chuguransky, S.; Williams, L.; Qureshi, M.; Salazar, G.A.; Sonnhammer, E.L.L.; Tosatto, S.C.E.; Paladin, L.; Raj, S.; Richardson, L.J.; et al. Pfam: The protein families database in 2021. Nucleic Acids Res. 2020, 49, D412–D419. [Google Scholar] [CrossRef]
- Klausen, M.S.; Jespersen, M.C.; Nielsen, H.; Jensen, K.K.; Jurtz, V.I.; Sønderby, C.K.; Sommer, M.O.A.; Winther, O.; Nielsen, M.; Petersen, B.; et al. NetSurfP-2.0: Improved prediction of protein structural features by integrated deep learning. Proteins Struct. Funct. Bioinform. 2019, 87, 520–527. [Google Scholar] [CrossRef] [Green Version]
- Fu, L.; Niu, B.; Zhu, Z.; Wu, S.; Li, W. CD-HIT: Accelerated for clustering the next-generation sequencing data. Bioinformatics 2012, 28, 3150–3152. [Google Scholar] [CrossRef]
- Wang, G.; Dunbrack, R.L. PISCES: A protein sequence culling server. Bioinformatics 2003, 19, 1589–1591. [Google Scholar] [CrossRef] [Green Version]
- Chambers, J.M.; Hastie, T.; Bates, D.M. Nonlinear Models. In Statistical Models in S; Chapman & Hall/CRC: Boca Raton, FL, USA, 1992; pp. 421–454. ISBN 0-534-16765-9. [Google Scholar]
- Darragh, A.J.; Garrick, D.J.; Moughan, P.J.; Hendriks, W.H. Correction for Amino Acid Loss during Acid Hydrolysis of a Purified Protein. Anal. Biochem. 1996, 236, 199–207. [Google Scholar] [CrossRef]
- Rodgers, G.M.; Conn, M.T. Homocysteine, an atherogenic stimulus, reduces protein C activation by arterial and venous endothelial cells. Blood 1990, 75, 895–901. [Google Scholar] [CrossRef] [Green Version]
- Mertens, D.; Loften, J. The Effect of Starch on Forage Fiber Digestion Kinetics In Vitro. J. Dairy Sci. 1980, 63, 1437–1446. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R. Multimodel Inference: Understanding AIC and BIC in Model Selection. Sociol. Methods Res. 2004, 33, 261–304. [Google Scholar] [CrossRef]
- Kogiso, T.; Moriyoshi, Y.; Shimizu, S.; Nagahara, H.; Shiratori, K. High-sensitivity C-reactive protein as a serum predictor of nonalcoholic fatty liver disease based on the Akaike Information Criterion scoring system in the general Japanese population. J. Gastroenterol. 2009, 44, 313–321. [Google Scholar] [CrossRef]
- Andres, J.; Benešová, M.; Chvosteková, M.; Fišerová, E. Optimization of Parameters in the Menzerath–Altmann Law, II. Acta Univ. Palacki. Olomuc. Fac. Rerum Nat. Math. 2014, 53, 5–28. [Google Scholar]
- Wang, Y.; Wagner, N.; Rondinelli, J.M. Symbolic Regression in Materials Science. MRS Commun. 2019, 9, 793–805. [Google Scholar] [CrossRef] [Green Version]
- Kim, D.-H.; Han, K.-H. Transient Secondary Structures as General Target-Binding Motifs in Intrinsically Disordered Proteins. Int. J. Mol. Sci. 2018, 19, 3614. [Google Scholar] [CrossRef] [Green Version]
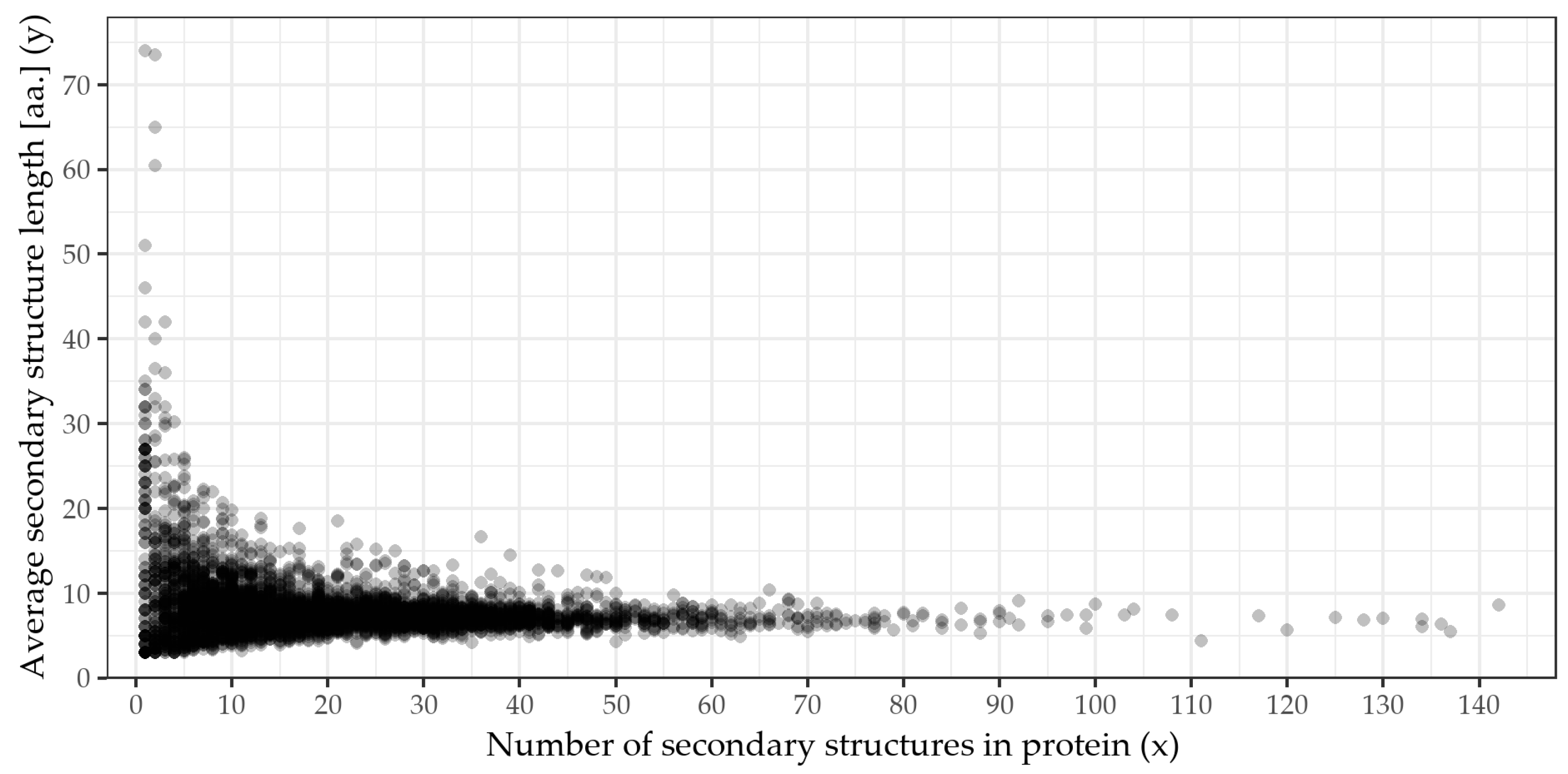

| Correlation | Result | 95% CI | p-Value |
|---|---|---|---|
| Pearson r | −0.219 | [−0.241, −0.199] | <0.001 |
| Spearman | −0.172 | [−0.204, −0.142] | <0.001 |
| Correlation ratio 1 | 0.394 | [0.352, 0.449] | <0.001 |
| (binned) Pearson r | −0.495 | [−0.572, −0.428] | <0.001 |
| (binned) Spearman | −0.620 | [−0.703, −0.513] | <0.001 |
| Model | a | b | c | d | s | AIC |
|---|---|---|---|---|---|---|
| 1 | 12.305 (±0.351) | −0.176 (±0.012) | 0.003 (±0.0004) | 10.072 | −68,085 | |
| 2 | 10.715 (±0.247) | −0.108 (±0.007) | 11.679 | −68,077 | ||
| 3 | 75.238 (±7.156) | 162.313 | −67,444 | |||
| 4 | 11.008 (±0.515) | 6.99 (±0.037) | 8.763 | −68,127 | ||
| 5 | 207.738 (±10.117) | 46.938 (±0.575) | 8.135 | −68,133 |
| Protein Subcellular Location | Frequency | Frequency in Outliers | Examples |
|---|---|---|---|
| Cell membrane | 168 (6.9%) | 23 (23.0%) | ATPF_MYCS2, CEIA_ECOLX, COX13_THET8 |
| Cell inner membrane | 103 (4.2%) | 16 (16.0%) | HPPA_THEMA, EMRD_ECOLI, MURJ_THEAB |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Matlach, V.; Dostál, D.; Novotný, M. Secondary Structures of Proteins Follow Menzerath–Altmann Law. Int. J. Mol. Sci. 2022, 23, 1569. https://doi.org/10.3390/ijms23031569
Matlach V, Dostál D, Novotný M. Secondary Structures of Proteins Follow Menzerath–Altmann Law. International Journal of Molecular Sciences. 2022; 23(3):1569. https://doi.org/10.3390/ijms23031569
Chicago/Turabian StyleMatlach, Vladimír, Daniel Dostál, and Marian Novotný. 2022. "Secondary Structures of Proteins Follow Menzerath–Altmann Law" International Journal of Molecular Sciences 23, no. 3: 1569. https://doi.org/10.3390/ijms23031569
APA StyleMatlach, V., Dostál, D., & Novotný, M. (2022). Secondary Structures of Proteins Follow Menzerath–Altmann Law. International Journal of Molecular Sciences, 23(3), 1569. https://doi.org/10.3390/ijms23031569






