Weak Point of SARS-CoV-2: Human and Viral Ion Channels under External Physical Fields
Abstract
:1. Introduction
2. Results and Discussion
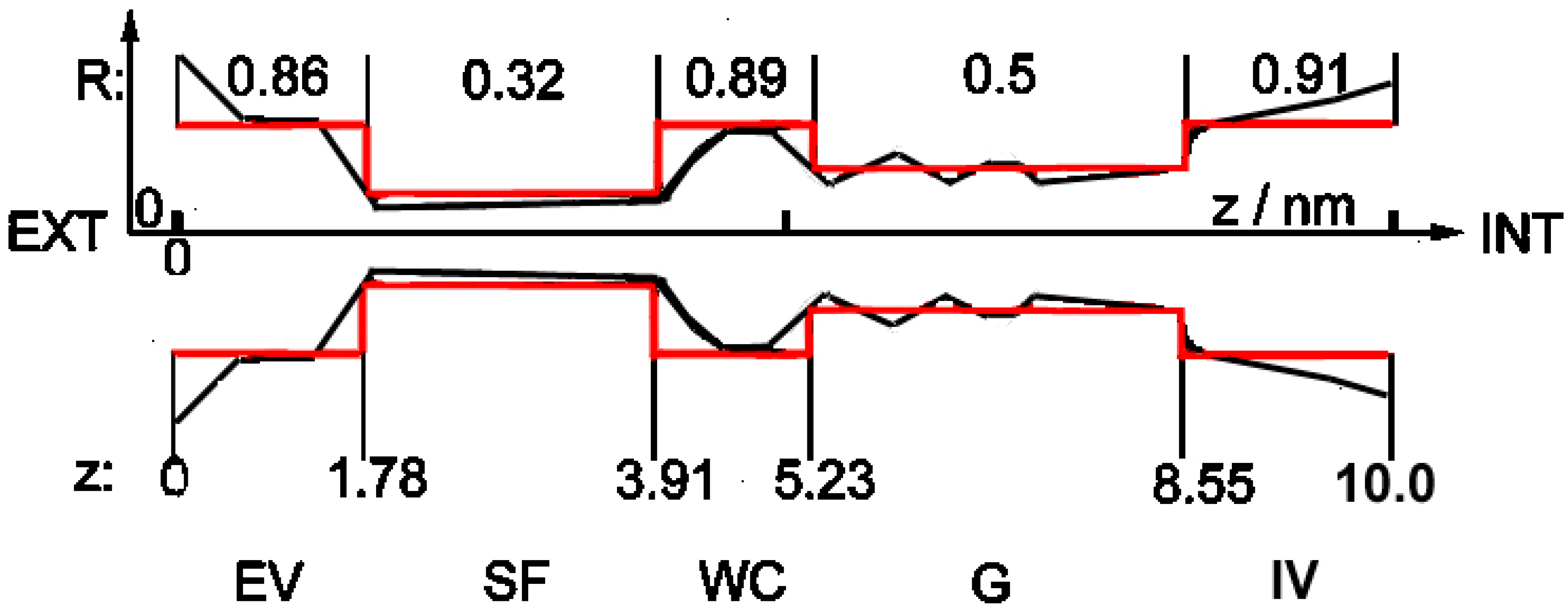
2.1. Structure of the Channel
2.2. The Model
- (i)
- The channel in this simplified shape is built of subsequent cylindrical segments with different radii (red structure in Figure 1). Cylindrical symmetry of the segments is assumed, but as noted above, the whole shape of the channel is strongly asymmetrical along the z-axis.
- (ii)
- The trajectory of only one ion at a time is analysed in detail; others remain in the background as charges.
- (iii)
- (iv)
- According to the observation in [3] that the SARS-CoV-2 E-channel has a very low charge in the selectivity filter region, and that there is some negative charge somewhere inside the channel (cf. above: Introduction), one constant charge inside the channel was introduced, located near the entrance from the external vestibule to the narrow internal parts. Three types of channels were examined: low-selectivity (ca. 3–5:1) viral with charge −0.01 e; medium-selectivity (ca. 90:1) viral with charge −2.5 e; and high-selectivity (above 1000:1) pro- and eukaryotic with charge −5.6 e, anion and cation charges being −1 e and +1 e, respectively.
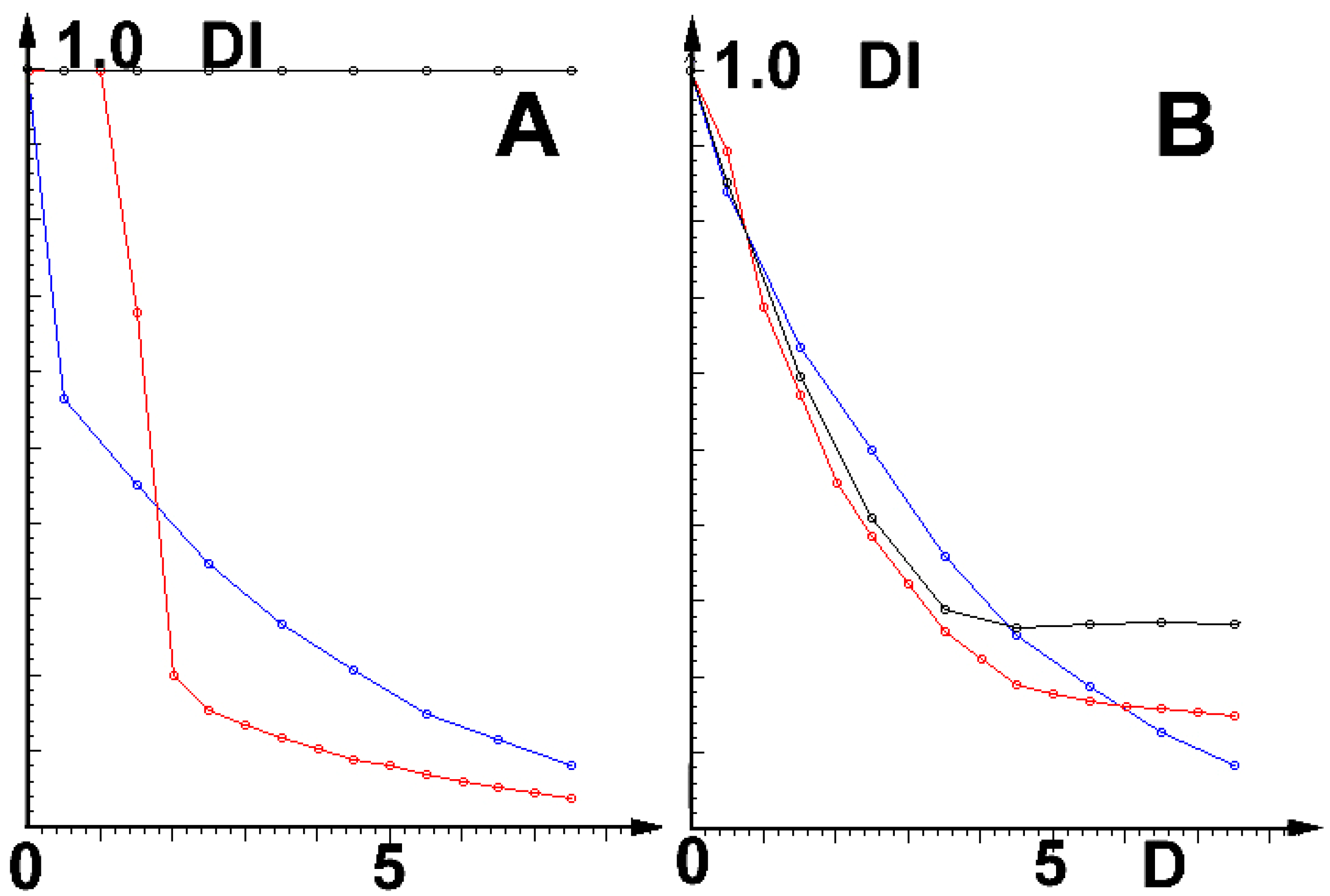
2.3. Simulations of Influence of External Physical Fields
2.4. Results
2.5. Discussion
3. Methods
3.1. Ionic Biochannels
3.1.1. Basic Properties
3.1.2. Comments
3.2. Details of the Model
- (i)
- Electrostatic interactions of ions with remaining ions, and with both static and induced charges within the channel itself;
- (ii)
- The differences in the concentration of given ions inside and outside the cell membrane (‘chemical’ force);
- (iii)
- (iv)
- Stochastic forces (noise): always present thermal noise (Gaussian White Noise) and more or less random influences of neighbour processes [18,19]; of note, the channel itself moves randomly in two dimensions inside the semi-fluid cell membrane [41]. This means that the Brownian motion of an ion is no longer normal diffusion (Wiener process) W(t) in external fields, but an indefinite anomalous one.
3.3. Equations of Motion
3.4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Toft-Bertelsen, T.L.; Jeppesen, M.G.; Tzortzini, E.; Xue, K.; Giller, K.; Becker, S.; Mujezinovic, A.; Bentzen, B.H.; BAndreas, L.; Kolocouris, A.; et al. Amantadine has potential for the treatment of COVID-19 because it inhibits known and novel ion channels encoded by SARS-CoV-2. Commun. Biol. 2021, 4, 1347. [Google Scholar] [CrossRef] [PubMed]
- Afaghi, P.; Lapolla, M.A.; Ghandi, K. Denaturation of the SARS-CoV-2 spike protein under non-thermal microwave radiation. Sci. Rep. 2021, 11, 23372. [Google Scholar] [CrossRef] [PubMed]
- Saurabh, K.; Solovchuk, M.; TonyWen-Hann, S. Investigating ion transport inside the pentameric ion channel encoded in COVID-19 E protein. Phys. Rev. E 2020, 102, 052408. [Google Scholar] [CrossRef] [PubMed]
- Cao, Y.; Yang, R.; Wang, W.; Lee, I.; Zhang, R.; Zhang, W.; Sun, J.; Xu, B.; Meng, X. Computational study of the ion and water permeation and transport mechanisms of the SARS-CoV-2 pentameric E protein channel. Front. Mol. Biosci. 2020, 7, 565797. [Google Scholar] [CrossRef] [PubMed]
- Kern, D.M.; Sorum, B.; Hoel, C.M.; Sridharan, S.; Remis, J.P.; Toso, D.B.; Brohawn, S.G. Cryo-EM structure of the SARS-CoV-2 3a ion channel in lipid nanodiscs. bioRxiv 2020. [Google Scholar] [CrossRef]
- Tomar, P.P.P.; Arkin, I.T. SARS-CoV-2 E protein is a potential ion channel that can be inhibited by Gliclazide and Memantine. Biochem. Biophys. Res. Commun. 2020, 530, 10–14. [Google Scholar] [CrossRef]
- McClenaghan, C.; Hanson, A.; Lee, S.-J.; Nichols, C.G. Coronavirus proteins as ion channels: Current and potential research. Front. Immun. 2020, 11, 73339. [Google Scholar] [CrossRef]
- Westerbeck, J.W.; Machamer, C.E. The infectious bronchitis coronavirus envelope protein alters golgi pH to protect the spike protein and promote the release of infectious virus. J. Vir. 2019, 93, e00015-19. [Google Scholar] [CrossRef] [Green Version]
- Vennema, H.; Godeke, G.J.; Rossen, J.; Voorhout, W.F.; Horzinek, M.C.; Opstelten, D.J.; Rottier, P.J. Nucleocapsid-independent assembly of coronavirus-like particles by co-expression of viral envelope protein genes. EMBO J. 1996, 15, 2020–2028. [Google Scholar] [CrossRef]
- Wilson, L.; Mckinlay, C.; Gage, P.; GEwart, G. SARS coronavirus E protein forms cation-selective ion channels. Virology 2004, 330, 322–331. [Google Scholar] [CrossRef]
- Wilson, L.; Mckinlay, C.; Gage, P. Hexamethylene amiloride blocks E protein ion channels and inhibits coronavirus replication. Virology 2006, 353, 294–306. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pepe, A.; SPietropaoli, S.; Vos, M.; Barba-Spaeth, G.; Zurzolo, C. Tunneling nanotubes provide a route for SARS-CoV-2 spreading. Sci. Adv. 2022, 8, eabo0171. [Google Scholar] [CrossRef] [PubMed]
- Compoint, M.; Ramseyer, C.; Huetz, P. Ab initio investigation of the atomic charges in the KcsA channel selectivity filter. Chem. Phys. Lett. 2004, 397, 510–515. [Google Scholar] [CrossRef]
- Allen, T.W.; Chung, S.H. Brownian dynamics study of an open-state KcsA potassium channel. Biochim. Biophys. Acta 2001, 515, 83–91. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nogueira, J.J.; Corry, B. Ion Channel Permeation and Selectivity in The Oxford Handbook of Neuronal Ion Channels; Bhattacharjee, A., Ed.; Oxford University Press: Oxford, UK, 2018; pp. 1–35. [Google Scholar]
- Noskov, S.; Roux, B. Ion selectivity in potassium channels. Biophys. Chem. 2006, 124, 279–291. [Google Scholar] [CrossRef]
- Roux, B. Ion channels and ion selectivity. Essays Biochem. 2017, 61, 201–209. [Google Scholar]
- Metzler, R. Brownian motion and beyond: First-passage, power spectrum, non- Gaussianity, and anomalous diffusion. J. Stat. Mech. 2019, 2019, 114003. [Google Scholar] [CrossRef] [Green Version]
- Fuliński, A. Fractional Brownian motions. Acta Phys. Pol. B 2020, 51, 1097–1129. [Google Scholar] [CrossRef]
- Vojta, T.; Skinner, S.; Metzler, R. Probability density of the fractional Langevin equation with reflecting walls. Phys. Rev. E 2019, 100, 042142. [Google Scholar] [CrossRef] [Green Version]
- Janušonis, S.; Detering, N.; Metzler, R.; Vojta, T. Serotonergic axons as fractional Brownian motion paths: Insights into the self-organization of regional densities. Front. Comput. Neurosci. 2020, 14, 00056. [Google Scholar] [CrossRef]
- Safdari, H.; Chechkin, A.V.; Jafari, G.R.; Metzler, R. Aging scaled Brownian motion. Phys. Rev. E 2015, 91, 042107. [Google Scholar] [CrossRef]
- Bernéche, S.; Roux, B. Energetics of ion conduction through the K+ channel. Nature 2001, 414, 73–77. [Google Scholar] [CrossRef]
- Makowiec, D.; Fuliński, A. Multifractal detrended fluctuation analysis as the estimator of long-range dependence. Acta Phys. Pol. B 2010, 41, 1025–1050. [Google Scholar]
- Fuliński, A.; Grzywna, Z.; Mellor, I.; Siwy, Z.; Usherwood, P.N.R. Non-Markovian character of ionic current fluctuations in membrane channels. Phys. Rev. E 1998, 58, 919–924. [Google Scholar] [CrossRef]
- Feynman, R.P.; Leighton, R.B.; Sands, M.L. The circular motion of a charged particle moving in a magnetic field. In The Feynman Lectures on Physics, The Definitive Edition Volume 2; Pearson/Addison-Wesley: Boston, MA, USA, 2006; Volume 3, ISBN 0-8053-9047-2. [Google Scholar]
- Duan, X.; Zhou, Q.; Wan JM, F.; Yu, A.C.H. Sonoporation generates downstream cellular impact after membrane resealing. Sci. Rep. 2021, 11, 5161. [Google Scholar] [CrossRef]
- Spohr, R. German Patent No. DE 2951376 C2. U.S. Patent 4369370, 1983. [Google Scholar]
- Siwy, Z.; Gu, Y.; A Spohr, H.; Baur, D.; Wolf-Reber, A.; Spohr, R.; Apel, P.; E Korchev, Y. Rectification and voltage gating of ion currents in a nanofabricated pore. Europhys. Lett. 2002, 60, 349. [Google Scholar] [CrossRef]
- Siwy, Z.; Behrends, J.; Fertig, N.; Fulinski, A.; Martin, C.R.; Neumann, R.; Trautmann, C.; Molares, T. European Patent No. EP 1 542 788 B1 (2006). U.S. Patent 7,708,871 B2, 2010. [Google Scholar]
- Siwy, Z.; Fuliński, A. Fabrication of a synthetic nanopore ion pump. Phys. Rev. Lett. 2002, 89, 198103. [Google Scholar] [CrossRef]
- Siwy, Z.; Fuliński, A. A nanodevice for rectfication and pumping ions. Am. J. Phys. 2004, 72, 567–574. [Google Scholar] [CrossRef] [Green Version]
- Siwy, Z.; Kosińska, I.D.; Fuliński, A.; Martin, C.R. Asymmetric diffusion through synthetic nanopores. Phys. Rev. Lett. 2005, 94, 048102. [Google Scholar] [CrossRef]
- Kosińska, I.D.; Fuliński, A. Asymmetric nanodiffusion. Phys. Rev. E 2005, 72, 011201. [Google Scholar] [CrossRef] [PubMed]
- Kosińska, I.D.; Fuliński, A. Asymmetries and anomalous phenomena in ionic transport through nanochannels. Acta Phys. Pol. B 2007, 38, 1631–1645. [Google Scholar]
- Fuliński, A. Exact nonmarkovianity measure based on time autocorrelation fuctions. Europhys. Lett. 2017, 118, 60002. [Google Scholar] [CrossRef]
- Vojta, T.; Halladay, S.; Skinner, S.; Janušonis, S.; Guggenberger, T.; Metzler, R. Reflected fractional Brownian motion in one and higher dimensions. Phys. Rev. E 2020, 102, 032108. [Google Scholar] [CrossRef] [PubMed]
- Siwy, Z.; Fuliński, A. Origin of 1/fα noise in membrane channel currents. Phys. Rev. Lett. 2002, 89, 158101. [Google Scholar] [CrossRef]
- Tasserit, C.; Koutsioubas, A.; Lairez, D.; Zalczer, G.; Clochard, M.C. Pink noise of ionic conductance through single artificial nanopores revisited. Phys. Rev. Lett. 2010, 105, 260602. [Google Scholar] [CrossRef] [Green Version]
- Bezrukov, S.M.; Winterhalter, M. Examining noise sources at the single-molecule level: 1/f noise of an open maltoporin channel. Phys. Rev. Lett. 2000, 85, 202–205. [Google Scholar] [CrossRef]
- Weigel, A.V.; Simon, B.; Tamkun, M.M.; Krapf, D. Ergodic and nonergodic processes coexist in the plasma membrane as observed by single-molecule tracking. Proc. Natl. Acad. Sci. USA 2011, 108, 6438. [Google Scholar] [CrossRef] [Green Version]
- Respondek, M.; Madl, T.; Go, C.; Golser, R.; Zangger, K. Mapping the orientation of helices in micelle-bound peptides by paramagnetic relaxation waves. J. Am. Chem. Soc. 2007, 129, 5228–5234. [Google Scholar] [CrossRef]
- Dinnon, K.H., 3rd; Leist, S.R.; Schäfer, A.; Edwards, C.E.; Martinez, D.R.; Montgomery, S.A.; West, A.; Yount, B.L., Jr.; Hou, Y.J.; Adams, L.E.; et al. A mouse-adapted model of SARS-CoV-2 to test COVID-19 counter- measures. Nature 2020, 586, 560–566. [Google Scholar] [CrossRef]
| SARS-CoV-2 | SARS-CoV-1 et al. | KcsA, Kv, et al. | |
|---|---|---|---|
| chbar10 | −0.01 | −2.5 | −5.6 |
| ∧c | −2.1 | −1.1 | −1.1 |
| ∧a | 0.5 | 0.32 | 0.01 |
| zbar1 | 4.0 | 2.5 | 1.77 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fuliński, A. Weak Point of SARS-CoV-2: Human and Viral Ion Channels under External Physical Fields. Int. J. Mol. Sci. 2022, 23, 15185. https://doi.org/10.3390/ijms232315185
Fuliński A. Weak Point of SARS-CoV-2: Human and Viral Ion Channels under External Physical Fields. International Journal of Molecular Sciences. 2022; 23(23):15185. https://doi.org/10.3390/ijms232315185
Chicago/Turabian StyleFuliński, Andrzej. 2022. "Weak Point of SARS-CoV-2: Human and Viral Ion Channels under External Physical Fields" International Journal of Molecular Sciences 23, no. 23: 15185. https://doi.org/10.3390/ijms232315185







