Hierarchical Coarse-Grained Strategy for Macromolecular Self-Assembly: Application to Hepatitis B Virus-Like Particles
Abstract
:1. Introduction
2. Methods and Materials
2.1. Framework Overview
2.2. Reference Structure HBcAg Dimer
2.3. Intermolecular Interaction Potential
2.3.1. Molecular Dynamics Simulations
2.3.2. Spatial Descriptors
2.3.3. Multivariant Estimation using Universal Kriging
2.3.4. Molecular Collisions
2.3.5. 2D Example of Kriging and Sampling Algorithm
2.3.6. Biased MD Sampling and Insertion of Empirical Data
2.3.7. Summary and Implementation
- 1.
- Molecular reference structure of all involved molecules from, e.g., a protein data bank. This reference structure has to be the same as used for the parameterization of the diffusion model [65].
- 2.
- Initial interaction potential sampling using MD and the outlined sampling methodology. (For large interaction spaces proximity sampling might be required for sufficient correlation data.)
- 3.
- Trend fitting in a lower dimensional interaction space of for all potential components.
- 4.
- Correlation analysis and sectional variogram fitting of trend-compensated residual R for all potential components. Identification of potential components with reasonable spatial continuity besides trend (only fulfilled by A-B potential).
- 5.
- Grid design based on interaction distance and memory size constraints.
- 6.
- Universal Kriging for multivariant estimation of interaction potential component residual R.
- 7.
- Molecular collision accounting as a function of molecular overlap and flexibility with increasing interaction potential.
- 8.
- Iterative refinement of field estimate based on estimation variance and extrema (potential minima/maxima, gradient maxima) localization and specification.
2.4. Diffusion Model
2.5. Usage and Implementation within the Molecular Discrete Element Method
2.5.1. Simulation Procedure
VLP Binding Agreement and Stability (SP1)
VLP Capsid Stability (SP2)
VLP Self-Assembly (SP3)
2.5.2. Postprocessing
3. Results and Discussion
3.1. HBcAg Interaction Potential and VLP Stability
3.1.1. Pure MD-Based Interaction Potential
MD Data
Convergence
Resulting Field
3.1.2. Biased MD Interaction Potential
3.1.3. MD-Based Interaction Potential with Empirical Data
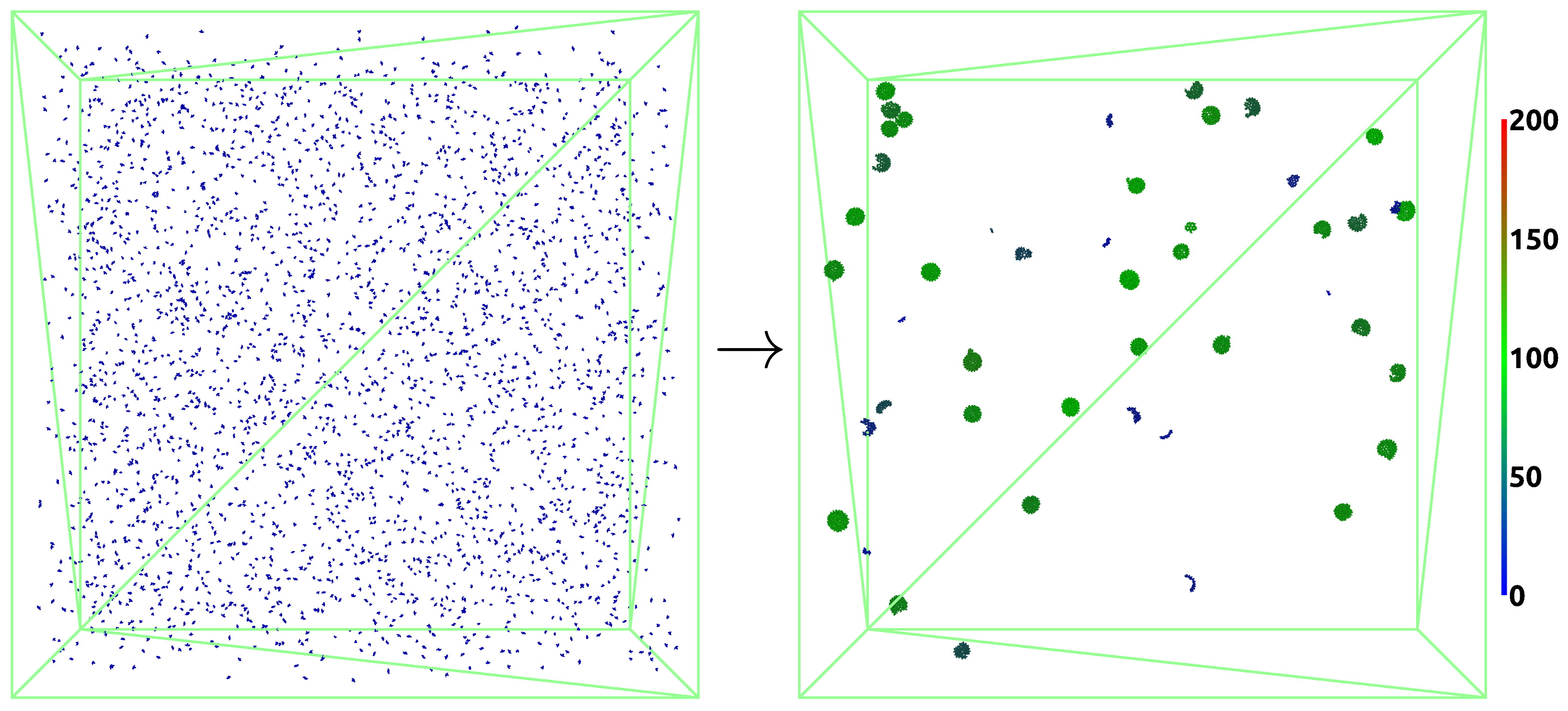
3.2. VLP Self-Assembly
3.2.1. Assembly Properties
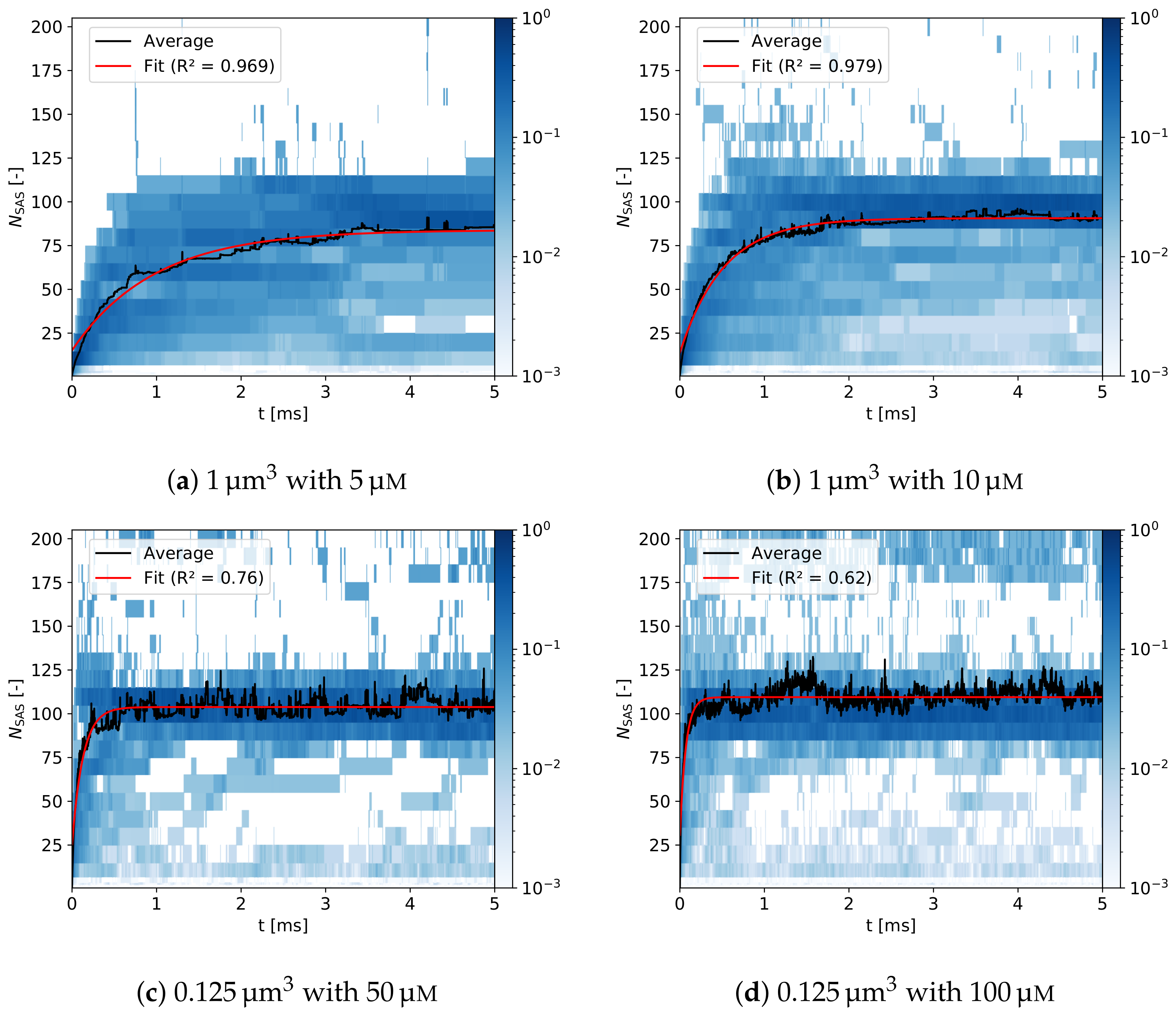
3.2.2. Assembly Kinetics
3.2.3. Assembly Pathways
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AA-MD | All-Atom Molecular Dynamics |
| ANN | Artificial Neural Networks |
| BD | Brownian Dynamics |
| BLUE | Best Linear Unbiased Estimate |
| CG-MD | Coarse-Grained Molecular Dynamics |
| CPU | Central Processing Unit |
| DEM | Discrete Element Method |
| DOF | Degree of Freedom |
| DPD | Dissipative Particle Dynamics |
| FF | Force Field |
| GPR | Gaussian Process Regression |
| GPU | Graphics Processing Unit |
| HBcAg | Hepatitis B Core Antigen |
| HBcAg | HBcAg Dimer |
| HBV | Hepatitis B Virus |
| LD | Langevin Dynamics |
| MDEM | Molecular Discrete Element Method |
| MD | Molecular Dynamics |
| NPT | Isothermal-Isobaric Ensemble |
| PBC | Periodic Boundary Conditions |
| PDB | Protein Data Bank |
| PME | Particle Mesh Ewald |
| PW | Polarizable Water |
| QM/MM | Quantum Mechanics/Molecular Mechanics |
| RMS | Root-Mean-Square |
| RMSD | Root-Mean-Square Distance |
| SAS | Self-Assembled Structure |
| SI | Supplementary Information |
| SPX | Simulation Procedure X |
| SVD | Singular Value Decomposition |
| UK | Universal Kriging |
| VLP | Virus-Like Particles |
References
- Vennelakanti, V.; Nazemi, A.; Mehmood, R.; Steeves, A.H.; Kulik, H.J. Harder, Better, Faster, Stronger: Large-Scale QM and QM/MM for Predictive Modeling in Enzymes and Proteins. Curr. Opin. Struct. Biol. 2022, 72, 9–17. [Google Scholar] [CrossRef] [PubMed]
- Hamelberg, D.; Mongan, J.; McCammon, J.A. Accelerated Molecular Dynamics: A Promising and Efficient Simulation Method for Biomolecules. J. Chem. Phys. 2004, 120, 11919–11929. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Earl, D.J.; Deem, M.W. Parallel Tempering: Theory, Applications, and New Perspectives. Phys. Chem. Chem. Phys. 2005, 7, 3910. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sugita, Y.; Okamoto, Y. Replica-Exchange Molecular Dynamics Method for Protein Folding. Chem. Phys. Lett. 1999, 314, 141–151. [Google Scholar] [CrossRef]
- Heilmann, N.; Wolf, M.; Kozlowska, M.; Sedghamiz, E.; Setzler, J.; Brieg, M.; Wenzel, W. Sampling of the Conformational Landscape of Small Proteins with Monte Carlo Methods. Sci. Rep. 2020, 10, 18211. [Google Scholar] [CrossRef] [PubMed]
- Kmiecik, S.; Gront, D.; Kolinski, M.; Wieteska, L.; Dawid, A.E.; Kolinski, A. Coarse-Grained Protein Models and Their Applications. Chem. Rev. 2016, 116, 7898–7936. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Saunders, M.G.; Voth, G.A. Coarse-Graining of Multiprotein Assemblies. Curr. Opin. Struct. Biol. 2012, 22, 144–150. [Google Scholar] [CrossRef]
- Joshi, S.Y.; Deshmukh, S.A. A Review of Advancements in Coarse-Grained Molecular Dynamics Simulations. Mol. Simul. 2021, 47, 786–803. [Google Scholar] [CrossRef]
- Noid, W.G. Perspective: Coarse-Grained Models for Biomolecular Systems. J. Chem. Phys. 2013, 139, 090901. [Google Scholar] [CrossRef]
- Onufriev, A.V.; Izadi, S. Water Models for Biomolecular Simulations. WIREs Comput. Mol. Sci. 2018, 8, e1347. [Google Scholar] [CrossRef]
- Beglov, D.; Roux, B. An Integral Equation To Describe the Solvation of Polar Molecules in Liquid Water. J. Phys. Chem. B 1997, 101, 7821–7826. [Google Scholar] [CrossRef]
- Kovalenko, A.; Hirata, F. Self-Consistent Description of a Metal–Water Interface by the Kohn–Sham Density Functional Theory and the Three-Dimensional Reference Interaction Site Model. J. Chem. Phys. 1999, 110, 10095–10112. [Google Scholar] [CrossRef]
- Palermo, G.; Bonvin, A.M.J.J.; Dal Peraro, M.; Amaro, R.E.; Tozzini, V. Editorial: Multiscale Modeling From Macromolecules to Cell: Opportunities and Challenges of Biomolecular Simulations. Front. Mol. Biosci. 2020, 7, 194. [Google Scholar] [CrossRef]
- Mansour, A.A.; Sereda, Y.V.; Yang, J.; Ortoleva, P.J. Prospective on Multiscale Simulation of Virus-Like Particles: Application to Computer-Aided Vaccine Design. Vaccine 2015, 33, 5890–5896. [Google Scholar] [CrossRef] [PubMed]
- Ayton, G.S.; Noid, W.G.; Voth, G.A. Multiscale Modeling of Biomolecular Systems: In Serial and in Parallel. Curr. Opin. Struct. Biol. 2007, 17, 192–198. [Google Scholar] [CrossRef]
- Tozzini, V. Coarse-Grained Models for Proteins. Curr. Opin. Struct. Biol. 2005, 15, 144–150. [Google Scholar] [CrossRef]
- Saunders, M.G.; Voth, G.A. Coarse-Graining Methods for Computational Biology. Annu. Rev. Biophys. 2013, 42, 73–93. [Google Scholar] [CrossRef]
- Coffey, W.T.; Kalmykov, Y.P. The Langevin Equation: With Applications to Stochastic Problems in Physics, Chemistry and Electrical Engineering; World Scientific: Singapore, 2004. [Google Scholar] [CrossRef]
- Paquet, E.; Viktor, H.L. Molecular Dynamics, Monte Carlo Simulations, and Langevin Dynamics: A Computational Review. BioMed Res. Int. 2015, 2015, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Van Gunsteren, W.; Berendsen, H.J.C. Algorithms for Brownian Dynamics. Mol. Phys. 1982, 45, 637–647. [Google Scholar] [CrossRef]
- Groot, R.D.; Warren, P.B. Dissipative Particle Dynamics: Bridging the Gap Between Atomistic and Mesoscopic Simulation. J. Chem. Phys. 1997, 107, 4423–4435. [Google Scholar] [CrossRef] [Green Version]
- De Jong, D.H.; Singh, G.; Bennett, W.F.D.; Arnarez, C.; Wassenaar, T.A.; Schäfer, L.V.; Periole, X.; Tieleman, D.P.; Marrink, S.J. Improved Parameters for the Martini Coarse-Grained Protein Force Field. J. Chem. Theory Comput. 2013, 9, 687–697. [Google Scholar] [CrossRef] [PubMed]
- Marrink, S.J.; Risselada, H.J.; Yefimov, S.; Tieleman, D.P.; De Vries, A.H. The MARTINI Force Field: Coarse Grained Model for Biomolecular Simulations. J. Phys. Chem. B 2007, 111, 7812–7824. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Monticelli, L.; Kandasamy, S.K.; Periole, X.; Larson, R.G.; Tieleman, D.P.; Marrink, S.J. The MARTINI Coarse-Grained Force Field: Extension to Proteins. J. Chem. Theory Comput. 2008, 4, 819–834. [Google Scholar] [CrossRef] [PubMed]
- Darré, L.; Machado, M.R.; Brandner, A.F.; González, H.C.; Ferreira, S.; Pantano, S. SIRAH: A Structurally Unbiased Coarse-Grained Force Field for Proteins with Aqueous Solvation and Long-Range Electrostatics. J. Chem. Theory Comput. 2015, 11, 723–739. [Google Scholar] [CrossRef] [PubMed]
- Machado, M.R.; Pantano, S. SIRAH Tools: Mapping, Backmapping and Visualization of Coarse-Grained Models. Bioinformatics 2016, 32, 1568–1570. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liwo, A.; Baranowski, M.; Czaplewski, C.; Gołaś, E.; He, Y.; Jagieła, D.; Krupa, P.; Maciejczyk, M.; Makowski, M.; Mozolewska, M.A.; et al. A Unified Coarse-Grained Model of Biological Macromolecules Based on Mean-Field Multipole–Multipole Interactions. J. Mol. Model. 2014, 20, 2306. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pulawski, W.; Jamroz, M.; Kolinski, M.; Kolinski, A.; Kmiecik, S. Coarse-Grained Simulations of Membrane Insertion and Folding of Small Helical Proteins Using the CABS Model. J. Chem. Inf. Model. 2016, 56, 2207–2215. [Google Scholar] [CrossRef]
- Berendsen, H.J. Simulating the Physical World: Hierarchical Modeling from Quantum Mechanics to Fluid Dynamics; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar] [CrossRef]
- Zwanzig, R.W. High-Temperature Equation of State by a Perturbation Method. I. Nonpolar Gases. J. Chem. Phys. 1954, 22, 1420–1426. [Google Scholar] [CrossRef]
- Torrie, G.; Valleau, J. Nonphysical Sampling Distributions in Monte Carlo Free-Energy Estimation: Umbrella Sampling. J. Comput. Phys. 1977, 23, 187–199. [Google Scholar] [CrossRef]
- Liwo, A.; Czaplewski, C.; Sieradzan, A.K.; Lipska, A.G.; Samsonov, S.A.; Murarka, R.K. Theory and Practice of Coarse-Grained Molecular Dynamics of Biologically Important Systems. Biomolecules 2021, 11, 1347. [Google Scholar] [CrossRef]
- Unke, O.T.; Chmiela, S.; Sauceda, H.E.; Gastegger, M.; Poltavsky, I.; Schütt, K.T.; Tkatchenko, A.; Müller, K.R. Machine Learning Force Fields. Chem. Rev. 2021, 121, 10142–10186. [Google Scholar] [CrossRef] [PubMed]
- Ye, H.; Xian, W.; Li, Y. Machine Learning of Coarse-Grained Models for Organic Molecules and Polymers: Progress, Opportunities, and Challenges. ACS Omega 2021, 6, 1758–1772. [Google Scholar] [CrossRef] [PubMed]
- Noé, F.; Tkatchenko, A.; Müller, K.R.; Clementi, C. Machine Learning for Molecular Simulation. Annu. Rev. Phys. Chem. 2020, 71, 361–390. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- John, S.T.; Csányi, G. Many-Body Coarse-Grained Interactions Using Gaussian Approximation Potentials. J. Phys. Chem. B 2017, 121, 10934–10949. [Google Scholar] [CrossRef] [PubMed]
- Stecher, T.; Bernstein, N.; Csányi, G. Free Energy Surface Reconstruction from Umbrella Samples Using Gaussian Process Regression. J. Chem. Theory Comput. 2014, 10, 4079–4097. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mones, L.; Bernstein, N.; Csányi, G. Exploration, Sampling, and Reconstruction of Free Energy Surfaces with Gaussian Process Regression. J. Chem. Theory Comput. 2016, 12, 5100–5110. [Google Scholar] [CrossRef] [Green Version]
- Arkhipov, A.; Freddolino, P.L.; Schulten, K. Stability and Dynamics of Virus Capsids Described by Coarse-Grained Modeling. Structure 2006, 14, 1767–1777. [Google Scholar] [CrossRef] [Green Version]
- Machado, M.R.; González, H.C.; Pantano, S. MD Simulations of Viruslike Particles with Supra CG Solvation Affordable to Desktop Computers. J. Chem. Theory Comput. 2017, 13, 5106–5116. [Google Scholar] [CrossRef]
- Cieplak, M.; Robbins, M.O. Nanoindentation of 35 Virus Capsids in a Molecular Model: Relating Mechanical Properties to Structure. PLoS ONE 2013, 8, e63640. [Google Scholar] [CrossRef] [Green Version]
- Marzinek, J.K.; Huber, R.G.; Bond, P.J. Multiscale Modelling and Simulation of Viruses. Curr. Opin. Struct. Biol. 2020, 61, 146–152. [Google Scholar] [CrossRef]
- Wynne, S.; Crowther, R.; Leslie, A. The Crystal Structure of the Human Hepatitis B Virus Capsid. Mol. Cell 1999, 3, 771–780. [Google Scholar] [CrossRef] [PubMed]
- Ludwig, C.; Wagner, R. Virus-Like Particles—Universal Molecular Toolboxes. Curr. Opin. Biotechnol. 2007, 18, 537–545. [Google Scholar] [CrossRef] [PubMed]
- Mohsen, M.O.; Zha, L.; Cabral-Miranda, G.; Bachmann, M.F. Major Findings and Recent Advances in Virus–Like Particle (VLP)-Based Vaccines. Semin. Immunol. 2017, 34, 123–132. [Google Scholar] [CrossRef] [PubMed]
- Hartzell, E.J.; Lieser, R.M.; Sullivan, M.O.; Chen, W. Modular Hepatitis B Virus-like Particle Platform for Biosensing and Drug Delivery. ACS Nano 2020, 14, 12642–12651. [Google Scholar] [CrossRef] [PubMed]
- Somiya, M.; Kuroda, S. Development of a Virus-Mimicking Nanocarrier for Drug Delivery Systems: The Bio-Nanocapsule. Adv. Drug Delivery Rev. 2015, 95, 77–89. [Google Scholar] [CrossRef] [PubMed]
- Birnbaum, F.; Nassal, M. Hepatitis B Virus Nucleocapsid Assembly: Primary Structure Requirements in the Core Protein. J. Virol. 1990, 64, 3319–3330. [Google Scholar] [CrossRef] [Green Version]
- Selzer, L.; Katen, S.P.; Zlotnick, A. The Hepatitis B Virus Core Protein Intradimer Interface Modulates Capsid Assembly and Stability. Biochemistry 2014, 53, 5496–5504. [Google Scholar] [CrossRef] [Green Version]
- Lutomski, C.A.; Lyktey, N.A.; Pierson, E.E.; Zhao, Z.; Zlotnick, A.; Jarrold, M.F. Multiple Pathways in Capsid Assembly. J. Am. Chem. Soc. 2018, 140, 5784–5790. [Google Scholar] [CrossRef]
- Selzer, L.; Zlotnick, A. Assembly and Release of Hepatitis B Virus. Cold Spring Harbor Perspect. Med. 2015, 5, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Lutomski, C.A.; Lyktey, N.A.; Zhao, Z.; Pierson, E.E.; Zlotnick, A.; Jarrold, M.F. Hepatitis B Virus Capsid Completion Occurs through Error Correction. J. Am. Chem. Soc. 2017, 139, 16932–16938. [Google Scholar] [CrossRef]
- Pierson, E.E.; Keifer, D.Z.; Selzer, L.; Lee, L.S.; Contino, N.C.; Wang, J.C.Y.; Zlotnick, A.; Jarrold, M.F. Detection of Late Intermediates in Virus Capsid Assembly by Charge Detection Mass Spectrometry. J. Am. Chem. Soc. 2014, 136, 3536–3541. [Google Scholar] [CrossRef] [PubMed]
- Zlotnick, A.; Mukhopadhyay, S. Virus Assembly, Allostery and Antivirals. Trends Microbiol. 2011, 19, 14–23. [Google Scholar] [CrossRef] [PubMed]
- Holmes, K.; Shepherd, D.A.; Ashcroft, A.E.; Whelan, M.; Rowlands, D.J.; Stonehouse, N.J. Assembly Pathway of Hepatitis B Core Virus-like Particles from Genetically Fused Dimers. J. Biol. Chem. 2015, 290, 16238–16245. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Böttcher, B.; Nassal, M. Structure of Mutant Hepatitis B Core Protein Capsids with Premature Secretion Phenotype. J. Mol. Biol. 2018, 430, 4941–4954. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.; Tycko, R. Simulated Self-Assembly of the HIV-1 Capsid: Protein Shape and Native Contacts Are Sufficient for Two-Dimensional Lattice Formation. Biophys. J. 2011, 100, 3035–3044. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Johnston, I.G.; Louis, A.A.; Doye, J.P.K. Modelling the Self-Assembly of Virus Capsids. J. Phys. Condens. Matter 2010, 22, 104101. [Google Scholar] [CrossRef] [Green Version]
- Levandovsky, A.; Zandi, R. Nonequilibirum Assembly, Retroviruses, and Conical Structures. Phys. Rev. Lett. 2009, 102, 198102. [Google Scholar] [CrossRef]
- Rapaport, D.C. Molecular Dynamics Study of T = 3 Capsid Assembly. J. Biol. Phys. 2018, 44, 147–162. [Google Scholar] [CrossRef]
- Cressie, N.A.C. Statistics for Spatial Data; Revised Edition ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2015. [Google Scholar]
- Webster, R.; Oliver, M.A. Geostatistics for Environmental Scientists; Wiley: Hoboken, NJ, USA, 2007. [Google Scholar]
- Wackernagel, H. Multivariate Geostatistics: An Introduction with Applications; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Lichtenstern, A. Kriging Methods in Spatial Statistics. Bachelor’s Thesis, Technische Universität München, München, Germany, 2013. [Google Scholar]
- Depta, P.N.; Jandt, U.; Dosta, M.; Zeng, A.P.; Heinrich, S. Toward Multiscale Modeling of Proteins and Bioagglomerates: An Orientation-Sensitive Diffusion Model for the Integration of Molecular Dynamics and the Discrete Element Method. J. Chem. Inf. Model. 2019, 59, 386–398. [Google Scholar] [CrossRef]
- Depta, P.N.; Dosta, M.; Heinrich, S. Data-Driven Multiscale Modeling of Self-Assembly and Hierarchical Structural Formation in Biological Macro-Molecular Systems. In High Performance Computing in Science and Engineering ’21; Nagel, W.E., Kröner, D.H., Resch, M.M., Eds.; Springer International Publishing: Cham, Switzerland, 2022. [Google Scholar]
- Geyer, T. Many-Particle Brownian and Langevin Dynamics Simulations with the Brownmove Package. BMC Biophys. 2011, 4, 7. [Google Scholar] [CrossRef] [Green Version]
- Leaver-Fay, A.; Tyka, M.; Lewis, S.M.; Lange, O.F.; Thompson, J.; Jacak, R.; Kaufman, K.W.; Renfrew, P.D.; Smith, C.A.; Sheffler, W.; et al. Rosetta3. In Methods in Enzymology; Elsevier: Amsterdam, The Netherlands, 2011; Volume 487, pp. 545–574. [Google Scholar] [CrossRef] [Green Version]
- Webb, B.; Sali, A. Comparative Protein Structure Modeling Using MODELLER. Curr. Protoc. Bioinf. 2016, 54, 5.6.1–5.6.37. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lindahl, E.; Abraham, M.J.; Hess, B.; Van Der Spoel, D. GROMACS 2020.1 Manual. Zenodo. 2020. Available online: https://doi.org/10.5281/ZENODO.3685920 (accessed on 29 April 2020).
- Yesylevskyy, S.O.; Schäfer, L.V.; Sengupta, D.; Marrink, S.J. Polarizable Water Model for the Coarse-Grained MARTINI Force Field. PLoS Comput. Biol. 2010, 6, e1000810. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High Performance Molecular Simulations Through Multi-Level Parallelism from Laptops to Supercomputers. SoftwareX 2015, 1–2, 19–25. [Google Scholar] [CrossRef] [Green Version]
- Berendsen, H.; van der Spoel, D.; van Drunen, R. GROMACS: A Message-Passing Parallel Molecular Dynamics Implementation. Comput. Phys. Commun. 1995, 91, 43–56. [Google Scholar] [CrossRef]
- Darden, T.; York, D.; Pedersen, L. Particle Mesh Ewald: An N Log(n) Method for Ewald Sums in Large Systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef] [Green Version]
- Bussi, G.; Donadio, D.; Parrinello, M. Canonical Sampling Through Velocity Rescaling. J. Chem. Phys. 2007, 126, 014101. [Google Scholar] [CrossRef] [Green Version]
- Hezaveh, S.; Zeng, A.P.; Jandt, U. Human Pyruvate Dehydrogenase Complex E2 and E3BP Core Subunits: New Models and Insights from Molecular Dynamics Simulations. J. Phys. Chem. B 2016, 120, 4399–4409. [Google Scholar] [CrossRef]
- Hezaveh, S.; Zeng, A.P.; Jandt, U. Investigation of Core Structure and Stability of Human Pyruvate Dehydrogenase Complex: A Coarse-Grained Approach. ACS Omega 2017, 2, 1134–1145. [Google Scholar] [CrossRef] [Green Version]
- Hezaveh, S.; Zeng, A.P.; Jandt, U. Full Enzyme Complex Simulation: Interactions in Human Pyruvate Dehydrogenase Complex. J. Chem. Inf. Model. 2018, 58, 362–369. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Postma, J.P.M.; van Gunsteren, W.F.; DiNola, A.; Haak, J.R. Molecular Dynamics with Coupling to an External Bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar] [CrossRef] [Green Version]
- Parrinello, M.; Rahman, A. Polymorphic Transitions in Single Crystals: A New Molecular Dynamics Method. J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar] [CrossRef]
- Nosé, S.; Klein, M. Constant Pressure Molecular Dynamics for Molecular Systems. Mol. Phys. 1983, 50, 1055–1076. [Google Scholar] [CrossRef]
- Long, A.E.; Myers, D.E. A New Form of the Cokriging Equations. Math. Geol. 1997, 29, 685–703. [Google Scholar] [CrossRef]
- Gómez-Hernández, J.J.; Cassiraga, E.F. Theory and Practice of Sequential Simulation. In Geostatistical Simulations; Armstrong, M., Dowd, P.A., Eds.; Springer: Dordrecht, The Netherlands, 1994; Volume 7, pp. 111–124. [Google Scholar] [CrossRef]
- Rotne, J.; Prager, S. Variational Treatment of Hydrodynamic Interaction in Polymers. J. Chem. Phys. 1969, 50, 4831–4837. [Google Scholar] [CrossRef]
- Yamakawa, H. Transport Properties of Polymer Chains in Dilute Solution: Hydrodynamic Interaction. J. Chem. Phys. 1970, 53, 436–443. [Google Scholar] [CrossRef]
- Khalili, M.; Liwo, A.; Jagielska, A.; Scheraga, H.A. Molecular Dynamics with the United-Residue Model of Polypeptide Chains. II. Langevin and Berendsen-Bath Dynamics and Tests on Model α-Helical Systems. J. Phys. Chem. B 2005, 109, 13798–13810. [Google Scholar] [CrossRef]
- Veitshans, T.; Klimov, D.; Thirumalai, D. Protein Folding Kinetics: Timescales, Pathways and Energy Landscapes in Terms of Sequence-Dependent Properties. Folding Des. 1997, 2, 1–22. [Google Scholar] [CrossRef] [Green Version]
- Dosta, M.; Skorych, V. MUSEN: An Open-Source Framework for GPU-Accelerated DEM Simulations. SoftwareX 2020, 12, 100618. [Google Scholar] [CrossRef]
- NVIDIA Corporation. CUDA Toolkit V11.2 Programming Guide; NVIDIA Corporation: Santa Clara, CA, USA, 2021. [Google Scholar]
- Gu, Z.; Gu, L.; Eils, R.; Schlesner, M.; Brors, B. Circlize Implements and Enhances Circular Visualization in R. Bioinformatics 2014, 30, 2811–2812. [Google Scholar] [CrossRef] [Green Version]
- Asor, R.; Schlicksup, C.J.; Zhao, Z.; Zlotnick, A.; Raviv, U. Rapidly Forming Early Intermediate Structures Dictate the Pathway of Capsid Assembly. J. Am. Chem. Soc. 2020, 142, 7868–7882. [Google Scholar] [CrossRef] [Green Version]
- Hagan, M.F.; Chandler, D. Dynamic Pathways for Viral Capsid Assembly. Biophys. J. 2006, 91, 42–54. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Venkatakrishnan, B.; Zlotnick, A. The Structural Biology of Hepatitis B Virus: Form and Function. Annu. Rev. Virol. 2016, 3, 429–451. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Böttcher, B.; Wynne, S.A.; Crowther, R.A. Determination of the Fold of the Core Protein of Hepatitis B Virus by Electron Cryomicroscopy. Nature 1997, 386, 88–91. [Google Scholar] [CrossRef] [PubMed]
- Hilmer, J.K.; Zlotnick, A.; Bothner, B. Conformational Equilibria and Rates of Localized Motion within Hepatitis B Virus Capsids. J. Mol. Biol. 2008, 375, 581–594. [Google Scholar] [CrossRef] [Green Version]
- Katen, S.; Zlotnick, A. Chapter 14 The Thermodynamics of Virus Capsid Assembly. Methods Enzymol. 2009, 455, 395–417. [Google Scholar] [CrossRef] [Green Version]
- Harms, Z.D.; Selzer, L.; Zlotnick, A.; Jacobson, S.C. Monitoring Assembly of Virus Capsids with Nanofluidic Devices. ACS Nano 2015, 9, 9087–9096. [Google Scholar] [CrossRef]
- Dryden, K.A.; Wieland, S.F.; Whitten-Bauer, C.; Gerin, J.L.; Chisari, F.V.; Yeager, M. Native Hepatitis B Virions and Capsids Visualized by Electron Cryomicroscopy. Mol. Cell 2006, 22, 843–850. [Google Scholar] [CrossRef]
- Roseman, A.M.; Berriman, J.A.; Wynne, S.A.; Butler, P.J.G.; Crowther, R.A. A Structural Model for Maturation of the Hepatitis B Virus Core. Proc. Natl. Acad. Sci. USA 2005, 102, 15821. [Google Scholar] [CrossRef] [Green Version]
- Seitz, S.; Urban, S.; Antoni, C.; Böttcher, B. Cryo-Electron Microscopy of Hepatitis B Virions Reveals Variability in Envelope Capsid Interactions. EMBO J. 2007, 26, 4160–4167. [Google Scholar] [CrossRef]
- Hillebrandt, N.; Vormittag, P.; Dietrich, A.; Wegner, C.H.; Hubbuch, J. Process Development for Cross-Flow Diafiltration-Based Vlp Disassembly: A Novel High-Throughput Screening Approach. Biotechnol. Bioeng. 2021, 118, 3926–3940. [Google Scholar] [CrossRef]
- Bruinsma, R.F.; Wuite, G.J.L.; Roos, W.H. Physics of Viral Dynamics. Nat. Rev. Phys. 2021, 3, 76–91. [Google Scholar] [CrossRef] [PubMed]
- Endres, D.; Zlotnick, A. Model-Based Analysis of Assembly Kinetics for Virus Capsids or Other Spherical Polymers. Biophys. J. 2002, 83, 1217–1230. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hagan, M.F.; Elrad, O.M. Understanding the Concentration Dependence of Viral Capsid Assembly Kinetics—the Origin of the Lag Time and Identifying the Critical Nucleus Size. Biophys. J. 2010, 98, 1065–1074. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zlotnick, A. Distinguishing Reversible from Irreversible Virus Capsid Assembly. J. Mol. Biol. 2007, 366, 14–18. [Google Scholar] [CrossRef] [Green Version]
- Zlotnick, A.; Johnson, J.M.; Wingfield, P.W.; Stahl, S.J.; Endres, D. A Theoretical Model Successfully Identifies Features of Hepatitis B Virus Capsid Assembly. Biochemistry 1999, 38, 14644–14652. [Google Scholar] [CrossRef]
- Schumacher, J.; Bacic, T.; Staritzbichler, R.; Daneschdar, M.; Klamp, T.; Arnold, P.; Jägle, S.; Türeci, Ö.; Markl, J.; Sahin, U. Enhanced Stability of a Chimeric Hepatitis B Core Antigen Virus-Like-Particle (HBcAg-VLP) by a C-Terminal Linker-Hexahistidine-Peptide. J. Nanobiotechnol. 2018, 16, 39. [Google Scholar] [CrossRef]
- Klamp, T.; Schumacher, J.; Huber, G.; Kühne, C.; Meissner, U.; Selmi, A.; Hiller, T.; Kreiter, S.; Markl, J.; Türeci, Ö.; et al. Highly Specific Auto-Antibodies against Claudin-18 Isoform 2 Induced by a Chimeric HBcAg Virus-Like Particle Vaccine Kill Tumor Cells and Inhibit the Growth of Lung Metastases. Cancer Res. 2011, 71, 516–527. [Google Scholar] [CrossRef]















| # | x | y | z | |||
|---|---|---|---|---|---|---|
| 1 | −2.74 | −0.74 | −3.10 | −0.48 | 0.98 | −0.32 |
| 2 | 1.47 | −0.91 | −4.14 | −0.88 | −1.05 | 0.67 |
| 3 | −3.01 | −0.70 | −3.08 | −2.72 | −1.05 | 3.03 |
| 4 | −0.65 | −0.77 | 4.25 | 2.72 | 0.92 | 2.76 |
| [m s] | [Mrad s] | ||||
|---|---|---|---|---|---|
| x | y | z | |||
| 87.69 | 72.27 | 71.48 | 12.05 | 7.46 | 7.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Depta, P.N.; Dosta, M.; Wenzel, W.; Kozlowska, M.; Heinrich, S. Hierarchical Coarse-Grained Strategy for Macromolecular Self-Assembly: Application to Hepatitis B Virus-Like Particles. Int. J. Mol. Sci. 2022, 23, 14699. https://doi.org/10.3390/ijms232314699
Depta PN, Dosta M, Wenzel W, Kozlowska M, Heinrich S. Hierarchical Coarse-Grained Strategy for Macromolecular Self-Assembly: Application to Hepatitis B Virus-Like Particles. International Journal of Molecular Sciences. 2022; 23(23):14699. https://doi.org/10.3390/ijms232314699
Chicago/Turabian StyleDepta, Philipp Nicolas, Maksym Dosta, Wolfgang Wenzel, Mariana Kozlowska, and Stefan Heinrich. 2022. "Hierarchical Coarse-Grained Strategy for Macromolecular Self-Assembly: Application to Hepatitis B Virus-Like Particles" International Journal of Molecular Sciences 23, no. 23: 14699. https://doi.org/10.3390/ijms232314699
APA StyleDepta, P. N., Dosta, M., Wenzel, W., Kozlowska, M., & Heinrich, S. (2022). Hierarchical Coarse-Grained Strategy for Macromolecular Self-Assembly: Application to Hepatitis B Virus-Like Particles. International Journal of Molecular Sciences, 23(23), 14699. https://doi.org/10.3390/ijms232314699








