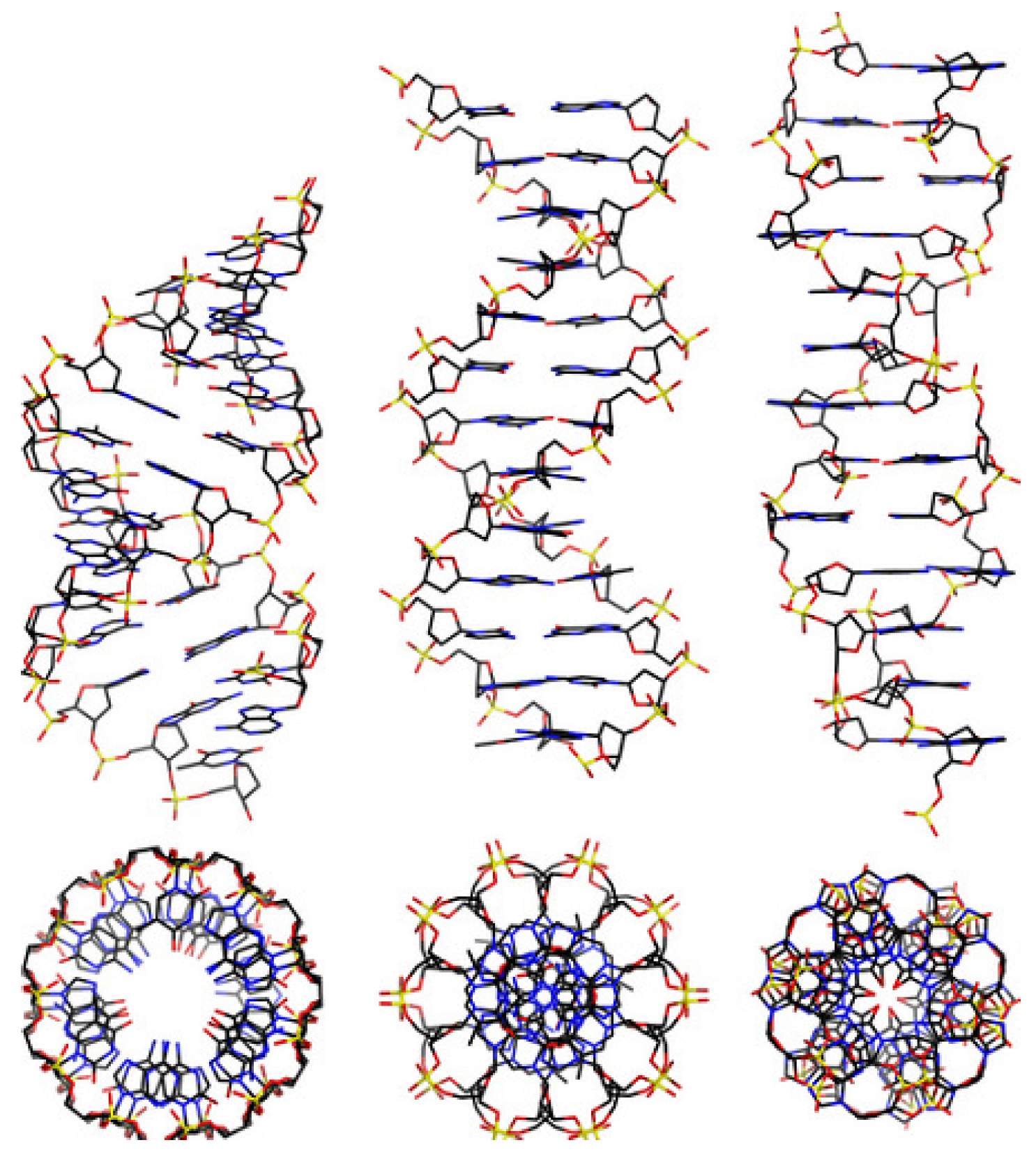
2.2. Finitely Generated Groups, Free Groups and Their Conjugacy Classes, and Aperiodicity of Sequences
The free group
on
r generators (of rank
r) consists of all distinct words that can be built from
r letters where two words are different unless their equality follows from the group axioms. The number of conjugacy classes of
of a given index
d is known and is a good signature of the isomorphism, or the closeness, of a group
to
. In the following, the cardinality structure of conjugacy classes of index
d in
is called the cardinality sequence (card seq) of
, and we need the cases from
r = 1 to 3 to correspond to the number of distinct bases in a DNA sequence. The card seq of
is in
Table 1 for the three sequences of interest in the context of DNA [
11].
Next, given a finitely generated group with a relation (rel) given by the sequence motif, we are interested in the card seq of its conjugacy classes. Often, the DNA motif in the sequence under investigation is close to that of a free group , with being the number of distinct bases involved in the motif. However, the finitely generated group , or or (where the are taken in the four bases A, T, G and C, and rel is the motif), may not be the free group , or or . The closeness of to can be checked by its signature in the finite range of indices of the card seq.
2.2.1. Groups Close to Free Groups and Aperiodicity of Sequences
According to reference [
5], aperiodicity correlates to the syntactical freedom of ordering rules. This statement was checked in the realm of transcription factors (Section 4 in [
4]). Let us introduce the concept of a general substitution rule in the context of free groups. A general substitution rule
on a finite alphabet
𝒜r on
r letters is an endomorphism of the corresponding free group
(Definition 4.1 in [
13]). The endomorphism property means the two relations
and
, for any
.
A special role is played by the subgroup of automorphisms of . We introduce the map from to the Abelian group in order to investigate the substitution rule with the tools of matrix algebra.
The map
induces a homomorphism
. Under
M,
maps to the general linear group of matrices with integer entries
. Given
, there is a unique mapping
that makes the map diagram commutative [
13] (p. 68). The substitution matrix
of
may be specified by its elements at row
i and column
j as follows:
This approach was applied to binding motifs of transcription factors [
4]. The binding motif rel in the finitely presented group
is split into appropriate segments so that
with the substitution rules
,
,
,
.
We are interested in the sequence of finitely generated groups
whose card seq is the same at each step
l and equal to the card seq of the free group
(in the finite range of indices that it is possible to check with the computer).
Under these conditions, (group) syntactical freedom correlates to the aperiodicity of sequences.
2.2.2. Aperiodicity of Substitutions
There is no definitive classification of aperiodic order, the intermediate between crystalline order and strong disorder, but in the context of substitution rules, some criteria can be found. First, we need a few definitions.
A non-negative matrix is one whose entries are non-negative numbers. A positive matrix M (denoted ) has at least one positive entry. A strictly positive matrix (denoted ) has all positive entries. An irreducible matrix is one for which there exists a non-negative integer k with for each pair . A primitive matrix M is one such that is a strictly positive matrix for some k.
A Perron–Frobenius (PF for short) eigenvector v of an irreducible non-negative matrix is the only one whose entries are positive: . The corresponding eigenvalue is called the PF eigenvalue.
We will use the following criterion (Corollary 4.3 in [
13]). A primitive substitution rule
of substitution matrix
with an irrational PF-eigenvalue is aperiodic.
A well-studied primitive substitution rule is the Fibonacci rule
of substitution matrix
and PF-eigenvalue equal to the golden ratio
(Example 4.6 in [
13]). As expected, the irrationality of
corresponds to the aperiodicity of the Fibonacci sequence.
The sequence of Fibonacci words is as follows:
The words have lengths equal to the Fibonacci numbers
All finitely generated groups whose relations have a card seq whose elements are 1s, as for the card seq of the free group . The Fibonacci sequence is our first example where group syntactical freedom correlates to aperiodicity.
2.2.3. A Four-Letter Sequence for the Transcription Factor of the Fos Gene
Let us now apply the method to a transcription factor of importance. The transcription factor of gene Fos has selected motif
[
14]. For this case, the four-letter generated group has a card seq similar to the free group
given in
Table 1.
We split rel into four segments so that
with the substitution maps
,
,
,
to produce the substitution sequence
The substitution matrix for this sequence is . It is a primitive matrix () whose eigenvalues follow from the vanishing of the polynomial . There are two real eigenvalues and , as well as two complex conjugate eigenvalues . The PF-eigenvalue is , with an eigenvector of (positive) entries . It follows that the selected sequence for the Fos gene is aperiodic.
All of the finitely generated groups
whose relations are
have a card seq whose elements are
which is the card seq of the free group
. For the Fos transcription factor, group syntactical freedom correlates to aperiodicity as expected.
Further examples are obtained in the context of DNA sequences for transcription factors (Section 4 in [
4]) and below, in relation to DNA conformations and telomeres.