3β-Corner Stability by Comparative Molecular Dynamics Simulations
Abstract
1. Introduction
2. Results
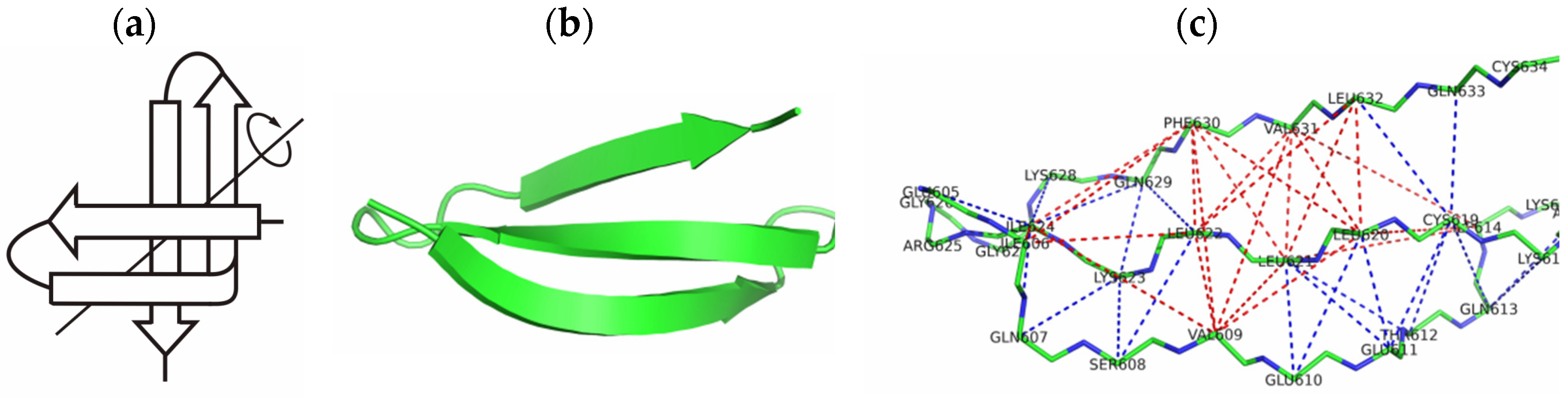
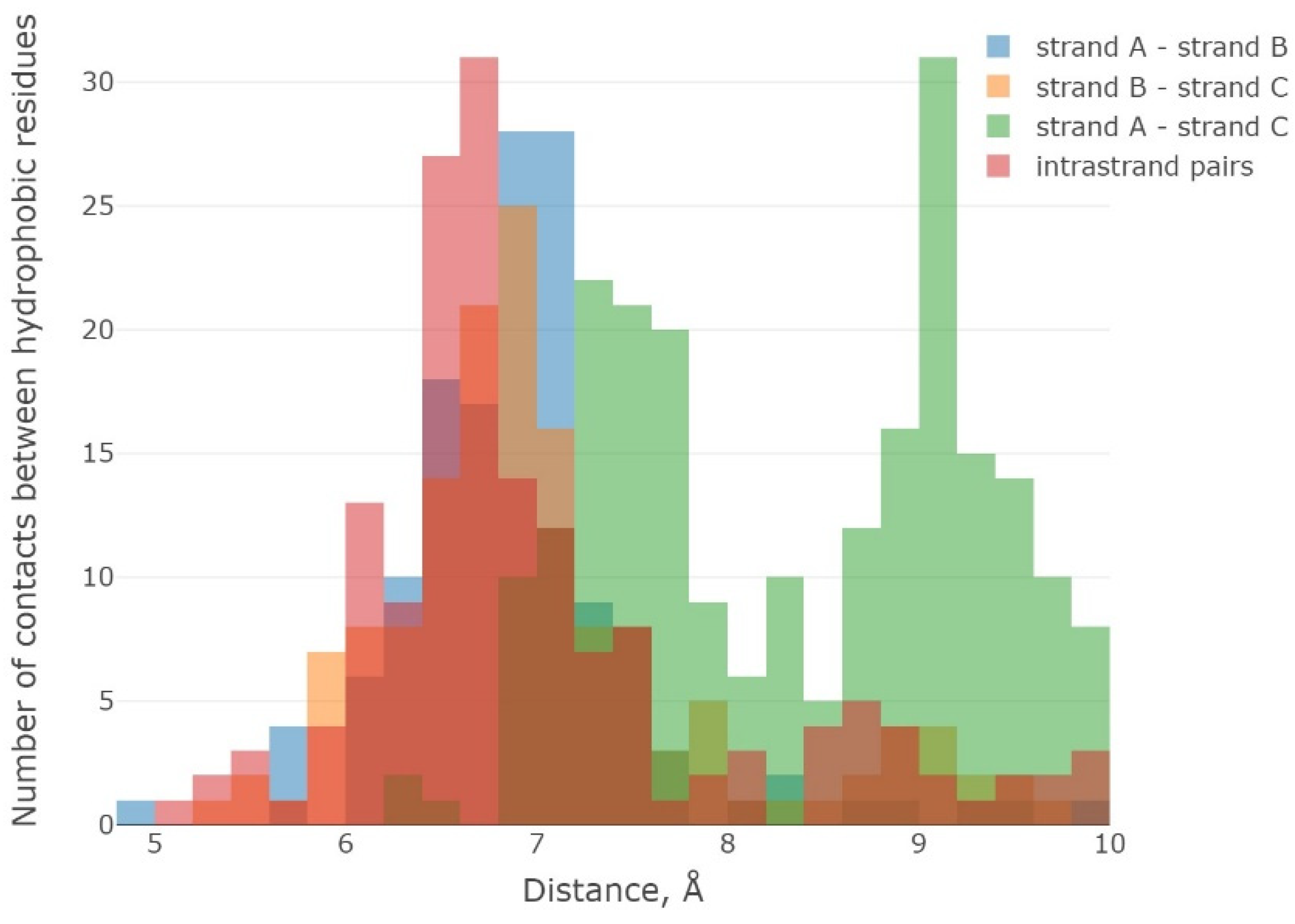
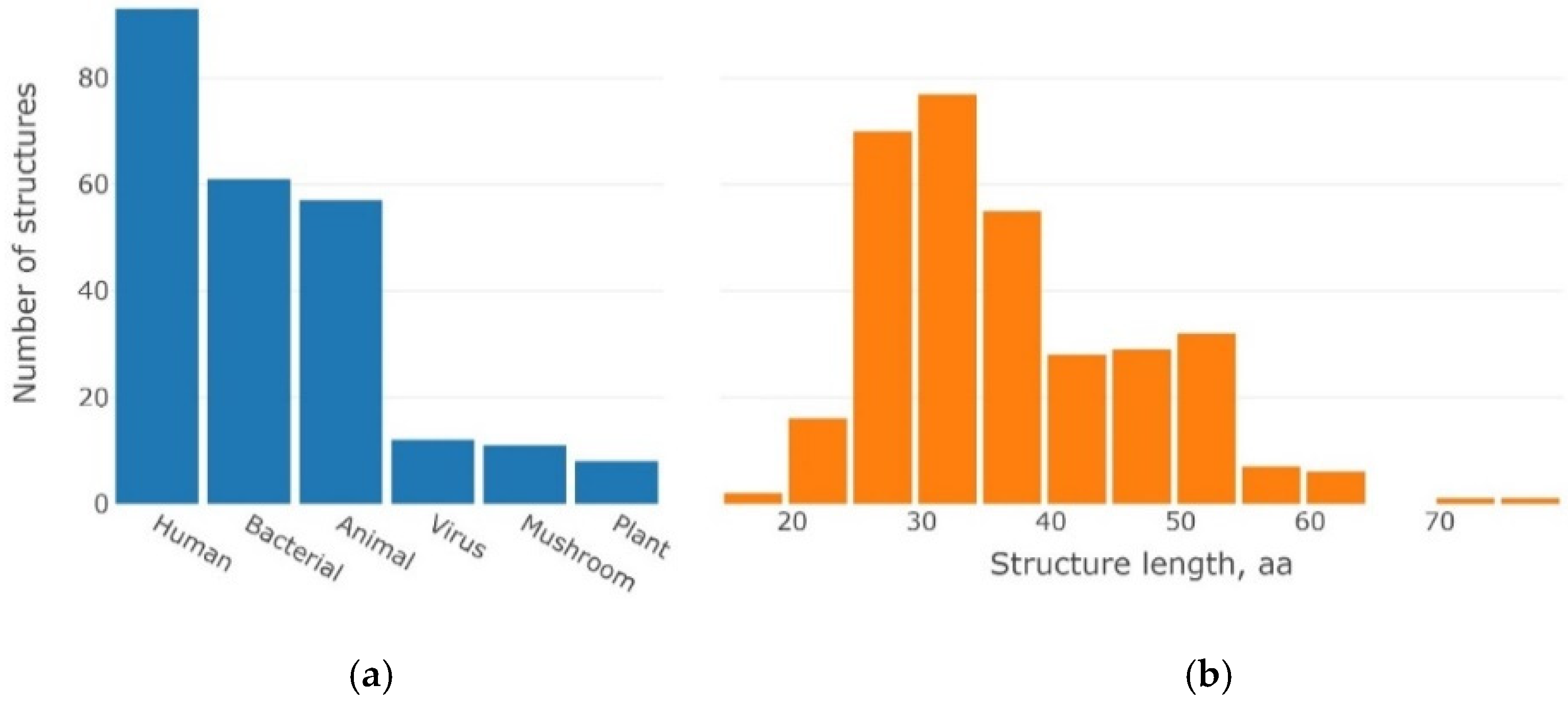
2.1. The 3β-Corner Motif as an Autonomous Structure
- -
- between the initial structure (PDB) and the structure outside the protein, it was equal to 2.8 Å;
- -
- between the initial structure and the structure in the composition of the protein, it was equal to 5.6 Å.
2.2. Control Experiments
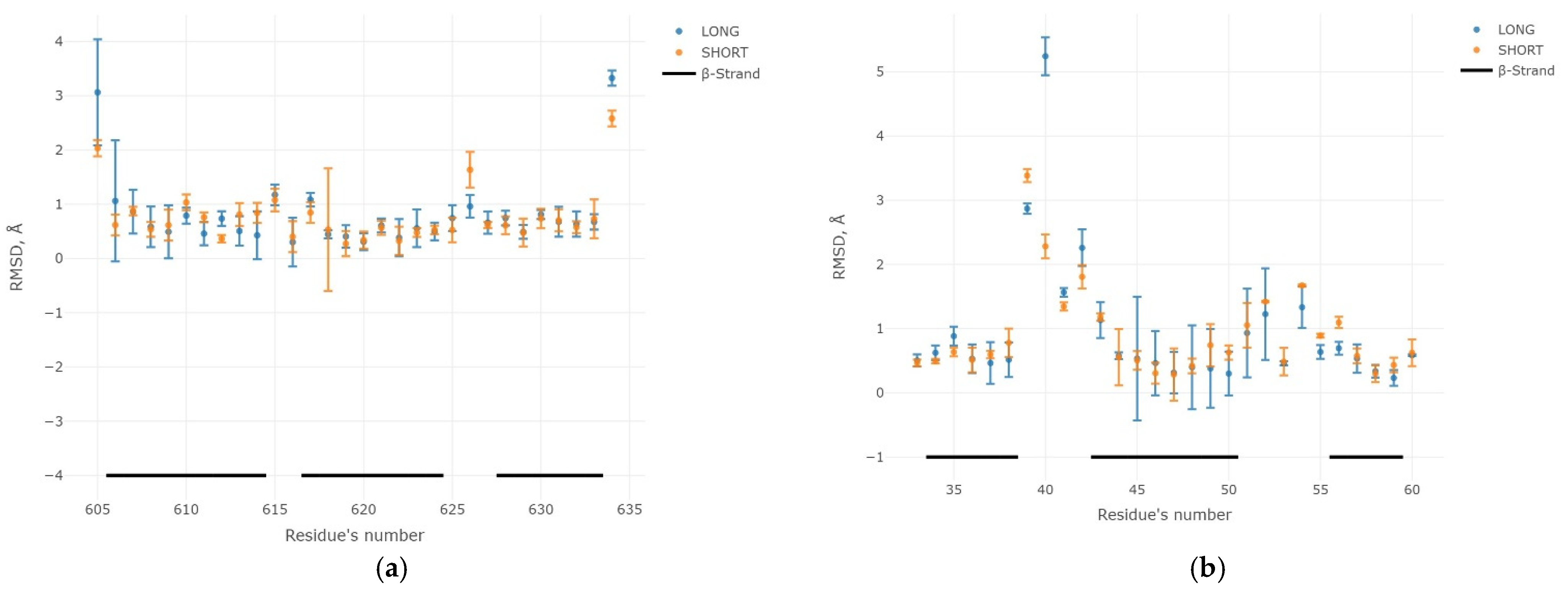
2.3. Results of the MD Experiment for 3β-Corners
3. Discussion
4. Materials and Methods
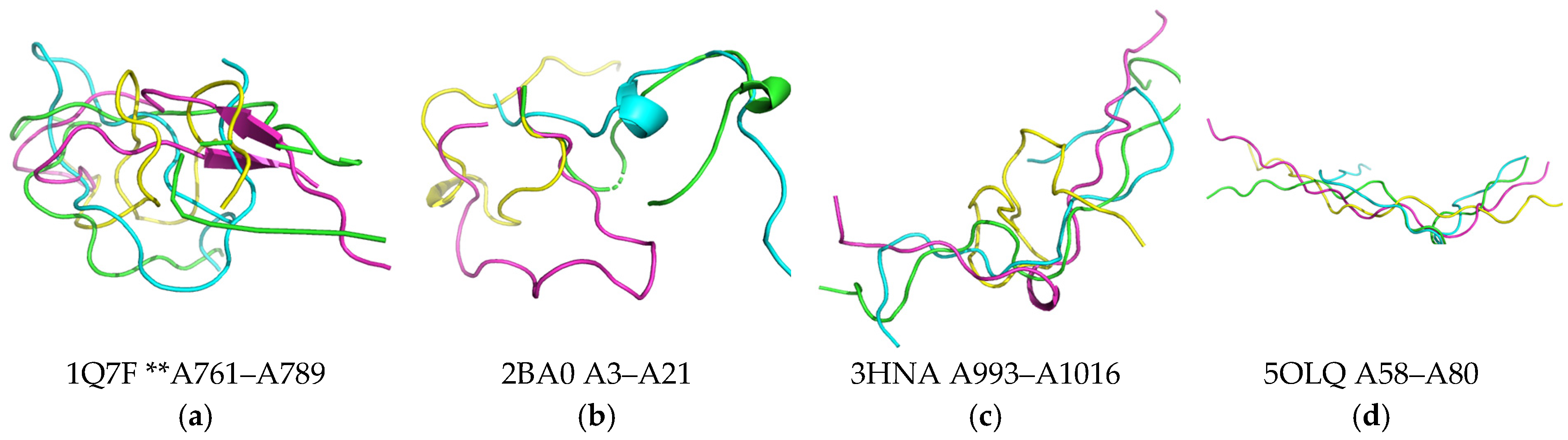
4.1. Dataset of 3β-Corner Structures
4.2. Molecular Dynamics Simulation
- -
- “long” dynamics, simulation duration 300 ns;
- -
- “short” dynamics, simulation duration 20 ns;
- -
- part of the whole protein, simulation duration of 300 ns.
- -
- root-mean-square deviation (RMSD) and gyration radius change (Rg);
- -
- solvent accessible surface area (SASA);
- -
- lifetime of major conformer;
- -
- change in torsion angles;
- -
- change in the number of hydrogen bonds.
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rao, S.T.; Rossmann, M.G. Comparison of Super-Secondary Structures in Proteins. J. Mol. Biol. 1973, 76, 241–256. [Google Scholar] [CrossRef]
- Levitt, M.; Chothia, C. Structural Patterns in Globular Proteins. Nature 1976, 261, 552–558. [Google Scholar] [CrossRef] [PubMed]
- Efimov, A.V. Standard Structures in Proteins. Prog. Biophys. Mol. Biol. 1993, 60, 201–239. [Google Scholar] [CrossRef]
- Efimov, A.V. Favoured Structural Motifs in Globular Proteins. Struct. Lond. Engl. 1993 1994, 2, 999–1002. [Google Scholar] [CrossRef]
- Efimov, A.V. Structural Trees for Protein Superfamilies. Proteins Struct. Funct. Bioinform. 1997, 28, 241–260. [Google Scholar] [CrossRef]
- Scholl, Z.N.; Yang, W.; Marszalek, P.E. Competing Pathways and Multiple Folding Nuclei in a Large Multidomain Protein, Luciferase. Biophys. J. 2017, 112, 1829–1840. [Google Scholar] [CrossRef]
- Xia, X.; Longo, L.M.; Sutherland, M.A.; Blaber, M. Evolution of a Protein Folding Nucleus. Protein Sci. Publ. Protein Soc. 2016, 25, 1227–1240. [Google Scholar] [CrossRef]
- Du, D.; Zhu, Y.; Huang, C.-Y.; Gai, F. Understanding the Key Factors That Control the Rate of β-Hairpin Folding. Proc. Natl. Acad. Sci. USA 2004, 101, 15915–15920. [Google Scholar] [CrossRef]
- Cruz, L.; Rao, J.S.; Teplow, D.B.; Urbanc, B. Dynamics of Metastable β-Hairpin Structures in the Folding Nucleus of Amyloid β-Protein. J. Phys. Chem. B 2012, 116, 6311–6325. [Google Scholar] [CrossRef]
- Rudnev, V.R.; Kulikova, L.I.; Nikolsky, K.S.; Malsagova, K.A.; Kopylov, A.T.; Kaysheva, A.L. Current Approaches in Supersecondary Structures Investigation. Int. J. Mol. Sci. 2021, 22, 11879. [Google Scholar] [CrossRef]
- Efimov, A.V. A Novel Super-Secondary Structure of Proteins and the Relation between the Structure and the Amino Acid Sequence. FEBS Lett. 1984, 166, 33–38. [Google Scholar] [CrossRef]
- Kmiecik, S.; Kolinski, A. Folding Pathway of the B1 Domain of Protein G Explored by Multiscale Modeling. Biophys. J. 2008, 94, 726–736. [Google Scholar] [CrossRef] [PubMed]
- Arnittali, M.; Rissanou, A.N.; Amprazi, M.; Kokkinidis, M.; Harmandaris, V. Structure and Thermal Stability of WtRop and RM6 Proteins through All-Atom Molecular Dynamics Simulations and Experiments. Int. J. Mol. Sci. 2021, 22, 5931. [Google Scholar] [CrossRef] [PubMed]
- Liwo, A.; Khalili, M.; Scheraga, H.A. Ab Initio Simulations of Protein-Folding Pathways by Molecular Dynamics with the United-Residue Model of Polypeptide Chains. Proc. Natl. Acad. Sci. USA 2005, 102, 2362–2367. [Google Scholar] [CrossRef]
- Hammarström, A.; Berndt, K.D.; Sillard, R.; Adermann, K.; Otting, G. Solution Structure of a Naturally-Occurring Zinc-Peptide Complex Demonstrates That the N-Terminal Zinc-Binding Module of the Lasp-1 LIM Domain Is an Independent Folding Unit. Biochemistry 1996, 35, 12723–12732. [Google Scholar] [CrossRef]
- Pérez-Alvarado, G.C.; Miles, C.; Michelsen, J.W.; Louis, H.A.; Winge, D.R.; Beckerle, M.C.; Summers, M.F. Structure of the Carboxy-Terminal LIM Domain from the Cysteine Rich Protein CRP. Nat. Struct. Biol. 1994, 1, 388–398. [Google Scholar] [CrossRef]
- Murzin, A.G.; Brenner, S.E.; Hubbard, T.; Chothia, C. SCOP: A Structural Classification of Proteins Database for the Investigation of Sequences and Structures. J. Mol. Biol. 1995, 247, 536–540. [Google Scholar] [CrossRef]
- Chandonia, J.-M.; Fox, N.K.; Brenner, S.E. SCOPe: Manual Curation and Artifact Removal in the Structural Classification of Proteins—Extended Database. J. Mol. Biol. 2017, 429, 348–355. [Google Scholar] [CrossRef]
- Youkharibache, P.; Veretnik, S.; Li, Q.; Stanek, K.A.; Mura, C.; Bourne, P.E. The Small β-Barrel Domain: A Survey-Based Structural Analysis. Struct. Lond. Engl. 1993 2019, 27, 6–26. [Google Scholar] [CrossRef]
- Murzin, A.G.; Lesk, A.M.; Chothia, C. Principles Determining the Structure of Beta-Sheet Barrels in Proteins. II. The Observed Structures. J. Mol. Biol. 1994, 236, 1382–1400. [Google Scholar] [CrossRef]
- Chothia, C.; Janin, J. Orthogonal Packing of Beta-Pleated Sheets in Proteins. Biochemistry 1982, 21, 3955–3965. [Google Scholar] [CrossRef] [PubMed]
- Heinig, M.; Frishman, D. STRIDE: A Web Server for Secondary Structure Assignment from Known Atomic Coordinates of Proteins. Nucleic Acids Res. 2004, 32 (Suppl. 2), W500–W502. [Google Scholar] [CrossRef] [PubMed]
- Kabsch, W.; Sander, C. Dictionary of Protein Secondary Structure: Pattern Recognition of Hydrogen-Bonded and Geometrical Features. Biopolymers 1983, 22, 2577–2637. [Google Scholar] [CrossRef] [PubMed]
- Xu, D.; Zhang, Y. Generating Triangulated Macromolecular Surfaces by Euclidean Distance Transform. PLoS ONE 2009, 4, e8140. [Google Scholar] [CrossRef] [PubMed]
- Taldaev, A.; Rudnev, V.; Kulikova, L.; Nikolsky, K.; Efimov, A.; Malsagova, K.; Kaysheva, A. Molecular Dynamics Study of Citrullinated Proteins Associated with the Development of Rheumatoid Arthritis. Proteomes 2022, 10, 8. [Google Scholar] [CrossRef]
- GROMACS Tutorial. A Guide to Molecular Dynamics Using GROMACS by Dimitar Dimitrov. Available online: https://static.igem.org/mediawiki/2021/d/d2/T--KCL_UK--UPDATEDGROMACSGUIDE.pdf (accessed on 15 August 2022).
- [Gmx-Users] Simulated Annealing Protocol. Available online: https://mailman-1.sys.kth.se/pipermail/gromacs.org_gmx-users/2012-March/069466.html (accessed on 15 August 2022).
- Water Models. Available online: https://water.lsbu.ac.uk/water/water_models.html (accessed on 15 August 2022).
- Molecular Dynamics Parameters (.mdp Options)—GROMACS 2022.3 Documentation. Available online: https://manual.gromacs.org/documentation/current/user-guide/mdp-options.html (accessed on 15 August 2022).



| Structure | SASA ± SD (Å2) | Rg ± SD | BH ± SD | RMSD ± SD (Å) |
|---|---|---|---|---|
| PDB ID 2E3H, chain A, region: 216–246 | ||||
| PDB structure * | 3202.64 | 1.3 | 18 | – |
| MD: 3β-corner ** | 3061.3 ± 150.4 | 1.23 ± 0.3 | 14 ± 1 | 2.77 ± 0.5 |
| MD: whole protein *** | 3606.075 ± 13.499 | 1.3 ± 0.04 | 16 ± 0 | 6.67 ± 0.72 |
| PDB ID 2E3I, chain A, region: A62–A93. | ||||
| PDB structure | 3335.75 | 1.2 | 22 | – |
| MD: 3β-corner | 3085.9 ± 130.3 | 1.19 ± 0.1 | 14 ± 1 | 2.1 ± 0.9 |
| MD: whole protein | 3846.33 ± 4.59 | 1.23 ± 0.01 | 19 ± 2 | 6.86 ± 0.37 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rudnev, V.R.; Nikolsky, K.S.; Petrovsky, D.V.; Kulikova, L.I.; Kargatov, A.M.; Malsagova, K.A.; Stepanov, A.A.; Kopylov, A.T.; Kaysheva, A.L.; Efimov, A.V. 3β-Corner Stability by Comparative Molecular Dynamics Simulations. Int. J. Mol. Sci. 2022, 23, 11674. https://doi.org/10.3390/ijms231911674
Rudnev VR, Nikolsky KS, Petrovsky DV, Kulikova LI, Kargatov AM, Malsagova KA, Stepanov AA, Kopylov AT, Kaysheva AL, Efimov AV. 3β-Corner Stability by Comparative Molecular Dynamics Simulations. International Journal of Molecular Sciences. 2022; 23(19):11674. https://doi.org/10.3390/ijms231911674
Chicago/Turabian StyleRudnev, Vladimir R., Kirill S. Nikolsky, Denis V. Petrovsky, Liudmila I. Kulikova, Anton M. Kargatov, Kristina A. Malsagova, Alexander A. Stepanov, Arthur T. Kopylov, Anna L. Kaysheva, and Alexander V. Efimov. 2022. "3β-Corner Stability by Comparative Molecular Dynamics Simulations" International Journal of Molecular Sciences 23, no. 19: 11674. https://doi.org/10.3390/ijms231911674
APA StyleRudnev, V. R., Nikolsky, K. S., Petrovsky, D. V., Kulikova, L. I., Kargatov, A. M., Malsagova, K. A., Stepanov, A. A., Kopylov, A. T., Kaysheva, A. L., & Efimov, A. V. (2022). 3β-Corner Stability by Comparative Molecular Dynamics Simulations. International Journal of Molecular Sciences, 23(19), 11674. https://doi.org/10.3390/ijms231911674







