Next Article in Journal
Anti-Inflammatory and Neuroprotective Effects of Morin in an MPTP-Induced Parkinson’s Disease Model
Previous Article in Journal
The Multifaceted Role of Signal Peptide-CUB-EGF Domain-Containing Protein (SCUBE) in Cancer
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
IJMS
Volume 23
Issue 18
10.3390/ijms231810576
ijms-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Modeling pKa of the Brønsted Bases as an Approach to the Gibbs Energy of the Proton in Acetonitrile

by
Zoran Glasovac
1,* and
Borislav Kovačević
2,*
1
Division of Organic Chemistry and Biochemistry, Ruđer Bošković Institute, Bijenička c. 54, HR-10000 Zagreb, Croatia
2
Division of Physical Chemistry, Ruđer Bošković Institute, Bijenička c. 54, HR-10000 Zagreb, Croatia
*
Authors to whom correspondence should be addressed.
Int. J. Mol. Sci. 2022, 23(18), 10576; https://doi.org/10.3390/ijms231810576
Submission received: 28 August 2022 / Revised: 7 September 2022 / Accepted: 8 September 2022 / Published: 12 September 2022
(This article belongs to the Section Physical Chemistry and Chemical Physics)
Browse Figures
Review Reports Versions Notes

Abstract

:
A simple but efficient computational approach to calculate pKa in acetonitrile for a set of phosphorus, nitrogen, and carbon bases was established. A linear function that describes relations between the calculated ΔG’a.sol(BH+) and pKa values was determined for each group of bases. The best model was obtained through the variations in the basis set, in the level of theory (density functionals or MP2), and in the continuum solvation model (IPCM, CPCM, or SMD). The combination of the IPCM/B3LYP/6-311+G(d,p) solvation approach with MP2/6-311+G(2df,p)//B3LYP/6-31G(d) gas-phase energies provided very good results for all three groups of bases with R2 values close to or above 0.99. Interestingly, the slopes and the intercepts of the obtained linear functions showed significant deviations from the theoretical values. We made a linear plot utilizing all the conducted calculations and all the structural variations and employed methods to prove the systematic nature of the intercept/slope dependence. The interpolation of the intercept to the ideal slope value enabled us to determine the Gibbs energy of the proton in acetonitrile, which amounted to −258.8 kcal mol−1. The obtained value was in excellent agreement with previously published results.

Graphical Abstract

1. Introduction

Considering that the deprotonation of the reactant is a crucial step in many organic reactions, organic (super)bases have wide applications as catalysts in organic synthesis [1,2]. Besides well-known guanidine derivatives, Schwesinger’s iminophosphoranes (phosphazenes) and vinamidines are probably the best-known examples [3,4,5,6,7,8,9]. During the last ten years, a significant amount of work has been conducted on the design and synthesis of triguanides [10] and their relatives termed BIG-bases [11], cyclopropenimines [12,13,14], and proton sponges based on phosphazene and cyclopropenimine subunits [15,16,17,18]. A common feature of all aforementioned (super)bases is the nitrogen atom that serves as a proton acceptor, and they are commonly termed nitrogen superbases (hereafter termed N-bases).
Despite recognizing phosphines as Brønsted bases, they are better known as ligands for transition metals [19]. Since the 1990s, many novel phosphines have been developed with a strong indication of their superbasic properties [20,21]. Perhaps, the most known phosphine superbases are proazaphosphatranes (Verkade bases) [22,23,24,25,26,27,28], tetramethylguanidinophosphines [29,30,31,32], and trisphosphazenophosphines (PP3) [33,34]. Tetramethylguanidinophosphines with measured THFpKa above 24 and ACNpKa above 29 [32,34,35,36,37] are comparable or even stronger bases than Schwesinger’s P2 phosphazenes, whereas trisphosphazenophosphines appear to be even stronger than P4 phosphazenes.
Other non-nitrogen superbases that came to attention in the last decade are phosphorous ylides, whose basicity limit is estimated to surpass those of phosphazenes [38]. For the ylides bearing Schwesinger’s P1 phosphazene subunits (P1 ylides), pKa of up to 33.5 in THF was measured, and this pKa value is comparable to Schwesinger’s P4-phosphazene base [39]. Ylide functionality was also employed in the synthesis of naphthalene-1,8-bisylide, the Proton Sponge® analog with high basicity and weak tendency to form an intramolecular hydrogen bond [40].
Hard work devoted to the design and measurements of novel non-nitrogen superbases has been generally supported by gas-phase basicity (GB) and pKa calculations with various success. Unlike nitrogen bases, the standard DFT theoretical models for the GB and pKa calculations of phosphines have previously led to significant errors. Utilizing B3LYP/6-311+G(2df,p)//B3LYP/6-31G(d) in combination with PCM HF/6-31G(d) solvation-energy calculations, Kovačević and Maksić [41] estimated ACNpKa of phosphazenyl phosphine (PP3H+) to ca 50, which appeared to be overestimation by ca 7 pKa units as shown later on [34,42]. This apparently originates from the substantial error in the computed GB of the P(N(Me)CH2CH2)3N (Verkade base), which served as a reference for pKa calculations. A year later, Koppel, Leito, and coworkers [37] measured the gas-phase basicity of the Verkade superbase and showed that the discrepancy against the B3LYP calculated value was higher than 20 kJ mol−1 (>4 kcal mol−1). DFT methods have also lead to the underestimation of the calculated basicity of tricyclohexylphosphine (PCy3), as demonstrated in a paper of Liu et al. [43]. According to their results, the MP2/6-311+G(2df,p)//B3LYP/6-31+G(d) approach outperformed all tested DFT methods. Nevertheless, the possibility of choosing an inappropriate reference base still remains.
The simplest approach to calculate the pKa values of species AH (acid) or BH+ (conjugate acid of base B) is based on the thermodynamic cycle [44] and can be expressed by Equation (1) [45].
pKa(AH/BH+) = ΔG’a,sol(AH/BH+)/ln(10)RT + Gsol(H+)/ln(10)RT
Equation (1) relies on the definition of ΔG’a,sol(AH/BH+), which stands for the reduced basicity of base A− or B in solution and equals difference in the Gibbs energies of the neutral and protonated forms of the acid/conjugate base pair. Gsol(H+) is the Gibbs energy of the proton in a given solvent; R is a general gas constant; and T is the temperature.
The separation of the Gibbs energy of deprotonation (ΔG’a,sol) from the Gibbs energy of the proton (Gsol(H+)) in a given solvent S allows the experimental data for Gsol(H+) to be used if available. Since the second term of the equation is a constant (for a given computational approach), Equation (1) could be used for the prediction of pKa even in a solvent for which the solvation energy of the proton is unknown. This is usually performed by creating a linear fit for a series of known bases, which at the same time serve as multiple and significantly more reliable reference points. The second problematic point in pKa calculations is the accuracy of the computed solvation energies of the neutral and protonated forms. Widely used continuum solvation models (CSMs) usually suffer from systematic errors, as it was shown by Klamt et al. [46,47], leading to the slope of the linear function that significantly differs from the ideal value, which amounts to 1/ln(10)RT. Nevertheless, linear functions that use the method-dependent slope and intercept employed by Perakylla [48] and by us [45,49] proved to be a powerful tool for predicting pKas, presumably due to the self-correction of the systematic errors [45]. Similarly, Busch et al. recently described the universal approach to pKa values in non-aqueous solvents from experimental data measured in water [50]. They emphasized a need for a scaling approach due to the shortcomings of the SMD solvation model. Besides that, the linear function given in Equation (1) also indicates a possibility for determining Gsol(H+) from measured pKas. Due to the high importance of Gsol(H+) [51], its evaluation from the intercept of such function seems very attractive and was already attempted by Matsui et al. by employing their AKB Scheme [52,53]. The AKB scheme is a mathematically slightly rewritten form of our approach in which the authors define the scaling factors that multiply the ideal slope in their fitting procedure. In line with comments on the systematic errors, ΔGsol(H+) values obtained using the AKB scheme significantly differ with respect to the employed computational method and the structure of the acid/base in question. Therefore, ΔGsol(H+) values obtained through the AKB scheme cannot be considered a good estimate unless highly accurate computational methods with scaling factors of 1 are used.
In this work, we present the results of our linear fitting approach to calculate the pKa values of neutral nitrogen, phosphorus, and carbon organic (super)bases. Due to the observed shortcomings of the B3LYP methods mentioned above, we considered that our original approach [45] needs improvement and decided to re-examine various computational methods, emphasizing the pKa values of phosphines. The accuracy of the gas-phase basicity calculations was tested by employing several density functionals and the MP2 level of theory. The solvation energies of neutrals and ions were calculated using the IPCM, CPCM, and SMD continuum solvation models. By taking advantage of several computational approaches used in this work, we found that a very good estimate of ΔGsol(H+), which is method and structure independent, may be derived from pKas through the “two–fit” approach. The second fit was introduced to overcome the systematic errors in pKa calculations inherited from the implicit solvation models [46].

2. Results and Discussion

The structures of phosphines with experimentally measured gas-phase basicity (GB) are given in Scheme 1.
We shall start our discussion with a brief comment on the derivatives with measured GBs. The experimental GBs of phosphines 1–10 (Table 1) were mostly reliable data taken from the NIST table or from the paper by Kaljurand et al. [37,43,54]. Phosphine 8 deserves a separate comment. The authors measured proton affinity PA(8) using the Cooks simple kinetic [55] and the bracketing technique [56], assuming similar entropies of protonation (ΔSp) of the measured and reference bases. However, ΔSp of the diamines used for the bracketing measurements was expected to significantly differ from that of phosphine 8. In these cases, GBs instead of PAs should be used [57,58,59]. Therefore, we recalculated GB(8) by taking the GB data of the reference bases and obtained 236 ± 3 kcal mol−1 (see Section S2 in Supplementary Materials). This value was used for the initial testing of the computational approaches in the gas phase.
The gas-phase basicity values of ten phosphines (Scheme 1) were calculated using seven different computational approaches, and the results were compared with the literature data [54].
The most difficult GB to reproduce was that of Verkade base 10, since all DFT approaches deviated by 6.2–12.7 kcal mol−1. MP2 calculations (models M5 and M6) provided a very good estimation of the GB, and they favorably compared with the value of 258.5 and 258.9 kcal mol−1 calculated using the G3B3 and G4 approaches, respectively. These two models also showed the best correlation data, with M5 being slightly closer to the ideal slope and intercept values of 1 and 0, respectively. On the other hand, the M6 model showed very close alignment to a trendline obtained for a set of nitrogen bases (Figure 1). The same comparison derived from the M1 data is given in Supplementary Materials (Figure S1). The result favored our corrected value for the GB of base 8 over the literature data.

3. Calculation of pKa

As mentioned in the Introduction, our approach to pKa is based on a simple thermodynamic cycle (Figure S2, Supplementary Materials). The choice of the model and a more detailed mathematical description of the calculation is given in the Supplementary Materials. The Gibbs energies of each species in solution (Gsol(B) and Gsol(BH+)) were obtained by adding the Gibbs energy of solvation (ΔG°s) to the gas-phase Gibbs energies of the neutral and protonated species. The reduced basicity in solution (ΔG’a,sol) was then calculated according to Equation (2).
ΔG’a,sol(BH+) = Gsol(B) − Gsol(BH+) = G(g)(B) + ΔG(s)(B) − G(g)(BH+) − ΔG(s)(BH+)
The calculated pKa values were then obtained from ΔG’a,sol(BH+) by applying a linear function (Equation (3)). The corrections for the change in the standard states of the neutral and protonated species canceled each other, while that of proton remains within the intercept (see Section S3 in Supplementary Materials).
pKa(BH+) = a × ΔG’a,sol(BH+) + b
where a and b are the slope and intercept obtained from the pKa vs. ΔG’a,sol(BH+) linear regression.
The Gibbs energies for a series of phosphorus bases (Scheme 2) were calculated using several DFT and MP2 approaches in combination with IPCM, CPCM, and SMD implicit solvation models (see Computational details). The ACNpKa(BH+) obtained using M6 gas-phase calculations are given in Table 2. The results obtained using other models are given in Tables S5–S7 in the Supplementary Materials.
Of the employed computational approaches, CPCM//M6 and IPCM//M6 showed the best overall agreement with the experimental results (Table 2 and Table S7). In both cases, the correlation coefficient, R2, was above 0.99. The mean unsigned error (MUE) and mean square root (RMS) on pKa were similar, being 1.0 or lower. The most pronounced differences were the slopes of the trendline, which amounted to 0.637 (IPCM//M6) and 0.690 (CPCM//M6), with both being significantly lower than the theoretical value of 0.733. The largest absolute deviations obtained using these approaches for base 37 were around 3 pKa units above the experimental value. The SMD1//M6 approach provided an almost ideal slope value, while the correlation coefficient significantly dropped to 0.977. The reason for that lay in the large absolute error calculated for the most basic derivatives going above 4.5 pKa units for base 35, while several bases deviated by 3 or more pKa units from the experimental value. Since all these three methods use the geometries and GBs calculated at the same level of theory, the quality of the correlation differences could only be attributed to the solvation model. We could note that the usage of the CPCM and IPCM solvation model decreased |Δ(pKa(35H+)| to 2.0 and 0.7, respectively, which was a significant improvement over the SMD1//M6 result. We also performed pKa calculations using several other computational schemes, and the results are given in Table S7 in the Supplementary Materials.
Interestingly, model SMD2//M3 provided very good estimates of pKa with a relatively high R2 value and an MUE below 1.0 pKa units. Bases 8, 10, and 14 deviated from the trendline by more than 3 units, which was presumably due to the gas-phase calculations. In this case, the MP2 single-point calculation did not improve the correlation. A comparison of IPCM//M5 and IPCM//M6 results revealed a minor but negative effect of the M06-2X/cc-pVDZ optimized geometries on the correlation quality. It is worth mentioning here that the relative trend of the pKa values of diphosphines 29–31 was only correctly interpreted using IPCM//M5. Among the other methods, SMD2//M3 provided very good estimates of pKa, but their relative trend was incorrect. All three methods based on M6 geometries underestimated pKa(31H+) and positioned it below 30 on the basicity scale.
The selected computational models were additionally tested against the set of nitrogen bases (Figure 2). The resulting trendlines were almost parallel to those obtained for phosphines. For the nitrogen bases, IPCM//M6 performed significantly better than CPCM//M6, giving an R2 value of 0.992, while the MUE and RMS amounted to 0.5 and 0.7, respectively. The results indicated a significant improvement over the IPCM//M1 approach recommended earlier [45]. The corresponding values for the CPCM//M6 were R2 = 0.977, MUE = 0.8, and RMS = 1.1, which made it less general than IPCM//M6. The SMD1//M6 approach provided results between the other two M6-based models, with the slope being the most similar to that obtained for phosphorus bases among all employed computational models. Again, SMD2//M3 was very good but not the best model, with quite a large difference in the slopes of the linear fits.
After establishing the best model for nitrogen and phosphorus bases, we tested it against a set of phosphorus ylides (Scheme 3) whose ACNpKa values were published by Leito and coworkers [39,68]. Most of these bases were measured in THF, and their pKa values in acetonitrile were estimated by linear regression. The calculated GBs, solvation energies, and ACNpKas are given in the Supplementary Materials (Tables S8 and S9). The correlation between the computed and experimental values is given in Figure 3.
Besides five significant outliers, the calculated ΔG’a.sol values correlated well against experimental ACNpKas. The correlation coefficient (R2) of 0.982 was slightly lower than those for P and N bases but could still be used with good confidence, as evidenced by the MUE of 0.5 and the RMS of 0.6. The relatively large slope was somewhat surprising, considering that we used IPCM as the solvation model. The slope deviation from the ideal value appeared to follow the hardness of the bases, being the largest for the nitrogen bases and lowest for the phosphorus ylides (C bases). The employed model did not give satisfactory results for the systems bearing three 2,6-disubstituted phenyl rings attached to the phosphorus (bases Y6, Y28, and Y29) and the bases containing phenyl and methyl substituents directly attached to the deprotonation center (Y28 and Y29). Somewhat surprising was a relatively large deviation of base Y27—structurally very similar to phosphazenes as well as trismesityl derivative Y6. The origin of these discrepancies is currently under investigation.

4. Estimation of ΔGsol(H+)

Before discussing the estimation of Gsol(H+), we need to make a clear semantic distinction between the literature value and the one obtained from the set of pKa calculations. Hereafter, we term them Glit(H+) and Gsol,calc(H+), respectively.
As already mentioned, the linear correlation approach used in this work (Supplementary Materials, Equation (S11)) should allow Gsol,calc(H+) to be estimated from the intercept. To test the validity of this idea and the influence of systematic errors, we calculated Gsol,calc(H+) for each employed method irrespective of its R2. All methods provided sufficiently good correlation coefficients (R2 > 0.95) to justify such a decision. Due to the systematic deviation from the ideal slope present in all correlations, Equation (3) was rewritten in the following form.
2.303RT × pKa(BH+) = m × ΔG’a,sol(BH+) + n
where m and n are the coefficients obtained from the correlation parameters and the intercept n includes Gsol(H+) (Equation (4)). Here, we should emphasize that our parameters m and n correspond to the k and C0 coefficients used in AKB scheme (Equation (4) in Ref. [52]).
The calculated m and n values, along with the calculated Gibbs energy of the proton in acetonitrile (Gsol,calc(H+)) are presented in Table 3.
To estimate whether the same scaling factor could be used for the slope and intercept, we calculated the value of n’ (Equation (5)) and compared it to m.
n’ = n/Glit(H+)
The literature value of Glit(H+) = −257.3 kcal mol−1 was obtained using Equation (6).
Glit(H+) = G°gas(H+) + ΔG°s(H+) + G°→*(H+)
where G°gas(H+) = −6.28 kcal mol−1, the literature value for ΔG°s(H+) is −252.9 [49] and the correction for the change in the standard state (G°→*(H+)) is 1.89 kcal mol−1.
Calculated parameters m and n’ showed mutual linear dependence (Figure 4a). Assuming m = n’, we obtained Gsol,calc(H+) ranging from −244 to −267 kcal mol−1 (Table 3), which corresponded to the results obtained using the AKB scheme [52,53]. One could notice that the linearity was kept even across the three different types of bases. The linear function with a non-zero intercept indicated that the intercept most likely contained two parts; one of them was not related to the Gibbs energy of the proton and should not be scaled with the same scaling factor. This issue was eliminated by modifying the second linear plot, as shown in Figure 4b.
To avoid the usage of any reference point (any published Glit(H+) in this case), we correlated the intercept n against m (Figure 4b), and the value of Gsol,calc(H+) was determined for m = 1 (the hypothetical, optimal result without systematic errors, G°sol,opt(H+)), which amounted to −258.8 kcal mol−1. Our estimate for the Gibbs solvation energy of the proton in acetonitrile (ΔG°s(H+)) of −254.4 kcal mol−1 was then calculated using Equation (6). The value fell in between those obtained by Carvalho and Pliego [69] and Rossini and Knapp [70]. The result was also very close to the standard Gibbs energy of solvation of a proton published by Fawcett [71]. We would like to emphasize here that the estimate was independent of the type of bases, whereas the selection of the computational model had a minor effect. The results showed that a very good estimate of ΔGsol(H+) could be derived from experimental pKa despite the systematic errors present in the continuum solvation model approaches.

5. Computational Details

All calculations were performed using the Gaussian09 program package [72]. The geometry optimizations and the single-point energy refinements were carried out using either B3LYP [73,74,75,76], M06-2X [77] density functionals, B2-PYLP [78] hybrid functional with perturbative correction or MP2 [79,80] calculations as defined in a list of the models. The minima on the Born–Oppenheimer potential energy surface were verified using a vibrational analysis. The solvation-energy contributions were calculated using the IPCM [81], SMD [82] or CPCM [83,84] continuum solvation model assuming the dielectric constant (ε) of acetonitrile to be either a default implemented value (35.688 for CPCM and SMD) or 36.64 (IPCM). Additionally, the non-standard parameters for IPCM calculations were used for the sake of consistency with our previous results on nitrogen bases, as well as to ensure good convergence [45]. The isodensity parameter of the molecular cavities in solution embracing the solute molecule was 4 × 10−4, and the angular integration weights over polar coordinates θ and φ were set to 100 and 20, respectively. The geometries of the optimized structures were visualized using MOLDEN5.9 [85,86].
List of models:
  • M1 = B3LYP/6-311+G(2df,p)//B3LYP/6-31G(d),
  • M2 = B3LYP(GD3)/6-311+G(2df,p)//B3LYP(GD3)/6-31+G(d),
  • M3 = M06-2X/aug-cc-pvtz//M06-2X/cc- pVDZ
  • M4 = M06-2X(GD3)/6-311++G(3df,2pd)//M06-2X/cc- pVDZ,
  • M5 = MP2(fc)/6-311+G(2df,p)//M06-2X/cc-pVDZ.
  • M6 = MP2(fc)/6-311+G(2df,p)//B3LYP/6-31G(d).
  • M7 = B2PLYP/6-311+G(2df,p)//B3LYP/6-31G(d)
  • IPCM = IPCM(ACN)/B3LYP/6-311+G(d,p)
  • CPCM = CPCM(ACN)/B3LYP/6-31G(d)
  • SMD1 = SMD(ACN)/M06-2X/6-31G(d)
  • SMD2 = SMD(ACN)/M06-2X/6-31+G(d,p)

6. Conclusions

Based on all examined correlations, IPCM//M6 and CPCM//M6 represented powerful approaches for the prediction of pKa in acetonitrile regardless of the type of bases, and the recommended equations for the IPCM//M6 model are as shown below.
N-Bases: pKa(BH+) = 0.601 × ΔG’a,sol(BH+) − 146.8
P-Bases: pKa(BH+) = 0.636 × ΔG’a,sol(BH+) − 158.5
C-Bases: pKa(BH+) = 0.705 × ΔG’a,sol(BH+) − 178.3
The SMD solvation model gave the smallest systematic deviation of the slope, which indicated the best estimate of the changes in the solvation energies. However, the scattering of the correlated data was more pronounced than for the other two approaches, and as such it was less reliable. Due to significant data scattering, we do not recommend using B3LYP calculations for either phosphines or ylides. M06-2X could be used in combination with correlation-consistent basis sets for phosphines, although a larger error could be expected for highly crowded systems such as tricyclohexylphosphine (8) and tris(t-butyl)phosphine (14).
Further, we showed that the approach for estimating the Gibbs energy of solvation of a proton could be applied as long as the reliable pKa values were measured. The approach compensated for the systematic errors inherently present in CSM calculations and provided values in a very good agreement with the literature ones. Malloum et al. were absolutely right in their statement: “... the accurate computation of the pKa of organic compounds in a given solvent is directly dependent on the accurate determination of the solvation free energy of the proton in that solvent.” [51]. However, the accurate determination of solvation-free energies is not a simple task. Expectedly, we obtained different systematic errors of the same method for the different classes of compounds. Within our approach, self-corrections of the systematic errors allowed us to obtain a very good estimate of the solvation-free energy of the proton in acetonitrile. The plots given in Figure 4 indicate that the approach was applicable regardless of whether we considered one or more classes of the organic bases and regardless of the employed computational models.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/ijms231810576/s1.

Author Contributions

Z.G. and B.K. equally contribute to calculation, data analysis, discussion, writing the manuscript and revising. All authors have read and agreed to the published version of the manuscript.

Funding

This work was financially supported by European Union through the European Regional Development Fund—the Competitiveness and Cohesion Operational Programme project “RAPTOVAX” (K.K.01.1.1.04.0099) and by Ministry of Science and Education of Croatia through the Program funding for academic year 2022.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data are available in this publication and Supplementary Materials.

Acknowledgments

Computations were mostly conducted on the Isabella cluster at the University computing center (SRCE) in Zagreb (https://www.srce.unizg.hr/isabella/), and their support is also greatly acknowledged.

Conflicts of Interest

The authors declare that they have no known competing financial interest or personal relationships that could have appeared to influence the work reported in this paper.

References

  1. Ishikawa, T.; Margetić, D. Superbases for organic synthesis: Guanidines, amidines, phosphaznes and related organocatalysts. In Perspectives; Ishikawa, T., Ed.; John Wiley & Sons, Ltd.: Chichester, UK, 2009; pp. 315–320. [Google Scholar]
  2. Puleo, T.R.; Sujansky, S.J.; Wright, S.E.; Bandar, J.S. Organic Superbases in Recent Synthetic Methodology Research. Chem. A Eur. J. 2021, 27, 4216–4229. [Google Scholar] [CrossRef] [PubMed]
  3. Schwesinger, R. Tricyclic 2,4-Diaminovinamidines– Readily Accessible, Very Strong CHN Bases. Angew. Chem. Int. Ed. Engl. 1987, 26, 1164–1165. [Google Scholar] [CrossRef]
  4. Schwesinger, R.; Missfeldt, M.; Peters, K.; von Schnering, H.G. Novel, Very Strongly Basic, Pentacyclic “Proton Sponges” with Vinamidine Structure. Angew. Chem. Int. Ed. Engl. 1987, 26, 1165–1167. [Google Scholar] [CrossRef]
  5. Schwesinger, R.; Schlemper, H. Peralkylated Polyaminophosphazenes—Extremely Strong, Neutral Nitrogen Bases. Angew. Chem. Int. Ed. Engl. 1987, 26, 1167–1169. [Google Scholar] [CrossRef]
  6. Schwesinger, R. Starke ungeladene Stickstoffbasen. Nachr. Chem. Tech. Lab. 1990, 38, 1214–1226. [Google Scholar] [CrossRef]
  7. Schwesinger, R.; Willaredt, J.; Schlemper, H.; Keller, M.; Schmitt, D.; Fritz, H. Novel, Very Strong, Uncharged Auxiliary Bases; Design and Synthesis of Monomeric and Polymer-Bound Triaminoiminophosphorane Bases of Broadly Varied Steric Demand. Chem. Ber. 1994, 127, 2435–2454. [Google Scholar] [CrossRef]
  8. Schwesinger, R.; Schlemper, H.; Hasenfratz, C.; Willaredt, J.; Dambacher, T.; Breuer, T.; Ottaway, C.; Fletschinger, M.; Boele, H.; Fritz, D.; et al. Extremly Strong, Uncharged Auxiliary Bases; Monomeric and polymer-Supported Polyaminophosphazenes (P2–P5). Liebigs Ann. 1996, 1996, 1055–1081. [Google Scholar] [CrossRef]
  9. Kaljurand, I.; Rodima, T.; Leito, I.; Koppel, I.A.; Schwesinger, R. Self-Consistent Spectrophotometric Basicity Scale in Acetonitrile Covering the Range between Pyridine and DBU. J. Org. Chem. 2000, 65, 6202–6208. [Google Scholar] [CrossRef]
  10. Štrukil, V.; Glasovac, Z.; Đilović, I.; Matković-Čalogović, D.; Šuman, L.; Kralj, M.; Eckert-Maksić, M. Triguanide Derivatives: Synthesis, Crystal Structure and Evaluation of the Proliferation Effect on Some Tumor Cell Lines. Eur. J. Org. Chem. 2012, 2012, 6785–6797. [Google Scholar] [CrossRef]
  11. Vazdar, K.; Kunetskiy, R.; Saame, J.; Kaupmees, K.; Leito, I.; Jahn, U. Very Strong Organosuperbases Formed by Combining Imidazole and Guanidine Bases: Synthesis, Structure, and Basicity. Angew. Chem. Int. Ed. 2014, 53, 1435–1438. [Google Scholar] [CrossRef]
  12. Petuškova, J.; Bruns, H.; Alcarazo, M. Cyclopropenylylidene-Stabilized Diaryl and Dialkyl Phosphenium Cations: Applications in Homogeneous Gold Catalysis. Angew. Chem. Int. Ed. 2011, 50, 3799–3802. [Google Scholar] [CrossRef]
  13. Bandar, J.S.; Lambert, T.H. Enantioselective Brønsted Base Catalysis with Chiral Cyclopropenimines. J. Am. Chem. Soc. 2012, 134, 5552–5555. [Google Scholar] [CrossRef]
  14. Bandar, J.S.; Lambert, T.H. Aminocyclopropenium Ions: Synthesis, Properties, and Applications. Synthesis 2013, 45, 2485–2498. [Google Scholar]
  15. Kögel, J.F.; Oelkers, B.; Kovačević, B.; Sundermeyer, J. A New Synthetic Pathway to the Second and Third Generation of Superbasic Bisphosphazene Proton Sponges: The Run for the Best Chelating Ligand for a Proton. J. Am. Chem. Soc. 2013, 35, 17768–17774. [Google Scholar] [CrossRef]
  16. Kögel, J.F.; Xie, X.; Baal, E.; Gesevičius, D.; Oelkers, B.; Kovačević, B.; Sundermeyer, J. Superbasic Alkyl-Substituted Bisphosphazene Proton Sponges: Synthesis, Structural Features, Thermodynamic and Kinetic Basicity, Nucleophilicity and Coordination Chemistry. Chem. Eur. J. 2014, 20, 7670–7685. [Google Scholar] [CrossRef]
  17. Belding, L.; Dudding, T. Synthesis and Theoretical Investigation of a 1,8-Bis(bis(diisopropylamino)cyclopropeniminyl)naphthalene Proton Sponge Derivative. Chem. Eur. J. 2014, 20, 1032–1037. [Google Scholar] [CrossRef]
  18. Belding, L.; Stoyanov, L.; Dudding, T. Synthesis, Theoretical Analysis, and Experimental pKa Determination of a Fluorescent, Nonsymmetric, In–Out Proton Sponge. J. Org. Chem. 2016, 81, 6–13. [Google Scholar] [CrossRef] [PubMed]
  19. Angelici, R.J. Basicities of Transition Metal Complexes from Studies of Their Heats of Protonation: A Guide to Complex Reactivity. Acc. Chem. Res. 1995, 28, 51–60. [Google Scholar] [CrossRef]
  20. Vazdar, K.; Margetić, D.; Kovačević, B.; Sundermeyer, J.; Leito, I.; Jahn, U. Design of Novel Uncharged Organic Superbases: Merging Basicity and Functionality. Acc. Chem. Res. 2021, 54, 3108–3123. [Google Scholar] [CrossRef]
  21. Weitkamp, R.F.; Neumann, B.; Stammler, H.-G.; Hoge, B. Phosphorus-Containing Superbases: Recent Progress in the Chemistry of Electron-Abundant Phosphines and Phosphazenes. Chem. Eur. J. 2021, 27, 10807–10825. [Google Scholar] [CrossRef]
  22. Tang, J.; Dopke, J.; Verkade, J.G. Synthesis of New Exceedingly Strong Non-ionic Bases: RN:P(MeNCH2CH2)3N. J. Am. Chem. Soc. 1993, 115, 5015–5020. [Google Scholar] [CrossRef]
  23. Verkade, J.G. Atranes: New Examples with Unexpected Properties. Acc. Chem. Res. 1993, 26, 483–489. [Google Scholar] [CrossRef]
  24. Verkade, J.G. Main Group Atranes: Chemical and Structural Features. Coord. Chem. Rev. 1994, 137, 233–295. [Google Scholar] [CrossRef]
  25. Wroblewski, A.E.; Pinkas, J.; Verkade, J.G. Strongly Basic Proazaphosphatranes: P(EtNCH2CH2)3N and P(iso-PrNCH2CH2)3N. Main Group Chem. 1995, 1, 69–79. [Google Scholar] [CrossRef]
  26. Verkade, J.G. P(RNCH2CH2)3N as Very Strong Non-Ionic Bases and Catalysts: Recent Advances and Applications. Phosphorus Sulfur Silicon Relat. Elem. 2002, 177, 1621–1631. [Google Scholar] [CrossRef]
  27. Verkade, J.G. P(RNCH2CH2)3N: Very Strong Non-Ionic Bases Useful in Organic Synthesis. Top. Curr. Chem. 2003, 223, 1–44. [Google Scholar]
  28. Verkade, J.G.; Kisanga, P.B. Recent Applications of Proazaphosphatranes in Organic Synthesis. Aldrichimica. Acta 2004, 37, 3–14. [Google Scholar] [CrossRef]
  29. Münchenberg, J.; Böge, O.; Fischer, A.K.; Jones, P.G.; Schmutzler, R. Synthesis and Structure of Tetraorganoguanidinyl–Substituted-Phosphorus–Halogen Compounds and of Tris–N–(N′,N′,N′′,N′′–Tetramethyl)–Guanidinyl Phosphonium Salts. Phosphorus Sulfur Silicon Relat. Elem. 1994, 86, 103–121. [Google Scholar] [CrossRef]
  30. Plack, V.; Münchenberg, J.; Thönnessen, H.; Jones, P.G.; Schmutzler, R. Synthesis of Stable N′,N′,N′′,N′′-Tetramethylguanidine-Substituted σ4(P)- and σ3(P)-Organophosphorus Compounds with N-Protonated P–N Bonds - The First σ3-Phosphorus-Substituted Ammonium Salts. Eur. J. Inorg. Chem. 1998, 1998, 865–875. [Google Scholar] [CrossRef]
  31. Freytag, M.; Plack, V.; Jones, P.G.; Schmutzler, R. Tris–N–(N′,N′,N″,N″–tetramethylguanidyl)phosphine Oxide – Synthesis and Reaction with Acids. Z. Naturforsch. B 2004, 59, 499–502. [Google Scholar]
  32. Buß, F.; Röthel, M.B.; Werra, J.A.; Rotering, P.; Wilm, L.F.B.; Daniliuc, C.G.; Löwe, P.; Dielmann, F. Tris(tetramethylguanidinyl)phosphine: The Simplest Non-ionic Phosphorus Superbase and Strongly Donating Phosphine Ligand. Chem. Eur. J. 2022, 28, e202104021. [Google Scholar] [CrossRef]
  33. Marchenko, A.P.; Koidan, G.N.; Pinchuk, A.M.; Kirsanov, A.V. Phosphorylated Phosphorimidic Triamides. Zh. Obshch. Khim. 1984, 54, 1774–1782. [Google Scholar]
  34. Ullrich, S.; Kovačević, B.; Xie, X.; Sundermeyer, J. Phosphazenyl Phosphines: The Most Electron-Rich Uncharged Phosphorus Brønsted and Lewis Bases. Angew. Chem. Int. Ed. 2019, 58, 10335–10339. [Google Scholar] [CrossRef]
  35. Mehlmann, P.; Dielmann, F. Switching the Electron-Donating Ability of Phosphines through Proton-Responsive Imidazolin-2-ylidenamino Substituents. Chem. Eur. J. 2019, 25, 2352–2357. [Google Scholar] [CrossRef]
  36. Kisanga, P.B.; Verkade, J.G.; Schwesinger, R. pKa Measurements of P(RNCH2CH3)3N. J. Org. Chem. 2000, 65, 5431–5432. [Google Scholar] [CrossRef]
  37. Kaljurand, I.; Koppel, I.A.; Kütt, A.; Rõõm, E.-I.; Rodima, T.; Koppel, I.; Mishima, M.; Leito, I. Experimental Gas-Phase Basicity Scale of Superbasic Phosphazenes. J. Phys. Chem. A 2007, 111, 1245–1250. [Google Scholar] [CrossRef]
  38. Leito, I.; Koppel, I.A.; Koppel, I.; Kaupmees, K.; Tshepelevitsh, S.; Saame, J. Basicity Limits of Neutral Organic Superbases. Angew. Chem. Int. Ed. 2015, 54, 9262–9265. [Google Scholar] [CrossRef]
  39. Saame, J.; Rodima, T.; Tshepelevitsh, S.; Kütt, A.; Kaljurand, I.; Haljasorg, T.; Koppel, I.A.; Leito, I. Experimental Basicities of Superbasic Phosphonium Ylides and Phosphazenes. J. Org. Chem. 2016, 81, 7349–7361. [Google Scholar] [CrossRef]
  40. Kögel, J.F.; Margetić, D.; Xie, X.; Finger, L.H.; Sundermeyer, J. A Phosphorus Bisylide: Exploring a New Class of Superbases with Two Interacting Carbon Atoms as Basicity Centers. Angew. Chem. Int. Ed. 2017, 56, 3090–3093. [Google Scholar] [CrossRef]
  41. Kovačević, B.; Maksić, Z.B. High Basicity of Phosphorus–Proton Affinity of Tris-(Tetramethylguanidinyl)phosphine and Tris-(Hexamethyltriaminophosphazenyl)phosphine by DFT Calculations. Chem. Commun. 2006, 2006, 1524–1526. [Google Scholar] [CrossRef]
  42. pKa(PP3H+) Was Measured in THF and Its Value in Acetonitrile Was Estimated to 43.4 Using the Correlation for the “Transfer between the Solvents”. Available online: https://analytical.chem.ut.ee/HA_UT/ (accessed on 27 August 2022).
  43. Liu, M.; Yang, I.; Buckley, B.; Lee, J.K. Proton Affinities of Phosphines versus N-Heterocyclic Carbenes. Org. Lett. 2010, 12, 4764–4767. [Google Scholar] [CrossRef]
  44. Liptak, M.D.; Shields, G.C. Accurate pKa Calculations for Carboxylic Acids Using Complete Basis Set and Gaussian-n Models Combined with CPCM Continuum Solvation Methods. J. Am. Chem. Soc. 2001, 123, 7314–7319. [Google Scholar] [CrossRef]
  45. Glasovac, Z.; Eckert-Maksić, M.; Maksić, Z.B. Basicity of Organic Bases and Superbases in Acetonitrile by the Polarized Continuum Model and DFT Calculations. New J. Chem. 2009, 33, 588–597. [Google Scholar] [CrossRef]
  46. Klamt, A.; Eckert, F.; Diedenhofen, M.; Beck, M.E. First Principles Calculations of Aqueous pKa Values for Organic and Inorganic Acids Using COSMO-RS Reveal an Inconsistency in the Slope of the pKa Scale. J. Phys. Chem. A 2003, 107, 9380–9386. [Google Scholar] [CrossRef] [Green Version]
  47. Eckert, F.; Leito, I.; Kaljurand, I.; Kütt, A.; Klamt, A.; Diedenhofen, M. Prediction of acidity in acetonitrile solution with COSMO-RS. J. Comput. Chem. 2009, 30, 799–810. [Google Scholar] [CrossRef]
  48. Peräkyllä, M. Ab Initio Quantum Mechanical Study on the Origin of the pK(a) Differences of the Proton Sponges 1,8-Bis(dimethylamino)naphthalene, 1,8-Bis(dimethylamino)-2,7-dimethoxynaphthalene, 1,6-Dimethyl-1,6-diazacyclodecane, and 1,6-Diazabicyclo[4.4.4]tetradecane. J. Org. Chem. 1996, 61, 7420–7425. [Google Scholar] [CrossRef]
  49. Kovačević, B.; Maksić, Z.B. Basicity of Some Organic Superbases in Acetonitrile. Org. Lett. 2001, 3, 1523–1526. [Google Scholar] [CrossRef]
  50. Busch, M.; Ahlberg, E.; Ahlberg, E.; Laasonen, K. How to Predict the pKa of Any Compound in Any Solvent. ACS Omega 2022, 7, 17369–17383. [Google Scholar] [CrossRef]
  51. Malloum, A.; Fifen, J.J.; Conradie, J. Determination of the Absolute Solvation Free Energy and Enthalpy of the Proton in Solutions. J. Mol. Liq. 2021, 322, 114919. [Google Scholar] [CrossRef]
  52. Matsui, T.; Baba, T.; Kamiyad, K.; Shigeta, Y. An Accurate Density Functional Theory Based Estimation of pKa Values of Polar Residues Combined with Experimental Data: From Amino acids to Minimal Proteins. Phys. Chem. Chem. Phys. 2012, 14, 4181–4187. [Google Scholar] [CrossRef]
  53. Fujiki, R.; Matsui, T.; Shigeta, Y.; Nakano, H.; Yoshida, N. Recent Developments of Computational Methods for pKa Prediction Based on Electronic Structure Theory with Solvation Models. J 2021, 4, 849–864. [Google Scholar] [CrossRef]
  54. Lias, S.G.; Bartmess, J.E.; Liebman, J.F.; Holmes, J.L.; Levin, R.D.; Mallard, W.G. “Ion Energetics Data” in NIST Chemistry WebBook, NIST Standard Reference Database Number 69; Linstrom, P.J., Mallard, W.G., Eds.; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2022.
  55. Cooks, R.G.; Kruger, T.L. Intrinsic Basicity Determination Using Metastable Ions. J. Am. Chem. Soc. 1977, 99, 1279–1281. [Google Scholar] [CrossRef]
  56. Bartmess, J.E. The bracketing method for determining the thermochemistry of ion-molecule reactions. In Encyclopedia of Mass Spectrometry; Elsevier: Amsterdam, The Netherlands, 2003; pp. 315–319. [Google Scholar]
  57. Cerda, B.A.; Wesdemiotis, C. Li+, Na+, and K+ Binding to the DNA and RNA Nucleobases. Bond Energies and Attachment Sites from the Dissociation of Metal Ion-Bound Heterodimers. J. Am. Chem. Soc. 1996, 118, 11884–11892. [Google Scholar] [CrossRef]
  58. Glasovac, Z.; Pavošević, F.; Štrukil, V.; Eckert-Maksić, M.; Schlangen, M.; Kretschmer, R. Toward Extension of the Gas-phase Basicity Scale by Novel Pyridine Containing Guanidines. Int. J. Mass Spectrom. 2013, 354–355, 113–122. [Google Scholar] [CrossRef]
  59. Glasovac, Z.; Eckert-Maksić, M.; Kaljurand, I.; Saame, J.; Leito, I. Gas phase Basicity of Biguanides – Comparison of the Equilibrium and the Kinetic Methods. Int. J. Mass Spectrom. 2019, 435, 61–68. [Google Scholar] [CrossRef]
  60. Haav, K.; Saame, J.; Kütt, A.; Leito, I. Basicity of Phosphanes and Diphosphanes in Acetonitrile. Eur. J. Org. Chem. 2012, 2012, 2167–2172. [Google Scholar] [CrossRef]
  61. Li, J.-N.; Fu, Y.; Liu, L.; Guo, Q.-X. First-Principle Predictions of Basicity of Organic Amines and Phosphines in Acetonitrile. Tetrahedron 2006, 62, 11801–11813. [Google Scholar] [CrossRef]
  62. Kaljurand, I.; Kütt, A.; Sooväli, L.; Rodima, T.; Mäemets, V.; Leito, I.; Koppel, I.A. Extension of the Self-Consistent Spectrophotometric Basicity Scale in Acetonitrile to a Full Span of 28 pKa Units:  Unification of Different Basicity Scales. J. Org. Chem. 2005, 70, 1019–1028. [Google Scholar] [CrossRef]
  63. Abdur-Rashid, K.; Fong, T.P.; Greaves, B.; Gusev, D.G.; Hinman, J.G.; Landau, S.E.; Lough, A.J.; Morris, R.H. An Acidity Scale for Phosphorus-Containing Compounds Including Metal Hydrides and Dihydrogen Complexes in THF:  Toward the Unification of Acidity Scales. J. Am. Chem. Soc. 2000, 122, 9155–9171. [Google Scholar] [CrossRef]
  64. Streuli, C.A. Determination of Basicity of Substituted Phosphines by Nonaqueous Titrimetry. Anal. Chem. 1960, 32, 985–987. [Google Scholar] [CrossRef]
  65. Greb, L.; Quack, S.; Schirmer, B.; Oña-Burgos, P.; Kaupmees, K.; Lõkov, M.; Leito, I.; Grimme, S.; Paradies, J. Electronic effects of triarylphosphines in metal-free hydrogen activation: A kinetic and computational study. Chem. Sci. 2013, 4, 2788–2796. [Google Scholar] [CrossRef]
  66. Tshepelevitsh, S.; Kütt, A.; Lõkov, M.; Kaljurand, I.; Saame, J.; Heering, A.; Plieger, P.; Vianello, R.; Leito, I. On the Basicity of Organic Bases in Different Media. Eur. J. Org. Chem. 2019, 2019, 6735–6748. [Google Scholar] [CrossRef]
  67. Mehlmann, P.; Mück-Lichtenfeld, C.; Tan, T.T.Y.; Dielmann, F. Tris(imidazolin-2-ylidenamino)phosphine: A Crystalline Phosphorus(III) Superbase That Splits Carbon Dioxide. Chem. Eur. J. 2017, 23, 5929–5933. [Google Scholar] [CrossRef]
  68. Himmel, D.; Goll, S.K.; Leito, I.; Krossing, I. Anchor Points for the Unified Brønsted Acidity Scale: The rCCC Model for the Calculation of Standard Gibbs Energies of Proton Solvation in Eleven Representative Liquid Media. Chem. Eur. J. 2011, 17, 5808–5826. [Google Scholar] [CrossRef]
  69. Carvalho, N.F.; Pliego, J.R. Cluster-continuum Quasichemical Theory Calculation of the Lithium Ion Solvation in Water, Acetonitrile and Dimethyl Sulfoxide: An Absolute Single-ion Solvation Free Energy Scale. Phys. Chem. Chem. Phys. 2015, 17, 26745–26755. [Google Scholar] [CrossRef]
  70. Rossini, E.; Knapp, E.-W. Proton Solvation in Protic and Aprotic Solvents. J. Comput. Chem. 2016, 37, 1082–1091. [Google Scholar] [CrossRef]
  71. Fawcett, W.R. The Ionic Work Function and its Role in Estimating Absolute Electrode Potentials. Langmuir 2008, 24, 9868–9875. [Google Scholar] [CrossRef]
  72. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian09. In Rev D. 01; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
  73. Becke, A.D. Density-functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
  74. Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti Correlation-energy Formula into a Functional of the Electron Density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
  75. Miehlich, B.; Savin, A.; Stoll, H.; Preuss, H. Results Obtained with the Correlation Energy Density Functionals of Becke and Lee, Yang and Parr. Chem. Phys. Lett. 1989, 157, 200–206. [Google Scholar] [CrossRef]
  76. Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
  77. Zhao, Y.; Truhlar, D.G. The M06 Suite of Density Functionals for Main Group Thermochemistry, Thermochemical Kinetics, Noncovalent Interactions, Excited States, and Transition Elements: Two New Functionals and Systematic Testing of Four M06-class Functionals and 12 Other Functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar]
  78. Grimme, S. Semiempirical hybrid density functional with perturbative second-order correlation. J. Chem. Phys. 2006, 124, 034108. [Google Scholar] [CrossRef] [PubMed]
  79. Møller, C.; Plesset, M.S. Note on an Approximation Treatment for Many-Electron Systems. Phys. Rev. 1934, 46, 0618–0622. [Google Scholar] [CrossRef]
  80. Frisch, M.J.; Head-Gordon, M.; Pople, J.A. Semi-direct Algorithms for the MP2 Energy and Gradient. Chem. Phys. Lett. 1990, 166, 281–289. [Google Scholar] [CrossRef]
  81. Foresman, J.B.; Keith, T.A.; Wiberg, K.B.; Snoonian, J.; Frisch, M.J. Solvent Effects. 5. Influence of Cavity Shape, Truncation of Electrostatics, and Electron Correlation on ab Initio Reaction Field Calculations. J. Phys. Chem. 1996, 100, 16098–16104. [Google Scholar] [CrossRef]
  82. Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef]
  83. Barone, V.; Cossi, M. Quantum Calculation of Molecular Energies and Energy Gradients in Solution by a Conductor Solvent Model. J. Phys. Chem. A 1998, 102, 1995–2001. [Google Scholar] [CrossRef]
  84. Cossi, M.; Rega, N.; Scalmani, G.; Barone, V. Energies, Structures, and Electronic Properties of Molecules in Solution with the C-PCM Solvation Model. J. Comp. Chem. 2003, 24, 669–681. [Google Scholar] [CrossRef]
  85. Schaftenaar, G.; Vlieg, E.; Vriend, G. Molden 2.0: Quantum chemistry meets proteins. J. Comp. Aided. Mol. Des. 2017, 31, 789–800. [Google Scholar] [CrossRef]
  86. Schaftenaar, G.; Nordik, J.H. Molden: A Pre- and Post-processing Program for Molecular and Electronic Structures. J. Comput. Aided Mol. Des. 2000, 14, 123–134. [Google Scholar] [CrossRef]
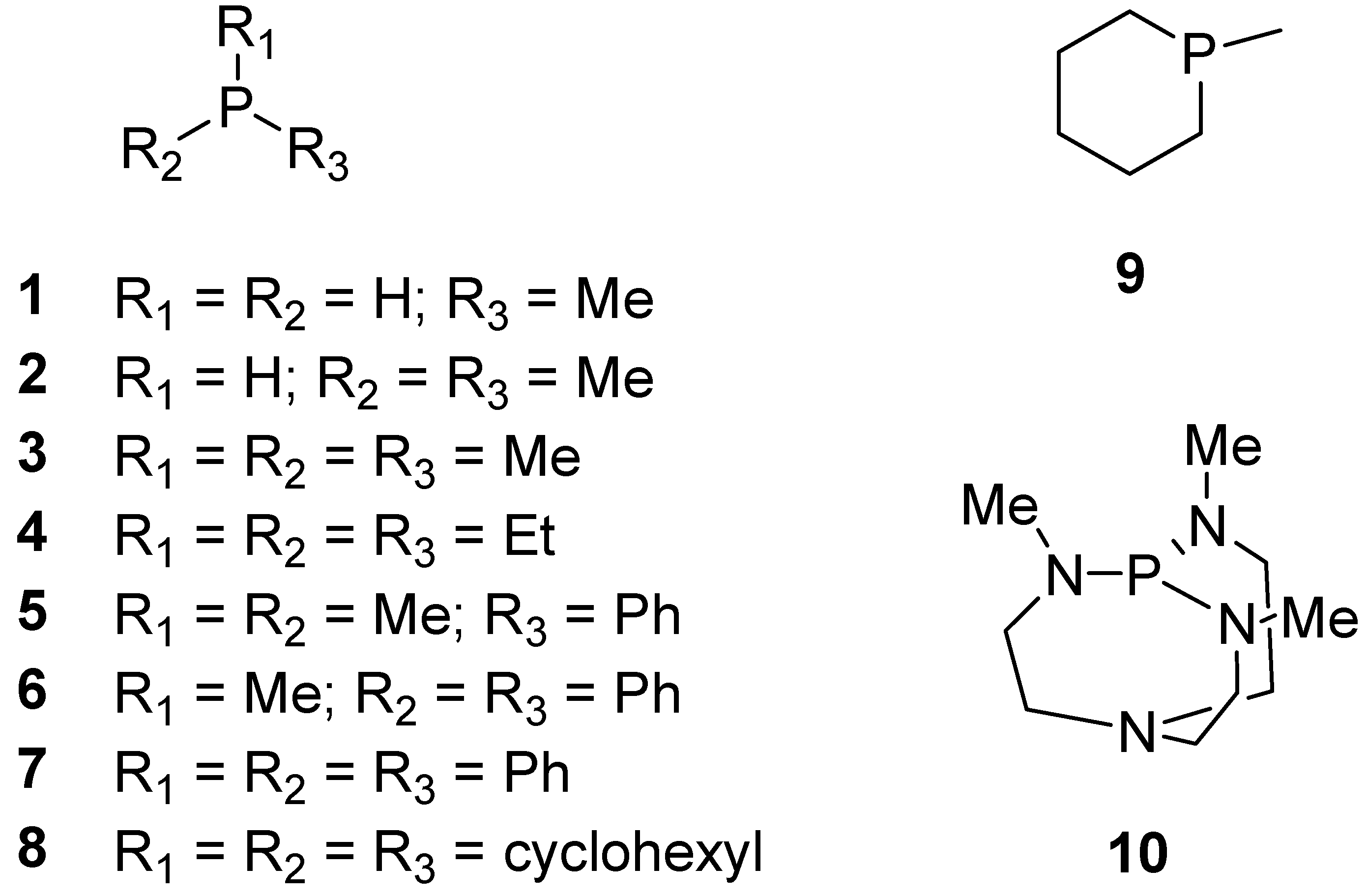
Ijms 23 10576 sch001 550
Scheme 1. Structures of the phosphine bases with measured gas-phase basicity.
Scheme 1. Structures of the phosphine bases with measured gas-phase basicity.
Ijms 23 10576 sch001
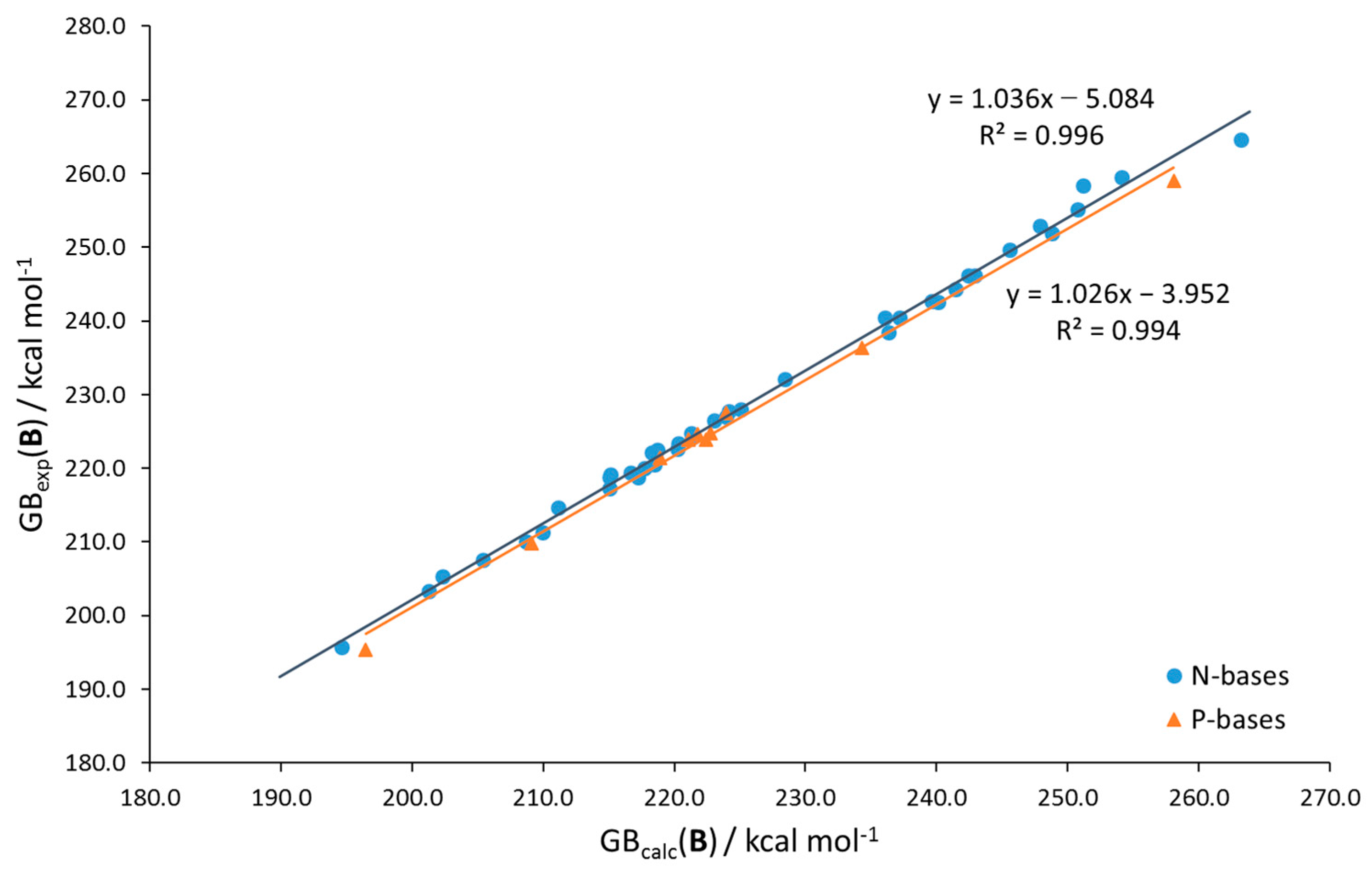
Ijms 23 10576 g001 550
Figure 1. Correlation of the experimental against calculated GB values for a set of nitrogen bases (blues circles) and selected phosphines (orange triangles). All GBcalc were calculated using the MP2(fc)/6-311+G(2df,p)//B3LYP/6-31G(d) approach (M6 model).
Figure 1. Correlation of the experimental against calculated GB values for a set of nitrogen bases (blues circles) and selected phosphines (orange triangles). All GBcalc were calculated using the MP2(fc)/6-311+G(2df,p)//B3LYP/6-31G(d) approach (M6 model).
Ijms 23 10576 g001
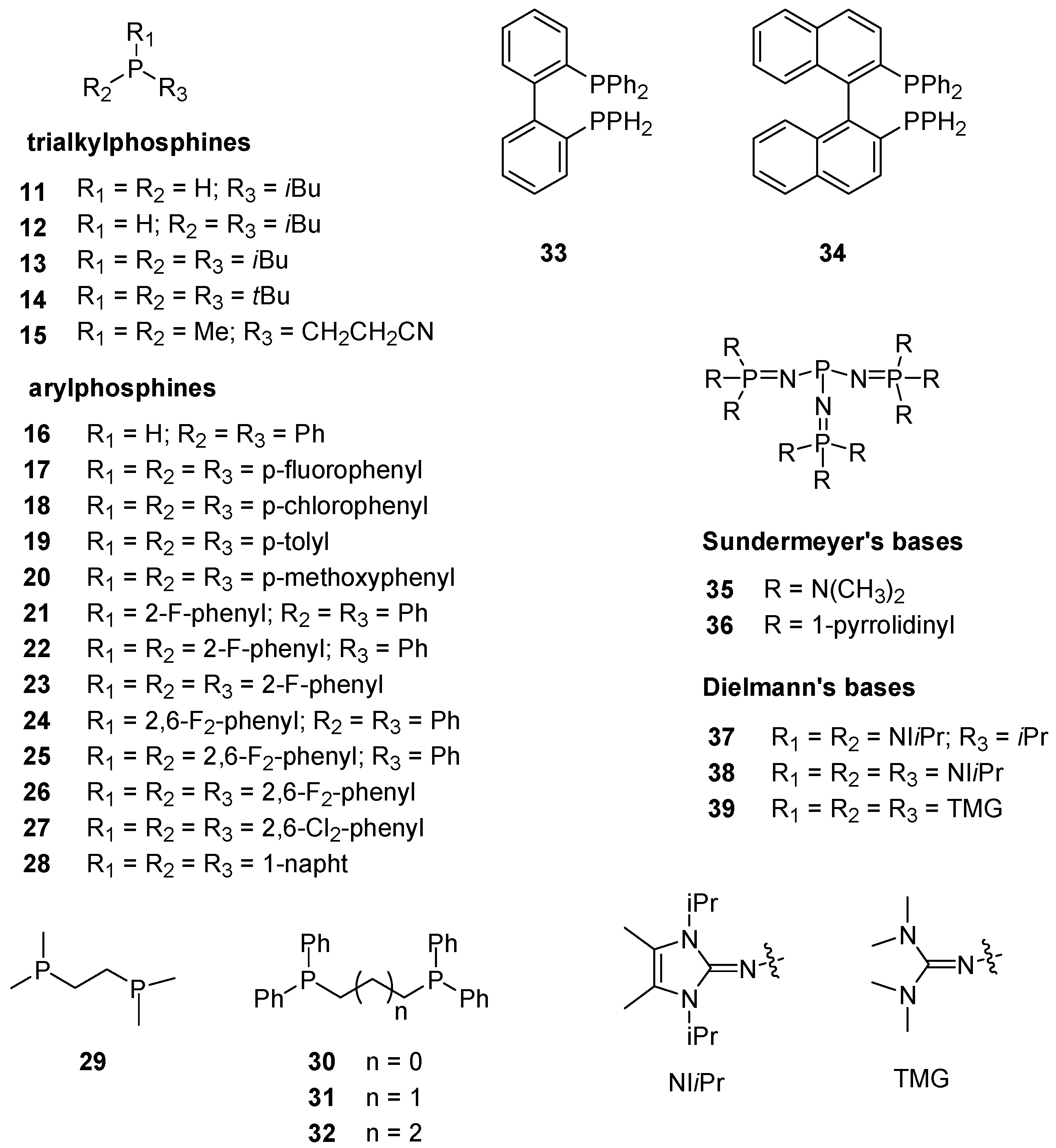
Ijms 23 10576 sch002 550
Scheme 2. Structures of phosphine bases with known pKa in acetonitrile.
Scheme 2. Structures of phosphine bases with known pKa in acetonitrile.
Ijms 23 10576 sch002
Ijms 23 10576 g002 550
Figure 2. Correlation of experimental pKa against ΔG’a,sol for N and P bases calculated at the (a) IPCM//M6, (b) CPCM//M6, (c) SMD1//M6, and (d) SMD2//M3 levels of theory.
Figure 2. Correlation of experimental pKa against ΔG’a,sol for N and P bases calculated at the (a) IPCM//M6, (b) CPCM//M6, (c) SMD1//M6, and (d) SMD2//M3 levels of theory.
Ijms 23 10576 g002
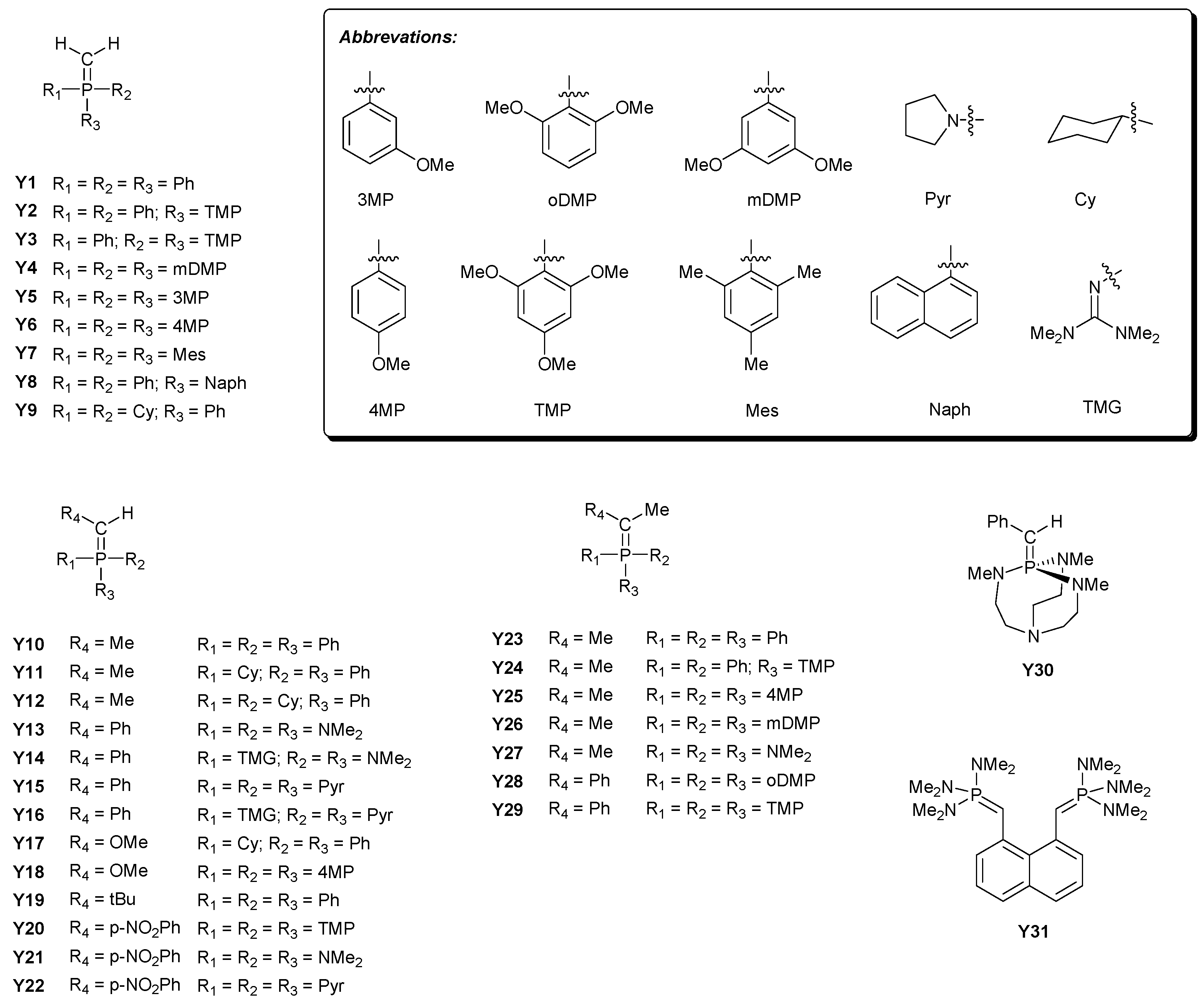
Ijms 23 10576 sch003 550
Scheme 3. Structures of ylides Y1–Y31 (carbon bases) with known pKa in acetonitrile.
Scheme 3. Structures of ylides Y1–Y31 (carbon bases) with known pKa in acetonitrile.
Ijms 23 10576 sch003
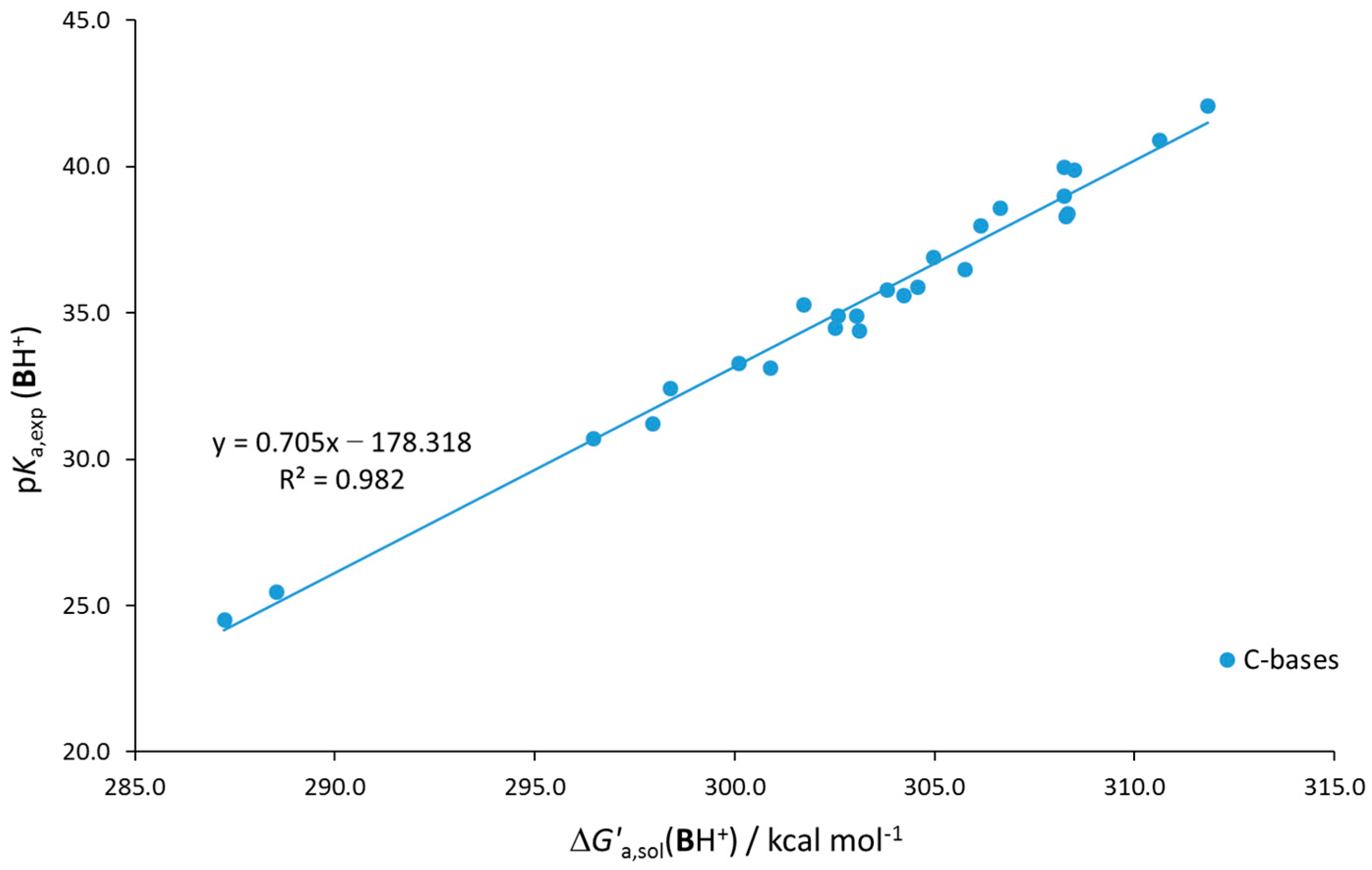
Ijms 23 10576 g003 550
Figure 3. Correlation of experimental pKa against the reduced Gibbs energy of dissociation (ΔG’a.sol(BH+)) obtained using the IPCM//M6 computational approach with off-liners excluded. MUE = 0.5, RMS = 0.6. Adding outliers to the correlation dropped R2 to 0.825, with MUE = 1.0 and RMS = 1.7.
Figure 3. Correlation of experimental pKa against the reduced Gibbs energy of dissociation (ΔG’a.sol(BH+)) obtained using the IPCM//M6 computational approach with off-liners excluded. MUE = 0.5, RMS = 0.6. Adding outliers to the correlation dropped R2 to 0.825, with MUE = 1.0 and RMS = 1.7.
Ijms 23 10576 g003
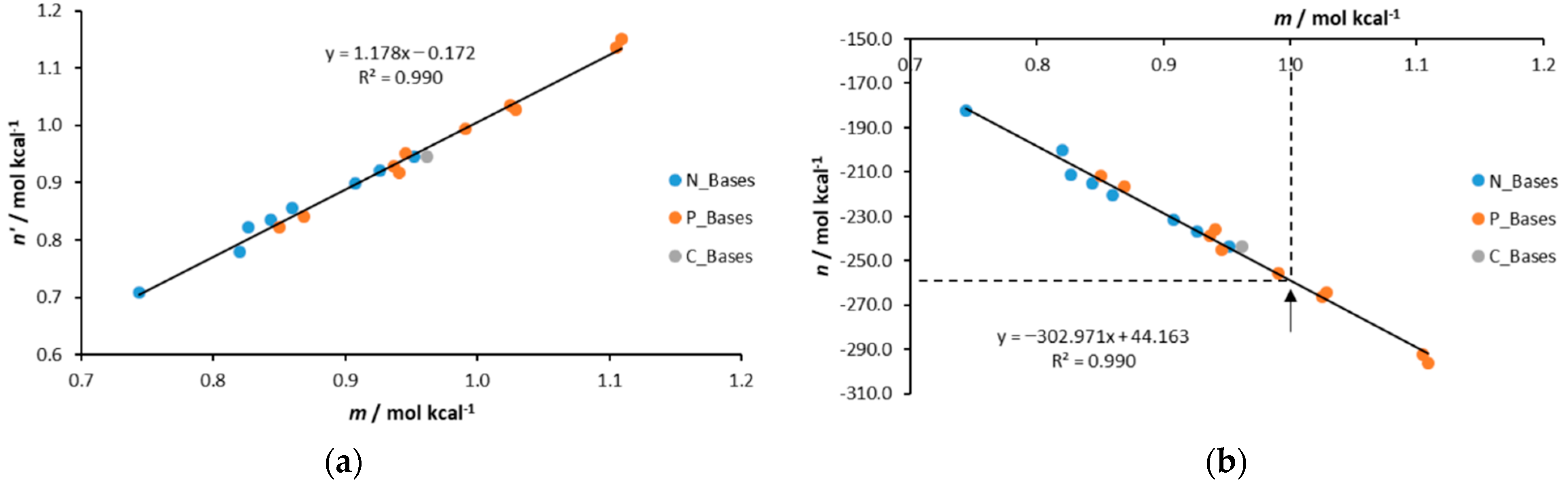
Ijms 23 10576 g004 550
Figure 4. Linear dependence of parameters (a) n’ against m and (b) n against m. (for the meaning of m, n, and n’, see Equations (4) and (5)). The arrow shows the interpolated point from which G°s,opt(H+) was calculated.
Figure 4. Linear dependence of parameters (a) n’ against m and (b) n against m. (for the meaning of m, n, and n’, see Equations (4) and (5)). The arrow shows the interpolated point from which G°s,opt(H+) was calculated.
Ijms 23 10576 g004
Table
Table 1. Comparison of the experimental and calculated gas-phase basicity values for the selected phosphine bases a.
Table 1. Comparison of the experimental and calculated gas-phase basicity values for the selected phosphine bases a.
BaseGB
expM1M2M3M4M5M6M7
1195.4196.9196.9194.5195.2196.6196.5199.7
2209.8210.6210.5207.5208.3209.2209.1213.3
3221.4221.5221.8217.4218.4218.7218.9224.1
4227.5227.4227.2223.3224.2223.7223.9229.7
5223.9225.3225.7220.3221.2221.3221.1227.6
6224.6227.0227.8221.9222.7221.9221.8229.9
7224.8229.2230.4223.5224.3222.5222.8232.0
8236.4
(241) b		239.4240.3235.3236.2234.7234.3242.6
9223.9225.8225.6221.8222.7222.3222.4228.5
10259.0252.8251.1249.2251.6258.8258.1257.0
slope
intercept
R2		 1.081
−19.1
0.975		1.084
−20.1
0.958		1.117
−22.8
0.986		1.091
−18.2
0.990		1.014
−1.5
0.992		1.026
−4.0
0.994		1.059
−17.3
0.979
a The employed computational models are as defined in Computational Details. b Derived from PA(8) = 249 kcal mol−1 [43] (see Supplementary Materials).
Table
Table 2. Comparison of calculated and experimental ACNpKas for protonated phosphines 3–39 a,b.
Table 2. Comparison of calculated and experimental ACNpKas for protonated phosphines 3–39 a,b.
Base BACNpKa
(BH+)		 //M6 Base BACNpKa
(BH+)		 //M6
exp.CPCMIPCMSMD1 exp.CPCMIPCMSMD1
315.5 b16.415.717.4224.6 j4.14.94.0
416.6 c16.015.117.4233.0 j2.73.62.2
512.7 b13.112.914.2245.2 j5.76.04.8
610.0 d9.99.810.2252.5 j2.73.72.0
77.6 b7.37.77.3260.7 j−0.30.5−2.1
816.1 e,f16.915.718.6271.7 j2.13.1−1.4
1032.9 g34.132.736.0286.6 j6.67.06.1
115.2 c6.25.57.42915.6 b15.214.016.5
1210.6 c11.710.212.9309.4 b9.49.09.6
1315.7 c15.413.816.8319.8 b9.79.010.1
1417.0 e17.917.420.03210.2 b9.38.29.5
1513.5 c12.311.714.1338.0 b7.78.66.2
164.2 h5.05.15.3347.8 b8.38.86.9
176.6 i5.76.76.43543.4 f,k41.442.738.8
185.4 i5.55.06.23645.4 f,k44.145.341.6
199.1 i8.38.58.13732.7 l32.432.431.7
2010.1 b9.910.910.13829.5 m32.532.631.3
216.1 j5.86.45.73938.8 n38.839.337.7
a
b
R2		 –0.690
−173.2
0.994		0.637
−158.8
0.993		0.726
−187.6
0.977
MUE
RMS		 –0.7
0.9		0.7
1.0		1.3
1.8
a For a definition of M6, see Table 1; CPCM = CPCM(ACN)/B3LYP/6-31G(d), IPCM = IPCM(ACN)/B3LYP/6-311+G(d,p), SMD1 = SMD(ACN)/M06-2X/6-31G(d). b Ref [60]. c Ref. [61]. d Ref [62]. e ACNpKa(14H+) was measured using the NMR method, while ACNpKa(8H+) was obtained from THFpKa(8H+); see Ref. [63]. f Conversion from THFpKa to ACNpKa was performed by employing the following equation: THFpKa = 0.92 × ACNpKa − 5.15; see Ref. [39]. g Ref. [36]. h Evaluated from half neutralization potential measured in nitromethane (Ref. [64]) and scaled to fit Leito’s data for 1H+, 5H+, 7H+, and 20H+. i Taken from Ref. [61] and scaled to fit Leito’s data for 1H+, 5H+, 7H+, and 20H+. j Refs. [65,66]. k Derived from THFpKa(35H+) = 34.9 and THFpKa(36H+) = 36.7 [34]. l Ref. [32]. m Ref. [35]. n Ref. [67].
Table
Table 3. Parameters m and n derived from the correlations used to estimate Gsol,calc(H+) a.
Table 3. Parameters m and n derived from the correlations used to estimate Gsol,calc(H+) a.
Methodmnn’Gsol,calc(H+) bΔ(Gsol,calc(H+))
Lit. data −257.3 c0.0
N_BasesIPCM//M10.744−182.1530.708−244.712.5
CPCM//M10.827−211.4190.822−255.81.5
SMD1//M10.860−220.4080.857−256.40.9
IPCM//M60.820−200.3670.779−244.412.9
CPCM//M60.908−231.4460.900−255.02.3
SMD1//M60.952−243.4670.946−255.71.5
SMD2//M30.844−214.8460.835−254.72.6
SMD2//M50.926−236.9720.921−255.81.5
P_BasesIPCM//M10.937−238.8650.929−254.82.4
CPCM//M11.029−264.2961.027−256.90.4
SMD1//M11.105−292.4041.137−264.67.3
IPCM//M60.869−216.3040.841−248.98.4
CPCM//M60.941−235.9240.917−250.66.7
SMD1//M60.991−255.5850.993−258.00.8
SMD2//M31.025−266.3741.035−260.02.7
SMD2//M50.946−244.7940.952−258.91.6
IPCM//M50.850−211.5620.822−248.98.4
SMD2//M21.109−296.0511.151−266.99.6
C_BasesIPCM//M60.962−243.3050.946−252.94.3
a Coefficients m and n are given in mol kcal−1, and Gsol,calc(H+) is given in kcal mol−1 (1 kcal = 4.184 kJ). b Gsol,calc(H+) = n/m. c The literature value for Glit(H+) was obtained using Equation (6).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Glasovac, Z.; Kovačević, B. Modeling pKa of the Brønsted Bases as an Approach to the Gibbs Energy of the Proton in Acetonitrile. Int. J. Mol. Sci. 2022, 23, 10576. https://doi.org/10.3390/ijms231810576

AMA Style

Glasovac Z, Kovačević B. Modeling pKa of the Brønsted Bases as an Approach to the Gibbs Energy of the Proton in Acetonitrile. International Journal of Molecular Sciences. 2022; 23(18):10576. https://doi.org/10.3390/ijms231810576

Chicago/Turabian Style

Glasovac, Zoran, and Borislav Kovačević. 2022. "Modeling pKa of the Brønsted Bases as an Approach to the Gibbs Energy of the Proton in Acetonitrile" International Journal of Molecular Sciences 23, no. 18: 10576. https://doi.org/10.3390/ijms231810576

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop