Monte Carlo Models for Sub-Chronic Repeated-Dose Toxicity: Systemic and Organ-Specific Toxicity
Abstract
:1. Introduction
2. Results
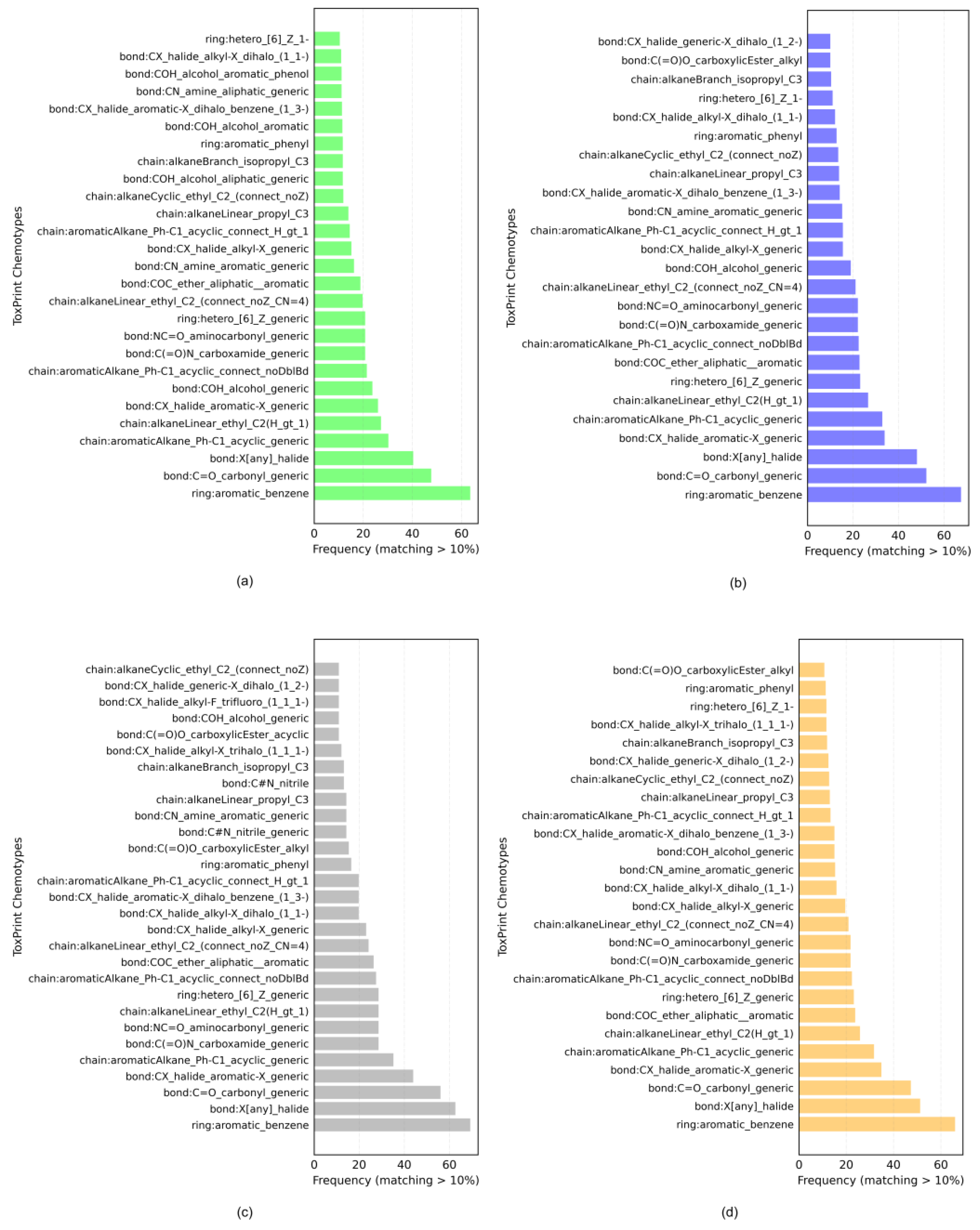
2.1. Characterization of the Datasets
2.2. Models Developed
2.2.1. General Models
2.2.2. Kidney Models
2.2.3. Brain Models
2.2.4. Liver Models
3. Discussion
3.1. Comparison with Other Models
4. Materials and Methods
4.1. Dataset Collection and Preparation
4.2. Characterization of the Datasets
4.3. Further Curation
4.4. Model Development and Optimal Descriptors
- (Cl.N)..1.1.A molecule contains one chlorine atom and one nitrogen atom;
- (Cl.N)..1.2.A molecule contains one chlorine atom and two nitrogen atoms;
- (Cl.N)..2.1.A molecule contains two chlorine atoms and one nitrogen atom.
4.5. Definition of the Applicability Domain
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- European Commission. Regulation (EC) No.1223/2009 of the European Parliament and of the Council of 30 November 2009 on Cosmetic Products. Off. J. Eur. Union 2009, 342, 59–209. [Google Scholar]
- Selvestrel, G.; Robino, F.; Baderna, D.; Manganelli, S.; Asturiol, D.; Manganaro, A.; Russo, M.Z.; Lavado, G.; Toma, C.; Roncaglioni, A.; et al. SpheraCosmolife: A new tool for the risk assessment of cosmetic products. ALTEX Altern. Anim. Exp. 2021, 38, 565–579. [Google Scholar] [CrossRef] [PubMed]
- European Commission. Regulation (EC) No 1907/ 2006 of the European Parliament and of the Council of 18 December 2006 concerning the Registration, Evaluation, Authorization and Restriction of Chemicals (REACH), Establishing a European Chemicals Agency, amending Directive 1999/45/EC and repealing Council Regulation (EEC) No 793/93 and Commission Regulation (EC) No 1488/94 as well as Council Directive 76/769/EEC and Commission Directives 91/155/EEC, 93/67/EEC, 93/105/EC and 2000/21/EC. Off. J. Eur. Union 2006, 1–849. [Google Scholar]
- SCCS. Scientific Committee on Consumer Safety (2021). SCCS Notes of Guidance for the Testing of Cosmetic Ingredients and Their Safety Evaluation 11th Revision; European Commission: Luxembourg, 2021; Volume SCCS/1628/21. [Google Scholar]
- Gadaleta, D.; Nicolotti, O. A k-NN algorithm for predicting oral sub-chronic toxicity in the rat. ALTEX Altern. Anim. Exp. 2014, 31, 4. [Google Scholar] [CrossRef] [Green Version]
- Gadaleta, D.; Marzo, M.; Toropov, A.A.; Toropova, A.; Lavado, G.J.; Escher, S.E.; Dorne, J.L.C.M.; Benfenati, E. Integrated In Silico Models for the Prediction of No-Observed-(Adverse)-Effect Levels and Lowest-Observed-(Adverse)-Effect Levels in Rats for Sub-chronic Repeated-Dose Toxicity. Chem. Res. Toxicol. 2020, 34, 247–257. [Google Scholar] [CrossRef]
- Galli, C.L.; Corsini, E.; Marinovich, M. Tossicologia, 3rd ed.; Piccin-Nuova Libraria: Padova, Italy, 2016. [Google Scholar]
- Sand, S.; Victorin, K.; Filipsson, A.F. The current state of knowledge on the use of the benchmark dose concept in risk assessment. J. Appl. Toxicol. 2008, 28, 405–421. [Google Scholar] [CrossRef] [PubMed]
- Pizzo, F.; Benfenati, E. In Silico Models for Repeated-Dose Toxicity (RDT): Prediction of the No Observed Adverse Effect Level (NOAEL) and Lowest Observed Adverse Effect Level (LOAEL) for Drugs. In In Silico Methods for Predicting Drug Toxicity, 1st ed.; Benfenati, E., Ed.; Springer: New York, NY, USA, 2016; pp. 163–176. [Google Scholar] [CrossRef]
- Toropov, A.A.; Toropova, A.P.; Pizzo, F.; Lombardo, A.; Gadaleta, D.; Benfenati, E. CORAL: Model for no observed adverse effect level (NOAEL). Mol. Divers. 2015, 19, 563–575. [Google Scholar] [CrossRef] [Green Version]
- Toropova, A.P.; Toropov, A.A.; Marzo, M.; Escher, S.E.; Dorne, J.L.; Georgiadis, N.; Benfenati, E. The application of new HARD-descriptor available from the CORAL software to building up NOAEL models. Food Chem. Toxicol. Int. J. Publ. Br. Ind. Biol. Res. Assoc. 2018, 112, 544–550. [Google Scholar] [CrossRef]
- Gramatica, P.; Sangion, A. A Historical Excursus on the Statistical Validation Parameters for QSAR Models: A Clarification Concerning Metrics and Terminology. J. Chem. Inf. Model. 2016, 56, 1127–1131. [Google Scholar] [CrossRef]
- Roy, K.; Kar, S. Chapter 3—How to Judge Predictive Quality of Classification and Regression Based QSAR Models? In Frontiers in Computational Chemistry; Ul-Haq, Z., Madura, J.D., Eds.; Bentham Science Publishers: Sharjah, United Arab Emirates, 2015; pp. 71–120. [Google Scholar] [CrossRef]
- Toropova, A.P.; Toropov, A.A. Does the Index of Ideality of Correlation Detect the Better Model Correctly? Mol. Inform. 2019, 38, 1800157. [Google Scholar] [CrossRef] [Green Version]
- Pizzo, F.; Gadaleta, D.; Benfenati, E. In Silico Models for Repeated-Dose Toxicity (RDT): Prediction of the No Observed Adverse Effect Level (NOAEL) and Lowest Observed Adverse Effect Level (LOAEL) for Drugs. In In Silico Methods for Predicting Drug Toxicity, 2nd ed.; Benfenati, E., Ed.; Springer: New York, NY, USA, 2022; pp. 241–258. [Google Scholar] [CrossRef]
- Berggren, E.; White, A.; Ouedraogo, G.; Paini, A.; Richarz, A.-N.; Bois, F.Y.; Exner, T.; Leite, S.; van Grunsven, L.A.; Worth, A.; et al. Ab initio chemical safety assessment: A workflow based on exposure considerations and non-animal methods. Comput. Toxicol. 2017, 4, 31–44. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cronin, M.T.D.; Enoch, S.J.; Mellor, C.L.; Przybylak, K.R.; Richarz, A.-N.; Madden, J.C. In Silico Prediction of Organ Level Toxicity: Linking Chemistry to Adverse Effects. Toxicol. Res. 2017, 33, 173–182. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- ICCR. Integrated Strategies for Safety Assessment of Cosmetic Ingredients: Part 2. 2018. Available online: https://www.iccr-cosmetics.org/topics-documents/5-integrated-strategies-for-safety-assesment (accessed on 23 July 2021).
- Russell, W.M.S.; Burch, R.L. The Principles of Humane Experimental Technique. Johns Hopkins Bloom. Sch. Public Health 1959. Available online: http://caat.jhsph.edu/principles/the-principles-of-humane-experimental-technique (accessed on 23 July 2021).
- Worth, A.; Barroso, J.; Bremer, S.; Burton, J.; Casati, S.; Coecke, S.; Corvi, R.; Desprez, B.; Dumont, C.; Gouliarmou, V.; et al. Alternative Methods for Regulatory Toxicology: A State of the Art Review. LU: Publications Office of the European Union. Joint Research Centre Institute for Health and Consumer Protection, Ispra (Italy). 2014. Available online: https://data.europa.eu/doi/10.2788/11111 (accessed on 23 July 2021).
- Benfenati, E.; Manganaro, A.; Gini, G. VEGA-QSAR: AI inside a platform for predictive toxicology. CEUR Workshop Proc. 2013, 1107, 21–28. [Google Scholar]
- OECD. Test No. 408: Repeated Dose 90-Day Oral Toxicity Study in Rodents; OECD Publishing: Paris, France, 2018; Available online: https://www.oecd-ilibrary.org/environment/test-no-408-repeated-dose-90-day-oral-toxicity-study-in-rodents_9789264070707-ee (accessed on 15 September 2021).
- Yang, C.; Barlow, S.M.; Jacobs, K.L.M.; Vitcheva, V.; Boobis, A.R.; Felter, S.P.; Arvidson, K.B.; Keller, D.; Cronin, M.T.; Enoch, S.; et al. Thresholds of Toxicological Concern for cosmetics-related substances: New database, thresholds, and enrichment of chemical space. Food Chem. Toxicol. 2017, 109, 170–193. [Google Scholar] [CrossRef]
- Watford, S.; Pham, L.L.; Wignall, J.; Shin, R.; Martin, M.T.; Friedman, K.P. ToxRefDB version 2.0: Improved utility for predictive and retrospective toxicology analyses. Reprod. Toxicol. 2019, 89, 145–158. [Google Scholar] [CrossRef]
- Dorne, J.; Richardson, J.; Livaniou, A.; Carnesecchi, E.; Ceriani, L.; Baldin, R.; Kovarich, S.; Pavan, M.; Saouter, E.; Biganzoli, F.; et al. EFSA’s OpenFoodTox: An open source toxicological database on chemicals in food and feed and its future developments. Environ. Int. 2021, 146, 106293. [Google Scholar] [CrossRef]
- Kovarich, S.; Ceriani, L.; Ciacci, A.; Baldin, R.; Perez Miguel, M.; Gibin, D.; Carnesecchi, E.; Roncaglioni, A.; Mostrag, A.; Tarkhov, A.; et al. OpenFoodTox: EFSA’s chemical hazards database. Zenodo 2020. [Google Scholar] [CrossRef]
- Escher, S.E.; Batke, M.; Hoffmann-Doerr, S.; Messinger, H.; Mangelsdorf, I. Interspecies extrapolation based on the RepDose database—A probabilistic approach. Toxicol. Lett. 2013, 218, 159–165. [Google Scholar] [CrossRef]
- Berthold, M.R.; Cebron, N.; Dill, F.; Gabriel, T.R.; Kötter, T.; Meinl, T.; Ohl, P.; Sieb, C.; Thiel, K.; Wiswedel, B. KNIME: The Konstanz Information Miner. In Data Analysis, Machine Learning and Applications; Springer: Berlin/Heidelberg, Germany, 2008; pp. 319–326. [Google Scholar]
- Gadaleta, D.; Lombardo, A.; Toma, C.; Benfenati, E. A new semi-automated workflow for chemical data retrieval and quality checking for modeling applications. J. Cheminform. 2018, 10, 60. [Google Scholar] [CrossRef] [Green Version]
- Ambure, P.; Gajewicz-Skretna, A.; Cordeiro, M.N.D.S.; Roy, K. New Workflow for QSAR Model Development from Small Data Sets: Small Dataset Curator and Small Dataset Modeler. Integration of Data Curation, Exhaustive Double Cross-Validation, and a Set of Optimal Model Selection Techniques. J. Chem. Inf. Model. 2019, 59, 4070–4076. [Google Scholar] [CrossRef]
- DTC. QSAR Modelling—Manual Small Dataset Curator and Small Dataset Modeler v. 1.0.0. 2020. Available online: https://sites.google.com/view/smalldatasetmodelling/manual-and-license (accessed on 13 February 2021).
- Kode, K.-C. Kode—Chemoinformatics. 2020. Available online: https://chm.kode-solutions.net/index.php (accessed on 4 May 2021).
- Toropova, A.P.; Toropov, A.A.; Benfenati, E.; Rallo, R.; Leszczynska, D.; Leszczynski, J. Development of Monte Carlo Approaches in Support of Environmental Research. In Advances in QSAR Modeling; Springer: Cham, Switzerland, 2017; Volume 24, pp. 453–469. [Google Scholar] [CrossRef]
- Toropova, A.P.; Toropov, A.A. Hybrid optimal descriptors as a tool to predict skin sensitization in accordance to OECD principles. Toxicol. Lett. 2017, 275, 57–66. [Google Scholar] [CrossRef] [PubMed]
- Lavado, G.J.; Baderna, D.; Carnesecchi, E.; Toropova, A.P.; Toropov, A.A.; Dorne, J.L.C.; Benfenati, E. QSAR models for soil ecotoxicity: Development and validation of models to predict reproductive toxicity of organic chemicals in the collembola Folsomia candida. J. Hazard. Mater. 2022, 423, 127236. [Google Scholar] [CrossRef] [PubMed]
- Manganelli, S.; Benfenati, E.; Manganaro, A.; Kulkarni, S.; Barton-Maclaren, T.S.; Honma, M. New Quantitative Structure–Activity Relationship Models Improve Predictability of Ames Mutagenicity for Aromatic Azo Compounds. Toxicol. Sci. 2016, 153, 316–326. [Google Scholar] [CrossRef] [PubMed]
- Toropov, A.A.; Toropova, A.P.; Benfenati, E.; Gini, G.; Puzyn, T.; Leszczynska, D.; Leszczynski, J. Novel application of the CORAL software to model cytotoxicity of metal oxide nanoparticles to bacteria Escherichia coli. Chemosphere 2012, 89, 1098–1102. [Google Scholar] [CrossRef]
- Toropov, A.; Toropova, A.; Martyanov, S.; Benfenati, E.; Gini, G.; Leszczynska, D.; Leszczynski, J. Comparison of SMILES and molecular graphs as the representation of the molecular structure for QSAR analysis for mutagenic potential of polyaromatic amines. Chemom. Intell. Lab. Syst. 2011, 109, 94–100. [Google Scholar] [CrossRef]
- Toropov, A.A.; Toropova, A.P. Modeling of acyclic carbonyl compounds normal boiling points by correlation weighting of nearest neighboring codes. J. Mol. Struct. THEOCHEM 2002, 581, 11–15. [Google Scholar] [CrossRef]
- Toropova, A.P.; Toropov, A.A.; Benfenati, E. The self-organizing vector of atom-pairs proportions: Use to develop models for melting points. Struct. Chem. 2021, 32, 967–971. [Google Scholar] [CrossRef]
- Toropov, A.A.; Toropova, A.P. Correlation intensity index: Building up models for mutagenicity of silver nanoparticles. Sci. Total Environ. 2020, 737, 139720. [Google Scholar] [CrossRef]
| Model | Set | n | R2 | CCC | IIC | Q2 | Q2F3 | RMSE | MAE | F |
|---|---|---|---|---|---|---|---|---|---|---|
| General | ||||||||||
| NOAEL | ||||||||||
| active training | 140 | 0.51 | 0.67 | 0.64 | 0.50 | 0.72 | 0.60 | 142 | ||
| passive training | 140 | 0.51 | 0.69 | 0.65 | 0.50 | 0.81 | 0.69 | 142 | ||
| calibration | 140 | 0.56 | 0.71 | 0.75 | 0.54 | 0.82 | 0.47 | 0.37 | 174 | |
| validation | 141 | 0.55 | 0.69 | 0.56 | 0.53 | 0.65 | 0.45 | 172 | ||
| LOAEL | ||||||||||
| active training | 142 | 0.55 | 0.71 | 0.70 | 0.54 | 0.66 | 0.50 | 173 | ||
| passive training | 142 | 0.55 | 0.68 | 0.51 | 0.53 | 0.72 | 0.57 | 168 | ||
| calibration | 137 | 0.51 | 0.63 | 0.71 | 0.49 | 0.48 | 0.71 | 0.56 | 138 | |
| validation | 137 | 0.53 | 0.63 | 0.59 | 0.32 | 0.72 | 0.53 | 149 | ||
| Kidney | ||||||||||
| NOAEL | ||||||||||
| active training | 95 | 0.50 | 0.67 | 0.67 | 0.48 | 0.56 | 0.48 | 94 | ||
| passive training | 95 | 0.52 | 0.54 | 0.57 | 0.51 | 0.73 | 0.64 | 103 | ||
| calibration | 45 | 0.62 | 0.78 | 0.78 | 0.58 | 0.86 | 0.32 | 0.27 | 70 | |
| validation | 45 | 0.59 | 0.75 | 0.70 | 0.84 | 0.33 | 0.27 | 62 | ||
| LOAEL | ||||||||||
| active training | 97 | 0.51 | 0.68 | 0.62 | 0.49 | 0.51 | 0.40 | 99 | ||
| passive training | 102 | 0.59 | 0.58 | 0.72 | 0.57 | 0.52 | 0.44 | 143 | ||
| calibration | 46 | 0.67 | 0.81 | 0.82 | 0.63 | 0.77 | 0.35 | 0.28 | 88 | |
| validation | 38 | 0.69 | 0.82 | 0.66 | 0.81 | 0.31 | 0.25 | 80 | ||
| Brain | ||||||||||
| NOAEL | ||||||||||
| active training | 23 | 0.55 | 0.71 | 0.57 | 0.46 | 0.67 | 0.59 | 26 | ||
| passive training | 22 | 0.61 | 0.42 | 0.64 | 0.52 | 0.75 | 0.68 | 31 | ||
| calibration | 23 | 0.58 | 0.74 | 0.76 | 0.51 | 0.88 | 0.31 | 0.26 | 28 | |
| validation | 22 | 0.53 | 0.67 | 0.68 | 0.81 | 0.35 | 0.28 | 23 | ||
| LOAEL | ||||||||||
| active training | 22 | 0.54 | 0.70 | 0.51 | 0.44 | 0.61 | 0.55 | 23 | ||
| passive training | 23 | 0.69 | 0.42 | 0.83 | 0.61 | 0.91 | 0.82 | 48 | ||
| calibration | 22 | 0.66 | 0.76 | 0.81 | 0.59 | 0.84 | 0.34 | 0.30 | 39 | |
| validation | 23 | 0.69 | 0.80 | 0.80 | 0.82 | 0.33 | 0.26 | 46 | ||
| Liver | ||||||||||
| NOAEL | ||||||||||
| active training | 97 | 0.76 | 0.86 | 0.72 | 0.75 | 0.38 | 0.29 | 297 | ||
| passive training | 94 | 0.73 | 0.83 | 0.78 | 0.72 | 0.44 | 0.34 | 247 | ||
| calibration | 30 | 0.78 | 0.83 | 0.89 | 0.75 | 0.82 | 0.35 | 0.28 | 103 | |
| validation | 31 | 0.55 | 0.73 | 0.54 | 0.55 | 0.54 | 0.38 | 35 | ||
| LOAEL | ||||||||||
| active training | 96 | 0.78 | 0.87 | 0.78 | 0.77 | 0.32 | 0.23 | 326 | ||
| passive training | 95 | 0.78 | 0.81 | 0.65 | 0.77 | 0.40 | 0.32 | 323 | ||
| calibration | 30 | 0.76 | 0.84 | 0.87 | 0.72 | 0.71 | 0.38 | 0.28 | 89 | |
| validation | 31 | 0.61 | 0.71 | 0.61 | 0.55 | 0.48 | 0.40 | 46 |
| Model | Set | n | R2 | Q2 | CCC | Q2F3 | RMSE | MAE | F | Reference |
|---|---|---|---|---|---|---|---|---|---|---|
| NOAEL | This work | |||||||||
| active training | 140 | 0.51 | 0.50 | 0.67 | 0.72 | 0.60 | 142 | |||
| passive training | 140 | 0.51 | 0.50 | 0.69 | 0.81 | 0.69 | 142 | |||
| calibration | 140 | 0.56 | 0.54 | 0.71 | 0.82 | 0.47 | 0.37 | 174 | ||
| validation | 141 | 0.55 | 0.69 | 0.53 | 0.65 | 0.45 | 172 | |||
| validation in AD (77%) | 109 | 0.61 | 0.74 | 0.69 | 0.52 | 0.38 | 171 | |||
| LOAEL | This work | |||||||||
| active training | 142 | 0.55 | 0.54 | 0.71 | 0.66 | 0.50 | 173 | |||
| passive training | 142 | 0.55 | 0.53 | 0.68 | 0.72 | 0.57 | 168 | |||
| calibration | 137 | 0.51 | 0.49 | 0.63 | 0.48 | 0.71 | 0.56 | 138 | ||
| validation | 137 | 0.53 | 0.63 | 0.32 | 0.72 | 0.53 | 149 | |||
| validation in AD (74%) | 102 | 0.51 | 0.64 | 0.55 | 0.58 | 0.45 | 105 | |||
| NOAEL | [6] | |||||||||
| training | 124 | 0.57 | 0.56 | 0.68 | 0.52 | 164 | ||||
| invisible training | 126 | 0.50 | 0.49 | 0.77 | 0.59 | 125 | ||||
| calibration | 38 | 0.61 | 0.55 | 0.67 | 0.49 | 56 | ||||
| validation | 38 | 0.65 | 0.68 | 0.52 | 68 | |||||
| validation in AD (87%) | 33 | 0.69 | 0.58 | 0.43 | ||||||
| LOAEL | [6] | |||||||||
| training | 124 | 0.55 | 0.53 | 0.66 | 0.51 | 147 | ||||
| invisible training | 126 | 0.45 | 0.43 | 0.80 | 0.63 | 102 | ||||
| calibration | 38 | 0.61 | 0.51 | 0.69 | 0.51 | 49 | ||||
| validation | 38 | 0.59 | 0.72 | 0.54 | 53 | |||||
| validation in AD (87%) | 33 | 0.62 | 0.59 | 0.44 | ||||||
| NOAEL | [10] | |||||||||
| training | 97 | 0.53 | 0.51 | 0.61 | 0.47 | 107 | ||||
| Test | 16 | 0.73 | 0.67 | 0.49 | 0.37 | 38 | ||||
| validation | 27 | 0.60 | 0.43 | 0.36 | 38 | |||||
| validation in AD (96%) | 26 | 0.61 | 0.42 |
| ID | Model | Initial Number of Compounds | Final Number of Compounds | Final Range Value mg/kg bw/Day (log) |
|---|---|---|---|---|
| M1 | General NOAEL | 573 | 561 | −1 to 3.591 |
| M2 | General LOAEL | 573 | 558 | −0.415 to 3.948 |
| M3 | Kidney NOAEL | 289 | 280 | 0.097 to 4.301 |
| M4 | Kidney LOAEL | 289 | 283 | 0.097 to 3.585 |
| M5 | Brain NOAEL | 91 | 90 | 0.248 to 4.301 |
| M6 | Brain LOAEL | 91 | 90 | 0.248 to 4.301 |
| M7 | Liver NOAEL | 353 | 252 | −0.432 to 3.499 |
| M8 | Liver LOAEL | 353 | 252 | −0.415 to 3.789 |
| Attribute | Description |
|---|---|
| S, SS, SSS | Single SMILES atom, a combination of two SMILES atoms and a combination of three SMILES atoms [36,37]. |
| EC1, EC2, EC3 | Morgan connectivity of first-, second- and third-order [38]. |
| NNC | Nearest neighbors codes [33,39]. |
| APP | Atom pair proportions weighted presence of F, Cl, Br, N, O, S, P, #, = [40]. |
| ID | α | β | γ | δ | x1 | x2 | x3 | y1 | y2 | y3 | y4 | IICw | CIIw | T* | N* |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| M1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0.25 | 0.30 | 1 | 30 |
| M2 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0.20 | 0 | 1 | 30 |
| M3 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0.25 | 0 | 1 | 10 |
| M4 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0.20 | 0 | 1 | 10 |
| M5 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0.50 | 0 | 1 | 33 |
| M6 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0.20 | 0 | 1 | 4 |
| M7 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0.15 | 0 | 2 | 15 |
| M8 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0.25 | 0 | 2 | 14 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Selvestrel, G.; Lavado, G.J.; Toropova, A.P.; Toropov, A.A.; Gadaleta, D.; Marzo, M.; Baderna, D.; Benfenati, E. Monte Carlo Models for Sub-Chronic Repeated-Dose Toxicity: Systemic and Organ-Specific Toxicity. Int. J. Mol. Sci. 2022, 23, 6615. https://doi.org/10.3390/ijms23126615
Selvestrel G, Lavado GJ, Toropova AP, Toropov AA, Gadaleta D, Marzo M, Baderna D, Benfenati E. Monte Carlo Models for Sub-Chronic Repeated-Dose Toxicity: Systemic and Organ-Specific Toxicity. International Journal of Molecular Sciences. 2022; 23(12):6615. https://doi.org/10.3390/ijms23126615
Chicago/Turabian StyleSelvestrel, Gianluca, Giovanna J. Lavado, Alla P. Toropova, Andrey A. Toropov, Domenico Gadaleta, Marco Marzo, Diego Baderna, and Emilio Benfenati. 2022. "Monte Carlo Models for Sub-Chronic Repeated-Dose Toxicity: Systemic and Organ-Specific Toxicity" International Journal of Molecular Sciences 23, no. 12: 6615. https://doi.org/10.3390/ijms23126615
APA StyleSelvestrel, G., Lavado, G. J., Toropova, A. P., Toropov, A. A., Gadaleta, D., Marzo, M., Baderna, D., & Benfenati, E. (2022). Monte Carlo Models for Sub-Chronic Repeated-Dose Toxicity: Systemic and Organ-Specific Toxicity. International Journal of Molecular Sciences, 23(12), 6615. https://doi.org/10.3390/ijms23126615










