Machine-Learning-Based Genome-Wide Association Studies for Uncovering QTL Underlying Soybean Yield and Its Components
Abstract
:1. Introduction
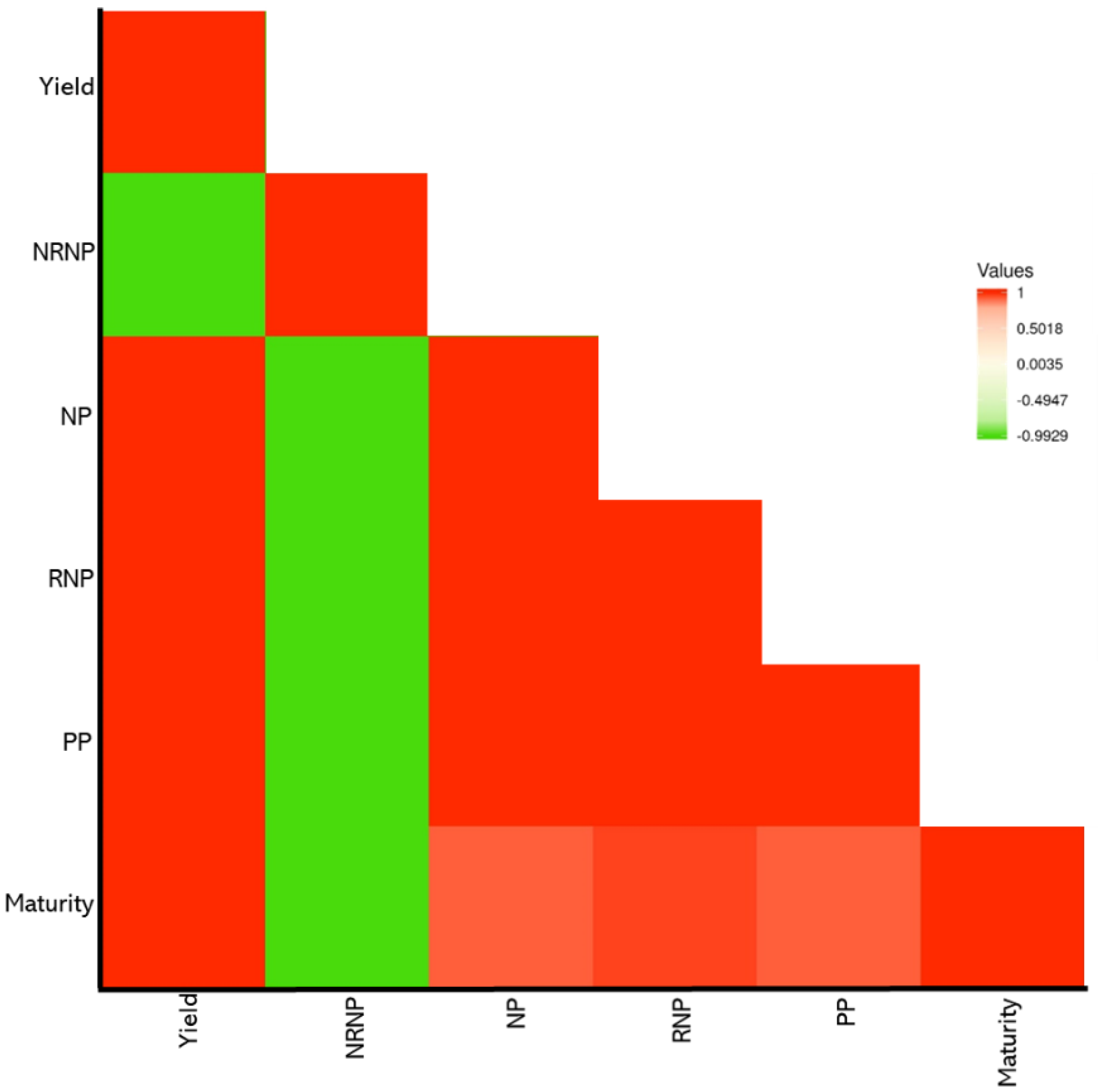
2. Results
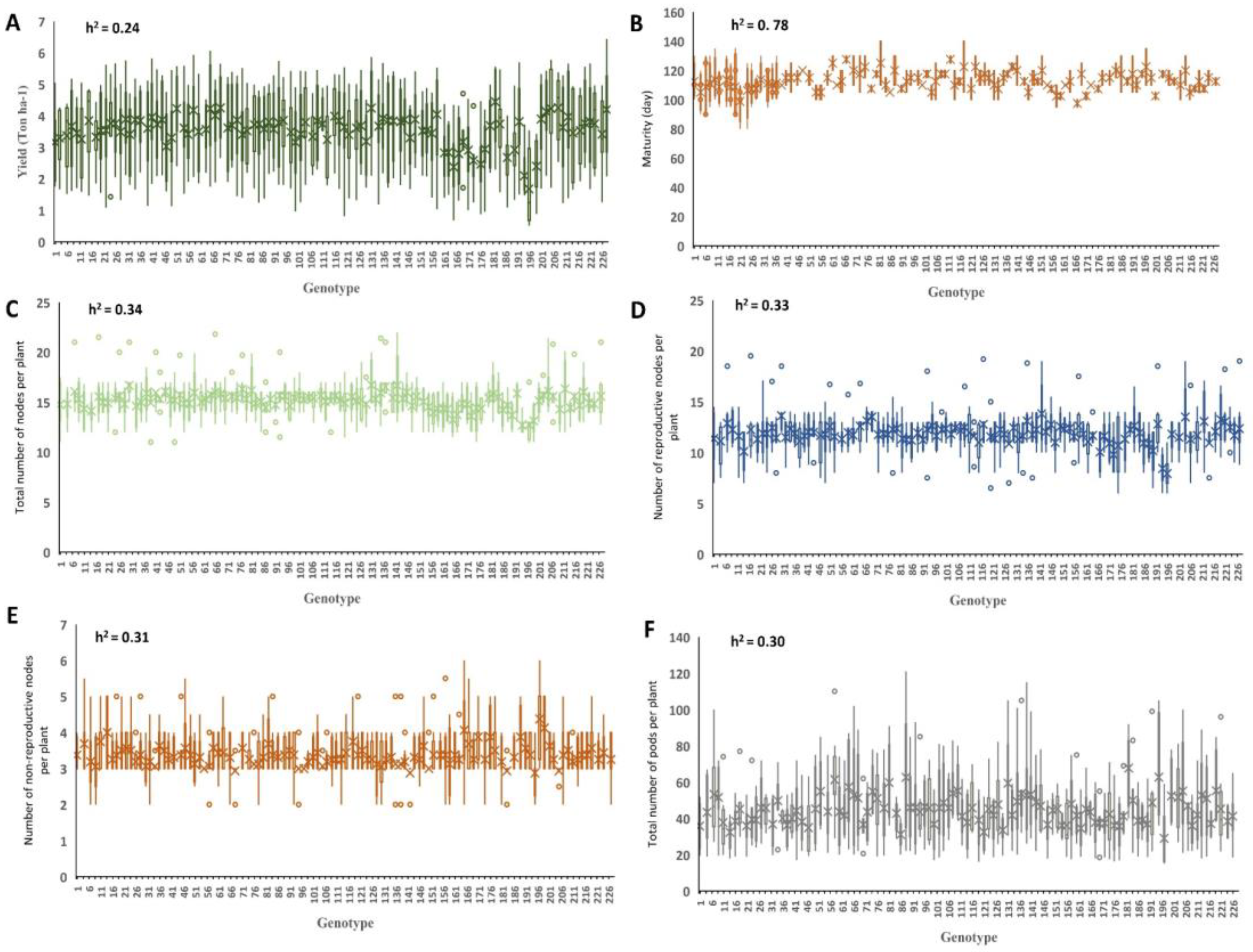
2.1. Phenotyping Evaluations
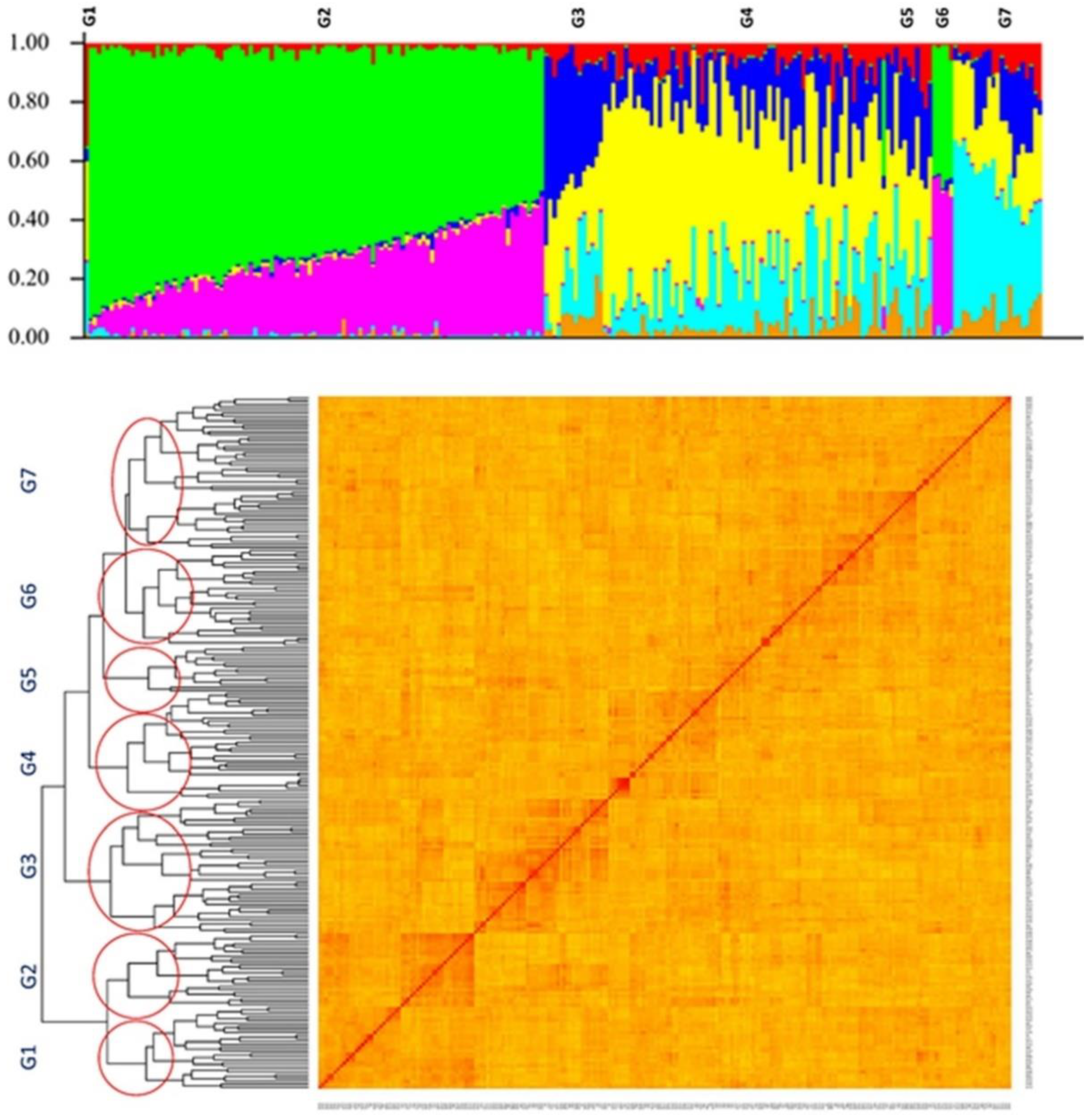
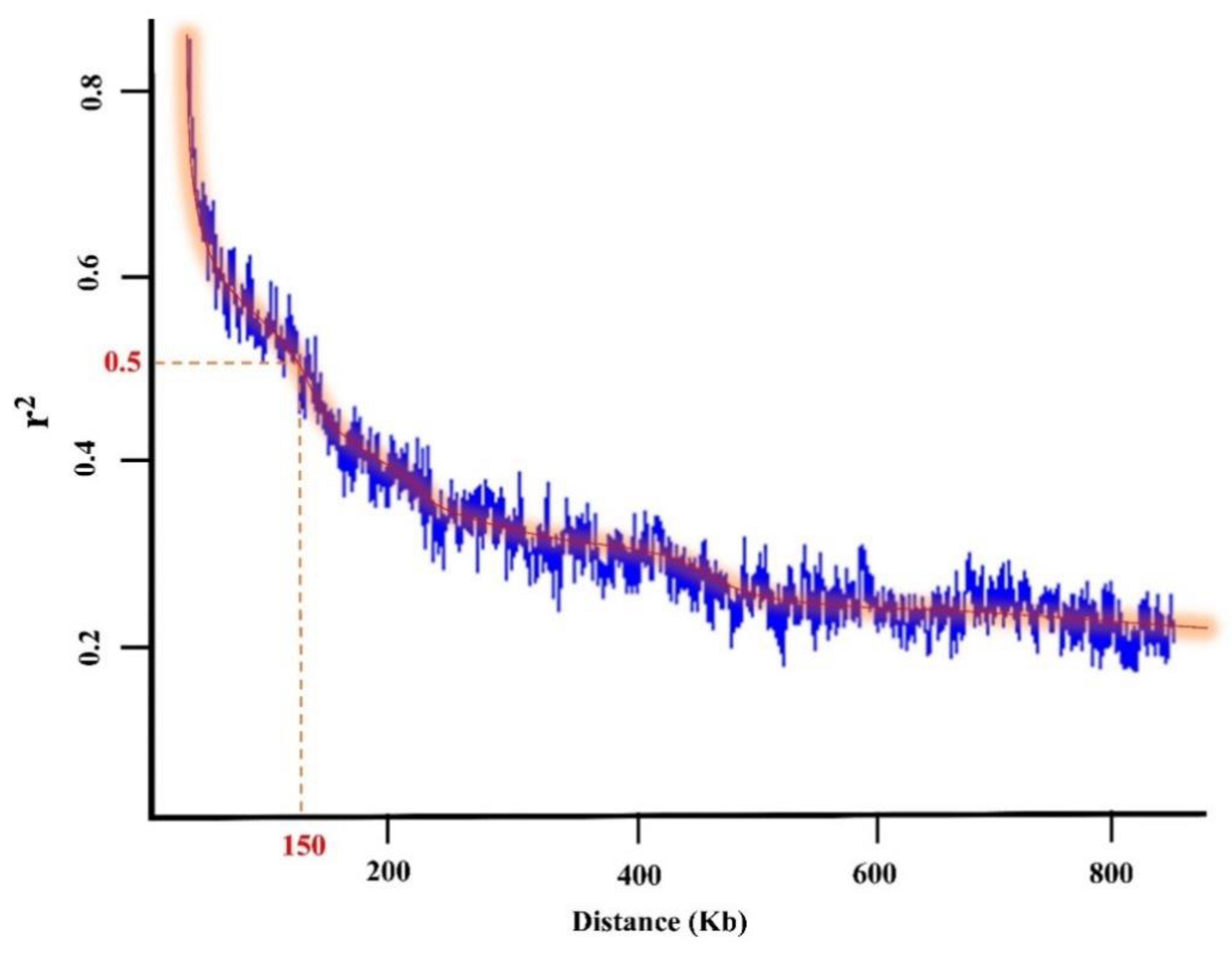
2.2. Population Structure and Kinship
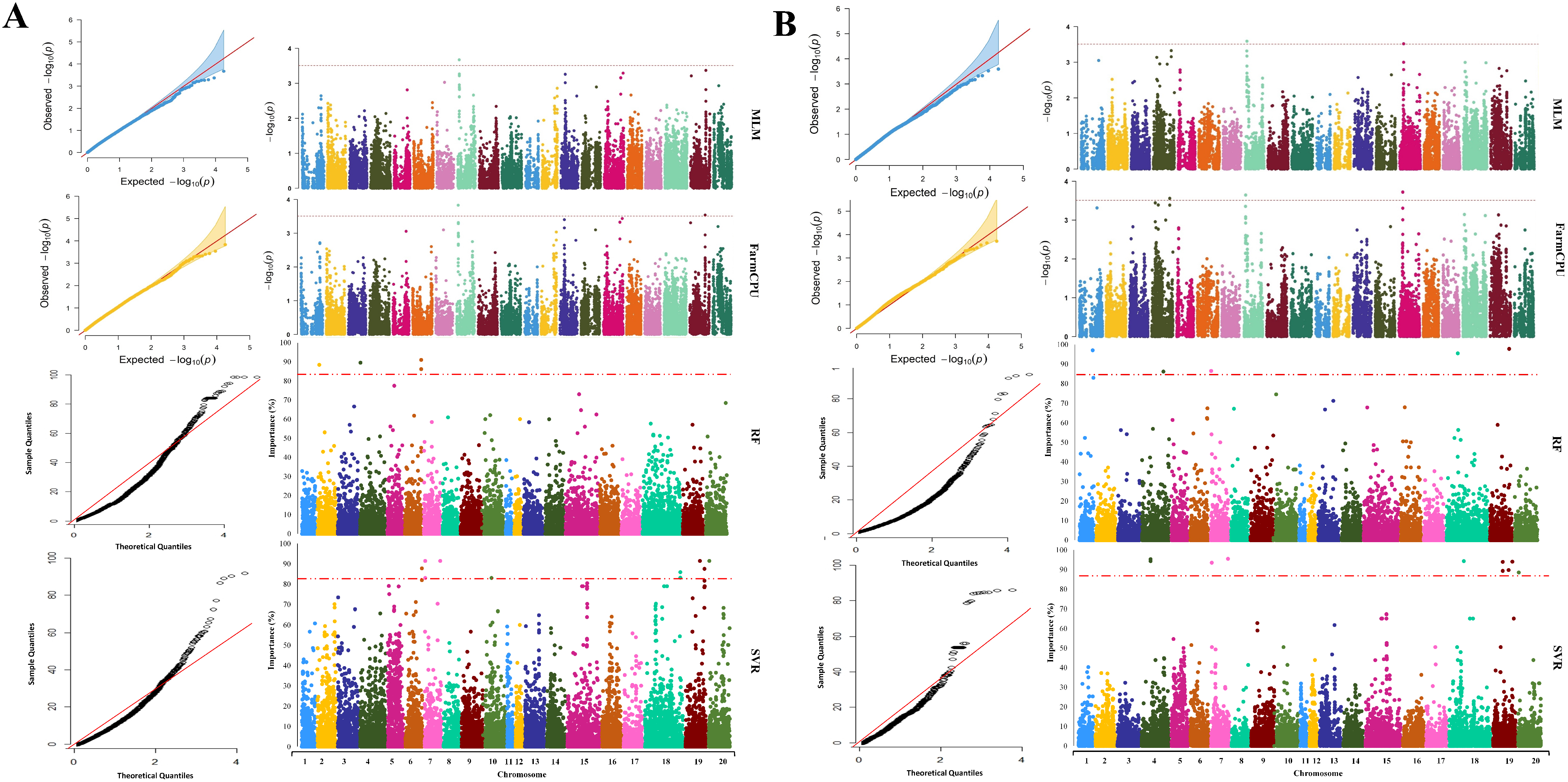
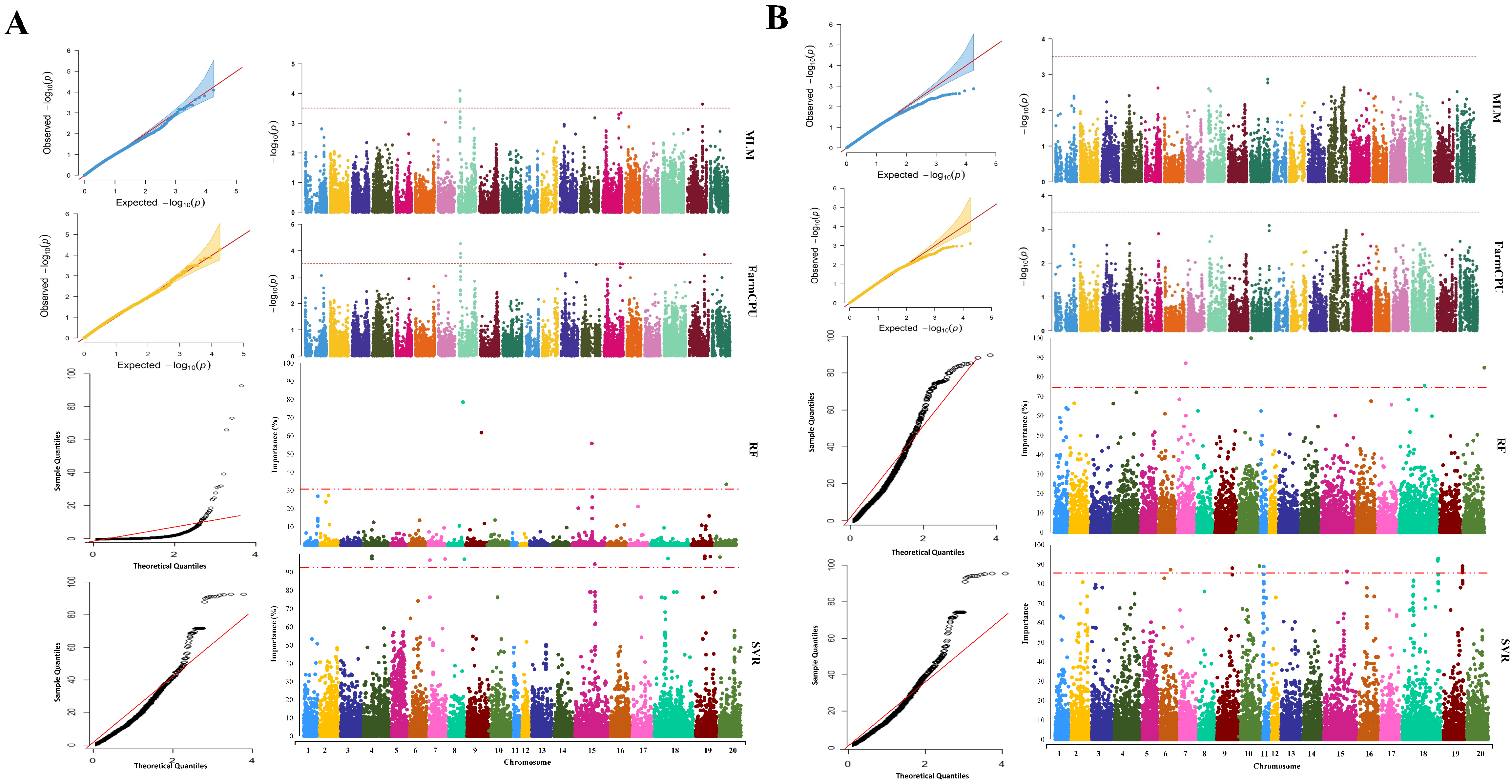
2.3. GWAS Analysis
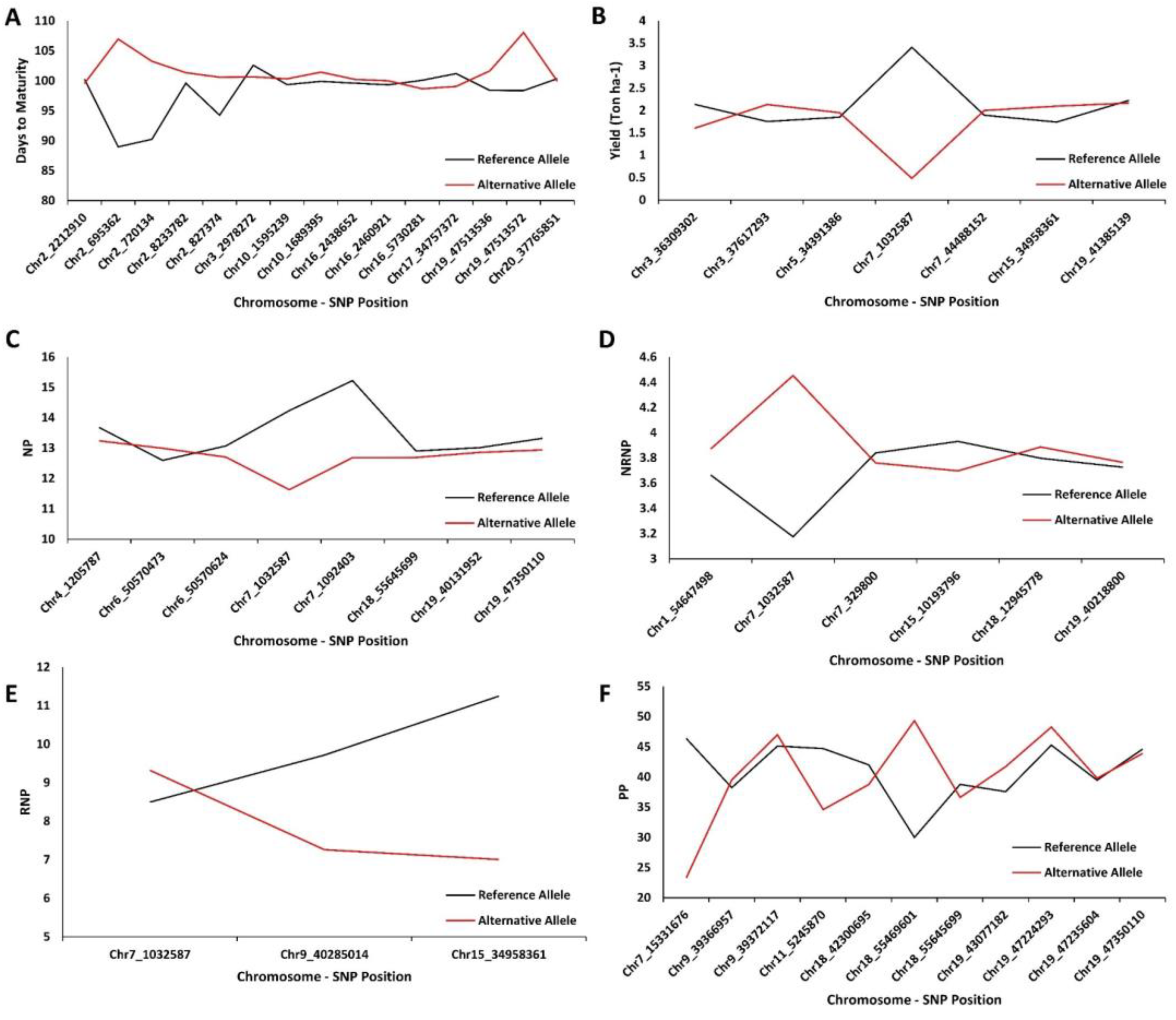
2.4. Extracting Candidate Genes Undelaying Detected QTL
3. Discussion
4. Materials and Methods
4.1. Population and Experimental Design
4.2. Phenotyping
4.3. Genotyping
4.4. Statistical Analyses
4.5. Analysis of Population Structure
4.6. Association Studies
4.7. Mixed Linear Model (MLM)
4.8. Fixed and Random Model Circulating Probability Unification (FarmCPU)
4.9. Random Forest (RF)
4.10. Support-Vector Regression (SVR)
4.11. Implementation of ML Algorithms in GWAS
4.12. Variable Importance Measurement
4.13. Extracting Candidate Genes Undelaying Detected QTL
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rębilas, K.; Klimek-Kopyra, A.; Bacior, M.; Zając, T. A model for the yield losses estimation in an early soybean (Glycine max (L.) Merr.) cultivar depending on the cutting height at harvest. Field Crop. Res. 2020, 254, 107846. [Google Scholar] [CrossRef]
- Xavier, A.; Rainey, K.M. Quantitative genomic dissection of soybean yield components. G3 Genes Genomes Genet. 2020, 10, 665–675. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Suhre, J.J.; Weidenbenner, N.H.; Rowntree, S.C.; Wilson, E.W.; Naeve, S.L.; Conley, S.P.; Casteel, S.N.; Diers, B.W.; Esker, P.D.; Specht, J.E. Soybean yield partitioning changes revealed by genetic gain and seeding rate interactions. Agron. J. 2014, 106, 1631–1642. [Google Scholar] [CrossRef] [Green Version]
- Mangena, P. Phytocystatins and their Potential Application in the Development of Drought Tolerance Plants in Soybeans (Glycine max L.). Protein Pept. Lett. 2020, 27, 135–144. [Google Scholar] [CrossRef] [PubMed]
- Richards, R. Breeding and Selecting for Drought Resistant Wheat. Drought Resistance in Crops with Emphasis on Rice. 1982. Available online: https://agris.fao.org/agris-search/search.do?recordID=XB8110524 (accessed on 1 March 2022).
- Reynolds, M. Application of Physiology in Wheat Breeding; Cimmyt: State of Mexico, Mexico, 2001. [Google Scholar]
- Pedersen, P.; Lauer, J.G. Response of soybean yield components to management system and planting date. Agron. J. 2004, 96, 1372–1381. [Google Scholar] [CrossRef] [Green Version]
- Yoosefzadeh-Najafabadi, M.; Tulpan, D.; Eskandari, M. Application of machine learning and genetic optimization algorithms for modeling and optimizing soybean yield using its component traits. PLoS ONE 2021, 16, e0250665. [Google Scholar]
- Robinson, A.P.; Conley, S.P.; Volenec, J.J.; Santini, J.B. Analysis of high yielding, early-planted soybean in Indiana. Agron. J. 2009, 101, 131–139. [Google Scholar] [CrossRef]
- Ma, B.; Dwyer, L.M.; Costa, C.; Cober, E.R.; Morrison, M.J. Early prediction of soybean yield from canopy reflectance measurements. Agron. J. 2001, 93, 1227–1234. [Google Scholar] [CrossRef] [Green Version]
- Xavier, A.; Jarquin, D.; Howard, R.; Ramasubramanian, V.; Specht, J.E.; Graef, G.L.; Beavis, W.D.; Diers, B.W.; Song, Q.; Cregan, P.B. Genome-wide analysis of grain yield stability and environmental interactions in a multiparental soybean population. G3 Genes Genomes Genet. 2018, 8, 519–529. [Google Scholar] [CrossRef] [Green Version]
- Kaler, A.S.; Gillman, J.D.; Beissinger, T.; Purcell, L.C. Comparing different statistical models and multiple testing corrections for association mapping in soybean and maize. Front. Plant Sci. 2020, 10, 1794. [Google Scholar] [CrossRef]
- Yoosefzadeh Najafabadi, M. Using Advanced Proximal Sensing and Genotyping Tools Combined with Bigdata Analysis Methods to Improve Soybean Yield. Ph.D. Thesis, University of Guelph, Guelph, ON, Canada, 2021. [Google Scholar]
- Yoosefzadeh-Najafabadi, M.; Earl, H.J.; Tulpan, D.; Sulik, J.; Eskandari, M. Application of Machine Learning Algorithms in Plant Breeding: Predicting Yield From Hyperspectral Reflectance in Soybean. Front. Plant Sci. 2021, 11, 2555. [Google Scholar] [CrossRef] [PubMed]
- Hesami, M.; Naderi, R.; Tohidfar, M.; Yoosefzadeh-Najafabadi, M. Development of support vector machine-based model and comparative analysis with artificial neural network for modeling the plant tissue culture procedures: Effect of plant growth regulators on somatic embryogenesis of chrysanthemum, as a case study. Plant Methods 2020, 16, 112. [Google Scholar] [CrossRef] [PubMed]
- Yoosefzadeh-Najafabadi, M.; Torabi, S.; Tulpan, D.; Rajcan, I.; Eskandari, M. Genome-Wide Association Studies of Soybean Yield-Related Hyperspectral Reflectance Bands Using Machine Learning-Mediated Data Integration Methods. Front. Plant Sci. 2021, 12, 777028. [Google Scholar] [CrossRef] [PubMed]
- Hesami, M.; Yoosefzadeh Najafabadi, M.; Adamek, K.; Torkamaneh, D.; Jones, A.M.P. Synergizing off-target predictions for in silico insights of CENH3 knockout in cannabis through CRISPR/CAS. Molecules 2021, 26, 2053. [Google Scholar] [CrossRef] [PubMed]
- Jafari, M.; Shahsavar, A. The application of artificial neural networks in modeling and predicting the effects of melatonin on morphological responses of citrus to drought stress. PLoS ONE 2020, 15, e0240427. [Google Scholar] [CrossRef] [PubMed]
- Tulpan, D. 311 A brief overview, comparison and practical applications of machine learning models. J. Anim. Sci. 2020, 98, 44–45. [Google Scholar] [CrossRef]
- Chen, J.H.; Verghese, A. Planning for the Known Unknown: Machine Learning for Human Healthcare Systems. Am. J. Bioeth. 2020, 20, 1–3. [Google Scholar] [CrossRef]
- Kim, G.B.; Kim, W.J.; Kim, H.U.; Lee, S.Y. Machine learning applications in systems metabolic engineering. Curr. Opin. Biotechnol. 2020, 64, 1–9. [Google Scholar] [CrossRef]
- Jordan, M.I.; Mitchell, T.M. Machine learning: Trends, perspectives, and prospects. Science 2015, 349, 255–260. [Google Scholar] [CrossRef]
- Szymczak, S.; Biernacka, J.M.; Cordell, H.J.; González-Recio, O.; König, I.R.; Zhang, H.; Sun, Y.V. Machine learning in genome-wide association studies. Genet. Epidemiol. 2009, 33, S51–S57. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Meinshausen, N. Quantile regression forests. J. Mach. Learn. Res. 2006, 7, 983–999. [Google Scholar]
- Ogutu, J.O.; Piepho, H.-P.; Schulz-Streeck, T. A comparison of random forests, boosting and support vector machines for genomic selection. BMC Proc. 2011, 5, S11. [Google Scholar] [CrossRef] [Green Version]
- Jamil, I.N.; Remali, J.; Azizan, K.A.; Muhammad, N.A.N.; Arita, M.; Goh, H.-H.; Aizat, W.M. Systematic Multi-Omics Integration (MOI) Approach in Plant Systems Biology. Front. Plant Sci. 2020, 11, 944. [Google Scholar] [CrossRef] [PubMed]
- Sun, S.; Wang, C.; Ding, H.; Zou, Q. Machine learning and its applications in plant molecular studies. Brief. Funct. Genom. 2020, 19, 40–48. [Google Scholar] [CrossRef]
- Su, Q.; Lu, W.; Du, D.; Chen, F.; Niu, B.; Chou, K.-C. Prediction of the aquatic toxicity of aromatic compounds to tetrahymena pyriformis through support vector regression. Oncotarget 2017, 8, 49359. [Google Scholar] [CrossRef] [Green Version]
- Auria, L.; Moro, R.A. Support Vector Machines (SVM) as a Technique for Solvency Analysis. SSRN Electron. J. 2008, 811. [Google Scholar]
- Hesami, M.; Jones, A.M.P. Application of artificial intelligence models and optimization algorithms in plant cell and tissue culture. Appl. Microbiol. Biotechnol. 2020, 104, 9449–9485. [Google Scholar] [CrossRef]
- Belayneh, A.; Adamowski, J.; Khalil, B.; Ozga-Zielinski, B. Long-term SPI drought forecasting in the Awash River Basin in Ethiopia using wavelet neural network and wavelet support vector regression models. J. Hydrol. 2014, 508, 418–429. [Google Scholar] [CrossRef]
- Duan, K.-B.; Rajapakse, J.C.; Wang, H.; Azuaje, F. Multiple SVM-RFE for gene selection in cancer classification with expression data. IEEE Trans. Nanobiosci. 2005, 4, 228–234. [Google Scholar] [CrossRef]
- Denton, S.M.; Salleb-Aouissi, A. A Weighted Solution to SVM Actionability and Interpretability. arXiv 2020, arXiv:2012.03372. [Google Scholar]
- Pepe, M.; Hesami, M.; Jones, A.M.P. Machine Learning-Mediated Development and Optimization of Disinfection Protocol and Scarification Method for Improved In Vitro Germination of Cannabis Seeds. Plants 2021, 10, 2397. [Google Scholar] [CrossRef] [PubMed]
- Yoosefzadeh-Najafabadi, M.; Tulpan, D.; Eskandari, M. Using Hybrid Artificial Intelligence and Evolutionary Optimization Algorithms for Estimating Soybean Yield and Fresh Biomass Using Hyperspectral Vegetation Indices. Remote Sens. 2021, 13, 2555. [Google Scholar] [CrossRef]
- Awad, M.; Khanna, R. Support vector regression. In Efficient Learning Machines; Springe: New York, NY, USA, 2015; pp. 67–80. [Google Scholar]
- Moellers, T.C.; Singh, A.; Zhang, J.; Brungardt, J.; Kabbage, M.; Mueller, D.S.; Grau, C.R.; Ranjan, A.; Smith, D.L.; Chowda-Reddy, R. Main and epistatic loci studies in soybean for Sclerotinia sclerotiorum resistance reveal multiple modes of resistance in multi-environments. Sci. Rep. 2017, 7, 3554. [Google Scholar] [CrossRef] [Green Version]
- Sonah, H.; O’Donoughue, L.; Cober, E.; Rajcan, I.; Belzile, F. Identification of loci governing eight agronomic traits using a GBS-GWAS approach and validation by QTL mapping in soya bean. Plant Biotechnol. J. 2015, 13, 211–221. [Google Scholar] [CrossRef] [PubMed]
- Kaler, A.S.; Dhanapal, A.P.; Ray, J.D.; King, C.A.; Fritschi, F.B.; Purcell, L.C. Genome-wide association mapping of carbon isotope and oxygen isotope ratios in diverse soybean genotypes. Crop Sci. 2017, 57, 3085–3100. [Google Scholar] [CrossRef]
- Fang, C.; Ma, Y.; Wu, S.; Liu, Z.; Wang, Z.; Yang, R.; Hu, G.; Zhou, Z.; Yu, H.; Zhang, M. Genome-wide association studies dissect the genetic networks underlying agronomical traits in soybean. Genome Biol. 2017, 18, 1–14. [Google Scholar] [CrossRef]
- Kan, G.; Zhang, W.; Yang, W.; Ma, D.; Zhang, D.; Hao, D.; Hu, Z.; Yu, D. Association mapping of soybean seed germination under salt stress. Mol. Genet. Genom. 2015, 290, 2147–2162. [Google Scholar] [CrossRef]
- Zhang, J.; Song, Q.; Cregan, P.B.; Nelson, R.L.; Wang, X.; Wu, J.; Jiang, G.-L. Genome-wide association study for flowering time, maturity dates and plant height in early maturing soybean (Glycine max) germplasm. BMC Genom. 2015, 16, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Mao, T.; Li, J.; Wen, Z.; Wu, T.; Wu, C.; Sun, S.; Jiang, B.; Hou, W.; Li, W.; Song, Q. Association mapping of loci controlling genetic and environmental interaction of soybean flowering time under various photo-thermal conditions. BMC Genom. 2017, 18, 415. [Google Scholar] [CrossRef]
- Bao, Y.; Kurle, J.E.; Anderson, G.; Young, N.D. Association mapping and genomic prediction for resistance to sudden death syndrome in early maturing soybean germplasm. Mol. Breed. 2015, 35, 18. [Google Scholar] [CrossRef] [Green Version]
- Leamy, L.J.; Zhang, H.; Li, C.; Chen, C.Y.; Song, B.-H. A genome-wide association study of seed composition traits in wild soybean (Glycine soja). BMC Genom. 2017, 18, 1–15. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wen, Z.; Tan, R.; Yuan, J.; Bales, C.; Du, W.; Zhang, S.; Chilvers, M.I.; Schmidt, C.; Song, Q.; Cregan, P.B. Genome-wide association mapping of quantitative resistance to sudden death syndrome in soybean. BMC Genom. 2014, 15, 1–11. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ray, J.D.; Dhanapal, A.P.; Singh, S.K.; Hoyos-Villegas, V.; Smith, J.R.; Purcell, L.C.; King, C.A.; Boykin, D.; Cregan, P.B.; Song, Q. Genome-wide association study of ureide concentration in diverse maturity group IV soybean [Glycine max (L.) Merr.] accessions. G3 Genes Genomes Genet. 2015, 5, 2391–2403. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dhanapal, A.P.; Ray, J.D.; Smith, J.R.; Purcell, L.C.; Fritschi, F.B. Identification of Novel Genomic Loci Associated with Soybean Shoot Tissue Macro and Micronutrient Concentrations. Plant Genome 2018, 11, 170066. [Google Scholar] [CrossRef] [PubMed]
- Hu, Z.; Zhang, D.; Zhang, G.; Kan, G.; Hong, D.; Yu, D. Association mapping of yield-related traits and SSR markers in wild soybean (Glycine soja Sieb. and Zucc.). Breed. Sci. 2014, 63, 441–449. [Google Scholar] [CrossRef] [Green Version]
- Contreras-Soto, R.I.; Mora, F.; de Oliveira, M.A.R.; Higashi, W.; Scapim, C.A.; Schuster, I. A genome-wide association study for agronomic traits in soybean using SNP markers and SNP-based haplotype analysis. PLoS ONE 2017, 12, e0171105. [Google Scholar]
- Li, Y.h.; Shi, X.h.; Li, H.h.; Reif, J.C.; Wang, J.j.; Liu, Z.x.; He, S.; Yu, B.s.; Qiu, L.j. Dissecting the genetic basis of resistance to soybean cyst nematode combining linkage and association mapping. Plant Genome 2016, 9. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Song, Q.; Cregan, P.B.; Jiang, G.-L. Genome-wide association study, genomic prediction and marker-assisted selection for seed weight in soybean (Glycine max). Theor. Appl. Genet. 2016, 129, 117–130. [Google Scholar] [CrossRef] [Green Version]
- Chang, H.-X.; Hartman, G.L. Characterization of insect resistance loci in the USDA soybean germplasm collection using genome-wide association studies. Front. Plant Sci. 2017, 8, 670. [Google Scholar] [CrossRef] [Green Version]
- Copley, T.R.; Duceppe, M.-O.; O’Donoughue, L.S. Identification of novel loci associated with maturity and yield traits in early maturity soybean plant introduction lines. BMC Genom. 2018, 19, 167. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.-h.; Reif, J.C.; Ma, Y.-s.; Hong, H.-l.; Liu, Z.-x.; Chang, R.-z.; Qiu, L.-j. Targeted association mapping demonstrating the complex molecular genetics of fatty acid formation in soybean. BMC Genom. 2015, 16, 841. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xavier, A.; Muir, W.M.; Rainey, K.M. Impact of imputation methods on the amount of genetic variation captured by a single-nucleotide polymorphism panel in soybeans. BMC Bioinform. 2016, 17, 55. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cook, D.E.; Bayless, A.M.; Wang, K.; Guo, X.; Song, Q.; Jiang, J.; Bent, A.F. Distinct copy number, coding sequence, and locus methylation patterns underlie Rhg1-mediated soybean resistance to soybean cyst nematode. Plant Physiol. 2014, 165, 630–647. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, J.; Wang, X.; Lu, Y.; Bhusal, S.J.; Song, Q.; Cregan, P.B.; Yen, Y.; Brown, M.; Jiang, G.-L. Genome-wide Scan for Seed Composition Provides Insights into Soybean Quality Improvement and the Impacts of Domestication and Breeding. Mol. Plant 2018, 11, 460–472. [Google Scholar] [CrossRef] [Green Version]
- Qin, J.; Song, Q.; Shi, A.; Li, S.; Zhang, M.; Zhang, B. Genome-wide association mapping of resistance to Phytophthora sojae in a soybean [Glycine max (L.) Merr.] germplasm panel from maturity groups IV and V. PLoS ONE 2017, 12, e0184613. [Google Scholar] [CrossRef]
- Vuong, T.; Sonah, H.; Meinhardt, C.; Deshmukh, R.; Kadam, S.; Nelson, R.; Shannon, J.; Nguyen, H. Genetic architecture of cyst nematode resistance revealed by genome-wide association study in soybean. BMC Genom. 2015, 16, 593. [Google Scholar] [CrossRef] [Green Version]
- Che, Z.; Liu, H.; Yi, F.; Cheng, H.; Yang, Y.; Wang, L.; Du, J.; Zhang, P.; Wang, J.; Yu, D. Genome-Wide Association Study Reveals Novel Loci for SC7 Resistance in a Soybean Mutant Panel. Front. Plant Sci. 2017, 8, 1771. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Tian, R.; Kamala, S.; Du, H.; Li, W.; Kong, Y.; Zhang, C. Identification and verification of pleiotropic QTL controlling multiple amino acid contents in soybean seed. Euphytica 2018, 214, 1–14. [Google Scholar] [CrossRef]
- Ray, J.D.; Dhanapal, A.P.; Singh, S.K.; Hoyos-Villegas, V.; Smith, J.R.; Purcell, L.C.; King, C.A.; Boykin, D.; Cregan, P.B.; Song, Q. Genome-wide association study (GWAS) of carbon isotope ratio (δ 13 C) in diverse soybean [Glycine max (L.) Merr.] genotypes. Theor. Appl. Genet. 2015, 128, 73–91. [Google Scholar]
- Priolli, R.H.G.; Campos, J.; Stabellini, N.; Pinheiro, J.; Vello, N. Association mapping of oil content and fatty acid components in soybean. Euphytica 2015, 203, 83–96. [Google Scholar] [CrossRef]
- Dhanapal, A.P.; Ray, J.D.; Singh, S.K.; Hoyos-Villegas, V.; Smith, J.R.; Purcell, L.C.; King, C.A.; Fritschi, F.B. Association mapping of total carotenoids in diverse soybean genotypes based on leaf extracts and high-throughput canopy spectral reflectance measurements. PLoS ONE 2015, 10, e0137213. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cooper, M.; van Eeuwijk, F.A.; Hammer, G.L.; Podlich, D.W.; Messina, C. Modeling QTL for complex traits: Detection and context for plant breeding. Curr. Opin. Plant Biol. 2009, 12, 231–240. [Google Scholar] [CrossRef] [PubMed]
- Hu, D.; Zhang, H.; Du, Q.; Hu, Z.; Yang, Z.; Li, X.; Wang, J.; Huang, F.; Yu, D.; Wang, H. Genetic dissection of yield-related traits via genome-wide association analysis across multiple environments in wild soybean (Glycine soja Sieb. and Zucc.). Planta 2020, 251, 39. [Google Scholar] [CrossRef] [PubMed]
- Kahlon, C.S.; Board, J.E. Growth dynamic factors explaining yield improvement in new versus old soybean cultivars. J. Crop Improv. 2012, 26, 282–299. [Google Scholar] [CrossRef]
- Herbert, S.; Litchfield, G. Partitioning Soybean Seed Yield Components 1. Crop Sci. 1982, 22, 1074–1079. [Google Scholar] [CrossRef]
- Sulistyo, A.; Sari, K. Correlation, path analysis and heritability estimation for agronomic traits contribute to yield on soybean. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Banda Aceh, Indonesia, 26–27 September 2018; p. 012034. [Google Scholar]
- Price, T.; Schluter, D. On the low heritability of life-history traits. Evolution 1991, 45, 853–861. [Google Scholar] [CrossRef]
- Cassell, B.G. Using Heritability for Genetic Improvement; Virginia Cooperative Extension: Blacksburg, VA, USA, 2009. [Google Scholar]
- Kaneko, H. Support vector regression that takes into consideration the importance of explanatory variables. J. Chemom. 2020, 35, e3327. [Google Scholar] [CrossRef]
- Lee, S.; Liang, X.; Woods, M.; Reiner, A.S.; Concannon, P.; Bernstein, L.; Lynch, C.F.; Boice, J.D.; Deasy, J.O.; Bernstein, J.L. Machine learning on genome-wide association studies to predict the risk of radiation-associated contralateral breast cancer in the WECARE Study. PLoS ONE 2020, 15, e0226157. [Google Scholar] [CrossRef]
- Williamson, B.D.; Gilbert, P.B.; Simon, N.R.; Carone, M. A unified approach for inference on algorithm-agnostic variable importance. arXiv 2020, arXiv:2004.03683 2020. [Google Scholar]
- Wu, Y.; Liu, Y. Variable selection in quantile regression. Stat. Sin. 2009, 801–817. [Google Scholar]
- Grömping, U. Variable importance assessment in regression: Linear regression versus random forest. Am. Stat. 2009, 63, 308–319. [Google Scholar] [CrossRef]
- Zhang, H.; Hao, D.; Sitoe, H.M.; Yin, Z.; Hu, Z.; Zhang, G.; Yu, D. Genetic dissection of the relationship between plant architecture and yield component traits in soybean (Glycine max) by association analysis across multiple environments. Plant Breed. 2015, 134, 564–572. [Google Scholar] [CrossRef]
- Pimentel, E.; Edel, C.; Emmerling, R.; Götz, K.-U. How imputation errors bias genomic predictions. J. Dairy Sci. 2015, 98, 4131–4138. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hwang, J.-U.; Song, W.-Y.; Hong, D.; Ko, D.; Yamaoka, Y.; Jang, S.; Yim, S.; Lee, E.; Khare, D.; Kim, K. Plant ABC transporters enable many unique aspects of a terrestrial plant’s lifestyle. Mol. Plant 2016, 9, 338–355. [Google Scholar] [CrossRef] [Green Version]
- Block, M.A.; Jouhet, J. Lipid trafficking at endoplasmic reticulum–chloroplast membrane contact sites. Curr. Opin. Cell Biol. 2015, 35, 21–29. [Google Scholar] [CrossRef]
- Kim, S.; Yamaoka, Y.; Ono, H.; Kim, H.; Shim, D.; Maeshima, M.; Martinoia, E.; Cahoon, E.B.; Nishida, I.; Lee, Y. AtABCA9 transporter supplies fatty acids for lipid synthesis to the endoplasmic reticulum. Proc. Natl. Acad. Sci. USA 2013, 110, 773–778. [Google Scholar] [CrossRef] [Green Version]
- Buzzell, R. Inheritance of a soybean flowering response to fluorescent-daylength conditions. Can. J. Genet. Cytol. 1971, 13, 703–707. [Google Scholar] [CrossRef]
- Watanabe, S.; Hideshima, R.; Xia, Z.; Tsubokura, Y.; Sato, S.; Nakamoto, Y.; Yamanaka, N.; Takahashi, R.; Ishimoto, M.; Anai, T. Map-based cloning of the gene associated with the soybean maturity locus E3. Genetics 2009, 182, 1251–1262. [Google Scholar] [CrossRef] [Green Version]
- Legris, M.; Ince, Y.Ç.; Fankhauser, C. Molecular mechanisms underlying phytochrome-controlled morphogenesis in plants. Nat. Commun. 2019, 10, 5219. [Google Scholar] [CrossRef] [Green Version]
- Casal, J.J. Photoreceptor signaling networks in plant responses to shade. Ann. Rev. Plant Biol. 2013, 64, 403–427. [Google Scholar] [CrossRef]
- De Wit, M.; Galvão, V.C.; Fankhauser, C. Light-mediated hormonal regulation of plant growth and development. Annu. Rev. Plant Biol. 2016, 67, 513–537. [Google Scholar] [CrossRef]
- Lambermon, M.H.; Fu, Y.; Kirk, D.A.W.; Dupasquier, M.; Filipowicz, W.; Lorković, Z.J. UBA1 and UBA2, two proteins that interact with UBP1, a multifunctional effector of pre-mRNA maturation in plants. Mol. Cell. Biol. 2002, 22, 4346–4357. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Kinoshita, T.; Pandey, S.; Ng, C.K.-Y.; Gygi, S.P.; Shimazaki, K.-i.; Assmann, S.M. Modulation of an RNA-binding protein by abscisic-acid-activated protein kinase. Nature 2002, 418, 793–797. [Google Scholar] [CrossRef] [PubMed]
- Kim, C.Y.; Bove, J.; Assmann, S.M. Overexpression of wound-responsive RNA-binding proteins induces leaf senescence and hypersensitive-like cell death. New Phytol. 2008, 180, 57–70. [Google Scholar] [CrossRef] [PubMed]
- Streitner, C.; Danisman, S.; Wehrle, F.; Schöning, J.C.; Alfano, J.R.; Staiger, D. The small glycine-rich RNA binding protein AtGRP7 promotes floral transition in Arabidopsis thaliana. Plant J. 2008, 56, 239–250. [Google Scholar] [CrossRef] [PubMed]
- Liu, F.; Quesada, V.; Crevillén, P.; Bäurle, I.; Swiezewski, S.; Dean, C. The Arabidopsis RNA-binding protein FCA requires a lysine-specific demethylase 1 homolog to downregulate FLC. Mol. Cell 2007, 28, 398–407. [Google Scholar] [CrossRef] [PubMed]
- Bäurle, I.; Dean, C. Differential interactions of the autonomous pathway RRM proteins and chromatin regulators in the silencing of Arabidopsis targets. PLoS ONE 2008, 3, e2733. [Google Scholar] [CrossRef] [Green Version]
- Na, J.-K.; Kim, J.-K.; Kim, D.-Y.; Assmann, S.M. Expression of potato RNA-binding proteins StUBA2a/b and StUBA2c induces hypersensitive-like cell death and early leaf senescence in Arabidopsis. J. Exp. Bot. 2015, 66, 4023–4033. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.H.; Ryu, H.-S.; Chung, K.S.; Posé, D.; Kim, S.; Schmid, M.; Ahn, J.H. Regulation of temperature-responsive flowering by MADS-box transcription factor repressors. Science 2013, 342, 628–632. [Google Scholar] [CrossRef]
- Hussin, S.H.; Wang, H.; Tang, S.; Zhi, H.; Tang, C.; Zhang, W.; Jia, G.; Diao, X. SiMADS34, an E-class MADS-box transcription factor, regulates inflorescence architecture and grain yield in Setaria italica. Plant Mol. Biol. 2021, 105, 419–434. [Google Scholar] [CrossRef]
- Gao, X.; Liang, W.; Yin, C.; Ji, S.; Wang, H.; Su, X.; Guo, C.; Kong, H.; Xue, H.; Zhang, D. The SEPALLATA-like gene OsMADS34 is required for rice inflorescence and spikelet development. Plant Physiol. 2010, 153, 728–740. [Google Scholar] [CrossRef] [Green Version]
- Ditta, G.; Pinyopich, A.; Robles, P.; Pelaz, S.; Yanofsky, M.F. The SEP4 gene of Arabidopsis thaliana functions in floral organ and meristem identity. Curr. Biol. 2004, 14, 1935–1940. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.; Teo, Z.W.N.; Bi, Y.; Song, S.; Xi, W.; Yang, X.; Yin, Z.; Yu, H. A conserved genetic pathway determines inflorescence architecture in Arabidopsis and rice. Dev. Cell 2013, 24, 612–622. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Severin, A.J.; Woody, J.L.; Bolon, Y.-T.; Joseph, B.; Diers, B.W.; Farmer, A.D.; Muehlbauer, G.J.; Nelson, R.T.; Grant, D.; Specht, J.E. RNA-Seq Atlas of Glycine max: A guide to the soybean transcriptome. BMC Plant Biol. 2010, 10, 160. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yin, Z.; Qi, H.; Mao, X.; Wang, J.; Hu, Z.; Wu, X.; Liu, C.; Xin, D.; Zuo, X.; Chen, Q. QTL mapping of soybean node numbers on the main stem and meta-analysis for mining candidate genes. Biotechnol. Biotechnol. Equip. 2018, 32, 915–922. [Google Scholar] [CrossRef] [Green Version]
- Lin, F.; Wani, S.H.; Collins, P.J.; Wen, Z.; Li, W.; Zhang, N.; McCoy, A.G.; Bi, Y.; Tan, R.; Zhang, S. QTL mapping and GWAS for identification of loci conferring partial resistance to Pythium sylvaticum in soybean (Glycine max (L.) Merr). Mol. Breed. 2020, 40, 1–11. [Google Scholar] [CrossRef]
- Song, J.; Sun, X.; Zhang, K.; Liu, S.; Wang, J.; Yang, C.; Jiang, S.; Siyal, M.; Li, X.; Qi, Z. Identification of QTL and genes for pod number in soybean by linkage analysis and genome-wide association studies. Mol. Breed. 2020, 40, 1–14. [Google Scholar] [CrossRef]
- Li, C.; Zou, J.; Jiang, H.; Yu, J.; Huang, S.; Wang, X.; Liu, C.; Guo, T.; Zhu, R.; Wu, X. Identification and validation of number of pod-and seed-related traits QTL s in soybean. Plant Breed. 2018, 137, 730–745. [Google Scholar] [CrossRef]
- Liu, B.; Liu, X.; Wang, C.; Li, Y.; Jin, J.; Herbert, S. Soybean yield and yield component distribution across the main axis in response to light enrichment and shading under different densities. Plant Soil Environ. 2010, 56, 384–392. [Google Scholar] [CrossRef] [Green Version]
- Rotundo, J.L.; Borrás, L.; Westgate, M.E.; Orf, J.H. Relationship between assimilate supply per seed during seed filling and soybean seed composition. Field Crop. Res. 2009, 112, 90–96. [Google Scholar] [CrossRef]
- Weber, H.; Borisjuk, L.; Wobus, U. Molecular physiology of legume seed development. Annu. Rev. Plant Biol. 2005, 56, 253–279. [Google Scholar] [CrossRef]
- Ruan, Y.-L.; Patrick, J.W.; Bouzayen, M.; Osorio, S.; Fernie, A.R. Molecular regulation of seed and fruit set. Trends Plant Sci. 2012, 17, 656–665. [Google Scholar] [CrossRef] [Green Version]
- Orozco-Arroyo, G.; Paolo, D.; Ezquer, I.; Colombo, L. Networks controlling seed size in Arabidopsis. Plant Reprod. 2015, 28, 17–32. [Google Scholar] [CrossRef] [PubMed]
- Le, B.H.; Cheng, C.; Bui, A.Q.; Wagmaister, J.A.; Henry, K.F.; Pelletier, J.; Kwong, L.; Belmonte, M.; Kirkbride, R.; Horvath, S. Global analysis of gene activity during Arabidopsis seed development and identification of seed-specific transcription factors. Proc. Natl. Acad. Sci. USA 2010, 107, 8063–8070. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sun, X.; Shantharaj, D.; Kang, X.; Ni, M. Transcriptional and hormonal signaling control of Arabidopsis seed development. Curr. Opin. Plant Biol. 2010, 13, 611–620. [Google Scholar] [CrossRef] [PubMed]
- Lepiniec, L.; Devic, M.; Roscoe, T.; Bouyer, D.; Zhou, D.-X.; Boulard, C.; Baud, S.; Dubreucq, B. Molecular and epigenetic regulations and functions of the LAFL transcriptional regulators that control seed development. Plant Reprod. 2018, 31, 291–307. [Google Scholar] [CrossRef]
- Pelletier, J.M.; Kwong, R.W.; Park, S.; Le, B.H.; Baden, R.; Cagliari, A.; Hashimoto, M.; Munoz, M.D.; Fischer, R.L.; Goldberg, R.B. LEC1 sequentially regulates the transcription of genes involved in diverse developmental processes during seed development. Proc. Natl. Acad. Sci. USA 2017, 114, E6710–E6719. [Google Scholar] [CrossRef] [Green Version]
- Figueiredo, D.D.; Köhler, C. Auxin: A molecular trigger of seed development. Genes Dev. 2018, 32, 479–490. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Hu, X.; Jiao, C.; Li, Z.; Fei, Z.; Yan, X.; Liu, C.; Wang, Y.; Wang, X. Transcriptome analyses of seed development in grape hybrids reveals a possible mechanism influencing seed size. BMC Genom. 2016, 17, 898. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Du, J.; Wang, S.; He, C.; Zhou, B.; Ruan, Y.-L.; Shou, H. Identification of regulatory networks and hub genes controlling soybean seed set and size using RNA sequencing analysis. J. Exp. Bot. 2017, 68, 1955–1972. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fehr, W.; Caviness, C.; Burmood, D.T.; Penington, J.S. Development description of soybean, Glycine max (L.) Mer. Crop Sci. 1971, 11, 929–931. [Google Scholar] [CrossRef]
- Sonah, H.; Bastien, M.; Iquira, E.; Tardivel, A.; Légaré, G.; Boyle, B.; Normandeau, É.; Laroche, J.; Larose, S.; Jean, M.; et al. An Improved Genotyping by Sequencing (GBS) Approach Offering Increased Versatility and Efficiency of SNP Discovery and Genotyping. PLoS ONE 2013, 8, e54603. [Google Scholar] [CrossRef] [Green Version]
- Torkamaneh, D.; Laroche, J.; Belzile, F. Fast-GBS v2.0: An analysis toolkit for genotyping-by-sequencing data. Genome 2020, 63, 577–581. [Google Scholar] [CrossRef] [PubMed]
- Goldberger, A.S. Best linear unbiased prediction in the generalized linear regression model. J. Am. Stat. Assoc. 1962, 57, 369–375. [Google Scholar] [CrossRef]
- Stroup, W.; Mulitze, D. Nearest neighbor adjusted best linear unbiased prediction. Am. Stat. 1991, 45, 194–200. [Google Scholar]
- Katsileros, A.; Drosou, K.; Koukouvinos, C. Evaluation of nearest neighbor methods in wheat genotype experiments. Commun. Biometry Crop Sci. 2015, 10, 115–123. [Google Scholar]
- Bowley, S. A Hitchhiker’s Guide to Statistics in Plant Biology; Any Old Subject Books: Guelph, ON, Canada, 1999. [Google Scholar]
- Raj, A.; Stephens, M.; Pritchard, J.K. fastSTRUCTURE: Variational inference of population structure in large SNP data sets. Genetics 2014, 197, 573–589. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Yeh, C.-T.E.; Ramamurthy, R.K.; Qi, X.; Fernando, R.L.; Dekkers, J.C.; Garrick, D.J.; Nettleton, D.; Schnable, P.S. Empirical comparisons of different statistical models to identify and validate kernel row number-associated variants from structured multi-parent mapping populations of maize. G3 Genes Genomes Genet. 2018, 8, 3567–3575. [Google Scholar] [CrossRef] [Green Version]
- Lipka, A.E.; Tian, F.; Wang, Q.; Peiffer, J.; Li, M.; Bradbury, P.J.; Gore, M.A.; Buckler, E.S.; Zhang, Z. GAPIT: Genome association and prediction integrated tool. Bioinformatics 2012, 28, 2397–2399. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yin, L.; Zhang, H.; Tang, Z.; Xu, J.; Yin, D.; Zhang, Z.; Yuan, X.; Zhu, M.; Zhao, S.; Li, X. rmvp: A memory-efficient, visualization-enhanced, and parallel-accelerated tool for genome-wide association study. Genom. Proteom. Bioinform. 2021, 19, 619–628. [Google Scholar] [CrossRef]
- Kuhn, M.; Wing, J.; Weston, S.; Williams, A.; Keefer, C.; Engelhardt, A.; Cooper, T.; Mayer, Z.; Kenkel, B.; Team, R.C. Package ‘caret’. R J. 2020, 223, 7. [Google Scholar]
- Wen, Y.-J.; Zhang, H.; Ni, Y.-L.; Huang, B.; Zhang, J.; Feng, J.-Y.; Wang, S.-B.; Dunwell, J.M.; Zhang, Y.-M.; Wu, R. Methodological implementation of mixed linear models in multi-locus genome-wide association studies. Brief. Bioinform. 2018, 19, 809. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.-B.; Feng, J.-Y.; Ren, W.-L.; Huang, B.; Zhou, L.; Wen, Y.-J.; Zhang, J.; Dunwell, J.M.; Xu, S.; Zhang, Y.-M. Improving power and accuracy of genome-wide association studies via a multi-locus mixed linear model methodology. Sci. Rep. 2016, 6, 19444. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bulik-Sullivan, B.K.; Loh, P.-R.; Finucane, H.K.; Ripke, S.; Yang, J.; Patterson, N.; Daly, M.J.; Price, A.L.; Neale, B.M. LD Score regression distinguishes confounding from polygenicity in genome-wide association studies. Nat. Genet. 2015, 47, 291–295. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, X.; Huang, M.; Fan, B.; Buckler, E.S.; Zhang, Z. Iterative usage of fixed and random effect models for powerful and efficient genome-wide association studies. PLoS Genet. 2016, 12, e1005767. [Google Scholar] [CrossRef] [PubMed]
- Botta, V.; Louppe, G.; Geurts, P.; Wehenkel, L. Exploiting SNP correlations within random forest for genome-wide association studies. PLoS ONE 2014, 9, e93379. [Google Scholar] [CrossRef] [Green Version]
- Cortes, C.; Vapnik, V. Support vector machine. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Fletcher, T. Support Vector Machines Explained; UCL: London, UK, 2008. [Google Scholar]
- Vapnik, V.N. Statistical Learning Theory; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Weston, J.; Mukherjee, S.; Chapelle, O.; Pontil, M.; Poggio, T.; Vapnik, V. Feature selection for SVMs. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 3–8 December 2001; pp. 668–674. [Google Scholar]
- Enoma, D.O.; Bishung, J.; Abiodun, T.; Ogunlana, O.; Osamor, V.C. Machine learning approaches to genome-wide association studies. J. King Saud Univ. Sci. 2022, 34, 101847. [Google Scholar] [CrossRef]
- Doerge, R.W.; Churchill, G.A. Permutation tests for multiple loci affecting a quantitative character. Genetics 1996, 142, 285–294. [Google Scholar] [CrossRef]
- Churchill, G.A.; Doerge, R.W. Empirical threshold values for quantitative trait mapping. Genetics 1994, 138, 963–971. [Google Scholar] [CrossRef]
- Benjamini, Y.; Hochberg, Y. Controlling the false discovery rate: A practical and powerful approach to multiple testing. J. R. Stat. Soc. Ser. B (Methodol.) 1995, 57, 289–300. [Google Scholar] [CrossRef]
- Siegmann, B.; Jarmer, T. Comparison of different regression models and validation techniques for the assessment of wheat leaf area index from hyperspectral data. Int. J. Remote Sens. 2015, 36, 4519–4534. [Google Scholar] [CrossRef]
- Lin, G.; Chai, J.; Yuan, S.; Mai, C.; Cai, L.; Murphy, R.W.; Zhou, W.; Luo, J. VennPainter: A tool for the comparison and identification of candidate genes based on Venn diagrams. PLoS ONE 2016, 11, e0154315. [Google Scholar] [CrossRef] [PubMed] [Green Version]

| GWAS Method | Chromosome | Peak SNP Position | Co-Located QTL | Reference |
|---|---|---|---|---|
| MLM | 2 | 2212910 | Sclero 3-g31 | [38] |
| 8233782 | Seed Weight 6-g1 | [39] | ||
| FarmCPU | 2 | 2212910 | Sclero 3-g31 | [38] |
| 8233766 | Seed Weight 6-g1 | [39] | ||
| 20 | 37765851 | WUE 2-g53 | [40] | |
| RF | 3 | 2978272 | Leaflet area 1-g2.1 | [41] |
| Leaflet width 1-g4.1 | [41] | |||
| Leaflet area 1-g2.2 | [41] | |||
| Leaflet width 1-g4.2 | [41] | |||
| Salt tolerance 1-g12 | [42] | |||
| 16 | 5730281 | Plant height 6-g17 | [43] | |
| Plant height 1-g17 | [43] | |||
| First flower 4-g63 | [44] | |||
| 17 | 34757372 | SDS root retention 1-g6 | [45] | |
| SVR | 2 | 695362 | Seed linolenic 2-g1 | [46] |
| Seed linolenic 2-g2 | [46] | |||
| 720134 | SDS 1-g12.1 | [47] | ||
| SDS 1-g12.2 | [47] | |||
| Ureide content 1-g2 | [48] | |||
| 827374 | SDS 1-g12.3 | [47] | ||
| 10 | 1595239 | Shoot Cu 1-g8 | [49] | |
| 1689395 | Seed oil 5-g3 | [39] | ||
| 16 | 2438652 | Reproductive period 4-g16 | [43] | |
| R8 full maturity 9-g2 | [43] | |||
| 2460921 | Reproductive period 2-g16 | [43] | ||
| R8 full maturity 2-g2 | [43] | |||
| 19 | 47513536 | R8 full maturity 4-g1 | [39] | |
| 47513572 | First flower 4-g81 | [44] |
| GWAS Method | Chromosome | Peak SNP Position | Co-Located QTL | Reference |
|---|---|---|---|---|
| MLM | 5 | 34391386 | Ureide content 1-g16.1 | [48] |
| Ureide content 1-g16.2 | [48] | |||
| FarmCPU | 5 | 34391386 | Ureide content 1-g16.1 | [48] |
| Ureide content 1-g16.2 | [48] | |||
| RF | 7 | 1032587 | WUE 2-g18 | [40] |
| SVR | 3 | 36309302 | First flower 4-g10 | [44] |
| First flower 3-g2 | [50] | |||
| Seed weight 4-g3 | [50] | |||
| Seed yield 4-g2 | [50] | |||
| R8 full maturity 3-g3 | [50] | |||
| 37617293 | Plant height 3-g17 | [51] | ||
| Leaflet shape 1-g1.1 | [41] | |||
| Leaflet shape 1-g1.2 | [41] | |||
| Leaflet shape 1-g1.3 | [41] | |||
| Seed set 1-g32.1 | [41] | |||
| Seed set 1-g32.2 | [41] | |||
| 7 | 44488152 | Seed yield 4-g4 | [50] | |
| 1032587 | WUE 2-g18 | [40] | ||
| 15 | 34958361 | SCN 5-g35 | [52] | |
| 19 | 41385139 | Seed weight 5-g20 | [53] | |
| Seed weight 4-g18 | [50] | |||
| Seed yield 4-g5 | [50] | |||
| Shoot Zn 1-g28.1 | [49] | |||
| Shoot Zn 1-g28.2 | [49] | |||
| Shoot Zn 1-g29.1 | [49] | |||
| Shoot Zn 1-g29.2 | [49] | |||
| Shoot Zn 1-g29.3 | [49] |
| GWAS Method | Chromosome | Peak SNP Position | Co-Located QTL | Reference |
|---|---|---|---|---|
| FarmCPU | 19 | 40131952 | Pubescence density 1-g17 | [54] |
| Seed weight 9-g5.1 | [55] | |||
| RF | 4 | 1205787 | Shoot Ca 1-g10 | [49] |
| 6 | 50570624 | Seed set 1-g51.1 | [41] | |
| Seed set 1-g43.1 | [41] | |||
| Seed set 1-g25.1 | [41] | |||
| Seed set 1-g43.2 | [41] | |||
| Seed set 1-g25.2 | [41] | |||
| Seed set 1-g51.2 | [41] | |||
| 50570473 | Seed set 1-g43.3 | [41] | ||
| Seed set 1-g51.3 | [41] | |||
| Seed set 1-g25.3 | [41] | |||
| Pod number 1-g3 | [41] | |||
| Seed palmitic 2-g2 | [41] | |||
| Seed long-chain faty acid 1-g22 | [41] | |||
| SVR | 6 | 50570624 | Seed set 1-g51.1 | [41] |
| Seed set 1-g43.1 | [41] | |||
| Seed set 1-g25.1 | [41] | |||
| Seed set 1-g43.2 | [41] | |||
| Seed set 1-g25.2 | [41] | |||
| Seed set 1-g51.2 | [41] | |||
| 50570473 | Seed set 1-g43.3 | [41] | ||
| Seed set 1-g51.3 | [41] | |||
| Seed set 1-g25.3 | [41] | |||
| Pod number 1-g3 | [41] | |||
| Seed palmitic 2-g2 | [41] | |||
| Seed long-chain faty acid 1-g22 | [41] | |||
| 7 | 1032587 | WUE 2-g18 | [40] | |
| 1092403 | WUE 2-g18 | [40] | ||
| First flower 3-g4 | [41] | |||
| 18 | 55645699 | Leaflet shape 1-g4.1 | [41] | |
| Leaflet shape 1-g4.2 | [41] | |||
| Leaflet shape 1-g4.3 | [41] | |||
| Seed stearic 4-g5 | [56] | |||
| Node number 1-g6.1 | [41] | |||
| Node number 1-g6.2 | [41] | |||
| Pod number 1-g1.1 | [41] | |||
| Pod number 1-g1.2 | [41] | |||
| Pode number 1-g1.3 | [41] | |||
| WUE 3-g31 | [40] | |||
| Seed weight, SoyNAM 14-g28 | [57] | |||
| Lodging, SoyNAM 4-g15 | [58] | |||
| Branching 1-g1.1 | [41] | |||
| Plant height 5-g4.2 | [41] | |||
| Plant height 5-g4.3 | [41] | |||
| Shoot p 1-g30 | [49] | |||
| 19 | 47350110 | Node number 1-g2.3 | [41] |
| GWAS Method | Chromosome | Peak SNP Position | Co-Located QTL | Reference |
|---|---|---|---|---|
| MLM | 15 | 10193796 | Seed protein 6-g2 | [59] |
| Seed Arg 1-g4 | [59] | |||
| Seed coat luster 1-g1.3 | [41] | |||
| FarmCPU | 15 | 10193796 | Seed protein 6-g2 | [59] |
| Seed Arg 1-g4 | [59] | |||
| Seed coat luster 1-g1.3 | [41] | |||
| RF | 1 | 54647498 | First flower 4-g2 | [44] |
| 7 | 329800 | Phytoph 2-g32 | [60] | |
| Phytoph 2-g7 | [60] | |||
| 18 | 12945778 | SCN 4-g14 | [61] | |
| 19 | 40218800 | Seed weight 9-g5.1 | [55] | |
| SVR | 7 | 1032587 | WUE 2-g18 | [40] |
| 19 | 40218800 | Seed weight 9-g5.1 | [55] |
| GWAS Method | Chromosome | Peak SNP Position | Co-Located QTL | Reference |
|---|---|---|---|---|
| RF | 9 | 40285014 | Shoot Fe 1-g8.1 | [49] |
| Shoot Fe 1-g8.2 | [49] | |||
| Shoot Fe 1-g8.3 | [49] | |||
| Shoot Fe 1-g9 | [49] | |||
| Shoot Fe 1-g10 | [49] | |||
| Shoot Fe 1-g11 | [49] | |||
| Soybean mosaic virus 2-g5 | [62] | |||
| 15 | 34958361 | SCN 5-g35 | [52] | |
| SVR | 7 | 1032587 | WUE 2-g18 | [40] |
| 15 | 34958361 | SCN 5-g35 | [52] |
| GWAS Method | Chromosome | Peak SNP Position | Co-Located QTL | Reference |
|---|---|---|---|---|
| RF | 7 | 15331676 | Seed weight, SoyNAM 14-g11 | [57] |
| SVR | 9 | 39366957 | Pod number 1-g4.1 | [41] |
| Pod number 1-g4.2 | [41] | |||
| Pod number 1-g4.3 | [41] | |||
| Seed thickness 2-g4 | [41] | |||
| 9 | 39372117 | Seed Thr 2-g1 | [63] | |
| Seed Ser 2-g1 | [63] | |||
| Seed Tyr 2-g2 | [63] | |||
| Seed Lys 2-g2 | [63] | |||
| Seed leu 2-g2 | [63] | |||
| Seed ile 2-g2 | [63] | |||
| Seed Ala 2-g2 | [63] | |||
| Seed Gly 2-g2 | [63] | |||
| 11 | 5245870 | Ureide content 1-g29 | [48] | |
| Pod number 1-g6 | [41] | |||
| 18 | 55645699 | Leaflet shape 1-g4.1 | [41] | |
| 55469601 | Leaflet shape 1-g4.2 | [41] | ||
| Leaflet shape 1-g4.3 | [41] | |||
| Seed stearic 4-g5 | [56] | |||
| Node number 1-g6.1 | [41] | |||
| Node number 1-g6.2 | [41] | |||
| Pode number 1-g1.1 | [41] | |||
| Pode number 1-g1.2 | [41] | |||
| Pode number 1-g1.3 | [41] | |||
| WUE 3-g31 | [64] | |||
| Seed weight, SoyNAM 14-g28 | [57] | |||
| Lodging, SoyNAM 4-g15 | [58] | |||
| Branching 1-g1.1 | [41] | |||
| Plant height 5-g4.2 | [41] | |||
| Plant height 5-g4.3 | [41] | |||
| Shoot p 1-g30 | [49] | |||
| Seed yield, SoyNAM 7-g19 | [58] | |||
| R8 full maturity, SoyNAM 13-g19 | [58] | |||
| Plant height 5-g4.3 | [41] | |||
| 19 | 43077182 | Seed weight 9-g5.2 | [55] | |
| Seed weight 5-g21 | [55] | |||
| First flower 5-g3 | [41] | |||
| First flower 5-g17 | [41] | |||
| 47235604 | First flower 4-g77 | [44] | ||
| Seed palmitic 1-g19 | [65] | |||
| 47350110 | Leaf carotenoid content 1-g14 | [66] | ||
| Ureide content 1-g50.3 | [48] | |||
| Ureide content 1-g50.4 | [48] | |||
| 47224293 | Node number 1-g2.3 | [41] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yoosefzadeh-Najafabadi, M.; Eskandari, M.; Torabi, S.; Torkamaneh, D.; Tulpan, D.; Rajcan, I. Machine-Learning-Based Genome-Wide Association Studies for Uncovering QTL Underlying Soybean Yield and Its Components. Int. J. Mol. Sci. 2022, 23, 5538. https://doi.org/10.3390/ijms23105538
Yoosefzadeh-Najafabadi M, Eskandari M, Torabi S, Torkamaneh D, Tulpan D, Rajcan I. Machine-Learning-Based Genome-Wide Association Studies for Uncovering QTL Underlying Soybean Yield and Its Components. International Journal of Molecular Sciences. 2022; 23(10):5538. https://doi.org/10.3390/ijms23105538
Chicago/Turabian StyleYoosefzadeh-Najafabadi, Mohsen, Milad Eskandari, Sepideh Torabi, Davoud Torkamaneh, Dan Tulpan, and Istvan Rajcan. 2022. "Machine-Learning-Based Genome-Wide Association Studies for Uncovering QTL Underlying Soybean Yield and Its Components" International Journal of Molecular Sciences 23, no. 10: 5538. https://doi.org/10.3390/ijms23105538
APA StyleYoosefzadeh-Najafabadi, M., Eskandari, M., Torabi, S., Torkamaneh, D., Tulpan, D., & Rajcan, I. (2022). Machine-Learning-Based Genome-Wide Association Studies for Uncovering QTL Underlying Soybean Yield and Its Components. International Journal of Molecular Sciences, 23(10), 5538. https://doi.org/10.3390/ijms23105538









