Biased Brownian Motion of KIF1A and the Role of Tubulin’s C-Terminal Tail Studied by Molecular Dynamics Simulation
Abstract
1. Introduction
2. Results
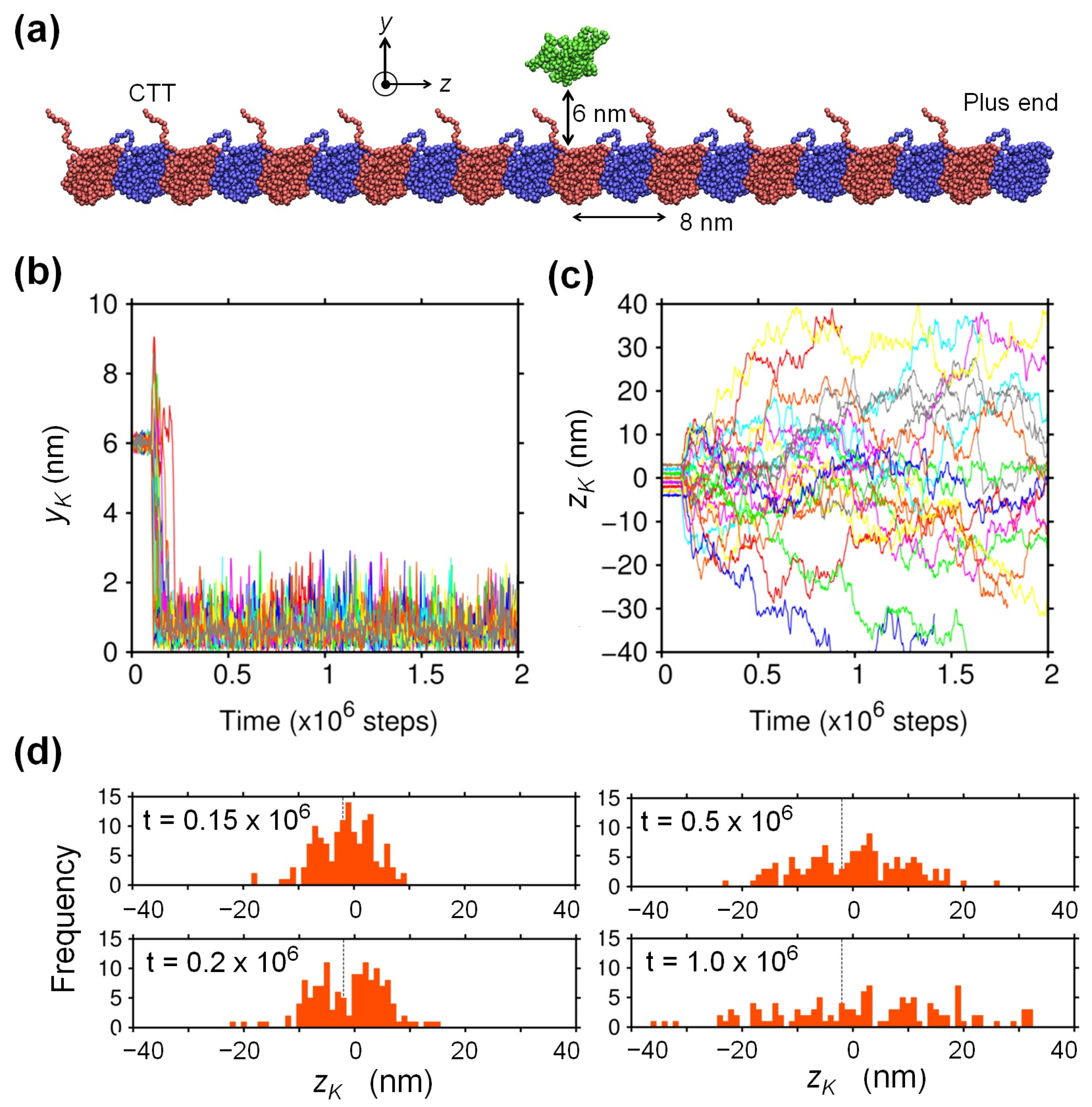
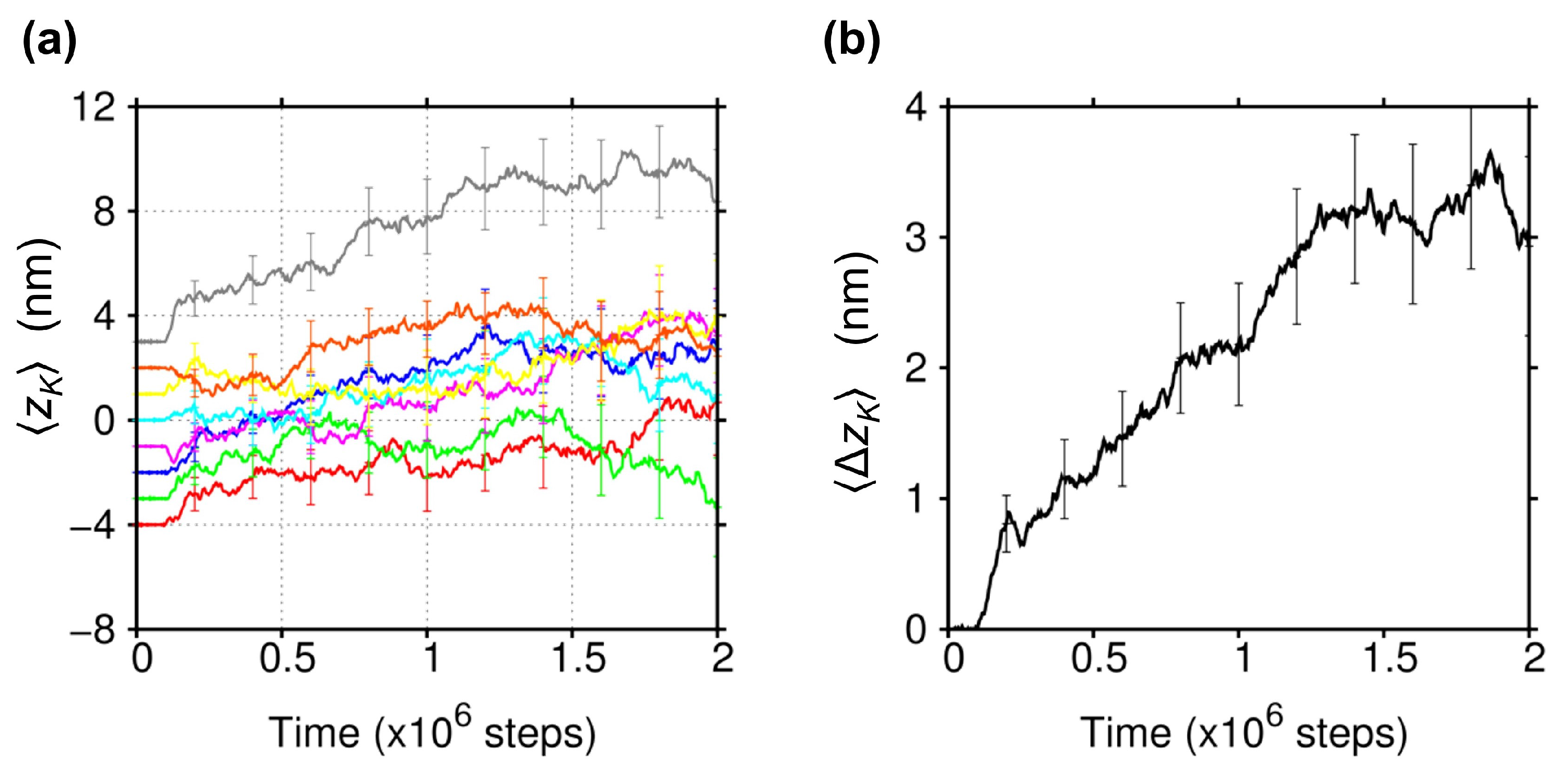
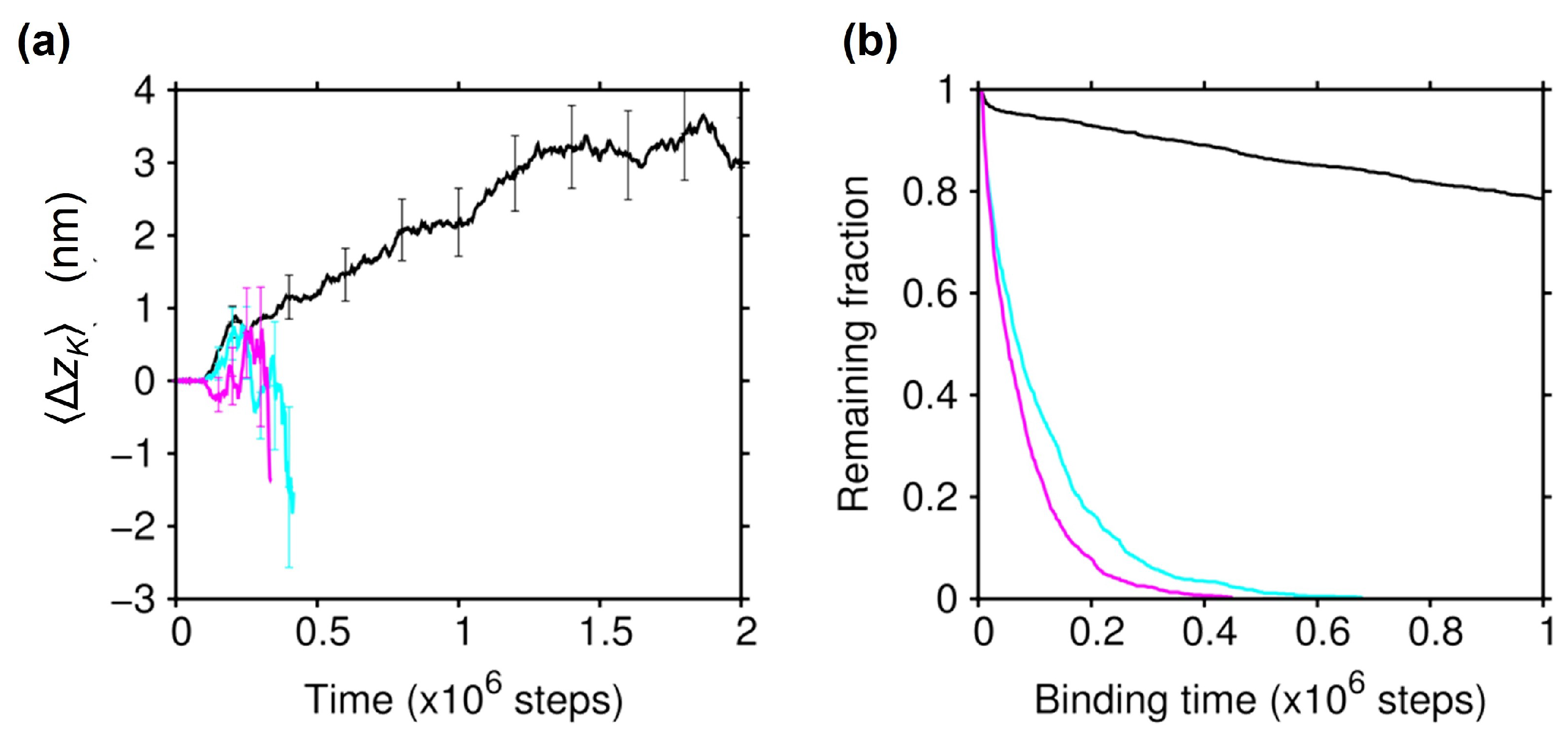
2.1. Biased Brownian Motion of KIF1A along the MT
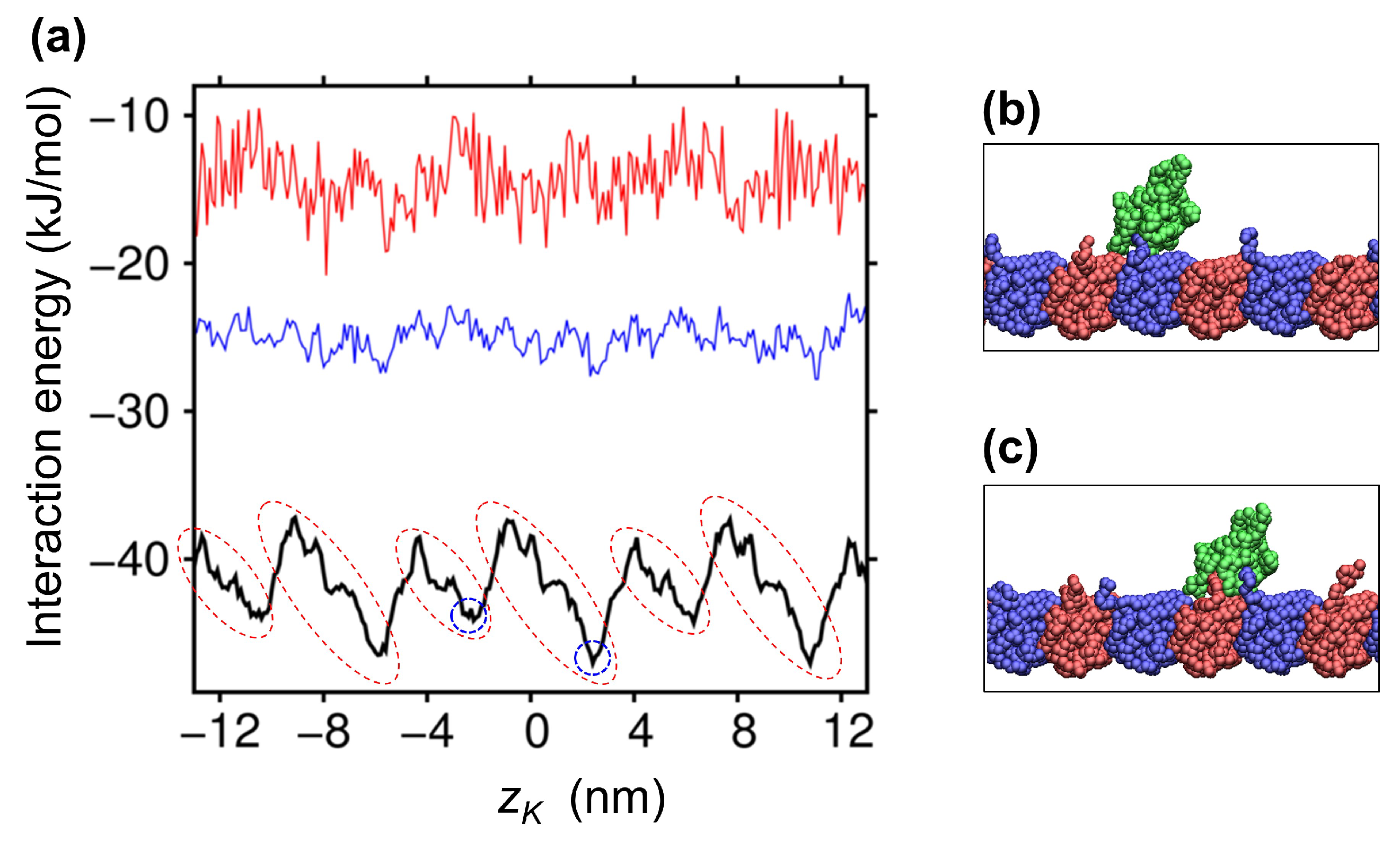
2.2. Ratchet-Like Energy Landscape for KIF1A-MT Interaction
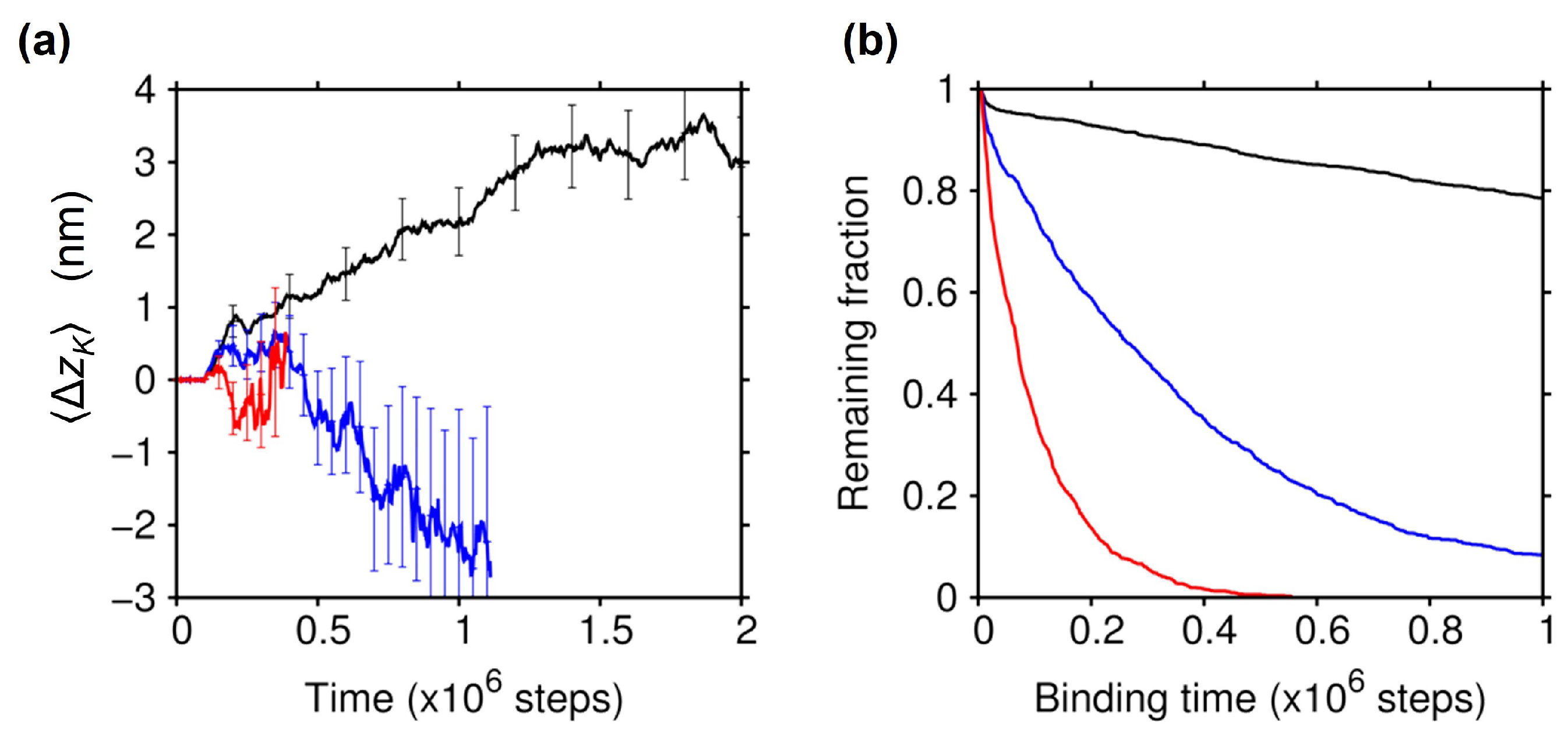
2.3. Effect of the Electrostatic Screening
2.4. Essential Role of the C-Terminal Tail of Tubulin
3. Discussion
4. Methods
4.1. System Setup
4.2. Intra-/Inter-Molecular Interactions
4.3. Molecular Dynamics
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Okada, Y.; Hirokawa, N. A processive single-headed motor: Kinesin superfamily protein KIF1A. Science 1999, 283, 1152–1157. [Google Scholar] [CrossRef] [PubMed]
- Hirokawa, N.; Noda, Y.; Tanaka, Y.; Niwa, S. Kinesin superfamily motor proteins and intracellular transport. Nat. Rev. Mol. Cell Biol. 2009, 10, 682–696. [Google Scholar] [CrossRef] [PubMed]
- Yonekawa, V.; Harada, A.; Okada, Y.; Funakoshi, T.; Kanai, Y.; Takei, Y.; Terada, S.; Noda, T.; Hirokawa, N. Defect in synaptic vesicle precursor transport and neuronal cell death in KIF1A motor protein-deficient mice. J. Cell Biol. 1998, 141, 431–441. [Google Scholar] [CrossRef] [PubMed]
- Pennings, M.; Schouten, M.I.; van Gaalen, J.; Meijer, R.P.; de Bot, S.T.; Kriek, M.; Saris, C.G.; van den Berg, L.H.; van Es, M.A.; Zuidgeest, D.M.; et al. KIF1A variants are a frequent cause of autosomal dominant hereditary spastic paraplegia. Eur. J. Hum. Genet. 2020, 28, 40–49. [Google Scholar] [CrossRef] [PubMed]
- Lo, K.Y.; Kuzmin, A.; Unger, S.M.; Petersen, J.D.; Silverman, M.A. KIF1A is the primary anterograde motor protein required for the axonal transport of dense-core vesicles in cultured hippocampal neurons. Neurosci. Lett. 2011, 491, 168–173. [Google Scholar] [CrossRef]
- Kondo, M.; Takei, Y.; Hirokawa, N. Motor protein KIF1A is essential for hippocampal synaptogenesis and learning enhancement in an enriched environment. Neuron 2012, 73, 743–757. [Google Scholar] [CrossRef]
- Vale, R.D.; Milligan, R.A. The way things move: Looking under the hood of molecular motor proteins. Science 2000, 288, 88–95. [Google Scholar] [CrossRef]
- Okada, Y.; Hirokawa, N. Mechanism of the single-headed processivity: Diffusional anchoring between the K-loop of kinesin and the C terminus of tubulin. Proc. Natl. Acad. Sci. USA 2000, 97, 640–645. [Google Scholar] [CrossRef]
- Okada, Y.; Higuchi, H.; Hirokawa, N. Processivity of the single-headed kinesin KIF1A through binding to tubulin. Nature 2003, 424, 574–577. [Google Scholar] [CrossRef]
- Hammond, J.W.; Cai, D.; Blasius, T.L.; Li, Z.; Jiang, Y.; Jih, G.T.; Meyhofer, E.; Verhey, K.J. Mammalian Kinesin-3 motors are dimeric in vivo and move by processive motility upon release of autoinhibition. PLoS Biol. 2009, 7, 0650–0663. [Google Scholar] [CrossRef] [PubMed]
- Lessard, D.V.; Zinder, O.J.; Hotta, T.; Verhey, K.J.; Ohi, R.; Berger, C.L. Polyglutamylation of tubulin’s C-terminal tail controls pausing and motility of kinesin-3 family member KIF1A. J. Biol. Chem. 2019, 294, 6353–6363. [Google Scholar] [CrossRef]
- Grant, B.J.; Gheorghe, D.; Zheng, W.; Alonso, M.; Huber, G.; Dlugosz, M.; McCammon, J.A.; Cross, R.A. Electrostatically biased binding of kinesin to microtubules. PLoS Biol. 2011, 9, e1001207. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Kanada, R.; Kuwata, T.; Kenzaki, H.; Takada, S. Structure-based molecular simulations reveal the enhancement of biased Brownian motions in single-headed kinesin. PLoS Comput. Biol. 2013, 9, e1002907. [Google Scholar] [CrossRef]
- Verhey, K.J.; Gaertig, J. The tubulin code. Cell Cycle 2007, 6, 2152–2160. [Google Scholar] [CrossRef] [PubMed]
- Janke, C.; Magiera, M.M. The tubulin code and its role in controlling microtubule properties and functions. Nat. Rev. Mol. Cell Biol. 2020, 21, 307–326. [Google Scholar] [CrossRef] [PubMed]
- Sirajuddin, M.; Rice, L.M.; Vale, R.D. Regulation of microtubule motors by tubulin isotypes and post-translational modifications. Nat. Cell Biol. 2014, 16, 335–344. [Google Scholar] [CrossRef]
- Bigman, L.S.; Levy, Y. Tubulin tails and their modifications regulate protein diffusion on microtubules. Proc. Natl. Acad. Sci. USA 2020, 117, 8876–8883. [Google Scholar] [CrossRef]
- Takano, M.; Terada, T.P.; Sasai, M. Unidirectional Brownian motion observed in an in silico single molecule experiment of an actomyosin motor. Proc. Natl. Acad. Sci. USA 2010, 107, 7769–7774. [Google Scholar] [CrossRef]
- Kamimura, S.; Mandelkow, E. Tubulin protofilaments and kinesin-dependent motility. J. Cell Biol. 1992, 118, 865–875. [Google Scholar] [CrossRef]
- Kikkawa, M.; Hirokawa, N. High-resolution cryo-EM maps show the nucleotide binding pocket of KIF1A in open and closed conformations. EMBO J. 2006, 25, 4187–4194. [Google Scholar] [CrossRef]
- Atilgan, A.R.; Durell, S.R.; Jernigan, R.L.; Demirel, M.C.; Keskin, O.; Bahar, I. Anisotropy of fluctuation dynamics of proteins with an elastic network model. Biophys. J. 2001, 80, 505–515. [Google Scholar] [CrossRef]
- Takano, M.; Higo, J.; Nakamura, H.K.; Sasai, M. On the model granularity to simulate protein dynamics: A biological physics view on biomolecular computing. Nat. Comput. 2004, 3, 377–393. [Google Scholar] [CrossRef]
- Sato, T.; Ohnuki, J.; Takano, M. Dielectric Allostery of Protein: Response of Myosin to ATP Binding. J. Phys. Chem. B 2016, 120, 13047–13055. [Google Scholar] [CrossRef] [PubMed]
- Sato, T.; Ohnuki, J.; Takano, M. Long-range coupling between ATP-binding and lever-arm regions in myosin via dielectric allostery. J. Chem. Phys. 2017, 147. [Google Scholar] [CrossRef]
- Sato, T.; Sasaki, T.; Ohnuki, J.; Umezawa, K.; Takano, M. Hydrophobic surface enhances electrostatic interaction in water. Phys. Rev. Lett. 2018, 121, 206002. [Google Scholar] [CrossRef] [PubMed]
- Okazaki, K.I.; Sato, T.; Takano, M. Temperature-enhanced association of proteins due to electrostatic interaction: A coarse-grained simulation of actin-myosin binding. J. Am. Chem. Soc. 2012, 134, 8918–8925. [Google Scholar] [CrossRef] [PubMed]
- Uchimura, S.; Oguchi, Y.; Katsuki, M.; Usui, T.; Osada, H.; Nikawa, J.I.; Ishiwata, S.; Muto, E. Identification of a strong binding site for kinesin on the microtubule using mutant analysis of tubulin. EMBO J. 2006, 25, 5932–5941. [Google Scholar] [CrossRef]
- Uchimura, S.; Oguchi, Y.; Hachikubo, Y.; Ishiwata, S.; Muto, E. Key residues on microtubule responsible for activation of kinesin ATPase. EMBO J. 2010, 29, 1167–1175. [Google Scholar] [CrossRef] [PubMed]
- Mizuhara, Y.; Parkin, D.; Umezawa, K.; Ohnuki, J.; Takano, M. Over-destabilization of protein-protein interaction in generalized Born model and utility of energy density integration cutoff. J. Phys. Chem. B 2017, 121, 4669–4677. [Google Scholar] [CrossRef] [PubMed]
- Eswar, N.; Webb, B.; Marti-Renom, M.A.; Madhusudhan, M.S.; Eramian, D.; Shen, M.Y.; Pieper, U.; Sali, A. Comparative protein structure modeling using MODELLER. Curr. Protoc. Protein Sci. 2007, 50, 1–31. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mizuhara, Y.; Takano, M. Biased Brownian Motion of KIF1A and the Role of Tubulin’s C-Terminal Tail Studied by Molecular Dynamics Simulation. Int. J. Mol. Sci. 2021, 22, 1547. https://doi.org/10.3390/ijms22041547
Mizuhara Y, Takano M. Biased Brownian Motion of KIF1A and the Role of Tubulin’s C-Terminal Tail Studied by Molecular Dynamics Simulation. International Journal of Molecular Sciences. 2021; 22(4):1547. https://doi.org/10.3390/ijms22041547
Chicago/Turabian StyleMizuhara, Yukinobu, and Mitsunori Takano. 2021. "Biased Brownian Motion of KIF1A and the Role of Tubulin’s C-Terminal Tail Studied by Molecular Dynamics Simulation" International Journal of Molecular Sciences 22, no. 4: 1547. https://doi.org/10.3390/ijms22041547
APA StyleMizuhara, Y., & Takano, M. (2021). Biased Brownian Motion of KIF1A and the Role of Tubulin’s C-Terminal Tail Studied by Molecular Dynamics Simulation. International Journal of Molecular Sciences, 22(4), 1547. https://doi.org/10.3390/ijms22041547




