Tunneling Quantum Dynamics in Ammonia
Abstract
1. Introduction
2. Quantum Hamilton Mechanics
3. Vibrational Eigenfunctions of Ammonia
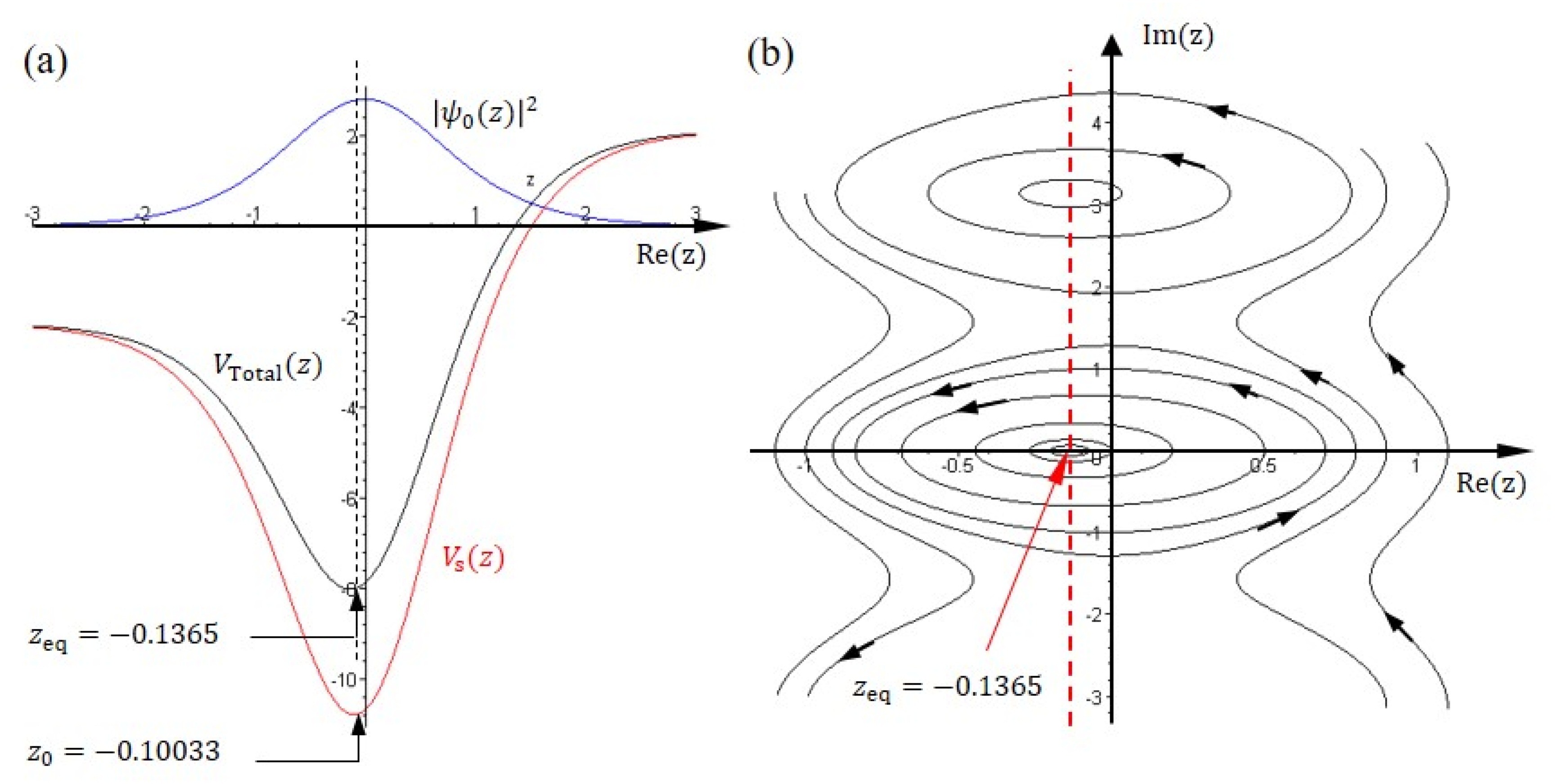
4. Nitrogen Dynamics in Single-Well Potential
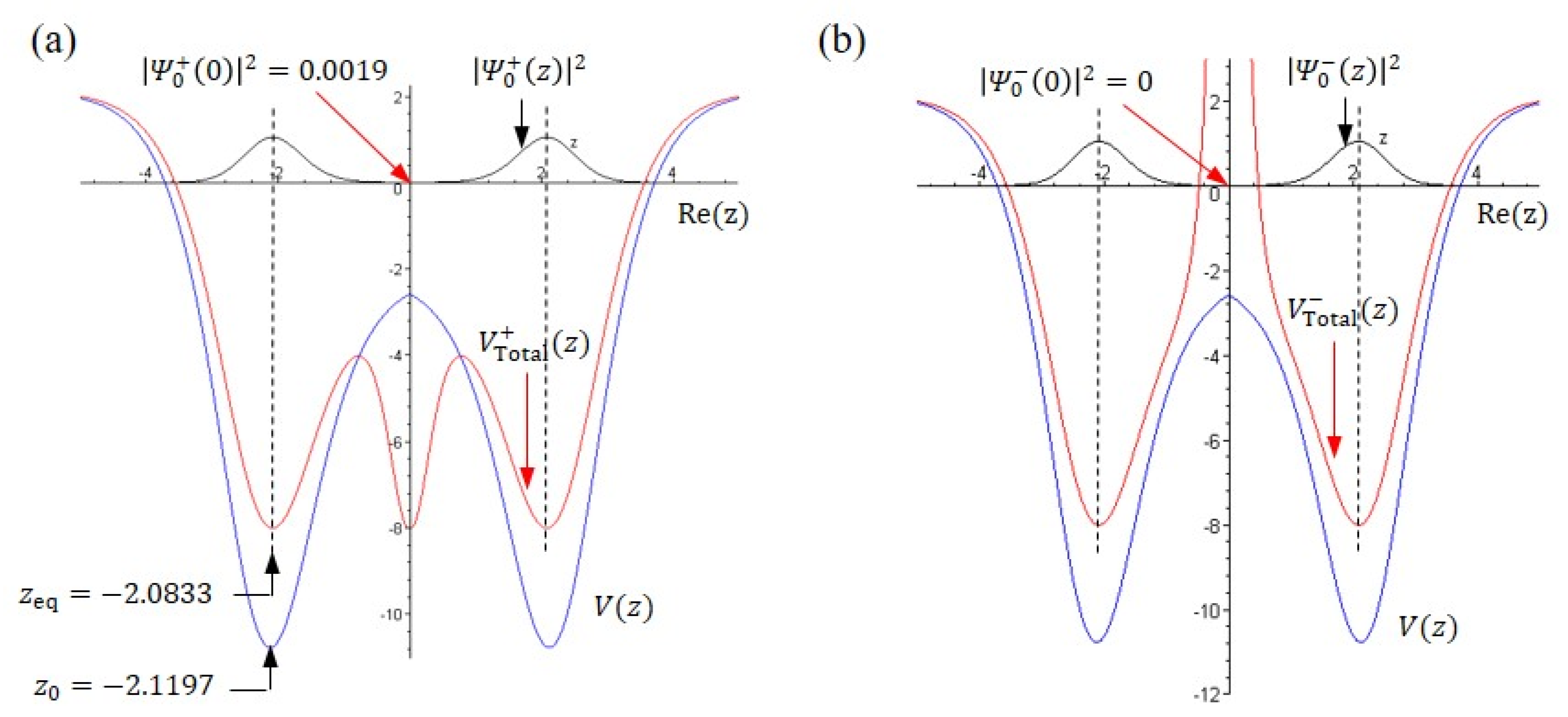
5. Tunneling Dynamic in Stationary States
5.1. Tunneling Trajectory in the Ground State
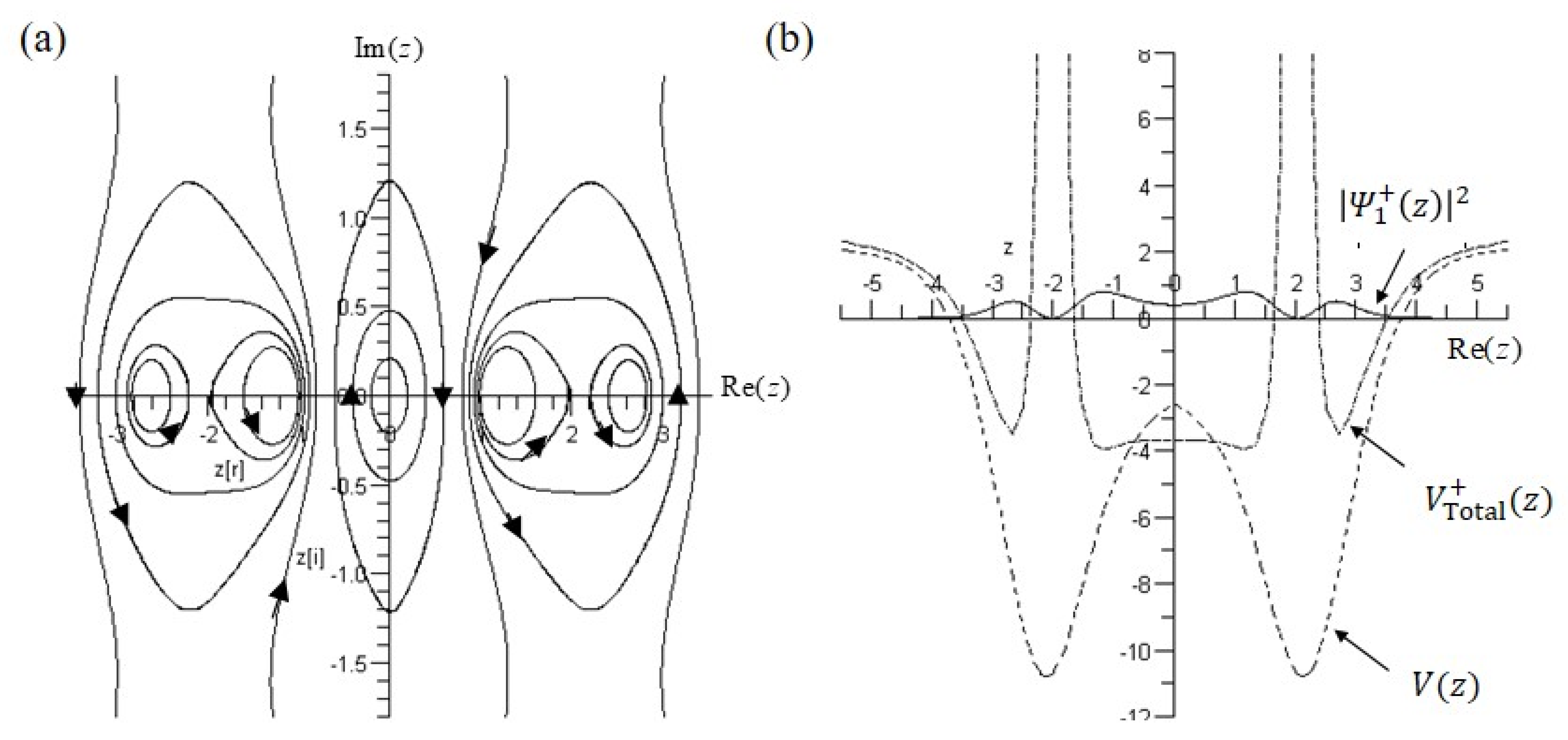
5.2. Tunneling Trajectory in the Excited States
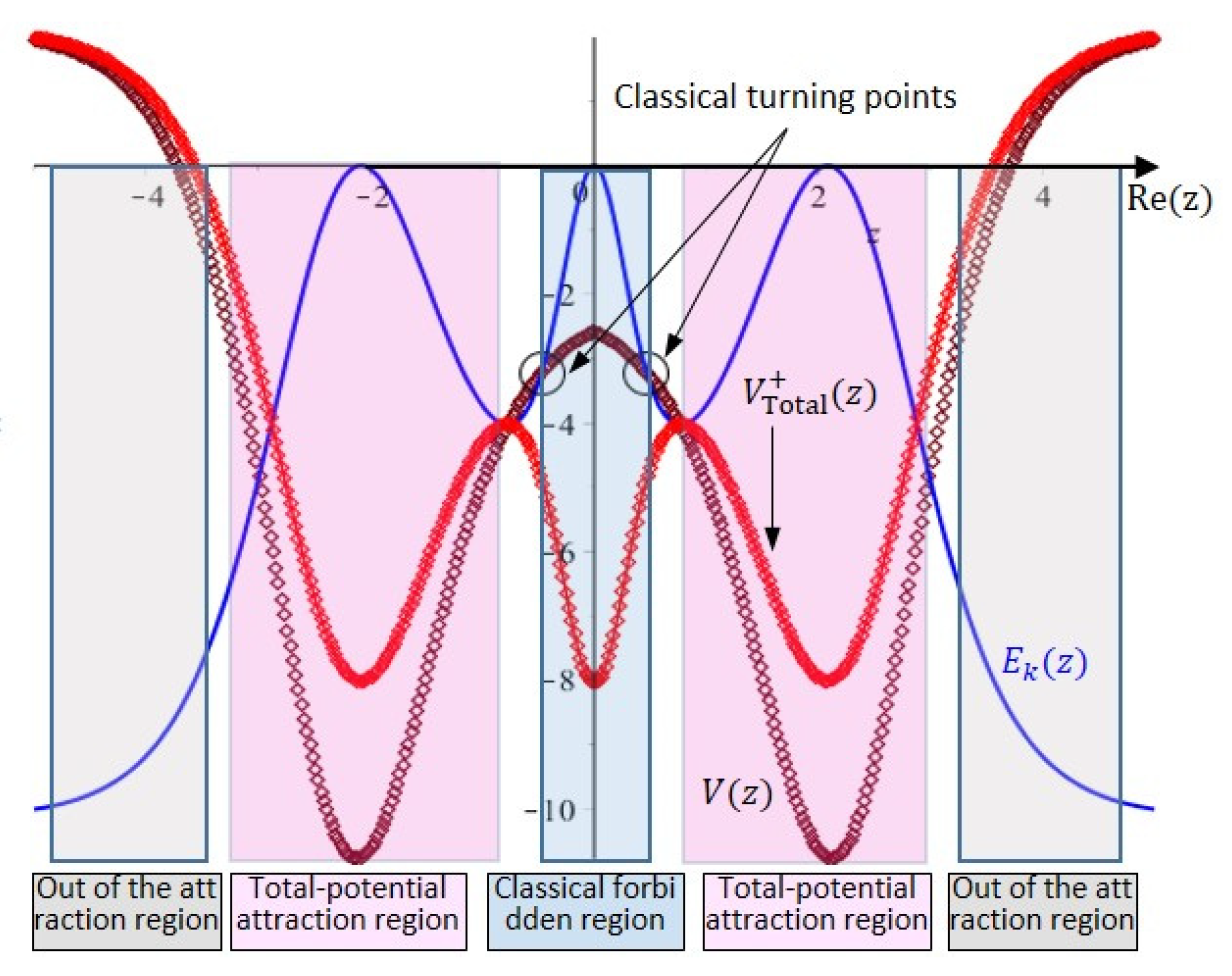
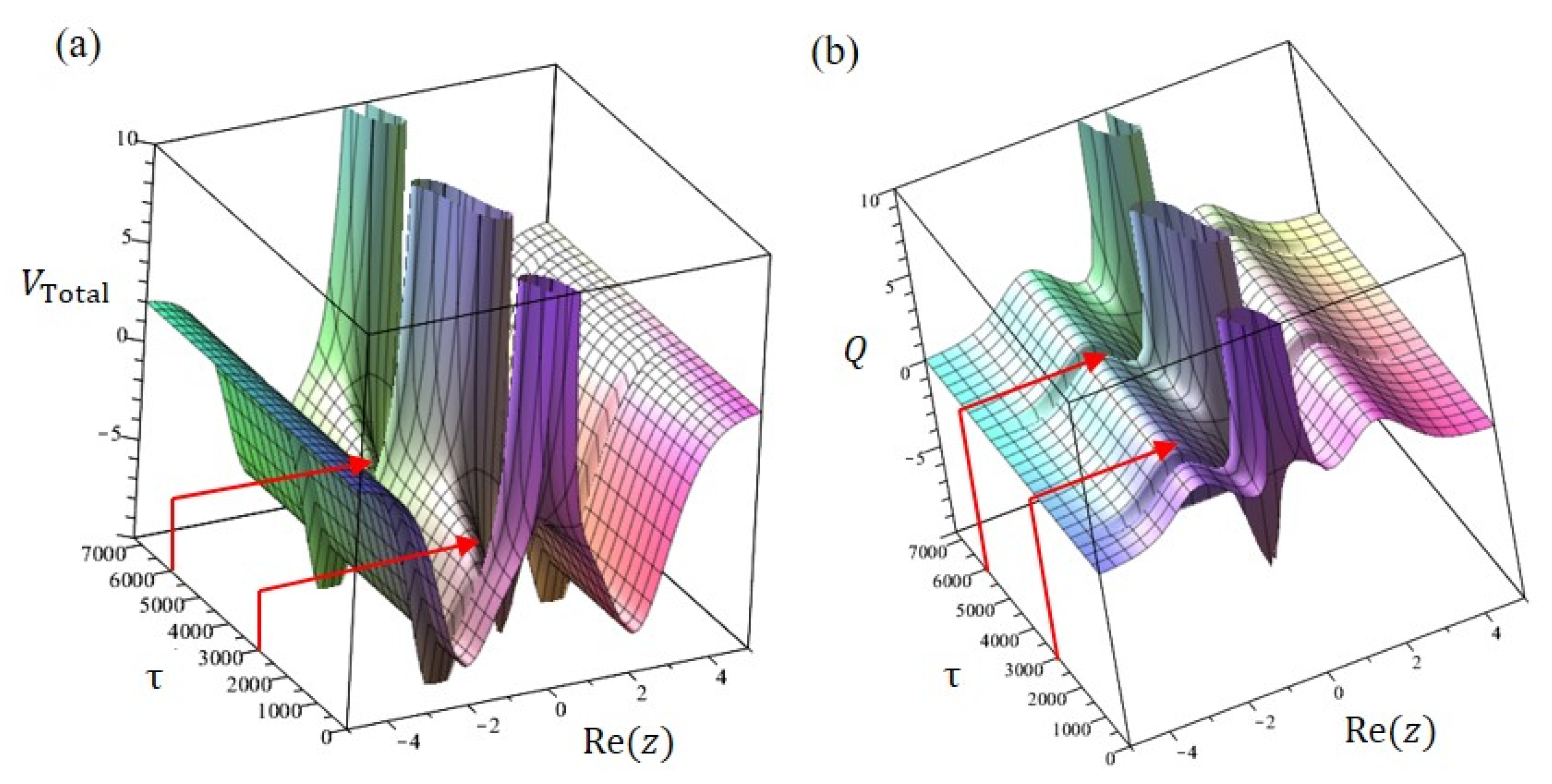
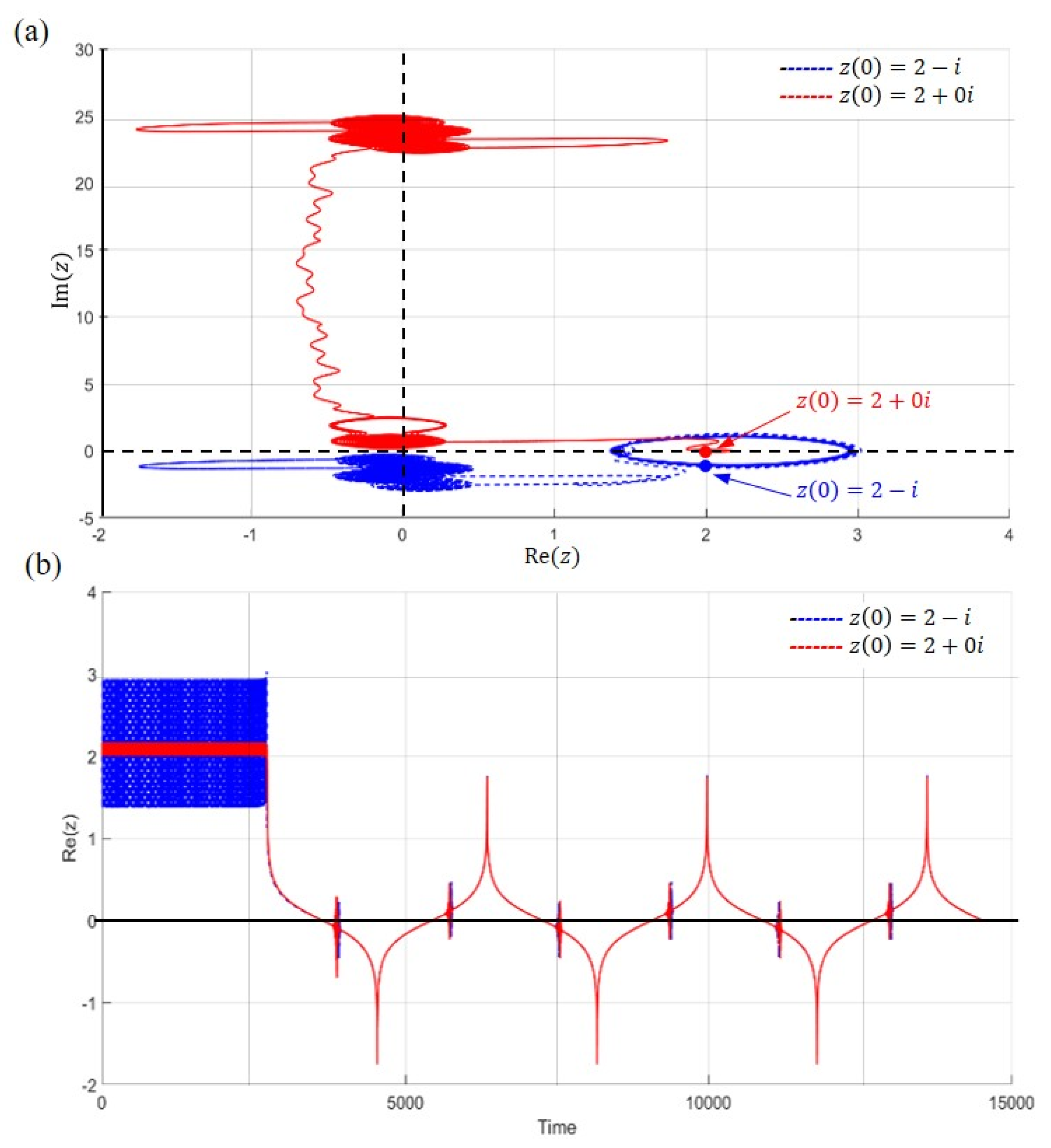
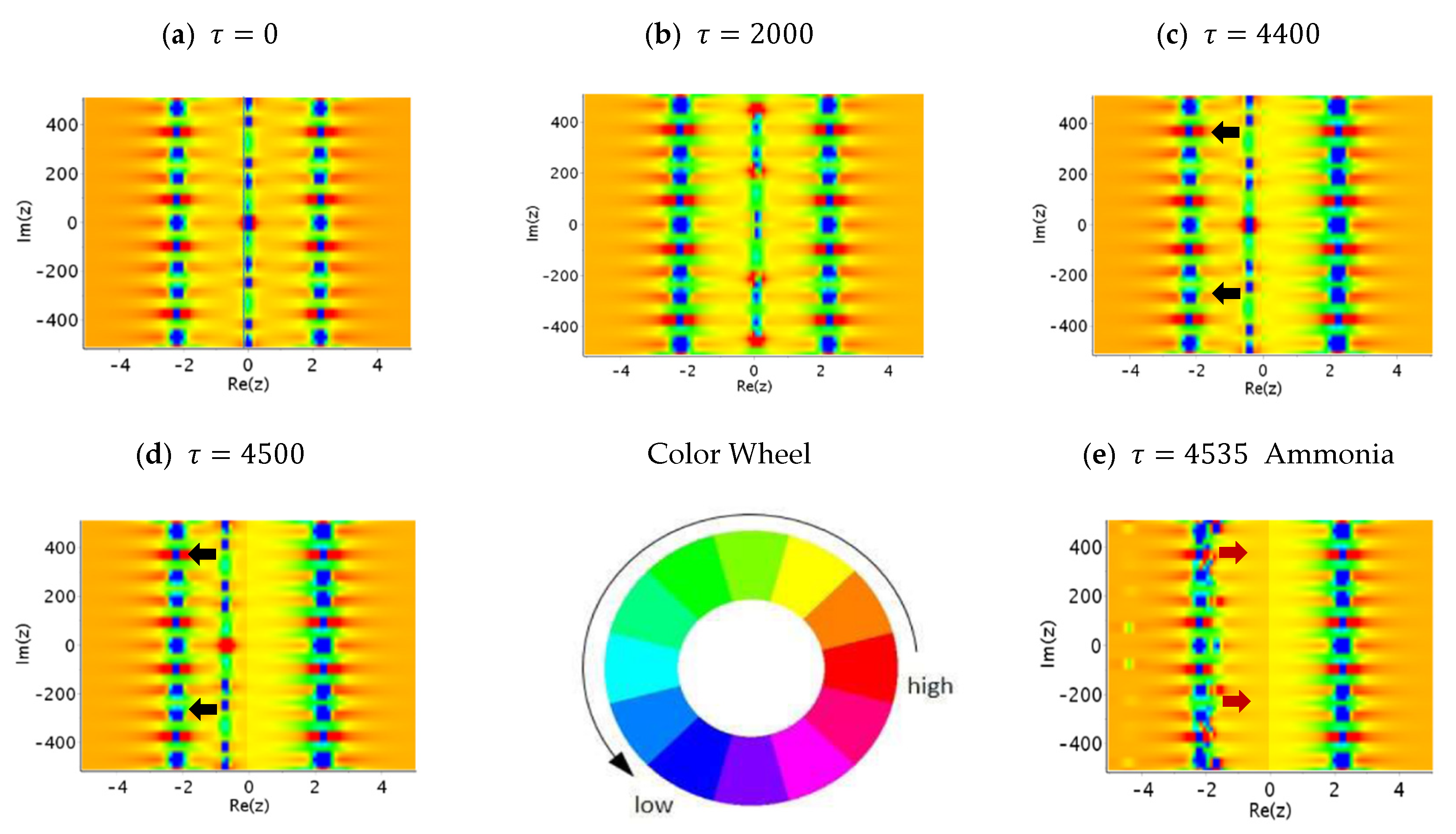
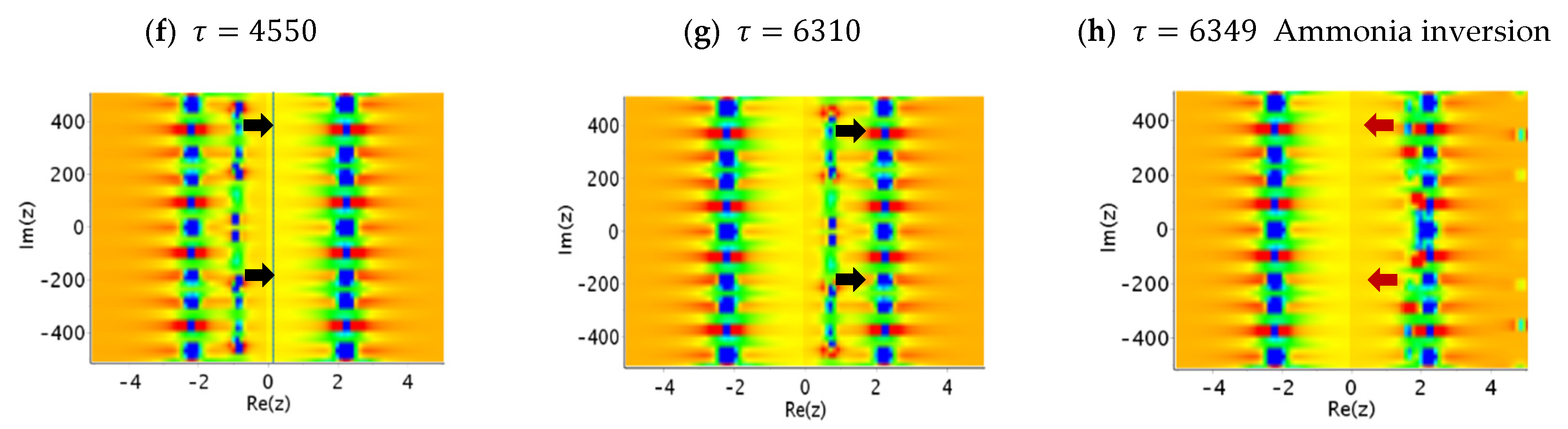
6. Tunneling Dynamics in Two-Level Transition States
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhong, S.Q.; Zhao, S.C.; Zhu, S.N. Photovoltaic properties enhanced by the tunneling effect in a coupled quantum dot photocell. Res. Phys. 2021, 4, 104094. [Google Scholar]
- Saldaña, J.C.E.; Vekris, A.; Žitko, R.; Steffensen, G.; Krogstrup, P.; Paaske, J.; Grove-Rasmussen, K.; Nygård, J. Two-impurity Yu-Shiba-Rusinov states in coupled quantum dots. Phys. Rev. B 2020, 102, 195143. [Google Scholar] [CrossRef]
- Guo, R.; Tao, L.; Li, M.; Liu, Z.; Lin, W.; Zhou, G.; Chen, X.; Liu, L.; Yan, X.; Tian, H.; et al. Interface-engineered electron and hole tunneling. Sci. Adv. 2021, 7, eabf1033. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Chen, S.; Yu, H.; Chen, J.; Yan, X.; Li, L.; Xu, M.-W. Overcoming the conductivity limit of insulator through tunneling-current junction welding: Ag @ PVP core–shell nanowire for high-performance transparent electrode. J. Mater. Chem. C 2021, 9, 3957–3968. [Google Scholar] [CrossRef]
- Huang, H.; Padurariu, C.; Ast, C.R. Tunneling dynamics between superconducting bound states at the atomic limit. Nat. Phys. 2020, 16, 1227–1231. [Google Scholar] [CrossRef]
- Gutzler, R.; Garg, M.; Kern, K. Light-matter interaction at atomic scales. Nat. Rev. Phys. 2021, 3, 441–453. [Google Scholar] [CrossRef]
- Belkadi, A.; Weerakkody, A.; Moddel, G. Demonstration of resonant tunneling effects in metal-double-insulator-metal (MI2M) diodes. Nat. Commun. 2021, 12, 2925. [Google Scholar] [CrossRef]
- Priya, G.L.; Venkatesh, M.; Samuel, T.S.A. Triple metal surrounding gate junctionless tunnel FET based 6T SRAM design for low leakage memory system. Silicon 2021, 13, 1691–1702. [Google Scholar] [CrossRef]
- Sharifi, F.; Gavilano, J.L.; Van Harlingen., D.J. Macroscopic quantum tunneling and thermal activation from metastable states in a dc SQUID. Phys. Rev. Lett. 1988, 61, 742–745. [Google Scholar] [CrossRef] [PubMed]
- Steinberg, A.M. How much time does a tunneling particle spend in the barrier region? Phys. Rev. Lett. 1995, 74, 2405–2409. [Google Scholar] [CrossRef] [PubMed]
- Xavier, A.L., Jr.; de Aguiar, M.A.M. Phase-space approach to the tunneling effect: A new semiclassical traversal time. Phys. Rev. Lett. 1997, 79, 3323–3326. [Google Scholar] [CrossRef]
- Ben-Nun, M.; Martinez, T.J. A multiple spawning approach to tunneling dynamics. J. Chem. Phys. 2000, 112, 6113. [Google Scholar] [CrossRef]
- Onishi, T.; Shudo, A.; Ikeda, K.S.; Takahashi, K. Semiclassical study on tunneling processes via complex-domain chaos. Phys. Rev. E 2003, 68, 056211. [Google Scholar] [CrossRef] [PubMed]
- Davies, P.C.W. Quantum tunneling time. Am. J. Phys. 2005, 73, 23–27. [Google Scholar] [CrossRef]
- Gradinaru, V.; Hagedorn, G.; Joye, A. Tunneling dynamics and spawning with adaptive semi-classical wave-packets. J. Chem. Phys. 2010, 132, 184108. [Google Scholar] [CrossRef]
- Landsman, A.S.; Keller, U. Attosecond science and the tunneling time problem. Phys. Rep. 2015, 547, 1–24. [Google Scholar] [CrossRef]
- Jensen, K.L.; Shiffler, D.A.; Lebowitz, J.L.; Cahay, M.; Petillo, J.J. Analytic Wigner distribution function for tunneling and trajectory models. J. Appl. Phys. 2019, 125, 114303. [Google Scholar] [CrossRef]
- Yusifsani, S.; Koleslk, M. Quantum tunneling time: Insights from an exactly solvable model. Phys. Rev. A 2020, 101, 052121. [Google Scholar] [CrossRef]
- Rivlin, T.; Pollak, E.; Dumont, R.S. Determination of the tunneling flight time as the reflected phase time. Phys. Rev. A 2021, 103, 012225. [Google Scholar] [CrossRef]
- Levit, S. Variational approach to tunneling dynamics. Application to hot superfluid fermi systems. Spontaneous and induced fission. Phys. Lett. B 2021, 813, 136042. [Google Scholar] [CrossRef]
- Bohm, D. A suggested interpretation of the quantum theory in terms of hidden variables. Phys. Rev. 1952, 85, 166–193. [Google Scholar] [CrossRef]
- Leacock, R.A.; Padgett, M.J. Hamilton-Jacobi theory and the quantum action variable. Phys. Rev. Lett. 1983, 50, 3–6. [Google Scholar] [CrossRef]
- Frisk, H. Properties of the trajectories in Bohmian mechanics. Phys. Lett. A 1997, 227, 139–142. [Google Scholar] [CrossRef]
- Holland, P.R. New trajectory interpretation of quantum mechanics. Found. Phys. 1998, 28, 881–991. [Google Scholar] [CrossRef]
- John, M.V. Modified de Broglie-Bohm approach to quantum mechanics. Found. Phys. Lett. 2002, 15, 329–343. [Google Scholar] [CrossRef]
- Mostacci, D.; Molinari, V.; Pizzio, F. Quantum macroscopic equations from Bohm potential and propagation of waves. Physica A 2008, 387, 6771–6777. [Google Scholar] [CrossRef]
- Dey, S.; Fring, A. Bohmian quantum trajectories from coherent states. Phys. Rev. A 2013, 88, 022116. [Google Scholar] [CrossRef]
- Chou, C.C. Trajectory approach to the Schrodinger-Langevin equation with linear dissipation for ground states. Ann. Phys. 2015, 362, 57–73. [Google Scholar] [CrossRef]
- Sanz, A.S.; Borondo, F.; Miret-Artes, S. Particle diffraction studied using quantum trajectories. J. Phys. Condens. Matter 2002, 14, 6109–6145. [Google Scholar] [CrossRef]
- Yang, C.D. Wave-particle duality in complex space. Ann. Phys. 2005, 319, 444–470. [Google Scholar] [CrossRef]
- Goldfarb, Y.; Degani, I.; Tannor, D.J. Bohmian mechanics with complex action: A new trajectory-based formulation of quantum mechanics. J. Chem. Phys. 2006, 125, 231103. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.D. Quantum Hamilton mechanics: Hamilton equations of quantum motion, origin of quantum operators, and proof of quantization axiom. Ann. Phys. 2006, 321, 2876–2926. [Google Scholar] [CrossRef]
- John, M.V. Probability and complex quantum trajectories. Ann. Phys. 2009, 324, 220–231. [Google Scholar] [CrossRef][Green Version]
- Bender, C.M.; Hook, D.W.; Meisinger, P.N.; Wang, Q.H. Probability density in the complex plane. Ann. Phys. 2010, 325, 2332–2362. [Google Scholar] [CrossRef]
- Anderson, A.G.; Bender, C.M. Complex trajectories in a classical periodic potential. J. Phys. A Math. Theor. 2012, 45, 45–60. [Google Scholar] [CrossRef][Green Version]
- Yang, C.D. Optimal guidance law in quantum mechanics. Ann. Phys. 2013, 338, 167–185. [Google Scholar] [CrossRef]
- Yang, C.D.; Su, K.C. Reconstructing interference fringes in slit experiments by complex quantum trajectories. Int. J. Quan. Chem. 2013, 113, 1253–1263. [Google Scholar] [CrossRef]
- Payandeh, F. Klein’s paradox and quantum Hamiltonian dynamics in complex spacetime. Mod. Phys. Lett. A 2014, 29, 1450095. [Google Scholar] [CrossRef]
- Chou, C.C. Complex quantum Hamilton-Jacobi equation with Bohmian trajectories: Application to the photodissociation dynamics of NOCI. J. Chem. Phys. 2014, 140, 104307. [Google Scholar] [CrossRef]
- Chou, C.C. Dissipative quantum trajectories in complex space: Damped harmonic oscillator. Ann. Phys. 2016, 373, 325–345. [Google Scholar] [CrossRef]
- Koch, W.; Tannor, D.J. Wavepacket revivals via complex trajectory propagation. Chem. Phys. Lett. 2017, 683, 306–314. [Google Scholar] [CrossRef][Green Version]
- Bracken, P. The complex quantum potential and wave-particle duality. Mod. Phys. Lett. B 2018, 32, 1850030. [Google Scholar] [CrossRef]
- Davidson, M. Bohmian trajectories for Kerr-Newman particles in complex space-time. Found. Phys. 2018, 48, 1590–1616. [Google Scholar] [CrossRef]
- Yang, C.D.; Han, S.Y. Trajectory interpretation of correspondence principle: Solution of nodal issue. Found. Phys. 2020, 50, 960–976. [Google Scholar] [CrossRef]
- Zhao, W.L.; Gong, P.; Wang, J.; Wang, Q. Chaotic dynamics of complex trajectory and its quantum signature. Chin. Phys. B 2020, 29, 120302. [Google Scholar] [CrossRef]
- Yang, C.D.; Han, S.Y. Extending quantum probability from real axis to complex plane. Entropy 2021, 23, 210. [Google Scholar] [CrossRef]
- Levkov, D.G.; Panin, A.G.; Sibiryakov, S.M. Complex trajectories in chaotic dynamical tunneling. Phys. Rev. E 2007, 76, 046209. [Google Scholar] [CrossRef]
- Yang, C.-D. Complex tunneling dynamics. Chaos Solitons Fractals 2007, 32, 312–345. [Google Scholar] [CrossRef]
- Mathew, K.; John, M.V. Tunneling in energy eigenstates and complex quantum trajectories. Quan. Stud. Math. Found. 2015, 2, 403–416. [Google Scholar] [CrossRef]
- Kocsis, S.; Braverman, B.; Ravets, S.; Stevens, M.J.; Mirin, R.P.; Shalm, L.K.; Steinberg, A.M. Observing the Average Trajectories of Single Photons in a Two-Slit Interferometer. Science 2011, 332, 1170–1173. [Google Scholar] [CrossRef] [PubMed]
- Murch, K.W.; Weber, S.J.; Macklin, C.; Siddiqi, I. Observing single quantum trajectories of a superconducting quantum bit. Nat. Cell Biol. 2013, 502, 211–214. [Google Scholar] [CrossRef]
- Roch, N.; Schwartz, M.; Motzoi, F.; Macklin, C.; Vijay, R.; Eddins, A.W.; Korotkov, A.N.; Whaley, K.B.; Sarovar, M.; Siddiqi, I. Observation of Measurement-Induced Entanglement and Quantum Trajectories of Remote Superconducting Qubits. Phys. Rev. Lett. 2014, 112, 170501. [Google Scholar] [CrossRef]
- Procopio, L.M.; Rozema, L.A.; Wong, Z.J.; Hamel, D.R.; O’Brien, K.; Zhang, X.; Dakić, B.; Walther, P. Single-photon test of hyper-complex quantum theories using a metamaterial. Nat. Commun. 2017, 8, 15044. [Google Scholar] [CrossRef] [PubMed]
- Rossi, M.; Mason, D.; Chen, J.; Schliesser, A. Observing and Verifying the Quantum Trajectory of a Mechanical Resonator. Phys. Rev. Lett. 2019, 123, 163601. [Google Scholar] [CrossRef]
- Zhou, Z.-Q.; Liu, X.; Kedem, Y.; Cui, J.-M.; Li, Z.-F.; Hua, Y.-L.; Li, C.-F.; Guo, G.-C. Experimental observation of anomalous trajectories of single photons. Phys. Rev. A 2017, 95, 042121. [Google Scholar] [CrossRef]
- Rubino, G.; Rozema, L.A.; Ebler, D.; Kristjánsson, H.; Salek, S.; Guérin, P.A.; Abbott, A.A.; Branciard, C.; Brukner, Č.; Chiribella, G.; et al. Experimental quantum communication enhancement by superposing trajectories. Phys. Rev. Res. 2021, 3, 013093. [Google Scholar] [CrossRef]
- Aharonov, Y.; Vaidman, D. How the result of a measurement of a component of the spin of a spin-1/2 particle can turn out to be 100. Phys. Rev. Lett. 1998, 60, 1351–1354. [Google Scholar] [CrossRef]
- Hofmann, H.F. On the role of complex phases in the quantum statistics of weak measurements. New J. Phys. 2011, 13, 103009. [Google Scholar] [CrossRef]
- Dressel, J.; Jordan, A.N. Significance of the imaginary part of the weak value. Phys. Rev. A 2012, 85, 012107. [Google Scholar] [CrossRef]
- Dressel, J.; Malik, M.; Miatto, F.; Jordan, A.; Boud, R. Colloquium: Understanding quantum weak values: Basic and applications. Rev. Mod. Phys. 2014, 85, 307–316. [Google Scholar] [CrossRef]
- Mori, T.; Tsutsui, I. Quantum trajectories based on the weak value. Prog. Theor. Exp. Phys. 2015, 2015, 043A01. [Google Scholar] [CrossRef]
- Rebufello, E.; Piacentini, F.; Avella, A.; de Souza, M.A.; Gramegna, M.; Dziewior, J.; Cohen, E.; Vaidman, L.; Degiovanni, I.P.; Genovese, M. Anomalous weak values via a single photon detection. Light. Sci. Appl. 2021, 10, 1–6. [Google Scholar] [CrossRef]
- Wu, K.-D.; Kondra, T.V.; Rana, S.; Scandolo, C.M.; Xiang, G.-Y.; Li, C.-F.; Guo, G.-C.; Streltsov, A. Operational Resource Theory of Imaginarity. Phys. Rev. Lett. 2021, 126, 090401. [Google Scholar] [CrossRef] [PubMed]
- Wu, K.-D.; Kondra, T.V.; Rana, S.; Scandolo, C.M.; Xiang, G.-Y.; Li, C.-F.; Guo, G.-C.; Streltsov, A. Resource theory of imaginarity: Quantification and state conversion. Phys. Rev. A 2021, 103, 032401. [Google Scholar] [CrossRef]
- Dennison, D.M.; Uhlenbeck, G.E. The Two-Minima Problem and the Ammonia Molecule. Phys. Rev. 1932, 41, 313–321. [Google Scholar] [CrossRef]
- Dennison, D.M.; Hardy, J.D. The parallel type absorption bands of ammonia. Phys. Rev. 1932, 39, 938–947. [Google Scholar]
- Rosen, N.; Morse, P.M. On the vibrations of polyatomic molecules. Phys. Rev. 1932, 42, 210–217. [Google Scholar] [CrossRef]
- Feynman, R.P.; Leighton, R.B.; Sands, M.; Treiman, S.B. The Feynman Lectures on Physics. Phys. Today 1964, 17, 45–46. [Google Scholar] [CrossRef]






| Equilibrium Positions | 0 | |||
| Tunneling Range | ||||
| Tunneling Frequency | Hz | Hz | Hz | |
| Equilibrium Positions | ||||
| Tunneling Range | - | 0 | ||
| Tunneling Frequency | Hz | Hz | Hz | |
| Equilibrium Positions | - | |||
| Tunneling Range | - | |||
| Tunneling Frequency | - | Hz | Hz | |
| Equilibrium Positions | - | - | ||
| Tunneling Range | - | - | −3.298~−3.145, 3.145~3.298 | |
| Tunneling Frequency | - | - | Hz | |
| Hz |
| Comparison | Tunneling Range | Energy Splitting | Tunneling Frequency |
|---|---|---|---|
| Experimental data | |||
| Theoretical results | - | ||
| Computation results |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, C.-D.; Han, S.-Y. Tunneling Quantum Dynamics in Ammonia. Int. J. Mol. Sci. 2021, 22, 8282. https://doi.org/10.3390/ijms22158282
Yang C-D, Han S-Y. Tunneling Quantum Dynamics in Ammonia. International Journal of Molecular Sciences. 2021; 22(15):8282. https://doi.org/10.3390/ijms22158282
Chicago/Turabian StyleYang, Ciann-Dong, and Shiang-Yi Han. 2021. "Tunneling Quantum Dynamics in Ammonia" International Journal of Molecular Sciences 22, no. 15: 8282. https://doi.org/10.3390/ijms22158282
APA StyleYang, C.-D., & Han, S.-Y. (2021). Tunneling Quantum Dynamics in Ammonia. International Journal of Molecular Sciences, 22(15), 8282. https://doi.org/10.3390/ijms22158282







