Multiscale Modeling of Wobble to Watson–Crick-Like Guanine–Uracil Tautomerization Pathways in RNA
Abstract
1. Introduction
2. Computational Methods and Details
2.1. QM
2.2. MD
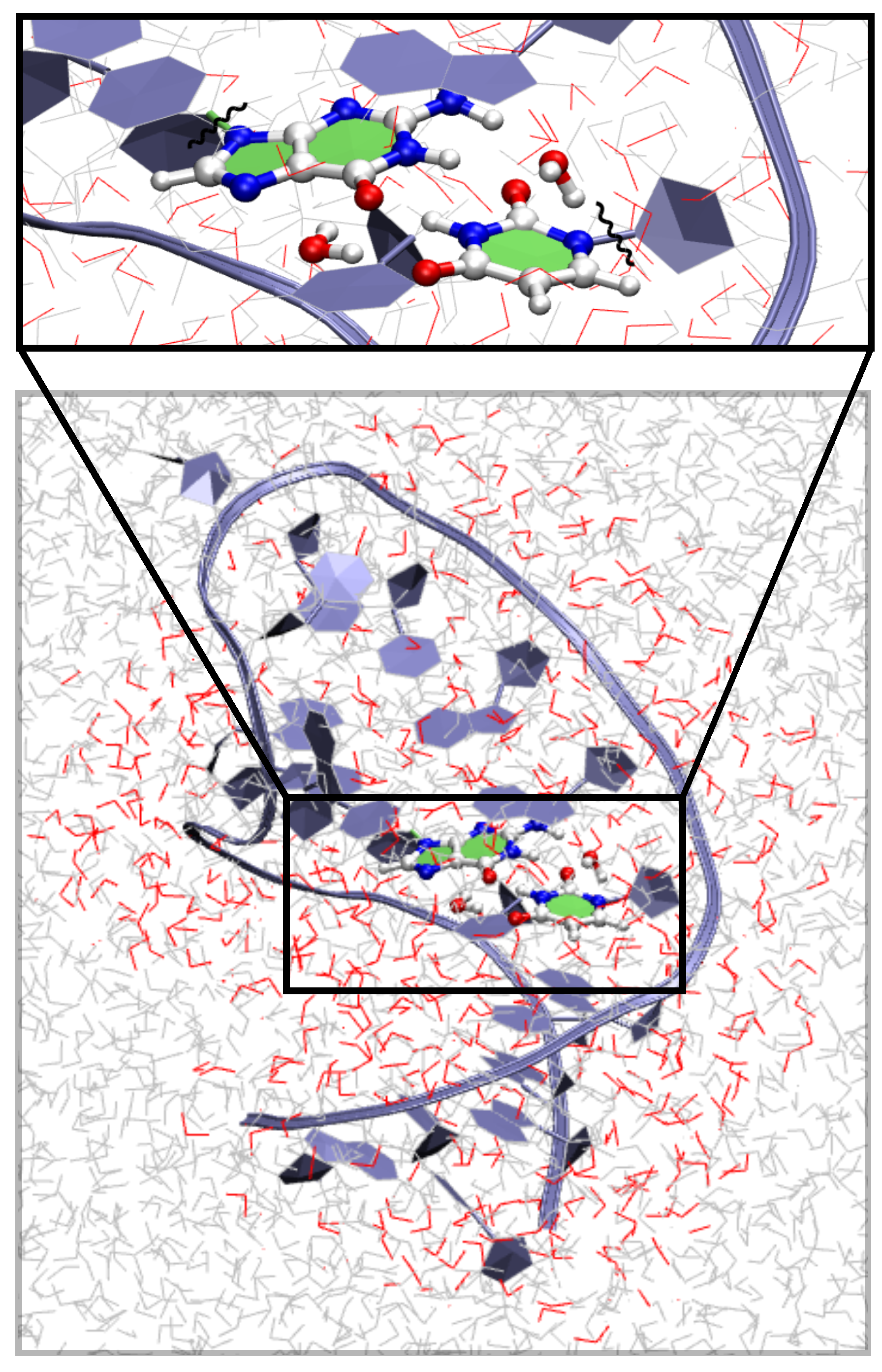
2.3. QM/MM
3. Results and Discussion
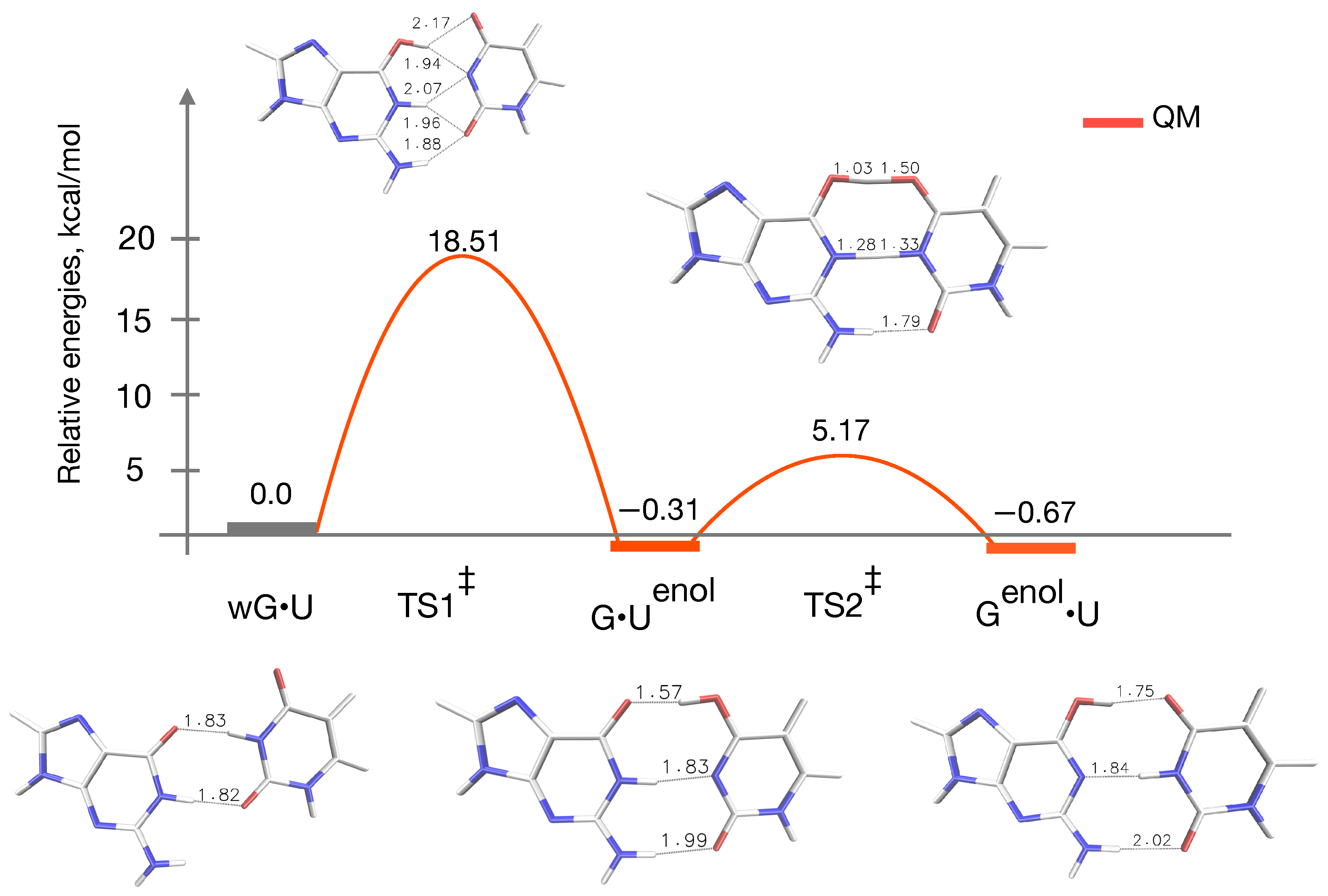
3.1. QM Profile without Microsolvation
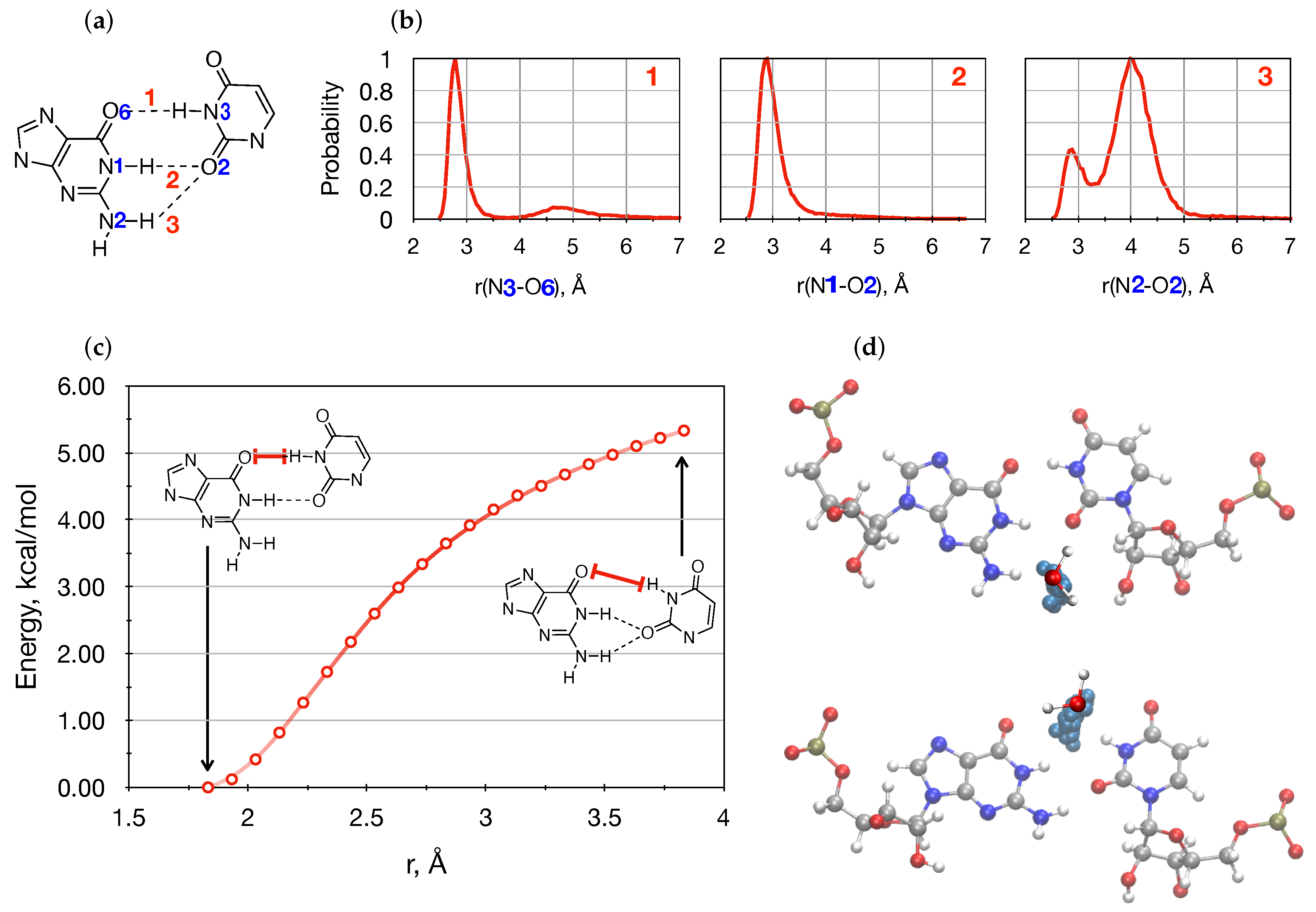
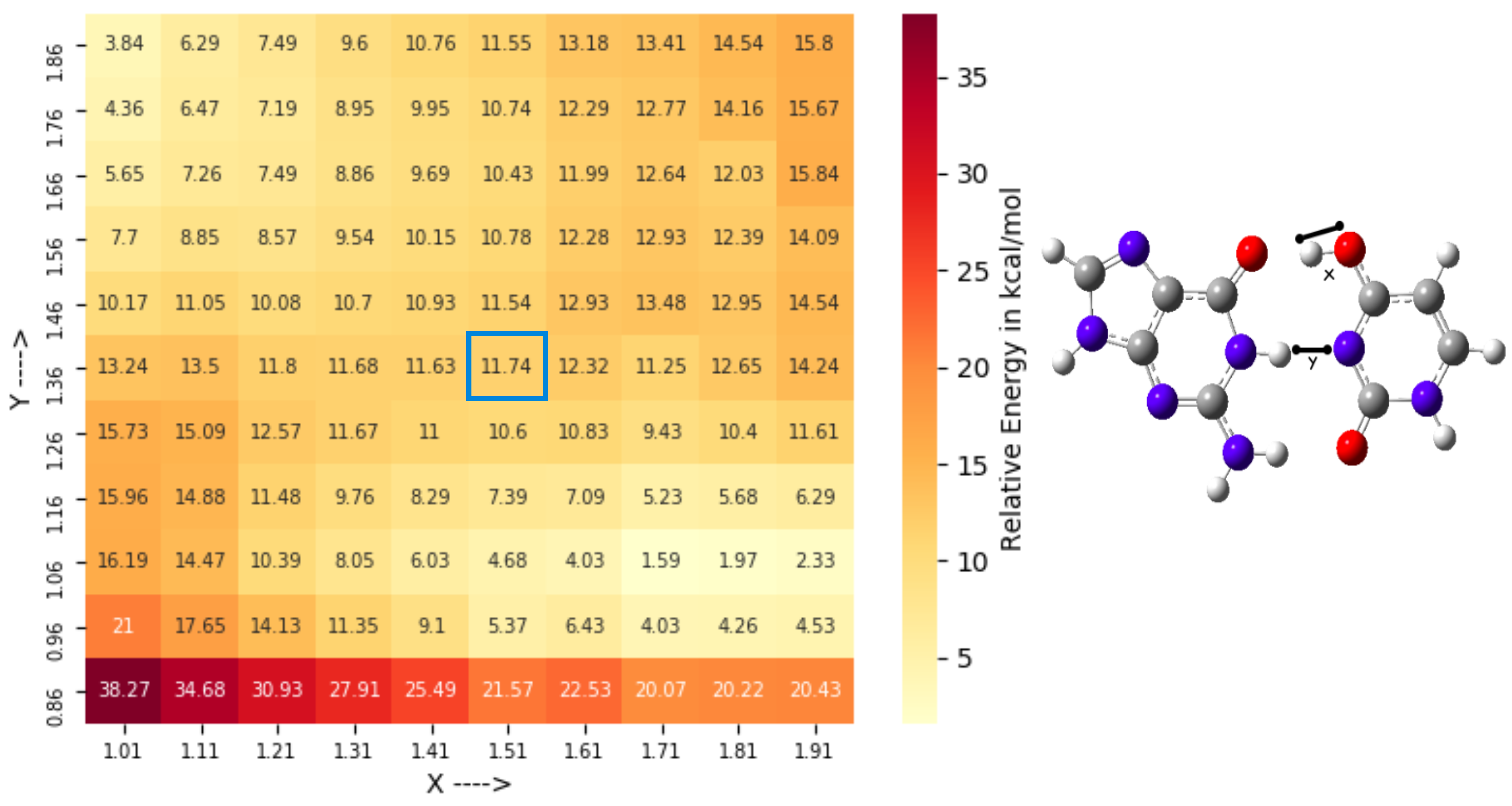
3.2. Conformational Space Sampling Using MD Simulations
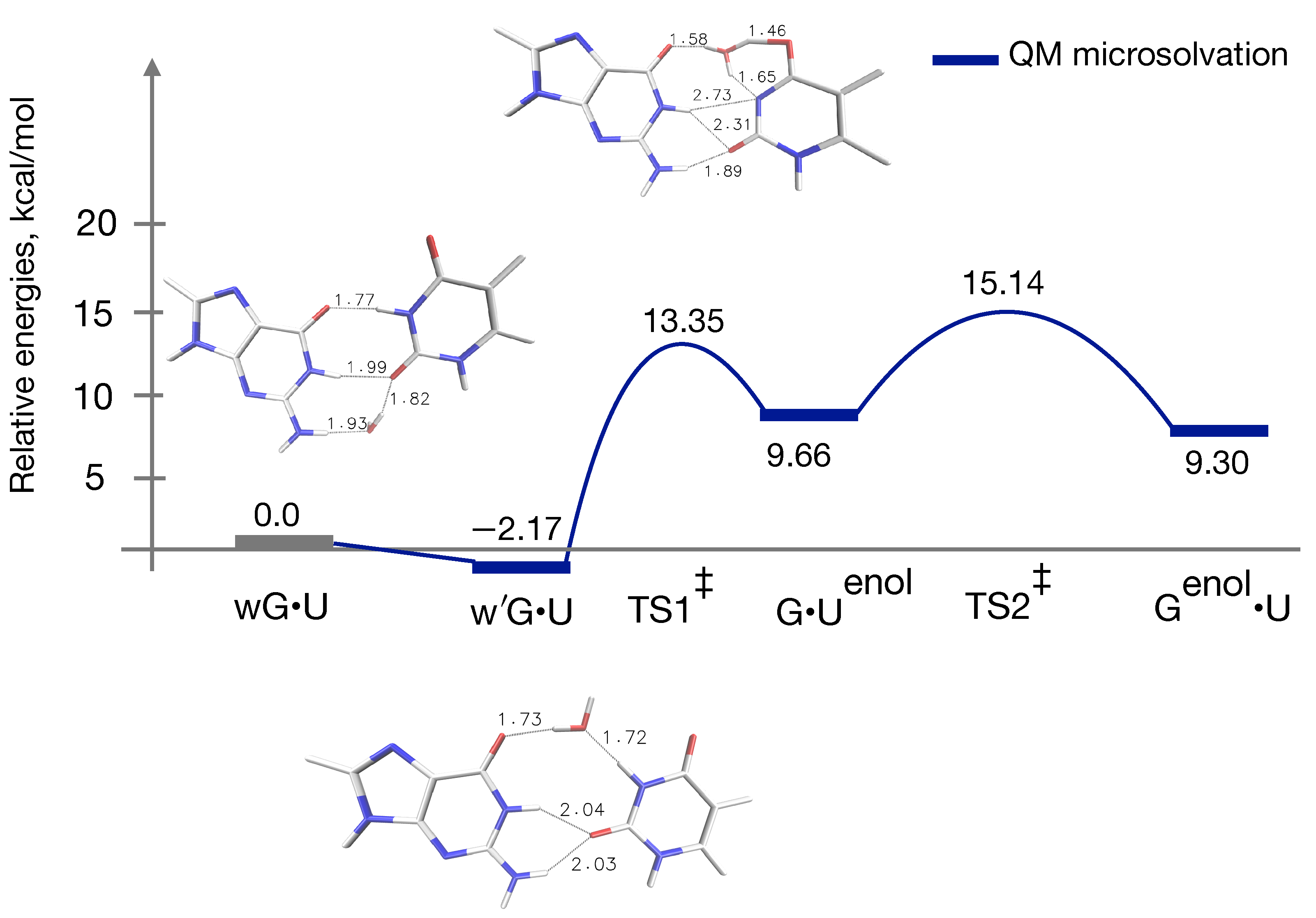
3.3. QM Profile Including Microsolvation
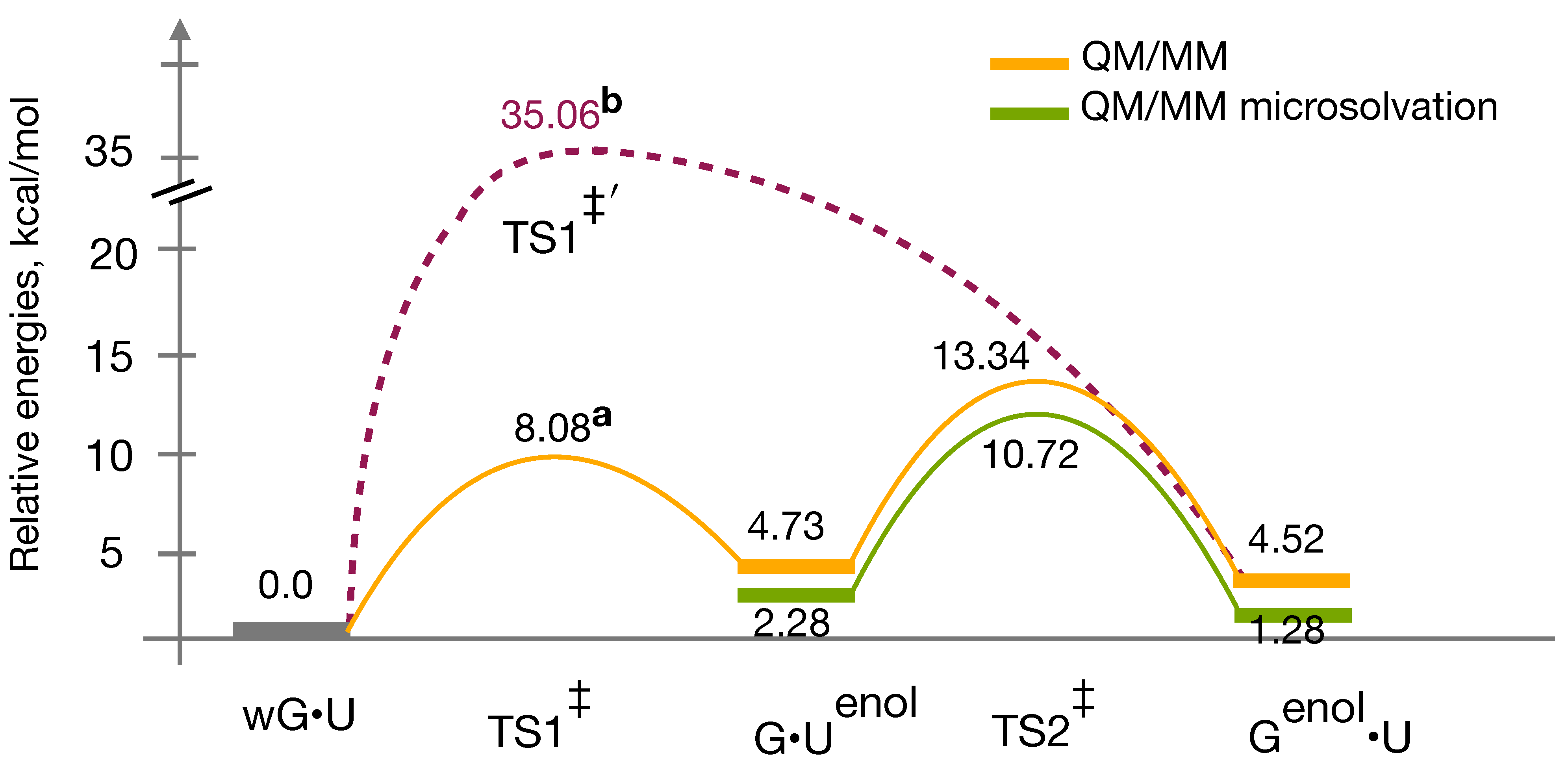
3.4. QM/MM Profile
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| QM/MM | Quantum Mechanics/Molecular Mechanics |
| MD | Molecular Dynamics |
| DFT | Density Functional Theory |
| NMR | Nuclear Magnetic Resonance |
| WC | Watson–Crick |
| guanine•uracil | G•U |
| DNA | Deoxyribonucleic Acid |
| RNA | Ribonucleic Acid |
References
- Watson, J.D.; Crick, F.H. Genetical implications of the structure of deoxyribonucleic acid. Nature 1953, 171, 964–967. [Google Scholar] [CrossRef]
- Topal, M.D.; Fresco, J.R. Complementary base pairing and the origin of substitution mutations. Nature 1976, 263, 285–289. [Google Scholar] [CrossRef]
- Draper, D.E. A guide to ions and RNA structure. RNA 2004, 10, 335–343. [Google Scholar] [CrossRef]
- Lipfert, J.; Doniach, S.; Das, R.; Herschlag, D. Understanding Nucleic Acid–Ion Interactions. Annu. Rev. Biochem. 2014, 83, 813–841. [Google Scholar] [CrossRef]
- Singh, V.; Fedeles, B.I.; Essigmann, J.M. Role of tautomerism in RNA biochemistry. RNA 2015, 21, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Gilbert, S.D.; Reyes, F.E.; Edwards, A.L.; Batey, R.T. Adaptive ligand binding by the purine riboswitch in the recognition of guanine and adenine analogs. Structure 2009, 17, 857–868. [Google Scholar] [CrossRef]
- Thore, S.; Frick, C.; Ban, N. Structural basis of thiamine pyrophosphate analogues binding to the eukaryotic riboswitch. J. Am. Chem. Soc. 2008, 130, 8116–8117. [Google Scholar] [CrossRef] [PubMed]
- Singh, V.; Peng, C.S.; Li, D.; Mitra, K.; Silvestre, K.J.; Tokmakoff, A.; Essigmann, J.M. Direct observation of multiple tautomers of oxythiamine and their recognition by the thiamine pyrophosphate riboswitch. ACS Chem. Biol. 2014, 9, 227–236. [Google Scholar] [CrossRef] [PubMed]
- Mulder, F.A.; Mittermaier, A.; Hon, B.; Dahlquist, F.W.; Kay, L.E. Studying excited states of proteins by NMR spectroscopy. Nat. Struct. Biol. 2001, 8, 932–935. [Google Scholar] [CrossRef]
- Early, T.A.; Olmsted, J., III; Kearns, D.R.; Lezius, A.G. Base pairing structure in the poly d (GT) double helix: Wobble base pairs. Nucleic Acids Res. 1978, 5, 1955–1970. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Hunter, W.N.; Brown, T.; Kneale, G.; Anand, N.N.; Rabinovich, D.; Kennard, O. The structure of guanosine-thymidine mismatches in B-DNA at 2.5-A resolution. J. Biol. Chem. 1987, 262, 9962–9970. [Google Scholar] [CrossRef]
- Brown, T.; Kennard, O.; Kneale, G.; Rabinovich, D. High-resolution structure of a DNA helix containing mismatched base pairs. Nature 1985, 315, 604–606. [Google Scholar] [CrossRef]
- Ho, P.; Frederick, C.; Quigley, G.; Van der Marel, G.; Van Boom, J.; Wang, A.; Rich, A. GT wobble base-pairing in Z-DNA at 1.0 A atomic resolution: The crystal structure of d (CGCGTG). EMBO J. 1985, 4, 3617–3623. [Google Scholar] [CrossRef]
- Bebenek, K.; Pedersen, L.C.; Kunkel, T.A. Replication infidelity via a mismatch with Watson–Crick geometry. Proc. Natl. Acad. Sci. USA 2011, 108, 1862–1867. [Google Scholar] [CrossRef]
- Wang, W.; Hellinga, H.W.; Beese, L.S. Structural evidence for the rare tautomer hypothesis of spontaneous mutagenesis. Proc. Natl. Acad. Sci. USA 2011, 108, 17644–17648. [Google Scholar] [CrossRef] [PubMed]
- Demeshkina, N.; Jenner, L.; Westhof, E.; Yusupov, M.; Yusupova, G. A new understanding of the decoding principle on the ribosome. Nature 2012, 484, 256–259. [Google Scholar] [CrossRef]
- Padermshoke, A.; Katsumoto, Y.; Masaki, R.; Aida, M. Thermally induced double proton transfer in GG and wobble GT base pairs: A possible origin of the mutagenic guanine. Chem. Phys. Lett. 2008, 457, 232–236. [Google Scholar] [CrossRef]
- Nomura, K.; Hoshino, R.; Shimizu, E.; Hoshiba, Y.; Danilov, V.I.; Kurita, N. DFT calculations on the effect of solvation on the tautomeric reactions for wobble Gua-Thy and canonical Gua-Cyt base-pairs. J. Mod. Phys. 2013, 4, 422–431. [Google Scholar] [CrossRef]
- Ol’ha, O.B.; Hovorun, D.M. New structural hypostases of the A· T and G· C Watson–Crick DNA base pairs caused by their mutagenic tautomerisation in a wobble manner: A QM/QTAIM prediction. RSC Adv. 2015, 5, 99594–99605. [Google Scholar]
- Brovarets’, O.O.; Hovorun, D.M. How many tautomerization pathways connect Watson–Crick-like G*· T DNA base mispair and wobble mismatches? J. Biomol. Struct. Dyn. 2015, 33, 2297–2315. [Google Scholar] [CrossRef] [PubMed]
- Maximoff, S.N.; Kamerlin, S.C.L.; Flori’an, J. DNA polymerase λ active site favors a mutagenic mispair between the enol form of deoxyguanosine triphosphate substrate and the keto form of thymidine template: A free energy perturbation study. J. Phys. Chem. B 2017, 121, 7813–7822. [Google Scholar] [CrossRef]
- Satpati, P.; Åqvist, J. Why base tautomerization does not cause errors in mRNA decoding on the ribosome. Nucleic Acids Res. 2014, 42, 12876–12884. [Google Scholar] [CrossRef] [PubMed]
- Hartono, Y.D.; Ito, M.; Villa, A.; Nilsson, L. Computational study of uracil tautomeric forms in the ribosome: The case of uracil and 5-oxyacetic acid uracil in the first anticodon position of tRNA. J. Phys. Chem. B 2018, 122, 1152–1160. [Google Scholar] [CrossRef] [PubMed]
- Kimsey, I.J.; Petzold, K.; Sathyamoorthy, B.; Stein, Z.W.; Al-Hashimi, H.M. Visualizing transient Watson–Crick-like mispairs in DNA and RNA duplexes. Nature 2015, 519, 315–320. [Google Scholar] [CrossRef]
- Szymanski, E.S.; Kimsey, I.J.; Al-Hashimi, H.M. Direct NMR evidence that transient tautomeric and anionic states in dG· dT form Watson–Crick-like base pairs. J. Am. Chem. Soc. 2017, 139, 4326–4329. [Google Scholar] [CrossRef]
- Kimsey, I.J.; Szymanski, E.S.; Zahurancik, W.J.; Shakya, A.; Xue, Y.; Chu, C.C.; Sathyamoorthy, B.; Suo, Z.; Al-Hashimi, H.M. Dynamic basis for dG• dT misincorporation via tautomerization and ionization. Nature 2018, 554, 195–201. [Google Scholar] [CrossRef]
- Orozco, M.; Hernández, B.; Luque, F.J. Tautomerism of 1-methyl derivatives of uracil, thymine, and 5-bromouracil. Is tautomerism the basis for the mutagenicity of 5-bromouridine? J. Phys. Chem. B 1998, 102, 5228–5233. [Google Scholar] [CrossRef]
- Hunter, W.N.; Kneale, G.; Brown, T.; Rabinovich, D.; Kennard, O. Refined crystal structure of an octanucleotide duplex with G· T mismatched base-pairs. J. Mol. Biol. 1986, 190, 605–618. [Google Scholar] [CrossRef]
- Koag, M.C.; Nam, K.; Lee, S. The spontaneous replication error and the mismatch discrimination mechanisms of human DNA polymerase β. Nucleic Acids Res. 2014, 42, 11233–11245. [Google Scholar] [CrossRef] [PubMed]
- Wu, E.Y.; Beese, L.S. The structure of a high fidelity DNA polymerase bound to a mismatched nucleotide reveals an “ajar” intermediate conformation in the nucleotide selection mechanism. J. Biol. Chem. 2011, 286, 19758–19767. [Google Scholar] [CrossRef]
- Xia, S.; Konigsberg, W.H. Mispairs with Watson-Crick base-pair geometry observed in ternary complexes of an RB69 DNA polymerase variant. Protein Sci. 2014, 23, 508–513. [Google Scholar] [CrossRef]
- Brovarets’, O.O.; Hovorun, D.M. The nature of the transition mismatches with Watson–Crick architecture: The G*· T or G· T* DNA base mispair or both? A QM/QTAIM perspective for the biological problem. J. Biomol. Struct. Dyn. 2015, 33, 925–945. [Google Scholar] [CrossRef] [PubMed]
- Li, P.; Rangadurai, A.; Al-Hashimi, H.M.; Hammes-Schiffer, S. Environmental Effects on Guanine-Thymine Mispair Tautomerization Explored with Quantum Mechanical/Molecular Mechanical Free Energy Simulations. J. Am. Chem. Soc. 2020, 142, 11183–11191. [Google Scholar] [CrossRef] [PubMed]
- Kazantsev, A.; Ignatova, Z. Tautomerization constraints the accuracy of codon-anticodon decoding. bioRxiv 2020. [Google Scholar] [CrossRef]
- Bevilacqua, P.C.; Yajima, R. Nucleobase catalysis in ribozyme mechanism. Curr. Opin. Chem. Biol. 2006, 10, 455–464. [Google Scholar] [CrossRef] [PubMed]
- Cochrane, J.C.; Strobel, S.A. Catalytic strategies of self-cleaving ribozymes. Acc. Chem. Res. 2008, 41, 1027–1035. [Google Scholar] [CrossRef]
- Weixlbaumer, A.; Murphy, F.V.; Dziergowska, A.; Malkiewicz, A.; Vendeix, F.A.; Agris, P.F.; Ramakrishnan, V. Mechanism for expanding the decoding capacity of transfer RNAs by modification of uridines. Nat. Struct. Mol. Biol. 2007, 14, 498–502. [Google Scholar] [CrossRef]
- Cantara, W.A.; Murphy, F.V.; Demirci, H.; Agris, P.F. Expanded use of sense codons is regulated by modified cytidines in tRNA. Proc. Natl. Acad. Sci. USA 2013, 110, 10964–10969. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Fedeles, B.I.; Singh, V.; Peng, C.S.; Silvestre, K.J.; Simi, A.K.; Simpson, J.H.; Tokmakoff, A.; Essigmann, J.M. Tautomerism provides a molecular explanation for the mutagenic properties of the anti-HIV nucleoside 5-aza-5, 6-dihydro-2’-deoxycytidine. Proc. Natl. Acad. Sci. USA 2014, 111, E3252–E3259. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian˜16 Revision C.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Dirac, P.A.M. Quantum Mechanics of Many-Electron Systems. Proc. R. Soc. Lond. A 1929, 123, 714–733. [Google Scholar]
- Slater, J.C. A Simplification of the Hartree-Fock Method. Phys. Rev. 1951, 81, 385–390. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Krishnan, R.; Binkley, J.S.; Seeger, R.; Pople, J.A. Self-consistent molecular orbital methods. XX. A basis set for correlated wave functions. J. Chem. Phys. 1980, 72, 650–654. [Google Scholar] [CrossRef]
- Clark, T.; Chandrasekhar, J.; Spitznagel, G.W.; Schleyer, P.V.R. Efficient diffuse function-augmented basis sets for anion calculations. III. The 3-21+ G basis set for first-row elements, Li–F. J. Comput. Chem. 1983, 4, 294–301. [Google Scholar] [CrossRef]
- Frisch, M.J.; Pople, J.A.; Binkley, J.S. Self-consistent molecular orbital methods 25. Supplementary functions for Gaussian basis sets. J. Chem. Phys. 1984, 80, 3265–3269. [Google Scholar] [CrossRef]
- Pietro, W.J.; Francl, M.M.; Hehre, W.J.; DeFrees, D.J.; Pople, J.A.; Binkley, J.S. Self-consistent molecular orbital methods. 24. Supplemented small split-valence basis sets for second-row elements. J. Am. Chem. Soc. 1982, 104, 5039–5048. [Google Scholar] [CrossRef]
- Dethoff, E.A.; Petzold, K.; Chugh, J.; Casiano-Negroni, A.; Al-Hashimi, H.M. Visualizing transient low-populated structures of RNA. Nature 2012, 491, 724–728. [Google Scholar] [CrossRef]
- Xu, X.; Zhao, P.; Chen, S.J. Vfold: A web server for RNA structure and folding thermodynamics prediction. PLoS ONE 2014, 9, e107504. [Google Scholar] [CrossRef]
- Phillips, J.C.; Braun, R.; Wang, W.; Gumbart, J.; Tajkhorshid, E.; Villa, E.; Chipot, C.; Skeel, R.D.; Kale, L.; Schulten, K. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005, 26, 1781–1802. [Google Scholar] [CrossRef] [PubMed]
- MacKerell, A.D., Jr.; Banavali, N.; Foloppe, N. Development and current status of the CHARMM force field for nucleic acids. Biopolym. Orig. Res. Biomol. 2000, 56, 257–265. [Google Scholar] [CrossRef]
- Mark, P.; Nilsson, L. Structure and dynamics of the TIP3P, SPC, and SPC/E water models at 298 K. J. Phys. Chem. A 2001, 105, 9954–9960. [Google Scholar] [CrossRef]
- Ryckaert, J.P.; Ciccotti, G.; Berendsen, H.J. Numerical integration of the cartesian equations of motion of a system with constraints: Molecular dynamics of n-alkanes. J. Comput. Phys. 1977, 23, 327–341. [Google Scholar] [CrossRef]
- Feller, S.E.; Zhang, Y.; Pastor, R.W.; Brooks, B.R. Constant pressure molecular dynamics simulation: The Langevin piston method. J. Chem. Phys. 1995, 103, 4613–4621. [Google Scholar] [CrossRef]
- Martyna, G.J.; Tobias, D.J.; Klein, M.L. Constant pressure molecular dynamics algorithms. J. Chem. Phys. 1994, 101, 4177–4189. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Metz, S.; Kästner, J.; Sokol, A.A.; Keal, T.W.; Sherwood, P. ChemShell—A modular software package for QM/MM simulations. WIREs Comput. Mol. Sci. 2014, 4, 101–110. [Google Scholar] [CrossRef]
- Neese, F. Software update: The ORCA program system, version 4.0. WIREs Comput. Mol. Sci. 2018, 8, e1327. [Google Scholar] [CrossRef]
- Brooks, B.R.; Brooks, C.L., III; Mackerell, A.D., Jr.; Nilsson, L.; Petrella, R.J.; Roux, B.; Won, Y.; Archontis, G.; Bartels, C.; Boresch, S.; et al. CHARMM: The biomolecular simulation program. J. Comput. Chem. 2009, 30, 1545–1614. [Google Scholar] [CrossRef]
- Sherwood, P.; de Vries, A.H.; Guest, M.F.; Schreckenbach, G.; Catlow, C.A.; French, S.A.; Sokol, A.A.; Bromley, S.T.; Thiel, W.; Turner, A.J.; et al. QUASI: A general purpose implementation of the QM/MM approach and its application to problems in catalysis. J. Mol. Struct. THEOCHEM 2003, 632, 1–28. [Google Scholar] [CrossRef]
- Denning, E.J.; Priyakumar, U.D.; Nilsson, L.; Mackerell, A.D., Jr. Impact of 2’-hydroxyl sampling on the conformational properties of RNA: Update of the CHARMM all-atom additive force field for RNA. J. Comput. Chem. 2011, 32, 1929–1943. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Smith, W.; Forester, T. DL_POLY_2.0: A general-purpose parallel molecular dynamics simulation package. J. Mol. Graph. 1996, 14, 136–141. [Google Scholar] [CrossRef]
- Kästner, J.; Carr, J.M.; Keal, T.W.; Thiel, W.; Wander, A.; Sherwood, P. DL-FIND: An open-source geometry optimizer for atomistic simulations. J. Phys. Chem. A 2009, 113, 11856–11865. [Google Scholar] [CrossRef]
- Billeter, S.R.; Turner, A.J.; Thiel, W. Linear scaling geometry optimisation and transition state search in hybrid delocalised internal coordinates. Phys. Chem. Chem. Phys. 2000, 2, 2177–2186. [Google Scholar] [CrossRef]
- Liu, D.C.; Nocedal, J. On the limited memory BFGS method for large scale optimization. Math. Program. 1989, 45, 503–528. [Google Scholar] [CrossRef]
- Banerjee, A.; Adams, N.; Simons, J.; Shepard, R. Search for stationary points on surfaces. J. Phys. Chem. 1985, 89, 52–57. [Google Scholar] [CrossRef]
- Pan, Y.; Priyakumar, U.D.; MacKerell, A.D. Conformational determinants of tandem GU mismatches in RNA: Insights from molecular dynamics simulations and quantum mechanical calculations. Biochemistry 2005, 44, 1433–1443. [Google Scholar] [CrossRef]
- Demeshkina, N.; Jenner, L.; Westhof, E.; Yusupov, M.; Yusupova, G. New structural insights into the decoding mechanism: Translation infidelity via a G· U pair with Watson–Crick geometry. FEBS Lett. 2013, 587, 1848–1857. [Google Scholar] [CrossRef] [PubMed]
- Rozov, A.; Demeshkina, N.; Westhof, E.; Yusupov, M.; Yusupova, G. Structural insights into the translational infidelity mechanism. Nat. Commun. 2015, 6, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Rozov, A.; Wolff, P.; Grosjean, H.; Yusupov, M.; Yusupova, G.; Westhof, E. Tautomeric G• U pairs within the molecular ribosomal grip and fidelity of decoding in bacteria. Nucleic Acids Res. 2018, 46, 7425–7435. [Google Scholar] [CrossRef]
- Loveland, A.B.; Demo, G.; Grigorieff, N.; Korostelev, A.A. Ensemble cryo-EM elucidates the mechanism of translation fidelity. Nature 2017, 546, 113–117. [Google Scholar] [CrossRef]
- Roßbach, S.; Ochsenfeld, C. Influence of coupling and embedding schemes on QM size convergence in QM/MM approaches for the example of a proton transfer in DNA. J. Chem. Theory Comput. 2017, 13, 1102–1107. [Google Scholar] [CrossRef] [PubMed]
- Pokorná, P.; Kruse, H.; Krepl, M.; Sponer, J. QM/MM calculations on protein–RNA complexes: Understanding limitations of classical MD simulations and search for reliable cost-effective QM methods. J. Chem. Theory Comput. 2018, 14, 5419–5433. [Google Scholar] [CrossRef] [PubMed]
- Naydenova, E.; Roßbach, S.; Ochsenfeld, C. QM/MM study of the uracil DNA glycosylase reaction mechanism: A competition between Asp145 and His148. J. Chem. Theory Comput. 2019, 15, 4344–4350. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chandorkar, S.; Raghunathan, S.; Jaganade, T.; Priyakumar, U.D. Multiscale Modeling of Wobble to Watson–Crick-Like Guanine–Uracil Tautomerization Pathways in RNA. Int. J. Mol. Sci. 2021, 22, 5411. https://doi.org/10.3390/ijms22115411
Chandorkar S, Raghunathan S, Jaganade T, Priyakumar UD. Multiscale Modeling of Wobble to Watson–Crick-Like Guanine–Uracil Tautomerization Pathways in RNA. International Journal of Molecular Sciences. 2021; 22(11):5411. https://doi.org/10.3390/ijms22115411
Chicago/Turabian StyleChandorkar, Shreya, Shampa Raghunathan, Tanashree Jaganade, and U. Deva Priyakumar. 2021. "Multiscale Modeling of Wobble to Watson–Crick-Like Guanine–Uracil Tautomerization Pathways in RNA" International Journal of Molecular Sciences 22, no. 11: 5411. https://doi.org/10.3390/ijms22115411
APA StyleChandorkar, S., Raghunathan, S., Jaganade, T., & Priyakumar, U. D. (2021). Multiscale Modeling of Wobble to Watson–Crick-Like Guanine–Uracil Tautomerization Pathways in RNA. International Journal of Molecular Sciences, 22(11), 5411. https://doi.org/10.3390/ijms22115411





