Kinematics Governing Mechanotransduction in the Sensory Hair of the Venus flytrap
Abstract
1. Introduction
2. Materials and Methods
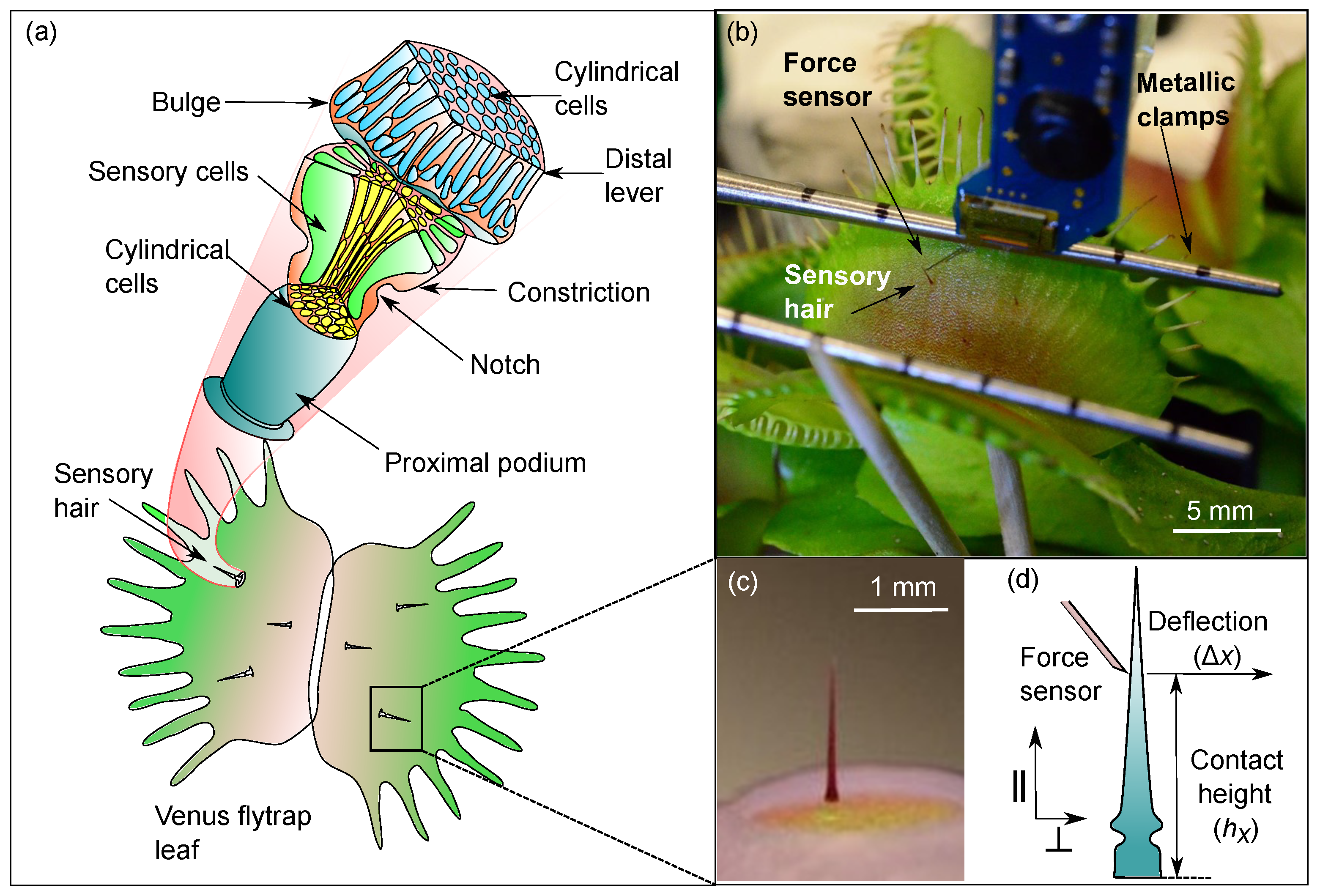
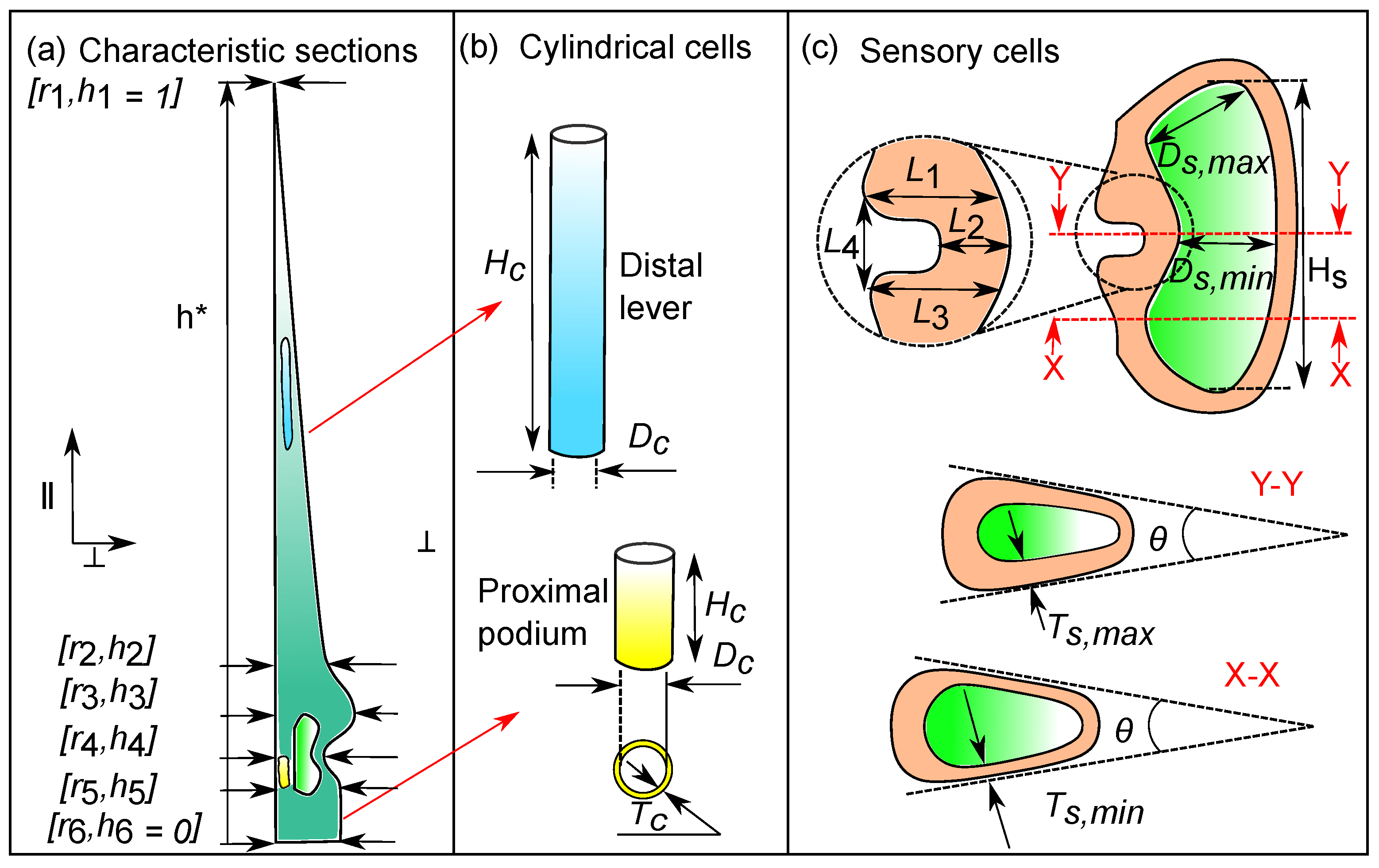
2.1. Anatomy of the Venus flytrap’s Sensory Hair
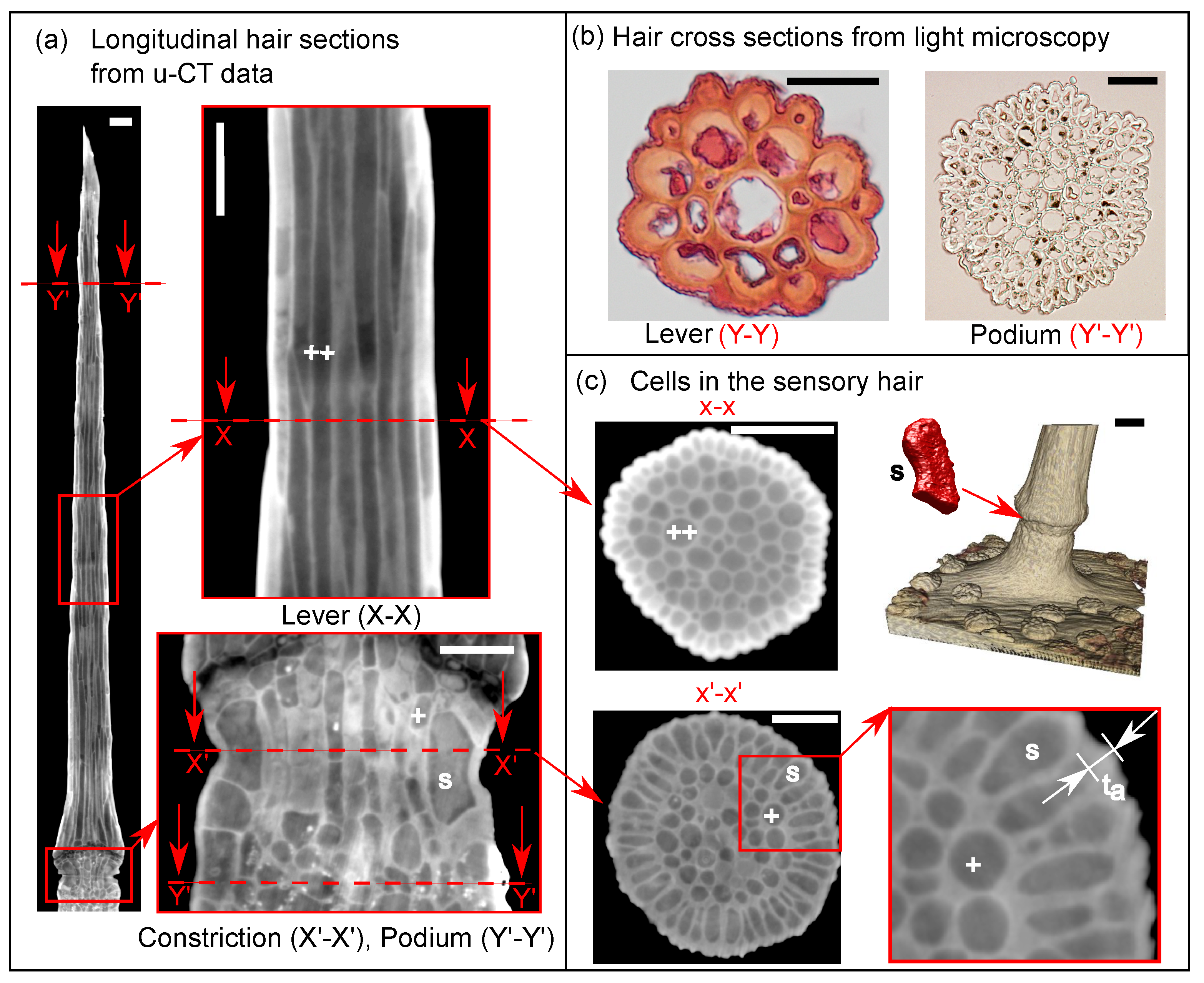
2.1.1. Micro-CT Imaging and Data Post-Processing
2.1.2. Light Microscopy for Cell Wall Thickness Measurements
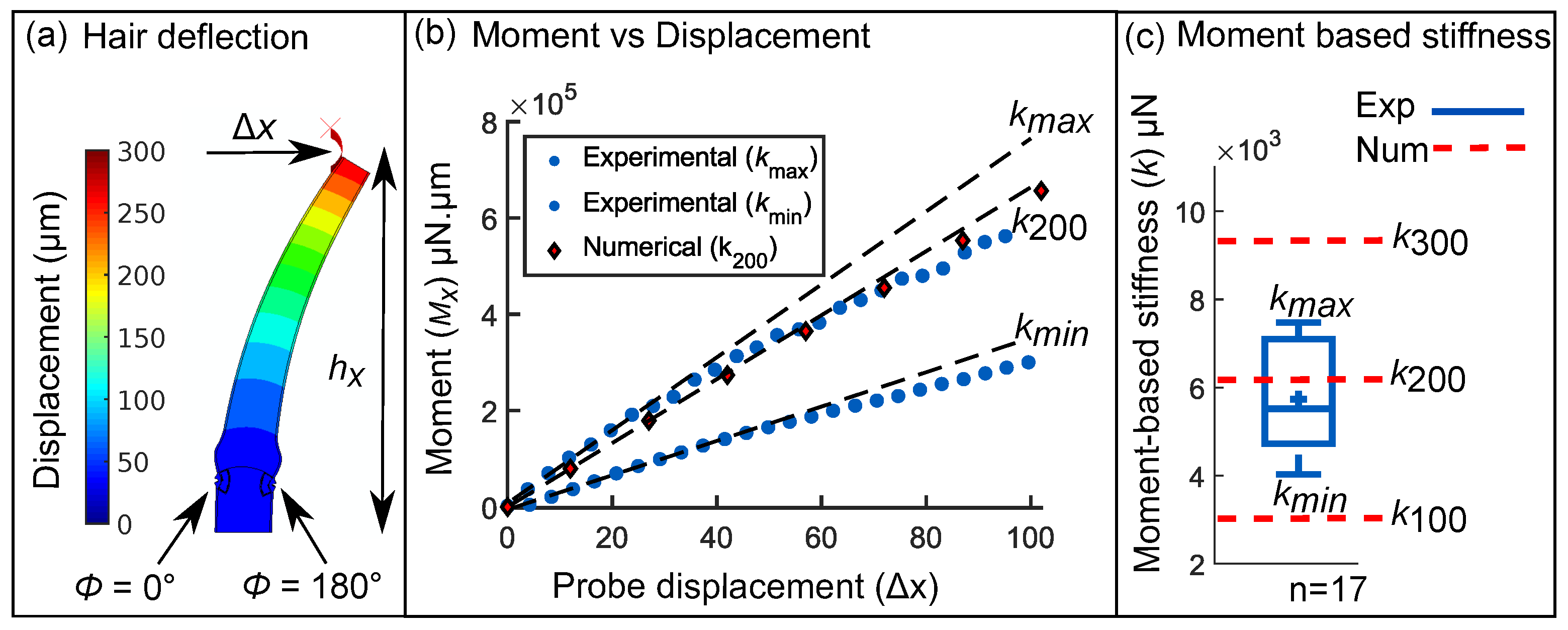
2.2. Force-Deflection Tests on Sensory Hairs
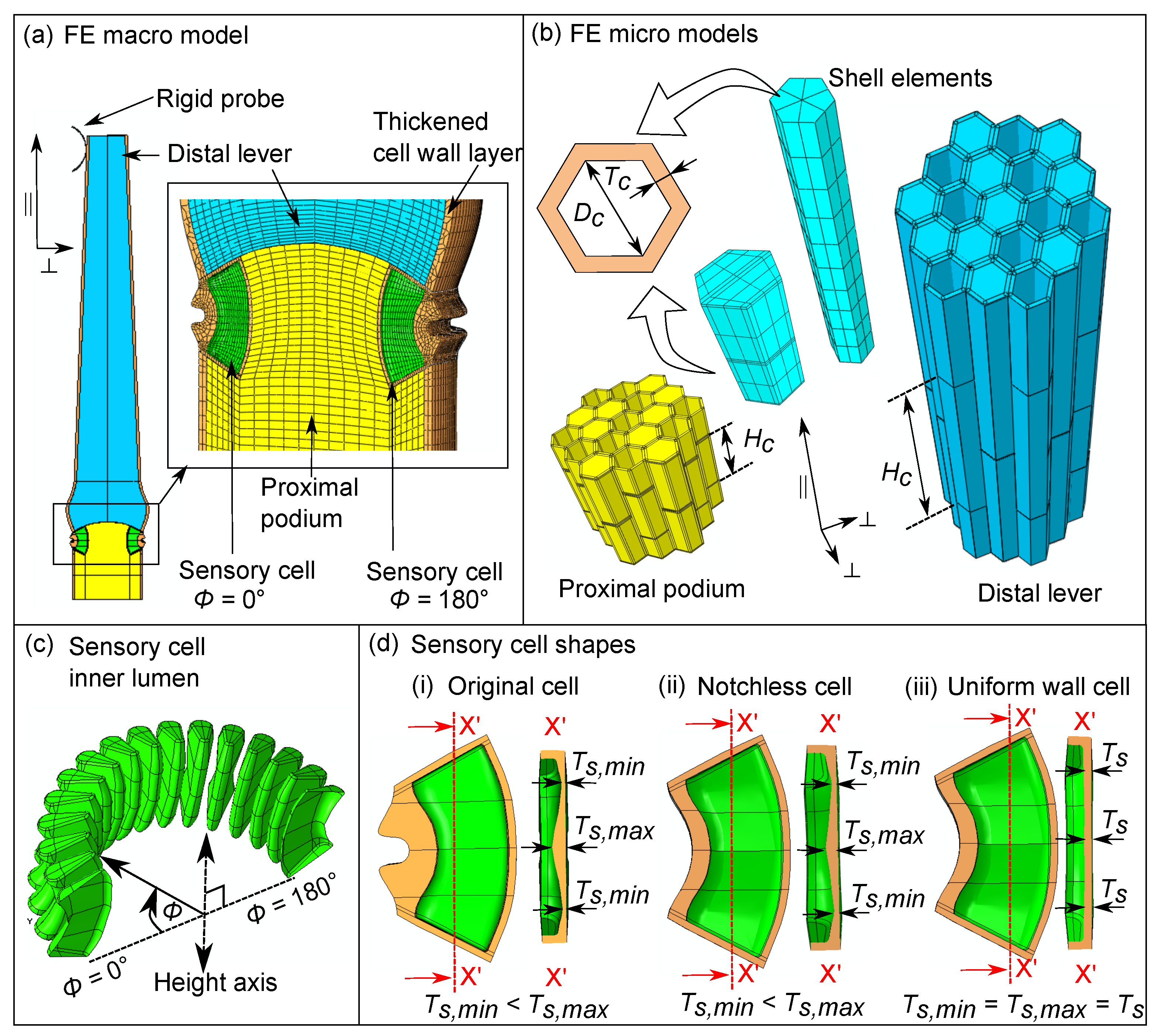
2.3. Multi-Scale Finite Element (FE) Model of the Sensory Hair
2.3.1. Homogenization of the Tissue Micro Models
2.3.2. Macro-Scale Numerical Hair Model and Deflection Simulations
2.3.3. Calculation of Mechanotransductive Properties
3. Results
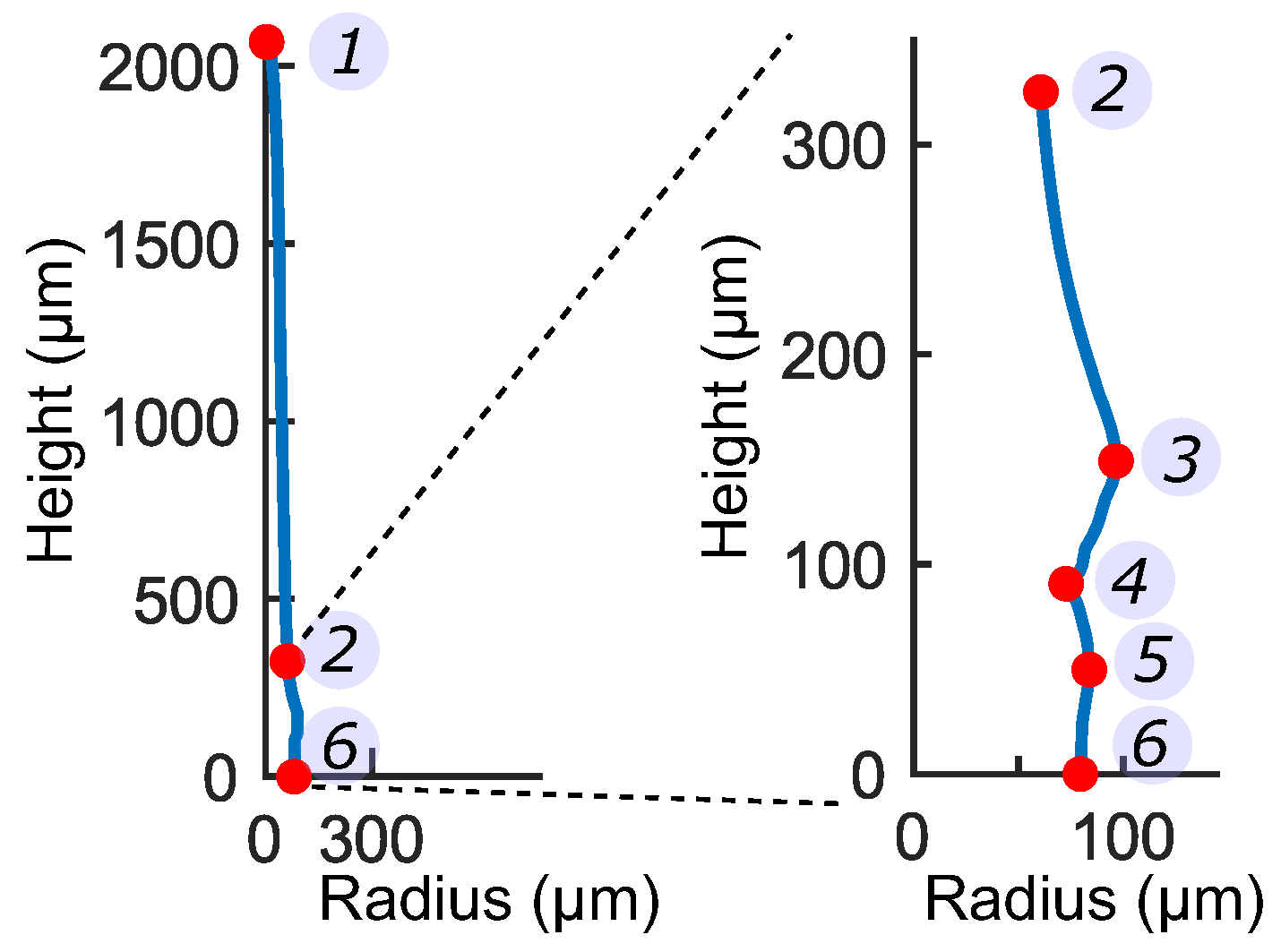
3.1. Representative Sensory Hair Morphology
3.2. Characteristic Cellular Shapes
3.3. Transverse Isotropic Compliance Tensors of Hair Tissues
3.4. Inverse Determination of Material Properties with Hair Stiffness
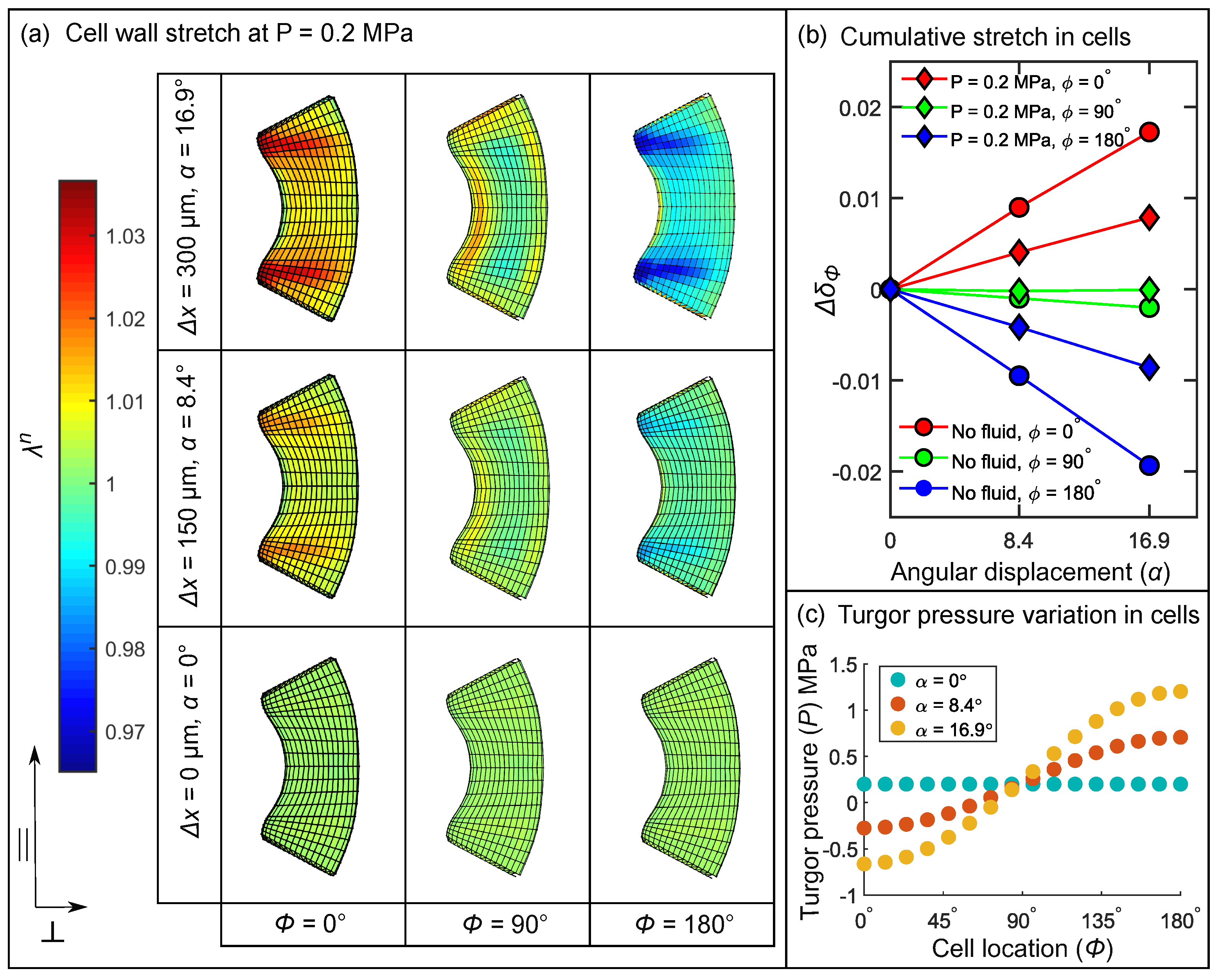
3.5. Stimulus Transformation onto Sensory Cells
3.5.1. Coarse-Grained Properties in Sensory Cells
3.5.2. Influence of Cellular Shape on the Stretch Pattern
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MSC | Mechanosensitive ion channel |
| AP | Action potential |
| FEM | Finite Element Method |
| TEM | Transmission Electron Microscopy |
| CT | Computed tomography |
| PEG | Polyethylene glycol |
| RP | Reference Point |
| O.C | Original cell |
| N.C | Notchless cell |
| U.C | Uniform walled cell |
| w.r.t | With respect to |
Appendix A
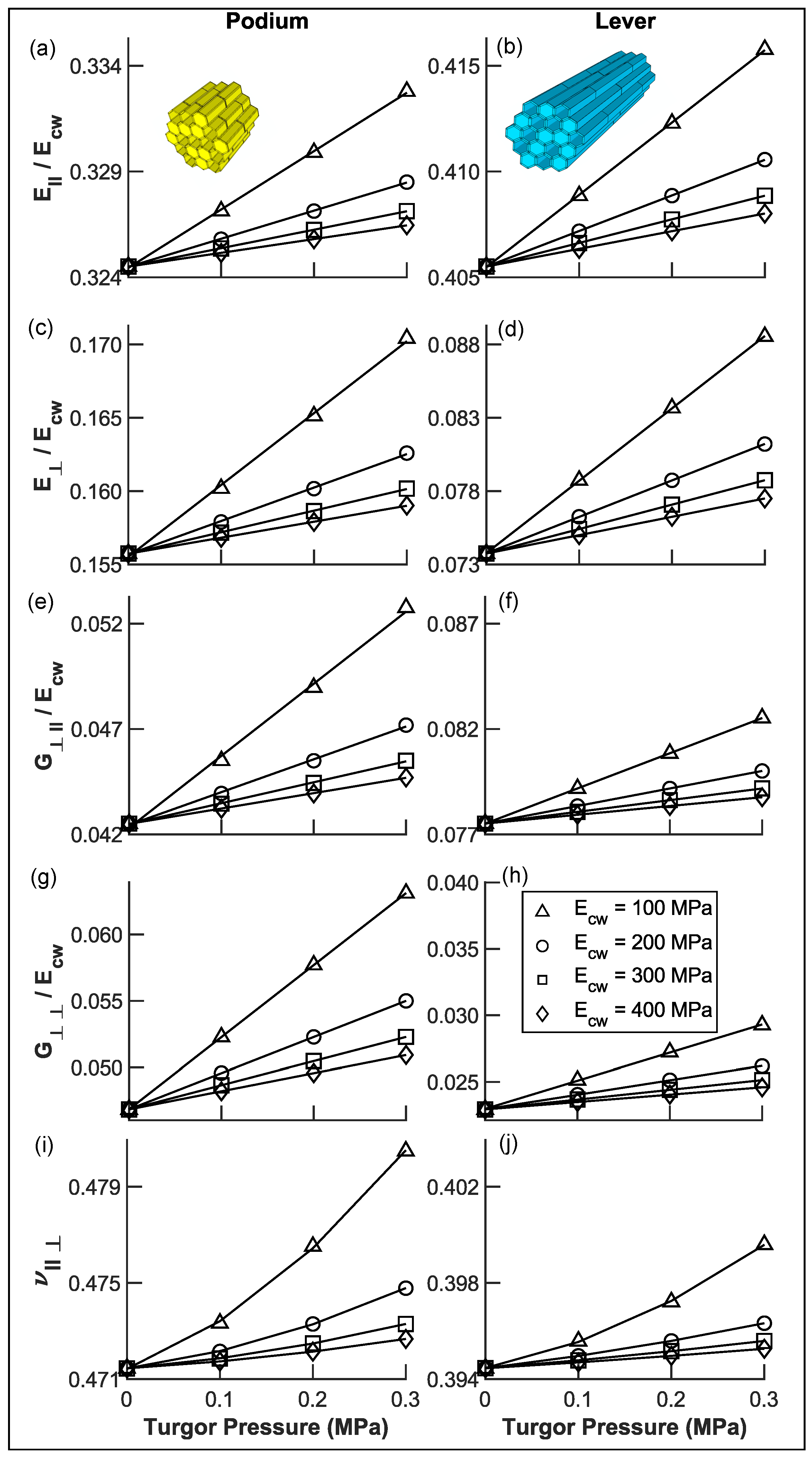
Appendix A.1. Calculated Tissue Properties
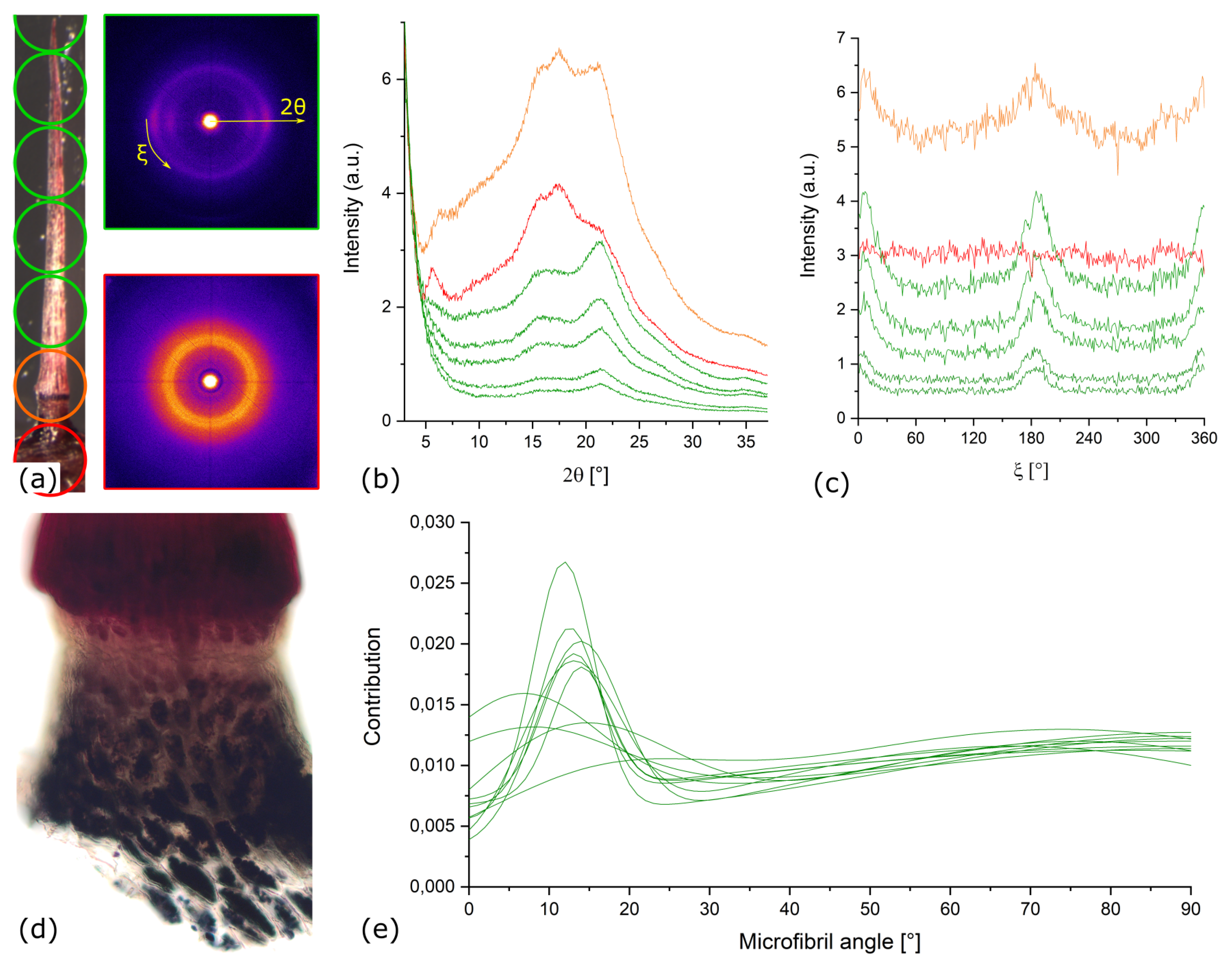
Appendix A.2. X-ray Diffraction
References
- Darwin, C. The correspondence of Charles Darwin, February 1873. In The Correspondence of Charles Darwin; Cambridge University Press: Cambridge, UK, 2014; Volume 21, p. 77. [Google Scholar]
- Forterre, Y.; Skotheim, J.M.; Dumais, J.; Mahadevan, L. How the Venus flytrap snaps. Nature 2005, 433, 421–425. [Google Scholar] [CrossRef] [PubMed]
- Hedrich, R. Ion Channels in Plants. Physiol. Rev. 2012, 92, 1777–1811. [Google Scholar] [CrossRef] [PubMed]
- Volkov, A.G.; Carrell, H.; Baldwin, A.; Markin, V.S. Electrical memory in Venus flytrap. Bioelectrochemistry 2009, 75, 142–147. [Google Scholar] [CrossRef] [PubMed]
- Curtis, M.A. Enumeration of plants growing spontaneously around Wilmington, North Carolina, with remarks on some new and obscure species. Boston J. Nat. Hist. 1834, 1, 82–141. [Google Scholar]
- Brown, W.H.; Sharp, L.W. The closing response in Dionaea. Bot. Gaz. 1910, 49, 290–302. [Google Scholar] [CrossRef]
- Haberlandt, G. Sinnesorgane im Pflanzenreich, 2nd ed.; Wilhelm Engelmann: Leipzig, Germany, 1906. [Google Scholar]
- Williams, M.E.; Mozingo, H.N. The Fine Structure of the Trigger Hair in Venus’s Flytrap. Am. J. Bot. 1971, 58, 532. [Google Scholar] [CrossRef]
- Scherzer, S.; Federle, W.; Al-Rasheid, K.A.S.; Hedrich, R. Venus flytrap trigger hairs are micronewton mechano-sensors that can detect small insect prey. Nat. Plants 2019, 5, 670–675. [Google Scholar] [CrossRef]
- Burri, J.T.; Saikia, E.; Läubli, N.F.; Vogler, H.; Wittel, F.K.; Rüggeberg, M.; Herrmann, H.J.; Burgert, I.; Nelson, B.J.; Grossniklaus, U. A single touch can provide sufficient mechanical stimulation to trigger Venus flytrap closure. PLoS Biol. 2020, 18, e3000740. [Google Scholar] [CrossRef]
- Suda, H.; Mano, H.; Toyota, M.; Fukushima, K.; Mimura, T.; Tsutsui, I.; Hedrich, R.; Tamada, Y.; Hasebe, M. Calcium dynamics during trap closure visualized in transgenic Venus flytrap. Nat. Plants 2020, 6, 1219–1224. [Google Scholar] [CrossRef]
- Sachs, F. Stretch-Activated Ion Channels: What Are They? Physiology 2010, 25, 50–56. [Google Scholar] [CrossRef]
- Haswell, E.; Phillips, R.; Rees, D. Mechanosensitive Channels: What Can They Do and How Do They Do It? Structure 2011, 19, 1356–1369. [Google Scholar] [CrossRef]
- Le Roux, A.L.; Quiroga, X.; Walani, N.; Arroyo, M.; Roca-Cusachs, P. The plasma membrane as a mechanochemical transducer. Philos. Trans. R. Soc. B 2019, 374, 20180221. [Google Scholar] [CrossRef] [PubMed]
- Stampanoni, M.; Groso, A.; Isenegger, A.; Mikuljan, G.; Chen, Q.; Bertrand, A.; Henein, S.; Betemps, R.; Frommherz, U.; Böhler, P.; et al. Trends in Synchrotron-Based Tomographic Imaging: The SLS Experience; Proc. SPIE: San Diego, CA, USA, 2006; Volume 6318. [Google Scholar]
- Paganin, D.; Mayo, S.C.; Gureyev, T.E.; Miller, P.R.; Wilkins, S.W. Simultaneous phase and amplitude extraction from a single defocused image of a homogeneous object. J. Microsc. 2002, 206, 33–40. [Google Scholar] [CrossRef] [PubMed]
- Marone, F.; Stampanoni, M. Regridding reconstruction algorithm for real-time tomographic imaging. J. Synchrotron Radiat. 2012, 19, 1029–1037. [Google Scholar] [CrossRef] [PubMed]
- Gierlinger, N.; Keplinger, T.; Harrington, M. Imaging of plant cell walls by confocal Raman microscopy. Nat. Protoc. 2012, 7, 1694–1708. [Google Scholar] [CrossRef]
- Smith, M. ABAQUS/Standard User’s Manual, Version 6.9; Dassault Systems Simulia Corp: Rhode Island, RI, USA, 2009. [Google Scholar]
- Gibson, L.J. The hierarchical structure and mechanics of plant materials. J. R. Soc. Interface 2012, 9, 2749–2766. [Google Scholar] [CrossRef]
- Steudle, E.; Zimmermann, U.; Lüttge, U. Effect of Turgor Pressure and Cell Size on the Wall Elasticity of Plant Cells. Plant Physiol. 1977, 59, 285–289. [Google Scholar] [CrossRef]
- Mozingo, H.N.; Klein, P.; Zeevi, Y.; Lewis, E.R. Venus’s Flytrap Observations by Scanning Electron Microscopy. Am. J. Bot. 1970, 57, 593. [Google Scholar] [CrossRef]
- Rüggeberg, M.; Saxe, F.; Metzger, T.H.; Sundberg, B.; Fratzl, P.; Burgert, I. Enhanced cellulose orientation analysis in complex model plant tissues. J. Struct. Biol. 2013, 183, 419–428. [Google Scholar] [CrossRef]
- Nikuni, Z. Studies on Starch Granules. Starch Stärke 1978, 30, 105–111. [Google Scholar] [CrossRef]
- Cheetham, N.W.; Tao, L. Variation in crystalline type with amylose content in maize starch granules: An X-ray powder diffraction study. Carbohyd. Polym. 1998, 36, 277–284. [Google Scholar] [CrossRef]
- Kawabata, A.; Takase, N.; Miyoshi, E.; Sawayama, S.; Kimura, T.; Kudo, K. Microscopic Observation and X-ray Diffractometry of Heat/Moisture-Treated Starch Granules. Starch Stärke 1994, 46, 463–469. [Google Scholar] [CrossRef]


| Tissue | Section | ||
|---|---|---|---|
| Distal lever (top) | [] | 0 | 1 |
| Distal lever (bottom) | [] | 0.032 | 0.174 |
| Bulge | [] | 0.050 | 0.079 |
| Notch | [] | 0.041 | 0.049 |
| Proximal podium (top) | [] | 0.045 | 0.029 |
| Proximal podium (bottom) | [] | 0.045 | 0 |
| Cell Type | Height (μm) | Diameter (μm) | Wall Thickness (μm) |
|---|---|---|---|
| Cylindrical cells (lever) | = 198.2 ± 46.3 | = 9.5 ± 1.1 | = 1.1 ± 0.2 |
| Cylindrical cells (podium) | = 27.2 ± 3.8 | = 13.9 ± 2.6 | = 1.1 ± 0.2 |
| Sensory cells | = 63.3 ± 4.8 | = 26.2 ± 3.4, = 20.8 ± 2.5 | = 2.8 ± 0.4, = 1.8 ± 0.5 |
| Proximal Podium | Distal Lever | |
|---|---|---|
| Cell height [μm] | 30 | 200 |
| Cell lumen diameter [μm] | 14 | 10 |
| Cell wall thickness [μm] | 1 | 1 |
| Cell wall Young’s modulus [] | 100–400 | |
| Cell wall Poisson’s number [-] | 0.3 | |
| Turgor pressure P [] | 0–0.3 | |
| Cell wall volume fraction [-] | 0.32 | 0.39 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saikia, E.; Läubli, N.F.; Burri, J.T.; Rüggeberg, M.; Schlepütz, C.M.; Vogler, H.; Burgert, I.; Herrmann, H.J.; Nelson, B.J.; Grossniklaus, U.; et al. Kinematics Governing Mechanotransduction in the Sensory Hair of the Venus flytrap. Int. J. Mol. Sci. 2021, 22, 280. https://doi.org/10.3390/ijms22010280
Saikia E, Läubli NF, Burri JT, Rüggeberg M, Schlepütz CM, Vogler H, Burgert I, Herrmann HJ, Nelson BJ, Grossniklaus U, et al. Kinematics Governing Mechanotransduction in the Sensory Hair of the Venus flytrap. International Journal of Molecular Sciences. 2021; 22(1):280. https://doi.org/10.3390/ijms22010280
Chicago/Turabian StyleSaikia, Eashan, Nino F. Läubli, Jan T. Burri, Markus Rüggeberg, Christian M. Schlepütz, Hannes Vogler, Ingo Burgert, Hans J. Herrmann, Bradley J. Nelson, Ueli Grossniklaus, and et al. 2021. "Kinematics Governing Mechanotransduction in the Sensory Hair of the Venus flytrap" International Journal of Molecular Sciences 22, no. 1: 280. https://doi.org/10.3390/ijms22010280
APA StyleSaikia, E., Läubli, N. F., Burri, J. T., Rüggeberg, M., Schlepütz, C. M., Vogler, H., Burgert, I., Herrmann, H. J., Nelson, B. J., Grossniklaus, U., & Wittel, F. K. (2021). Kinematics Governing Mechanotransduction in the Sensory Hair of the Venus flytrap. International Journal of Molecular Sciences, 22(1), 280. https://doi.org/10.3390/ijms22010280