DockingApp RF: A State-of-the-Art Novel Scoring Function for Molecular Docking in a User-Friendly Interface to AutoDock Vina
Abstract
1. Introduction
2. Materials and Methods
2.1. Datasets
2.2. Features Selection
- intermolecular contacts of the pharmacophoric types (phCo),
- variations of the solvent-accessible surface area upon binding (ΔSASA) and
- AutoDock Vina’s unweighted energy terms.
2.2.1. Intermolecular Contacts
2.2.2. Solvent Accessible Surface Area
2.2.3. Vina’s Energy Terms
2.3. Performance Metrics and Errors Evaluation
3. Results and Implementation
3.1. Model Comparison
3.2. Contribution of the Features
3.3. CASF-2013 Core Set Results
3.4. CASF-2016 Core Set Results
3.5. Docking Power and Screening Power Testing
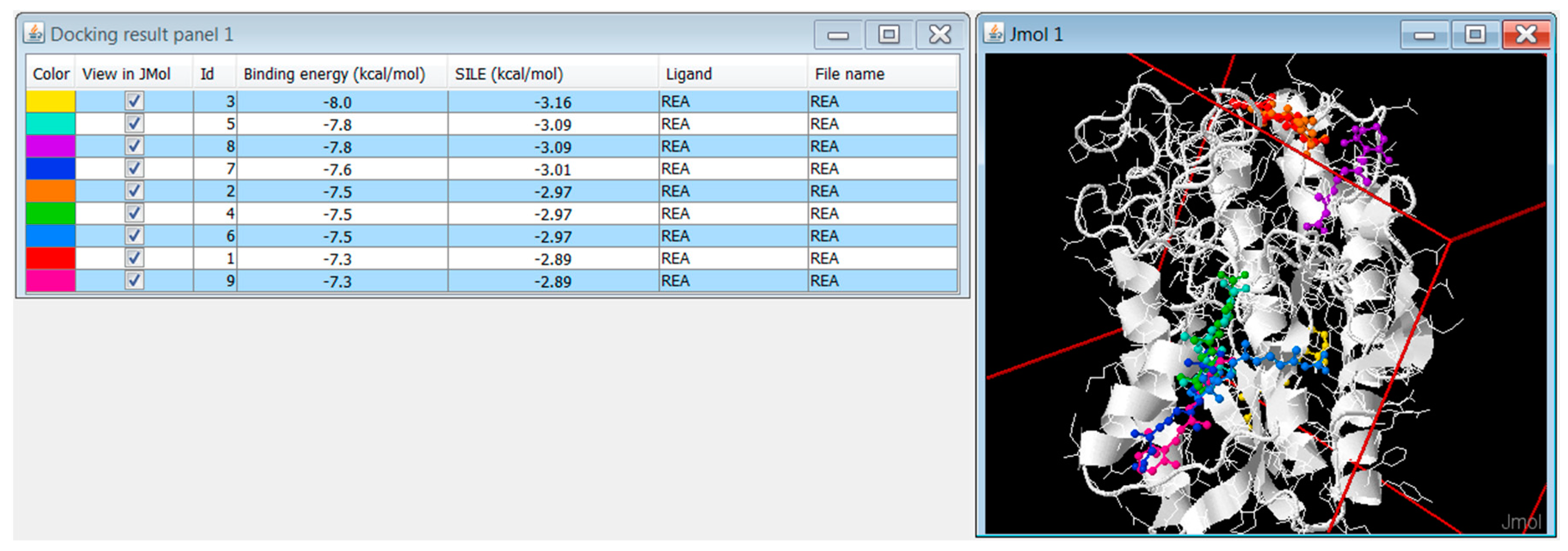
3.6. DockingApp RF’s Implementation and New Features
3.6.1. Replicated Docking
3.6.2. Extension of the Drug Library Collection
3.6.3. DockingApp RF’s Additional Functionalities
3.6.4. Technology, Requirements, Availability and Execution Times
4. Discussion
5. Future Development
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| SF | Scoring function |
| ML | Machine learning |
| CNN | convolution neural network |
| LR | Linear regression |
| RF | Random forest |
| SVM | Support vector machine |
| KNN | K-nearest neighbor |
| R | Pearson’s correlation coefficient |
| MAE | Mean absolute error |
| RMSE | Root mean squared error |
| SD | Standard deviation |
| SASA | Solvent accessible surface area |
References
- DiMasi, J.A.; Grabowski, H.G.; Hansen, R.W. Innovation in the pharmaceutical industry: New estimates of R&D costs. J. Health Econ. 2016, 47, 20–33. [Google Scholar] [PubMed]
- Mignani, S.; Huber, S.; Tomas, H.; Rodrigues, J.; Majoral, J.P. Why and how have drug discovery strategies in pharma changed? What are the new mindsets? Drug Discov. Today 2016, 21, 239–249. [Google Scholar] [CrossRef] [PubMed]
- Wong, C.H.; Siah, K.W.; Lo, A.W. Estimation of clinical trial success rates and related parameters. Biostatistics 2019, 20, 273–286. [Google Scholar] [CrossRef] [PubMed]
- Sliwoski, G.; Kothiwale, S.; Meiler, J.; Lowe, E.W., Jr. Computational methods in drug discovery. Pharm. Rev. 2014, 66, 334–395. [Google Scholar] [CrossRef] [PubMed]
- Danishuddin, M.; Khan, A.U. Structure based virtual screening to discover putative drug candidates: Necessary considerations and successful case studies. Methods 2015, 71, 135–145. [Google Scholar] [CrossRef]
- Ban, F.; Dalal, K.; Li, H.; Leblanc, E.; Rennie, P.S.; Cherkasov, A. Best Practices of Computer-Aided Drug Discovery: Lessons Learned from the Development of a Preclinical Candidate for Prostate Cancer with a New Mechanism of Action. J. Chem. Inf. Model. 2017, 57, 1018–1028. [Google Scholar] [CrossRef] [PubMed]
- Usha, T.; Shanmugarajan, D.; Goyal, A.K.; Kumar, C.S.; Middha, S.K. Recent Updates on Computer-aided Drug Discovery: Time for a Paradigm Shift. Curr. Top. Med. Chem. 2018, 17, 3296–3307. [Google Scholar] [CrossRef]
- Chaput, L.; Mouawad, L. Efficient conformational sampling and weak scoring in docking programs? Strategy of the wisdom of crowds. J. Cheminf. 2017, 9, 37. [Google Scholar] [CrossRef]
- Böhm, H.J.; Stahl, M. The Use of Scoring Functions in Drug Discovery Applications. In Reviews in Computational Chemistry; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2003; Chapter 2; pp. 41–87. [Google Scholar] [CrossRef]
- Gilson, M.K.; Given, J.A.; Head, M.S. A new class of models for computing receptor-ligand binding affinities. Chem. Biol. 1997, 4, 87–92. [Google Scholar] [CrossRef]
- Zou, X.; Sun, Y.; Kuntz, I.D. Inclusion of solvation in ligand binding free energy calculations using the generalized-born model. J. Am. Chem Soc. 1999, 121, 8033–8043. [Google Scholar] [CrossRef]
- Meng, E.C.; Shoichet, B.K.; Kuntz, I.D. Automated docking with grid-based energy evaluation. J. Comput. Chem. 1992, 13, 505–524. [Google Scholar] [CrossRef]
- Morris, G.M.; Huey, R.; Lindstrom, W.; Sanner, M.F.; Belew, R.K.; Goodsell, D.S.; Olson, A.J. AutoDock4 and AutoDockTools4: Automated docking with selective receptor flexibility. J. Comput. Chem. 2009, 30, 2785–2791. [Google Scholar] [CrossRef] [PubMed]
- Muegge, I. PMF scoring revisited. J. Med. Chem. 2006, 49, 5895–5902. [Google Scholar] [CrossRef] [PubMed]
- Velec, H.F.; Gohlke, H.; Klebe, G. DrugScoreCSD-knowledge-based scoring function derived from small molecule crystal data with superior recognition rate of near-native ligand poses and better affinity prediction. J. Med. Chem. 2005, 48, 6296–6303. [Google Scholar] [CrossRef]
- Liu, J.; Wang, R. Classification of current scoring functions. J. Chem. Inf. Model. 2015, 55, 475–482. [Google Scholar] [CrossRef]
- Eldridge, M.D.; Murray, C.W.; Auton, T.R.; Paolini, G.V.; Mee, R.P. Empirical scoring functions: I. The development of a fast empirical scoring function to estimate the binding affinity of ligands in receptor complexes. J. Comput. Aided Mol. Des. 1997, 11, 425–445. [Google Scholar] [CrossRef]
- Trott, O.; Olson, A.J. AutoDock Vina: Improving the speed and accuracy of docking with a new scoring function, efficient optimization, and multithreading. J. Comput. Chem. 2010, 31, 455–461. [Google Scholar] [CrossRef]
- Guedes, I.A.; Pereira, F.S.; Dardenne, L.E. Empirical scoring functions for structure-based virtual screening: Applications, critical aspects, and challenges. Front. Pharm. 2018, 9, 1089. [Google Scholar] [CrossRef]
- Jiménez, J.; Škali, M.; Martínez-Rosell, G.; De Fabritiis, G. KDEEP: Protein-Ligand Absolute Binding Affinity Prediction via 3D-Convolutional Neural Networks. J. Chem. Inf. Modeling 2018, 58, 287–296. [Google Scholar] [CrossRef]
- Li, H.; Leung, K.; Wong, M.; Ballester, J.P. Improving AutoDock Vina Using Random Forest: The Growing Accuracy of Binding Affinity Prediction by the Effective Exploitation of Larger Data Sets. Mol. Inform. 2015, 34, 115–126. [Google Scholar] [CrossRef]
- Nguyen, D.D.; Wei, G.W. AGL-Score: Algebraic Graph Learning Score for Protein–Ligand Binding Scoring, Ranking, Docking, and Screening. J. Chem. Inf. Model. 2019, 59, 3291–3304. [Google Scholar] [CrossRef] [PubMed]
- Zheng, L.; Fan, J.; Mu, Y. OnionNet: A Multiple-Layer Intermolecular-Contact-Based Convolutional Neural Network for Protein–Ligand Binding Affinity Prediction. ACS Omega 2019, 4, 15956–15965. [Google Scholar] [CrossRef] [PubMed]
- Stepniewska-Dziubinska, M.M.; Zielenkiewicz, P.; Siedlecki, P. Development and evaluation of a deep learning model for protein-ligand binding affinity prediction. Bioinformatics 2018, 34, 3666–3674. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Sze, K.H.; Lu, G.; Ballester, P.J. Machine-learning scoring functions for structure-based drug lead optimization. Wires Comput. Mol. Sci. 2020, e1465. [Google Scholar] [CrossRef]
- Shen, C.; Hu, Y.; Wang, Z.; Zhang, X.; Pang, J.; Wang, G.; Zhong, H.; Xu, L.; Cao, D.; Hou, T. Beware of the generic machine learning-based scoring functions in structure-based virtual screening. Brief. Bioinform. 2020. [Google Scholar] [CrossRef] [PubMed]
- DiMuzio, E.; Toti, D.; Polticelli, F. DockingApp: A user friendly interface for facilitated docking simulations with AutoDock Vina. J. Comput. Aided Mol. Des. 2017, 31, 213–218. [Google Scholar] [CrossRef]
- Li, Y.; Han, L.; Liu, Z.; Wang, R. Comparative Assessment of Scoring Functions on an Updated Benchmark: 2. Evaluation Methods and General Results. J. Chem. Inf. Model. 2014, 54, 1717–1736. [Google Scholar] [CrossRef]
- Su, M.; Yang, Q.; Du, Y.; Feng, G.; Liu, Z.; Li, Y.; Wang, R. Comparative Assessment of Scoring Functions: The CASF-2016 Update. J. Chem. Inf. Model. 2019, 59, 895–913. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Biau, G. Analysis of a Random Forests Model. J. Mach. Learn. Res. 2012, 13, 1063–1095. [Google Scholar]
- Liu, Z.; Li, Y.; Han, L.; Liu, J.; Zhao, Z.; Nie, W.; Liu, Y.; Wang, R. PDB-wide collection of binding data: Current status of the PDBbind database. Bioinformatics 2015, 31, 405–412. [Google Scholar] [CrossRef] [PubMed]
- Wei, D.; Jiang, Q.; Wei, Y.; Wang, S. A novel hierarchical clustering algorithm for gene sequences. BMC Bioinf. 2012, 13, 174. [Google Scholar] [CrossRef] [PubMed]
- Boyles, F.; Deane, C.M.; Morris, G. Learning from the Ligand: Using Ligand-Based Features to Improve Binding Affinity Prediction. Bioinformatics 2019. [Google Scholar] [CrossRef]
- Landrum, G. RDKit: Open-source Cheminformatics, 2006. Int. J. Mol. Sci. 2020. submitted. [Google Scholar]
- Ballester, P.J.; Mitchell, J.B.O. A machine learning approach to predicting protein-ligand binding affinity with applications to molecular docking. Bioinformatics 2010, 26, 1169–1175. [Google Scholar] [CrossRef] [PubMed]
- Mooij, W.T.M.; Verdonk, M.L. General and targeted statistical potentials for protein-ligand interactions. Proteins Struct. Funct. Bioinform. 2005, 61, 272–287. [Google Scholar] [CrossRef] [PubMed]
- Wójcikowski, M.; Ballester, P.J.; Siedlecki, P. Performance of machine-learning scoring functions in structure-based virtual screening. Sci. Rep. 2017, 7, 46710. [Google Scholar] [CrossRef]
- Macari, G.; Toti, D.; Moro, C.D.; Polticelli, F. Fragment-Based Ligand-Protein Contact Statistics: Application to Docking Simulations. Int J. Mol. Sci. 2019, 20, 2499. [Google Scholar] [CrossRef]
- Ballester, P.J.; Schreyer, A.; Blundell, T.L. Does a More Precise Chemical Description of Protein-Ligand Complexes Lead to More Accurate Prediction of Binding Affinity? J. Chem. Inf. Model. 2014, 54, 944–955. [Google Scholar] [CrossRef]
- Jiang, L.; Rizzo, R.C. Pharmacophore-Based Similarity Scoring for DOCK. J. Phys. Chem. B 2015, 119, 1083–1102. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, Y. Improving scoring-docking-screening powers of protein-ligand scoring functions using random forest. J. Comput. Chem. 2017, 38, 169–177. [Google Scholar] [CrossRef] [PubMed]
- Santos-Martins, D.; Fernandes, P.A.; Ramos, M.J. Calculation of distribution coefficients in the SAMPL5 challenge from atomic solvation parameters and surface areas. J. Comput. Aided Mol. Des. 2016, 30, 1079–1086. [Google Scholar] [CrossRef]
- Ignjatovic, M.M.; Caldararu, O.; Dong, G.; Munoz-Gutierrez, C.; Adasme-Carreno, F.; Ryde, U. Binding-affinity predictions of HSP90 in the D3R Grand Challenge 2015 with docking, MM/GBSA, QM/MM, and free-energy simulations. J. Comput. Aided Mol. Des. 2016, 30, 707. [Google Scholar] [CrossRef] [PubMed]
- Duan, R.; Xu, X.; Zou, X. Lessons learned from participating in D3R 2016 Grand Challenge 2: Compounds targeting the farnesoid X receptor. J. Comput. Aided Mol. Des. 2018, 32, 103–111. [Google Scholar] [CrossRef]
- Yan, Z.; Wang, J. Optimizing the affinity and specificity of ligand binding with the inclusion of solvation effect. Proteins Struct. Funct. Bioinform. 2015, 83, 1632–1642. [Google Scholar] [CrossRef] [PubMed]
- Mitternacht, S. FreeSASA: An open source C library for solvent accessible surface area calculations. F1000Research 2016, 5, 189. [Google Scholar] [CrossRef]
- Wang, R.; Lai, L.; Wang, S. Further development and validation of empirical scoring functions for structure-based binding affinity prediction. J. Comput. Aided Mol. Des. 2002, 16, 11–26. [Google Scholar] [CrossRef]
- Arrouchi, H.; Lakhlili, W.; Ibrahimi, A. Re-positioning of known drugs for Pim-1 kinase target using molecular docking analysis. Bioinformation 2019, 15, 116–120. [Google Scholar] [CrossRef]
- Gu, S.; Fu, W.Y.; Fu, A.K.; Tong, E.P.S.; Ip, F.C.; Huang, X.; Ip, N.Y. Identification of new EphA4 inhibitors by virtual screening of FDA-approved drugs. Sci. Rep. 2018, 8, 7377. [Google Scholar] [CrossRef]
- Brindha, S.; Sundaramurthi, J.C.; Velmurugan, D.; Vincent, S.; Gnanadoss, J.J. Docking-based virtual screening of known drugs against murE of Mycobacterium tuberculosis towards repurposing for TB. Bioinformation 2016, 12, 368–372. [Google Scholar] [CrossRef]
- Law, V.; Knox, C.; Djoumbou, Y.; Jewison, T.; Guo, A.C.; Liu, Y.; Maciejewski, A.; Arndt, D.; Wilson, M.C.; Neveu, V.; et al. DrugBank 4.0: Shedding new light on drug metabolism. Nucleic Acids Res. 2014, 42, D1091–D1097. [Google Scholar] [CrossRef] [PubMed]
- Irwin, J.J.; Shoichet, B.K. ZINC—A free database of commercially available compounds for virtual screening. J. Chem. Inf. Model. 2005, 45, 177–182. [Google Scholar] [CrossRef] [PubMed]
- O’Boyle, N.M.; Banck, M.; James, C.A.; Morley, C.; Vandermeersch, T.; Hutchison, G.R. Open Babel: An open chemical toolbox. J. Cheminf. 2011, 3, 33. [Google Scholar] [CrossRef] [PubMed]
- Bjerrum, E.J. Machine learning optimization of cross docking accuracy. Comput. Biol. Chem. 2016, 62, 133–144. [Google Scholar] [CrossRef]
- Zhang, H.; Liao, L.; Saravanan, K.M.; Yin, P.; Wei, Y. DeepBindRG: A deep learning based method for estimating effective protein–ligand affinity. PeerJ 2019, 7, e7362. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M.; et al. ImageNet Large Scale Visual Recognition Challenge. Int. J. Comput. Vis. 2015, 115, 211–252. [Google Scholar] [CrossRef]
- Caprari, S.; Toti, D.; Hung, L.V.; Stefano, M.D.; Polticelli, F. ASSIST: A fast versatile local structural comparison tool. Bioinformatics 2014, 30. [Google Scholar] [CrossRef]
- Hung, L.V.; Caprari, S.; Bizai, M.; Toti, D.; Polticelli, F. LIBRA: LIgand Binding site Recognition Application. Bioinformatics 2015, 31. [Google Scholar] [CrossRef]
- Toti, D.; Hung, L.V.; Tortosa, V.; Brandi, V.; Polticelli, F. LIBRA-WA: A web application for ligand binding site detection and protein function recognition. Bioinformatics 2018, 34. [Google Scholar] [CrossRef]
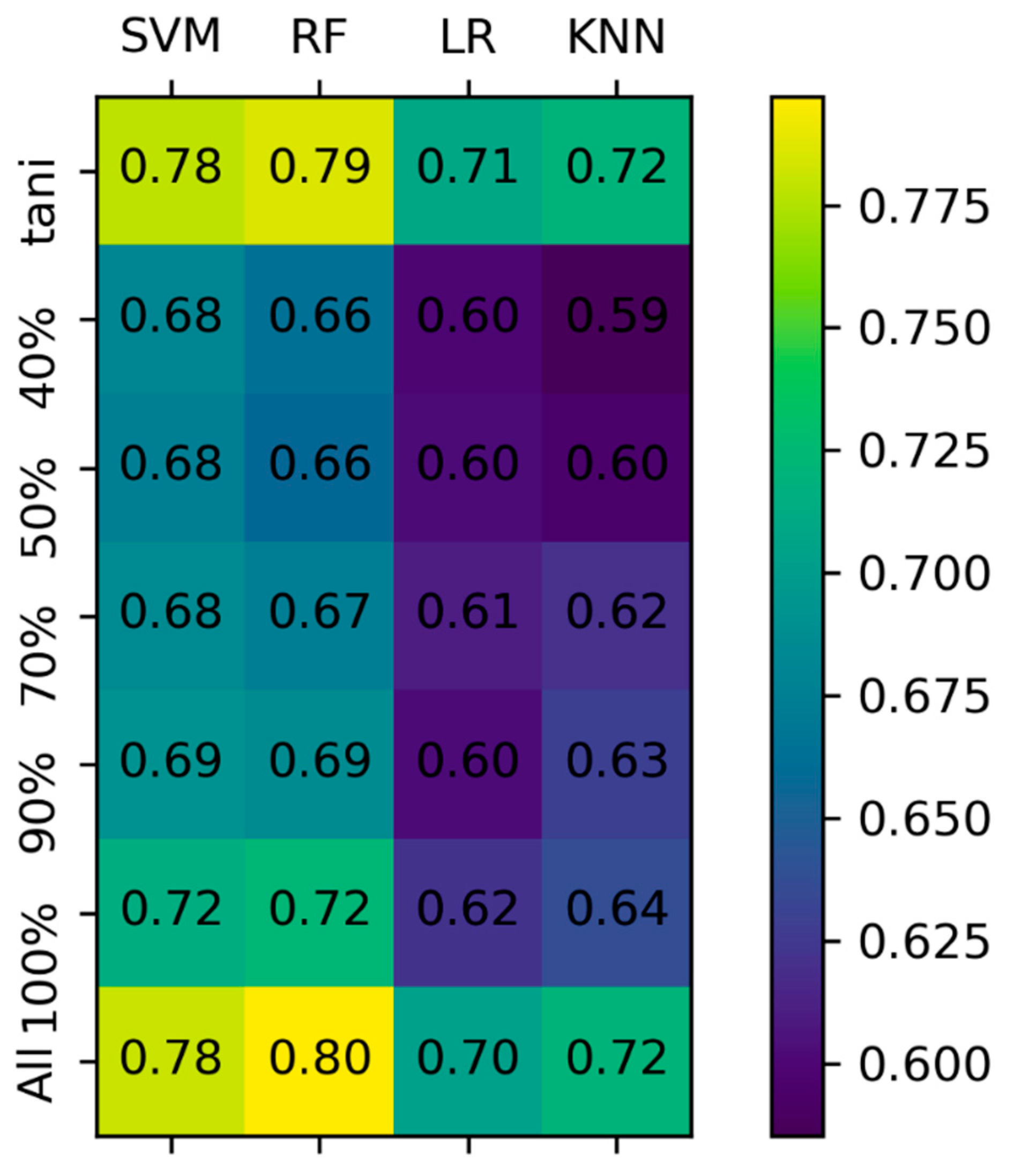
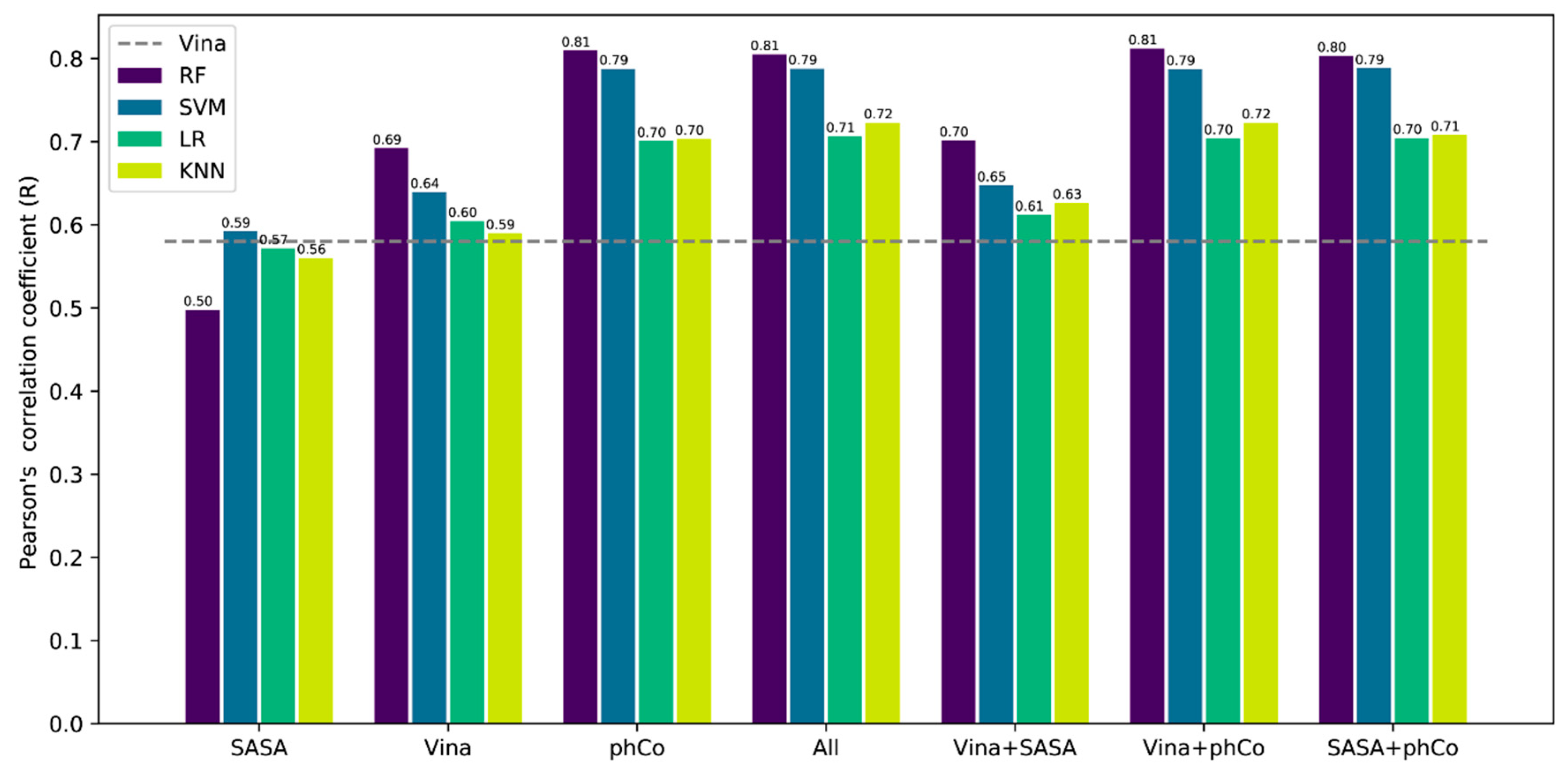
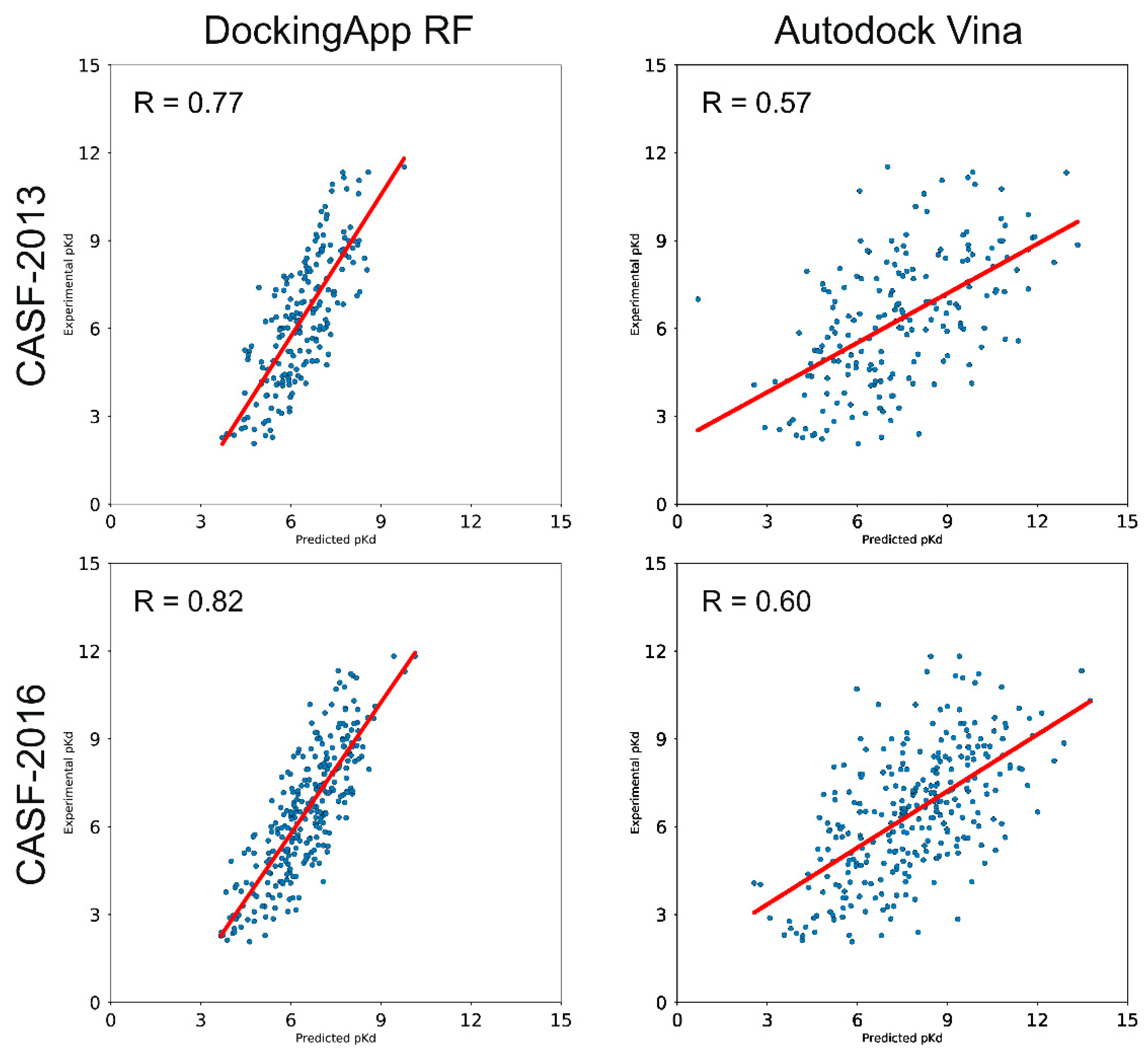
| Benchmark | Training-Set | n. Complexes | Test Set | n. Complexes |
|---|---|---|---|---|
| CASF-2013 | PDBBindv2013 refined set | 2764 | PDBBindv2013 core set | 195 |
| CASF-2016 | PDBBindv2016 refined set | 3772 | PDBBindv2016 core set | 285 |
| CASF-combined | PDBBindv2018 general set 100 | 12,002 | PDBBindv2013 core set + PDBBindv2016 core set | 370 |
| CASF-combined | PDBBindv2018 general set 90 | 10,943 | PDBBindv2013 core set + PDBBindv2016 core set | 370 |
| CASF-combined | PDBBindv2018 general set 70 | 10,523 | PDBBindv2013 core set + PDBBindv2016 core set | 370 |
| CASF-combined | PDBBindv2018 general set 50 | 10,173 | PDBBindv2013 core set + PDBBindv2016 core set | 370 |
| CASF-combined | PDBBindv2018 general set 40 | 9597 | PDBBindv2013 core set + PDBBindv2016 core set | 370 |
| CASF-combined | PDBBindv2018general set Tani | 13,194 | PDBBindv2013 core set + PDBBindv2016 core set | 370 |
| Pharmacophore Type | SYBYL Atom Type |
|---|---|
| P = Positive | N.4 (4 *) |
| N.2 (3 *) | |
| N.pl3 (C.cat) | |
| N = Negative | O (C (2 O or S [*])) |
| O (P (2 O or S [*])) | |
| O (S (3 O [*])) | |
| S (C (4 *)) [*] | |
| S (C (2 (O or S [*]))) | |
| DA = Donor-acceptor | O (H) |
| N.3 (H) | |
| N.2 (H) | |
| N.pl3 (H) | |
| S (H) | |
| D = Donor | N.ar (H) |
| N.am (H) | |
| A = Acceptor | O Default |
| N.3 | |
| N.1 | |
| N.ar (2 *) | |
| N.pl3 | |
| S [3 *] | |
| AR = Aromatic | N.ar |
| C.ar | |
| H = Hydrophobic | C [N] [O] [F] [P] [S] |
| PL = Polar | N.am |
| S (3 *) | |
| C (N) (O) (F) (P) (S) | |
| P | |
| HA = Halogen | F |
| Cl | |
| Br | |
| I |
| CASF-2013 | ||||
| SF | R | SD | RMSE | MAE |
| AGL-SCORE | 0.79 | n.a. | 1.97 | n.a. |
| DockingApp RF * | 0.79 | 1.26 | 1.38 | 1.13 |
| OnionNet * | 0.78 | 1.45 | 1.50 | 1.21 |
| DockingApp RF | 0.77 | 1.41 | 1.55 | 1.31 |
| RF-Score-v2 | 0.74 | 1.50 | 1.60 | n.a. |
| RF-Score-v3 | 0.74 | 1.50 | 1.59 | n.a. |
| Pafnucy * | 0.70 | 1.61 | 1.62 | 1.51 |
| ΔVinaRF20 | 0.69 | 1.64 | n.a. | n.a. |
| DeepBindRG | 0.64 | 1.73 | 1.82 | 1.48 |
| X-Score [48] | 0.61 | 1.78 | n.a. | n.a. |
| AutoDock Vina | 0.57 | n.a. | 2.4 | 1.95 |
| CASF-2016 | ||||
| SF | R | SD | RMSE | MAE |
| AGL-SCORE | 0.83 | n.a. | 1.73 | n.a. |
| DockingApp RF * | 0.83 | 1.26 | 1.38 | 1.13 |
| DockingApp RF | 0.82 | 1.26 | 1.38 | 1.13 |
| KDeep | 0.82 | n.a. | 1.27 | n.a. |
| OnionNet * | 0.82 | 1.26 | 1.28 | 0.98 |
| RF-Score-v2 | 0.81 | 1.28 | 1.42 | n.a. |
| RF-Score-v3 | 0.80 | n.a. | 1.39 | n.a. |
| Pafnucy * | 0.78 | 1.37 | 1.42 | 1.13 |
| ΔVinaXGB * | 0.80 | 1.32 | n.a. | n.a. |
| ΔVinaRF20 * | 0.73 | 1.26 | n.a. | n.a. |
| X-Score [48] | 0.63 | 1.69 | n.a. | n.a. |
| AutoDock Vina | 0.60 | n.a. | 2.35 | 1.94 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Macari, G.; Toti, D.; Pasquadibisceglie, A.; Polticelli, F. DockingApp RF: A State-of-the-Art Novel Scoring Function for Molecular Docking in a User-Friendly Interface to AutoDock Vina. Int. J. Mol. Sci. 2020, 21, 9548. https://doi.org/10.3390/ijms21249548
Macari G, Toti D, Pasquadibisceglie A, Polticelli F. DockingApp RF: A State-of-the-Art Novel Scoring Function for Molecular Docking in a User-Friendly Interface to AutoDock Vina. International Journal of Molecular Sciences. 2020; 21(24):9548. https://doi.org/10.3390/ijms21249548
Chicago/Turabian StyleMacari, Gabriele, Daniele Toti, Andrea Pasquadibisceglie, and Fabio Polticelli. 2020. "DockingApp RF: A State-of-the-Art Novel Scoring Function for Molecular Docking in a User-Friendly Interface to AutoDock Vina" International Journal of Molecular Sciences 21, no. 24: 9548. https://doi.org/10.3390/ijms21249548
APA StyleMacari, G., Toti, D., Pasquadibisceglie, A., & Polticelli, F. (2020). DockingApp RF: A State-of-the-Art Novel Scoring Function for Molecular Docking in a User-Friendly Interface to AutoDock Vina. International Journal of Molecular Sciences, 21(24), 9548. https://doi.org/10.3390/ijms21249548








