Exclusion Zone Phenomena in Water—A Critical Review of Experimental Findings and Theories
Abstract
:1. Introduction
2. Background
3. Pollack’s Key Experimental Findings and Replications
4. The Structure Change Theory
4.1. Testing the Structure Change Theory with Neutron Radiography
4.2. Testing for Structure Change with Optical Birefringence Measurement
5. Alternative Explanations for EZ Phenomena
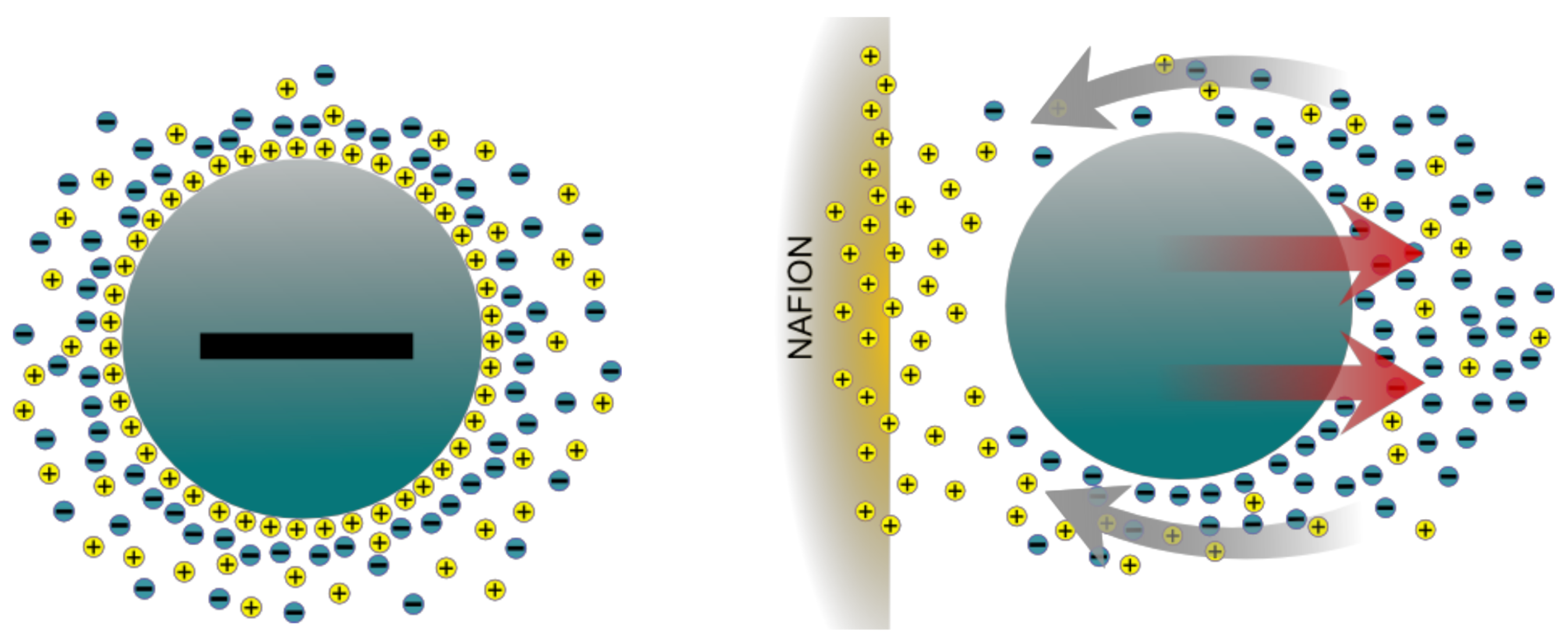
5.1. Diffusiophoresis
5.2. EZs at Metal Surfaces: Van Der Waals Repulsion and Quantum Phenomena
5.3. Other Possible Mechanisms and Experimental Confounds
- Dissolution of Nafion, during which polymer strands diffusing out of the gel push the beads away from the surface.
- A “brush mechanism” in which closely spaced long elastic polymer strands keep the beads away by entropic forces.
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chen, C.S.; Chung, W.J.; Hsu, I.C.; Wu, C.M.; Chin, W.C. Force field measurements within the exclusion zone of water. J. Biol. Phys. 2011, 38, 113–120. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Musa, S.; Florea, D.; van Loon, S.; Wyss, H.; Huyghe, J.M. Interfacial Water: Unexplained Phenomena. In Proceedings of the Fifth Biot Conference on Poromechanics, Vienna, Austria, 10–12 July 2013. [Google Scholar]
- Huszár, I.; Mártonfalvi, Z.; Laki, A.; Iván, K.; Kellermayer, M. Exclusion-Zone Dynamics Explored with Microfluidics and Optical Tweezers. Entropy 2014, 16, 4322–4337. [Google Scholar] [CrossRef] [Green Version]
- Gudkov, S.; Astashev, M.; Bruskov, V.; Kozlov, V.; Zakharov, S.; Bunkin, N. Self-oscillating Water Chemiluminescence Modes and Reactive Oxygen Species Generation Induced by Laser Irradiation; Effect of the Exclusion Zone Created by Nafion. Entropy 2014, 16, 6166–6185. [Google Scholar] [CrossRef] [Green Version]
- Jabs, H.; Rubik, B. Self-Organization at Aqueous Colloid-Membrane Interfaces and an Optical Method to Measure the Kinetics of Exclusion Zone Formation. Entropy 2014, 16, 5954–5975. [Google Scholar] [CrossRef] [Green Version]
- Florea, D.; Musa, S.; Huyghe, J.M.R.; Wyss, H.M. Long-range repulsion of colloids driven by ion exchange and diffusiophoresis. Proc. Natl. Acad. Sci. USA 2014, 111, 6554–6559. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bunkin, N.F.; Ignatiev, P.S.; Kozlov, V.A.; Shkirin, A.V.; Zakharov, S.D.; Zinchenko, A.A. Study of the Phase States of Water Close to Nafion Interface. Water J. 2013, 4, 129–154. [Google Scholar]
- Yakhno, T.A.; Yakhno, V.G. On the interaction of water with hydrophilic surfaces. Russ. J. Biol. Phys. Chem. 2018, 3, 9–18. [Google Scholar]
- Spencer, P.D.; Riches, J.D.; Williams, E.D. Exclusion zone water is associated with material that exhibits proton diffusion but not birefringent properties. Fluid Phase Equilibria 2018, 466, 103–109. [Google Scholar] [CrossRef]
- Sharma, A.; Adams, C.; Cashdollar, B.D.; Li, Z.; Nguyen, N.V.; Sai, H.; Shi, J.; Velchuru, G.; Zhu, K.Z.; Pollack, G.H. Effect of Health-Promoting Agents on Exclusion-Zone Size. Dose-Response 2018, 16, 155932581879693. [Google Scholar] [CrossRef]
- Esplandiu, M.J.; Reguera, D.; Fraxedas, J. Electrophoretic origin of long-range repulsion of colloids near water/Nafion interfaces. Soft Matter 2020, 16, 3717–3726. [Google Scholar] [CrossRef]
- Zheng, J.; Chin, W.; Khijniak, E.; Khijniak, E.; Pollack, G.H. Surfaces and interfacial water: Evidence that hydrophilic surfaces have long-range impact. Adv. Colloid Interface Sci. 2006, 127, 19–27. [Google Scholar] [CrossRef] [PubMed]
- Pedroza, L.S.; Poissier, A.; Fernández-Serra, M.V. Local order of liquid water at metallic electrode surfaces. J. Chem. Phys. 2015, 142, 034706. [Google Scholar] [CrossRef] [PubMed]
- Chai, B.; Mahtani, A.G.; Pollack, G.H. Unexpected presence of solute-free zones at metal-water interfaces. Contemp. Mater. 2012, 3, 1. [Google Scholar] [CrossRef] [Green Version]
- Sulbarán, B.; Toriz, G.; Allan, G.G.; Pollack, G.H.; Delgado, E. The dynamic development of exclusion zones on cellulosic surfaces. Cellulose 2014, 21, 1143–1148. [Google Scholar] [CrossRef]
- Pedregal-Cortés, R.; Toriz, G.; Delgado, E.; Pollack, G.H. Interfacial water and its potential role in the function of sericin against biofouling. Biofouling 2019, 35, 732–741. [Google Scholar] [CrossRef] [PubMed]
- Ball, P. Water as an Active Constituent in Cell Biology. Chem. Rev. 2008, 108, 74–108. [Google Scholar] [CrossRef]
- Drost-Hansen, W. Structure of Water Near Solid Interfaces. Ind. Eng. Chem. 1969, 61, 10–47. [Google Scholar] [CrossRef]
- Drost-Hansen, W. Phase transitions in biological systems: Manifestations of cooperative processes in vicinal water. Ann. N. Y. Acad. Sci. 1973, 204, 100–112. [Google Scholar] [CrossRef]
- Fenter, P.; Sturchio, N.C. Mineral–water interfacial structures revealed by synchrotron X-ray scattering. Prog. Surf. Sci. 2004, 77, 171–258. [Google Scholar] [CrossRef]
- Verdaguer, A.; Sacha, G.M.; Bluhm, H.; Salmeron, M. Molecular Structure of Water at Interfaces: Wetting at the Nanometer Scale. Chem. Rev. 2006, 106, 1478–1510. [Google Scholar] [CrossRef]
- Maccarini, M. Water at solid surfaces: A review of selected theoretical aspects and experiments on the subject. Biointerphases 2007, 2, MR1–MR15. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ling, G.N. A new theoretical foundation for the polarized-oriented multilayer theory of cell water and for inanimate systems demonstrating long-range dynamic structuring of water molecules. Physiol. Chem. Phys. Med. NMR 2003, 35, 91–130. [Google Scholar]
- Deryagin, B.V.; Golovanov, M.V. Electromagnetic nature of forces of repulsion forming aureoles around cells. Colloid J. USSR 1986, 48, 209–211. [Google Scholar]
- Shen, Y.R.; Ostroverkhov, V. Sum-Frequency Vibrational Spectroscopy on Water Interfaces: Polar Orientation of Water Molecules at Interfaces. Chem. Rev. 2006, 106, 1140–1154. [Google Scholar] [CrossRef] [PubMed]
- Catalano, J.G. Weak interfacial water ordering on isostructural hematite and corundum (001) surfaces. Geochim. Cosmochim. Acta 2011, 75, 2062–2071. [Google Scholar] [CrossRef]
- Eftekhari-Bafrooei, A.; Borguet, E. Effect of Hydrogen-Bond Strength on the Vibrational Relaxation of Interfacial Water. J. Am. Chem. Soc. 2010, 132, 3756–3761. [Google Scholar] [CrossRef] [PubMed]
- Ebbinghaus, S.; Kim, S.J.; Heyden, M.; Yu, X.; Heugen, U.; Gruebele, M.; Leitner, D.M.; Havenith, M. An extended dynamical hydration shell around proteins. Proc. Natl. Acad. Sci. USA 2007, 104, 20749–20752. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Elton, D.C.; Fernández-Serra, M.V. Polar nanoregions in water: A study of the dielectric properties of TIP4P/2005, TIP4P/2005f and TTM3F. J. Chem. Phys. 2014, 140, 124504. [Google Scholar] [CrossRef] [Green Version]
- Elton, D.C. Understanding the Dielectric Properties of Water. Ph.D. Thesis, Stony Brook University, Stony Brook, NY, USA, 2016. [Google Scholar]
- Chaplin, M. A proposal for the structuring of water. Biophys. Chem. 2000, 83, 211–221. [Google Scholar] [CrossRef]
- Zheng, J.M.; Pollack, G.H. Long-range forces extending from polymer-gel surfaces. Phys. Rev. E 2003, 68, 031408. [Google Scholar] [CrossRef] [Green Version]
- Klimov, A.; Pollack, G.H. Visualization of Charge-Carrier Propagation in Water. Langmuir 2007, 23, 11890–11895. [Google Scholar] [CrossRef] [PubMed]
- Park, J.S.; Choi, J.H.; Woo, J.J.; Moon, S.H. An electrical impedance spectroscopic (EIS) study on transport characteristics of ion-exchange membrane systems. J. Colloid Interface Sci. 2006, 300, 655–662. [Google Scholar] [CrossRef] [PubMed]
- Pollack, G. The Fourth Phase of Water: Beyond Solid, Liquid, and Vapor; Ebner & Sons: Seattle, WA, USA, 2013. [Google Scholar]
- Hwang, S.G.; Hong, J.K.; Sharma, A.; Pollack, G.H.; Bahng, G. Exclusion zone and heterogeneous water structure at ambient temperature. PLoS ONE 2018, 13, e0195057. [Google Scholar] [CrossRef] [PubMed]
- Ying, Z.; Takizawa, S.; Lohwacharin, J. Spontaneous Particle Separation and Salt Rejection by Hydrophilic Membranes. Water J. 2015, 7. [Google Scholar] [CrossRef]
- Chai, B.; Yoo, H.; Pollack, G.H. Effect of Radiant Energy on Near-Surface Water. J. Phys. Chem. B 2009, 113, 13953–13958. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zheng, J.-M.; Wexler, A.; Pollack, G.H. Effect of buffers on aqueous solute-exclusion zones around ion-exchange resins. J. Colloid Interface Sci. 2009, 332, 511–514. [Google Scholar] [CrossRef] [Green Version]
- Figueroa, X.A.; Pollack, G.H. Exclusion-zone formation from discontinuous nafion surfaces. Int. J. Des. Nat. Ecodynamics 2011, 6, 286–296. [Google Scholar] [CrossRef]
- Oehr, K.; LeMay, P. The Case for Tetrahedral Oxy-subhydride (TOSH) Structures in the Exclusion Zones of Anchored Polar Solvents Including Water. Entropy 2014, 16, 5712–5720. [Google Scholar] [CrossRef] [Green Version]
- Giudice, E.D.; Tedeschi, A.; Vitiello, G.; Voeikov, V. Coherent structures in liquid water close to hydrophilic surfaces. J. Phys. Conf. Ser. 2013, 442, 012028. [Google Scholar] [CrossRef] [Green Version]
- Elia, V.; Napoli, E.; Germano, R.; Oliva, R.; Roviello, V.; Niccoli, M.; Amoresano, A.; Naviglio, D.; Ciaravolo, M.; Trifuoggi, M.; et al. New chemical-physical properties of water after iterative procedure using hydrophilic polymers: The case of paper filter. J. Mol. Liq. 2019, 296, 111808. [Google Scholar] [CrossRef]
- Giudice, E.D.; Spinetti, P.R.; Tedeschi, A. Water Dynamics at the Root of Metamorphosis in Living Organisms. Water 2010, 2, 566–586. [Google Scholar] [CrossRef] [Green Version]
- Giudice, E.; Voeikov, V.; Tedeschi, A.; Vitiello, G. The Origin and the Special Role of Coherent Water in Living Systems; Research Signpost: Trivandrum, India, 2015; Volume 37661, pp. 95–111. [Google Scholar] [CrossRef]
- Bier, M.; Pravica, D. Limits on Quantum Coherent Domains in Liquid Water. Acta Phys. Pol. B 2018, 49, 1717. [Google Scholar] [CrossRef] [Green Version]
- So, E.; Stahlberg, R.; Pollack, G.H. Exclusion zone as intermediate between ice and water. In Water and Society; WIT Press: Southampton, UK, 2011. [Google Scholar]
- Fedyakin, N.N. Change in the structure of water during condensation in capillaries. Kolloid Zhurnal 1962, 24, 497. [Google Scholar]
- Hasted, J.B. Water and “polywater”. Contemp. Phys. 1971, 12, 133–152. [Google Scholar] [CrossRef]
- Segarra-Martí, J.; Roca-Sanjuán, D.; Merchán, M. Can the Hexagonal Ice-like Model Render the Spectroscopic Fingerprints of Structured Water? Feedback from Quantum-Chemical Computations. Entropy 2014, 16, 4101–4120. [Google Scholar] [CrossRef] [Green Version]
- Chai, B.; Pollack, G.H. Solute-Free Interfacial Zones in Polar Liquids. J. Phys. Chem. B 2010, 114, 5371–5375. [Google Scholar] [CrossRef] [Green Version]
- Skinner, L.B.; Benmore, C.J.; Shyam, B.; Weber, J.K.R.; Parise, J.B. Structure of the floating water bridge and water in an electric field. Proc. Natl. Acad. Sci. USA 2012, 109, 16463–16468. [Google Scholar] [CrossRef] [Green Version]
- Fuchs, E.C.; Bitschnau, B.; Woisetschläger, J.; Maier, E.; Beuneu, B.; Teixeira, J. Neutron scattering of a floating heavy water bridge. J. Phys. D: Appl. Phys. 2009, 42, 065502. [Google Scholar] [CrossRef]
- Chai, B.; Zheng, J.; Zhao, Q.; Pollack, G.H. Spectroscopic Studies of Solutes in Aqueous Solution. J. Phys. Chem. A 2008, 112, 2242–2247. [Google Scholar] [CrossRef] [PubMed]
- Dibble, W.E.; Kaszyk, J.; Tiller, W.A. Bulk Water with Exclusion Zone Water Characteristics: Experimental Evidence of Interaction With a Non-physical Agent. Water J. 2014, 6. [Google Scholar] [CrossRef]
- Bielski, B.H.J.; Cabelli, D.E.; Arudi, R.L.; Ross, A.B. Reactivity of HO2/O-2 Radicals in Aqueous Solution. J. Phys. Chem. Ref. Data 1985, 14, 1041–1100. [Google Scholar] [CrossRef]
- Janik, I.; Tripathi, G.N.R. The nature of the superoxide radical anion in water. J. Chem. Phys. 2013, 139, 014302. [Google Scholar] [CrossRef] [PubMed]
- Matheson, I.B.C.; Lee, J. The Absorption Spectrum of Superoxide Anion in Dimethylsulfoxide. Spectrosc. Lett. 1969, 2, 117–119. [Google Scholar] [CrossRef]
- Czapski, G.; Dorfman, L.M. Pulse Radiolysis Studies. V. Transient Spectra and Rate Constants in Oxygenated Aqueous Solutions. J. Phys. Chem. 1964, 68, 1169–1177. [Google Scholar] [CrossRef]
- Pokorný, J.; Pokorný, J.; Foletti, A.; Kobilková, J.; Vrba, J.; Vrba, J. Mitochondrial Dysfunction and Disturbed Coherence: Gate to Cancer. Pharmaceuticals 2015, 8, 675–695. [Google Scholar] [CrossRef] [Green Version]
- Hwang, S.G.; Lee, H.S.; Lee, B.C.; Bahng, G. Effect of Antioxidant Water on the Bioactivities of Cells. Int. J. Cell Biol. 2017, 2017, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Tychinsky, V.P. Extension of the concept of an anomalous water component to images of T-cell organelles. J. Biomed. Opt. 2014, 19, 126008. [Google Scholar] [CrossRef] [Green Version]
- Spencer, P. Examining Claims of Long-Range Molecular Order in Water Molecules. Master’s Thesis, Queensland University of Technology, Brisbane City, Australia, 2018. [Google Scholar]
- Takenaka, N.; Sugimoto, K.; Takami, S.; Sugioka, K.; Tsukada, T.; Adschiri, T.; Saito, Y. Application of Neutron Radiography to Flow Visualization in Supercritical Water. Phys. Procedia 2013, 43, 264–268. [Google Scholar] [CrossRef] [Green Version]
- Das, R.; Pollack, G.H. Charge-Based Forces at the Nafion–Water Interface. Langmuir 2013, 29, 2651–2658. [Google Scholar] [CrossRef] [PubMed]
- Totland, C.; Nerdal, W. Experimental Determination of Water Molecular Orientation near a Silica Surface Using NMR Spectroscopy. J. Phys. Chem. C 2016, 120, 5052–5058. [Google Scholar] [CrossRef]
- Yoo, H.; Baker, D.R.; Pirie, C.M.; Hovakeemian, B.; Pollack, G.H. Characteristics of water adjacent to hydrophilic interfaces. In Water: The Forgotten Biological Molecule; Pan Stanford Publishing: Staford, CA, USA, 2016. [Google Scholar]
- Shokr, M.; Sinha, N. Laboratory Techniques for Revealing the Structure of Polycrystalline Ice. In Sea Ice; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2015; pp. 231–269. [Google Scholar]
- Tychinsky, V. High Electric Susceptibility is the Signature of Structured Water in Water-Containing Objects. Water J. 2011, 3, 95–99. [Google Scholar]
- Schurr, J.M.; Fujimoto, B.S.; Huynh, L.; Chiu, D.T. A Theory of Macromolecular Chemotaxis. J. Phys. Chem. B 2013, 117, 7626–7652. [Google Scholar] [CrossRef]
- Schurr, J.M. Phenomena Associated with Gel–Water Interfaces. Analyses and Alternatives to the Long-Range Ordered Water Hypothesis. J. Phys. Chem. B 2013, 117, 7653–7674. [Google Scholar] [CrossRef] [PubMed]
- Pollack, G.H. Comment on “A Theory of Macromolecular Chemotaxis” and “Phenomena Associated with Gel–Water Interfaces. Analyses and Alternatives to the Long-Range Ordered Water Hypothesis”. J. Phys. Chem. B 2013, 117, 7843–7846. [Google Scholar] [CrossRef] [PubMed]
- Ovchinnikova, K.; Pollack, G.H. Can Water Store Charge? Langmuir 2009, 25, 542–547. [Google Scholar] [CrossRef]
- Seger, B.; Vinodgopal, K.; Kamat, P.V. Proton Activity in Nafion Films: Probing Exchangeable Protons with Methylene Blue. Langmuir 2007, 23, 5471–5476. [Google Scholar] [CrossRef] [PubMed]
- Phonyiem, M.; Chaiwongwattana, S.; Lao-ngam, C.; Sagarik, K. Proton transfer reactions and dynamics of sulfonic acid group in Nafion®. Phys. Chem. Chem. Phys. 2011, 13, 10923. [Google Scholar] [CrossRef]
- Devanathan, R.; Venkatnathan, A.; Rousseau, R.; Dupuis, M.; Frigato, T.; Gu, W.; Helms, V. Atomistic Simulation of Water Percolation and Proton Hopping in Nafion Fuel Cell Membrane. J. Phys. Chem. B 2010, 114, 13681–13690. [Google Scholar] [CrossRef]
- Kreuer, K.D.; Ise, M.; Fuchs, A.; Maier, J. Proton and water transport in nano-separated polymer membranes. J. Phys. IV 2000, 10, Pr7-279–Pr7-281. [Google Scholar] [CrossRef]
- Musumeci, F.; Pollack, G.H. High electrical permittivity of ultrapure water at the water–platinum interface. Chem. Phys. Lett. 2014, 613, 19–23. [Google Scholar] [CrossRef]
- Fajín, J.L.C.; Cordeiro, M.N.D.S.; Gomes, J.R.B. Density Functional Theory Study of the Water Dissociation on Platinum Surfaces: General Trends. J. Phys. Chem. A 2014, 118, 5832–5840. [Google Scholar] [CrossRef]
- Ninno, A.D. Dynamics of formation of the Exclusion Zone near hydrophilic surfaces. Chem. Phys. Lett. 2017, 667, 322–326. [Google Scholar] [CrossRef]
- Hamaker, H. The London—van der Waals attraction between spherical particles. Physica 1937, 4, 1058–1072. [Google Scholar] [CrossRef]
- Lifshitz, E.M. The theory of molecular attractive forces between solids. Sov. Phys. JETP 1956, 2, 73–83. [Google Scholar]
- Van Zwol, P.J.; Palasantzas, G. Repulsive Casimir forces between solid materials with high-refractive-index intervening liquids. Phys. Rev. A 2010, 81, 062502. [Google Scholar] [CrossRef] [Green Version]
- Zhao, R.; Koschny, T.; Economou, E.N.; Soukoulis, C.M. Repulsive Casimir forces with finite-thickness slabs. Phys. Rev. B 2011, 83, 075108. [Google Scholar] [CrossRef] [Green Version]
- Milling, A.; Mulvaney, P.; Larson, I. Direct Measurement of Repulsive van der Waals Interactions Using an Atomic Force Microscope. J. Colloid Interface Sci. 1996, 180, 460–465. [Google Scholar] [CrossRef]
- Munday, J.N.; Capasso, F.; Parsegian, V.A. Measured long-range repulsive Casimir–Lifshitz forces. Nature 2009, 457, 170–173. [Google Scholar] [CrossRef]
- Meurk, A.; Luckham, P.F.; Bergström, L. Direct Measurement of Repulsive and Attractive van der Waals Forces between Inorganic Materials. Langmuir 1997, 13, 3896–3899. [Google Scholar] [CrossRef]
- woo Lee, S.; Sigmund, W.M. AFM study of repulsive van der Waals forces between Teflon AF™ thin film and silica or alumina. Colloids Surfaces A Physicochem. Eng. Asp. 2002, 204, 43–50. [Google Scholar] [CrossRef]
- Bevan, M.A.; Prieve, D.C. Direct Measurement of Retarded van der Waals Attraction. Langmuir 1999, 15, 7925–7936. [Google Scholar] [CrossRef]
- woo Lee, S.; Sigmund, W.M. Repulsive van der Waals Forces for Silica and Alumina. J. Colloid Interface Sci. 2001, 243, 365–369. [Google Scholar] [CrossRef]
- Israelachvili, J.N. Intermolecular and Surface Forces; Elsevier: San Diego, CA, USA, 2011. [Google Scholar]
- He, X.; Zhou, Y.; Wen, X.; Shpilman, A.A.; Ren, Q. Effect of Spin Polarization on the Exclusion Zone of Water. J. Phys. Chem. B 2018, 122, 8493–8502. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez-Fortuño, F.J.; Zayats, A.V. Repulsion of polarised particles from anisotropic materials with a near-zero permittivity component. Light. Sci. Appl. 2016, 5, e16022. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bunkin, N.F.; Shkirin, A.V.; Kozlov, V.A.; Ninham, B.W.; Uspenskaya, E.V.; Gudkov, S.V. Near-surface structure of Nafion in deuterated water. J. Chem. Phys. 2018, 149, 164901. [Google Scholar] [CrossRef]
- Bunkin, N.F.; Bashkina, U.A.; Bolikov, N.G.; Bereza, I.S.; Molchanov, I.I.; Kozlov, V.A. Study of the luminescence from polymeric membrane swollen in water with various content of deuterium; isotopic effects. J. Phys. Conf. Ser. 2019, 1348, 012030. [Google Scholar] [CrossRef]
- Almeida, S.H.D.; Kawano, Y. Ultraviolet-visible spectra of Nafion membrane. Eur. Polym. J. 1997, 33, 1307–1311. [Google Scholar] [CrossRef]
- Horinek, D.; Serr, A.; Geisler, M.; Pirzer, T.; Slotta, U.; Lud, S.Q.; Garrido, J.A.; Scheibel, T.; Hugel, T.; Netz, R.R. Peptide adsorption on a hydrophobic surface results from an interplay of solvation, surface, and intrapeptide forces. Proc. Natl. Acad. Sci. USA 2008, 105, 2842–2847. [Google Scholar] [CrossRef] [Green Version]
- Richert, R.; Agapov, A.; Sokolov, A.P. Appearance of a Debye process at the conductivity relaxation frequency of a viscous liquid. J. Chem. Phys. 2011, 134, 104508. [Google Scholar] [CrossRef]
- Chaplin, M. Self-generation of colligative properties at hydrophilic surfaces. arXiv 2012, arXiv:1203.0206. [Google Scholar]
- Chaplin, M. Self-Generation of Colligative Properties at Interfaces. Available online: http://www1.lsbu.ac.uk/water/colligative_generation.html (accessed on 14 September 2019).
- Rohani, M.; Pollack, G.H. Flow through Horizontal Tubes Submerged in Water in the Absence of a Pressure Gradient: Mechanistic Considerations. Langmuir 2013, 29, 6556–6561. [Google Scholar] [CrossRef] [PubMed]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elton, D.C.; Spencer, P.D.; Riches, J.D.; Williams, E.D. Exclusion Zone Phenomena in Water—A Critical Review of Experimental Findings and Theories. Int. J. Mol. Sci. 2020, 21, 5041. https://doi.org/10.3390/ijms21145041
Elton DC, Spencer PD, Riches JD, Williams ED. Exclusion Zone Phenomena in Water—A Critical Review of Experimental Findings and Theories. International Journal of Molecular Sciences. 2020; 21(14):5041. https://doi.org/10.3390/ijms21145041
Chicago/Turabian StyleElton, Daniel C., Peter D. Spencer, James D. Riches, and Elizabeth D. Williams. 2020. "Exclusion Zone Phenomena in Water—A Critical Review of Experimental Findings and Theories" International Journal of Molecular Sciences 21, no. 14: 5041. https://doi.org/10.3390/ijms21145041





