Self-Repair in Cacti Branches: Comparative Analyses of Their Morphology, Anatomy, and Biomechanics
Abstract
1. Introduction
2. Results
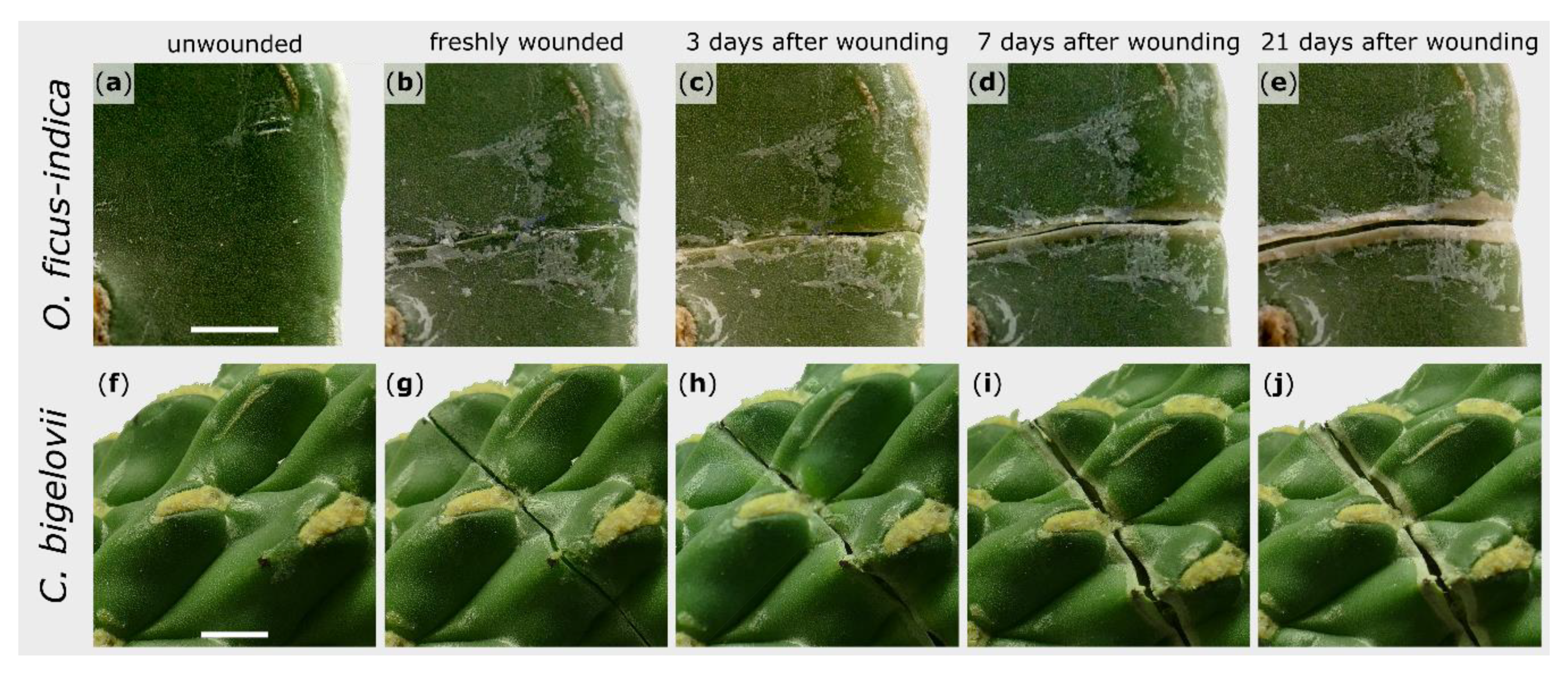
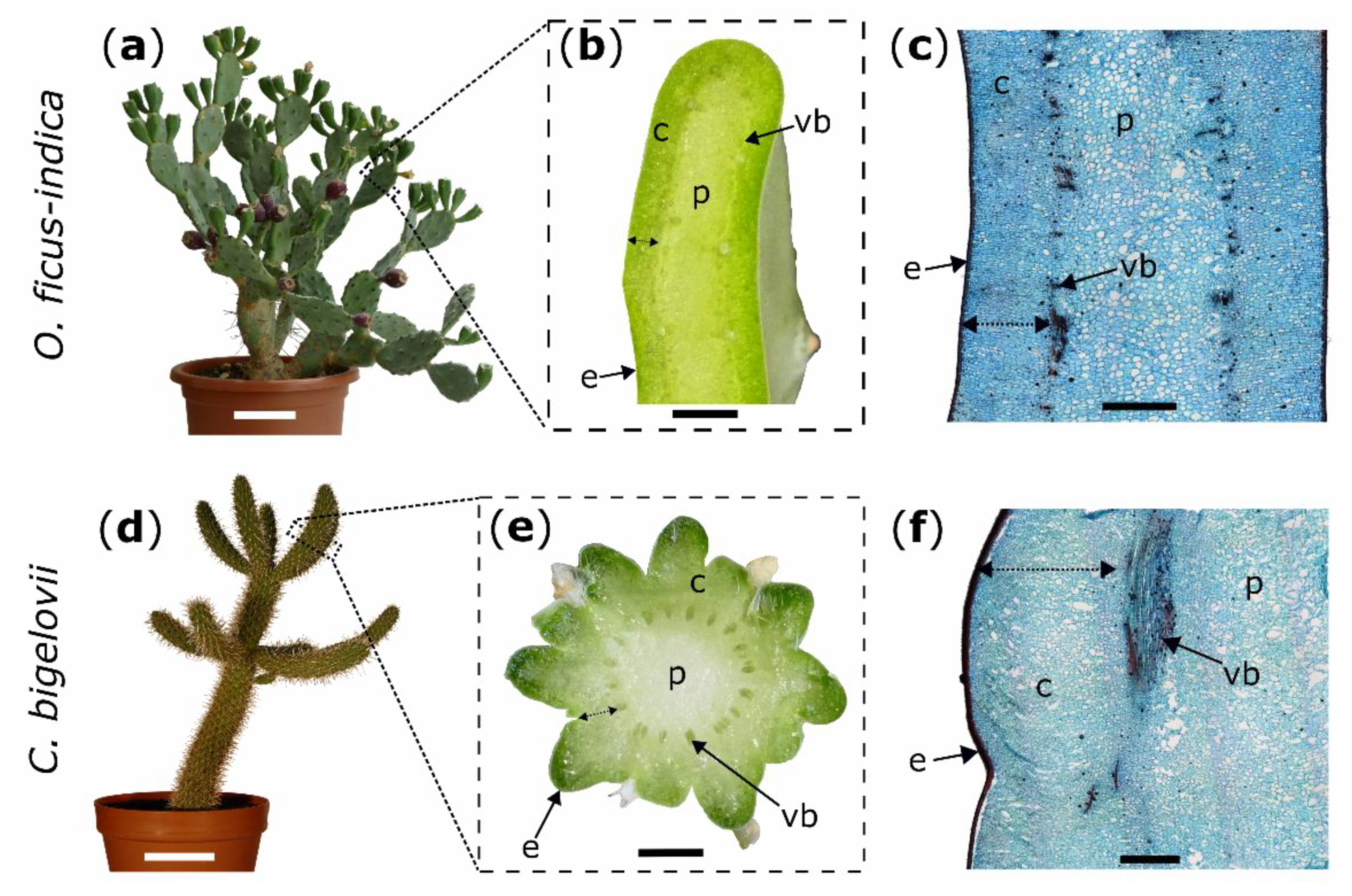
2.1. Macroscopic Observations
2.2. Microscopic Observations
2.3. Biomechanics
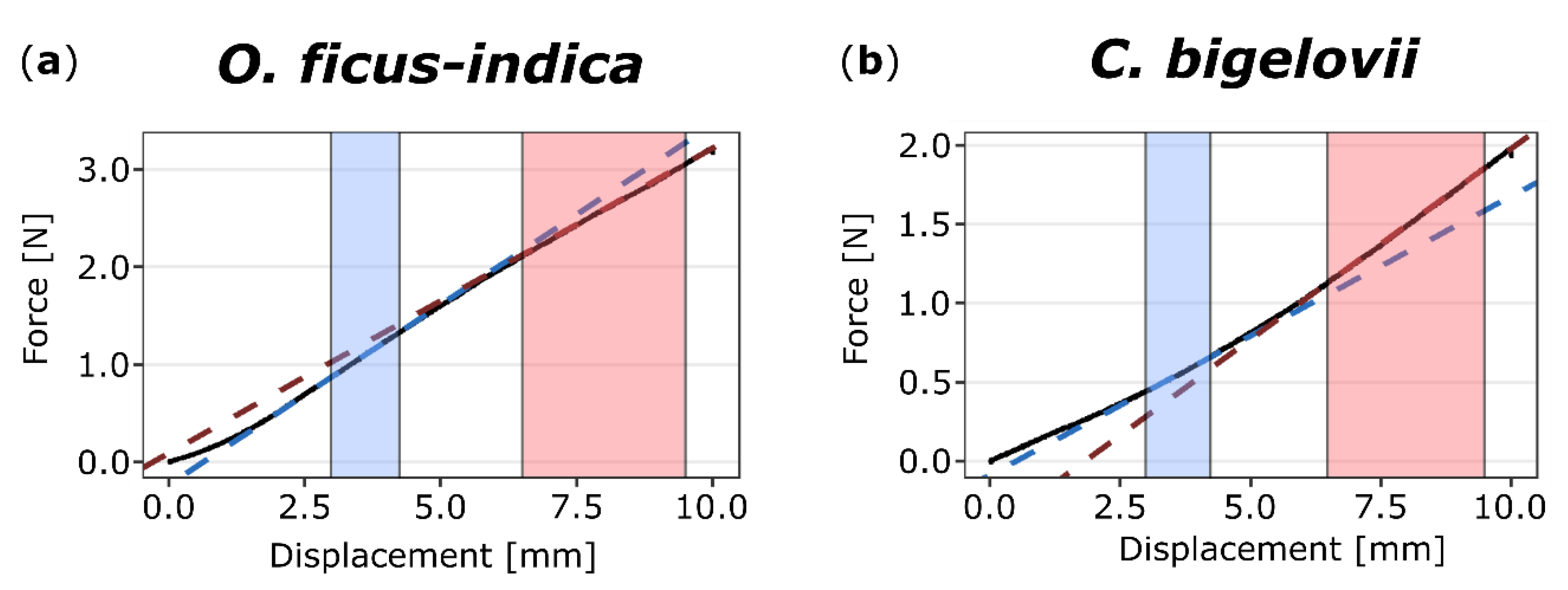
2.3.1. Bilinear Behavior
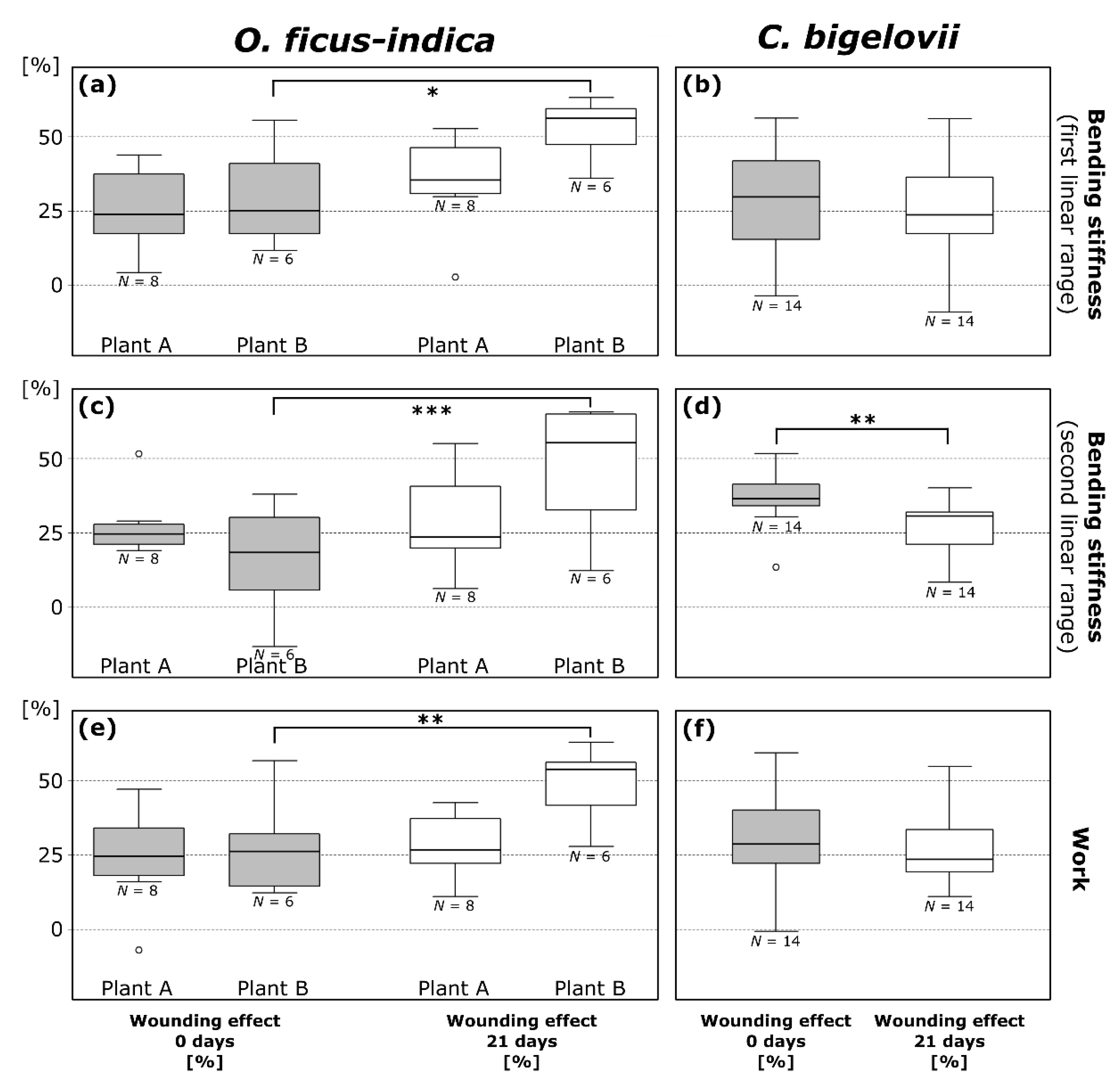
2.3.2. Bending Stiffness
2.3.3. Work
2.3.4. Bending Elastic Modulus
2.3.5. Synopsis of Biomechanical Performance
2.3.6. Relative Water Content
3. Discussion
3.1. Morphological and Anatomical Repair-Effects: Restoration of Structural Integrity
3.2. Biomechanical Repair-Effects: Restoration of Mechanical Integrity
4. Materials and Methods
4.1. Plant Material and Treatment
4.2. Wounding
4.3. Macroscopic Observations
4.4. Anatomy
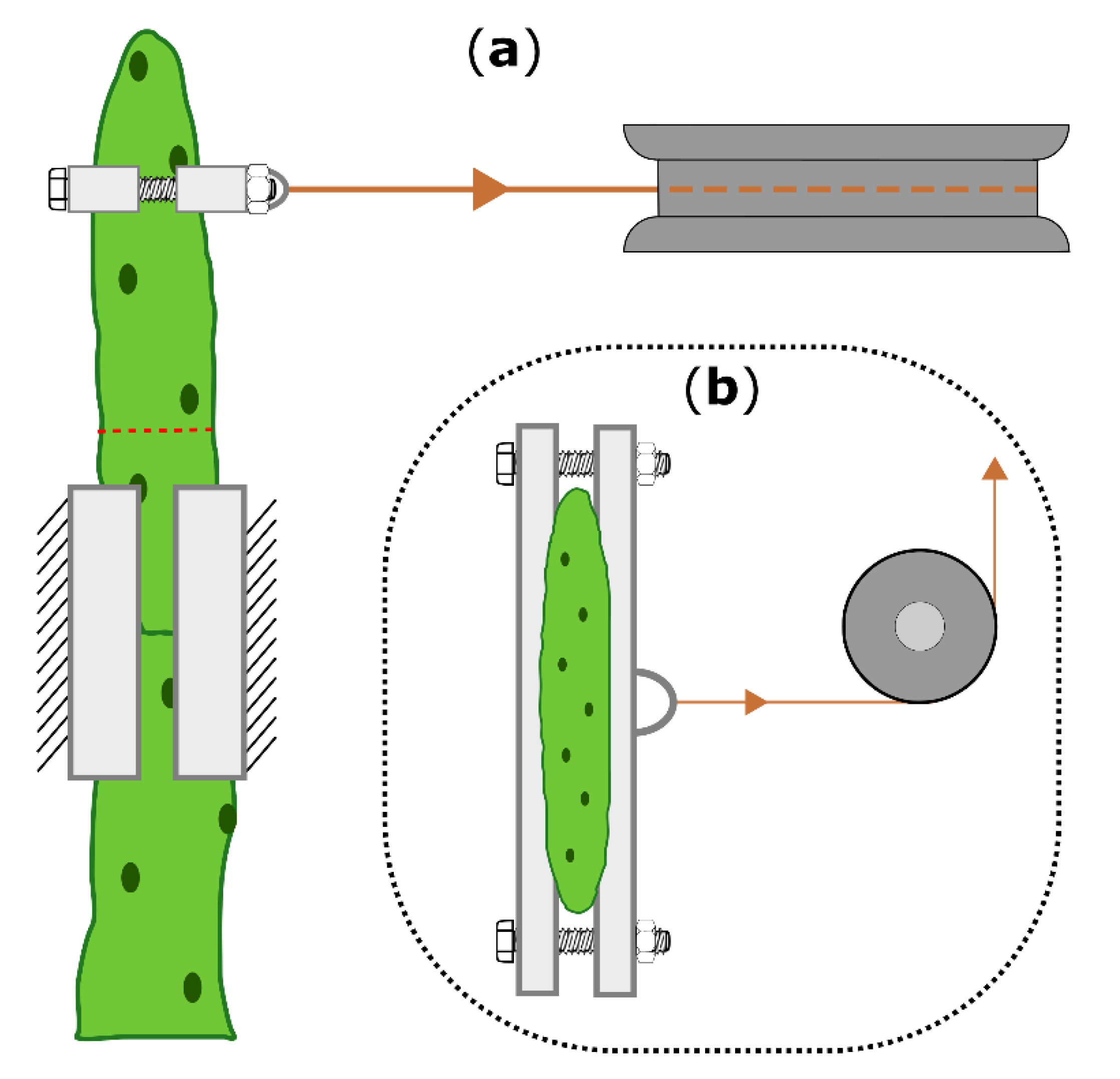
4.5. Biomechanical Testing
4.6. Wounding Effect and Healing Effect
4.7. Bending Elastic Modulus
4.8. Relative Water Content
4.9. Statistics
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| WE | Wounding effect |
| HE | Healing effect |
| SD | Standard deviation |
| IQR | Interquartile range |
| E | Bending elastic modulus |
| I | Axial second moment of area |
| RWC | Relative water content |
| STL | Stereolithography |
| CAD | Computer-aided design |
| COM | Center of mass |
| EI | Bending stiffness |
| uv | Unwounded value |
| wv | Wounded value |
Appendix A
| Parameter Comparison | O. ficus-indica Plants A and B n = 14 | C. bigelovii Plants C, D, and E n = 14 |
|---|---|---|
| BS 1 1 | ||
| —2 | t = −0.441, df = 9.438, p = 0.669 (1) n.s. | Df = 2, Sum Sq = 293, Mean Sq = 146.5, F = 0.391, p = 0.685 (5) n.s. |
| —3 | t = −2.647, df = 11.804, p = 0.0216 (1) * | Df = 2, Sum Sq = 350, Mean Sq = 175.2, F = 0.514, p = 0.612 (5) n.s. |
| —4 | t = 1.519, df = 11.616, p = 0.155 (1) n.s. | Df = 2, Sum Sq = 1102, Mean Sq = 551.2, F = 4.36, p = 0.0403 Tukey’s test: all p > 0.055 (5,7) n.s. |
| BS 2 5 | ||
| — | W = 32, p = 0.345 (3) n.s. | Df = 2, Sum Sq = 32.1, Mean Sq = 16.04, F = 0.162, p = 0.853 (5) n.s. |
| — | t = 1.832, df = 9.158, p = 0.0996 (1) n.s. | Df = 2, Sum Sq = 44.7, Mean Sq = 22.35, F = 0.228, p = 0.8 (5) n.s. |
| — | t = 3.652, df = 11.084, p = 0.00376 (1) ** | Df = 2, Sum Sq = 5.59, Mean Sq = 2.796, F = 0.124, p = 0.885 (5) n.s. |
| Work | ||
| — | t = 0.446, df = 10.945, p = 0.665 (1) n.s. | Df = 2, Sum Sq = 46.3, Mean Sq = 23.16, F = 0.085, p = 0.92 (5) n.s. |
| — | t = 3.343, df = 9.704, p = 0.00777 (1) ** | χ2 = 2.143, df = 2, p = 0.343 (6) n.s. |
| — | t = 2.113, df = 11.653, p = 0.0569 (1) n.s. | Df = 2, Sum Sq = 306, Mean Sq = 153.0, F = 1.227, p = 0.33 (5) n.s. |
| Plant | BS 1 1 | BS 2 4 | Work |
|---|---|---|---|
| O. ficus-indica | |||
| Plant A (N = 8) | t = 1.4159, df = 7, p = 0.1997 (2) n.s. | V = 16, p = 0.8438 (4) n.s. | t = −0.6040, df = 7, p = 0.565 (2) n.s. |
| Plant B (N = 6) | t = 3.5331, df = 5, p = 0.0167 (2) * | t = 7.2921, df = 5, p = 0.00076 (2) *** | t = −4.528, df = 5, p = 0.0062 (2) ** |
| C. bigelovii | |||
| Plant C (n = 5) | t = -3.0339, df = 4, p = 0.039 (2) * | t = −3.8951, df = 4, p = 0.0176 (2) * | V = 14, p = 0.125 (4) n.s. |
| Plant D (n = 4) | t = 0.58275, df = 3, p = 0.601 (2) n.s. | t = −4.9121, df = 3, p = 0.0162 (2) * | t = −0.1308, df = 3, p = 0.904 (2) n.s. |
| Plant E (n = 5) | t = 1.142, df = 4, p = 0.3172 (2) n.s. | t = −4.4061, df = 4, p = 0.0116 (2) * | t = 0.6218, df = 4, p = 0.5677 (2) n.s. |
References
- Speck, O.; Speck, T. An overview of bioinspired and biomimetic self-repairing materials. Biomimetics 2019, 4, 26. [Google Scholar] [CrossRef] [PubMed]
- Addicott, F.T. Abscission; University of California Press: Berkeley, CA, USA; Los Angeles, CA, USA, 1982; ISBN 0520042883. [Google Scholar]
- Gulfishan, M.; Jahan, A.; Bhat, T.A.; Sahab, D. Plant senescence and organ abscission. In Senescence Signalling and Control in Plants, 1st ed.; Sarwat, M., Tuteja, N., Eds.; Academic Press: London, UK, 2019; pp. 255–272. ISBN 9780128131879. [Google Scholar]
- Lipetz, J. Wound-Healing in higher plants. In International Review of Cytology; Bourne, G.H., Danielli, J.F., Eds.; Academic Press: New York, NY, USA, 1970; Volume 27, pp. 1–28. ISBN 978-0-12-364327-8. [Google Scholar]
- Speck, T.; Bauer, G.; Flues, F.; Oelker, K.; Rampf, M.; Schüssele, A.C.; Von Tapavicza, M.; Bertling, J.; Luchsinger, R.; Nellesen, A.; et al. Bio-inspired self-healing materials. In Materials Design Inspired by Nature; Fratzl, P., Dunlop, J.W.C., Weinkamer, R., Eds.; Royal Society of Chemistry: Cambridge, UK, 2013; pp. 359–389. ISBN 978-1-84973-553-7. [Google Scholar]
- Speck, O.; Schlechtendahl, M.; Borm, F.; Kampowski, T.; Speck, T. Humidity-dependent wound sealing in succulent leaves of Delosperma cooperi—An adaptation to seasonal drought stress. Beilstein J. Nanotechnol. 2018, 9, 175–186. [Google Scholar] [CrossRef] [PubMed]
- Harrington, M.J.; Speck, O.; Speck, T.; Wagner, S.; Weinkamer, R. Biological archetypes for self-healing materials. In Self-Healing Materials; Hager, M.D., Van der Zwaag, S., Schubert, U.S., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 307–344. ISBN 978-3-319-32776-1. [Google Scholar]
- Bauer, G.; Speck, T. Restoration of tensile strength in bark samples of Ficus benjamina due to coagulation of latex during fast self-healing of fissures. Ann. Bot. 2012, 109, 807–811. [Google Scholar] [CrossRef]
- Anandan, S.; Rudolph, A.; Speck, T.; Speck, O. Comparative morphological and anatomical study of self-repair in succulent cylindrical plant organs. Flora 2018, 241, 1–7. [Google Scholar] [CrossRef]
- Konrad, W.; Flues, F.; Schmich, F.; Speck, T.; Speck, O. An analytic model of the self-sealing mechanism of the succulent plant Delosperma cooperi. J. Theor. Biol. 2013, 336, 96–109. [Google Scholar] [CrossRef]
- Benson, L. The Cacti of the United States and Canada; Stanford University Press: Stanford, CA, USA, 1982; ISBN 0-8047-0863-0. [Google Scholar]
- Bobich, E.G.; North, G.B. Structural implications of succulence: Architecture, anatomy, and mechanics of photosynthetic stem succulents, pachycauls, and leaf succulents. In Perspectives in Biophysical Plant Ecophysiology: A Tribute to Park S. Nobel; De La Barrera, E., Smith, W.K., Eds.; Univ. Nacional Autónoma de México: Mexico City, Mexico, 2009; pp. 3–38. ISBN 978-0578006765. [Google Scholar]
- Coutant, M.W. Wound periderm in certain cacti. Bull. Torrey Bot. Club 1918, 45, 353–364. [Google Scholar] [CrossRef]
- Molina-Freaner, F.; Tinoco-Ojanguren, C.; Niklas, K.J. Stem biomechanics of three columnar cacti from the Sonoran Desert. Am. J. Bot. 1998, 85, 1082–1090. [Google Scholar] [CrossRef]
- Niklas, K.J.; Molina-Freaner, F.; Tinoco-Ojanguren, C.; Hogan, C.J.; Paolillo, D.J. On the mechanical properties of the rare endemic cactus Stenocereus eruca and the related species S. gummosus. Am. J. Bot. 2003, 90, 663–674. [Google Scholar] [CrossRef]
- Niklas, K.J.; Molina-Freaner, F.; Tinoco-Ojanguren, C. Biomechanics of the columnar cactus Pachycereus pringlei. Am. J. Bot. 1999, 86, 767–775. [Google Scholar] [CrossRef]
- Schwager, H.; Masselter, T.; Speck, T.; Neinhuis, C. Functional morphology and biomechanics of branch-stem junctions in columnar cacti. Proc. Biol. Sci. 2013, 280, 20132244. [Google Scholar] [CrossRef]
- Nobel, P.S.; Meyer, R.W. Biomechanics of cladodes and cladode-cladode junctions for Opuntia ficus-indica (Cactaceae). Am. J. Bot. 1991, 78, 1252–1259. [Google Scholar] [CrossRef]
- Bobich, E.G.; Nobel, P.S. Cladode junction regions and their biomechanics for arborescent platyopuntias. Int. J. Plant Sci. 2002, 163, 507–517. [Google Scholar] [CrossRef]
- Bobich, E.G.; Nobel, P.S. Vegetative reproduction as related to biomechanics, morphology and anatomy of four cholla cactus species in the Sonoran Desert. Ann. Bot. 2001, 87, 485–493. [Google Scholar] [CrossRef][Green Version]
- GBIF Secretariat. Opuntia ficus-indica (L.) Mill. Available online: https://www.gbif.org/species/5384064 (accessed on 8 January 2020).
- GBIF Secretariat. Cylindropuntia bigelovii (Engelm.) F.M.Knuth. Available online: https://www.gbif.org/species/7282821 (accessed on 8 January 2020).
- Bobich, E.G.; Nobel, P.S. Biomechanics and anatomy of cladode junctions for two Opuntia (Cactaceae) species and their hybrid. Am. J. Bot. 2001, 88, 391–400. [Google Scholar] [CrossRef]
- Gibson, A.C.; Nobel, P.S. The Cactus Primer; Harvard University Press: Cambridge, MA, USA, 1986; ISBN 9780674281721. [Google Scholar]
- Nobel, P.S. Cacti. Biology and Uses; University of California Press: Berkeley, CA, USA; Los Angeles, CA, USA, 2002; ISBN 0520231570. [Google Scholar]
- Lucas, S.S.; Von Tapavicza, M.; Schmidt, A.M.; Bertling, J.; Nellesen, A. Study of quantification methods in self-healing ceramics, polymers and concrete: A route towards standardization. J. Intel. Mat. Syst. Str. 2016, 27, 2577–2598. [Google Scholar] [CrossRef]
- Diesendruck, C.E.; Sottos, N.R.; Moore, J.S.; White, S.R. Biomimetic self-healing. Angew. Chem. Int. Ed. 2015, 54, 10428–10447. [Google Scholar] [CrossRef]
- Cohades, A.; Branfoot, C.; Rae, S.; Bond, I.; Michaud, V. Progress in self-healing fiber-reinforced polymer composites. Adv. Mater. Interfaces 2018, 5, 1800177. [Google Scholar] [CrossRef]
- Conde, L.F. Anatomical comparisons of five species of Opuntia (Cactaceae). Ann. Mo. Bot. Gard. 1975, 62, 425–473. [Google Scholar] [CrossRef]
- Trachtenberg, S.; Mayer, A.M. Composition and properties of Opuntia ficus-indica mucilage. Phytochemistry 1981, 20, 2665–2668. [Google Scholar] [CrossRef]
- Johnson, A.; Koehl, M. Maintenance of dynamic strain similarity and environmental stress factor in different flow habitats: Thallus allometry and material properties of a giant kelp. J. Exp. Bot. 1994, 195, 381–410. [Google Scholar]
- Speck, T.; Speck, O.; Emanns, A.; Spatz, H.-C. Biomechanics and functional anatomy of hollow stemmed sphenopsids: III. Equisetum hyemale. Bot. Acta 1998, 111, 366–376. [Google Scholar] [CrossRef]
- Spatz, H.; Kohler, L.; Niklas, K.J. Mechanical behaviour of plant tissues: Composite materials or structures? J. Exp. Bot. 1999, 202, 3269–3272. [Google Scholar]
- Köhler, L.; Speck, T.; Spatz, H.C. Micromechanics and anatomical changes during early ontogeny of two lianescent Aristolochia species. Planta 2000, 210, 691–700. [Google Scholar] [CrossRef]
- Harder, D.L.; Hurd, C.L.; Speck, T. Comparison of mechanical properties of four large, wave-exposed seaweeds. Am. J. Bot. 2006, 93, 1426–1432. [Google Scholar] [CrossRef] [PubMed]
- Yan, L.L.; Yu, B.; Han, B.; Chen, C.Q.; Zhang, Q.C.; Lu, T.J. Compressive strength and energy absorption of sandwich panels with aluminum foam-filled corrugated cores. Compos. Sci. Technol. 2013, 86, 142–148. [Google Scholar] [CrossRef]
- Niklas, K.J. Plant Biomechanics: An Engineering Approach to Plant Form and Function; University of Chicago press: Chicago, IL, USA, 1992; ISBN 0226586308. [Google Scholar]
- Mauseth, J.D. Wide-band tracheids are present in almost all species of Cactaceae. J. Plant Res. 2004, 117, 69–76. [Google Scholar] [CrossRef]
- Kampowski, T.; Mylo, M.D.; Poppinga, S.; Speck, T. How water availability influences morphological and biomechanical properties in the one-leaf plant Monophyllaea horsfieldii. R. Soc. Open Sci. 2018, 5, 171076. [Google Scholar] [CrossRef]
- Kampowski, T.; Demandt, S.; Poppinga, S.; Speck, T. Kinematical, structural and mechanical adaptations to desiccation in poikilohydric Ramonda myconi (Gesneriaceae). Front. Plant Sci. 2018, 9, 1701. [Google Scholar] [CrossRef]
- Caliaro, M.; Schmich, F.; Speck, T.; Speck, O. Effect of drought stress on bending stiffness in petioles of Caladium bicolor (Araceae). Am. J. Bot. 2013, 100, 2141–2148. [Google Scholar] [CrossRef]
- Nobel, P.S.; Cavelier, J.; Andrade, J.L. Mucilage in cacti: Its apoplastic capacitance, associated solutes, and influence on tissue water relations. J. Exp. Bot. 1992, 43, 641–648. [Google Scholar] [CrossRef]
- Paul-Victor, C.; Dalle Vacche, S.; Sordo, F.; Fink, S.; Speck, T.; Michaud, V.; Speck, O. Effect of mechanical damage and wound healing on the viscoelastic properties of stems of flax cultivars (Linum usitatissimum L. cv. Eden and cv. Drakkar). PLoS ONE 2017, 12, e0185958. [Google Scholar] [CrossRef]
- Speck, O.; Schmauder, K.; Speck, T.; Paul-Victor, C. Wound reactions in stems of Leonurus cardiaca: A morphological, anatomical, and biomechanical study. Botany 2020, 98, 81–89. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019. [Google Scholar]
- Fox, J.; Weisberg, S. An R Companion to Applied Regression, 3rd ed.; Sage: Thousand Oaks, CA, USA, 2019; ISBN 9781544336473. [Google Scholar]
- Zeileis, A.; Wiel, M.A.; Hornik, K.; Hothorn, T. Implementing a class of permutation tests: The coin package. J. Stat. Softw. 2008, 28, 1–23. [Google Scholar]
- Signorell, A.; Aho, K.; Alfons, A.; Anderegg, N.; Aragon, T.; Arppe, A. DescTools: Tools for Descriptive Statistics; R Package Version 0.99; R Foundation for Statistical Computing: Vienna, Austria, 2016; Volume 18. [Google Scholar]
- Wickham, H. Ggplot2: Elegant Graphics for Data Analysis; Springer: New York, NY, USA, 2009; ISBN 978-0-387-98141-3. [Google Scholar]
- Hothorn, T.; Bretz, F.; Westfall, P. Simultaneous inference in general parametric models. Biom. J. 2008, 50, 346–363. [Google Scholar] [CrossRef]
- Revelle, W. psych: Procedures for Psychological, Psychometric, and Personality Research; Northwestern University: Evanston, IL, USA, 2017. [Google Scholar]

| Bending Stiffness Ratio | ||||
|---|---|---|---|---|
| States | Unwounded | Wounded | Healed | All States 1 |
| Sample size (N) | 14 | 14 | 14 | 42 |
| O. ficus-indica | 0.88 ± 0.14 | 0.95 ± 0.21 | 0.95 ± 0.13 | 0.93 ± 0.17 |
| C. bigelovii | 1.16 ± 0.13 | 1.07 ± 0.17 | 1.18 ± 0.18 | 1.14 ± 0.17 |
| O. ficus-indica | C. bigelovii | ||||
|---|---|---|---|---|---|
| Plant A | Plant B | Plant C | Plant D | Plant E | |
| Sample size (N) | 8 | 6 | 5 | 4 | 5 |
| Bending stiffness first linear range (Nmm2) | |||||
| unwounded | 13,048 (7589) | 17,978 (3541) | 12,759 (1530) | 16,588 (4637) | 15,534 (3383) |
| wounded | 9274 (6221) | 13,470 (5669) | 8873 (343) | 11,619 (1036) | 12,355 (502) |
| healed | 8598 (2206) | 9001 (4307) | 10,423 (938) | 12,303 (1384) | 11,334 (690) |
| Bending stiffness second linear range (Nmm2) | |||||
| unwounded | 10,548 (7755) | 16,746 (7017) | 16,715 (3664) | 19,016 (1995) | 18,804 (1685) |
| wounded | 7863 (5932) | 13,650 (6718) | 9447 (2109) | 11,963 (1308) | 12,020 (506) |
| healed | 7766 (2829) | 7777 (4434) | 11,356 (987) | 13,509 (1577) | 12,941 (942) |
| Work (Nmm) | |||||
| unwounded | 7.4 (3.2) | 11.6 (1.8) | 8.6 (0.6) | 10.6 (3.3) | 10.0 (1.0) |
| wounded | 5.9 (4.0) | 8.5 (4.2) | 6.1 (0.4) | 7.5 (0.5) | 7.8 (0.6) |
| healed | 5.8 (1.5) | 5.6 (1.5) | 6.6 (0.6) | 7.9 (1.4) | 7.2 (0.6) |
| O. ficus-indica | C. bigelovii | ||||||
|---|---|---|---|---|---|---|---|
| Plant A | Plant B | Pooled Data | Plant C | Plant D | Plant E | Pooled Data | |
| Sample size (N) | 8 | 6 | 14 | 5 | 4 | 5 | 14 |
| of bending stiffness first linear range (%) | |||||||
| −15.22 (30.52) | −22.03 * (28.49) | −17.80 ** (21.06) | 14.88 * (2.45) | −1.93 (20.83) | −6.70 (0.75) | 2.44 (20.44) | |
| of bending stiffness second linear range (%) | |||||||
| −1.47 (25.88) | −31.21 *** (11.53) | 12.32 * (8.74) | 8.72 * (4.91) | 9.48 * (2.90) | 9.72 *** (7.04) | ||
| of work (%) | |||||||
| 1.59 (26.39) | −19.00 ** (10.68) | −14.96 * (27.16) | 5.92 (2.76) | 6.12 (9.78) | −5.44 (20.43) | 5.30 (12.12) | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mylo, M.D.; Krüger, F.; Speck, T.; Speck, O. Self-Repair in Cacti Branches: Comparative Analyses of Their Morphology, Anatomy, and Biomechanics. Int. J. Mol. Sci. 2020, 21, 4630. https://doi.org/10.3390/ijms21134630
Mylo MD, Krüger F, Speck T, Speck O. Self-Repair in Cacti Branches: Comparative Analyses of Their Morphology, Anatomy, and Biomechanics. International Journal of Molecular Sciences. 2020; 21(13):4630. https://doi.org/10.3390/ijms21134630
Chicago/Turabian StyleMylo, Max D., Friederike Krüger, Thomas Speck, and Olga Speck. 2020. "Self-Repair in Cacti Branches: Comparative Analyses of Their Morphology, Anatomy, and Biomechanics" International Journal of Molecular Sciences 21, no. 13: 4630. https://doi.org/10.3390/ijms21134630
APA StyleMylo, M. D., Krüger, F., Speck, T., & Speck, O. (2020). Self-Repair in Cacti Branches: Comparative Analyses of Their Morphology, Anatomy, and Biomechanics. International Journal of Molecular Sciences, 21(13), 4630. https://doi.org/10.3390/ijms21134630








