A Simple Method to Measure Renal Function in Swine by the Plasma Clearance of Iohexol
Abstract
:1. Introduction
2. Results
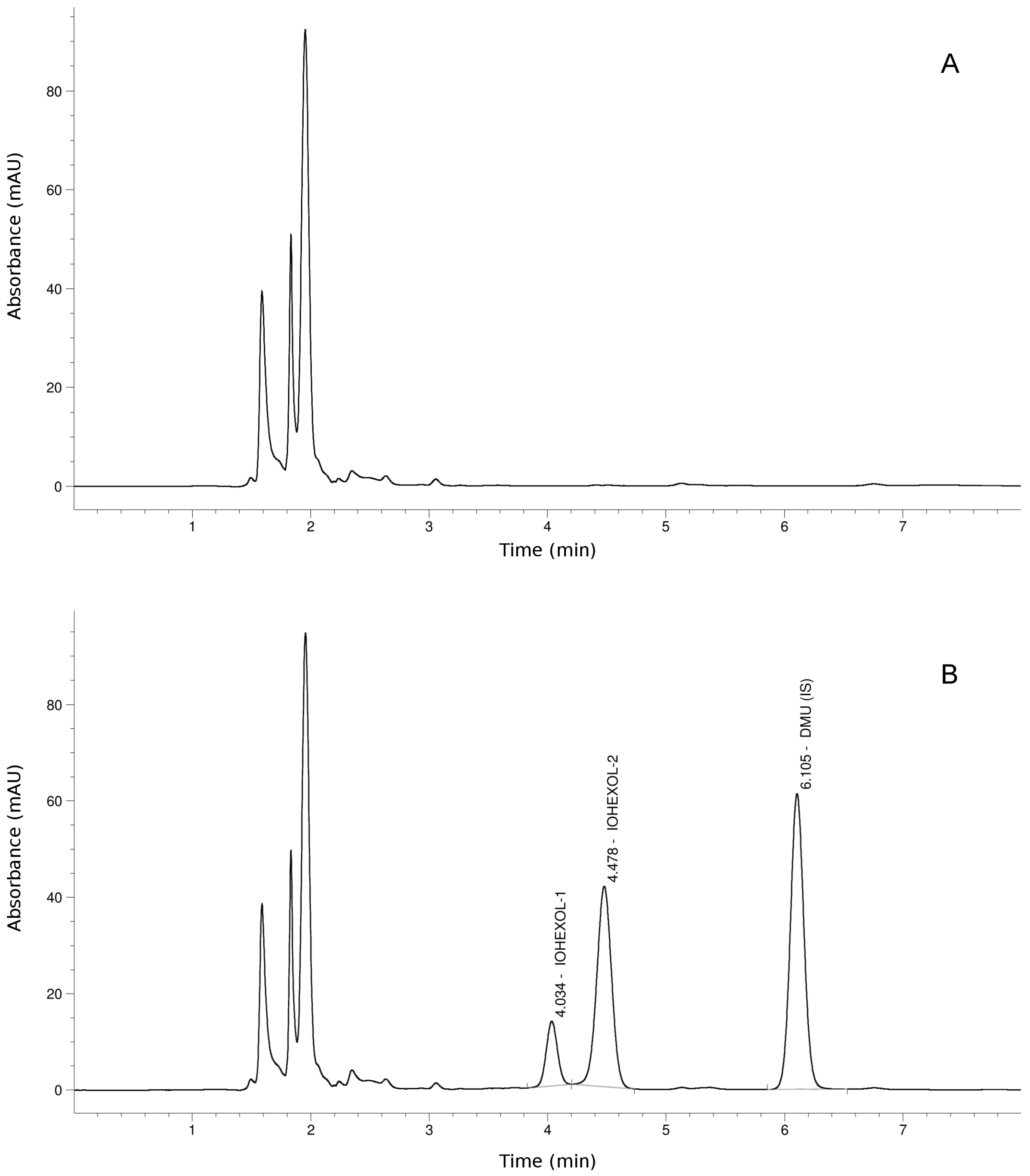
2.1. Iohexol Plasma Analysis
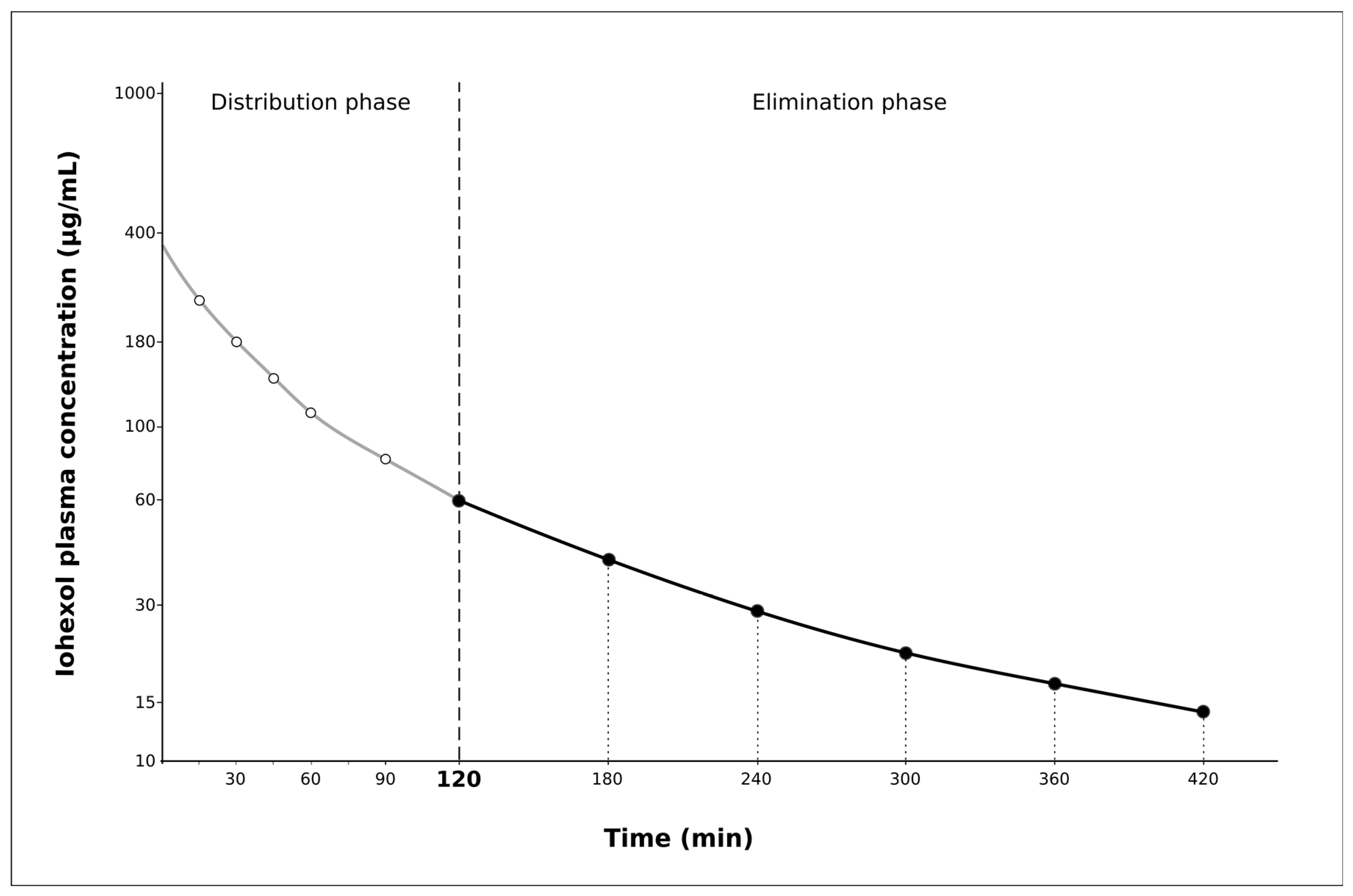
2.2. Pharmacokinetic Clearance Profiles
2.3. Test Group
2.4. Correction Formula
2.5. Validation Group
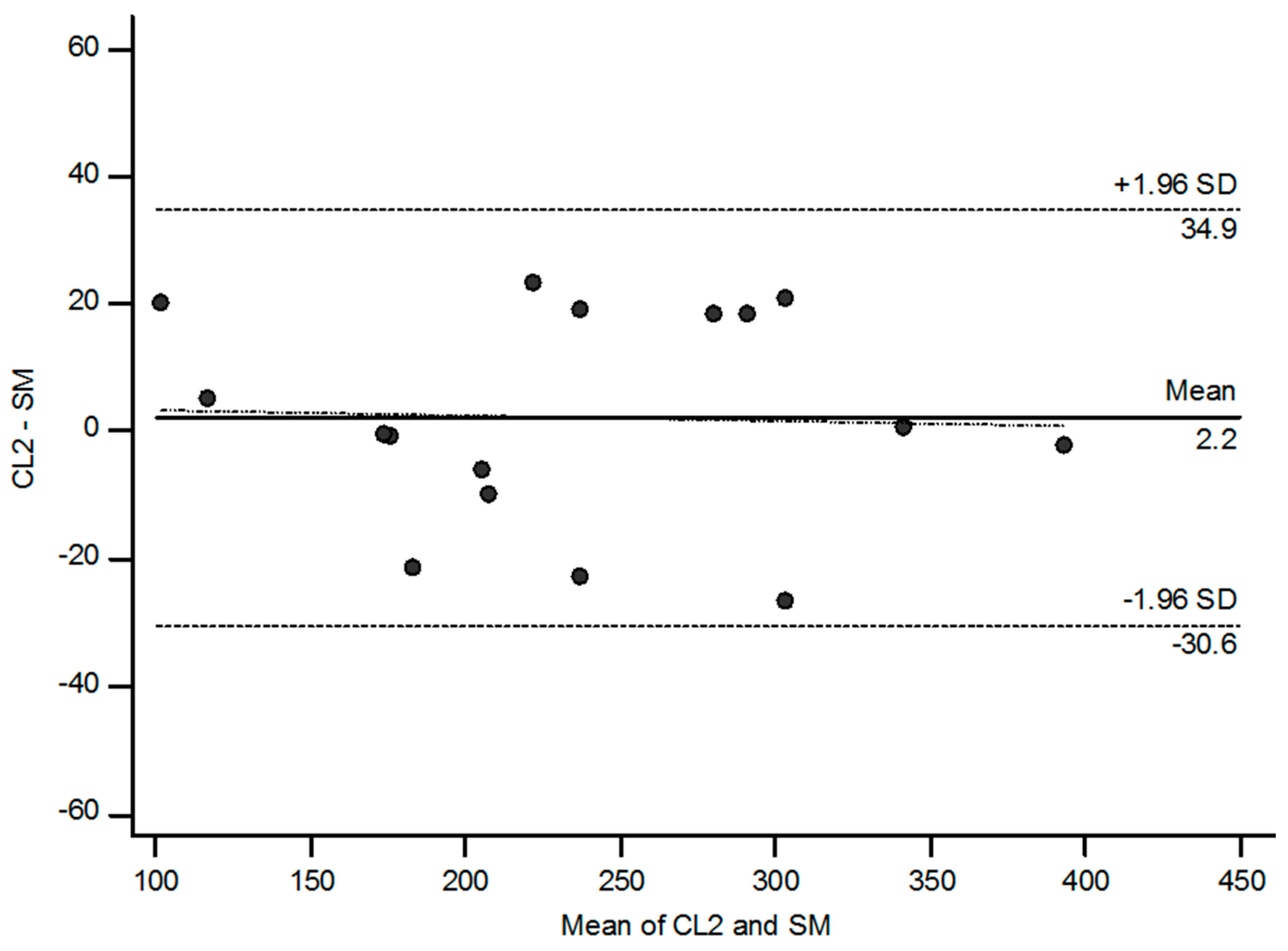
2.6. Analysis of Agreement
2.7. Reproducibility Study
2.8. Sensitivity Analysis
2.9. Calibration and Quality Control Standards
3. Discussion
4. Material and Methods
4.1. Ethics Statement
4.2. Experimental Design
4.3. Iohexol Measurements
4.4. Calibration and Quality Control Standards
4.5. Pharmacokinetic Analyses: One- and Two-Compartment Models
4.6. Developing a Correction Formula to Simplify the Method
4.7. Reproducibility Study
4.8. Sensitivity Analysis
4.9. Pharmacokinetic Analysis
4.10. Statistical Analysis: Tests of Agreement
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Houdebine, L.M. The Mouse as an Animal Model for Human Diseases. In The Laboratory Mouse; Hedrich, H., Ed.; Academic Press: Cambridge, MA, USA, 2004; pp. 99–110. [Google Scholar]
- Muhammad, S. Nephrotoxic nephritis and glomerulonephritis: Animal model versus human disease. Br. J. Biomed. Sci. 2014, 71, 168–171. [Google Scholar] [CrossRef] [PubMed]
- Betz, B.; Conway, B.R. Recent advances in animal models of diabetic nephropathy. Nephron Exp. Nephrol. 2014, 126, 191–195. [Google Scholar] [CrossRef] [PubMed]
- Herrmann, S.M.; Sethi, S.; Fervenza, F.C. Membranous nephropathy: The start of a paradigm shift. Curr. Opin. Nephrol. Hypertens. 2012, 21, 203–210. [Google Scholar] [CrossRef] [PubMed]
- Taylor, C.M.; Williams, J.M.; Lote, C.J.; Howie, A.J.; Thewles, A.; Wood, J.A.; Milford, D.V.; Raafat, F.; Chant, I.; Rose, P.E. A laboratory model of toxin-induced hemolytic uremic syndrome. Kidney Int. 1999, 55, 1367–1374. [Google Scholar] [CrossRef] [PubMed]
- Yokota, S.D.; Benyajati, S.; Dantzler, W.H. Comparative aspects of glomerular filtration in vertebrates. Ren. Physiol. 1985, 8, 193–221. [Google Scholar] [CrossRef] [PubMed]
- Davies, B.; Morris, T. Physiological parameters in laboratory animals and humans. Pharm. Res. 1993, 10, 1093–1095. [Google Scholar] [CrossRef] [PubMed]
- Sachs, D.H. The pig as a potential xenograft donor. Vet. Immunol. Immunopathol. 1994, 43, 185–191. [Google Scholar] [CrossRef]
- Tumbleson, M.E.; Schook, L.B. Advances in Swine in Biomedical Research; Tumbleson, M.E., Schook, L.B., Eds.; Plenum Press: New York, NY, USA, 1996; Volume 1, pp. 1–4. [Google Scholar]
- Cibulskyte, D.; Pedersen, M.; Hjelm-Poulsen, J.; Hansen, H.E.; Madsen, M.; Mortensen, J. The pharmacokinetics and acute renal effects of oral microemulsion ciclosporin A in normal pigs. Int. Immunopharmacol. 2006, 6, 627–634. [Google Scholar] [CrossRef] [PubMed]
- Lodrup, A.B.; Karstoft, K.; Dissing, T.H.; Nyengaard, J.R.; Pedersen, M. The association between renal function and structural parameters: A pig study. BMC Nephrol. 2008, 23, 18. [Google Scholar] [CrossRef] [PubMed]
- Kidney Disease Outcome Quality Initiative. Clinical practice guidelines for chronic kidney disease: Evaluation, classification and stratification. Am. J. Kidney Dis. 2002, 39, S1–S246. [Google Scholar]
- GBD 2013 Mortality and Causes of Death Collaborators. Global, regional, and national age-sex specific all-cause and cause-specific mortality for 240 causes of death, 1990–2013: A systematic analysis for the Global Burden of Disease Study 2013. Lancet 2015, 385, 117–171. [Google Scholar] [CrossRef]
- Levey, A.S.; Inker, L.A.; Coresh, J. GFR estimation: From physiology to public health. Am. J. Kidney Dis. 2014, 63, 820–834. [Google Scholar] [CrossRef] [PubMed]
- Delanaye, P.; Melsom, T.; Ebert, N.; Bäck, S.E.; Mariat, C.; Cavalier, E.; Björk, J.; Christensson, A.; Nyman, U.; Porrini, E.; et al. Iohexol plasma clearance for measuring glomerular filtration rate in clinical practice and research: A review. Part 2: Why to measure glomerular filtration rate with iohexol? Clin. Kidney J. 2016, 9, 700–704. [Google Scholar] [CrossRef] [PubMed]
- Delanaye, P.; Ebert, N.; Melsom, T.; Gaspari, F.; Mariat, C.; Cavalier, E.; Björk, J.; Christensson, A.; Nyman, U.; Porrini, E.; et al. Iohexol plasma clearance for measuring glomerular filtration rate in clinical practice and research: A review. Part 1: How to measure glomerular filtration rate with iohexol? Clin. Kidney J. 2016, 9, 682–699. [Google Scholar] [CrossRef] [PubMed]
- Odlind, B.; Hällgren, R.; Sohtell, M.; Lindström, B. Is 125I iothalamate an ideal marker for glomerular filtration? Kidney Int. 1985, 27, 9–16. [Google Scholar] [CrossRef] [PubMed]
- Zurth, C. Mechanism of renal excretion of various X-ray contrast materials in rabbits. Investig. Radiol. 1984, 19, 110–115. [Google Scholar] [CrossRef]
- Nilsson-Ehle, P.; Grubb, A. New markers for the determination of GFR: Iohexol clearance and cystatin C serum concentration. Kidney Int. Suppl. 1994, 47, S17–S19. [Google Scholar] [PubMed]
- Donadio, C.; Tramonti, G.; Giordani, R.; Lucchetti, A.; Calderazzi, A.; Bassani, L.; Bianchi, C. Effects on renal hemodynamics and tubular function of the contrast medium iohexol in renal patients. Ren. Fail. 1990, 12, 141–146. [Google Scholar] [CrossRef] [PubMed]
- Frennby, B.; Sterner, G.; Almén, T.; Chai, C.M.; Jönsson, B.A.; Månsson, S. Clearance of iohexol, 51Cr-EDTA and endogenous creatinine for determination of glomerular filtration rate in pigs with reduced renal function: A comparison between different clearance techniques. Scand. J. Clin. Lab. Investig. 1997, 57, 241–252. [Google Scholar] [CrossRef]
- Lundqvist, S.; Hietala, S.O.; Karp, K. Experimental studies comparing iohexol and 51Cr-EDTA for glomerular filtration rate measurements. Acta Radiol. 1993, 36, 58–63, three Rs concept. Altern. Lab. Anim. 1995, 23, 298–304. [Google Scholar] [CrossRef] [PubMed]
- Russell, W.M. The development of the Anim Care. Lab. Anim. Care 1969, 19, 403–405. [Google Scholar]
- Bröchner-Mortensen, J. A simple method for the determination of glomerular filtration rate. Scand. J. Clin. Lab. Investig. 1972, 30, 271–274. [Google Scholar] [CrossRef]
- Colson, P.; Saussine, M.; Séguin, J.R.; Cuchet, D.; Chaptal, P.A.; Roquefeuil, B. Hemodynamic effects of anesthesia in patients chronically treated with angiotensin converting enzyme inhibitors. Anesth. Analg. 1992, 74, 805–808. [Google Scholar] [CrossRef] [PubMed]
- Fusellier, M.; Desfontis, J.C.; Madec, S.; Gautier, F.; Debailleul, M.; Gogny, M. Influence of three anesthetic protocols on glomerular filtration rate in dogs. Am. J. Vet. Res. 2007, 68, 807–811. [Google Scholar] [CrossRef] [PubMed]
- Finco, D.R.; Braselton, W.E.; Cooper, T.A. Relationship between plasma iohexol clearance and urinary exogenous creatinine clearance in dogs. J. Vet. Intern. Med. 2001, 15, 368–373. [Google Scholar] [CrossRef] [PubMed]
- Gaspari, F.; Perico, N.; Matalone, M.; Signorini, O.; Azzollini, N.; Mister, M.; Remuzzi, G. Precision of plasma clearance of iohexol for estimation of GFR in patients with renal disease. J. Am. Soc. Nephrol. 1998, 9, 310–313. [Google Scholar] [PubMed]
- Miyagawa, Y.; Takemura, N.; Hirose, H. Evaluation of a single sampling method for Estimation of plasma iohexol clearance in dogs and cats with various kidney functions. J. Vet. Med. Sci. 2010, 72, 271–278. [Google Scholar] [CrossRef] [PubMed]
- Krutzén, E.; Bäck, S.E.; Nilsson-Ehle, I.; Nilsson-Ehle, P. Plasma clearance of a new contrast agent, iohexol: A method for the assessment of glomerular filtration rate. J. Lab. Clin. Med. 1984, 104, 955–961. [Google Scholar] [PubMed]
- Rocco, M.V.; Buckalew, V.M., Jr.; Moore, L.C.; Shihabi, Z.K. Measurement of glomerular filtration rate using nonradioactive Iohexol: Comparison of two one-compartment models. Am. J. Nephrol. 1996, 16, 138–143. [Google Scholar] [CrossRef] [PubMed]
- Dove, C.R.; Alworth, L.C. Blood collection from the orbital sinus of swine. Lab. Anim. 2015, 44, 383–384. [Google Scholar] [CrossRef] [PubMed]
- Huhn, R.G.; Osweiler, G.D.; Switzer, W.P. Application of the orbital sinus bleeding technique to swine. Lab. Anim. Care 1969, 19, 403–405. [Google Scholar] [PubMed]
- Luis-Lima, S.; Gaspari, F.; Porrini, E.; García-González, M.; Batista, N.; Bosa-Ojeda, F.; Oramas, J.; Carrara, F.; González-Posada, J.M.; Marrero, D.; et al. Measurement of glomerular filtration rate: Internal and external validations of the iohexol plasma clearance technique by HPLC. Clin. Chim. Acta 2014, 430, 84–85. [Google Scholar] [CrossRef] [PubMed]
- Bland, J.M.; Altman, D.G. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet 1986, 1, 307–310. [Google Scholar] [CrossRef]
- Lin, L.; Hedayat, A.; Wu, W. Statistical Tools for Measuring Agreement; Springer: New York, NY, USA, 2012. [Google Scholar]
- Lin, L.; Hedayat, A.; Sinha, B.; Yang, M. Statistical methods in assessing agreement: Models, issues, and tools. J. Am. Stat. Assoc. 2002, 97, 257–270. [Google Scholar] [CrossRef]
| Test Group | |||||||
| CASE | Weight ** | CL2 * | CL1 * | SM * | SM–CL2 (%) | BM * | BM–CL2 (%) |
| 1 | 113 | 119.6 | 150.4 | 114.6 | −4.2 | 121.5 | 1.6 |
| 2 | 122 | 172.6 | 236.3 | 194.3 | 12.5 | 166.1 | −3.8 |
| 3 | 138 | 225.8 | 301.6 | 248.7 | 10.1 | 188.1 | −16.7 |
| 4 | 132 | 233.8 | 255.4 | 210.8 | −9.9 | 173.6 | −25.8 |
| 5 | 101 | 175.8 | 216.4 | 176.7 | 0.5 | 157.4 | −10.5 |
| 6 | 210 | 341.8 | 433.1 | 341.4 | −0.1 | 200.6 | −41.3 |
| 7 | 209 | 300.5 | 345.6 | 282.1 | −6.1 | 196.9 | −34.5 |
| 8 | 212 | 392.0 | 527.4 | 394.4 | 0.6 | 183.7 | −53.1 |
| mean ± SD | 155 ± 47 | 245 ± 93 | 308 ± 123 | 245 ± 91 | 190 ± 26 | ||
| Validation Group | |||||||
| Weight ** | CL2 * | CL1 * | SM * | SM–CL2 | BM * | BM–CL2 | |
| 9 | 106 | 173.7 | 213.7 | 174.2 | 0.3 | 156.1 | −10.2 |
| 10 | 182 | 246.8 | 275.9 | 227.9 | −7.7 | 180.7 | −26.8 |
| 11 | 116 | 112.1 | 128.0 | 92.2 | −17.8 | 106.9 | −4.7 |
| 12 | 159 | 289.9 | 394.6 | 316.6 | 9.2 | 201.3 | −30.6 |
| 13 | 156 | 202.8 | 253.5 | 209.1 | 3.1 | 172.9 | −14.8 |
| 14 | 176 | 289.6 | 331.2 | 271.4 | −6.3 | 194.5 | −32.8 |
| 15 | 115 | 202.8 | 257.7 | 212.7 | 4.9 | 174.4 | −14.0 |
| 16 | 188 | 313.9 | 360.9 | 293.2 | −6.6 | 198.9 | −36.6 |
| mean ± SD | 150 ± 33 | 229 ± 69 | 277 ± 85 | 225 ± 71 | 181 ± 31 | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luis-Lima, S.; García-Contreras, C.; Vázquez-Gómez, M.; Astiz, S.; Carrara, F.; Gaspari, F.; Negrín-Mena, N.; Jiménez-Sosa, A.; Jiménez-Hernández, H.; González-Bulnes, A.; et al. A Simple Method to Measure Renal Function in Swine by the Plasma Clearance of Iohexol. Int. J. Mol. Sci. 2018, 19, 232. https://doi.org/10.3390/ijms19010232
Luis-Lima S, García-Contreras C, Vázquez-Gómez M, Astiz S, Carrara F, Gaspari F, Negrín-Mena N, Jiménez-Sosa A, Jiménez-Hernández H, González-Bulnes A, et al. A Simple Method to Measure Renal Function in Swine by the Plasma Clearance of Iohexol. International Journal of Molecular Sciences. 2018; 19(1):232. https://doi.org/10.3390/ijms19010232
Chicago/Turabian StyleLuis-Lima, Sergio, Consolación García-Contreras, Marta Vázquez-Gómez, Susana Astiz, Fabiola Carrara, Flavio Gaspari, Natalia Negrín-Mena, Alejandro Jiménez-Sosa, Hugo Jiménez-Hernández, Antonio González-Bulnes, and et al. 2018. "A Simple Method to Measure Renal Function in Swine by the Plasma Clearance of Iohexol" International Journal of Molecular Sciences 19, no. 1: 232. https://doi.org/10.3390/ijms19010232
APA StyleLuis-Lima, S., García-Contreras, C., Vázquez-Gómez, M., Astiz, S., Carrara, F., Gaspari, F., Negrín-Mena, N., Jiménez-Sosa, A., Jiménez-Hernández, H., González-Bulnes, A., & Porrini, E. (2018). A Simple Method to Measure Renal Function in Swine by the Plasma Clearance of Iohexol. International Journal of Molecular Sciences, 19(1), 232. https://doi.org/10.3390/ijms19010232