Effect of Acetyl Group on Mechanical Properties of Chitin/Chitosan Nanocrystal: A Molecular Dynamics Study
Abstract
:1. Introduction
2. Results and Discussions
2.1. Structure of Chitin/Chitosan Nanocrystal
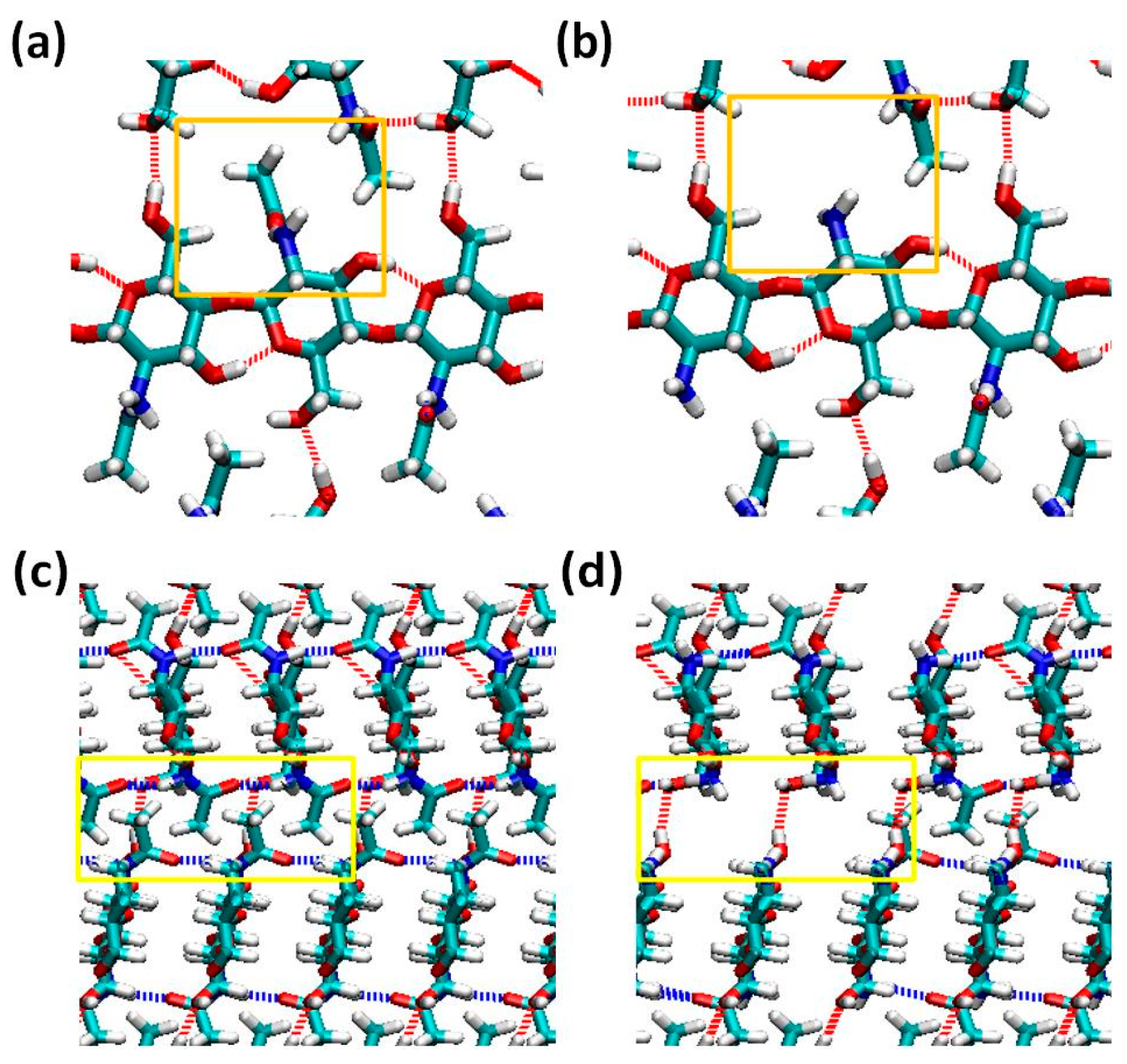
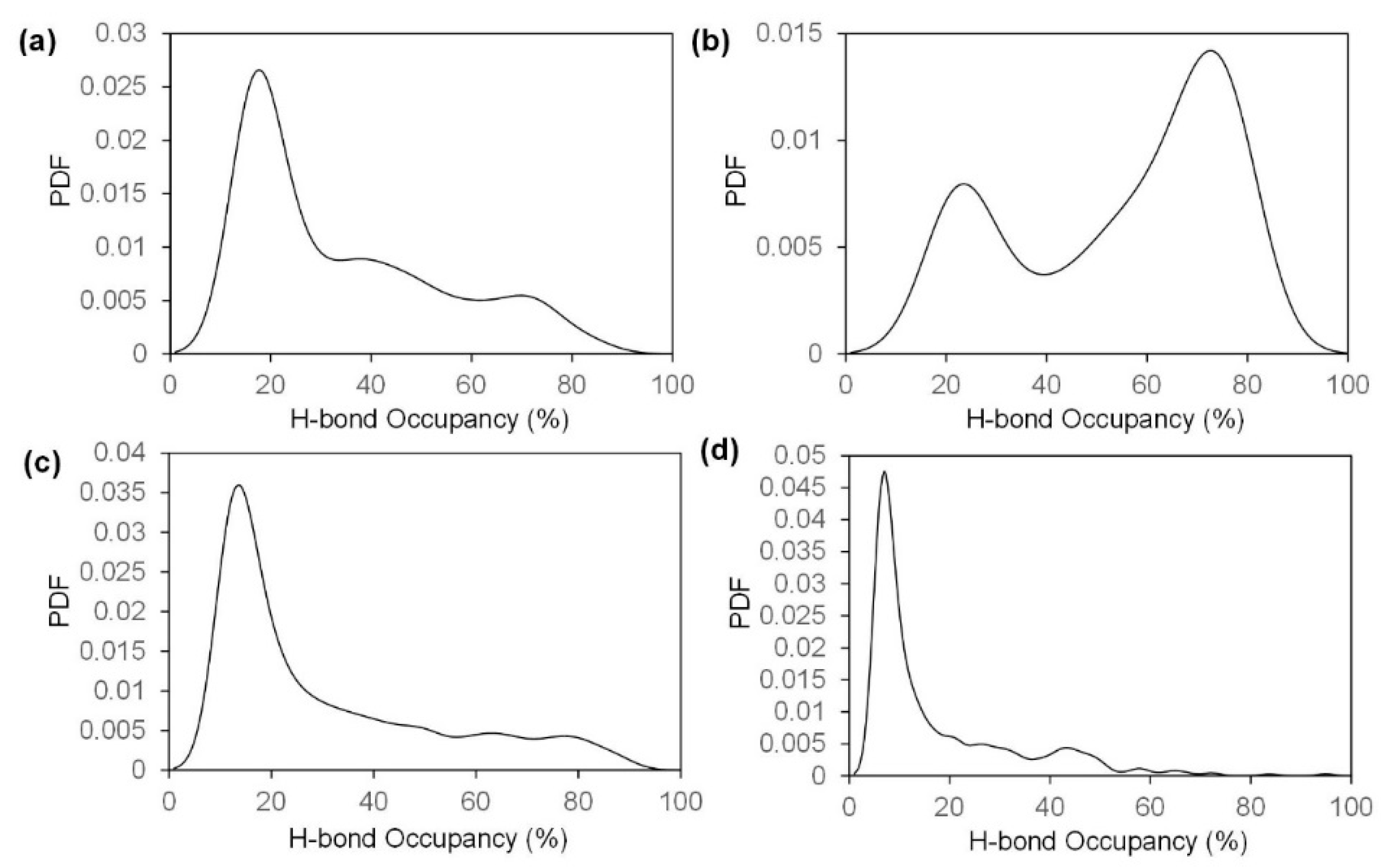
2.2. Fracture and Stress-Strain Behavior
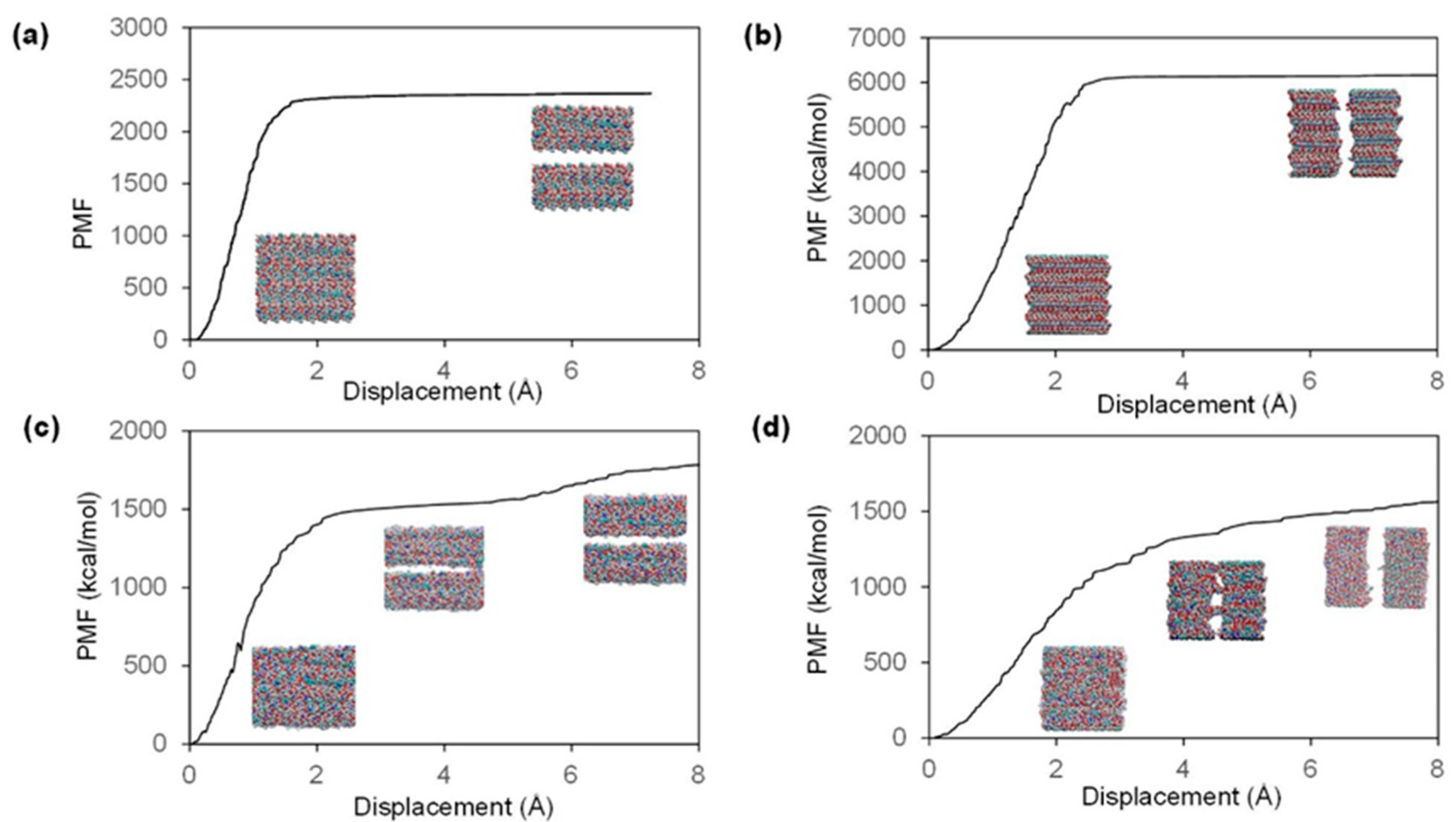

| Model | Direction | Ultimate Stress (GPa) | Fracture Strain (%) | Stiffness (GPa) |
|---|---|---|---|---|
| Chitin | Inter-chain | 0.551 | 5.29 | 22.58 |
| Inter-sheet | 0.936 | 7.45 | 21.13 | |
| 85% Chitosan | Inter-chain | 0.372 | 6.22 | 13.39 |
| Inter-sheet | 0.419 | 8.82 | 11.98 |
2.3. The Role of Acetyl Group
3. Methods
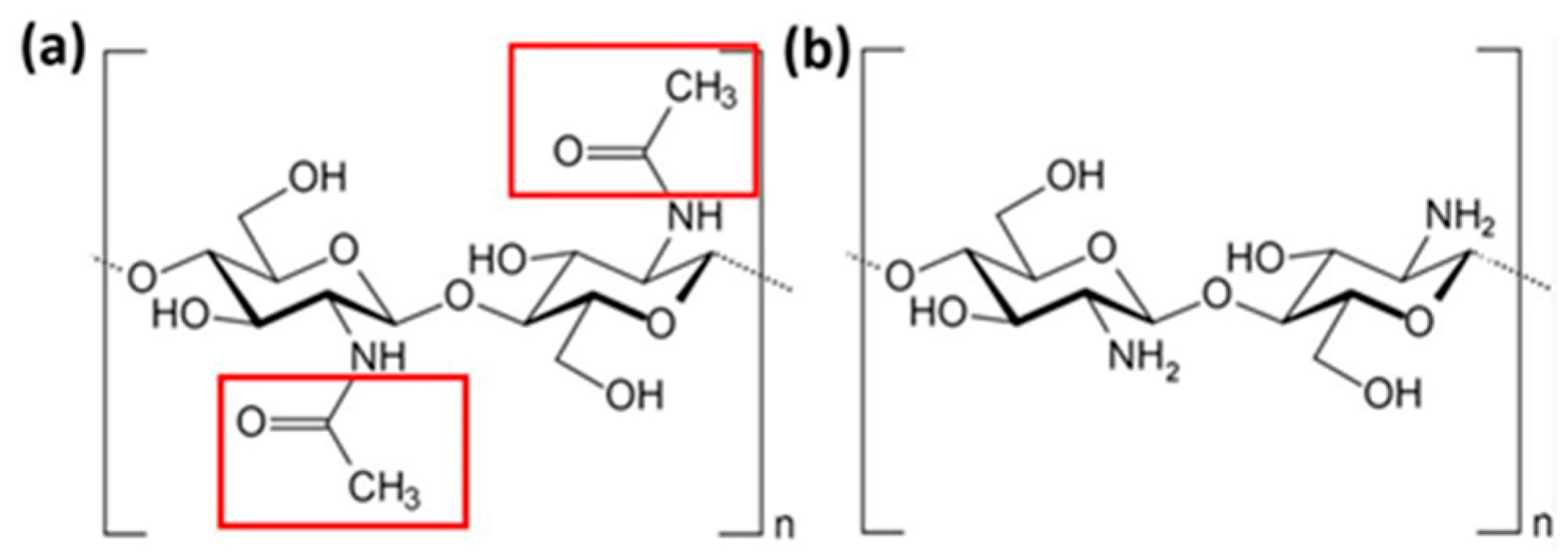
3.1. Atomistic Models
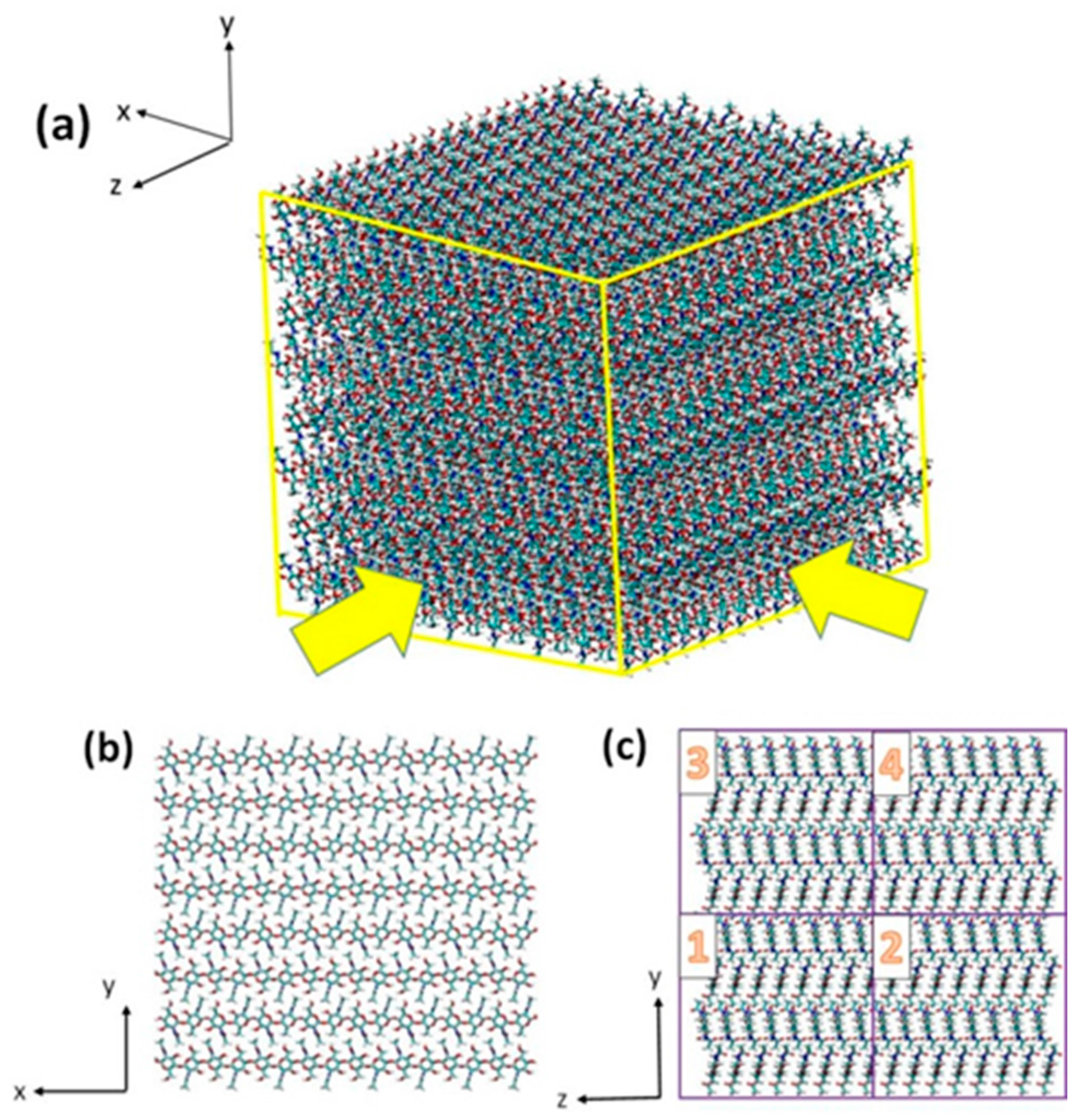
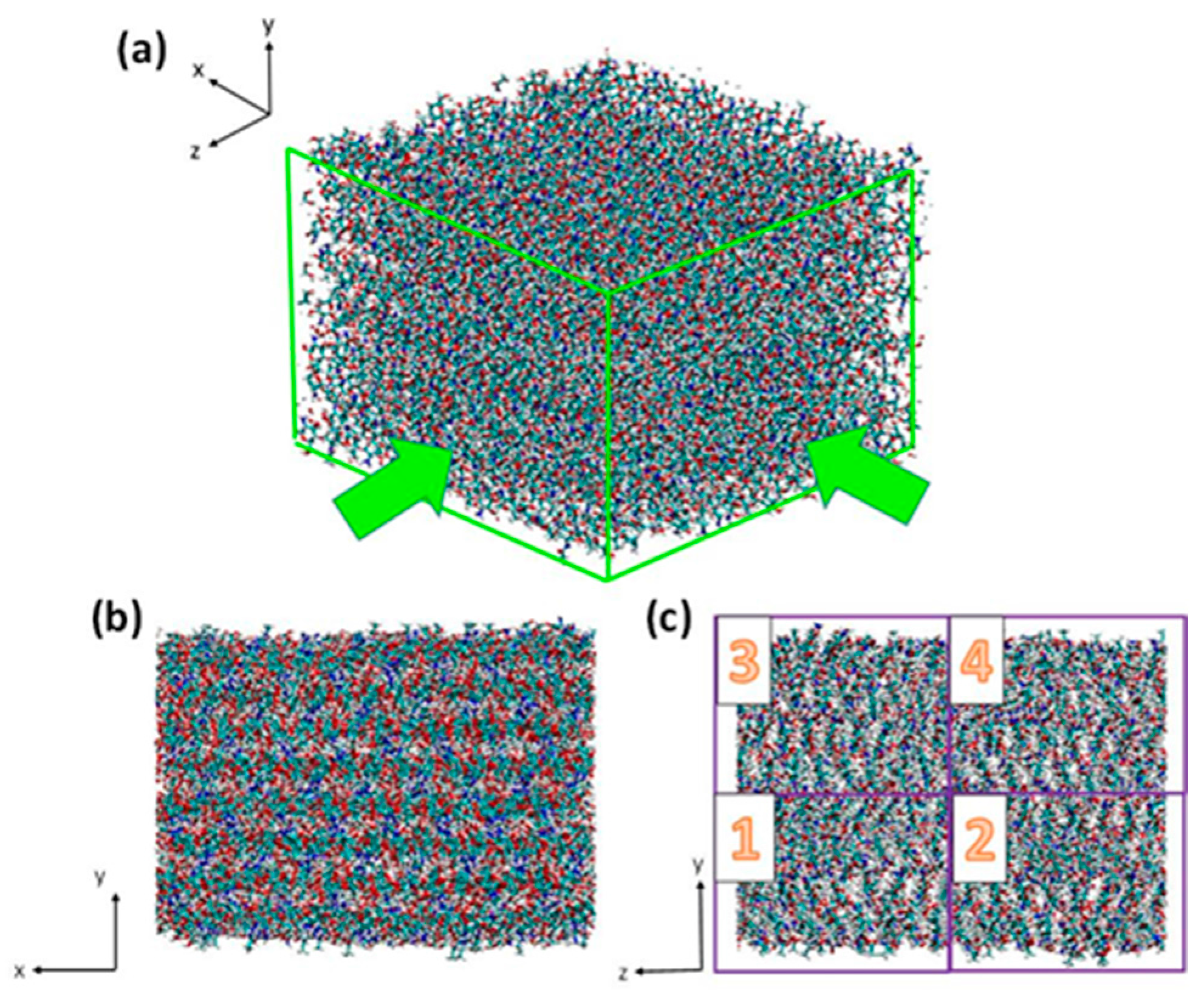
3.2. Simulation Details
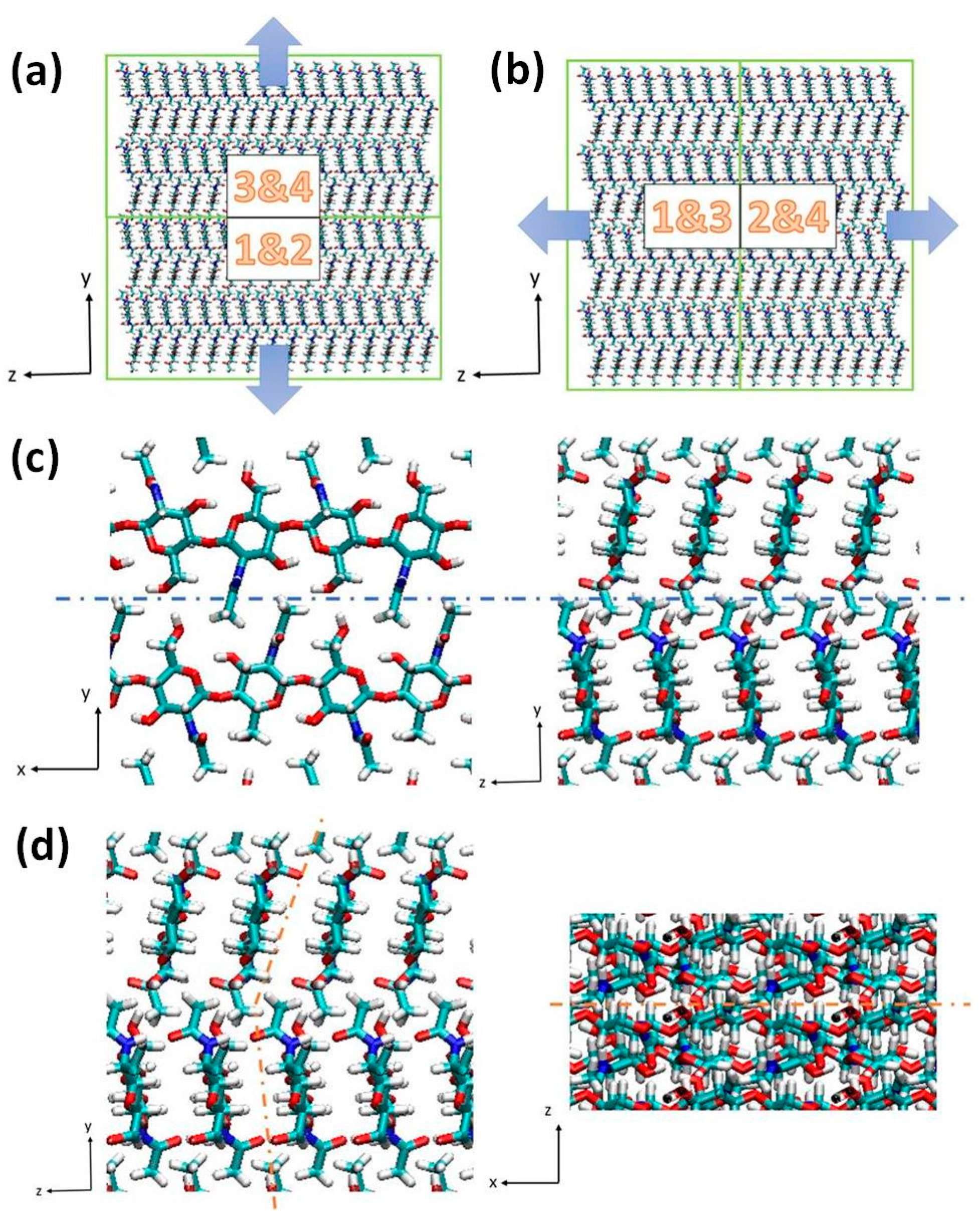
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ehrlich, H. Chitin and collagen as universal and alternative templates in biomineralization. Int. Geol. Rev. 2010, 52, 661–699. [Google Scholar] [CrossRef]
- Ehrlich, H. Biological Materials of Marine Origin; Springer: Berlin, Germany, 2010. [Google Scholar]
- Wysokowski, M.; Petrenko, I.; Stelling, A.; Stawski, D.; Jesionowski, T.; Ehrlich, H. Poriferan chitin as a versatile template for extreme biomimetics. Polymers 2015, 7, 235–265. [Google Scholar] [CrossRef]
- Rinaudo, M. Chitin and chitosan: Properties and applications. Prog. Polym. Sci. 2006, 31, 603–632. [Google Scholar] [CrossRef]
- Nikolov, S.; Fabritius, H.; Petrov, M.; Friák, M.; Lymperakis, L.; Sachs, C.; Raabe, D.; Neugebauer, J. Robustness and optimal use of design principles of arthropod exoskeletons studied by ab initio-based multiscale simulations. J. Mech. Behav. Biomed. Mater. 2011, 4, 129–145. [Google Scholar] [CrossRef] [PubMed]
- Yang, F.C.; Peters, R.D.; Dies, H.; Rheinstädter, M.C. Hierarchical, self-similar structure in native squid pen. Soft Matter 2014, 10, 5541–5549. [Google Scholar] [CrossRef] [PubMed]
- Brunner, E.; Richthammer, P.; Ehrlich, H.; Paasch, S.; Simon, P.; Ueberlein, S.; van Pée, K.H. Chitin-based organic networks: An integral part of cell wall biosilica in the diatom Thalassiosira pseudonana. Angew. Chem. Int. Ed. 2009, 48, 9724–9727. [Google Scholar] [CrossRef] [PubMed]
- Ehrlich, H.; Maldonado, M.; Spindler, K.D.; Eckert, C.; Hanke, T.; Born, R.; Goebel, C.; Simon, P.; Heinemann, S.; Worch, H. First evidence of chitin as a component of the skeletal fibers of marine sponges. Part I. Verongidae (Demospongia: Porifera). J. Exp. Zool. B 2007, 308, 347–356. [Google Scholar] [CrossRef] [PubMed]
- Bo, M.; Bavestrello, G.; Kurek, D.; Paasch, S.; Brunner, E.; Born, R.; Galli, R.; Stelling, A.L.; Sivkov, V.N.; Petrova, O.V.; et al. Isolation and identification of chitin in the black coral Parantipathes larix (Anthozoa: Cnidaria). Int. J. Biol. Macromol. 2012, 51, 129–137. [Google Scholar] [CrossRef] [PubMed]
- Moussian, B.; Schwarz, H.; Bartoszewski, S.; Nüsslein-Volhard, C. Involvement of chitin in exoskeleton morphogenesis in Drosophila melanogaster. J. Morphol. 2005, 264, 117–130. [Google Scholar] [CrossRef] [PubMed]
- Raabe, D.; Romano, P.; Sachs, C.; Fabritius, H.; Al-Sawalmih, A.; Yi, S.B.; Servos, G.; Hartwig, H. Microstructure and crystallographic texture of the chitin–protein network in the biological composite material of the exoskeleton of the lobster Homarus americanus. Mater. Sci. Eng. A 2006, 421, 143–153. [Google Scholar] [CrossRef]
- Vincent, J.F. Arthropod cuticle: A natural composite shell system. Compos. A Appl. Sci. Manuf. 2002, 33, 1311–1315. [Google Scholar] [CrossRef]
- Falini, G.; Fermani, S.; Ripamonti, A. Crystallization of calcium carbonate salts into β-chitin scaffold. J. Inorg. Biochem. 2002, 91, 475–480. [Google Scholar] [CrossRef]
- Ehrlich, H.; Janussen, D.; Simon, P.; Bazhenov, V.V.; Shapkin, N.P.; Erler, C.; Mertig, M.; Born, R.; Heinemann, S.; Hanke, T. Nanostructural organization of naturally occurring composites-Part II: Silica-chitin-based biocomposites. J. Nanomater. 2008, 2008, 54. [Google Scholar] [CrossRef]
- Ehrlich, H.; Simon, P.; Carrillo-Cabrera, W.; Bazhenov, V.V.; Botting, J.P.; Ilan, M.; Ereskovsky, A.V.; Muricy, G.; Worch, H.; Mensch, A. Insights into chemistry of biological materials: Newly discovered silica-aragonite-chitin biocomposites in demosponges. Chem. Mater. 2010, 22, 1462–1471. [Google Scholar] [CrossRef]
- Percot, A.; Viton, C.; Domard, A. Optimization of chitin extraction from shrimp shells. Biomacromolecules 2003, 4, 12–18. [Google Scholar] [CrossRef] [PubMed]
- Badwan, A.A.; Rashid, I.; al Omari, M.M.; Darras, F.H. Chitin and chitosan as direct compression excipients in pharmaceutical applications. Mar. Drugs 2015, 13, 1519–1547. [Google Scholar] [CrossRef] [PubMed]
- Ehrlich, H.; Ilan, M.; Maldonado, M.; Muricy, G.; Bavestrello, G.; Kljajic, Z.; Carballo, J.; Schiaparelli, S.; Ereskovsky, A.; Schupp, P. Three-dimensional chitin-based scaffolds from Verongida sponges (Demospongiae: Porifera). Part I. Isolation and identification of chitin. Int. J. Biol. Macromol. 2010, 47, 132–140. [Google Scholar] [CrossRef] [PubMed]
- Yu, Z.; Xu, Z.; Lau, D. Effect of acidity on chitin–protein interface: A molecular dynamics study. BioNanoScience 2014, 4, 207–215. [Google Scholar] [CrossRef]
- No, H.K.; Meyers, S.P. Preparation and characterization of chitin and chitosan—A review. J. Aquat. Food Prod. Technol. 1995, 4, 27–52. [Google Scholar] [CrossRef]
- Palpandi, C.; Shanmugam, V.; Shanmugam, A. Extraction of chitin and chitosan from shell and operculum of mangrove gastropod Nerita (Dostia) crepidularia Lamarck. Int. J. Med. Med. Sci. 2009, 1, 198–205. [Google Scholar]
- Martinou, A.; Kafetzopoulos, D.; Bouriotis, V. Chitin deacetylation by enzymatic means: Monitoring of deacetylation processes. Carbohydr. Res. 1995, 273, 235–242. [Google Scholar] [CrossRef]
- Brugnerotto, J.; Lizardi, J.; Goycoolea, F.; Argüelles-Monal, W.; Desbrieres, J.; Rinaudo, M. An infrared investigation in relation with chitin and chitosan characterization. Polymer 2001, 42, 3569–3580. [Google Scholar] [CrossRef]
- Miserez, A.; Schneberk, T.; Sun, C.; Zok, F.W.; Waite, J.H. The transition from stiff to compliant materials in squid beaks. Science 2008, 319, 1816–1819. [Google Scholar] [CrossRef] [PubMed]
- Nishino, T.; Matsui, R.; Nakamae, K. Elastic modulus of the crystalline regions of chitin and chitosan. J. Polym. Sci. B Polym. Phys. 1999, 37, 1191–1196. [Google Scholar] [CrossRef]
- Vincent, J.F.; Wegst, U.G. Design and mechanical properties of insect cuticle. Arthropod Struct. Dev. 2004, 33, 187–199. [Google Scholar] [CrossRef] [PubMed]
- Lange, F.; Radford, K. Fracture energy of an epoxy composite system. J. Mater. Sci. 1971, 6, 1197–1203. [Google Scholar] [CrossRef]
- Jin, K.; Feng, X.; Xu, Z. Mechanical properties of chitin-protein interfaces: A molecular dynamics study. BioNanoScience 2013, 3, 312–320. [Google Scholar] [CrossRef]
- Dunlop, J.W.C.; Fratzl, P. Multilevel architectures in natural materials. Scr. Mater. 2013, 68, 8–12. [Google Scholar] [CrossRef]
- Yu, Z.; Lau, D. Molecular dynamics study on stiffness and ductility in chitin-protein composite. J. Mater. Sci. 2015, 50, 7149–7157. [Google Scholar] [CrossRef]
- Reed, A.E.; Curtiss, L.A.; Weinhold, F. Intermolecular interactions from a natural bond orbital, donor-acceptor viewpoint. Chem. Rev. 1988, 88, 899–926. [Google Scholar] [CrossRef]
- Fenniri, H.; Mathivanan, P.; Vidale, K.L.; Sherman, D.M.; Hallenga, K.; Wood, K.V.; Stowell, J.G. Helical rosette nanotubes: Design, self-assembly, and characterization. J. Am. Chem. Soc. 2001, 123, 3854–3855. [Google Scholar] [CrossRef] [PubMed]
- Ruiz, L.; VonAchen, P.; Lazzara, T.D.; Xu, T.; Keten, S. Persistence length and stochastic fragmentation of supramolecular nanotubes under mechanical force. Nanotechnology 2013, 24, 195103. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Sasaki, T.; Irie, S.; Sakurai, K. A novel biomass-ionic liquid platform for the utilization of native chitin. Polymer 2008, 49, 2321–2327. [Google Scholar] [CrossRef]
- Knowles, T.P.; Fitzpatrick, A.W.; Meehan, S.; Mott, H.R.; Vendruscolo, M.; Dobson, C.M.; Welland, M.E. Role of intermolecular forces in defining material properties of protein nanofibrils. Science 2007, 318, 1900–1903. [Google Scholar] [CrossRef] [PubMed]
- Park, S.; Khalili-Araghi, F.; Tajkhorshid, E.; Schulten, K. Free energy calculation from steered molecular dynamics simulations using Jarzynski’s equality. J. Chem. Phys. 2003, 119, 3559–3566. [Google Scholar] [CrossRef]
- Lange, F. Fracture energy and strength behavior of a sodium borosilicate glass-Al2O3 composite system. J. Am. Ceram. Soc. 1971, 54, 614–620. [Google Scholar] [CrossRef]
- Sinko, R.; Mishra, S.; Ruiz, L.; Brandis, N.; Keten, S. Dimensions of biological cellulose nanocrystals maximize fracture strength. ACS Macro Lett. 2013, 3, 64–69. [Google Scholar] [CrossRef]
- Keten, S.; Buehler, M.J. Geometric confinement governs the rupture strength of H-bond assemblies at a critical length scale. Nano Lett. 2008, 8, 743–748. [Google Scholar] [CrossRef] [PubMed]
- Dunlop, J.W.C.; Fratzl, P. Biological composites. Annu. Rev. Mater. Res. 2010, 40, 1–24. [Google Scholar] [CrossRef]
- Yu, Z.; Lau, D. Development of a coarse-grained α-chitin model on the basis of MARTINI forcefield. J. Mol. Model. 2015, 21, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Sila, A.; Mlaik, N.; Sayari, N.; Balti, R.; Bougatef, A. Chitin and chitosan extracted from shrimp waste using fish proteases aided process: Efficiency of chitosan in the treatment of unhairing effluents. J. Polym. Environ. 2013, 22, 78–87. [Google Scholar] [CrossRef]
- Min, B.M.; Lee, S.W.; Lim, J.N.; You, Y.; Lee, T.S.; Kang, P.H.; Park, W.H. Chitin and chitosan nanofibers: electrospinning of chitin and deacetylation of chitin nanofibers. Polymer 2004, 45, 7137–7142. [Google Scholar] [CrossRef]
- Jia, Z.; Shen, D. Effect of reaction temperature and reaction time on the preparation of low-molecular-weight chitosan using phosphoric acid. Carbohydr. Polym. 2002, 49, 393–396. [Google Scholar] [CrossRef]
- Cheng, C.Y.; Li, Y.K. An Aspergillus chitosanase with potential for large-scale preparation of chitosan oligosaccharides. Biotechnol. Appl. Biochem. 2000, 32, 197–203. [Google Scholar] [CrossRef] [PubMed]
- Lorenzo, A.C.; Caffarena, E.R. Elastic properties, Young’s modulus determination and structural stability of the tropocollagen molecule: A computational study by steered molecular dynamics. J. Biomech. 2005, 38, 1527–1533. [Google Scholar] [CrossRef] [PubMed]
- Tam, L.H.; Lau, D. Moisture effect on the mechanical and interfacial properties of epoxy-bonded material system: An atomistic and experimental investigation. Polymer 2015, 57, 132–142. [Google Scholar] [CrossRef]
- Lau, D.; Broderick, K.; Buehler, M.J.; Büyüköztürk, O. A robust nanoscale experimental quantification of fracture energy in a bilayer material system. Proc. Natl. Acad. Sci. USA 2014, 111, 11990–11995. [Google Scholar] [CrossRef] [PubMed]
- Lau, D.; Büyüköztürk, O.; Buehler, M.J. Characterization of the intrinsic strength between epoxy and silica using a multiscale approach. J. Mater. Res. 2012, 27, 1787–1796. [Google Scholar] [CrossRef]
- Pearson, F.; Marchessault, R.; Liang, C. Infrared spectra of crystalline polysaccharides. V. Chitin. J. Polym. Sci. 1960, 43, 101–116. [Google Scholar] [CrossRef]
- Petrov, M.; Lymperakis, L.; Friák, M.; Neugebauer, J. Ab Initio Based conformational study of the crystalline α-chitin. Biopolymers 2013, 99, 22–34. [Google Scholar] [CrossRef] [PubMed]
- Tang, W.J.; Fernandez, J.G.; Sohn, J.J.; Amemiya, C.T. Chitin is endogenously produced in vertebrates. Curr. Biol. 2015, 25, 897–900. [Google Scholar] [CrossRef] [PubMed]
- Ganguly, S. Antimicrobial properties from naturally derived substances useful for food preservation and shelf-life extension—A review. Int. J. Bioassays 2013, 2, 929–931. [Google Scholar]
- Sarasam, A.; Madihally, S.V. Characterization of chitosan-polycaprolactone blends for tissue engineering applications. Biomaterials 2005, 26, 5500–5508. [Google Scholar] [CrossRef] [PubMed]
- Kurita, K.; Tomita, K.; Tada, T.; Ishii, S.; Nishimura, S.I.; Shimoda, K. Squid chitin as a potential alternative chitin source: Deacetylation behavior and characteristic properties. J. Polym. Sci. A Polym. Chem. 1993, 31, 485–491. [Google Scholar] [CrossRef]
- Huang, J.; MacKerell, A.D. CHARMM36 all-atom additive protein force field: Validation based on comparison to NMR data. J. Comput. Chem. 2013, 34, 2135–2145. [Google Scholar] [CrossRef] [PubMed]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Park, S.; Schulten, K. Calculating potentials of mean force from steered molecular dynamics simulations. J. Chem. Phys. 2004, 120, 5946–5961. [Google Scholar] [CrossRef] [PubMed]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, J.; Yu, Z.; Lau, D. Effect of Acetyl Group on Mechanical Properties of Chitin/Chitosan Nanocrystal: A Molecular Dynamics Study. Int. J. Mol. Sci. 2016, 17, 61. https://doi.org/10.3390/ijms17010061
Cui J, Yu Z, Lau D. Effect of Acetyl Group on Mechanical Properties of Chitin/Chitosan Nanocrystal: A Molecular Dynamics Study. International Journal of Molecular Sciences. 2016; 17(1):61. https://doi.org/10.3390/ijms17010061
Chicago/Turabian StyleCui, Junhe, Zechuan Yu, and Denvid Lau. 2016. "Effect of Acetyl Group on Mechanical Properties of Chitin/Chitosan Nanocrystal: A Molecular Dynamics Study" International Journal of Molecular Sciences 17, no. 1: 61. https://doi.org/10.3390/ijms17010061
APA StyleCui, J., Yu, Z., & Lau, D. (2016). Effect of Acetyl Group on Mechanical Properties of Chitin/Chitosan Nanocrystal: A Molecular Dynamics Study. International Journal of Molecular Sciences, 17(1), 61. https://doi.org/10.3390/ijms17010061








