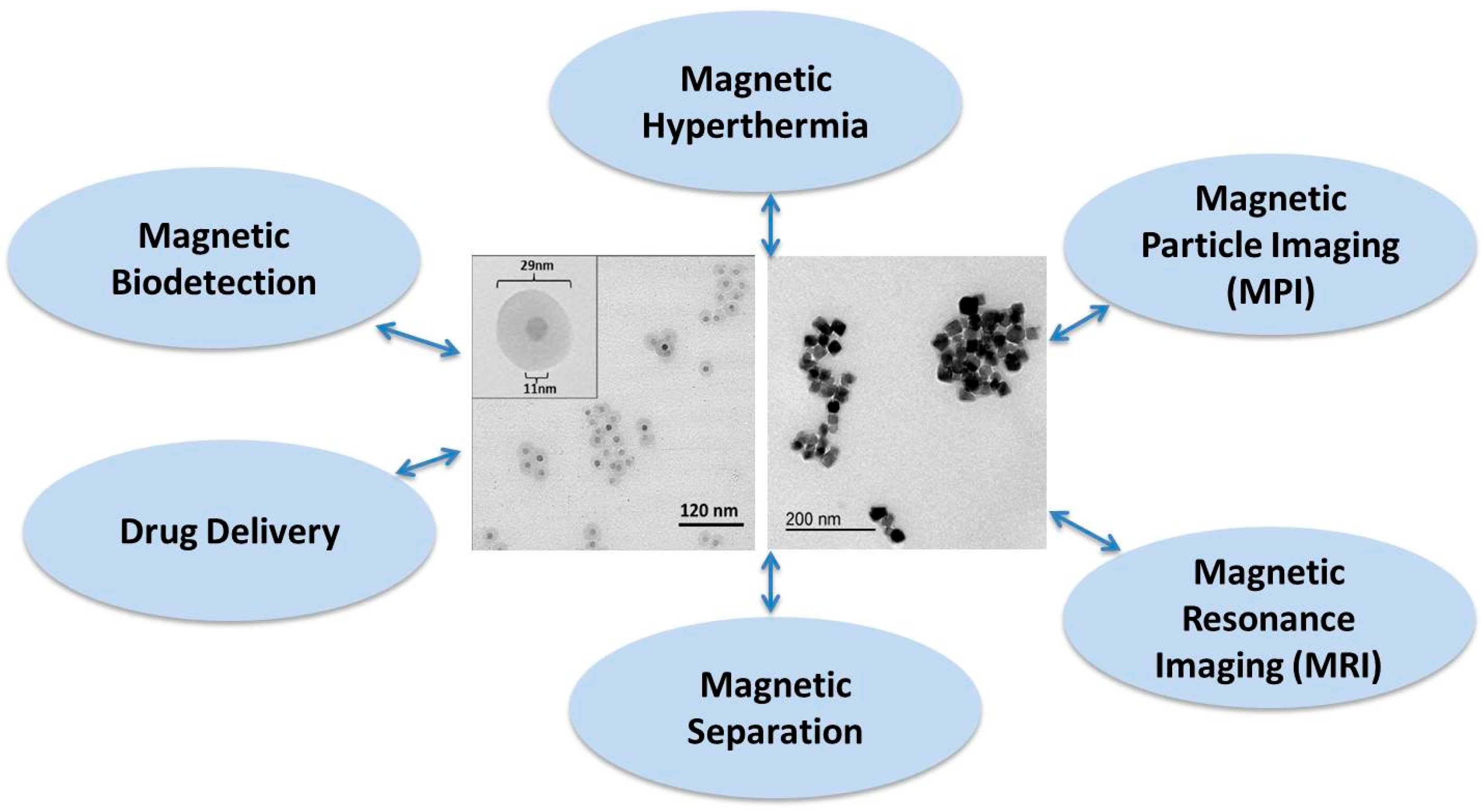
1. Introduction
Single-core magnetic iron oxide nanoparticles with sizes from a few nanometers and iron oxide based multi-core particles with sizes up to several micrometers can be found in several biomedical applications in the areas of diagnosis, therapy, actuation and imaging [
1,
2]. Magnetic nanoparticle systems can act as binding sites and nanosensors in magnetic biosensor detection systems, they can be local heat sources in magnetic hyperthermia to kill cancerous cells, they facilitate separation steps in immunoassays, they can act as drug carriers in targeting procedures or they can act as imaging agents in magnetic resonance imaging or magnetic particle imaging [
1,
2]. In many of these biomedical applications, the parameters of the particle size distribution, both for the single- and multi-core particles, are important to know and to control during the synthesis process. Some biomedical applications using magnetic nanoparticles (MNPs) are illustrated in
Figure 1.
Figure 1.
Biomedical applications of magnetic nanoparticles. Both single- and multi-core magnetic nanoparticle systems as shown in the TEM images are used in the applications.
Figure 1.
Biomedical applications of magnetic nanoparticles. Both single- and multi-core magnetic nanoparticle systems as shown in the TEM images are used in the applications.
MNPs can be investigated in immobilized state or suspended in a liquid. The latter is relevant for many biomedical applications. Measurements on immobilized MNPs provide important information on structural and magnetic properties of the metal oxide MNP cores. Immobilization of MNPs can be reached in several ways: air drying, freeze drying, embedding in gel, sugar or gypsum, or by other methods. It has been observed that the magnetic behavior of immobilized samples depends on the actual method of immobilization, which will alter the local environment and organization of the MNPs. Nevertheless, the interpretation of measurement data of immobilized MNP can be based on well-established models. The ensemble behavior of immobilized MNPs, in most cases, does not represent the suspension behavior, firstly because the interaction of the particles and the suspension medium is missing and secondly, because the average separation and thus the dipolar interaction energy between the particles have changed. MNP suspensions, on the other hand, make up realistic samples for the ensemble behavior, but the model-based interpretation might become highly complicated due to field-dependent changes in MNP organization and interactions (e.g., chain formation), which have to be included in the interpretation of measurement data. These effects may further depend on the degree of dilution of the MNPs in the suspension medium, which should also be taken into account.
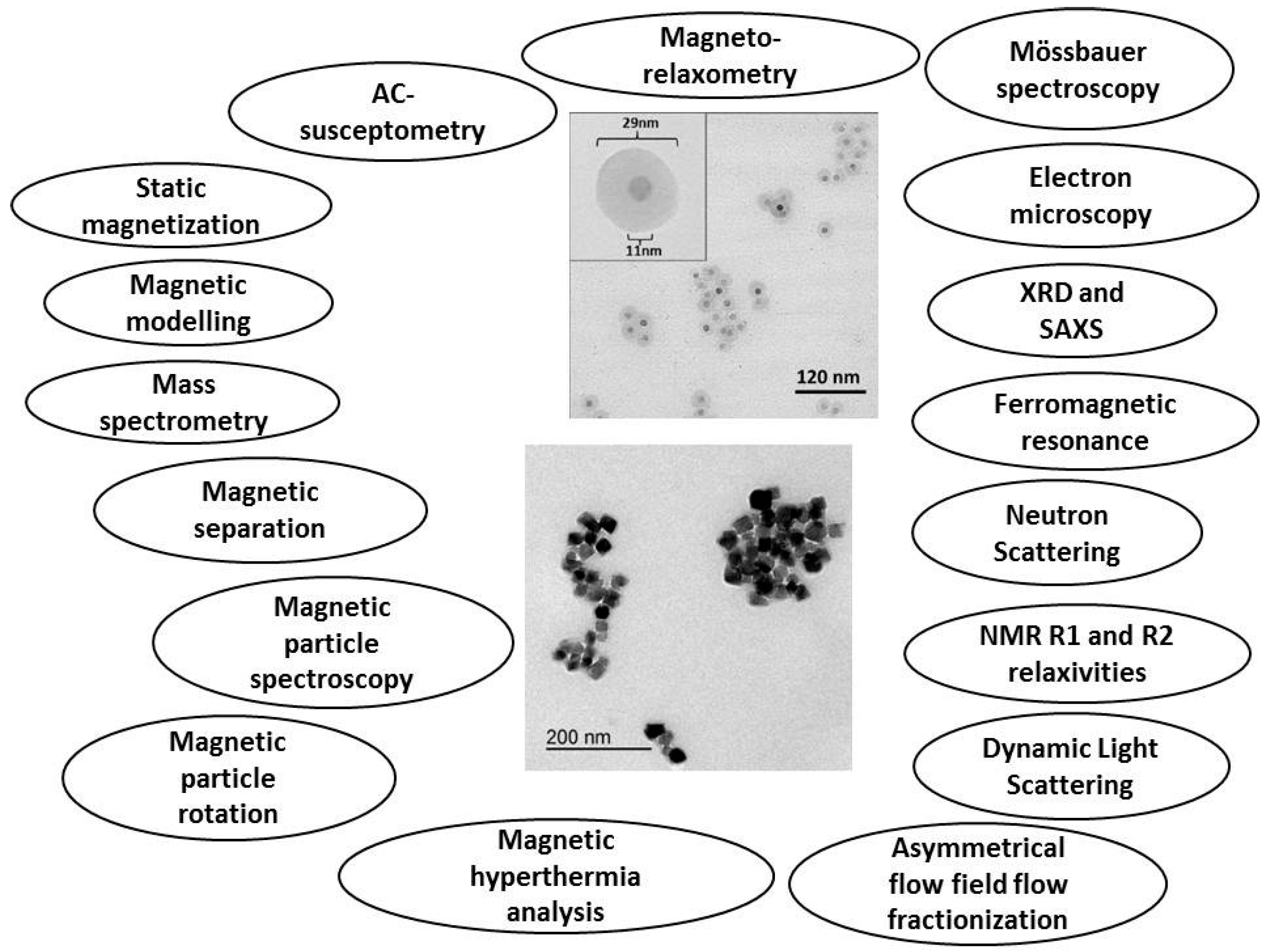
Although MNPs have been researched and applied already for a considerable number of years, so far there exists no standardized way of characterizing and expressing their main physicochemical properties. This represents a considerable obstacle for introducing new MNP-based biomedical and clinical applications, for example Magnetic Particle Imaging (MPI). Within the EU FP7 project, NanoMag, as a possible means to improve this situation, we have formulated a tentative normative document for a standardized MNP description. This document will then iteratively be rewritten and updated, in strong collaboration with MNP manufacturers, appliers, end-users and other socioeconomic groups interested in MNPs. Eventually, the knowledge and result obtained in the NanoMag project can enter a standardization process as it is mediated by the European Committee for Standardization and the European Committee for Electrotechnical Standardization (CEN/CENELEC) or the International Organization for Standardization (ISO). A stakeholder committee consisting of 15 industrial, medical and academic organizations guides the NanoMag project regarding standardization and exploitation. The four-year NanoMag project focused on nanometrology standardization methods for MNPs was launched in November 2013. The project involves research institutes, universities, companies as well as national metrology institutes. The main objectives of this project are to improve and redefine existing analysis methods and models and to develop new standardized analysis methods and models for MNPs. Using improved manufacturing technologies, the NanoMag project will synthesize MNPs with specific properties, characterize them with a multitude of techniques (focusing on both structural and magnetic properties), and bring the experimental results together to obtain a self-consistent picture, which describes, e.g., how structural and magnetic properties are interrelated. This extensive project aims to define the standard measurements and techniques required to classify and characterize magnetic nanoparticle systems and to be used for quality control during synthesis of magnetic nanoparticles. A detailed description of the project can be found on the NanoMag website [
3]. In the NanoMag project, we use basic analysis and more advanced analysis techniques as well as more application oriented methods, summarized in
Figure 2. A detailed description of the analysis methods for MNP systems is available now and allows the selection of a tailored analysis strategy depending on target properties, economical effort other application aspects.
MNPs synthesized within the project as well as selected commercially available nanoparticles are characterized and analyzed with the techniques and methods that are shown in
Figure 2. The results are used to identify and standardize analysis methods for MNPs. All of the analysis methods shown in
Figure 2 have been used in the first two years of the NanoMag project.
Figure 2.
Analysis techniques used in the NanoMag project for the characterization and analysis of synthesized single- and multi-core nanoparticles shown in the TEM (transmission electron microscopy) images in the middle of the figure.
Figure 2.
Analysis techniques used in the NanoMag project for the characterization and analysis of synthesized single- and multi-core nanoparticles shown in the TEM (transmission electron microscopy) images in the middle of the figure.
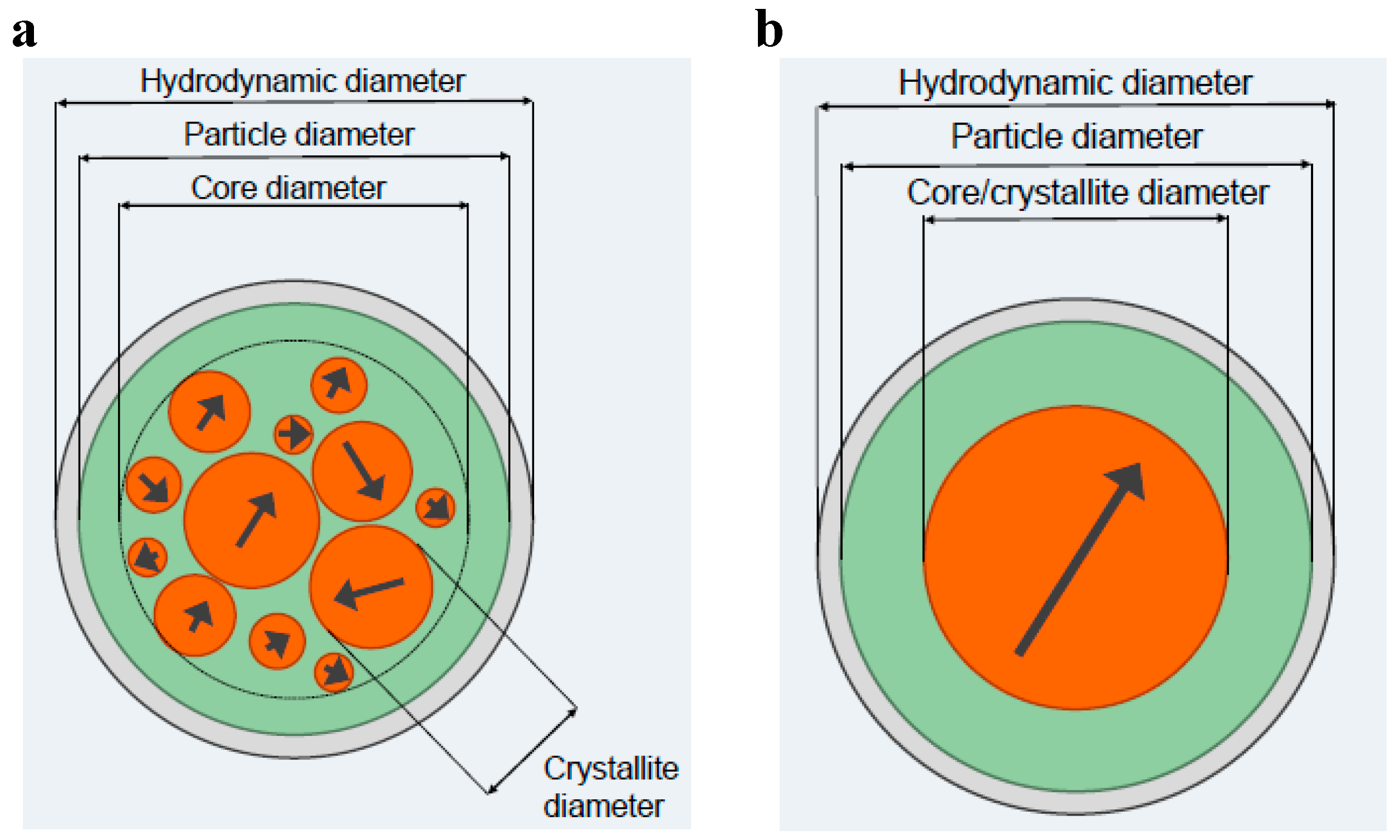
Since the behaviour of MNPs in a suspension crucially depends on their physical properties (for instance, the mean size and the distribution of sizes of both the nanocrystals and the physical particles as well as the hydrodynamic size and surface charge that determine the colloidal stability) and the type of MNP systems (single- or multi-core particle system), it is of vital importance for different biomedical applications that the analysis methods used to determine the physical parameters are well defined and standardized. In the description of the structural composition of a typical iron oxide based MNP suspension, there should be a clear distinction between the different compartments of the suspension: metal oxide cores, organic coating and suspension medium (see
Figure 3). A single-core magnetic nanoparticle can be defined as a particle containing only a single nanocrystal that can be further coated and functionalized at the surface for colloidal stability and also for use in specific applications (e.g., specific binding to different analytes). A multi-core particle can be defined as a particle containing several nanocrystals either densely or loosely packed within the multi-core structure. The surface of the multi-core particle can also be coated and functionalized. We have earlier presented a review of synthesis of single-core and multi-core particles [
4]. The magnetic properties of single-core and multi-core particles depend on both the properties of the nanocrystals (such as their size distribution) and in the case of multi-core particles how the nanocrystals are distributed in the multi-core structure [
5,
6]. Schematic pictures of single- and multi-core particles are shown in
Figure 3.
Figure 3.
Schematic pictures of magnetic (a) multi-core particles and (b) single-core particles. The definitions of the size parameters of the two different particle types are also shown in the figure. See the text for an explanation of the compartments.
Figure 3.
Schematic pictures of magnetic (a) multi-core particles and (b) single-core particles. The definitions of the size parameters of the two different particle types are also shown in the figure. See the text for an explanation of the compartments.
The particle size parameters for a multi-core particle system can be defined according to their (I) nanocrystal size (crystallite diameter); (II) the core diameter where the nanocrystals are positioned; (III) the particle diameter due to the particle matrix (for instance starch or dextran) and surface coating and/or surface functionalization; and (IV) the hydrodynamic diameter if the particles are dispersed in a carrier liquid (for instance water), which may be different from the physical particle size due to the solvation zone near the particle surface that is dragged along with the particle when it rotates. For the single-core particle only one single-domain nanocrystal is within the particle and the defined particle size parameters are the same as for the multi-core particle except that the core size is the same as the nanocrystal size.
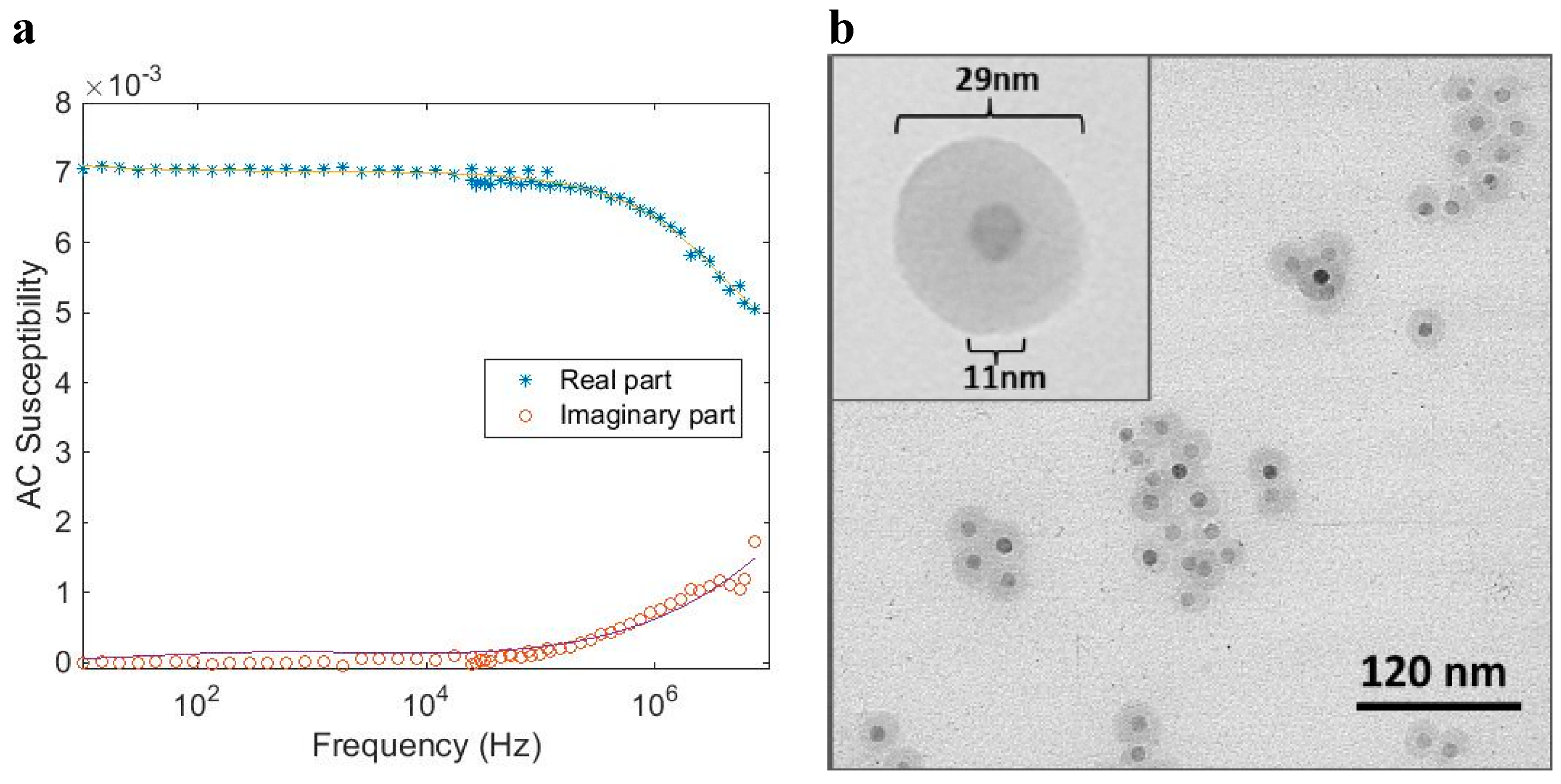
Magnetic relaxation in a MNP system dispersed in a carrier liquid can be divided in particles that undergo internal Néel relaxation where the magnetic moment within the nanocrystals rotates due to thermal activation and is decoupled from the particle rotation. The other relaxation mechanism is the Brownian relaxation where the particle physically rotates and the magnetic moments of the nanocrystals are blocked in a specific direction in the particles and the total effective particle magnetic moment is coupled to the particle and rotates with the same rate as the particle itself [
5]. Both processes may take place simultaneously. However, the faster process will dominate the overall magnetic relaxation behavior of the particle system.
MNP systems (both single- and multi-core nanoparticles) may contain small nanocrystals that show fast internal magnetic relaxation (Néel relaxation) and larger nanocrystals that are thermally blocked. An ensemble of single-core particles, with a typical relaxation time shorter than the specific time scale of the measurement (for instance defined by the measurement excitation frequency in AC susceptometry measurements), behaves as a superparamagnetic material and shows a magnetic response in phase with the applied magnetic field. When the time scale of the measurement is of the same order of magnitude as the relaxation time, the magnetic response of the particle ensemble will lag behind the magnetic field excitation and have a non-zero out-of-phase component.
The Néel relaxation time in zero magnetic field and assuming no magnetic interactions between the nanocrystals is:
where τ
0 is the intrinsic relaxation time of the magnetic nanocrystals,
K the magnetic anisotropy,
VC the volume of the nanocrystals,
k the Boltzmann constant and
T is the temperature.
The Brownian relaxation time is:
where
VH is the hydrodynamic volume (given by 4π
rH3/3, where
rH is the hydrodynamic radius) of the magnetic nanoparticles (taking into account the particle surface layer and the volume of carrier liquid the particles drags along when rotating) of the particles and η is the viscosity of the carrier liquid in which the particles are dispersed. The total relaxation time, τ
eff, the magnetic nanoparticles will undergo is given by the effective relaxation time combining both the Néel and Brownian relaxation time according to:
A corresponding relaxation frequency
fR can be defined as
where τ can be the Néel relaxation time (Equation (1)), Brownian relaxation time (Equation (2)) or the effective relaxation time (Equation (3)). The relaxation frequency,
fR, can approximately be seen in the AC susceptibility
vs. excitation frequency,
i.e., AC susceptometry (ACS) response in the same frequency range as the peak in the out of phase component and a decrease in the in-phase component.
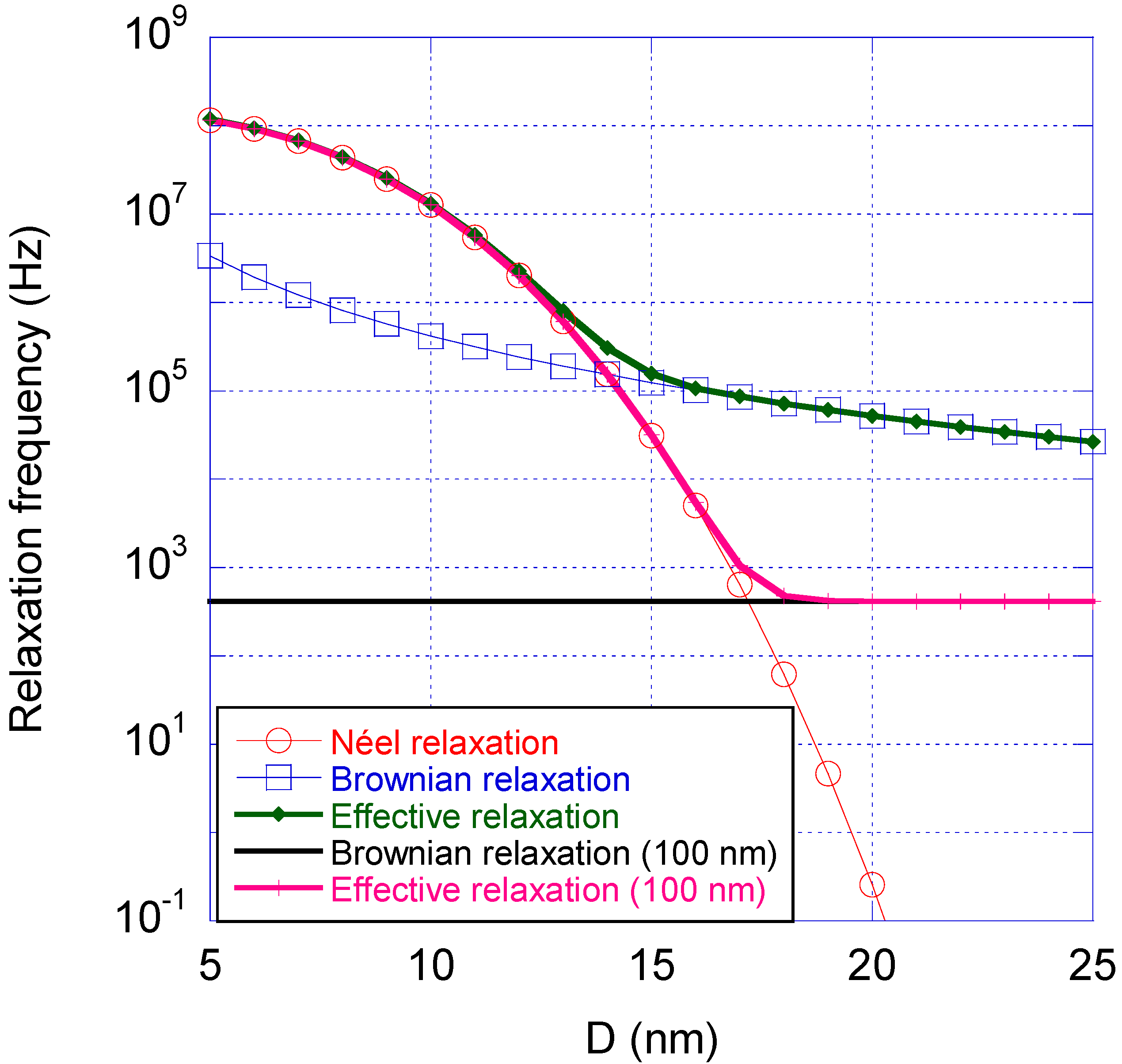
Figure 4 shows calculated values of the Néel, Brownian and effective relaxation frequencies
vs. nanocrystal diameter for a single-core particle with a physical size equal to the magnetic size and a physical size equal to 100 nm, respectively. The parameters determining whether Néel or Brownian relaxation dominates for a magnetic nanoparticle system dispersed in a carrier liquid at a given temperature, are the mean sizes, size distribution, the magnetic material properties (through the magnetic anisotropy) and the viscous properties of the liquid (through the viscosity of the carrier liquid). At a specific temperature, the Néel relaxation depends mainly on the intrinsic properties of the nanocrystals (size and magnetic anisotropy) whereas the Brownian relaxation depends mainly external properties (carrier liquid viscosity). Both the Néel and Brownian relaxation mechanisms are affected by nanocrystal interactions and by the magnitude of the applied external measurement field (which is not taken into account in
Figure 4).
Figure 4 shows that small nanocrystals relax via the Néel process, whereas larger nanocrystals relax via the Brownian process. The crossover size is in the case shown in
Figure 4 is about 15 nm. If instead the nanocrystals are placed in a particle matrix with diameter of 100 nm the crossover size between Néel and Brownian relaxation is about 18 nm, see
Figure 4.
Figure 4.
Magnetic relaxation time vs. the nanocrystal size (D is the diameter of the nanocrystals) for an iron oxide based nano-sized particle system dispersed in water at room temperature, showing the Néel relaxation frequency (red), Brownian relaxation frequency (blue) and the effective relaxation frequency (green). The figure also shows the Brownian relaxation frequency of a particle with diameter 100 nm (black) and the effective relaxation (magenta) a nanocrystal will undergo positioned in that particle matrix. The parameters of nano-sized iron oxide nanocrystals used in this figure were K = 20 kJ/m3, τ0 = 10−9 s, η = 10−3 Pa·s and zero shell thickness of the nanocrystals.
Figure 4.
Magnetic relaxation time vs. the nanocrystal size (D is the diameter of the nanocrystals) for an iron oxide based nano-sized particle system dispersed in water at room temperature, showing the Néel relaxation frequency (red), Brownian relaxation frequency (blue) and the effective relaxation frequency (green). The figure also shows the Brownian relaxation frequency of a particle with diameter 100 nm (black) and the effective relaxation (magenta) a nanocrystal will undergo positioned in that particle matrix. The parameters of nano-sized iron oxide nanocrystals used in this figure were K = 20 kJ/m3, τ0 = 10−9 s, η = 10−3 Pa·s and zero shell thickness of the nanocrystals.
Dynamic magnetic properties of magnetic nanoparticle systems can be analyzed by using ACS (AC susceptometry) analysis and MRX (magnetorelaxometry) analysis (magnetic moment
vs. time after switching off the magnetizing field). Several earlier studies using ACS and MRX analysis for determining dynamic magnetic properties and particle size parameters in MNP systems has been carried out [
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15].
The frequency dependent complex magnetic AC susceptibility can be described by the in-phase component, χ′, (real part) and the out-of-phase component, χ′′, (imaginary part) according to:
In order to extract MNP parameters from the AC susceptometry data we use ACS models depending on the class of particle system investigated.
AC susceptibility model for single-core particles is described by the following relation [
7]:
f(
rC) is the number-weighted nanocrystal size distribution (log-normal function is used),
rH =
rC + δ where
rC is the magnetic nanocrystal radius,, ω = 2π
f where
f is the excitation frequency and
C is a pre-factor (including temperature, intrinsic saturation magnetization and particle density), δ is the thickness of the shell surrounding the nanocrystals, and χ
high is the high frequency value of the in-phase part of the susceptibility. This high frequency relaxation process is probably due to the intra-potential-well contribution of the nanocrystals to the AC susceptibility [
5,
7].
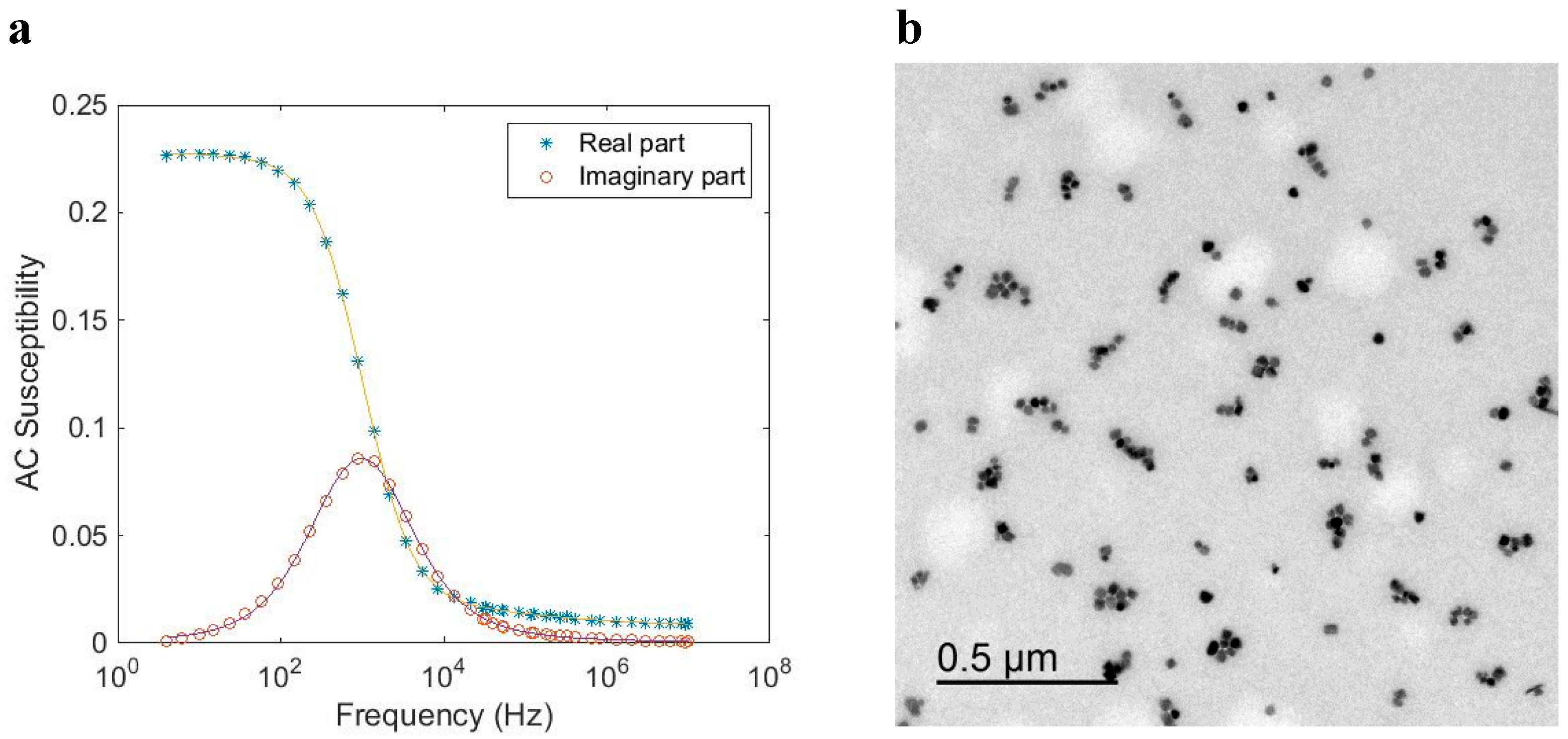
The multi-core model is used for multi-core structured particles that undergo Brownian relaxation. Since the nanocrystals in the multi-core can magnetically interact with each other, non-interacting models for the (I) dynamic AC response and (II) the Néel relaxation time cannot be used. Instead we use a mean value for the DC (static) susceptibility,
<χ
0B>, in the Debye model. The mean value of <χ
0B> is then the average DC susceptibility value of the multi-core particle system. Thus, we picture each multi-core particle as a magnetic site with a mean value susceptibility <χ
0B>. Since we use a mean value of the susceptibility, <χ
0B>, we make the approximation that all multi-core particles contributes equally to the DC susceptibility. The AC susceptibility response can then be expressed as [
8]:
where
f(
rH) is the hydrodynamic particle size distribution (log-normal function is used). It has been shown in many earlier studies that using the above model that the determined hydrodynamic size distribution and mean particle sizes by fitting data to Equation (7), resembles very well the intensity weighed size distribution and the Z-average size as determined by DLS analysis [
5,
6,
7,
9].
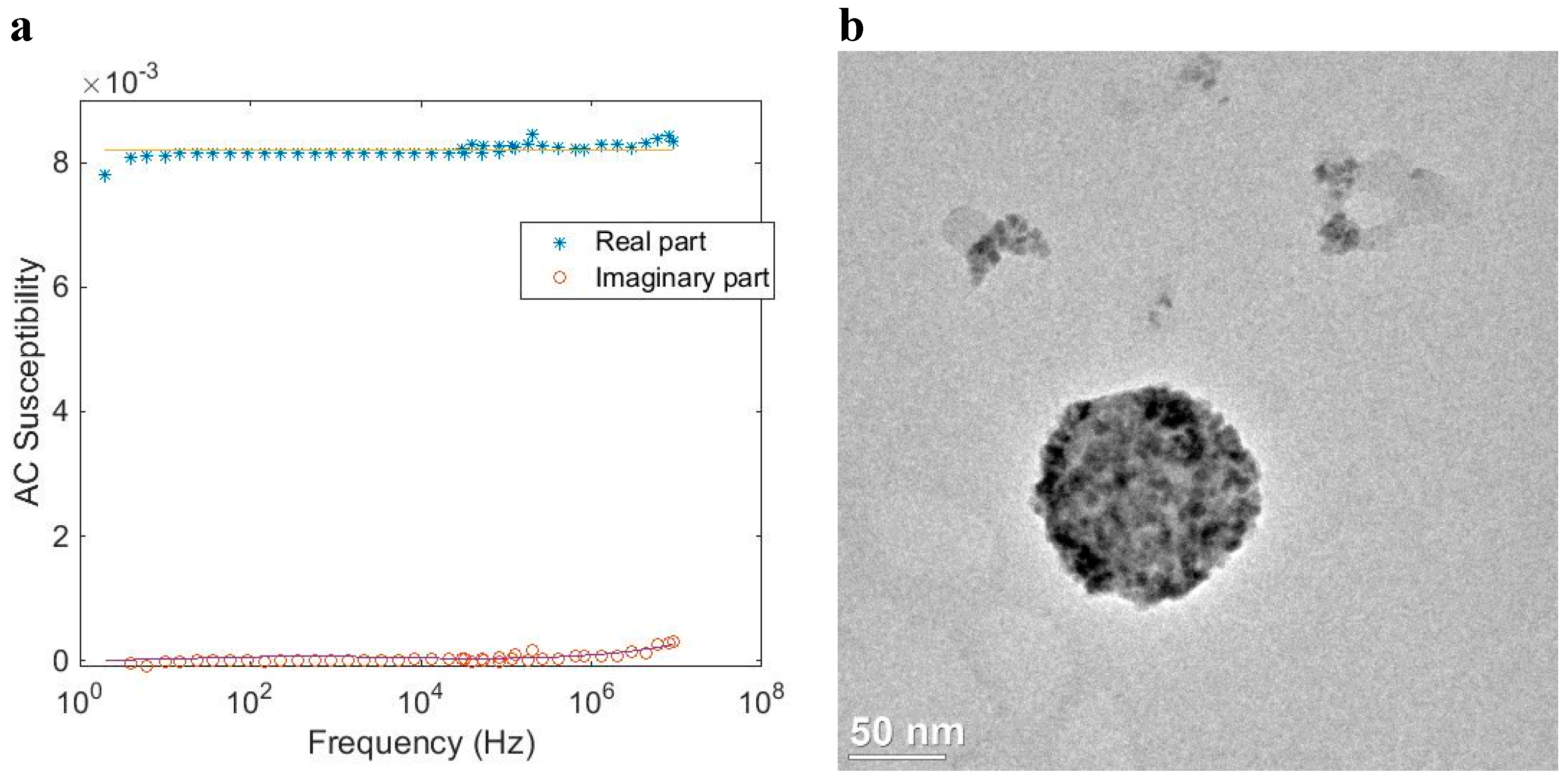
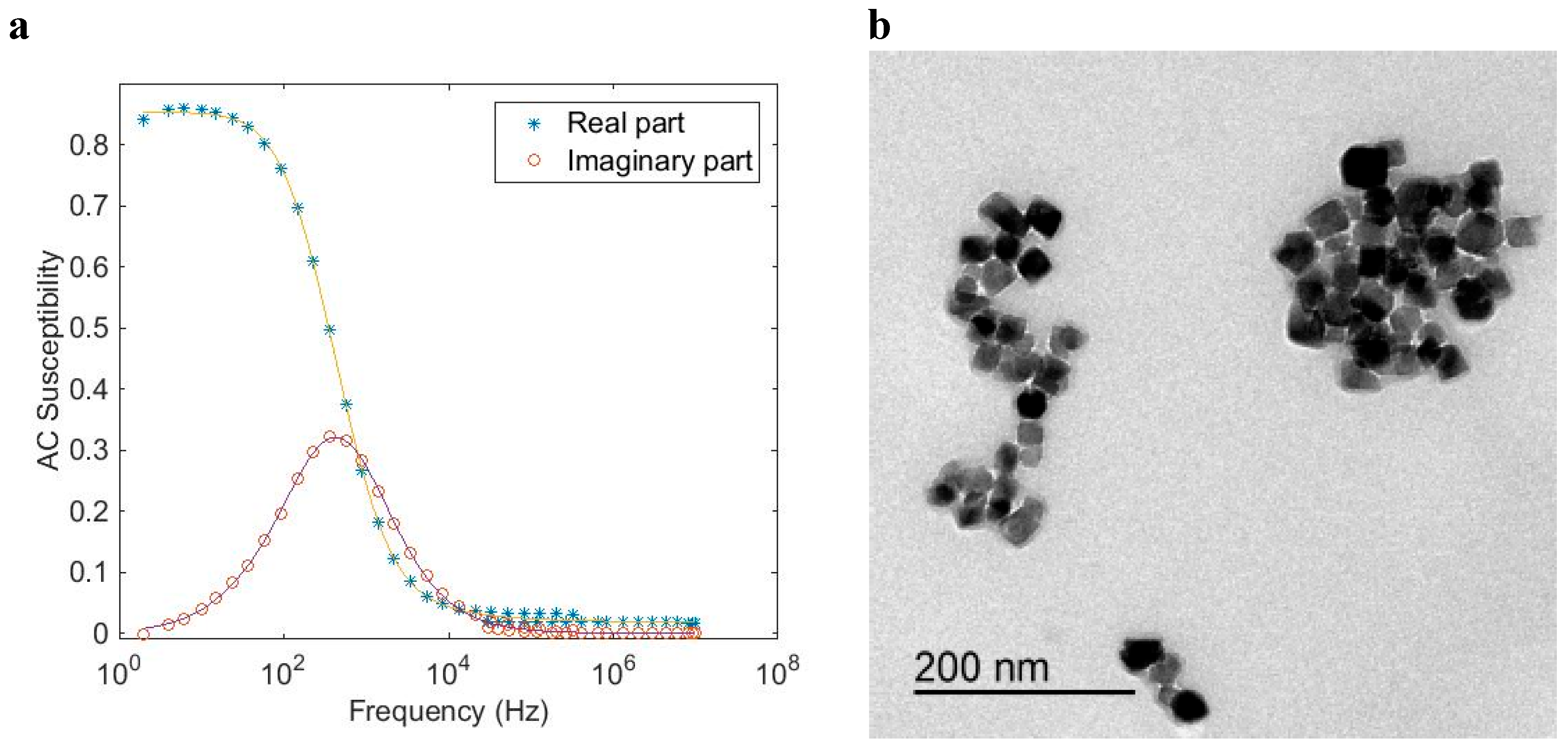
Using the same approximation as described in connection to Equation (7) for multi-core particle systems that shows a mixture of both Brownian and Néel relaxation, the AC susceptibility model for multi-core particles (Equation (7)) is combined with a Cole–Cole expression for the Néel relaxation part, according to [
8]:
where χ
0N gives the Néel DC susceptibility contribution, and α is the Cole–Cole parameter for the Néel relaxation part (0 < α < 1) that sets the width of the relaxation distribution. In addition, also in this case, it has been shown in earlier studies that using the above equation that the determined size distribution resembles very well the intensity weighed size distribution as determined by dynamic light scattering analysis.
The models given in Equations (6)–(8) are used to extract magnetic nanoparticle properties by fitting the models to the experimental data. The results for different particle types are given in chapter 2, where magnetic nanoparticle systems are classified according to their magnetic relaxation properties and their particle size parameters. Other similar AC susceptometry models can be used in order to extract size parameters of magnetic nanoparticle systems [
10,
11]. Models are also used to analyse the MRX data in order to extract for instance particle size parameters [
12,
13,
14].
We are not able to, in a single article, present the result from all analyzing techniques in the NanoMag project. In this article, we will concentrate on the result regarding some synthesis of single- and multi-core nanoparticles in the NanoMag project and how to classify these particle systems, by analysing their magnetic relaxation properties using ACS and also taking into account their nanocrystal size and particle size and morphology using transmission electron microscopy (TEM) and dynamic light scattering (DLS) data. MRX analysis is also used as complementary magnetic relaxation measuring technique in order to verify the ACS relaxation measurements presented in chapter 2. TEM analysis gives the number weighted size distribution, while the DLS analysis gives primarily the intensity weighted (∝) size distribution (and Z-average size). When comparing the results of the determined mean sizes from each analysis technique for each of the particle systems, as given in chapter 2, we take into account the different weighting of the size distribution for the different measuring techniques.