The Cross-Bridge of Skeletal Muscle Is Not Synchronized Either by Length or Force Step
Abstract
:1. Introduction
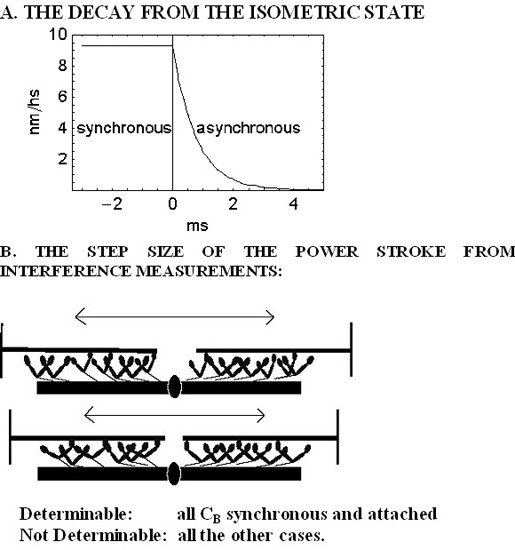
2. Results
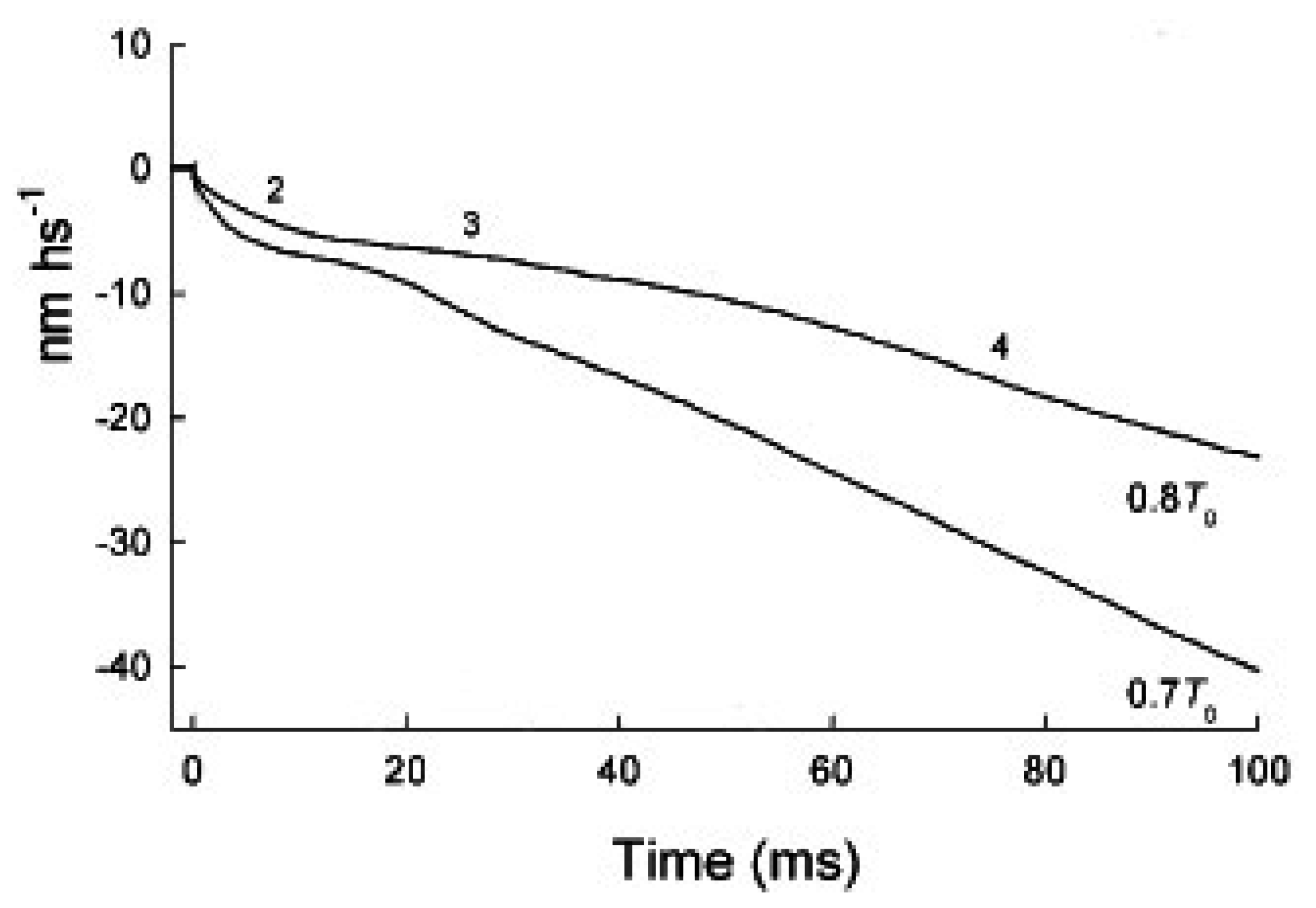
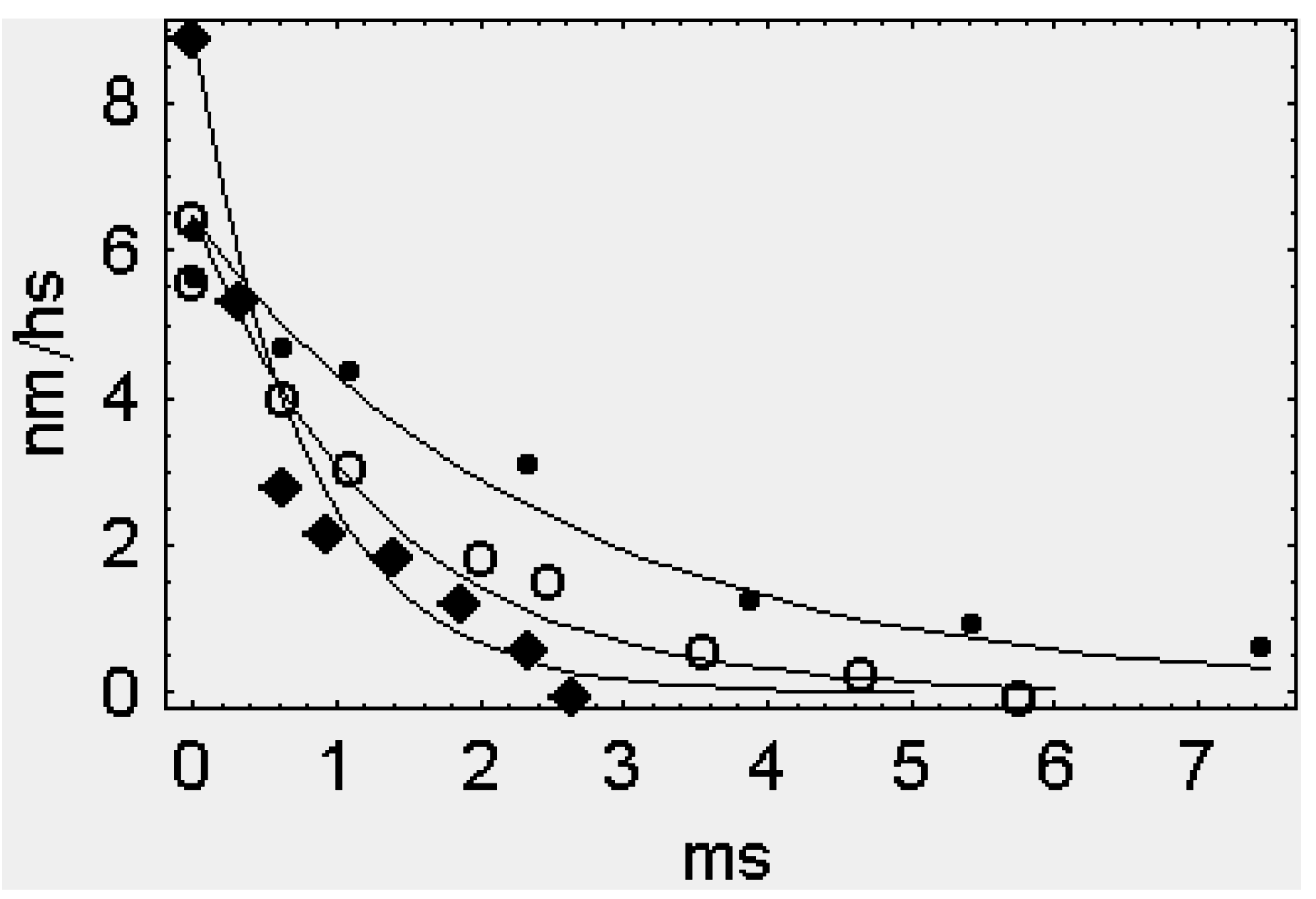
2.1. The Rapid Phase 2 Cannot Be Related to the Synchronous Execution of the Working Stroke
2.2. In Phase 2 the Change of the Interference Distance Is Not Solely Related to the Power Stroke
2.2.1. The First Model
| Attached, Tilt Angle | Detached, Tilt Angle | Hypothetical Stroke (nm) | ΔID (nm) |
|---|---|---|---|
| 70° | none | 5.643 | 5.643 |
| 50° | none | 10.606 | 10.606 |
| 70° | 60° | 5.643 | 2.764 |
| 50° | 60° | 10.606 | 5.194 |
2.2.2. The Second Model
The Attached Head Domains
The Detached Head Domains
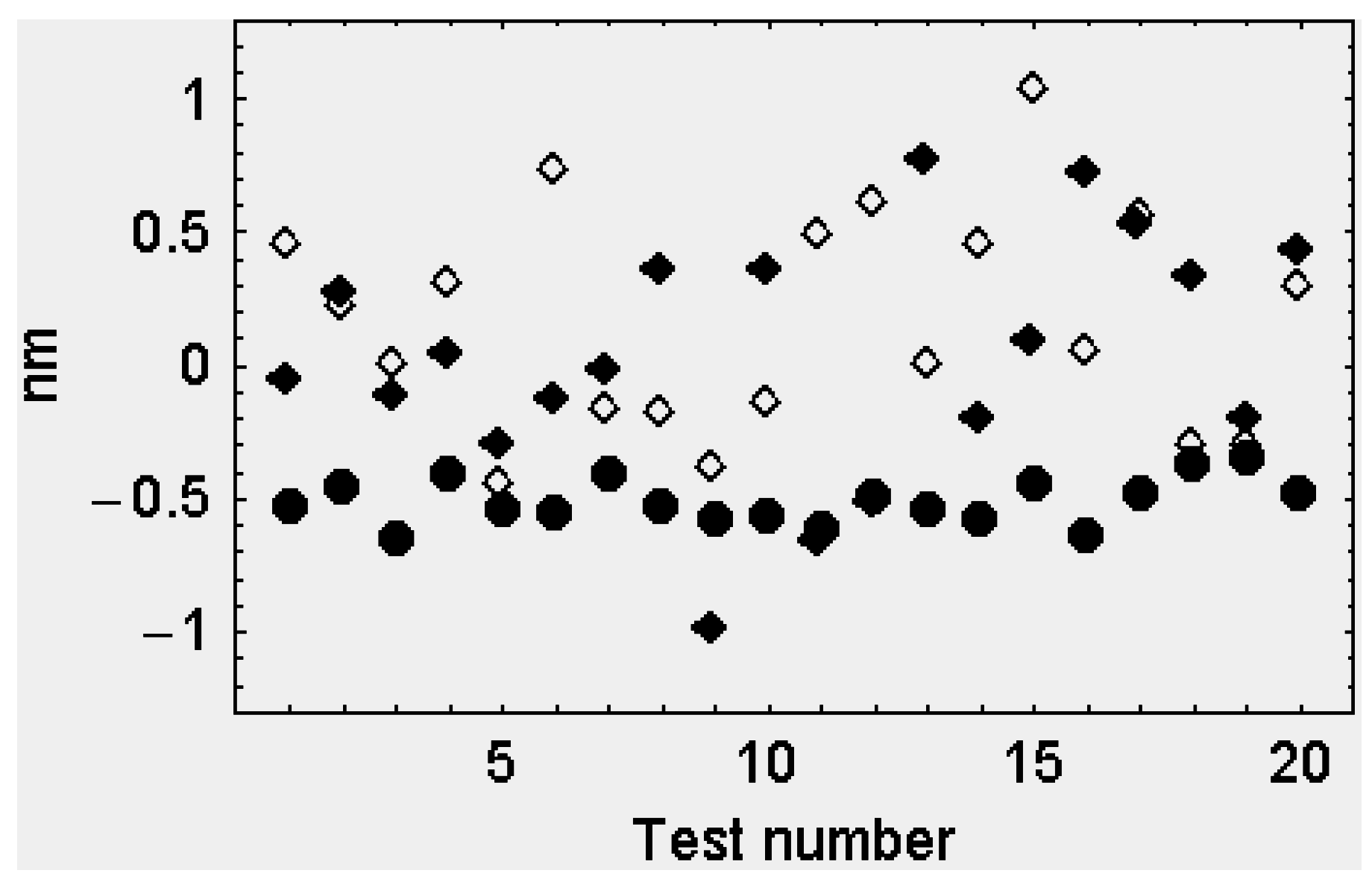
3. Discussion
4. Experimental Section
4.1. Cross-Bridge Synchronization
4.2. The Center of Mass of an Array of Cross-Bridges
5. Conclusions
Author Contributions
Appendix A
Appendix B
Conflicts of Interest
References
- Huxley, A.F.; Simmons, R.M. Proposed mechanism of force generation in striated muscle. Nature 1971, 233, 533–538. [Google Scholar] [CrossRef] [PubMed]
- Piazzesi, G.; Lucii, L.; Lombardi, V. The size and the speed of the working stroke of muscle myosin and its dependence on the force. J. Physiol. 2002, 545, 145–151. [Google Scholar] [CrossRef] [PubMed]
- Reconditi, M.; Linari, M.; Lucii, L.; Stewart, A.; Sun, Y.B.; Boesecke, P.; Narayanan, T.; Fischetti, R.F.; Irving, T.; Piazzesi, G.; et al. The myosin motor in muscle generates a smaller and slower working stroke at higher load. Nature 2004, 428, 578–581. [Google Scholar] [CrossRef] [PubMed]
- Reconditi, M. Recent improvements in small angle X-ray diffraction for the study of muscle physiology. Rep. Prog. Phys. 2006, 69, 2709–2759. [Google Scholar] [CrossRef] [PubMed]
- Piazzesi, G.; Reconditi, M.; Linari, M.; Lucii, L.; Bianco, P.; Brunello, E.; Decostre, V.; Stewart, A.; Gore, D.B.; Irving, T.C.; et al. Skeletal muscle performance determined by modulation of number of myosin motors rather than motor force or stroke size. Cell 2007, 131, 784–795. [Google Scholar] [CrossRef] [PubMed]
- Linari, M.; Piazzesi, G.; Lombardi, V. The effct of myofilament compliance on kinetics and force generation by myosin motors in muscle. Biophys. J. 2009, 96, 583–592. [Google Scholar] [CrossRef] [PubMed]
- Linari, M.; Caremani, M.; Lombardi, V. A kinetic model that explains the effect of inorganic phosphate on the mechanics and energetics of isometric contraction of fast skeletal muscle. Proc. Biol. Sci. 2010, 277, 19–27. [Google Scholar] [CrossRef] [PubMed]
- Nucciotti, V.; Stringari, C.; Sacconi, L.; Vanzi, F.; Fusia, L.; Linari, M.; Piazzesi, G.; Lombardi, V.; Pavone, F.S. Probing myosin structural conformation in vivo by second-harmonic generation microscopy. Proc. Natl. Acad. Sci. USA 2010, 107, 7763–7768. [Google Scholar] [CrossRef] [PubMed]
- Reconditi, M.; Brunello, E.; Linari, M.; Bianco, P.; Narayanan, T.; Panine, P.; Piazzesi, G.; Lombardi, V.; Irving, M. Motion of myosin heads domain during activation and force development in skeletal muscle. Proc. Natl. Acad. Sci. USA 2011, 108, 7236–7240. [Google Scholar] [CrossRef] [PubMed]
- Caremani, M.; Melli, L.; Dolfi, M.; Lombardi, V.; Linari, M. The working stroke of the myosin II motor in muscle is not tightly coupled to release of orthophosphate from its active site. J. Physiol. 2013, 591, 5187–5205. [Google Scholar] [CrossRef] [PubMed]
- Squire, J.M. The Structural Basis of Muscle Contraction; Plenum: New York, NY, USA, 1981. [Google Scholar]
- Woledge, R.C.; Barclay, C.J.; Curtin, N.A. Temperature change as a probe of muscle crossbridge kinetics: A review and discussion. Proc. Biol. Sci. 2009, 276, 2685–2695. [Google Scholar] [CrossRef] [PubMed]
- Craig, R. Structure of A-segments from frog and rabbit skeletal muscle. J. Mol. Biol. 1977, 109, 69–81. [Google Scholar] [CrossRef]
- Rome, E. Structural studies by X-ray diffraction of striated muscle permeated with certain ions and proteins. Cold Spring Harb. Symp. Quant. Biol. 1972, 37, 331–339. [Google Scholar] [CrossRef]
- Bordas, J.; Lowy, J.; Svensson, A.; Harries, J.A.; Diakun, G.P.; Gandy, J.; Miles, C.; Mant, R.G.; Towns-Andres, E. X-ray evidence that in contracting live frog muscles there exist two different populations of myosin heads. Biophys. J. 1995, 68, 99s–104s. [Google Scholar] [PubMed]
- Huxley, H.E. Discussion. Biophys. J. 1995, 68, 104s. [Google Scholar]
- Rayment, Y.; Rypnievski, W.R.; Schmidt-Base, K.; Smith, R.; Tomchick, D.R.; Winkelmann, D.A.; Wesenberg, G.; Holden, M. Three-dimensional structure of myosin subfragment-1: A molecular motor. Science 1993, 261, 50–58. [Google Scholar] [CrossRef] [PubMed]
- Huxley, H.E.; Reconditi, M.; Stewart, A.; Irving, T. X-ray interference studies of cross-bridge action in muscle contraction: Evidence from quick release. J. Mol. Biol. 2006, 363, 743–761. [Google Scholar] [PubMed]
- Grazi, E.; Pozzati, S. The contribution of the elastic reaction is severely underestimated in studies on myofibril contraction. Int. J. Mol. Sci. 2009, 10, 942–953. [Google Scholar] [CrossRef] [PubMed]
- Huxley, H.E. Past, present and future experiments on muscle. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2000, 355, 539–543. [Google Scholar] [CrossRef] [PubMed]
- Huxley, H.E.; Reconditi, M.; Stewart, A.; Irving, T. X-ray interference studies of crossbridge action in muscle contraction: Evidence from muscle during steady shortening. J. Mol. Biol. 2006, 363, 762–772. [Google Scholar] [CrossRef] [PubMed]
- Grazi, E. Experimental basis of the hypothesis on the mechanism of skeletal muscle contraction. Muscles Ligaments Tendons J. 2011, 1, 77–84. [Google Scholar] [PubMed]
- Hill, T.L. Theoretical formalism for the sliding filament model of contraction of striated muscle. Part I. Prog. Biophys. Mol. Biol. 1974, 28, 267–340. [Google Scholar] [CrossRef]
- Grazi, E. A highly non-ideal solution: The contractile system of skeletal muscle. Eur. Biophys. J. 2000, 29, 535–541. [Google Scholar] [CrossRef] [PubMed]
- Grazi, E. Water and muscle contraction. Int. J. Mol. Sci. 2008, 9, 1435–1452. [Google Scholar] [CrossRef] [PubMed]
- Knupp, C.; Offer, G.; Ranatunga, K.W.; Squire, J.M. Probing muscle myosin motor action: X-ray (M3 and M6). Interference measurements report motor domain not lever arm movement. J. Mol. Biol. 2009, 390, 168–181. [Google Scholar] [CrossRef] [PubMed]
- Fusi, L.; Reconditi, M.; Linari, M.; Brunello, E.; Elangovan, R.; Lombardi, V.; Piazzesi, G. The mechanism of the resistance to stretch of isometrically contracting single muscle fibres. J. Physiol. 2010, 583, 495–510. [Google Scholar] [CrossRef] [PubMed]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grazi, E. The Cross-Bridge of Skeletal Muscle Is Not Synchronized Either by Length or Force Step. Int. J. Mol. Sci. 2015, 16, 12064-12075. https://doi.org/10.3390/ijms160612064
Grazi E. The Cross-Bridge of Skeletal Muscle Is Not Synchronized Either by Length or Force Step. International Journal of Molecular Sciences. 2015; 16(6):12064-12075. https://doi.org/10.3390/ijms160612064
Chicago/Turabian StyleGrazi, Enrico. 2015. "The Cross-Bridge of Skeletal Muscle Is Not Synchronized Either by Length or Force Step" International Journal of Molecular Sciences 16, no. 6: 12064-12075. https://doi.org/10.3390/ijms160612064
APA StyleGrazi, E. (2015). The Cross-Bridge of Skeletal Muscle Is Not Synchronized Either by Length or Force Step. International Journal of Molecular Sciences, 16(6), 12064-12075. https://doi.org/10.3390/ijms160612064