Chemical Bonding: The Orthogonal Valence-Bond View
Abstract
:1. Introduction
1.1. Bonding and Bonds
2. Covalent Bonding and Chemical Reactions
3. OVB Reading of FORS Wave Functions
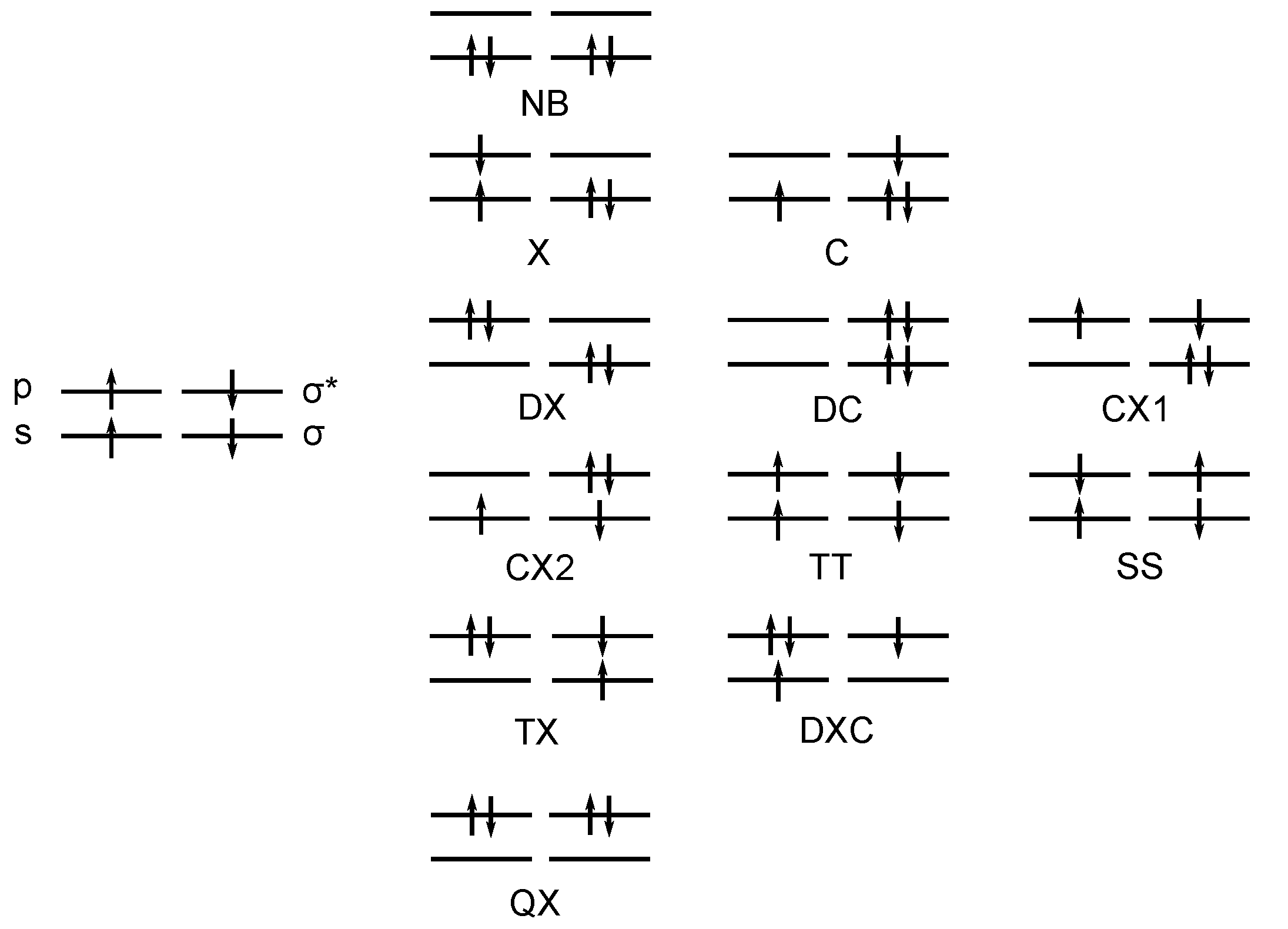
3.1. The Carbene Dimerization
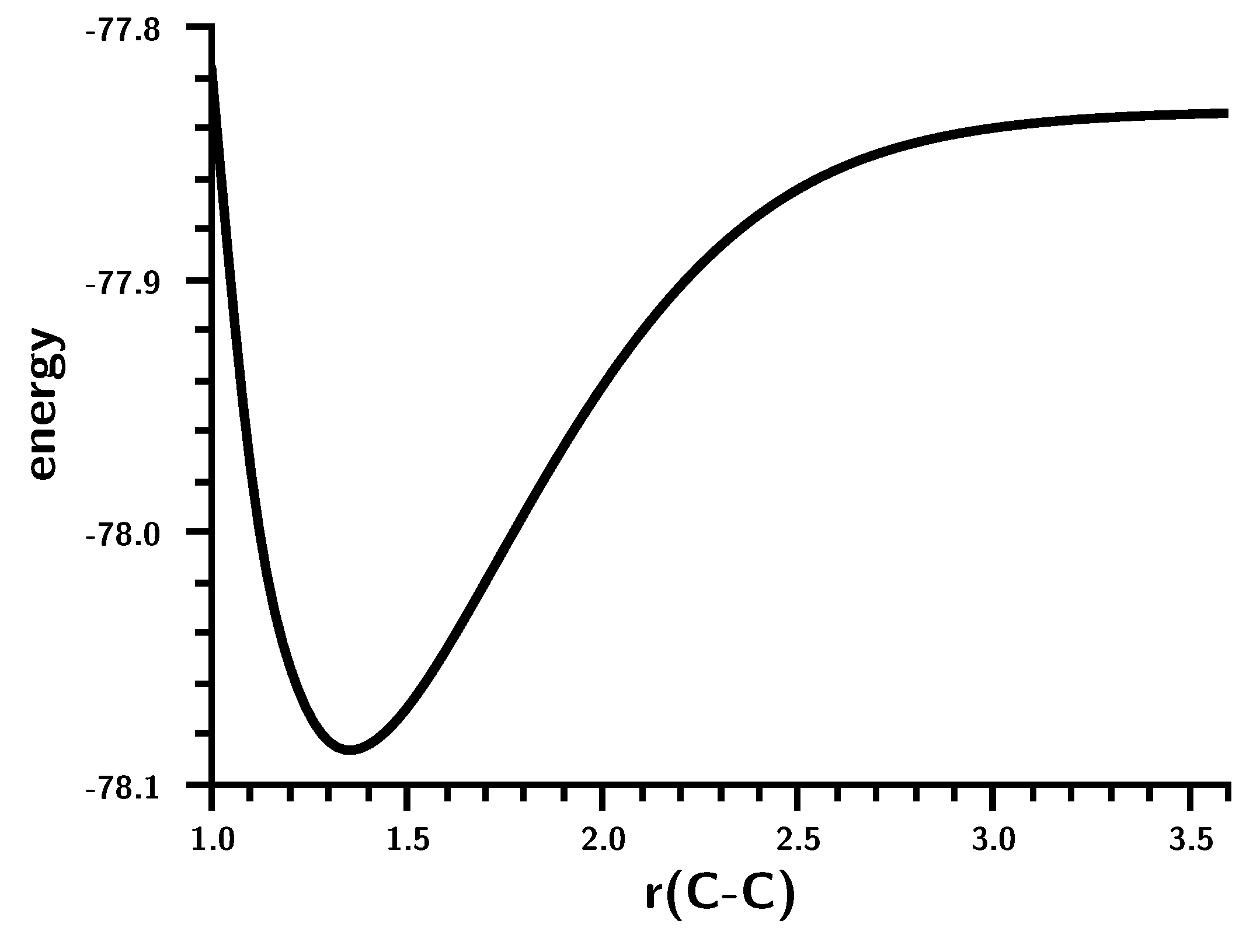
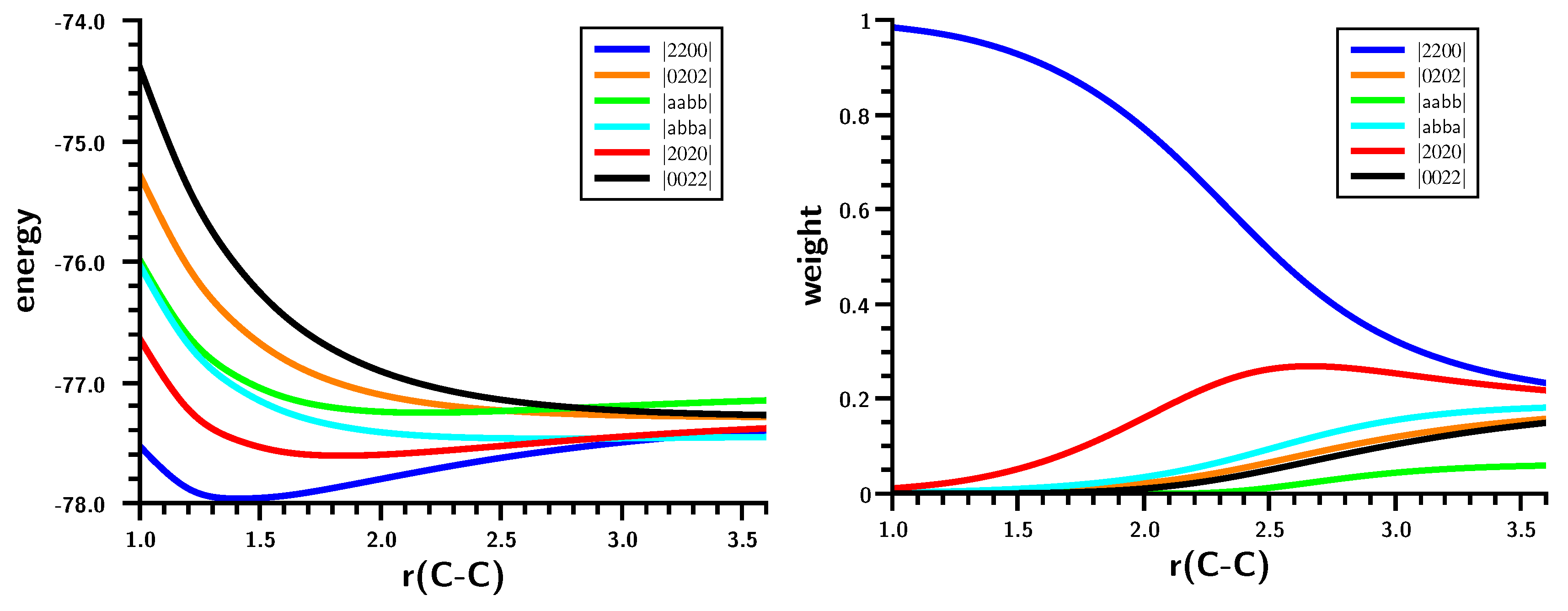
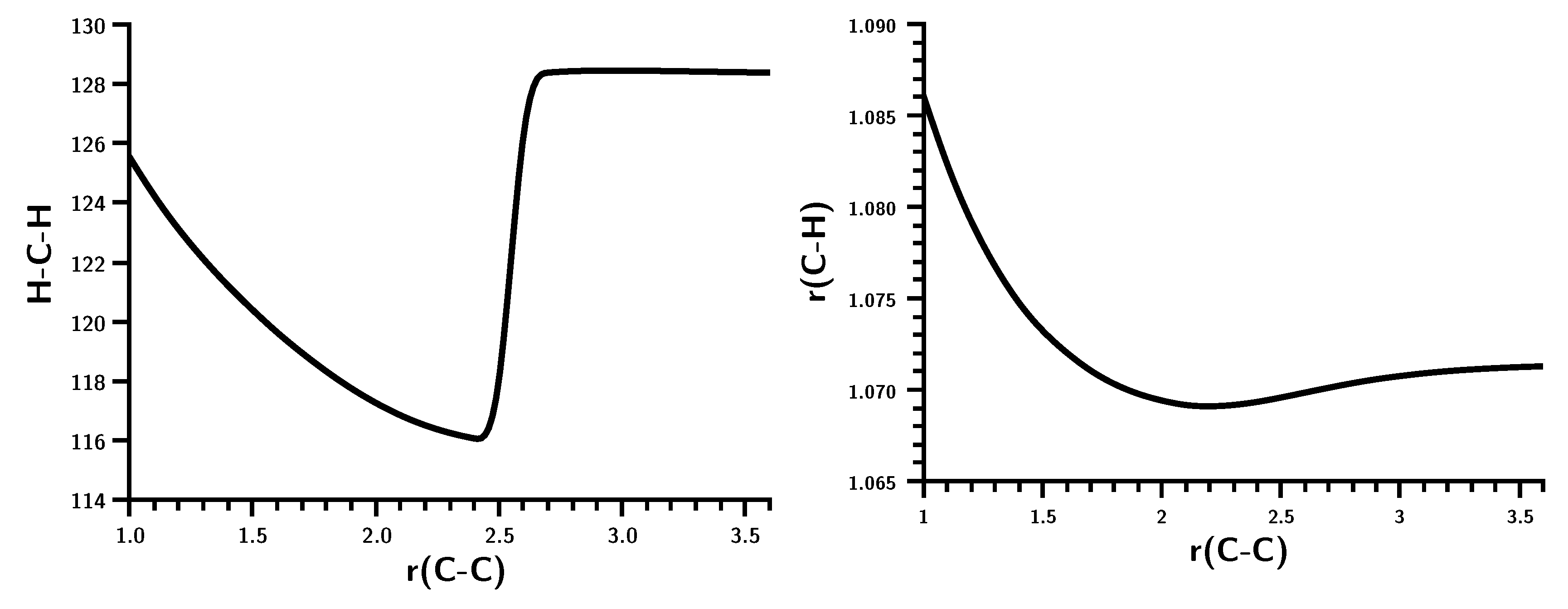
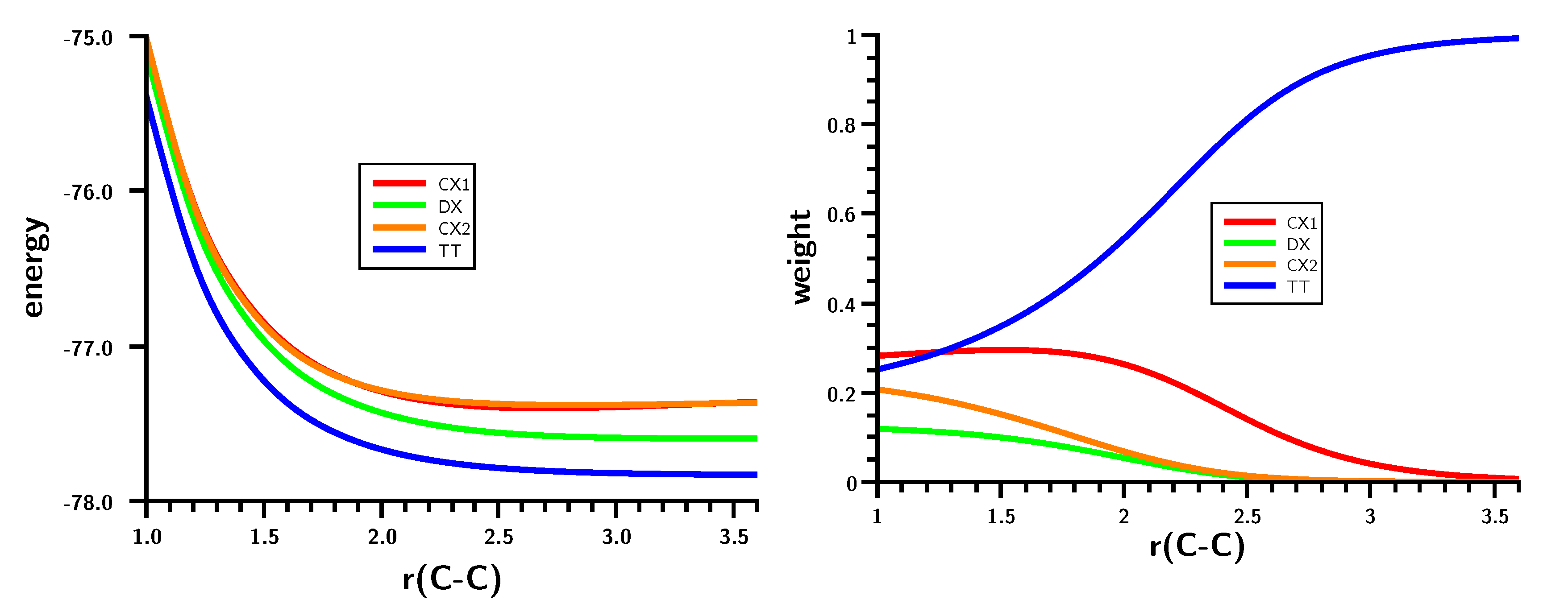
3.2. The Silylene Dimerization in D2h
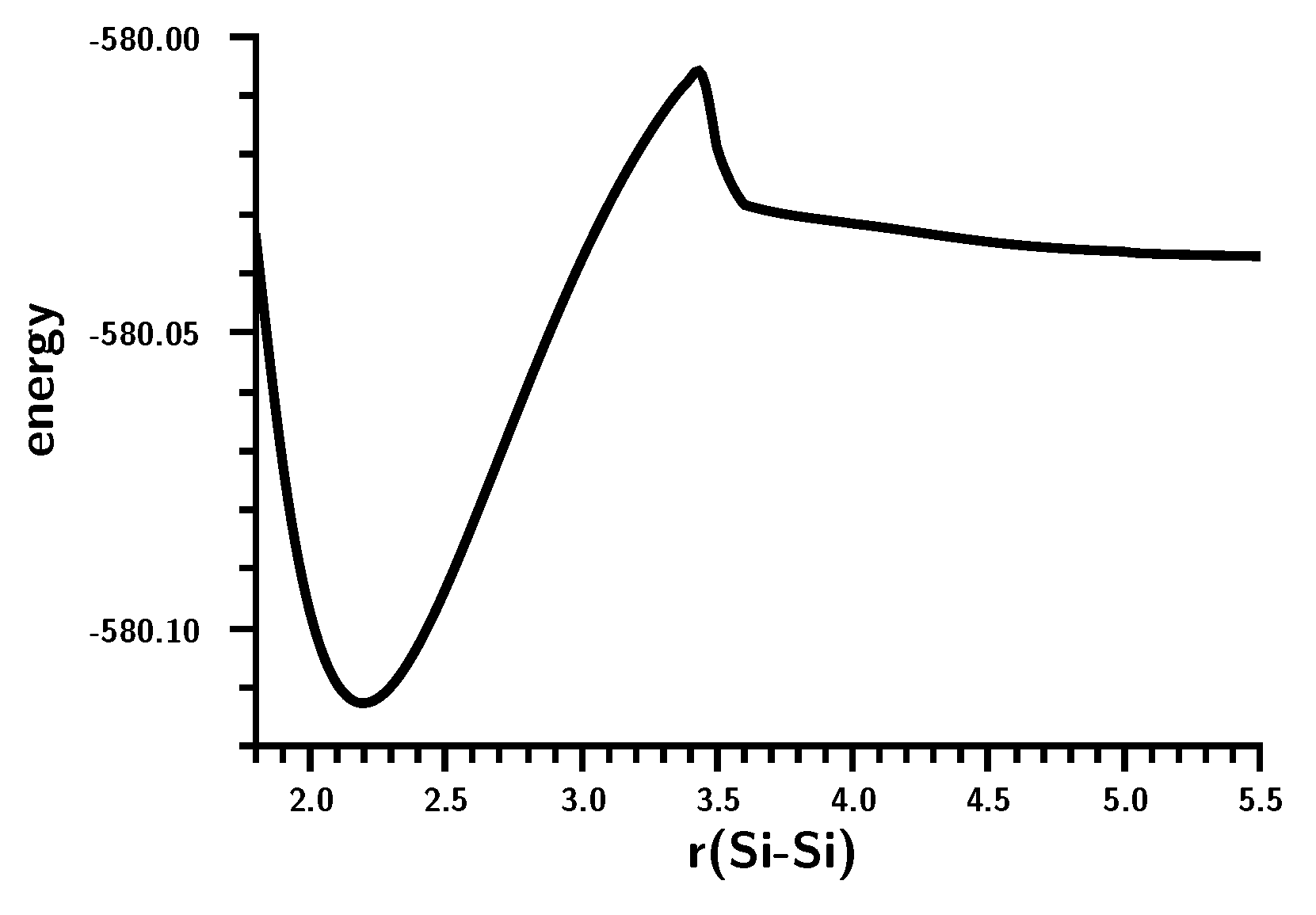
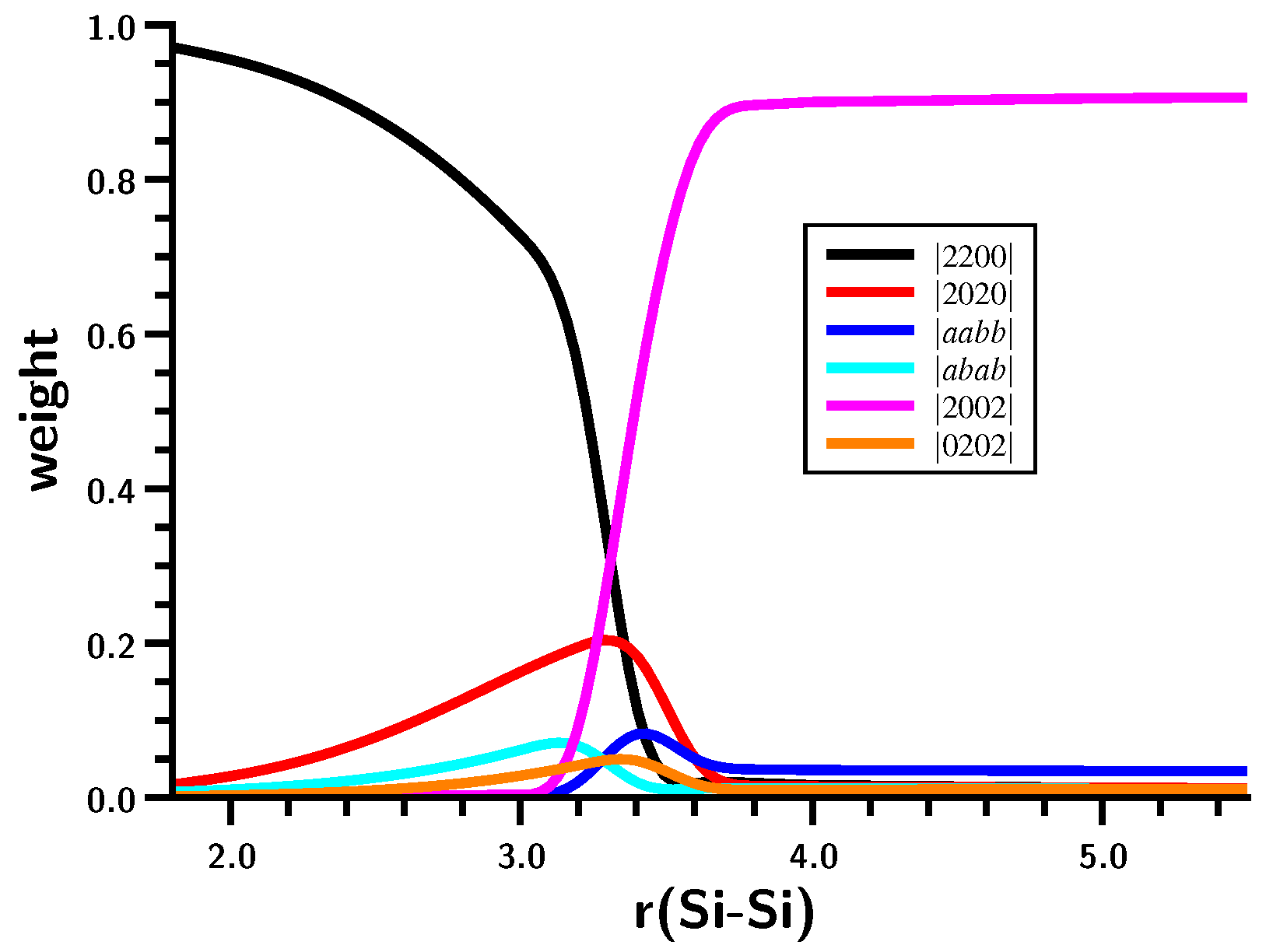
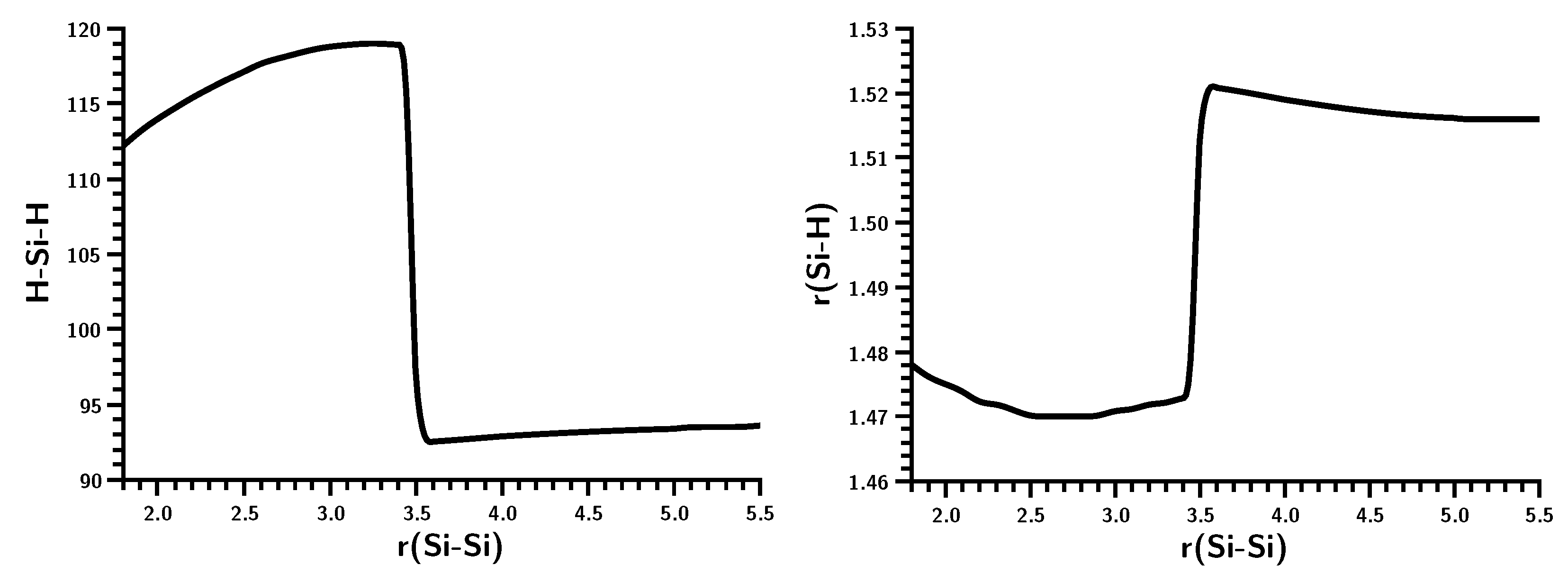
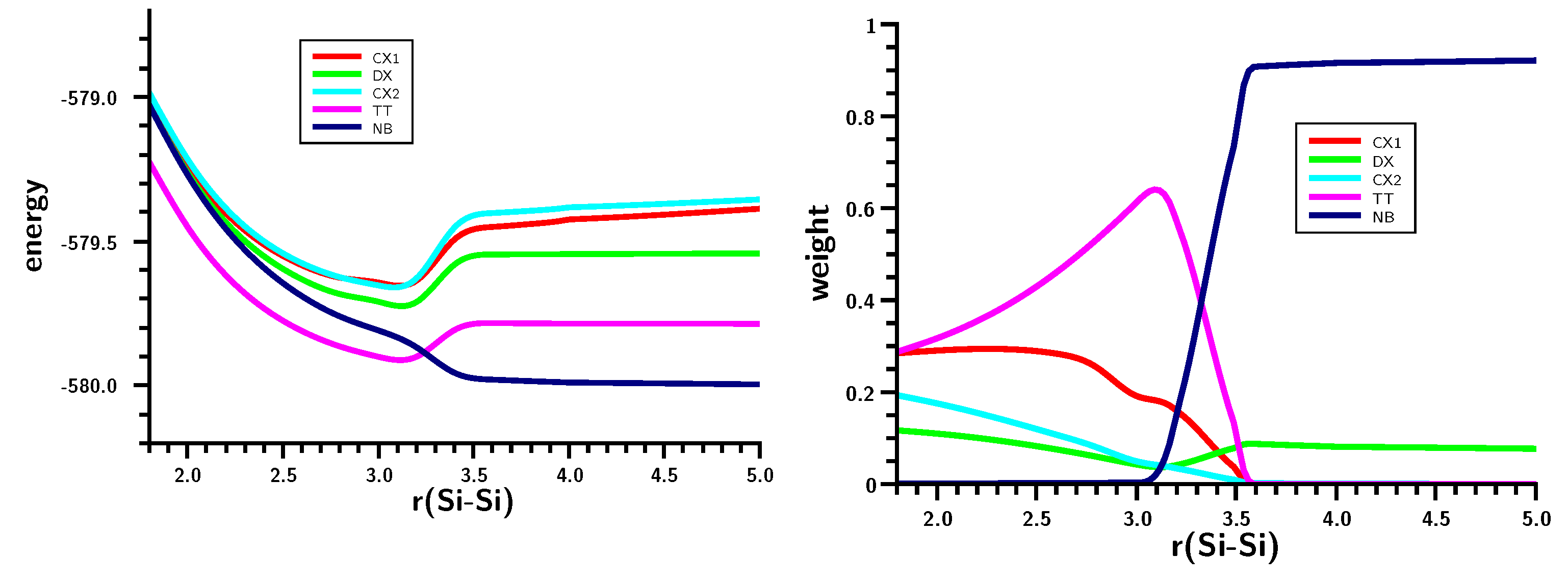
3.3. The Silylene Dimerization in C2h
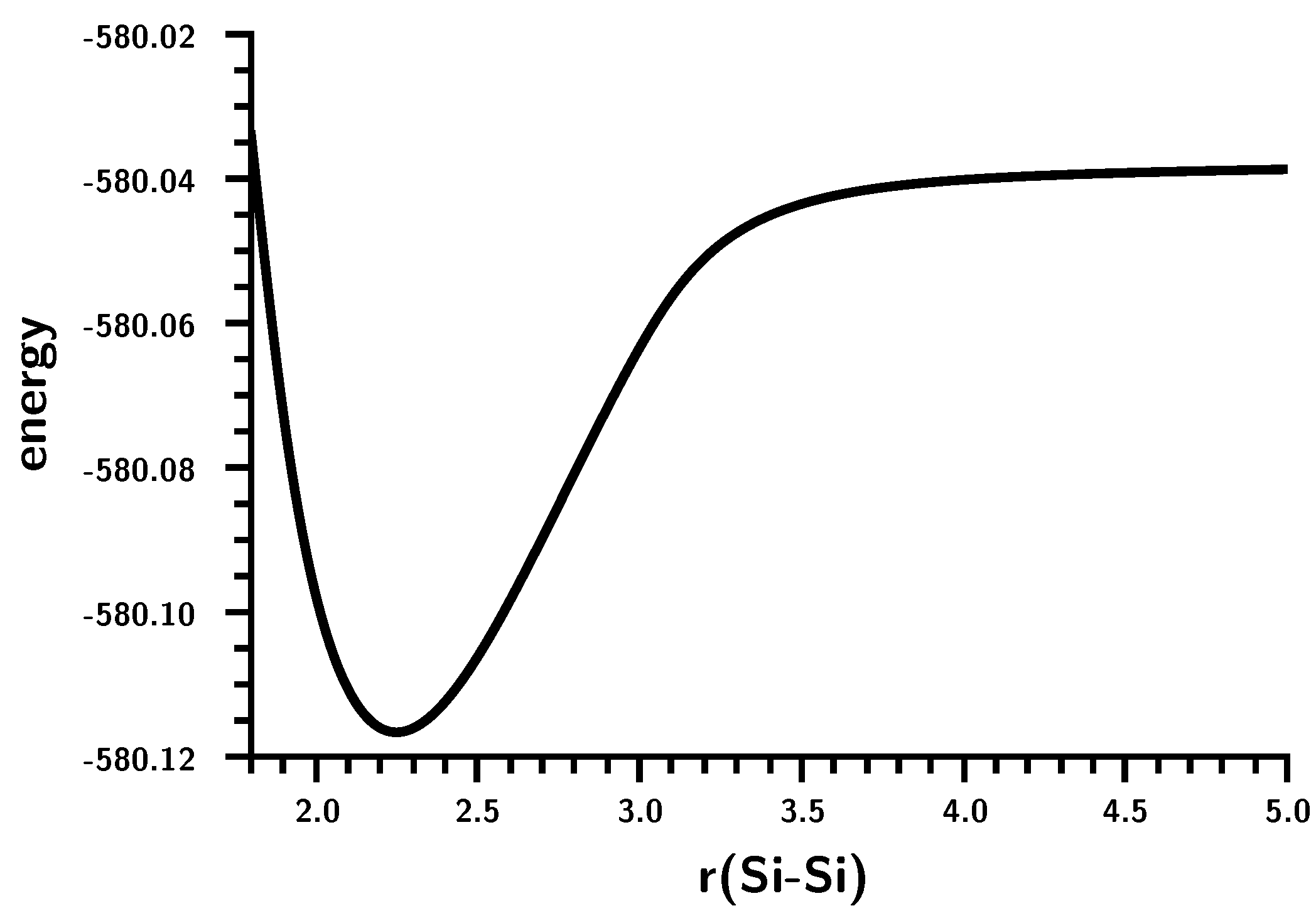
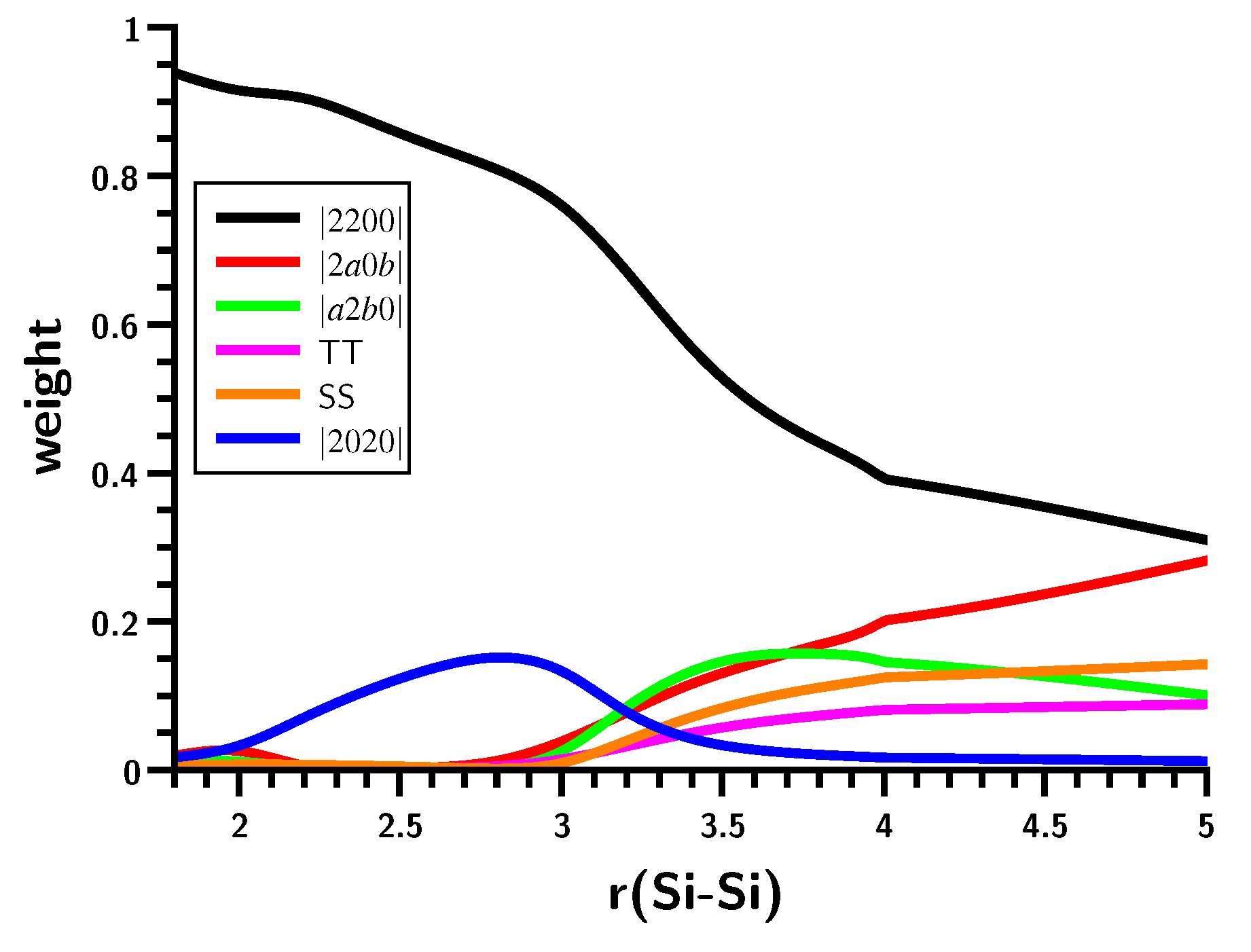

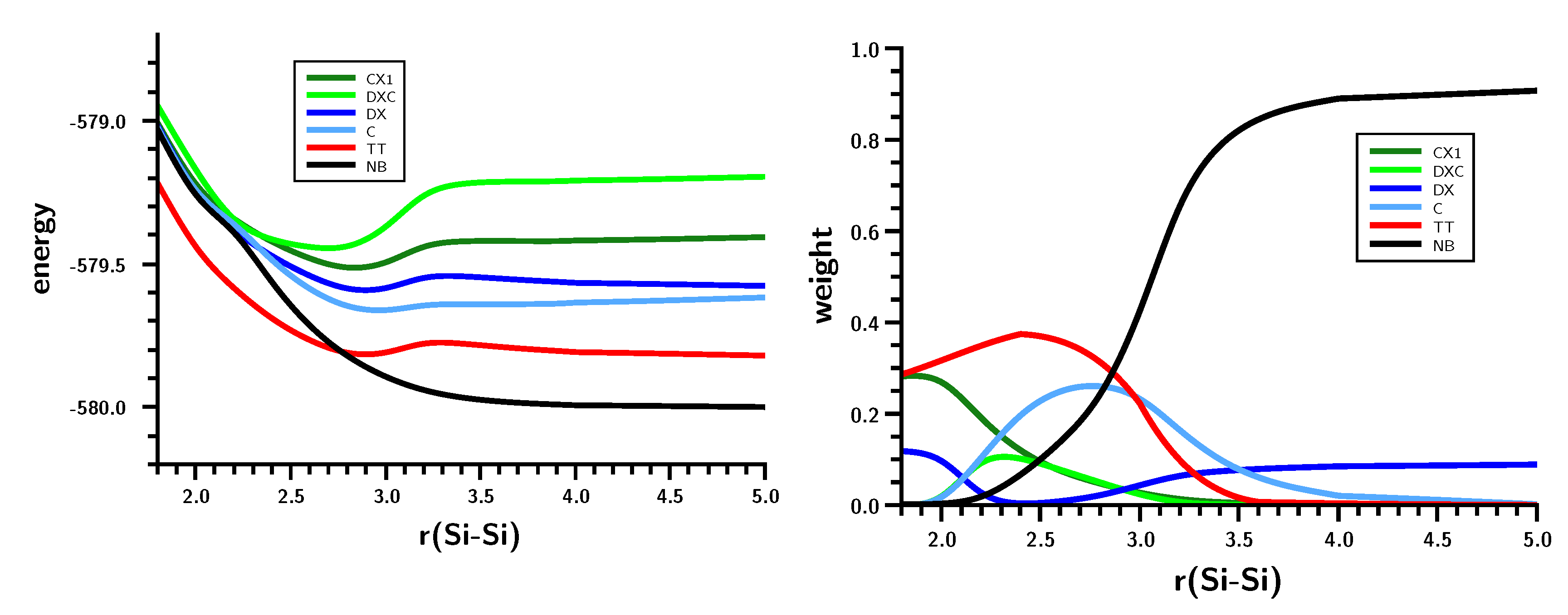
3.4. The Insertion of Carbene into H2
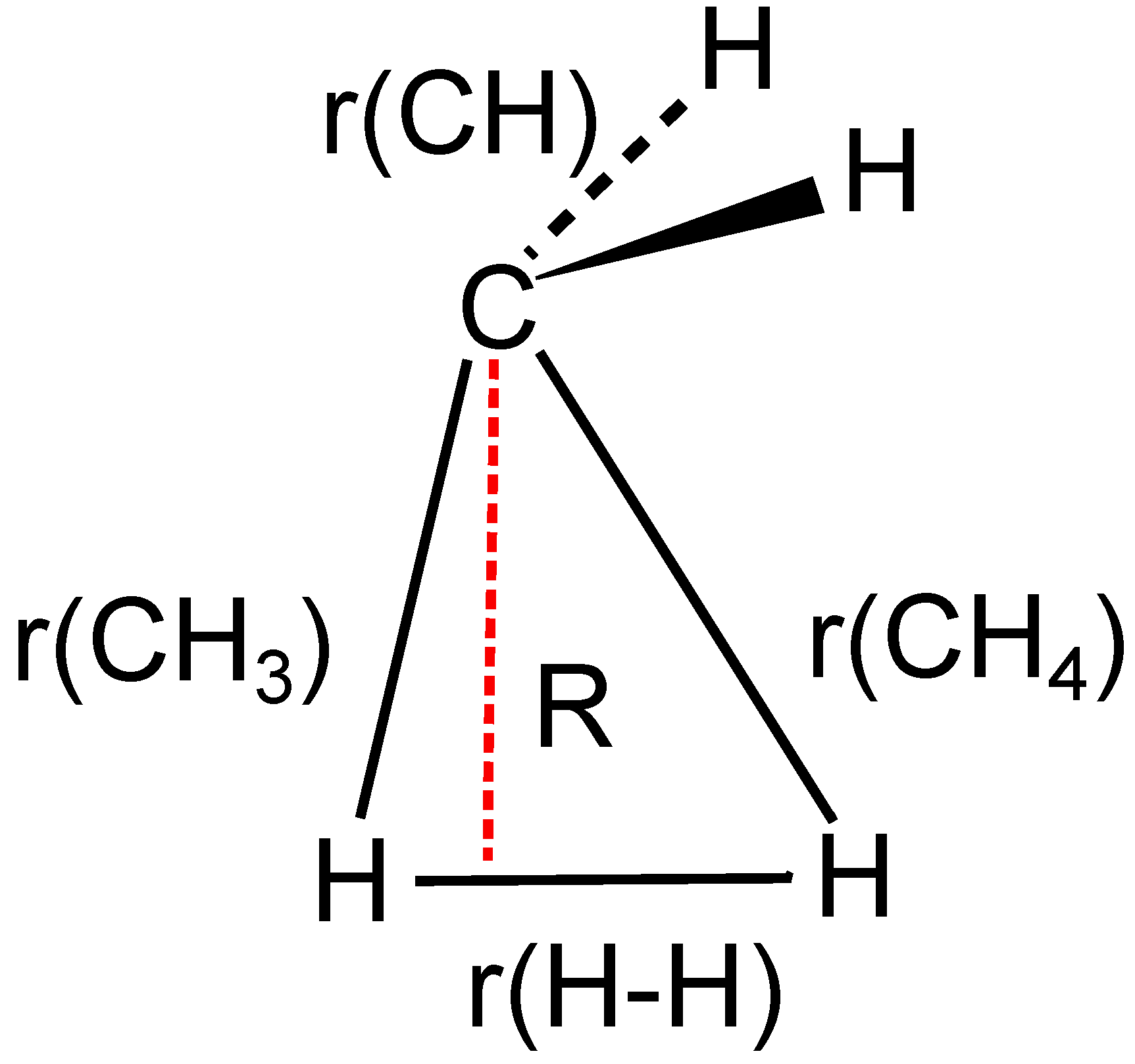
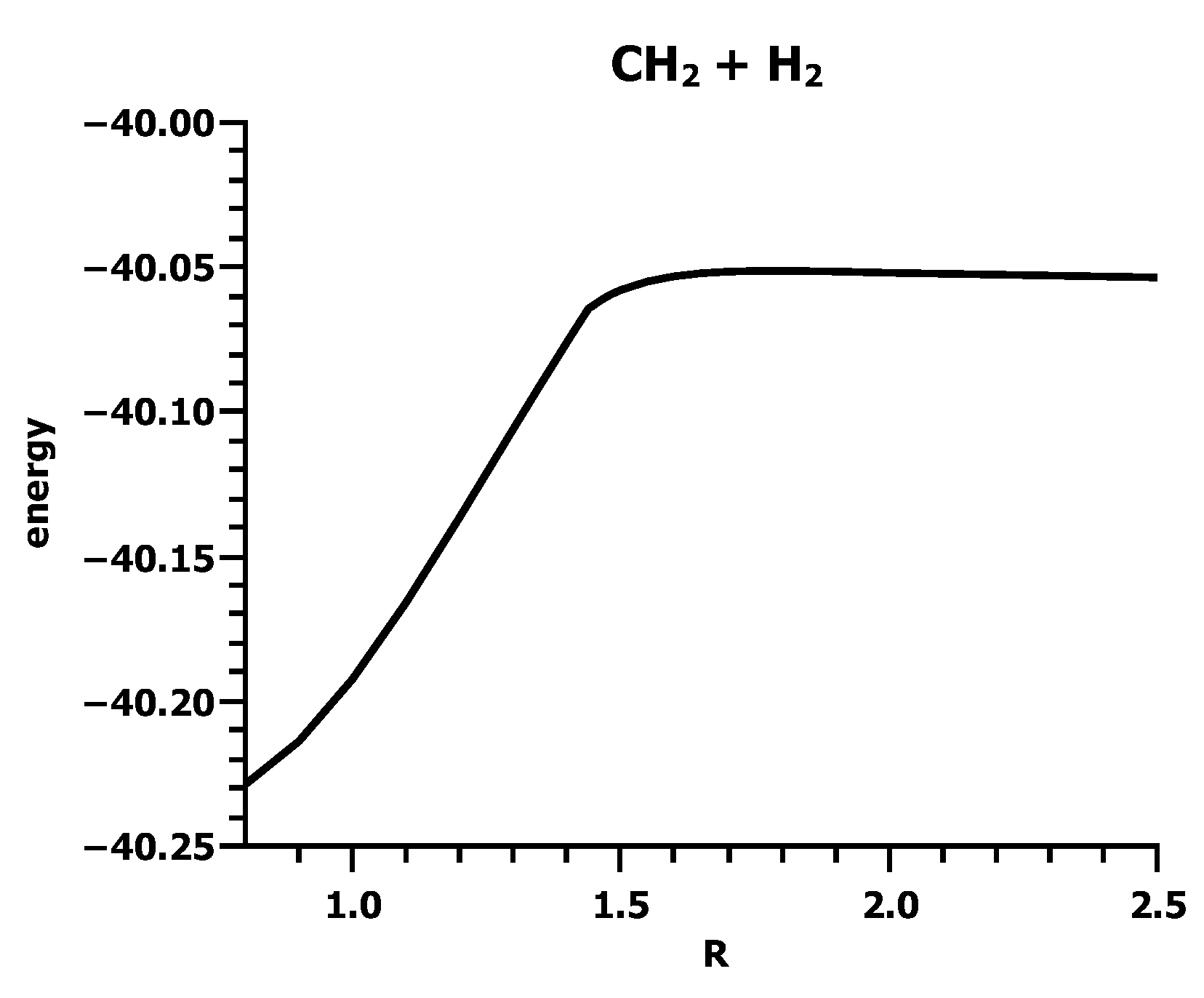
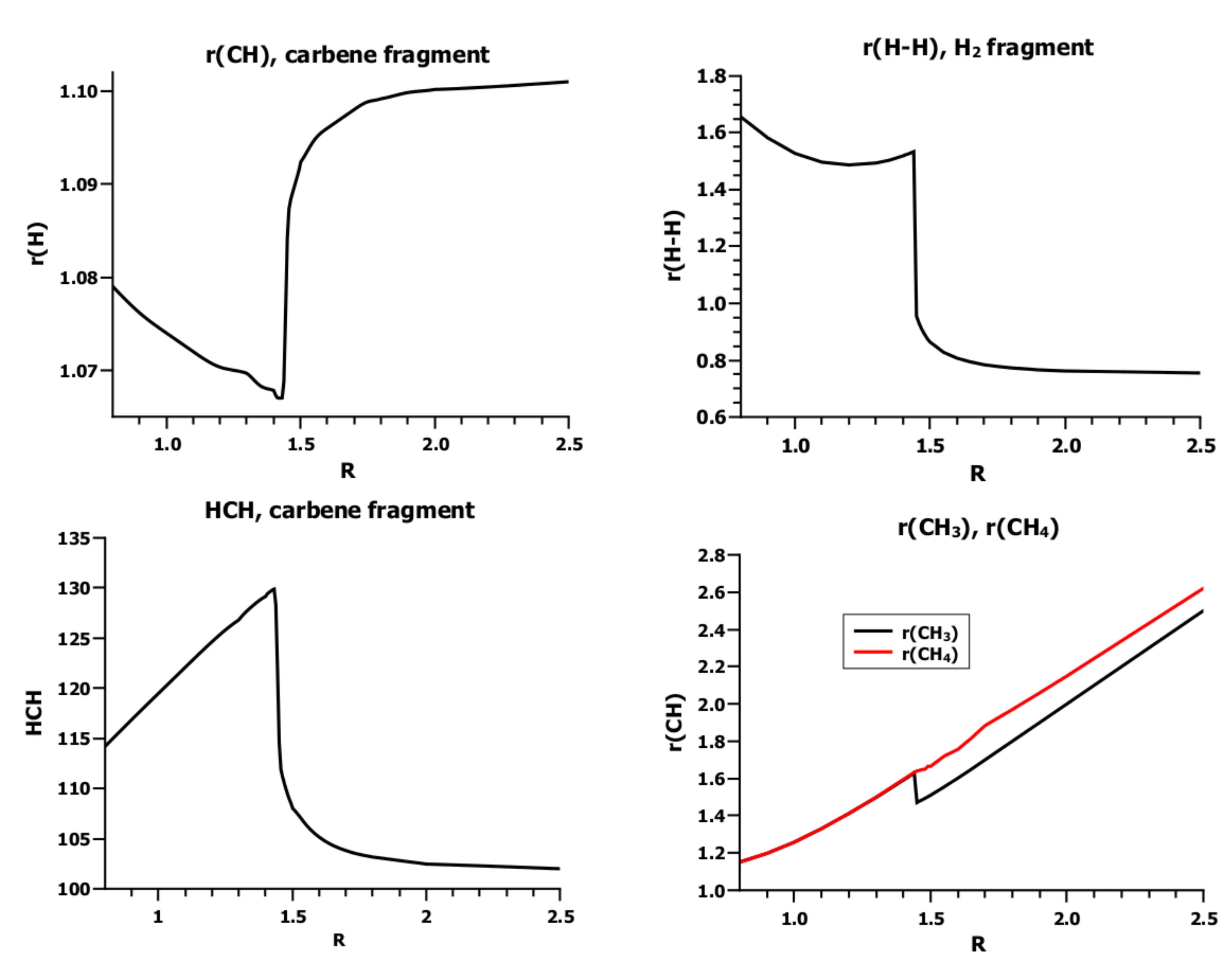
4. What We Can Learn from the OVB Analysis
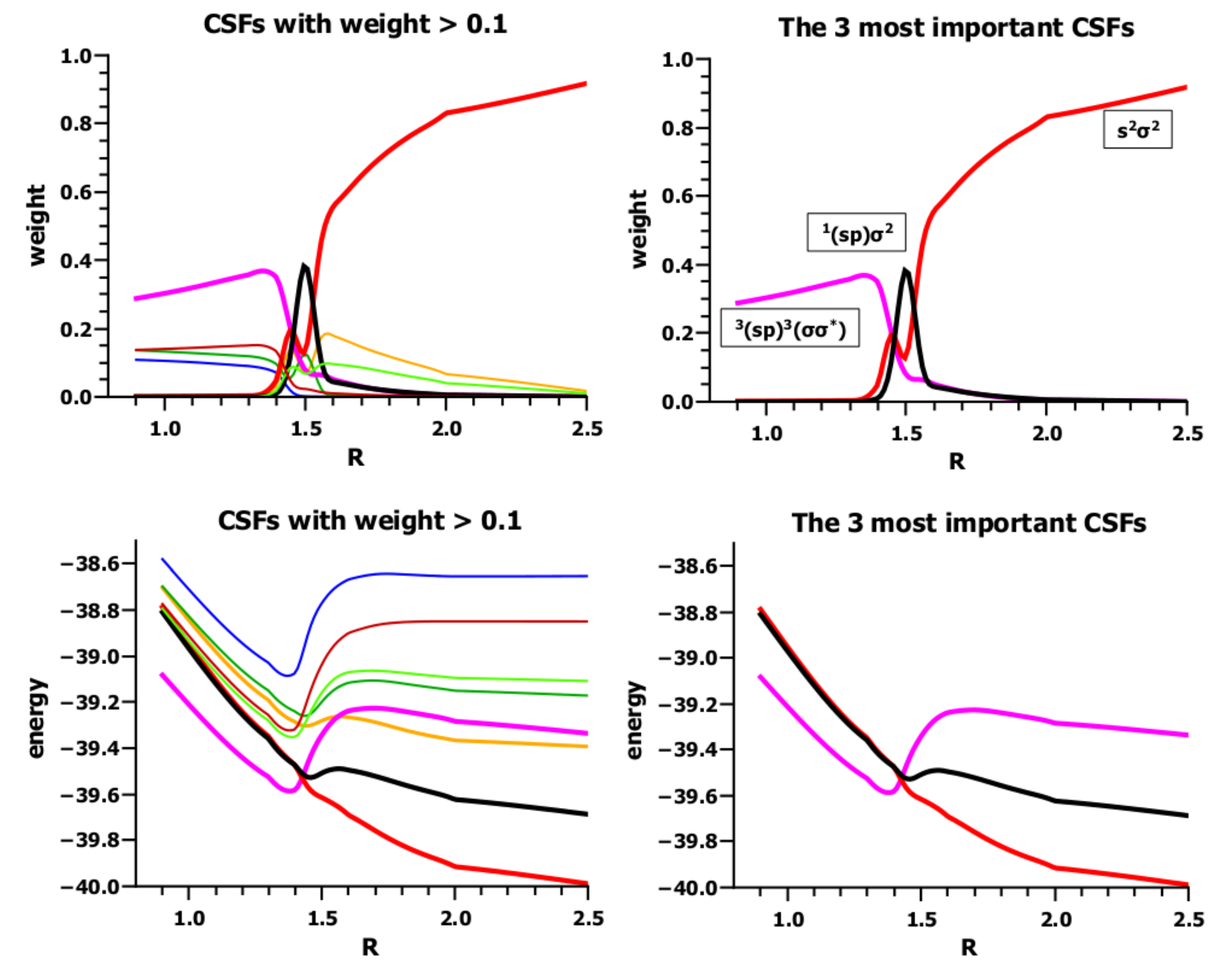
5. The Differences between Conventional VB and OVB
5.1. The Basis of Conventional VB
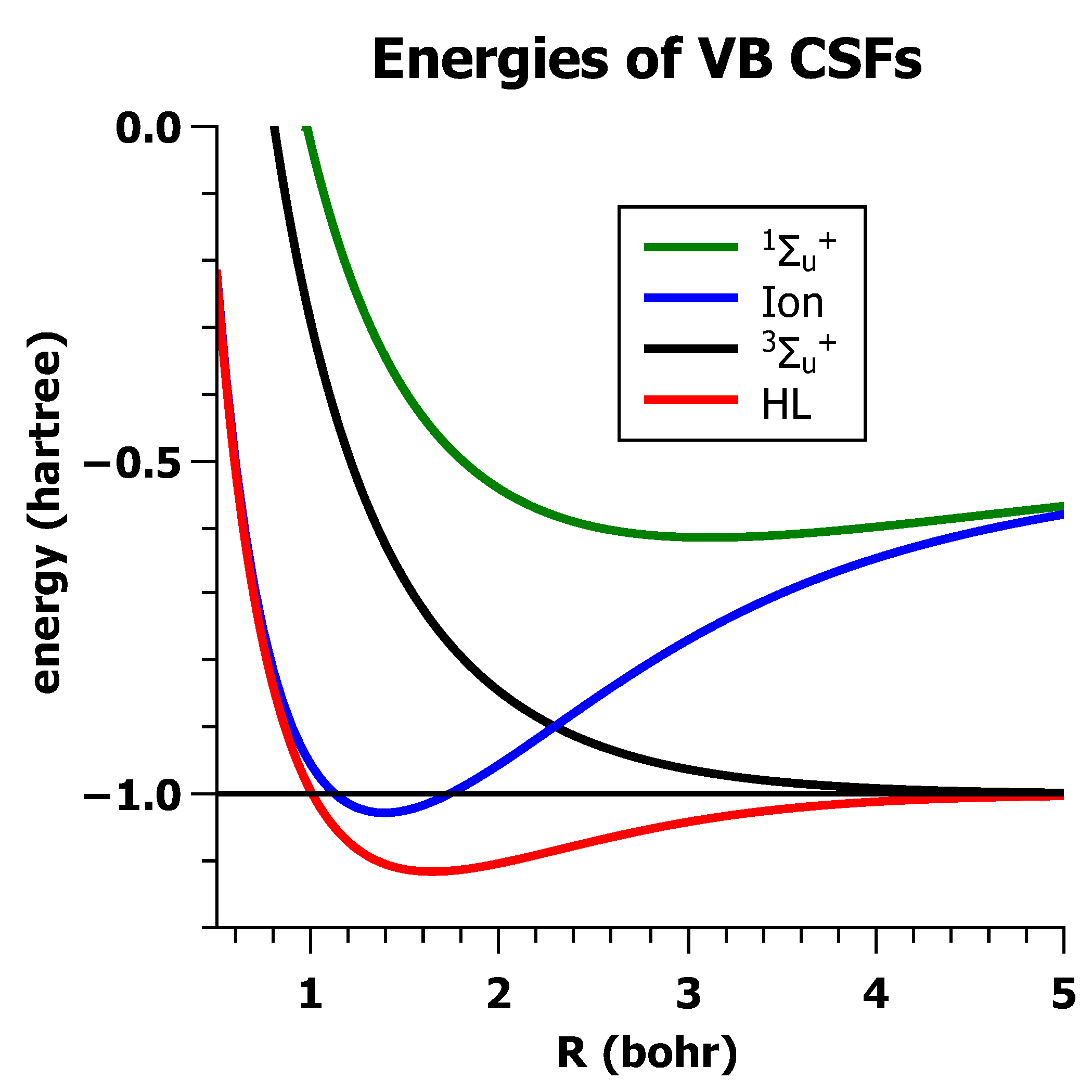
5.2. The Non-Orthogonality of VB-CSFs
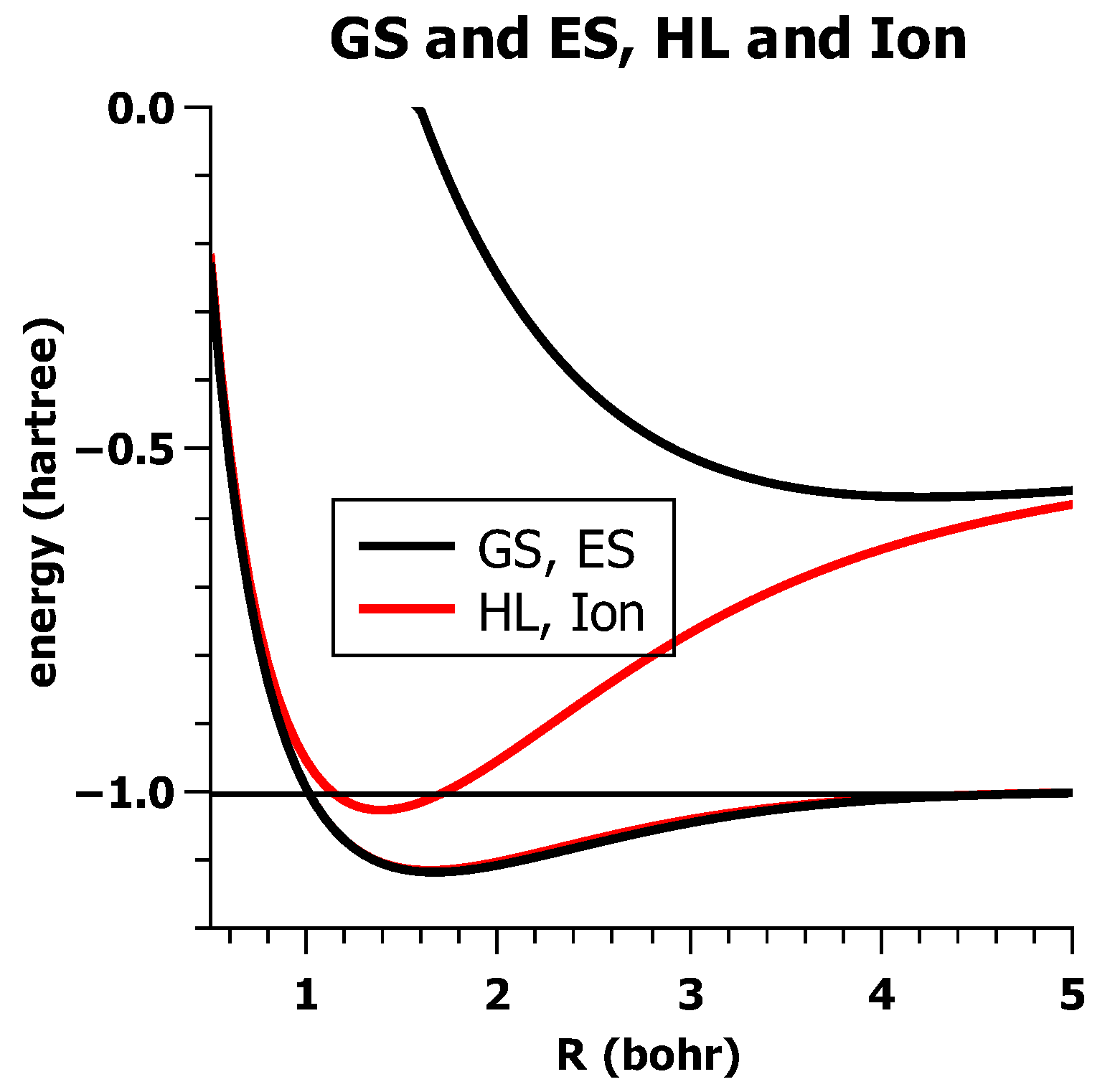
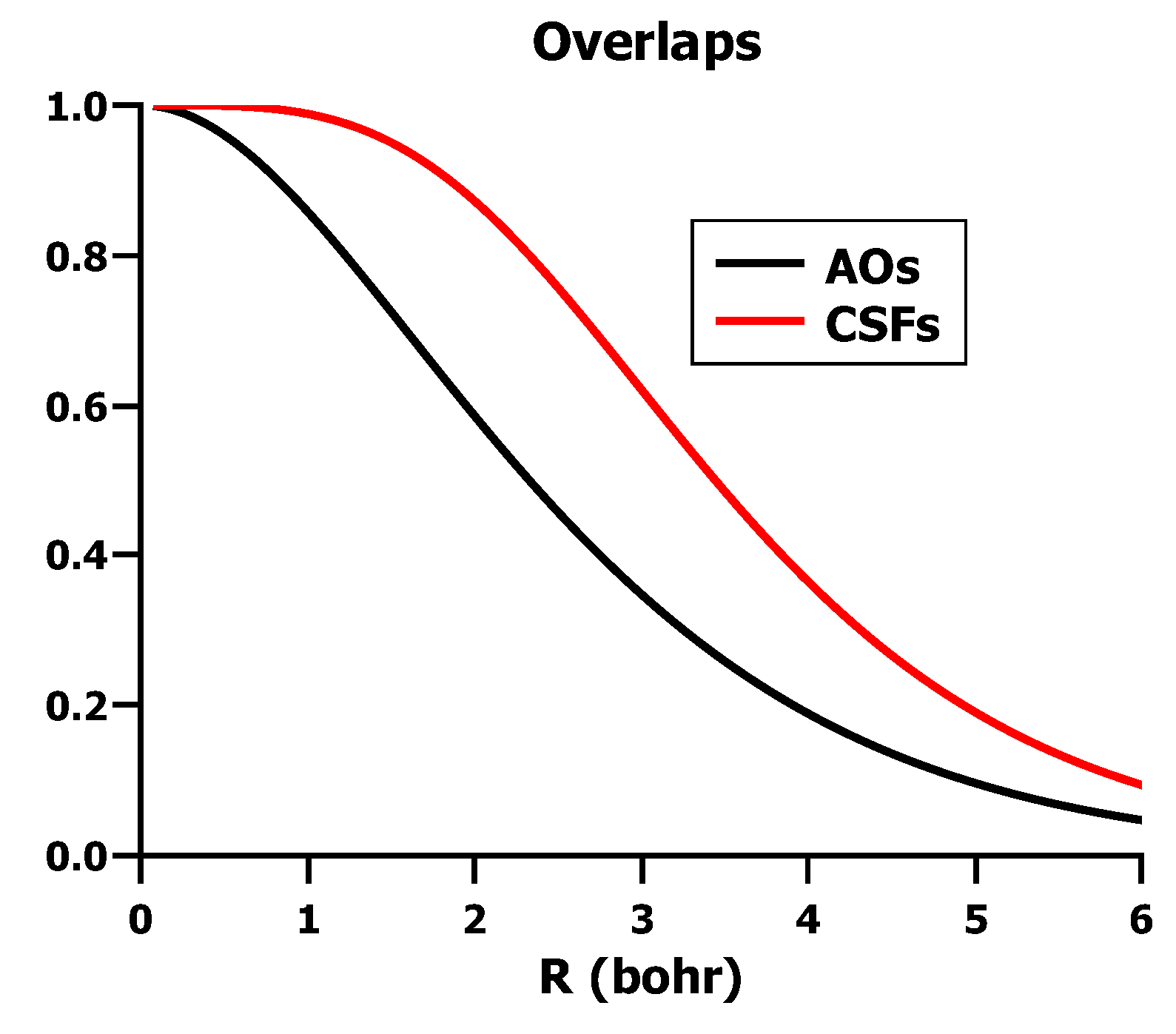
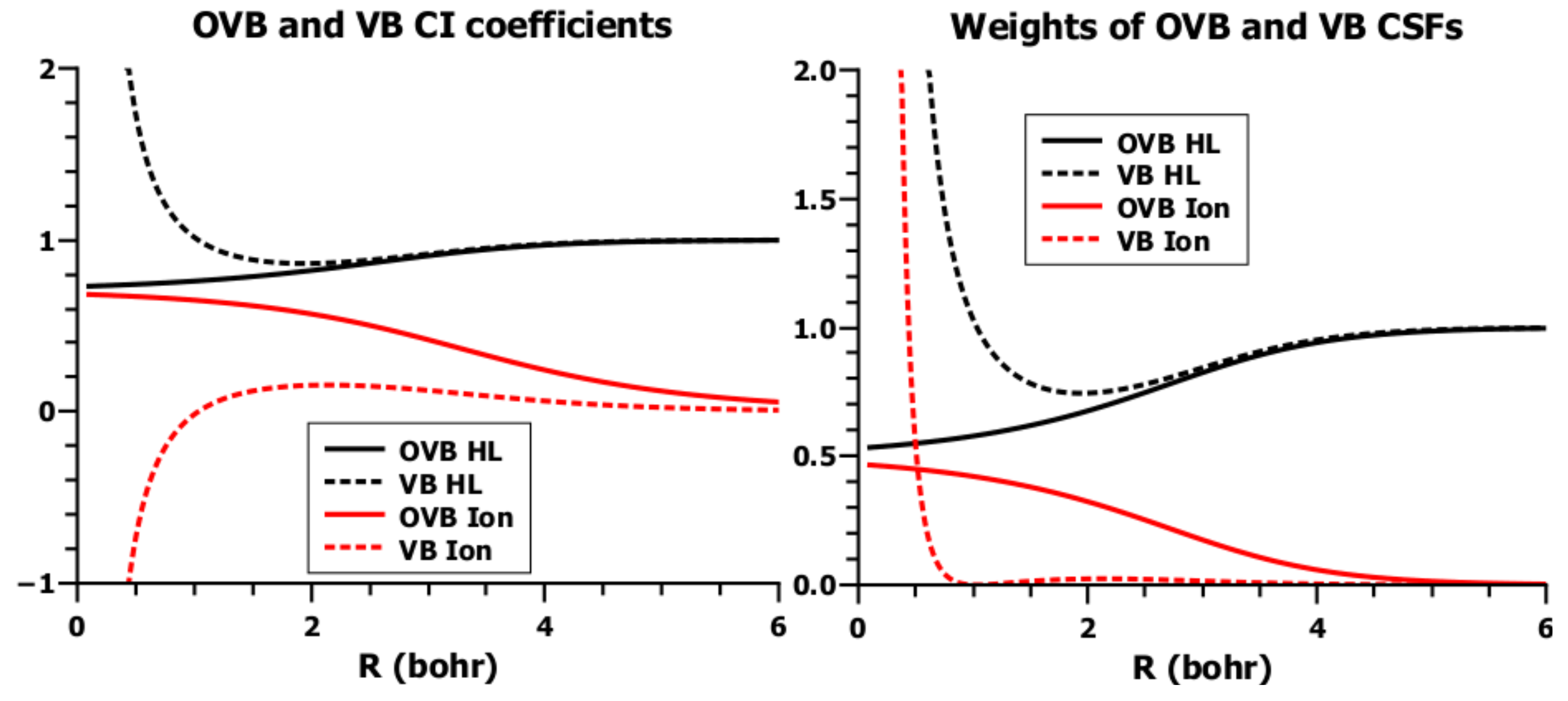
5.3. The Role of Interference in Conventional VB
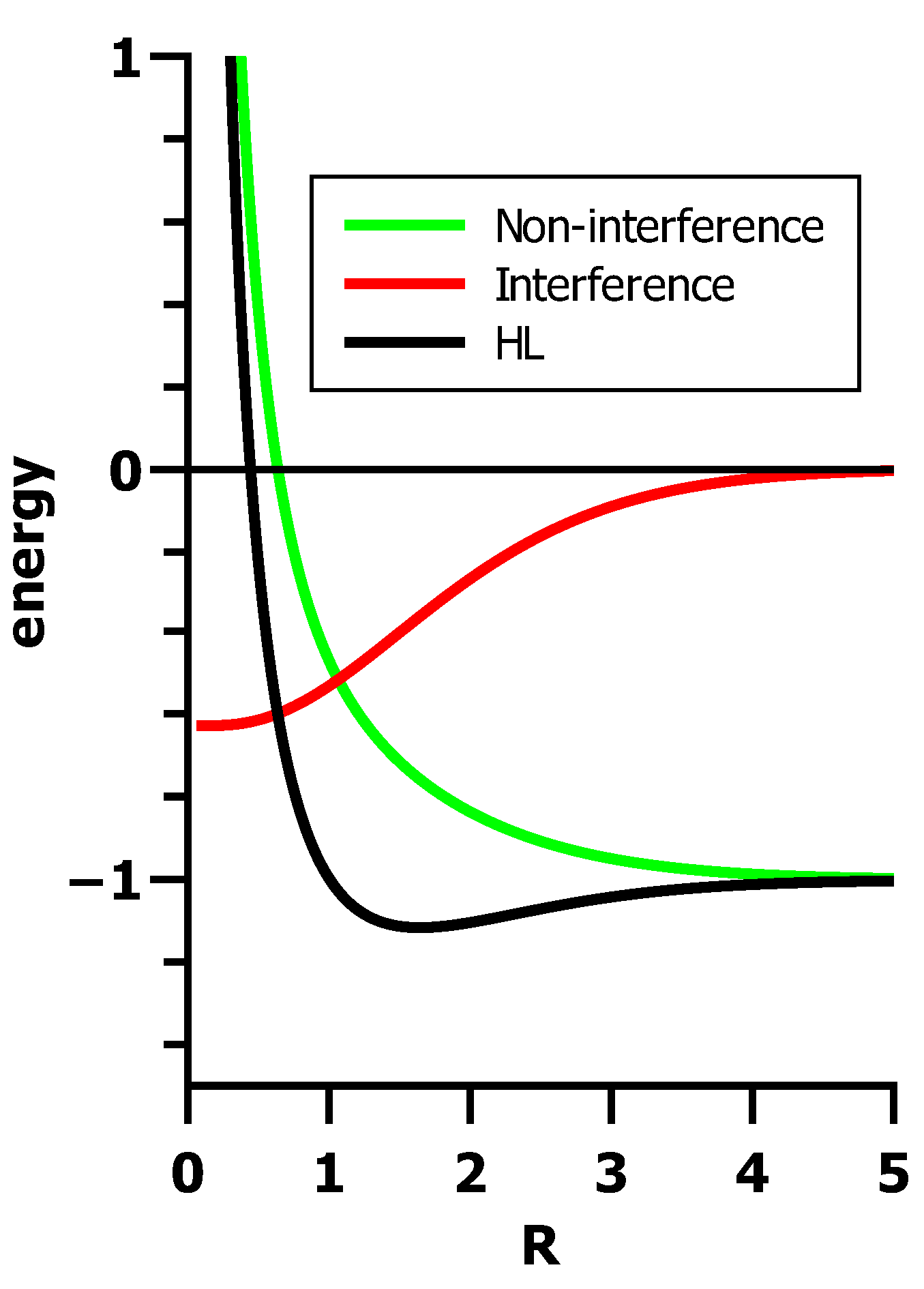
5.4. Orthogonal VB
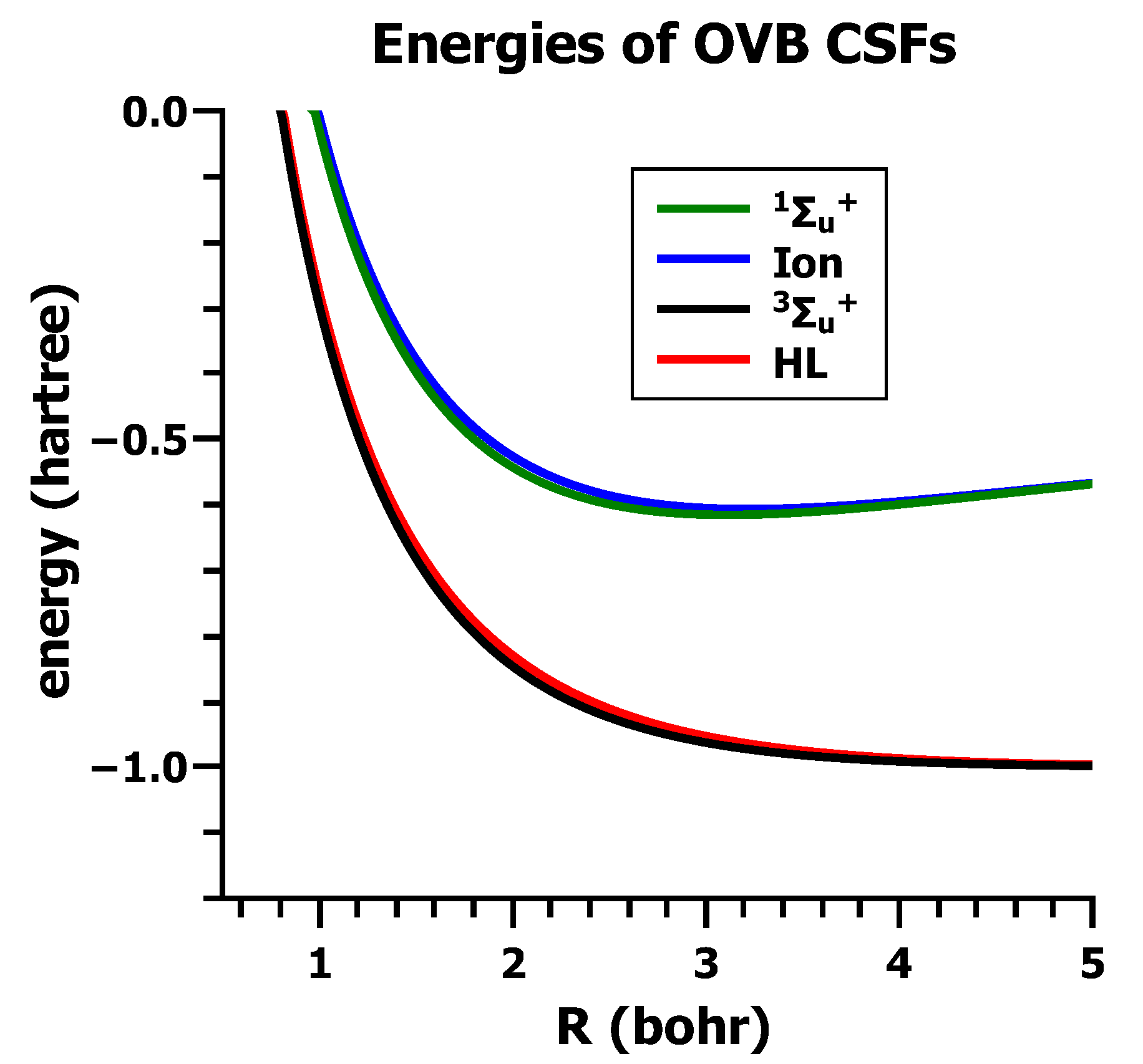
5.5. OVB and Chemical Bonding
- (1)
- Covalent bonding is the result of the lowering of kinetic energy through inter-atomic electron delocalization, called electron-sharing. Delocalization is caused by constructive interference during the superposition of hydrogen AOs. The electrostatic interactions due to charge accumulation in the internuclear region are not bonding, as is frequently claimed, but debonding.
- (2)
- Electron-sharing is accompanied by intra-atomic contraction and polarization. Contraction causes a decrease in the intra-atomic electrostatic energy and an increase in the intra-atomic kinetic energy in the deformed atoms in the molecule.
- (3)
- Intra-atomic contraction enhances the inter-atomic lowering of the kinetic energy and, thus, contributes to energy minimization.
- (4)
- The antagonistic changes of intra-atomic and inter-atomic energy contributions cause a variational competition between electrostatic and kinetic energy; the wave function that achieves the optimal total energy is obtained by variational optimization.
- (5)
- The atom-centered orbitals describing the deformed atoms are quasi-AOs; their shape depending on the distance between the interacting atoms. Near equilibrium distance, they are more contracted than the free AOs, causing the lowering of electrostatic energy; at larger distances, they may be even more expanded than in the free atom, because then the electron can better expand into spatial regions not available for the electron in the free atom when the AOs are superimposed.
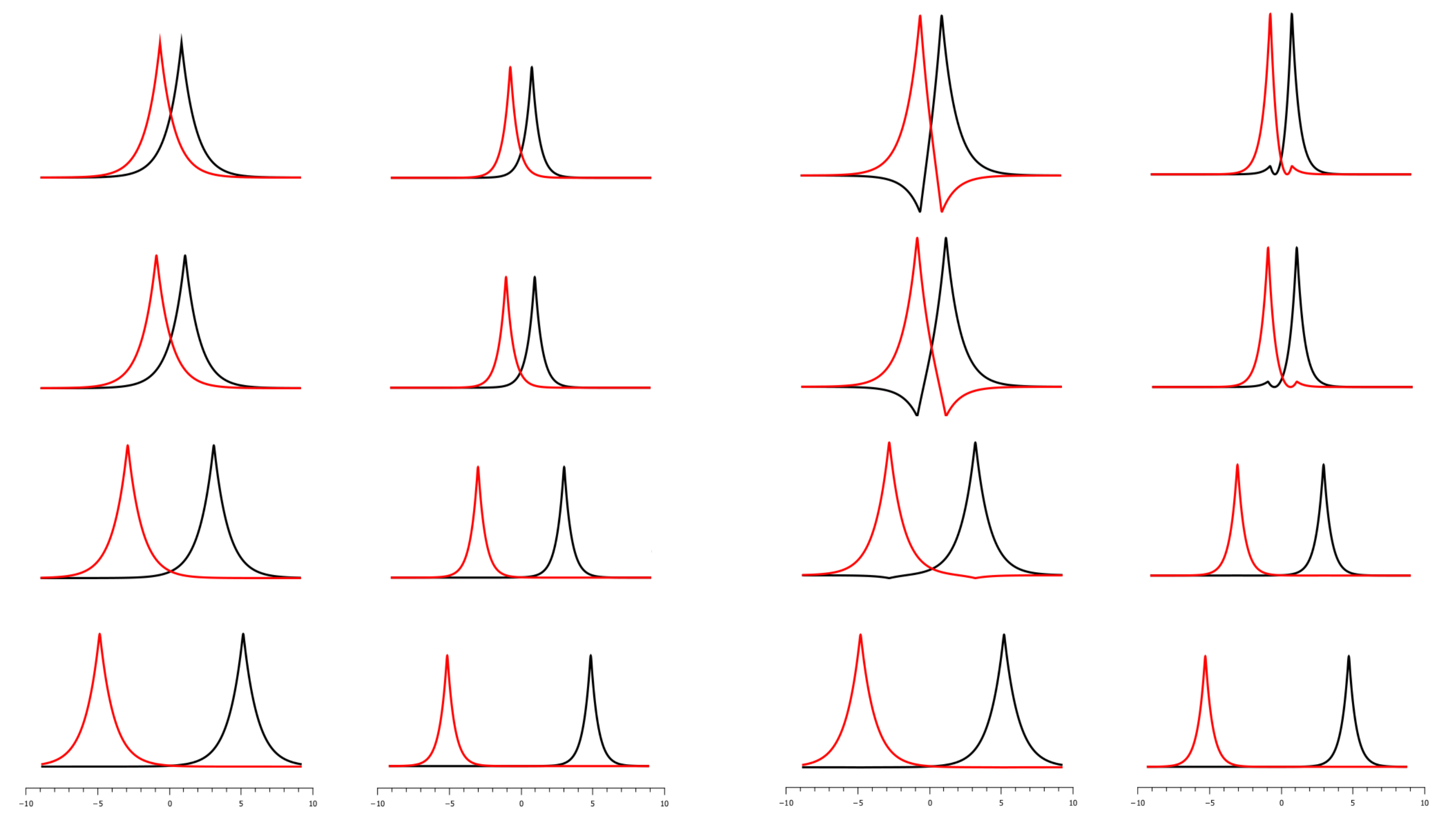
5.6. Diabaticity of OVB CSFs
6. Discussion
7. Computational Methods
8. Conclusions
Acknowledgments
Conflicts of Interest
References
- Cartwright, N. How the Laws of Physics Lie; Oxford University Press: New York, NY, USA, 1983. [Google Scholar]
- Hacking, I. Representing and Intervening; Cambridge University Press: Cambridge, UK, 1983. [Google Scholar]
- Giere, R.N. Science without Laws; The University of Chicago Press: Chicago, IL, USA, 1999. [Google Scholar]
- Giere, R.N. Explaining Science. A Cognitive Approach; The University of Chicago Press: Chicago, IL, USA, 1988. [Google Scholar]
- Gelfert, A. Manipulative success and the unreal. Int. Stud. Phil. Sci. 2003, 17, 245–263. [Google Scholar] [CrossRef]
- Frenking, G. Unicorns in the world of chemical bonding models. J. Comp. Chem. 2007, 28, 15–24. [Google Scholar] [CrossRef]
- Falkenburg, B. Particle Methaphysics; Springer: Berlin, Germany, 2010. [Google Scholar]
- Jeffrey, G.A. An Introduction to Hydrogen Bonding; Oxford University Press: New York, NY, USA, 1997. [Google Scholar]
- Stone, A. The Theory of Intermolecular Forces, 2nd Ed. ed; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Hoja, J.; Sax, A.F.; Szalewicz, K. Is electrostatics sufficient to describe hydrogen-bonding interactions? Chem. Eur. J. 2014, 20, 2292–2300. [Google Scholar] [CrossRef] [PubMed]
- Levine, R.D. Molecular Reaction Dynamics; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Schmidt, M.W.; Gordon, M.S. The construction and interpretation of MCSCF wavefunctions. Ann. Rev. Phys. Chem. 1998, 49, 233–266. [Google Scholar] [CrossRef]
- Roos, B.O. The complete active space self-consistent field method and its applications in electronic structure calculations. Adv. Chem. Phys. 1987, 69, 399–445. [Google Scholar]
- Roos, B.O. The multiconfigurational (MC) self-consistent field (SCF) theory. In Lecture Notes in Quantum Chemistry; Roos, B., Ed.; Springer: Berlin, Germany, 1992; pp. 177–254. [Google Scholar]
- Ruedenberg, K.; Sundberg, K.R. MCSCF studies of chemical reactions: Natural reaction orbitals. In Quantum Science; Calais, J.L., Goscinski, O., Linderberg, J., Öhrn, Y., Eds.; Plenum: New York, NY, USA, 1976; pp. 505–515. [Google Scholar]
- Cheung, L.M.; Sundberg, K.R.; Ruedenberg, K. Dimerization of carbene to ethylene. J. Am. Chem. Soc. 1978, 100, 8024–8025. [Google Scholar] [CrossRef]
- Cheung, L.M.; Sundberg, K.R.; Ruedenberg, K. Electronic rearrangements during chemical reactions II. Planar dissociation of ethylene. Int. J. Quantum Chem. 1979, 16, 1003–1039. [Google Scholar]
- Ruedenberg, K.; Schmidt, Michael, W.; Gilbert, Mary, M.; Elbert, S.T. Are atoms intrinsic to molecular electronic wave functions? I . The FORS model. Chem. Phys. 1982, 71, 41–49. [Google Scholar] [CrossRef]
- Ruedenberg, K.; Schmidt, M.W.; Gilbert, M.M.; Elbert, S.T. Are atoms intrinsic to molecular electronic wave functions? III . Analysis of FORS configurations. Chem. Phys. 1982, 71, 65–78. [Google Scholar] [CrossRef]
- Ruedenberg, K.; Schmidt, M.W.; Gilbert, M.M. Are atoms intrinsic to molecular electronic wave functions? II . Analysis of FORS orbitals. Chem. Phys. 1982, 51–64. [Google Scholar] [CrossRef]
- Feller, D.F.; Schmidt, M.W.; Ruedenberg, K. Concerted dihydrogen exchange between ethane and ethylene. SCF and FORS calculations of the barrier. J. Am. Chem. Soc. 1982, 104, 960–967. [Google Scholar] [CrossRef]
- Sax, A.F. Localization of molecular orbitals on fragments. J. Comp. Chem. 2012, 33, 495–1510. [Google Scholar] [CrossRef]
- Bunker, P.R.; Jensen, P.; Kraemer, W.P.; Beardsworth, R. The potential surface of X 3B1 methylene (CH2) and the singlet-triplet splitting. J. Chem. Phys. 1986, 85, 3724. [Google Scholar] [CrossRef]
- Dubois, I. The absorption spectrum of the free SiH−2 radical. Can. J. Phys. 1968, 46, 2485. [Google Scholar] [CrossRef]
- Balasubramanian, K.; McLean, A.D. The singlet-triple energy separation in silylene. J. Chem. Phys. 1986, 85, 5117. [Google Scholar] [CrossRef]
- Petek, H.; Nesbitt, D.J.; Darwin, D.C.; Ogilby, P.R.; Moore, C.B.; Ramsay, D.A. Analysis of CH2 ã1A1 (1,0,0) and (0,0,1) Coriolis-coupled states, ã1A1 − 3B1 spin-orbit coupling, and the equilibrium structure of CH2ã1A1 state. J. Chem. Phys. 1989, 91, 6566. [Google Scholar] [CrossRef]
- Shaik, S.S.; Hiberty, P.C. A Chemist’s Guide to Valence Bond Theory; Wiley-Interscience: Hoboken, NJ, USA, 2008; p. 316. [Google Scholar]
- Chirgwin, B.H.; Coulson, C.A. The electronic structure of conjugated systems. VI. Proc. R. Soc. Lond. Ser. A 1950, 201, 196. [Google Scholar] [CrossRef]
- Schmalz, T.G. A valence bond view of fullerenes. In Valence Bond Theory; Cooper, D.L., Ed.; Elsevier: New York, NY, USA, 2002; p. 535. [Google Scholar]
- Coulson, C.A.; Fisher, I. Notes on the molecular orbital treatment of the hydrogen molecule. Phil. Mag. 1949, 40, 386. [Google Scholar] [CrossRef]
- Goddard, W.A. Improved quantum theory of many-electron systems. II. The basic method. Phys. Rev. 1967, 157, 81. [Google Scholar] [CrossRef]
- Wannier, G. The structure of electronic excitation levels in insulating crystals. Phys. Rev. 1937, 52, 191. [Google Scholar] [CrossRef]
- Löwdin, P.O. On the non-orthogonality problem connected with the use of atomic wave functions in the theory of molecules and crystals. J. Chem. Phys. 1950, 18, 365. [Google Scholar]
- Pople, J.A. Electron interaction in unsaturated hydrocarbons. Trans. Faraday Soc. 1953, 49, 1375. [Google Scholar] [CrossRef]
- Pariser, R.; Parr, R.G. A semi-empirical theory of the electronic spectra and electronic structure of complex unsaturated molecules. I. J. Chem. Phys. 1953, 21, 466. [Google Scholar] [CrossRef]
- Pariser, R.; Parr, R.G. A semi-empirical theory of the electronic spectra and electronic structure of complex unsaturated molecules. II . J. Chem. Phys. 1953, 21, 767. [Google Scholar] [CrossRef]
- Fischer-Hjalmars, I. Zero differential overlap in π-electron theories . Adv. Quantum Chem. 1965, 2, 25. [Google Scholar]
- Fischer-Hjalmars, I. Deduction of the zero differential overlap approximation from an orthogonal atomic orbital basis . J. Chem. Phys. 1965, 42, 1962. [Google Scholar] [CrossRef]
- Fischer-Hjalmars, I. Orbital basis of zero differential overlap. In Modern Quantum Chemistry; Volume 1, Sinanoglu, O., Ed.; Academic Press: New York, NY, USA, 1965; pp. 185–193. [Google Scholar]
- Slater, J.C. Note on orthogonal atomic orbitals. J. Chem. Phys 1951, 19, 220. [Google Scholar] [CrossRef]
- McWeeny, R. The valence bond theory of molecular structure. I. Orbital theories and the valence-bond method. Proc. R. Soc. Lond. Ser. A 1954, 223, 63. [Google Scholar]
- Malrieu, J.P.; Angeli, C.; Cimiraglia, R. On the relative merits of non-orthogonal and orthogonal valence bond methods illustrated on the hydrogen molecule. J. Chem. Educ. 2008, 85, 150. [Google Scholar] [CrossRef]
- Slater, J.C. Quantum Theory of Molecules and Solids, vol. 1; McGraw-Hill Book Company: New York, NY, USA, 1963; p. 74. [Google Scholar]
- Pilar, F.L. Elementary Quantum Chemistry; McGraw-Hill Book Company: New York, NY, USA, 1968; p. 569. [Google Scholar]
- Gallup, G.A. A short history of VB theory. In Valence Bond Theory; Cooper, D.L., Ed.; Elsevier: New York, NY, USA, 2002; p. 29. [Google Scholar]
- Ruedenberg, K. The physical nature of the chemical bond. Rev. Mod. Phys. 1962, 34, 326. [Google Scholar] [CrossRef]
- Edmiston, C.; Ruedenberg, K. Chemical binding in the water molecule. J. Phys. Chem. 1964, 68, 1628. [Google Scholar] [CrossRef]
- Feinberg, M.J.; Ruedenberg, K.; Mehler, E. The origin of binding and antibinding in the hydrogen molecule-ion. Adv. Quantum Chem. 1970, 5, 27–98. [Google Scholar]
- Feinberg, M.J.; Ruedenberg, K. Paradoxical role of the kinetic-energy operator in the formation of the covalent bond. J. Chem. Phys. 1971, 54, 1495. [Google Scholar] [CrossRef]
- Feinberg, M.J.; Ruedenberg, K. Heteropolar one-electron bond. J. Chem. Phys. 1971, 55, 5804. [Google Scholar] [CrossRef]
- Ruedenberg, K. The nature of the chemical bond: An energetic view. In Localization and Delocalization in Quantum Chemistry; Volume 1, Daudel, R., Ed.; Reidel: Dordrecht, The Netherlands, 1975; p. 223. [Google Scholar]
- Ruedenberg, K.; Schmidt, M.W. Why does electron sharing lead to covalent bonding? A variational analysis. J. Comp. Chem. 2007, 28, 391. [Google Scholar] [CrossRef]
- Ruedenberg, K.; Schmidt, M.W. Physical understanding through variational reasoning: Electron sharing and covalent bonding. J. Phys. Chem. A 2009, 113, 1954. [Google Scholar] [CrossRef] [PubMed]
- Bitter, T.; Ruedenberg, K.; Schwarz, W.H.E. Towards a physical understanding of electron-sharing two-center bonds. I. General aspects. J. Comp. Chem. 2007, 28, 411. [Google Scholar] [CrossRef]
- Bitter, T.; Wang, S.G.; Ruedenberg, K.; Schwarz, W.H.E. Towards a physical understanding of electron-sharing two-center bonds. II. Pseudo-potential based analysis of diatomic molecules. Theor. Chem. Acc. 2010, 127, 237. [Google Scholar] [CrossRef]
- Schmidt, M.W.; Ivanic, J.; Ruedenberg, K. Covalent bonds are created by the drive of electron waves to lower their kinetic energy through expansion. J. Chem. Phys. 2014, 140, 1204104. [Google Scholar]
- Schmidt, M.W.; Ivanic, J.; Ruedenberg, K. The physical origin of covalent bonding. In The Chemical Bond. Fundamental Aspects of Chemical Bonding; Frenking, G., Shaik, S., Eds.; Wiley-VCH: Dordrecht, The Netherlands, 2014. [Google Scholar]
- Hubbard, J. Electron correlation in narrow energy bands. Proc. R. Soc. Lond. Ser. A 1963, 276, 238. [Google Scholar] [CrossRef]
- Hubbard, J. Electron correlation in narrow energy bands. III. An improved solution. Proc. R. Soc. Lond. Ser. A 1964, 281, 401. [Google Scholar] [CrossRef]
- Atchity, G.; Ruedenberg, K. Determination of diabatic states through enforcement of configurational uniformity. Theor. Chem. Acc. 1997, 97, 47–58. [Google Scholar]
- Angeli, C.; Cimiraglia, R.; Malrieu, J.P. Non-orthogonal and orthogonal valence bond wavefunctions in the hydrogen molecule: The diabatic view. Mol. Phys. 2013, 111, 1069–1077. [Google Scholar] [CrossRef]
- Nakamura, H.; Truhlar, D. The direct calculation of diabatic states based on configurational uniformity. J. Chem. Phys. 2001, 115, 10353–10372. [Google Scholar] [CrossRef]
- Nakamura, H.; Truhlar, D. Direct diabatization of electronic states by the fourfold way. II. Dynamical correlation and rearrangement processes. J. Chem. Phys. 2002, 117, 5576–5593. [Google Scholar] [CrossRef]
- Nakamura, H.; Truhlar, D. Extension of the fourfold way for calculation of global diabatic potential energy surfaces of complex, multiarrangement, non-Born-Oppenheimer systems: Application to HNCO (S0, S1). J. Chem. Phys. 2003, 118, 6816–6829. [Google Scholar] [CrossRef]
- Kabbaj, O.K.; Volatron, F.; Malrieu, J.P. A nearly diabatic description of SN2 reactions: The collinear model. Chem. Phys. Lett. 1988, 147, 353–358. [Google Scholar] [CrossRef]
- Kabbaj, O.K.; Lepetit, M.B.; Malrieu, J.P.; Sini, G.; Hiberty, P.C. SN2 reactions as Two-State Problems: Diabatic MO-CI Calculations on , Li2H−, , and ClCH3Cl−. J. Am. Chem. Soc. 1991, 113, 5619–5627. [Google Scholar] [CrossRef]
- Malrieu, J.P.; Guihery, N.; Calzado, C.J.; Angeli, C. Bond electron pair: Its relevance and analysis from the quantum chemistry point of view. J. Comp. Chem. 2007, 28, 35–50. [Google Scholar] [CrossRef]
- Lennard-Jones, J. New ideas in chemistry. Adv. Sci. 1954, 11, 136–148. [Google Scholar]
- Scemama, A.; Caffarel, M.; Savin, A. Maximum probability domains from quantum monte carlo calculations. J. Comp. Chem. 2007, 28, 442–454. [Google Scholar] [CrossRef]
- Lüchow, A. Maxima of |Ψ|2: A connection between quantum mechanics and Lewis structures. J. Comp. Chem. 2014, 35, 854–864. [Google Scholar] [CrossRef]
- Schmidt, M.W.; Baldridge, K.K.; Boatz, J.A.; Elbert, S.T.; Gordon, M.S.; Jensen, J.H.; Koseki, S.; Matsunaga, N.; Nguyen, K.A.; Su, S.J.; et al. General atomic and molecular electronic structure system. J. Comp. Chem. 1993, 14, 1347–1363. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sax, A.F. Chemical Bonding: The Orthogonal Valence-Bond View. Int. J. Mol. Sci. 2015, 16, 8896-8933. https://doi.org/10.3390/ijms16048896
Sax AF. Chemical Bonding: The Orthogonal Valence-Bond View. International Journal of Molecular Sciences. 2015; 16(4):8896-8933. https://doi.org/10.3390/ijms16048896
Chicago/Turabian StyleSax, Alexander F. 2015. "Chemical Bonding: The Orthogonal Valence-Bond View" International Journal of Molecular Sciences 16, no. 4: 8896-8933. https://doi.org/10.3390/ijms16048896
APA StyleSax, A. F. (2015). Chemical Bonding: The Orthogonal Valence-Bond View. International Journal of Molecular Sciences, 16(4), 8896-8933. https://doi.org/10.3390/ijms16048896




