First Principles Study on the Electronic Properties of Zn64Sb64−xTex Solid Solution (x = 0, 2, 3, 4)
Abstract
:1. Introduction
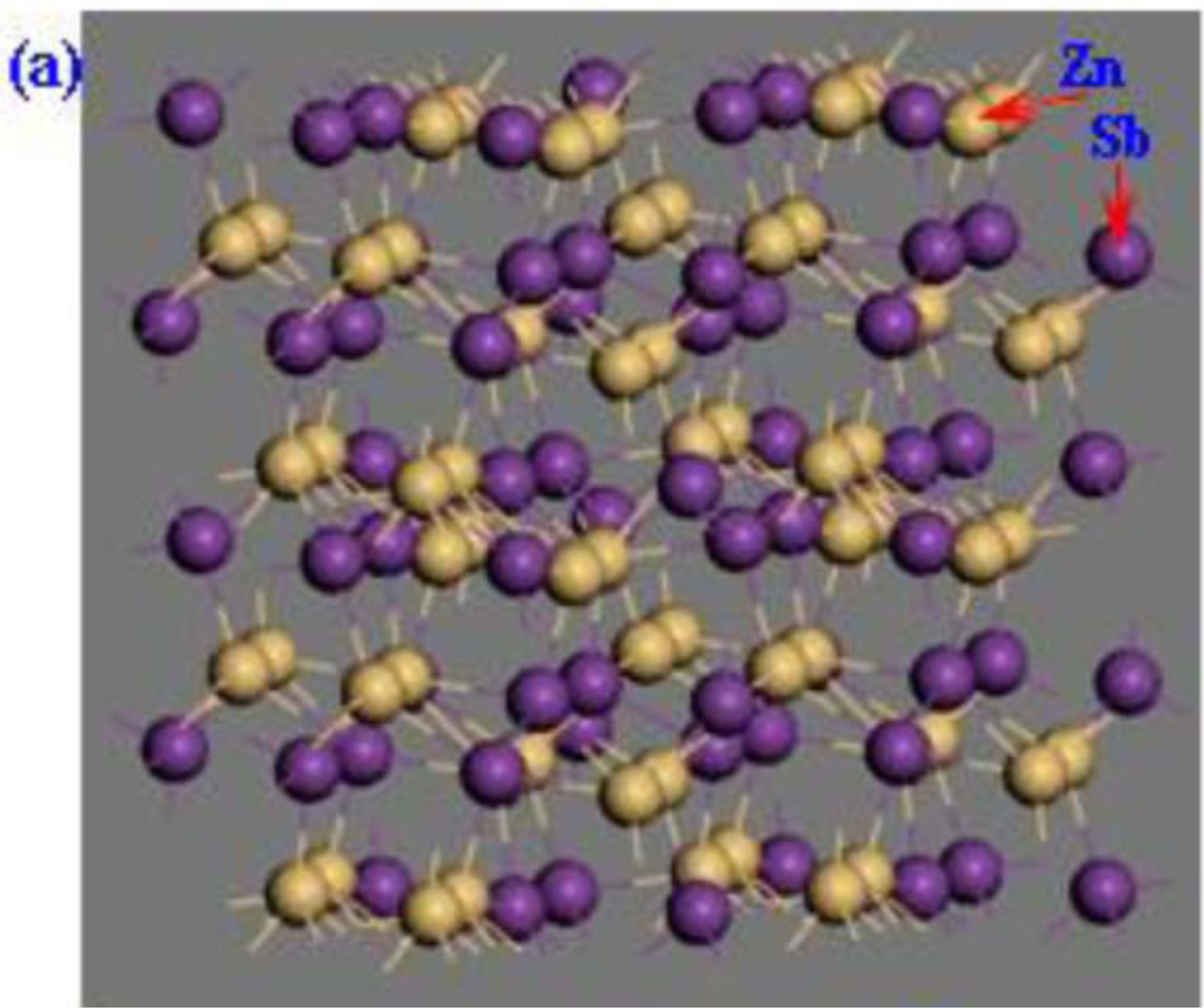
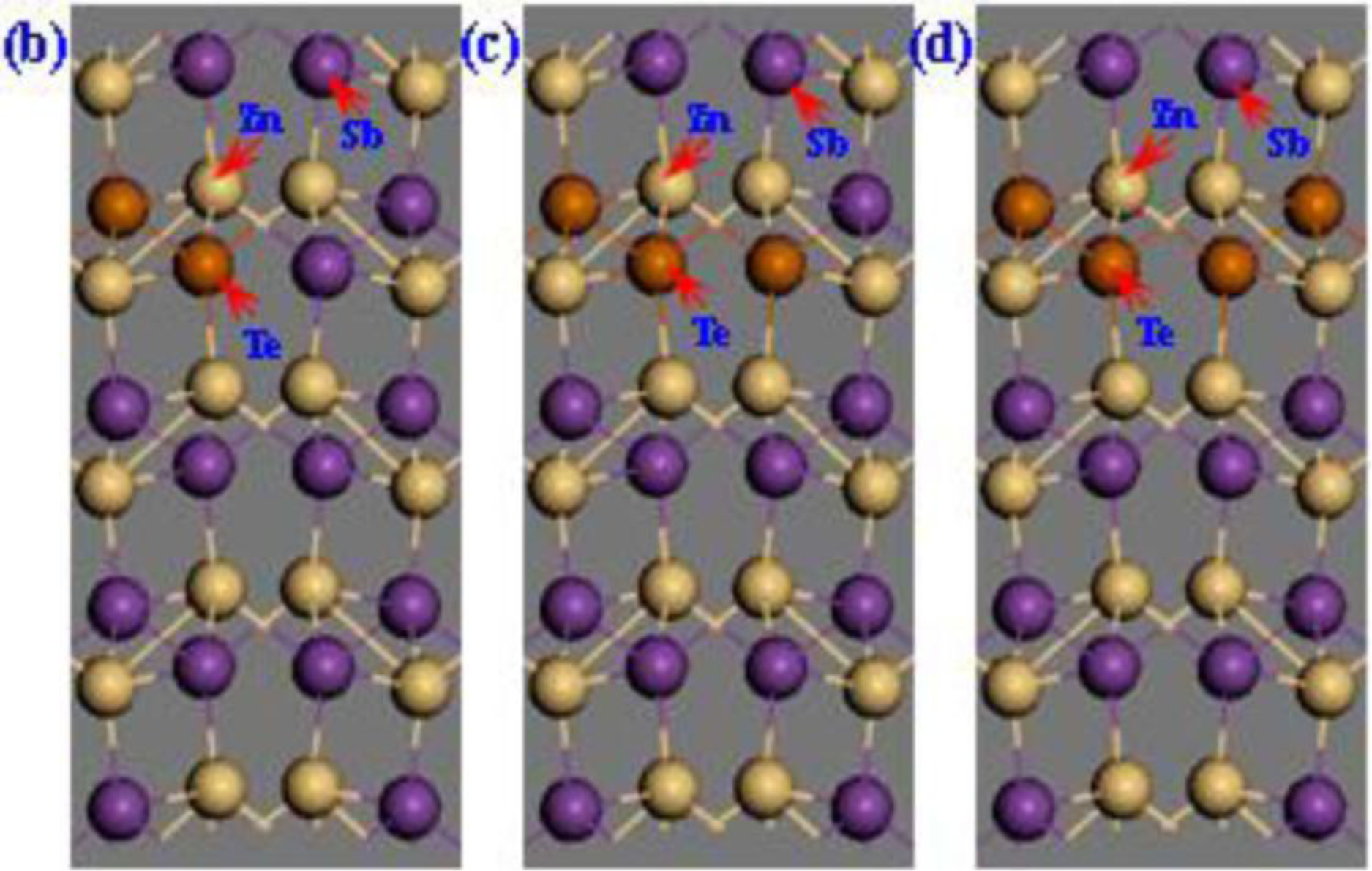
2. Calculation Models and Methods
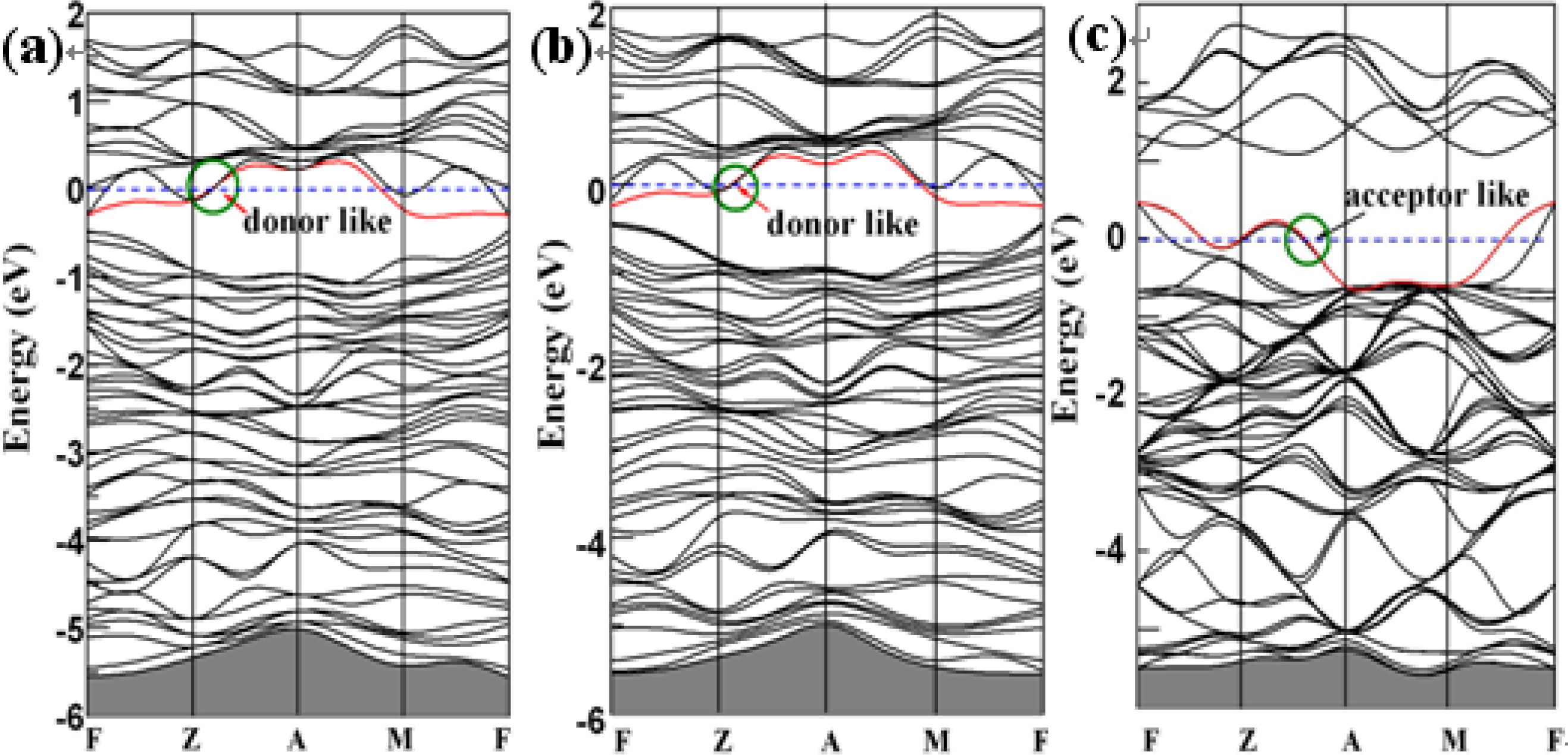
3. Results and Discussion
4. Conclusions
Acknowledgments
References
- Tapiero, M; Tarabichi, S; Gies, JG; Noguet, C; Zielinger, JP; Christensen, M; Robino, M; Herion, J. Preparation and characterization of Zn4Sb4. Sol. Energy Mater 1985, 12, 257–274. [Google Scholar]
- Zhang, LT; Tsutsui, M; Ito, K; Yamaguchi, M. Thermoelectric properties of Zn4Sb3 thin films prepared by magnetron sputtering. Thin Solid Films 2003, 443, 84–90. [Google Scholar]
- Nakamoto, G; Kinshita, K; Kurisu, M. Thermal expansion anomalies at high temperatures near stoichiometric Zn4Sb3 composition. J. Alloys Compd 2007, 436, 65–68. [Google Scholar]
- Gau, HJ; Yu, JL; Wu, CC; Kuo, YK; Ho, CH. Thermoelectric properties of Zn–Sb alloys doped with In. J. Alloys Compd 2009, 480, 73–75. [Google Scholar]
- Mozharivskyj, Y; Janssen, Y; Harringa, JL; Kracher, A; Tsokol, AO; Miller, GJ. Zn13Sb10: A structural and landau theoretical analysis of its phase transitions. Chem. Mater 2006, 18, 822–831. [Google Scholar]
- Mozharivskyj, Y; Pecharsky, AO; Budko, S; Miller, GJ. A Promising thermoelectric material: Zn4Sb3 or Zn6−δSb5. Its composition, structure, stability, and polymorphs. structure and Stability of Zn1−δSb. Chem. Mater 2004, 16, 1580–1589. [Google Scholar]
- Abou-Zeid, A; Shneider, G. Te-doped n-type ZnSb. Phys. Status Solidi A 1971, 6, 101–103. [Google Scholar]
- Ueda, T; Okamura, C; Noda, Y; Hasezaki, K. Effect of Tellurium doping on the thermoelectric properties of ZnSb. Mater. Trans 2009, 50, 2473–2475. [Google Scholar]
- Zeng, W; Liu, TM. Hydrogen sensing characteristics and mechanism of nanosize TiO2 dope with metallic ions. Phys. B Condens. Matter 2010, 405, 564–568. [Google Scholar]
- Zeng, W; Liu, TM; Wang, ZC; Tsukimto, S; Saito, M; Ikuhara, Y. Oxygen Adsorption on Anatase TiO2 (101) and (001) surfaces from first principles. Mater. Trans 2010, 51, 171–175. [Google Scholar]
- Yamada, Y. Band Structure Calculation of ZnSb. Phys. Status. Solidi. B 1978, 85, 723–732. [Google Scholar]
- Boulet, P; Record, MC. Structural investigation of the Zn1−xCdxSb solid solution by density-functional theory approach. Solid State Sci 2010, 12, 26–32. [Google Scholar]
- Mikhaylushkin, AS; Nylen, J; Haussermann, U. Structure and bonding of Zinc Antimonides: Complex frameworks and narrow band gaps. Chem. Eur. J 2005, 11, 4912–4920. [Google Scholar]
- Cartera, FL; Mazelsky, R. The ZnSb structure; A further enquiry. J. Phys. Chem. Solid 1964, 25, 571–581. [Google Scholar]
- Kresse, G; Furthmuller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar]
- Perdew, JP; Wang, Y. Accurate and simple density functional for the electronic exchange energy: Generalized gradient approximation. Phys. Rev. B 1986, 33, 8800–8802. [Google Scholar]
- Sjöstedt, E; Nordstrom, L; Singh, DJ. An alternative way of linearizing the augmented plane-wave method. Solid State Commun 2000, 114, 15–20. [Google Scholar]
- Keloglus, YP; Fedorko, AS. Model explanation for extremums of properties in ZnSb–CdSb system. Izv. Vyssh. Uchebn. Zaved. Fiz 1970, 7, 151. [Google Scholar]
- Mann, O; Fregland, W. Mechanism of formation and electronic structure of semiconducting ZnSb nanoclusters electrodeposited from an ionic liquid. Electrochim. Acta 2007, 53, 518–524. [Google Scholar]
- Caillat, T; Fleurial, J-P; Borshchersky, AJ. Preparation and thermoelectric properties of semiconducting Zn4Sb3. Phys. Chem. Solid 1997, 58, 1119–1125. [Google Scholar]
- Yu, X; Si, P; Hou, Q; Kong, X; Cheng, W. First-principles study on the bandgap modulation of Be and Mg co-doped ZnO systems. Phys. B 2009, 404, 1794–1798. [Google Scholar]



© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Zhao, J.-H.; Han, E.-J.; Liu, T.-M.; Zeng, W. First Principles Study on the Electronic Properties of Zn64Sb64−xTex Solid Solution (x = 0, 2, 3, 4). Int. J. Mol. Sci. 2011, 12, 3162-3169. https://doi.org/10.3390/ijms12053162
Zhao J-H, Han E-J, Liu T-M, Zeng W. First Principles Study on the Electronic Properties of Zn64Sb64−xTex Solid Solution (x = 0, 2, 3, 4). International Journal of Molecular Sciences. 2011; 12(5):3162-3169. https://doi.org/10.3390/ijms12053162
Chicago/Turabian StyleZhao, Jian-Hua, Er-Jing Han, Tian-Mo Liu, and Wen Zeng. 2011. "First Principles Study on the Electronic Properties of Zn64Sb64−xTex Solid Solution (x = 0, 2, 3, 4)" International Journal of Molecular Sciences 12, no. 5: 3162-3169. https://doi.org/10.3390/ijms12053162
APA StyleZhao, J.-H., Han, E.-J., Liu, T.-M., & Zeng, W. (2011). First Principles Study on the Electronic Properties of Zn64Sb64−xTex Solid Solution (x = 0, 2, 3, 4). International Journal of Molecular Sciences, 12(5), 3162-3169. https://doi.org/10.3390/ijms12053162




