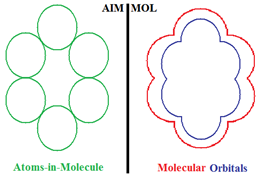
Compactness Aromaticity of Atoms in Molecules
Abstract
:1. Introduction
2. Methods
2.1. Quantum Compactness Aromaticity
2.2. Reactivity Indices-Based Aromaticity
2.2.1. Geometric Index of Reactivity: Polarizability
2.2.2. Energetic Indices of Reactivity: Electronegativity and Chemical Hardness
2.3. Quantum Methods for Molecular Orbitals
2.3.1. General Mono-Electronic Orbitals’ Equations
2.3.2. Semi-empirical Approximations
- By neglecting the differential overlap (NDO) through the mono-atomic orbitalic constraint:leaving with the simplified integrals:thus reducing the number of bielectronic integrals, while the tri- and tetra-centric integrals are all neglected;
- By neglecting the diatomic differential overlap (NDDO) of the bi-atomic orbitals:that implies the actual simplifications:when overlaps (or contractions) of atomic orbitals on different atoms are neglected.
2.3.2.1. NDO Methods
2.3.2.2. NDDO Methods
2.3.3. Ab initio Methods
2.3.3.1. Hartree-Fock Method
2.3.3.2. Density Functional Theory Methods
- B3-LYP: advanced by Becke by empirical comparisons against very accurate results and contains the exchange contribution (20% HF + 8% Slater + 81% Becke88) added to the correlation energy (81% LYP + 19% VWN) [135];
- B3-PW91: was developed also by Becke with PW91 correlation instead of LYP;
- EDF1: was optimized for a specific basis set (6–31 + G*) and represent a rearrangement of Becke88 with LYP functionals with slightly different parameters, being an improvement over B3-LYP and Becke88-LYP combinations;
- Becke-97: is a hybrid exchange-correlation functional appeared by extending the g(x) of Equation (66) as a power series containing three terms with an admixture of 19.43% HF exchange [136].
3. Application on Basic Aromatics Scales
- Aroma1 Rule: the mono-benzenoid compounds have systematically higher aromaticity than those of double-ring benzenoids; yet, this is the generalized version of the rule demanding that the benzene aromaticity is always higher than that of naphthalene, for instance; however, further generalization respecting the poly-ring benzenoids is anticipated albeit it should be systematically proved by appropriate computations;
- Aroma2 Rule: C-replaced benzenoids are more aromatic than substituted benzenoids, e.g., Pyridine and Pyrimidine vs. Phenol and Aniline ordering aromaticity in Table 2; this rule extends the substituted versus addition rules in aromaticity historical definition (see Introduction);
- Aroma3 Rule: double-C-replaced annulens have greater aromaticity than mono-C-replaced annulenes, e.g., APyrimidine > APyridine; this is a sort of continuation of the previous rule in the sense that as more Carbons are replaced in aromatic rings, higher aromaticity is provided; further generalization to poly-replacements to poly-ring benzenoids is also envisaged;
- Aroma4 Rule: hydroxyl-substitution to annulene produces more aromatic (stable) compounds than the correspondent amine-substitution; e.g., this rule is fulfilled by mono-benzenoids and is maintained also by the double-benzene-rings no matter the stereoisomers considered; due to the fact the π electrons provided by Oxygen in hydroxyl-group substituted to annulene ring is greater than those released by Nitrogen in annulene ring by the amine-group substitution this rule is formally justified, while the generalization for hydroxyl- versus amine- substitution to poly-ring annulens may be equally advanced for further computational confirmation;
- Aroma5 Rule: for double ring annulens the α position is more aromatic for hydroxyl-substitution while β position is more aromatic for amine-substitution than their β and α counterparts, respectively; this rule may be justified in the light of the Aroma4 Rule above employing the inverse role the Oxygen and Nitrogen plays in furnished (π + free pair) electrons to annulens rings: while for Oxygen the higher atomic charge may be positioned closer to the common bond between annulens’ rings–thus favoring the alpha position, the lesser Nitrogen atomic charge should be located as much belonging to one annulene ring only–thus favoring the beta position; such inversion behavior is justified by the existing of free electrons on the NH2- group that as closely are to the benzenic ring as much favors its stability against further electrophilic attack–as is the case of beta position of 2-Naphtalenamine in Table 2; extensions to the poly-ring annulens may be also investigated.
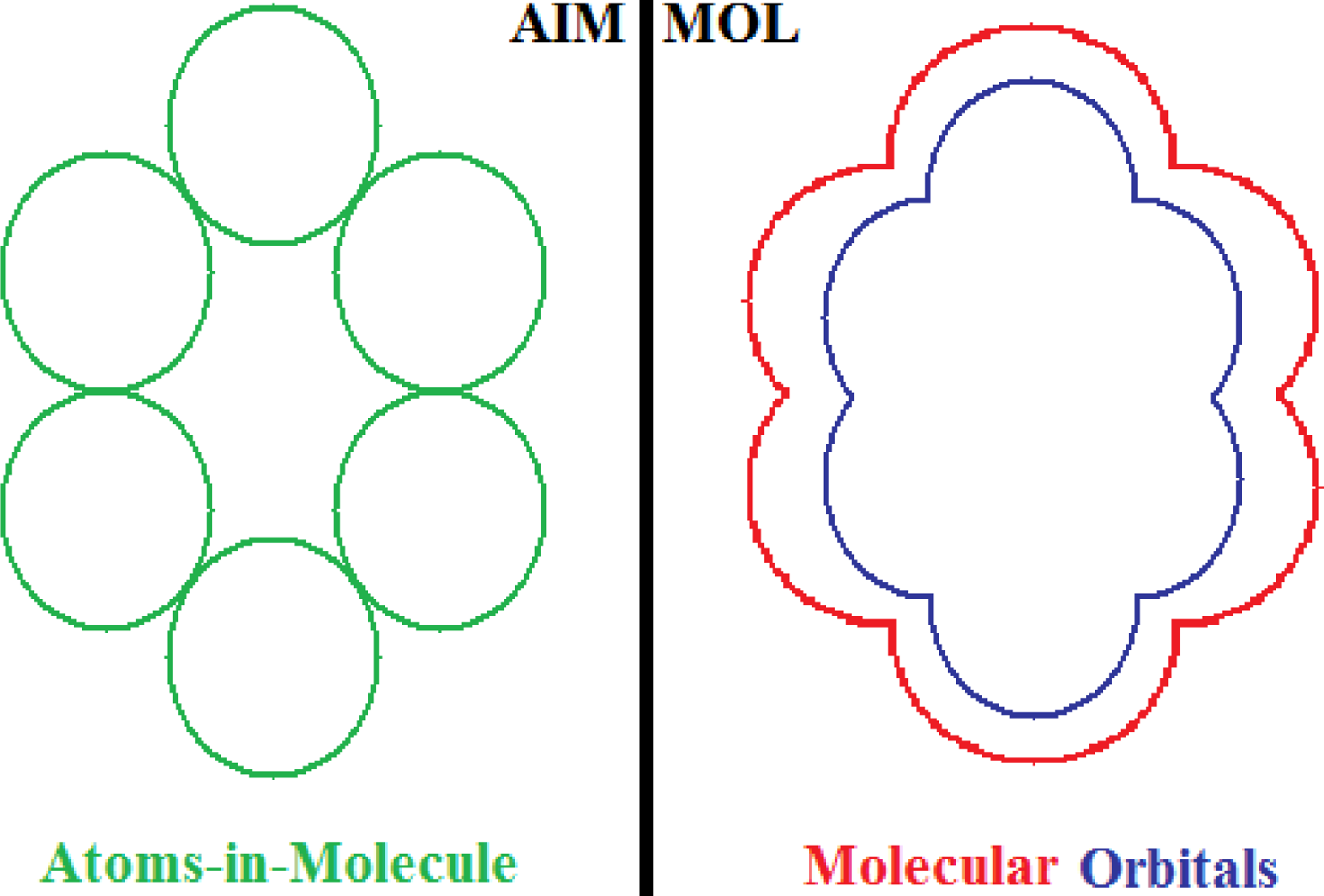
- No semi-empirical quantum method, in general, satisfies the first rule of aromaticity, Aroma1, in the sense that the trend in Figure 2a (and Table 3) displays rather growing aromaticity character from mono- to double-benzenoid rings; the same behavior is common also to HF computational environment, perhaps due to the close relationships with approximations made in semi-empirical approaches; instead, all other ab initio methods considered, including that without exchange and correlation terms in Equations (57), do fulfill the Aroma1 rule;
- The remaining aromaticity Aroma2–5 rules are generally not adapted with any of the semi-empirical methods, except the MINDO3 (the most advanced and accurate method from the NDO approximations) fulfilling the Aroma3 rule regarding the ordering of mono- versus bi- CH- replacement group by Nitrogen on benzenoid ring. Interestingly, the Aroma3 rule is then not satisfied by any of the ab initio quantum methods;
- Aroma2 rule about the comparison between the CH- replacement group and the H- substitution to the mono ring benzene seems being in accordance only with HF and ab initio without exchange-correlation environments leading with the idea the electronegativity based- aromaticity of substitution and replacement groups is not so sensitive to the spin and correlation effects, being of primarily Coulombic nature;
- Hydroxyl- versus amine- substitution aromaticity appears that is not influenced by spin and correlation in electronegativity based- ordering aromaticity since only the no-exchange and correlation computational algorithm agrees with Aroma4 Rule;
- α- versus β- stereoisomeric position influence in aromaticity ordering is respected only by the HF scheme of computation and by no other combination, either semi-empirical or ab initio.
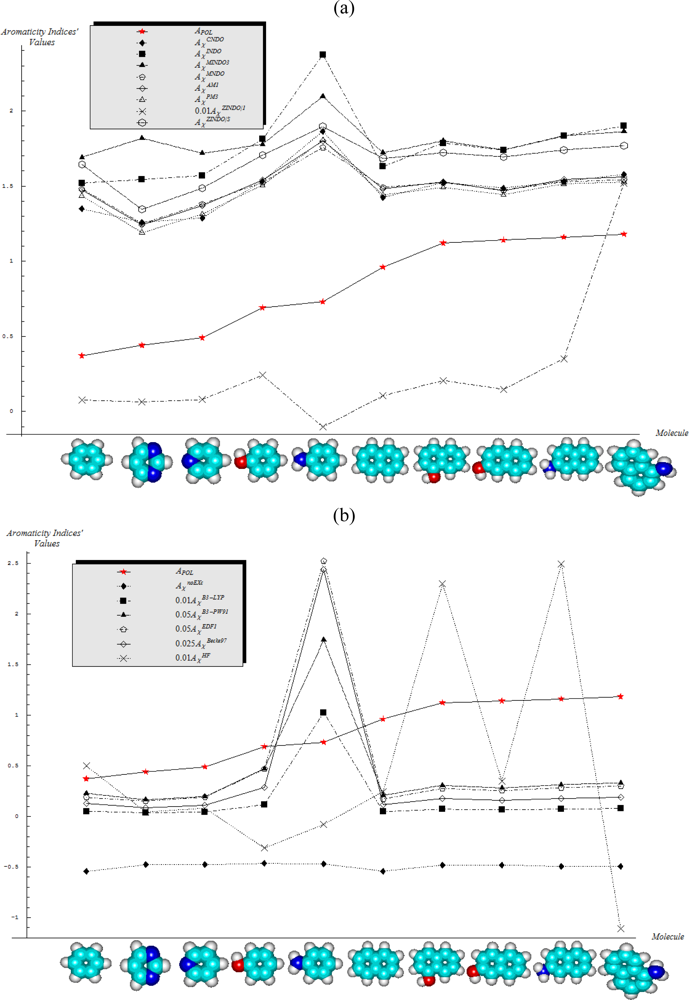
- Semi-empirical methods are equally appropriate in producing agreement with Aroma1 and Aroma4 rules in what concerns the aromaticity behavior for the mono- versus bi- ring annulens and hydroxyl- versus amine- substitution to either of them, respectively;
- Aroma2 and Aroma3 rules are slightly better fulfilled by the semi-empirical than the ab initio quantum frameworks in modeling the aromaticity performance of the mono- versus bi- CH- replaced groups and both of them against the H- substituted on benzenic rings, respectively;
- The stereoisomeric effects comprised by the Aroma5 rule is not modeled by the chemical hardness compactness aromaticity by any of its computed scales, neither semi-empirical or ab initio.
- With CNDO and INDO methods, the electronegativity based-aromaticity is more oriented towards the AIM limit of Figure 1, while chemical hardness based- aromaticity merely models the MOL limit of chemical bonding, see Table 3. This agrees with the basic principles of chemical reactivity according to which electronegativity drives the atomic encountering in forming the transition state towards chemical bond, while chemical hardness refines the bond by the aid of maximum hardness principle [59,67];
- The MINDO3, MNDO, AM1, PM3, and ZINDO/S all display in Table 3 the exclusively AIM limit in assessing aromaticity in bonding, yet with electronegativity based values systematically higher than those based on chemical hardness–this way respecting in some degree the empirical rule stating that the electronegativity stands as the first order effect in reactivity, while the chemical hardness corrects in the second order the bonding stability, according with the basic differential definitions of Equations (14) and (19), respectively;
- ZINDO/1 differs both from ZINDO/S and by the rest of semi-empirical methods of the last group, while giving qualitative results in the same manner as CNDO and INDO, in the sense of higher absolute (positively defined) electronegativity based-respecting the chemical hardness based-aromaticities, yet with significant quantitative values over unity (i.e., the transition state as the instable equilibrium between AIM and MOL limits), see Table 3. This means that the transitional elements’ orbitals inclusion without further refinements of ZINDO/S exacerbates the Coulombic atoms-in-molecule effects, i.e., the stability (aromaticity) of bonding is mostly to be acquired in the pre-bonding stage of the AIM limit;
- Somehow with the same qualitative-quantitative behavior as ZINDO/1 is the HF computed aromaticities indices of Table 4; however, the negative values as well as exceeding the AIM unity limit of electronegativity based-aromaticities appear now as multiple-recordings, while the resulted chemical hardness aromaticity is the closest respecting the unity limit of transition state prescribed by Equation (1). Together, this information shows that the HF computational framework merely models the pre-bonding AIM and the post-bonding MOL stages by electronegativity and chemical hardness reactivity indices, respectively;
- The reverse case to HF computing stands the no-exchange-and-correlation (noEX-C) values in Table 4, according to which the electronegativity based aromaticity, beside the negative values, are all in sub-unity range, so being associated with post-bonding MOL limit. This corroborates the situation with the supra-unitary recordings of chemical hardness based-aromaticity outputs, specific to pre-bonding AIM, the resulted reactivity picture is completely reversed respecting that accustomed for electronegativity and chemical hardness reactivity principles [54]. Therefore, it is compulsory to consider at least the electronic spin through exchange contributions (as in the HF case), not only conceptually, but also computationally for achieving a consistent picture of reactivity, not only of the aromaticity;
- The last situation is restored by using the hybrid functionals of DFT, i.e., B3-LYP, B3-PW91, EDF1, and Becke97 in Table 4, with the help of which electronegativity based-aromaticity regains its supremacy over that computed with the chemical hardness AIM and MOL limits in bonding. Although, no explicit sub-unity MOL limit of Equation (1) is obtained with chemical hardness aromaticity computation, the recorded values are enough close to unity, while those based on electronegativity are more than twice further away from unity, to can say that the reactivity principles are fairly respected within these quantum methods, i.e., when Aχ and Aη are situated in the AIM and MOL limiting sides of chemical bonding, respectively.
4. Conclusions
- the molecule viewed as composed of the constituent atoms (AIM) and
- the molecule viewed from its spectra of molecular orbitals (MOL).
- having a viable quantum definition (since the quantum nature of electrons and nucleus are assumed as responsible for molecular stability/reactivity/aromaticity); and
- having a reality at both the atomic and molecular levels.
- Aroma1: the greater effect on aromaticity by mono- over bi-(poly-) benzenic rings;
- Aroma2: the greater effect on aromaticity by CH- replaced group over H- substituted group on benzenic rings;
- Aroma3: the greater effect on aromaticity by bi- (poly-) over mono- CH- replaced group on benzenic rings;
- Aroma4: the greater effect on aromaticity by OH- group over NH2- substituted groups on benzenic rings;
- Aroma5: the greater effect on aromaticity by the stereoisomers with substituted group having the lowest atomic charge contribution (or the lowest free valence or largest bonding order, e.g., OH- substituted group) to the benzenic rings, unless free electrons on that group exist (e.g., NH2- substituted group) in which case the rule is inversed.
- there is preferable computing aromaticity in an absolute manner, i.e., for each molecule based on its pre- and post- bonding properties (as is the present compactness definition, for instance) without involving other referential molecule, as is often case in the fashioned aromaticity scales;
- the comparison between various aromaticity absolute scales is to be done respecting that one based on a structural or reactivity index with attested observational character (as is the present polarizability based- aromaticity);
- the rules derived from the absolute aromaticity scale based on observable quantum index should be considered for further guidance for the rest of aromaticity scales considered;
- the aromaticity concept, although currently associated with stability character of molecules, seems to not depending on correlation and sometimes neither by exchange effects.
Acknowledgments
Appendix: New Hydrogenic Polarizability Formula
| Atom | Radius [Å] | Pol [Å]3 | χ [eV] | η [eV] |
|---|---|---|---|---|
| H | 0.529 | 0.666 | 7.18 | 6.45 |
| C | 0.49 | 0.529 | 6.24 | 4.99 |
| N | 0.41 | 0.310 | 6.97 | 7.59 |
| O | 0.35 | 0.193 | 7.59 | 6.14 |
| Compound | Structure | Polarizability [Å]3 | AIM-Indices | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Formula Name CAS Index (πe−) | AIM | Molecule | Conventional | PAIM | Molec | AP | χAIM | ηAIM | |
| Vol | PMOL | ||||||||
| C6H6 Benzene 71-43-2 I (6) |  |  |  | 7.17 | 328.11 | 19.58 | 0.37 | 6.68 | 5.63 |
| C4H4N2 Pyrimidine 289-95-2 II (6) |  |  |  | 5.40 | 306.46 | 12.19 | 0.44 | 6.73 | 5.93 |
| C5H5N Pyridine 110-86-1 III (6) |  |  |  | 6.29 | 320.75 | 12.76 | 0.49 | 6.70 | 5.76 |
| C6H6O Phenol 108-95-2 IV (8) | 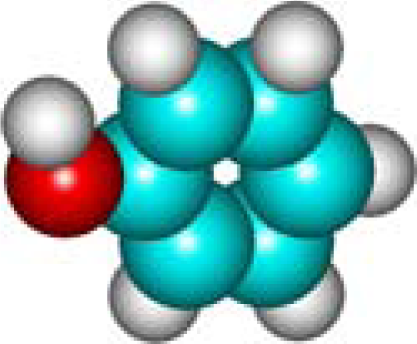 | 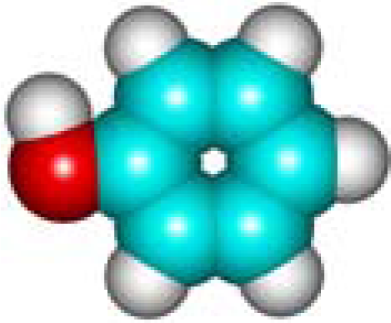 |  | 7.37 | 356.91 | 10.65 | 0.69 | 6.74 | 5.66 |
| C6H7N Aniline 62-53-3 V (8) |  |  |  | 8.15 | 371.73 | 11.09 | 0.73 | 6.73 | 5.79 |
| C10H8 Naphthalene 91-20-3 VI (10) |  |  |  | 10.62 | 463.84 | 11.07 | 0.96 | 6.63 | 5.55 |
| C10H8O 1-Naphthol 90-15-3 VII (12) |  |  |  | 10.82 | 483.88 | 9.63 | 1.12 | 6.67 | 5.58 |
| C10H8O 2-Naphthalelon 135-19-3 VIII (12) |  |  |  | 10.82 | 478.39 | 9.52 | 1.14 | 6.67 | 5.58 |
| C10H9N 2-Naphthalenamine 91-59-8 IX (12) |  |  |  | 11.60 | 501.54 | 9.98 | 1.16 | 6.67 | 5.66 |
| C10H9N 1-Naphthalenamine 134-32-7 X (12) |  |  |  | 11.60 | 496.11 | 9.87 | 1.18 | 6.67 | 5.66 |
| Compound | CNDO | INDO | MINDO3 | MNDO | AM1 | PM3 | ZINDO/1 | ZINDO/S | |
|---|---|---|---|---|---|---|---|---|---|
| Index | Property | ||||||||
| I | ELUMO | 3.892207 | 4.451804 | 1.26534 | 0.3681966 | 0.514791 | 0.3440638 | 7.970686 | 0.7950159 |
| –EHOMO | 13.80296 | 13.24336 | 9.165875 | 9.391555 | 9.591248 | 9.652767 | 9.724428 | 8.927967 | |
| χ | 4.96 | 4.40 | 3.95 | 4.51 | 4.54 | 4.65 | 0.88 | 4.07 | |
| η | 8.85 | 8.85 | 5.22 | 4.88 | 5.05 | 4.998 | 8.85 | 4.86 | |
| AEL | 1.35 | 1.52 | 1.69 | 1.48 | 1.472 | 1.435 | 7.62 | 1.64 | |
| AHard | 0.64 | 0.64 | 1.08 | 1.15 | 1.11 | 1.13 | 0.64 | 1.16 | |
| II | ELUMO | 2.709499 | 3.147036 | 0.951945 | –0.3960558 | –0.2959276 | –0.6894529 | 6.422883 | –0.3419995 |
| –EHOMO | 13.39755 | 11.86692 | 8.356924 | 10.36822 | 10.56194 | 10.62456 | 8.527512 | 9.67323 | |
| χ | 5.34 | 4.36 | 3.70 | 5.38 | 5.43 | 5.66 | 1.05 | 5.01 | |
| η | 8.05 | 7.51 | 4.65 | 4.99 | 5.13 | 4.968 | 7.48 | 4.67 | |
| AEL | 1.26 | 1.54 | 1.82 | 1.25 | 1.24 | 1.19 | 6.40 | 1.34 | |
| AHard | 0.74 | 0.79 | 1.274 | 1.189 | 1.16 | 1.19 | 0.79 | 1.271 | |
| III | ELUMO | 3.051321 | 3.521359 | 1.011715 | –0.02136767 | 0.1085682 | –0.1944273 | 6.909242 | 0.01985455 |
| –EHOMO | 13.45145 | 12.06075 | 8.813591 | 9.692185 | 9.903634 | 10.0075 | 8.598721 | 9.040296 | |
| χ | 5.20 | 4.27 | 3.90 | 4.86 | 4.90 | 5.10 | 0.84 | 4.51 | |
| η | 8.25 | 7.79 | 4.91 | 4.84 | 5.01 | 4.91 | 7.75 | 4.53 | |
| AEL | 1.29 | 1.57 | 1.718 | 1.38 | 1.37 | 1.31 | 7.93 | 1.49 | |
| AHard | 0.6980 | 0.74 | 1.17 | 1.191 | 1.15 | 1.17 | 0.74 | 1.272 | |
| IV | ELUMO | 3.718175 | 4.275294 | 1.085692 | 0.1763786 | 0.3450922 | 0.2196551 | 7.706827 | 0.6566099 |
| –EHOMO | 12.51092 | 11.71605 | 8.669437 | 9.022056 | 9.108171 | 9.169341 | 8.265366 | 8.557631 | |
| χ | 4.40 | 3.72 | 3.79 | 4.42 | 4.38 | 4.47 | 0.28 | 3.95 | |
| η | 8.11 | 8.00 | 4.88 | 4.60 | 4.73 | 4.69 | 7.99 | 4.61 | |
| AEL | 1.53 | 1.81 | 1.78 | 1.52 | 1.538 | 1.506 | 24.13 | 1.71 | |
| AHard | 0.6975 | 0.71 | 1.16 | 1.23 | 1.20 | 1.21 | 0.71 | 1.23 | |
| V | ELUMO | 4.002921 | 4.61612 | 1.360785 | 0.5461559 | 0.7090454 | 0.5768315 | 8.106442 | 0.8517742 |
| –EHOMO | 11.22051 | 10.28413 | 7.783539 | 8.207099 | 8.186989 | 8.028173 | 6.803807 | 7.95583 | |
| χ | 3.61 | 2.83 | 3.21 | 3.83 | 3.74 | 3.73 | –0.65 | 3.55 | |
| η | 7.61 | 7.45 | 4.57 | 4.38 | 4.45 | 4.30 | 7.46 | 4.40 | |
| AEL | 1.86 | 2.37 | 2.10 | 1.76 | 1.80 | 1.806 | –10.33 | 1.89 | |
| AHard | 0.76 | 0.78 | 1.266 | 1.323 | 1.3017 | 1.35 | 0.78 | 1.31 | |
| VI | ELUMO | 2.172528 | 2.757336 | 0.4589255 | –0.3423392 | –0.2855803 | –0.4525464 | 6.197386 | –0.04161556 |
| –EHOMO | 11.48051 | 10.89619 | 8.165956 | 8.544642 | 8.660414 | 8.746719 | 7.4545 | 7.835637 | |
| χ | 4.65 | 4.07 | 3.85 | 4.44 | 4.47 | 4.60 | 0.63 | 3.939 | |
| η | 6.83 | 6.83 | 4.31 | 4.10 | 4.19 | 4.15 | 6.83 | 3.90 | |
| AEL | 1.42 | 1.63 | 1.721 | 1.49 | 1.48 | 1.441 | 10.55 | 1.68 | |
| AHard | 0.81 | 0.81 | 1.29 | 1.35 | 1.33 | 1.34 | 0.81 | 1.42 | |
| VII | ELUMO | 2.192621 | 2.79537 | 0.5106197 | –0.3850094 | –0.2975906 | –0.4355633 | 6.210848 | –0.06489899 |
| –EHOMO | 10.95387 | 10.26489 | 7.918682 | 8.376475 | 8.441528 | 8.514781 | 6.859143 | 7.681855 | |
| χ | 4.38 | 3.73 | 3.70 | 4.38 | 4.37 | 4.48 | 0.32 | 3.87 | |
| η | 6.57 | 6.53 | 4.21 | 4.00 | 4.07 | 4.04 | 6.54 | 3.81 | |
| AEL | 1.52 | 1.79 | 1.80 | 1.52 | 1.53 | 1.49 | 20.58 | 1.72 | |
| AHard | 0.85 | 0.85 | 1.32 | 1.40 | 1.37 | 1.38 | 0.85 | 1.47 | |
| VIII | ELUMO | 2.534854 | 3.128462 | 0.5805296 | –0.3075339 | –0.2500397 | –0.3581562 | 6.510067 | 0.08197734 |
| –EHOMO | 11.50232 | 10.80223 | 8.246805 | 8.747499 | 8.821697 | 8.887013 | 7.405916 | 7.956836 | |
| χ | 4.48 | 3.84 | 3.83 | 4.53 | 4.54 | 4.62 | 0.45 | 3.937 | |
| η | 7.02 | 6.97 | 4.41 | 4.22 | 4.29 | 4.26 | 6.96 | 4.02 | |
| AEL | 1.49 | 1.74 | 1.74 | 1.47 | 1.471 | 1.443 | 14.89 | 1.69 | |
| AHard | 0.795 | 0.80 | 1.26 | 1.322 | 1.302 | 1.31 | 0.80 | 1.39 | |
| IX | ELUMO | 2.228869 | 2.844 | 0.5107521 | –0.3597778 | –0.2714103 | –0.4318241 | 6.286494 | –0.01188275 |
| –EHOMO | 10.94335 | 10.11959 | 7.783869 | 8.371226 | 8.367208 | 8.374782 | 6.666291 | 7.655258 | |
| χ | 4.36 | 3.64 | 3.64 | 4.37 | 4.32 | 4.40 | 0.19 | 3.83 | |
| η | 6.59 | 6.48 | 4.15 | 4.01 | 4.05 | 3.97 | 6.48 | 3.82 | |
| AEL | 1.53 | 1.83 | 1.83 | 1.53 | 1.544 | 1.515 | 35.12 | 1.74 | |
| AHard | 0.86 | 0.87 | 1.36 | 1.41 | 1.40 | 1.43 | 0.87 | 1.48 | |
| X | ELUMO | 2.22685 | 2.840066 | 0.5115107 | –0.3805175 | –0.2805806 | –0.4578161 | 6.326563 | –0.00408988 |
| –EHOMO | 10.68815 | 9.865701 | 7.676749 | 8.272097 | 8.261106 | 8.2799 | 6.414326 | 7.540981 | |
| χ | 4.23 | 3.51 | 3.58 | 4.33 | 4.27 | 4.37 | 0.04 | 3.77 | |
| η | 6.46 | 6.35 | 4.09 | 3.95 | 3.99 | 3.91 | 6.37 | 3.77 | |
| AEL | 1.58 | 1.90 | 1.86 | 1.54 | 1.56 | 1.53 | 152.0 | 1.77 | |
| AHard | 0.88 | 0.89 | 1.38 | 1.43 | 1.42 | 1.45 | 0.89 | 1.50 | |
| Compound | DFT | Hartree-Fock | |||||
|---|---|---|---|---|---|---|---|
| Index | Property | noEX-C | B3-LYP | B3-PW91 | EDF1 | Becke97 | |
| I | ELUMO | 15.69352 | 2.52946 | 2.398649 | 1.561805 | 2.512676 | 7.234344 |
| –EHOMO | –8.870216 | 5.158205 | 5.338667 | 4.430191 | 5.165561 | 7.502962 | |
| χ | –12.28 | 1.31 | 1.47 | 1.43 | 1.33 | 0.13 | |
| η | 3.41 | 3.84 | 3.87 | 3.00 | 3.84 | 7.37 | |
| AEL | –0.54 | 5.08 | 4.54 | 4.66 | 5.04 | 49.74 | |
| AHard | 1.65 | 1.46 | 1.46 | 1.88 | 1.47 | 0.76 | |
| II | ELUMO | 15.11303 | 0.9238634 | 0.7736028 | –0.04114805 | 0.9030221 | 5.579984 |
| –EHOMO | –13.04602 | 4.744987 | 4.883547 | 3.513406 | 4.728943 | 8.695125 | |
| χ | –14.08 | 1.91 | 2.05 | 1.78 | 1.91 | 1.56 | |
| η | 1.03 | 2.83 | 2.83 | 1.74 | 2.82 | 7.14 | |
| AEL | –0.478 | 3.52 | 3.27 | 3.79 | 3.52 | 4.32 | |
| AHard | 5.74 | 2.09 | 2.096 | 3.42 | 2.106 | 0.83 | |
| III | ELUMO | 15.34953 | 1.622094 | 1.477663 | 0.6587179 | 1.60312 | 6.284506 |
| –EHOMO | –12.73475 | 4.751619 | 4.893573 | 3.484843 | 4.739381 | 7.943096 | |
| χ | –14.04 | 1.56 | 1.71 | 1.41 | 1.57 | 0.83 | |
| η | 1.31 | 3.19 | 3.186 | 2.07 | 3.1713 | 7.11 | |
| AEL | –0.477 | 4.28 | 3.92 | 4.74 | 4.27 | 8.08 | |
| AHard | 4.41 | 1.81 | 1.81 | 2.78 | 1.82 | 0.81 | |
| IV | ELUMO | 16.5171 | 2.596515 | 2.475588 | 1.716375 | 2.584044 | 7.102361 |
| –EHOMO | –12.45941 | 3.760901 | 3.909865 | 2.872823 | 3.758234 | 6.672404 | |
| χ | –14.49 | 0.58 | 0.72 | 0.58 | 0.59 | –0.21 | |
| η | 2.03 | 3.18 | 3.193 | 2.29 | 3.1711 | 6.89 | |
| AEL | –0.465 | 11.58 | 9.40 | 11.66 | 11.48 | –31.35 | |
| AHard | 2.79 | 1.78 | 1.77 | 2.47 | 1.78 | 0.82 | |
| V | ELUMO | 16.5102 | 2.963498 | 2.848121 | 2.077958 | 2.949314 | 7.449772 |
| –EHOMO | –12.06327 | 3.094653 | 3.234635 | 2.291472 | 3.087551 | 5.765693 | |
| χ | –14.29 | 0.07 | 0.19 | 0.11 | 0.07 | –0.84 | |
| η | 2.22 | 3.03 | 3.04 | 2.18 | 3.02 | 6.61 | |
| AEL | –0.471 | 102.63 | 34.82 | 63.04 | 97.37 | –7.99 | |
| AHard | 2.60 | 1.91 | 1.90 | 2.65 | 1.92 | 0.88 | |
| VI | ELUMO | 14.5038 | 1.290144 | 1.146572 | 0.4413206 | 1.267581 | 5.544161 |
| –EHOMO | –10.0267 | 4.156837 | 4.331527 | 3.541704 | 4.159986 | 6.084805 | |
| χ | –12.27 | 1.43 | 1.59 | 1.55 | 1.45 | 0.27 | |
| η | 2.24 | 2.72 | 2.74 | 1.99 | 2.71 | 5.81 | |
| AEL | –0.54 | 4.63 | 4.16 | 4.28 | 4.58 | 24.53 | |
| AHard | 2.48 | 2.04 | 2.03 | 2.79 | 2.05 | 0.95 | |
| VII | ELUMO | 15.40361 | 1.534507 | 1.39925 | 0.7539564 | 1.51676 | 5.631796 |
| –EHOMO | –12.32641 | 3.422596 | 3.578508 | 2.691508 | 3.420128 | 5.689867 | |
| χ | –13.87 | 0.94 | 1.09 | 0.97 | 0.95 | 0.03 | |
| η | 1.54 | 2.48 | 2.49 | 1.72 | 2.47 | 5.66 | |
| AEL | –0.481 | 7.07 | 6.12 | 6.88 | 7.01 | 229.72 | |
| AHard | 3.63 | 2.25 | 2.24 | 3.24 | 2.26 | 0.99 | |
| VIII | ELUMO | 15.48911 | 1.614079 | 1.472582 | 0.8028092 | 1.593253 | 5.815819 |
| –EHOMO | –12.3533 | 3.699537 | 3.860561 | 2.910033 | 3.698387 | 6.201466 | |
| χ | –13.92 | 1.04 | 1.19 | 1.05 | 1.05 | 0.19 | |
| η | 1.57 | 2.66 | 2.67 | 1.86 | 2.65 | 6.01 | |
| AEL | –0.479 | 6.40 | 5.59 | 6.33 | 6.34 | 34.59 | |
| AHard | 3.56 | 2.10 | 2.093 | 3.01 | 2.109 | 0.93 | |
| IX | ELUMO | 15.08743 | 1.524559 | 1.389197 | 0.7397588 | 1.502934 | 5.626748 |
| –EHOMO | –11.85368 | 3.370883 | 3.52209 | 2.624703 | 3.369097 | 5.680253 | |
| χ | –13.47 | 0.92 | 1.07 | 0.94 | 0.93 | 0.03 | |
| η | 1.62 | 2.45 | 2.46 | 1.68 | 2.44 | 5.65 | |
| AEL | –0.495 | 7.23 | 6.25 | 7.08 | 7.15 | 249.32 | |
| AHard | 3.50 | 2.31 | 2.30 | 3.36 | 2.32 | 1.00 | |
| X | ELUMO | 15.12512 | 1.53895 | 1.404091 | 0.7564005 | 1.518818 | 5.640772 |
| –EHOMO | –11.90494 | 3.264767 | 3.41559 | 2.541048 | 3.262239 | 5.520739 | |
| χ | –13.52 | 0.86 | 1.01 | 0.89 | 0.87 | –0.06 | |
| η | 1.61 | 2.40 | 2.41 | 1.65 | 2.39 | 5.58 | |
| AEL | –0.494 | 7.73 | 6.63 | 7.47 | 7.65 | –111.14 | |
| AHard | 3.52 | 2.36 | 2.35 | 3.43 | 2.37 | 1.01 | |
| Aromaticity Rules Quantum Methods | Aroma1 | Aroma2 | Aroma3 | Aroma4 | Aroma5 | |
|---|---|---|---|---|---|---|
| Semi-empirical | CNDO | − | − | − | − | − |
| INDO | − | − | − | − | − | |
| MINDO3 | − | − | × | − | − | |
| MNDO | − | − | − | − | − | |
| AM1 | − | − | − | − | − | |
| PM3 | − | − | − | − | − | |
| ZINDO/1 | − | − | − | − | − | |
| ZINDO/S | − | − | − | − | − | |
| Ab initio | noEXc | × | × | − | × | − |
| B3-LYP | × | − | − | − | − | |
| B3-PW91 | × | − | − | − | − | |
| EDF1 | × | − | − | − | − | |
| Becke97 | × | − | − | − | − | |
| Hartree-Fock | − | × | − | − | × | |
| Aromaticity Rules Quantum Methods | Aroma1 | Aroma2 | Aroma3 | Aroma4 | Aroma5 | |
|---|---|---|---|---|---|---|
| Semi-empirical | CNDO | × | − | − | × | − |
| INDO | × | − | − | × | − | |
| MINDO3 | × | − | − | × | − | |
| MNDO | × | − | × | × | − | |
| AM1 | × | × | − | × | − | |
| PM3 | × | × | − | × | − | |
| ZINDO/1 | × | − | − | × | − | |
| ZINDO/S | × | − | × | × | − | |
| Ab initio | noEXc | − | − | − | − | − |
| B3-LYP | × | − | − | × | − | |
| B3-PW91 | × | − | − | × | − | |
| EDF1 | − | − | − | × | − | |
| Becke97 | × | − | − | × | − | |
| Hartree-Fock | × | × | − | × | − | |
References
- Kekulé, AF. Untersuchungen uber aromatische Verbindungen. Liebigs Ann. Chem 1866, 137, 129–136. [Google Scholar]
- Thomson, JJ. On the structure of the molecule and chemical combination. Philos. Mag 1921, 41, 510–538. [Google Scholar]
- Hückel, E. Quantentheoretische Beiträge zum Benzolproblem. Z. Physik 1931, 70, 204–286. [Google Scholar]
- Julg, A; Françoise, P. Recherches sur la géométrie de quelques hydrocarbures non-alternants: son influence sur les énergies de transition, une nouvelle définition de l'aromaticité. Theor. Chem. Acta 1967, 8, 249–259. [Google Scholar]
- Boldyrev, AI; Wang, LS. All-Metal Aromaticity and Antiaromaticity. Chem. Rev 2005, 105, 3716–3757. [Google Scholar]
- Doering, WV; Detert, F. Cycloheptatrienylium oxide. J. Am. Chem. Soc 1951, 73, 876–877. [Google Scholar]
- Chattaraj, PK; Sarkar, U; Roy, DR. Electronic structure principles and aromaticity. J. Chem. Edu 2007, 84, 354–358. [Google Scholar]
- Mandado, M; Moa, MJG; Mosquera, RA. Exploring basic chemical concepts with the quantum theory of atoms in molecules. In Progress in Quantum Chemistry Research; Hoffman, EO, Ed.; Nova Science Publishers: New York, NY, USA, 2007; pp. 1–57. [Google Scholar]
- Katritzky, AR; Topson, RD. The σ and π inductive effects. J. Chem. Edu 1971, 48, 427–431. [Google Scholar]
- Schleyer, PVR; Maerker, C; Dransfeld, A; Jiao, H; Eikema Hommes, NJRV. Nucleus-independent chemical shifts: A simple and efficient aromaticity probe. J. Am. Chem. Soc 1996, 118, 6317–6318. [Google Scholar]
- Chen, Z; Wannere, CS; Corminboeuf, C; Puchta, R; Schleyer, PVR. Nucleus-Independent Chemical Shifts (NICS) as an aromaticity criterion. Chem. Rev 2005, 105, 3842–3888. [Google Scholar]
- Moran, D; Simmonett, AC; Leach, FE; Allen, WD; Schleyer, PVR; Schaeffer, HF, III. Popular theoretical methods predict benzene and arenes to be nonplanar. J. Am. Chem. Soc 2006, 128, 9342–9343. [Google Scholar]
- Randić, M. Aromaticity and conjugation. J. Am. Chem. Soc 1977, 99, 444–450. [Google Scholar]
- Gutman, I; Milun, M; Trinastić, N. Graph theory and molecular orbitals. 19. Nonparametric resonance energies of arbitrary conjugated systems. J. Am. Chem. Soc 1977, 99, 1692–1704. [Google Scholar]
- Balaban, AT; Schleyer, PVR; Rzepa, HS. Crocker, not armit and robinson, begat the six aromatic electrons. Chem. Rev 2005, 105, 3436–3447. [Google Scholar]
- Ciesielski, A; Krygowski, TM; Cyranski, MK; Dobrowolski, MA; Balaban, AT. Are thermodynamic and kinetic stabilities correlated? A topological index of reactivity toward electrophiles used as a criterion of aromaticity of polycyclic benzenoid hydrocarbons. J. Chem. Inf. Model 2009, 49, 369–376. [Google Scholar]
- Ciesielski, A; Krygowski, TM; Cyrański, MK; Dobrowolski, MA; Aihara, J. Graph–topological approach to magnetic properties of benzenoid hydrocarbons. Phys. Chem. Chem. Phys 2009, 11, 11447–11455. [Google Scholar]
- Tarko, L. Aromatic molecular zones and fragments. 2008, 24–45. [Google Scholar]
- Tarko, L; Putz, MV. On electronegativity and chemical hardness relationships with aromaticity. J. Math. Chem 2010, 47, 487–495. [Google Scholar]
- Kruszewski, J; Krygowski, TM. Definition of aromaticity basing on the harmonic oscillator model. Tetrahedron Lett 1972, 13, 3839–3842. [Google Scholar]
- Krygowski, TM. Crystallographic studies of inter- and intramolecular interactions reflected in aromatic character of π-electron systems. J. Chem. Inf. Comput. Sci. (actually J. Chem. Inf. Model) 1993, 33, 70–78. [Google Scholar]
- Pauling, L; Wheland, GW. The nature of the chemical bond. V. The quantum-mechanical calculation of the resonance energy of benzene and naphthalene and the hydrocarbon free radicals. J. Chem. Phys 1933, 1, 362–375. [Google Scholar]
- Pauling, L; Sherman, J. The nature of the chemical bond. VI. The calculation from thermochemical data of the energy of resonance of molecules among several electronic structures. J. Chem. Phys 1933, 1, 606–618. [Google Scholar]
- Wheland, GW. The Theory of Resonance and Its Application to Organic Chemistry; Wiley: New York, NY, USA, 1944. [Google Scholar]
- Hess, BA; Schaad, LJ. Hückel molecular orbital π resonance energies. Benzenoid hydrocarbons. J. Am. Chem. Soc 1971, 93, 2413–2416. [Google Scholar]
- Dauben, HJ, Jr; Wilson, JD; Laity, JL. Diamagnetic susceptibility exaltation as a criterion of aromaticity. J. Am. Chem. Soc 1968, 90, 811–813. [Google Scholar]
- Flygare, WH. Magnetic interactions in molecules and an analysis of molecular electronic charge distribution from magnetic parameters. Chem. Rev 1974, 74, 653–687. [Google Scholar]
- Schleyer, PvR; Maerker, C; Dransfeld, A; Jiao, H; Hommes, NJRvE. Nucleus-Independent Chemical Shifts: A simple and efficient aromaticity probe. J. Am. Chem. Soc 1996, 118, 6317–6318. [Google Scholar]
- Chen, Z; Wannere, CS; Corminboeuf, C; Puchta, R; Schleyer, PvR. Nucleus-Independent Chemical Shifts (NICS) as an Aromaticity Criterion. Chem. Rev 2005, 105, 3842–3888. [Google Scholar]
- Feixas, F; Matito, E; Poater, J; Solà, M. On the performance of some aromaticity indices: A critical assessment using a test set. J. Comput. Chem 2008, 29, 1543–1554. [Google Scholar]
- Giambiagi, M; de Giambiagi, MS; dos Santos, CD; de Figueiredo, AP. Multicenter bond indices as a measure of aromaticity. Phys. Chem. Chem. Phys 2000, 2, 3381–3392. [Google Scholar]
- Bultinck, P; Ponec, R; van Damme, S. Multicenter bond indices as a new measure of aromaticity in polycyclic aromatic hydrocarbons. J. Phys. Org. Chem 2005, 18, 706–718. [Google Scholar]
- Poater, J; Fradera, X; Duran, M; Solà, M. An Insight into the Local Aromaticities of Polycyclic Aromatic Hydrocarbons and Fullerenes. Chem. Eur. J 2003, 9, 1113–1122. [Google Scholar]
- Matito, E; Poater, J; Duran, M; Solà, M. An analysis of the changes in aromaticity and planarity along the reaction path of the simplest Diels–Alder reaction. Exploring the validity of different indicators of aromaticity. J. Mol. Struct. (Theochem) 2005, 727, 165–171. [Google Scholar]
- Matito, E; Duran, M; Solà, M. The aromatic fluctuation index (FLU): A new aromaticity index based on electron delocalization. J. Chem. Phys 2005, 122, 014109. [Google Scholar]
- Matito, E; Salvador, P; Duran, M; Solà, M. Aromaticity measures from Fuzzy-Atom Bond Orders (FBO). The Aromatic fluctuation (FLU) and the para-delocalization (PDI) indexes. J. Phys. Chem. A 2006, 110, 5108–5113. [Google Scholar]
- Cioslowski, J; Matito, E; Solà, M. Properties of aromaticity indices based on the one-electron density matrix. J. Phys. Chem. A 2007, 111, 6521–6525. [Google Scholar]
- Putz, MV. On absolute aromaticity within electronegativity and chemical hardness reactivity pictures. MATCH Commun. Math. Comput. Chem 2010, 64, 391–418. [Google Scholar]
- Brinck, T; Murray, JS; Politzer, P. Polarizability and volume. J. Chem. Phys 1993, 98, 4305–4307. [Google Scholar]
- Hati, S; Datta, D. Hardness and electric dipole polarizability. Atoms and clusters. J. Phys. Chem 1994, 98, 10451–10454. [Google Scholar]
- Waller, I. Stark's effect of the second order with hydrogen and the Rydberg correction of the spectrum of He and Li. Z. Physik 1926, 38, 635–646. [Google Scholar]
- Epstein, PS. The Stark effect from the point of view of Schrödinger’s quantum theory. Phys. Rev 1926, 28, 695–710. [Google Scholar]
- Hassé, HR. The polarizability of the helium atom and the lithium ion. Proc. Cambridge Phil. Soc 1930, 26, 542–555. [Google Scholar]
- McDowell, HK; Porter, RN. Reduced free-particle Green's functions in quantum-mechanical perturbation calculations. J. Chem. Phys 1976, 65, 658–672. [Google Scholar]
- McDowell, HK. Exact static dipole polarizabilities for the excited S states of the hydrogen atom. J. Chem. Phys 1976, 65, 2518–2522. [Google Scholar]
- Delone, NB; Krainov, VP. Multiphoton Processes in Atoms; Springer: Berlin, Germany, 1994. [Google Scholar]
- Krylovetsky, AA; Manakov, NL; Marmo, SI. Quadratic Stark effect and dipole dynamic polarizabilities of Hydrogen-like levels. Laser Phys 1997, 7, 781–796. [Google Scholar]
- Bratsch, SG. Electronegativity equalization with Pauling units. J. Chem. Edu 1984, 61, 588–590. [Google Scholar]
- Bratsch, SG. A group electronegativity method with Pauling units. J. Chem. Edu 1985, 62, 101–104. [Google Scholar]
- Parr, RG; Donnelly, RA; Levy, M; Palke, WE. Electronegativity: The density functional viewpoint. J. Chem. Phys 1978, 68, 3801–3808. [Google Scholar]
- Sen, KD; Jørgenson, CD. Structure and Bonding; Springer: Berlin, Germany, 1987; Volume 66. [Google Scholar]
- Putz, MV. Contributions within Density Functional Theory with Applications to Chemical Reactivity Theory and Electronegativity; Dissertation Com.: Parkland, FL, USA, 2003. [Google Scholar]
- Putz, MV. Systematic formulation for electronegativity and hardness and their atomic scales within density functional softness theory. Int. J. Quantum Chem 2006, 106, 361–386. [Google Scholar]
- Putz, MV. Absolute and Chemical Electronegativity and Hardness; Nova Science Publishers: New York, NY, USA, 2008. [Google Scholar]
- Putz, MV. Quantum and electrodynamic versatility of electronegativity and chemical hardness. In Quantum Frontiers of Atoms and Molecules; Putz, MV, Ed.; Nova Science Publishers: New York, NY, USA, 2010; Chapter 11, in press. [Google Scholar]
- Koopmans, T. Ordering of wave functions and eigenvalues to the individual electrons of an atom. Physica 1934, 1, 104–110. [Google Scholar]
- Sanderson, RT. Principles of electronegativity Part I. General nature. J. Chem. Edu 1988, 65, 112–119. [Google Scholar]
- Mortier, WJ; Genechten, KV; Gasteiger, J. Electronegativity equalization: application and parametrization. J. Am. Chem. Soc 1985, 107, 829–835. [Google Scholar]
- Putz, MV. Maximum hardness index of quantum acid-base bonding. MATCH Commun. Math. Comput. Chem 2008, 60, 845–868. [Google Scholar]
- Pearson, RG. Hard and Soft Acids and Bases; Dowden, Hutchinson & Ross: Stroudsberg, PA, USA, 1973. [Google Scholar]
- Pearson, RG. Hard and soft acids and bases—the evolution of a chemical concept. Coord. Chem. Rev 1990, 100, 403–425. [Google Scholar]
- Putz, MV; Russo, N; Sicilia, E. On the application of the HSAB principle through the use of improved computational schemes for chemical hardness evaluation. J. Comput. Chem 2004, 25, 994–1003. [Google Scholar]
- Pearson, RG. Chemical Hardness: Applications from Molecules to Solids; Wiley-VCH: Weinheim, Germany, 1997. [Google Scholar]
- Sen, KD; Mingos, DMP. Structure and Bonding; Springer: Berlin, Gernay, 1993; Volume 80. [Google Scholar]
- Parr, RG; Yang, W. Density Functional Theory of Atoms and Molecules; Oxford University Press: New York, NY, USA, 1989. [Google Scholar]
- Putz, MV. Density functionals of chemical bonding. Int. J. Mol. Sci 2008, 9, 1050–1095. [Google Scholar]
- Parr, RG; Chattaraj, PK. Principle of maximum hardness. J. Am. Chem. Soc 1991, 113, 1854–1855. [Google Scholar]
- Putz, MV. Semiclassical electronegativity and chemical hardness. J. Theor. Comput. Chem 2007, 6, 33–47. [Google Scholar]
- Dirac, PAM. Quantum mechanics of many-electron systems. Proc. Roy. Soc. (London) 1929, A123, 714–733. [Google Scholar]
- Löwdin, P-O. On the non-orthogonality problem connected with the use of atomic wave functions in the theory of molecules and crystals. J. Chem. Phys 1950, 18, 365–376. [Google Scholar]
- Löwdin, P-O. Some remarks on the resemblance theorems associated with various orthonormalization procedures. Int. J. Quantum Chem 1993, 48, 225–232. [Google Scholar]
- Hoffmann, R. An extended Hückel theory. I. Hydrocarbons. J. Chem. Phys 1963, 39, 1397–1412. [Google Scholar]
- Roothaan, C. C.J. New developments in molecular orbital theory. Rev. Mod. Phys 1951, 23, 69–89. [Google Scholar]
- Pople, JA; Nesbet, RK. Self-consistent orbitals for radicals. J. Chem. Phys 1954, 22, 571–572. [Google Scholar]
- Pople, JA; Beveridge, DV. Approximate Molecular Orbital Theory; McGraw-Hill: New York, NY, USA, 1970. [Google Scholar]
- Pople, JA; Santry, DP; Segal, GA. Approximate self-consistent molecular orbital theory. I. Invariant procedures. J. Chem. Phys 1965, 43, S129–S135. [Google Scholar]
- Pople, JA; Segal, GA. Approximate self-consistent molecular orbital theory. II. Calculations with complete neglect of differential overlap. J. Chem. Phys 1965, 43, S136–S151. [Google Scholar]
- Pople, JA; Segal, GA. Approximate self-consistent molecular orbital theory. III. CNDO results for AB2 and AB3 systems. J. Chem.Phys 1966, 44, 3289–3297. [Google Scholar]
- Oleari, L; DiSipio, L; De Michelis, G. The evaluation of the one-centre integrals in the semi-empirical molecular orbital theory. Mol. Phys 1966, 10, 97–109. [Google Scholar]
- Slater, JI. Quantum Theory of Atomic Structure; McGraw-Hill Book Company: New York, NY, USA, 1960. [Google Scholar]
- Baird, NC; Dewar, MJS. Ground states of σ-bonded molecules. IV. The MINDO method and its application to hydrocarbons. J. Chem. Phys 1969, 50, 1262–1275. [Google Scholar]
- Dewar, MJS; Hasselbach, E. Ground states of .sigma.-bonded molecules. IX. MINDO [modified intermediate neglect of differential overlap]/2 method. J. Am. Chem. Soc 1970, 92, 590–598. [Google Scholar]
- Dewar, MJS; Lo, DH. Ground states of sigma-bonded molecules. XVII. Fluorine compounds. J. Am. Chem. Soc 1972, 94, 5296–5303. [Google Scholar]
- Bingham, RC; Dewar, MJS; Lo, DH. Ground states of molecules. XXV. MINDO/3. Improved version of the MINDO semiempirical SCF-MO method. J. Am. Chem. Soc 1975, 97, 1285–1293. [Google Scholar]
- Bingham, RC; Dewar, MJS; Lo, DH. Ground states of molecules. XXVI. MINDO/3 calculations for hydrocarbons. J. Am. Chem. Soc 1975, 97, 1294–1301. [Google Scholar]
- Bingham, RC; Dewar, MJS; Lo, DH. Ground states of molecules. XXVII. MINDO/3 calculations for carbon, hydrogen, oxygen, and nitrogen species. J. Am. Chem. Soc 1975, 97, 1302–1306. [Google Scholar]
- Bingham, RC; Dewar, MJS; Lo, DH. Ground states of molecules. XXVIII. MINDO/3 calculations for compounds containing carbon, hydrogen, fluorine, and chlorine. J. Am. Chem. Soc 1975, 97, 1307–1311. [Google Scholar]
- Dewar, MJS; Lo, DH; Ramsden, CA. Ground states of molecules. XXIX. MINDO/3 calculations of compounds containing third row elements. J. Am. Chem. Soc 1975, 97, 1311–1318. [Google Scholar]
- Murrell, JN; Harget, AJ. Semi-empirical Self-consistent-field Molecular Orbital Theory of Molecules; Wiley Interscience: New York, NY, USA, 1971. [Google Scholar]
- Ohno, K. Some remarks on the Pariser-Parr-Pople method. Theor. Chim. Acta 1964, 2, 219–227. [Google Scholar]
- Klopman, G. A semiempirical treatment of molecular structures. II. Molecular terms and application to diatomic molecules. J. Am. Chem. Soc 1964, 86, 4550–4557. [Google Scholar]
- Pople, JA; Beveridge, DL; Dobosh, PA. Approximate self-consistent molecular-orbital theory. V. Intermediate neglect of differential overlap. J. Chem. Phys 1967, 47, 2026–2034. [Google Scholar]
- Dewar, MJS; Thiel, W. Ground states of molecules. 38. The MNDO method. Approximations and parameters. J. Am. Chem. Soc 1977, 99, 4899–4907. [Google Scholar]
- Dewar, MJS; McKee, ML. Ground states of molecules. 41. MNDO results for molecules containing boron. J. Am. Chem. Soc 1977, 99, 5231–5241. [Google Scholar]
- Dewar, MJS; Rzepa, HS. Ground states of molecules. 40. MNDO results for molecules containing fluorine. J. Am. Chem. Soc 1978, 100, 58–67. [Google Scholar]
- Davis, LP; Guidry, RM; Williams, JR; Dewar, MJS; Rzepa, HS. MNDO calculations for compounds containing aluminum and boron. J. Comp. Chem 1981, 2, 433–445. [Google Scholar]
- Dewar, MJS; Storch, DM. Development and use of quantum molecular models. 75. Comparative tests of theoretical procedures for studying chemical reactions. J. Am. Chem. Soc 1985, 107, 3898–3902. [Google Scholar]
- Thiel, W. Semiempirical methods: current status and perspectives. Tetrahedron 1988, 44, 7393–7408. [Google Scholar]
- Clark, TA. Handbook of Computational Chemistry; John Wiley and Sons: New York, NY, USA, 1985. [Google Scholar]
- Dewar, MJS; Zoebisch, EG; Healy, EF; Stewart, JJP. Development and use of quantum mechanical molecular models. 76. AM1: A new general purpose quantum mechanical molecular model. J. Am. Chem. Soc 1985, 107, 3902–3909. [Google Scholar]
- Dewar, MJS; Dieter, KM. Evaluation of AM1 calculated proton affinities and deprotonation enthalpies. J. Am. Chem. Soc 1986, 108, 8075–8086. [Google Scholar]
- Stewart, JJP. MOPAC: A semiempirical molecular orbital program. J. Comp. Aided Mol. Design 1990, 4, 1–103. [Google Scholar]
- Stewart, JJP. Optimization of parameters for semiempirical methods. I. Method. J. Comput. Chem 1989, 10, 209–220. [Google Scholar]
- Stewart, JJP. Optimization of parameters for semiempirical methods. II. Applications. J. Comput. Chem 1989, 10, 221–264. [Google Scholar]
- Del Bene, J; Jaffé, HH. Use of the CNDO method in spectroscopy. I. Benzene, pyridine, and the diazines. J. Chem. Phys 1968, 48, 1807–1814. [Google Scholar]
- Del Bene, J; Jaffé, HH. Use of the CNDO method in spectroscopy. II. Five-membered rings. J. Chem. Phys 1968, 48, 4050–4056. [Google Scholar]
- Del Bene, J; Jaffé, HH. Use of the CNDO method in spectroscopy. III. Monosubstituted benzenes and pyridines. J. Chem. Phys 1968, 49, 1221–1229. [Google Scholar]
- Ridley, JE; Zerner, MC. Triplet states via intermediate neglect of differential overlap: Benzene, Pyridine and the Diazines. Theor. Chim. Acta 1976, 42, 223–236. [Google Scholar]
- Bacon, AD; Zerner, MC. An intermediate neglect of differential overlap theory for transition metal complexes: Fe, Co and Cu chlorides. Theor. Chim. Acta 1979, 53, 21–54. [Google Scholar]
- Stavrev, KK; Zerner, MC; Meyer, TJ. Outer-sphere charge-transfer effects on the spectroscopy of the [Ru(NH3)5(py)]2+ Complex. J. Am. Chem. Soc 1995, 117, 8684–8685. [Google Scholar]
- Stavrev, KK; Zerner, MC. On the Jahn–Teller effect on Mn2+ in zinc-blende ZnS crystal. J. Chem. Phys 1995, 102, 34–39. [Google Scholar]
- Cory, MG; Stavrev, KK; Zerner, MC. An examination of the electronic structure and spectroscopy of high- and low-spin model ferredoxin via several SCF and CI techniques. Int. J. Quant. Chem 1997, 63, 781–795. [Google Scholar]
- Anderson, WP; Edwards, WD; Zerner, MC. Calculated spectra of hydrated ions of the first transition-metal series. Inorg. Chem 1986, 25, 2728–2732. [Google Scholar]
- Anderson, WP; Cundari, TR; Zerner, MC. An intermediate neglect of differential overlap model for second-row transition metal species. Int. J. Quantum Chem 1991, 39, 31–45. [Google Scholar]
- Boys, SF. Electronic wavefunctions. I. A general method of calculation for stationary states of any molecular system. Proc. Roy. Soc 1950, A200, 542–554. [Google Scholar]
- Szabo, A; Ostlund, NS. Modern Quantum Chemistry - Introduction to Advanced Electronic Structure Theory; Dover Publications Inc.: New York, NY, USA, 1996. [Google Scholar]
- Clementi, E; Roetti, C. Roothaan-Hartree-Fock atomic wavefunctions: Basis functions and their coefficients for ground and certain excited states of neutral and ionized atoms, Z ≤ 54. At. Data Nucl. Data Tables 1974, 14, 177–478. [Google Scholar]
- Hehre, WJ; Stewart, RF; Pople, JA. Self-consistent molecular-orbital methods. I. Use of Gaussian expansions of Slater-type atomic orbitals. J. Chem. Phys 1969, 51, 2657–2665. [Google Scholar]
- Collins, JB; Schleyer, PvR; Binkley, JS; Pople, JA. Self-consistent molecular orbital methods. XVII. Geometries and binding energies of second-row molecules. A comparison of three basis sets. J. Chem. Phys 1976, 64, 5142–5152. [Google Scholar]
- Stewart, RF. Small Gaussian expansions of Slater-type orbitals. J. Chem. Phys 1970, 52, 431–439. [Google Scholar]
- Hartree, DR. The wave mechanics of an atom with a non-Coulomb central field. Proc. Cam. Phil. Soc 1928, 24, 89–111. [Google Scholar]
- Hartree, DR. The wave mechanics of an atom with a noncoulomb central field. Part I. Theory and methods. Part II. Some results and discussions. Proc. Cam. Phil. Soc 1928, 24, 111–132. [Google Scholar]
- Hartree, DR. The Calculation of Atomic Structures; John Wiley and Sons: New York, NY, USA, 1957. [Google Scholar]
- Fock, V. Näherungsmethode zur Lösung des quantenmechanischen Mehrkörperproblems. Z. Physik 1930, 61, 126–140. [Google Scholar]
- Kohn, W; Sham, LJ. Self-consistent equations including exchange and correlation effects. Phys. Rev 1965, 140, A1133–A1138. [Google Scholar]
- Johnson, BG; Gill, PMW; Pople, JA. The performance of a family of density functional methods. J. Chem. Phys 1993, 98, 5612–5627, Erratum: Johnson, B.G. J. Chem. Phys. 1994, 101, 9202. [Google Scholar]
- Slater, JC. Quantum Theory of Molecules and Solids; McGraw-Hill: New York, NY, USA, 1974; Volume 4. [Google Scholar]
- Becke, AD. Density-functional exchange energy approximation with correct asymptotic behaviour. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar]
- Perdew, JP; Chevary, JA; Vosko, SH; Jackson, KA; Pederson, MR; Sing, DJ; Fiolhais, C. Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B 1992, 46, 667–6687. [Google Scholar]
- Senatore, G; March, NH. Recent progress in the field of electron correlation. Rev. Mod. Phys 1994, 66, 445–479. [Google Scholar]
- Lee, C; Yang, W; Parr, RG. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar]
- Miehlich, B; Savin, A; Stoll, H; Preuss, H. Results obtained with the correlation energy density functionals of Becke and Lee, Yang and Parr. Chem. Phys. Lett 1989, 157, 200–206. [Google Scholar]
- Gill, PMW; Johnson, BG; Pople, JA; Frisch, MJ. The performance of the Becke-Lee-Yang-Parr (B-LYP) density functional theory with various basis-sets. Chem. Phys. Lett 1992, 197, 499–505. [Google Scholar]
- Vosko, SH; Wilk, L; Nusair, M. Accurate spin-dependent electron liquid correlation energies for local spin density calculations: a critical analysis. Can. J. Phys 1980, 58, 1200–1211. [Google Scholar]
- Becke, AD. Density-functional thermochemistry. III. The role of exact exchange. J Chem Phys 1993, 98, 5648–5653. [Google Scholar]
- Becke, AD. Density-functional thermochemistry. V. Systematic optimization of exchange-correlation functionals. J. Chem. Phys 1997, 107, 8554–8561. [Google Scholar]
- Putz, MV; Russo, N; Sicilia, E. Atomic radii scale and related size properties from density functional electronegativity formulation. J. Phys. Chem 2003, 107, 5461–5465. [Google Scholar]
- Program Package, Single Point, Minimal Basis Set-for Ab Initio Methods; HyperChem 7.01; Hypercube, Inc.: Gainesville, FL, USA, 2002.
- Putz, MV. Electronegativity: quantum observable. Int. J. Quantum Chem 2009, 109, 733–738. [Google Scholar]
- Bethe, H; Jackiw, R. Intermediate Quantum Mechanics, 2nd ed; Benjamin: New York, NY, USA, 1968; Chapter 11. [Google Scholar]
- Jackiw, R. Quantum mechanical sum rules. Phys. Rev 1967, 157, 1220–1225. [Google Scholar]
- Thomas, W. Uber die Zahl der Dispersionselectronen, die einem starionären Zustande zugeordnet sind. Naturwissenschaftern 1925, 13, 510–525. [Google Scholar]
- Kuhn, W. Regarding the total strength of a condition from outgoing absorption lines. Z. Phys 1925, 33, 408–412. [Google Scholar]
- Reiche, F; Thomas, W. Uber die Zahl der dispersionselektronen, die einem stationären Zustand zugeordnet sind. Z. Phys 1925, 34, 510–525. [Google Scholar]
- Mehra, J; Rechenberg, H. The Historical Development of Quantum Theory: The Formulation of Matrix Mechanics and its Modifications 1925–1926; Springer-Verlag: New York, NY, USA, 1982; Chapter IV. [Google Scholar]
- Bethe, H. Theory of the passage of fast corpuscular rays through matter (Translated). In Selected Works of Hans A Bethe with Commentary (World Scientific Series in 20th Century Physics); Bethe, H, Ed.; World Scientific: Singapore, 1997; Volume 18, pp. 77–154. [Google Scholar]
- Morse, PM; Feshbach, H. Methods of Theoretical Physics; McGraw-Hill: New York, NY, USA, 1953. [Google Scholar]
© 2010 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Putz, M.V. Compactness Aromaticity of Atoms in Molecules. Int. J. Mol. Sci. 2010, 11, 1269-1310. https://doi.org/10.3390/ijms11041269
Putz MV. Compactness Aromaticity of Atoms in Molecules. International Journal of Molecular Sciences. 2010; 11(4):1269-1310. https://doi.org/10.3390/ijms11041269
Chicago/Turabian StylePutz, Mihai V. 2010. "Compactness Aromaticity of Atoms in Molecules" International Journal of Molecular Sciences 11, no. 4: 1269-1310. https://doi.org/10.3390/ijms11041269
APA StylePutz, M. V. (2010). Compactness Aromaticity of Atoms in Molecules. International Journal of Molecular Sciences, 11(4), 1269-1310. https://doi.org/10.3390/ijms11041269