1. Introduction
Isothermal titration calorimetry [
1] is a fundamental quantitative biochemical tool for characterizing intermolecular interactions, such as protein-ligand, protein-protein, drug-DNA and protein-DNA. It uses stepwise injections of one reagent into a calorimetric cell containing the second reagent to measure the heat of the reaction for both exothermic and endothermic processes.
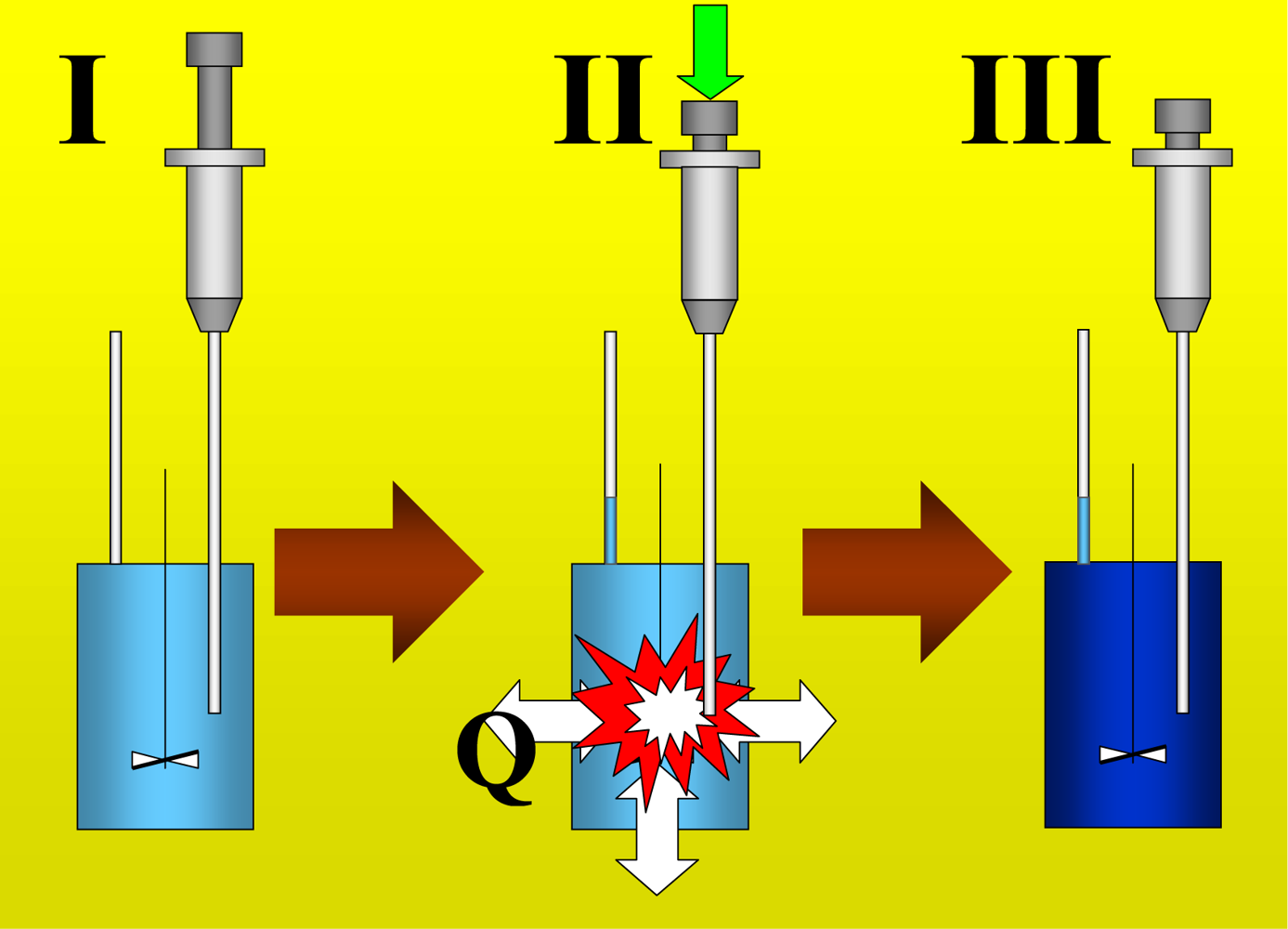
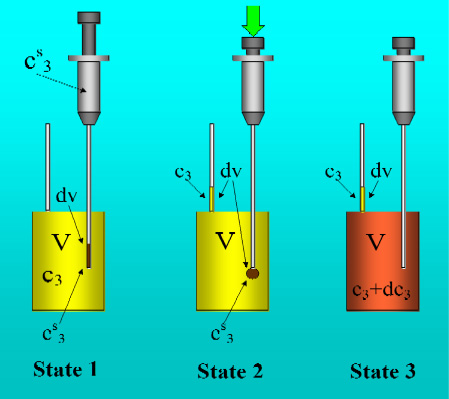
Figure 1 shows the basic performance of a titration in an isothermal titration calorimeter with full cells. The titration cell (I) is composed of a vessel, a syringe containing a second liquid and a drainage capillary, through which liquid in excess is removed from the full cell upon introduction of a new liquid from the syringe. The vessel is maintained at a constant temperature, and the interior liquid is stirred to achieve homogeneity.
When the liquid of the vessel interior (see
Figure 1-I) is titrated with the amount of liquid in the syringe heat flows from or to the vessel (
Figure 1-II); this heat flow is measured and recorded by a suitable electronic system. At this time, a volume of liquid equal to that of the titrant liquid exits the vessel through the drainage capillary (
Figure 1-II). In the final state (1-III), the interior of the vessel contains the two liquids that are completely mixed at a known composition and the drainage capillary holds an amount of liquid with a different composition. Thus, it is possible to consider an effective volume in the vessel in which a determinate amount of heat is produced (or adsorbed) and in which the concentrations are known. Importantly, this effective volume is constant throughout the titration process. If the cell is half-full, however, this assumption is not necessarily correct, because the volume of sample varies in the process of titration. In this work, we consider only full cell titration calorimeters.
Table 1 shows a list of isothermal titration calorimeters that are currently commercially available. The majority of these calorimeters use the full cells method.
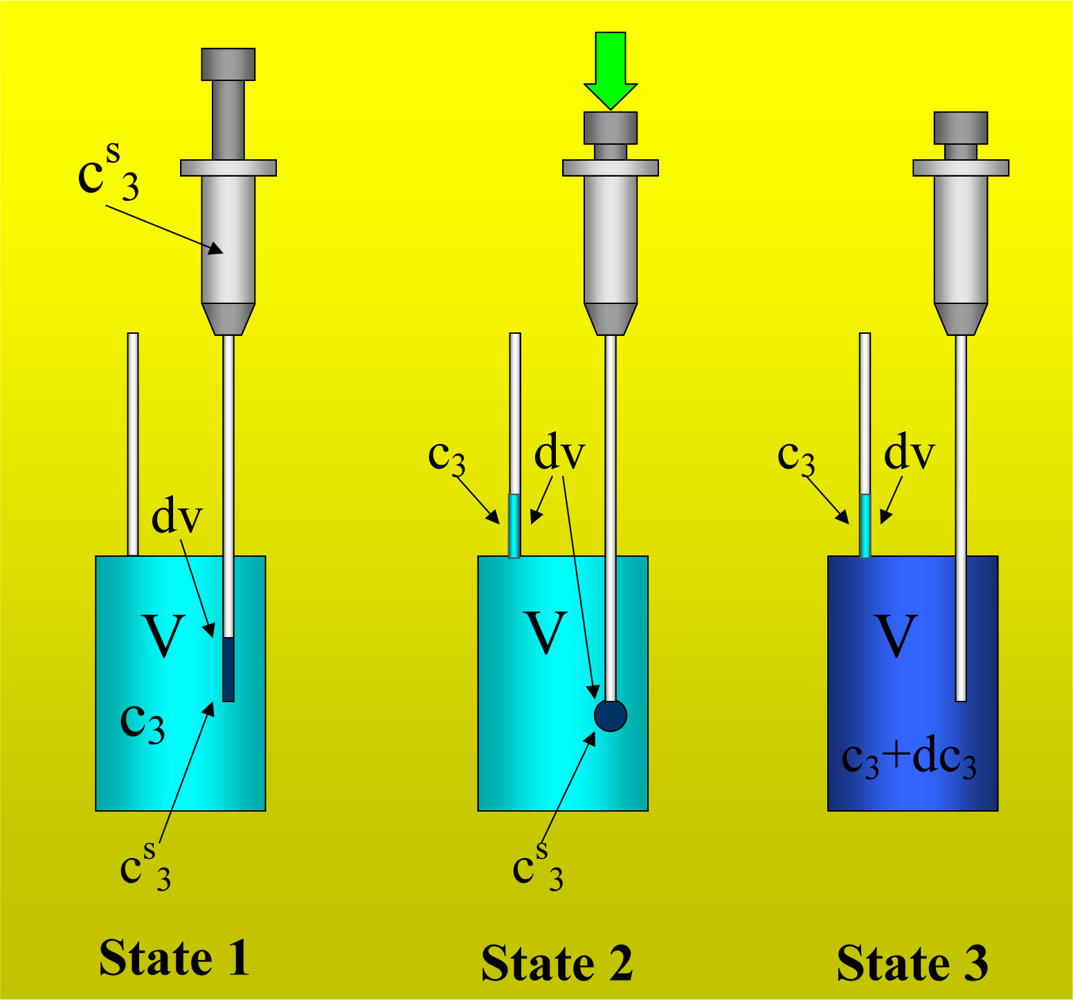
It is commonly accepted that with a suitable procedure involving simple titration experiments [
2], it is possible to measure the heat of interaction between two components (components 2 and 3) in a solvent (component 1). In a first experiment, a solution of component 2 in the solvent (component 1) is titrated with a stock solution of component 3 in the same solvent. The contributions to the heat that is measured are the heat of interaction between the components 2 and 3, the heats of dilution of components 2 and 3, and the heats of interaction between the component 3 and the different parts of the experimental setup (vessel walls, stirrer and syringe needle). In a second experiment the solvent (component 1) is titrated with the stock solution.
This experiment is carried out using the same conditions as the first experiment. In this case, the contributions to the heat measured are the heat of dilution of the component 3 and the interaction with the different parts of the experimental setup. In the third experiment the solution of component 2 in the solvent is titrated with the solvent and the heat of dilution of component 2 is the contribution to the heat measured. In the fourth experiment the solvent is titrated with the solvent.
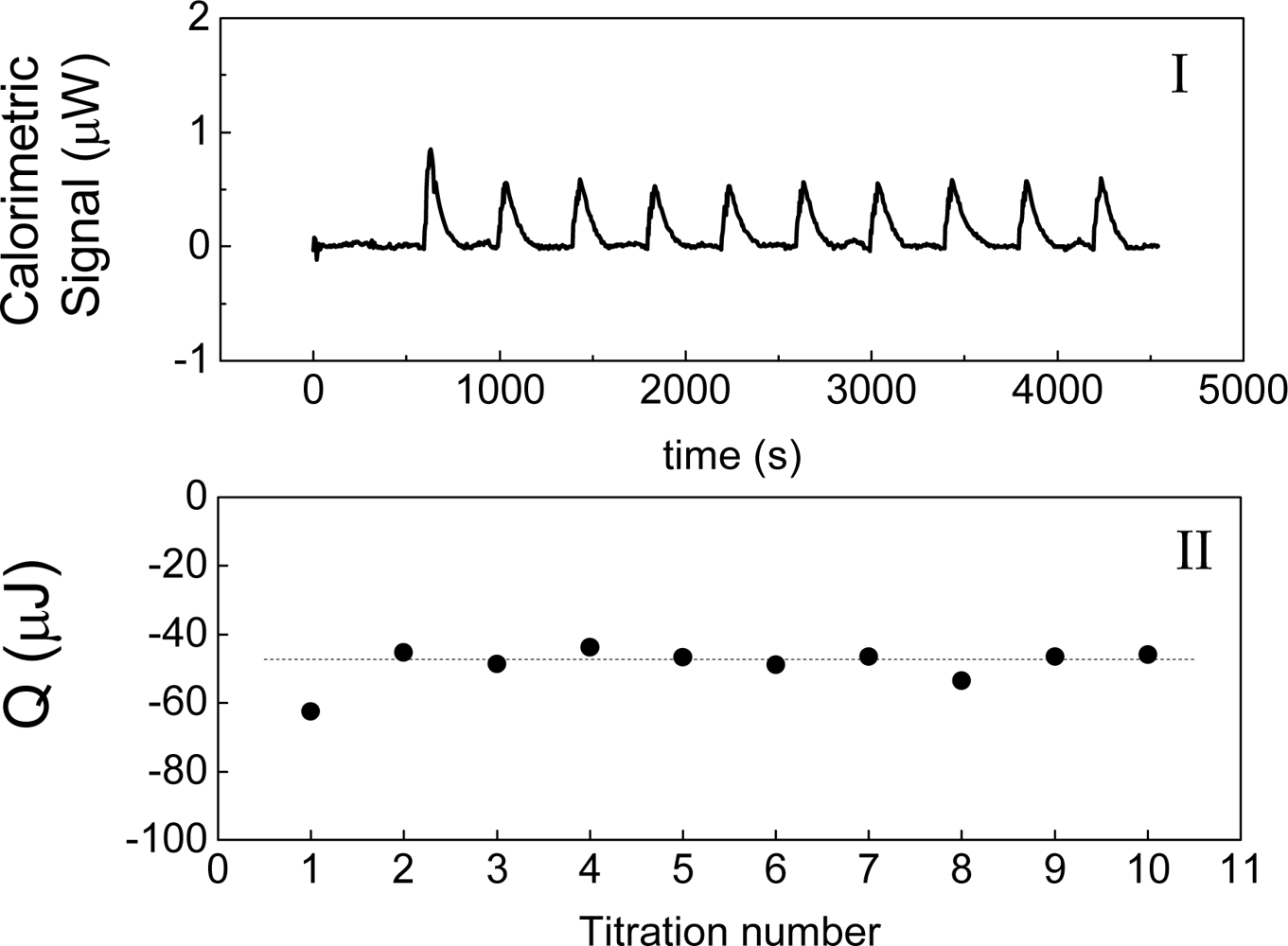
Figure 2 shows an example of this experiment, in which water is titrated with water. The heat of interaction is interpreted as the following balance:
The fourth experiment takes part in the protocol because its contribution appears also in experiments one, second and three. From a practical point of view, the heats of experiments 3 and 4 are negligible since they are usually insignificant [
2]. In this way,
Equation (1) takes the form [
1,
2]:
Because all processes in the above protocol are carried out at constant pressure, the measured heat is usually interpreted in terms of the following Equation [
3]:
where ΔH is the difference in enthalpy between the final and the initial estates, and Q is the heat measured by the calorimeter. The heat of interaction that is obtained from the above protocol is usually interpreted as the enthalpy of interaction.
It is interesting to note that the origin of the protocol shown in
Equations (1) and
(2) is empirical. The use of the set of
Equations (1) and
(2) to obtain heats of interaction seems reasonable and reliable, and it is supported by a considerable amount of experimental evidence; nonetheless, we do not have a rigorous demonstration that this heat can be considered as a heat of interaction. Thus, we do not know if this interpretation is exact or if it is an approximation. If it is an approximation, it would be useful to know under what conditions it can be applied. It is also very interesting to note that
Equation (3) is inconsistent with the considerations made in the protocol shown in the
Equations (1) and
(2). If for example, we consider the titration of water in water, the initial state is a volume V of pure water, and the final state after titration is this volume V of pure water. The difference in enthalpy for this system is zero. From
Equation (3), the expected heat for this experiment is zero, against the experimental result shown in
Figure 2. Without the
Equation (3) the problem now is the following: can we interpret the heats obtained by
Equations (1) and
(2) as enthalpies of interaction?
In this paper, we address the above problem and the physical meaning of the heat obtained from the given protocol based on the typical performance of an isothermal titration with full cells which is described in
Figure 1. We first aimed to find a new equation to replace the equation Q = ΔH [
Equation (3)]. Next, we determined how the concentrations of different components vary after the titration. Then, we calculated the heats involved in the titration process. We also applied a set of thermodynamic tools that were developed in our previous works [
4–
6]. We consider the hypothesis that the solutions are sufficiently diluted. This hypothesis was mathematically implemented, supposing that the molar (or specific) thermodynamic properties could be described by a Taylor expansion of the first order (high diluted region). Another concept that we applied is the “fraction of a system”. A fraction of a system is a thermodynamic entity (with internal composition) that groups several components. This concept is essential for working with multicomponent systems at infinite dilution.
We observed that the heat measured in an experiment where solvent is titrated with itself has its origin in the work required for to inject the volume of titrant. For this reason it can be named as “heat of injection”. In addition, we see that the heat involved per mol of titrant when the titration is infinitesimally small is related to its partial molar enthalpy of interaction at infinite dilution and its molar partial volume of interaction also at infinite dilution. That is, using the full-cell method, the heat measured by the calorimeter when the above protocol is employed is the partial molar enthalpy of interaction only when the variation in the molar partial volume of interaction can be neglected. This fact is true in binding events where protein unfolding is involved.
4. Discussion
As it has been stated previously, a measured heat is obtained experimentally when a liquid is titrated with itself.
Figure 2 shows the measurement of this heat when water is titrated with water at 30 °C. This result agrees with those that have been obtained by other authors [
2]. This heat has been named as “blank machine” [
2] or “instrumental heat” and its origin could be attributed to a possible difference in temperatures between the titrated volume and the cell. In the case of
Figure 2, the room temperature was 20 °C and the temperature cell was 30 °C. That is, if a difference in temperature existed, the initial temperature T
i of the titrant volume would be less than the final temperature T
f. According to equation:
where Q
inj is the heat obtained from the injection, m the mass of the titrant volume, c
p the specific heat capacity and ΔT = T
f - T
i we would expect a heat positive. The heat shown on
Figure 2 is negative and therefore it is not possible to explain the heat observed on
Figure 2 in terms of a “blank machine” or an “instrumental heat”. The merit of the equation ΔH = W
inj + Q [
Equation (9)] is that it allows to take into account a heat measured by the calorimeter when a liquid is titrated with itself and the sign of this heat. Because it is necessary to apply work to the system in order to introduce an amount of liquid into the cell and push out an equivalent amount of liquid, this work must be positive. Since in this case Q
inj = -W
inj, the heat measured must to be negative. The heat shown in
Figures 2-II agrees with this prediction.
Contributions to Q
inj can be several as for example the friction between liquids (relative viscosities) and the friction between the liquid and the narrow bore tube of the needle. Recently [
8] the following equation has been proposed that gives the temperature rise in a fluid from frictional flow in a tube:
where ΔT is the difference in temperature in K, μ is the fluid viscosity in centipoises, l is the length of the tube in cm, v’ is the volumetric flow rate in cm
3 min
−1, ρ is the fluid density in g cm
3, C is the fluid heat capacity in J g
−1 K
−1, and d is the tube diameter in cm. For water flowing through a 0.4 mm diameter tube 30 cm long at 1 cm
3 min
−1, ΔT = 0.002 K. As it is stated by
Equation (88) ΔT depends on the nature of the fluid through its viscosity, density and heat capacity, on the geometry of the calorimetric system through the diameter and length of the needle and to the conditions of the experiment through the volume flow rate. When combining
Equations (87) and
(88) it results an expected influence of the volumetric flow rate (v’) in Q
inj. This fact was shown experimentally in the Figure 2.7 of ref. [
2].
Figure 5 shows the calorimetric signal of the titration of toluene with toluene. Unlike in
Figure 1 in which all peaks are exothermic, in this case a minimum with a negative value (endothermic peak) was recorded. Usually, the syringe is at the temperature of the room, and the cell is at the fixed temperature of the experiment. This endothermic peak can be explained by the large volume of titration (which is 15% of the volume of the cell) and the difference in temperature between the cell and the room.
Therefore we can state that a characteristic of isothermal titration calorimetry is the necessity of very small volume according to two considerations: first, with a large volume, the temperature of the experiment is not kept constant, second, the validity of
Equation (81) imposes very small titration volumes in order to assume that the heat obtained following the experimental the protocol is related to a partial molar enthalpy of interaction at infinite dilution and to a term proportional to a partial molar volume of interaction also at infinite dilution.
In
Equation (86), we have two contributions to the heat obtained from the given protocol. One is the partial molar enthalpy of interaction of component 3 within the limit of infinite dilution (Δh
Δ3;1,2). The second contribution is – ρ
1h
1Δv
Δ3;1,2. This term represents the enthalpy of a volume of solvent Δv
Δ3;1,2 as a consequence of the protocol employed. In addition to this, it is possible to demonstrate that when the interactions between two components are maximum, the heat dq
3;1,2/dns
3 obtained is zero. In a previous work [
5], we demonstrated that if the plot of j
oF;1 as function of a variable of composition is linear for a range of compositions of F, then the interactions between the components of the fraction are maximum in that range. The composition variable employed was the mass fraction of component 3 in the fraction (t
f3).
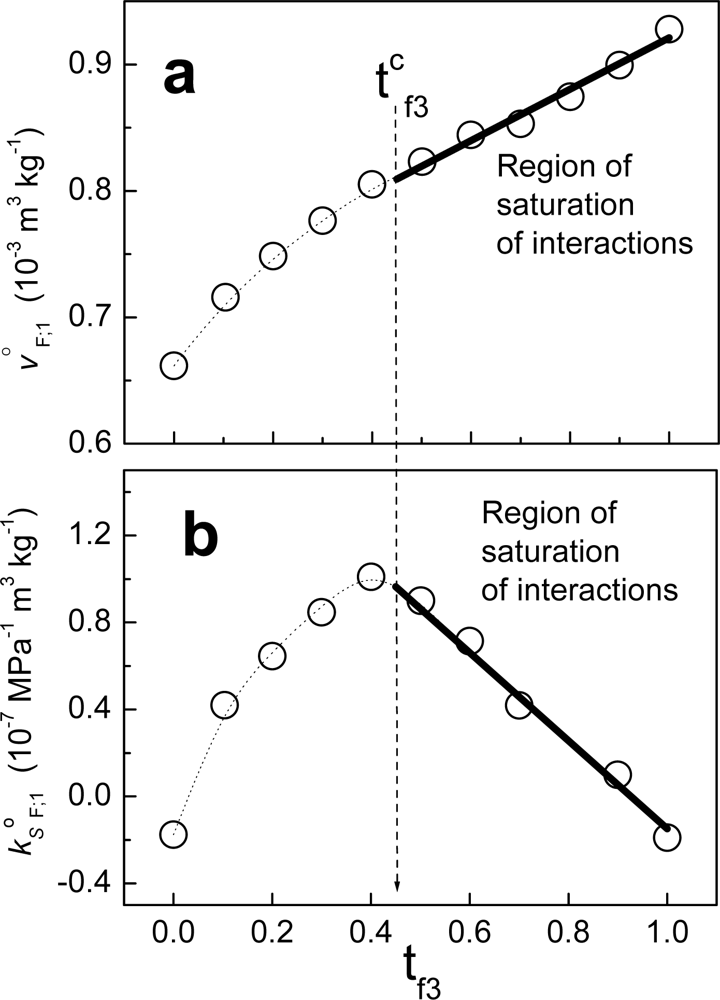
Figure 6 shows an example when fraction F is composed of non-charged polymeric particles (component 2) and a cationic surfactant (component 3). The solvent in this case is water. From zero to t
f3, the behavior is non-linear. Considering that the value tc
f3 in units of molar fractions is x
cf3, at this composition the partial property of F takes the value:
where x
f2= 1-x
f3. Above the value xc
f3, j
oF;1 can be written as:
where:
and X
f2= 1-X
f3. When we write jΔ
2;1,3 and j
Δ3;1,2, we assume [
4–
6] that concomitantly component 2 is in the presence of components 1 and 3 and component 3 is in the presence of components 1 and 2. Thus the notation j
oF;1 = x
f2 j
Δ2;1,3 + x
f3 j
Δ3;1,2 indicates that, F is composed of components 2 and 3, which are interacting in a medium (component 1). On the other hand, j
o2;1 and j
o3;1 indicate that component 2 is alone in component 1 and that component 3 is alone in component 1. Therefore, if we write j
oF;1 = x
f2 j
o2;1 + x
f3 j
o3;1 we assume that fraction F is composed of components 2 and 3, which are not interacting.
This is the case for
Equation (90), where fraction F is composed of a fraction of constant composition (with partial property j
oF;1(xc
f3)) and an amount of component 3 (with partial property j
o3;1) and these components are not interacting. In other words [
5,
6], in a region of saturation of interactions, component 2 is interacting with a part of component 3 to form a fraction with constant composition. A fraction with constant composition is named a “pseudo-component [
4–
6].” This pseudo-component, composed of 2 and a part of 3, does not interact with the rest of component 3. A saturation of interactions is related to the formation of pseudo-components.
By substituting the equation for j
oF;1 in the region of saturation (
Equation (90)) in the equation for calculating j
o3;1,2 from j
oF;1 (
Equation (117)) and bearing in mind that:
we obtain that:
Substituting this result into
Equation (86) we obtained that in the region of saturation of interactions:
Another interesting problem in isothermal titration calorimetry is the following: is there a relationship between the experiments carried out when component 3 is the titrant and when component 2 is the titrant? We can answer this question as follows: the heat generated when component 3 is the titrant can be obtained from (86), dq
3;1,2/dns
3. In the same way, the heat obtained when component 2 is the titrant can be written as:
This is an equation of the Gibbs-Duhem type that relates the heats of interaction obtained when components 2 and 3 are the titrant components.
From equation ΔH = Q it is commonly assumed the heat measured by an ITC can be related to the variation of enthalpy; many papers and books in biochemistry and biophysics have reported results on this link. In this work, we have demonstrated that the equation ΔH = Q does not hold for isothermal titration calorimetry and that the true equation is ΔH = W
inj + Q, which involves a term of work. In addition, we have found that the heat obtained from the usual protocol employed in the determination of the heat of interaction dq
3;1,2/dns
3 between two components (
Equation (86)) involves both a variation of enthalpy and a variation of volume. In general Δv
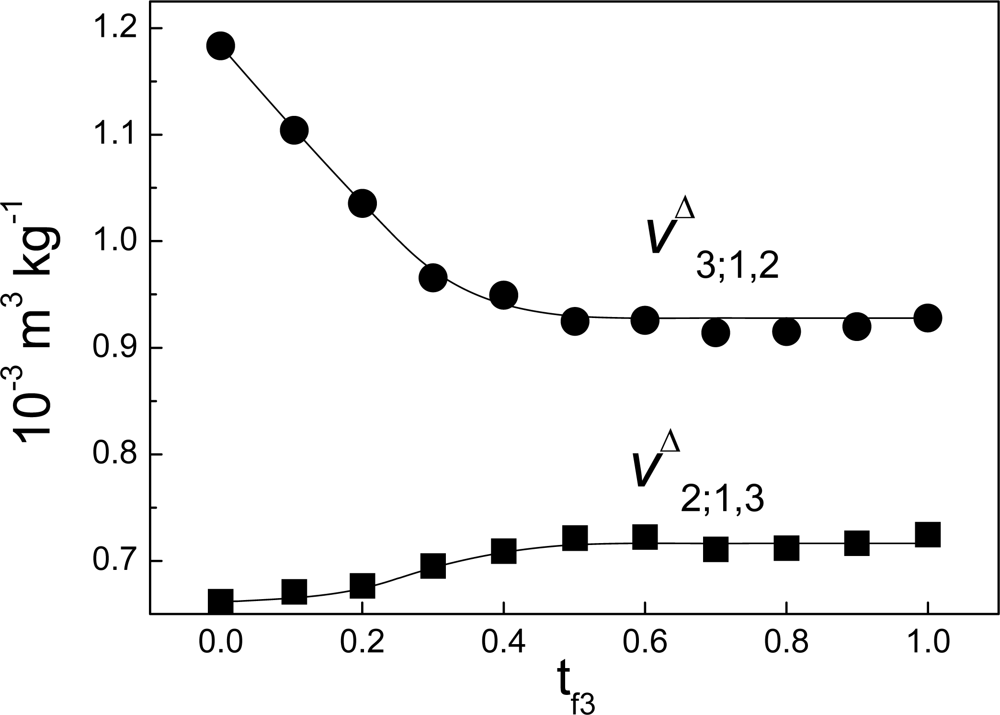
Δ3;1,2 is not zero. As example of this,
Figure 7 shows the case of the interaction between non-charged polymeric particles and a surfactant. On the other hand, if there were no link between the variation of enthalpy and the heat of interaction measured by ITC this would affect the results of heats of interaction obtained with the technique, particularly in biophysical applications. This paradox can be solved as follows: models have been proposed [
9–
11] that indicate that the variation in volume for protein unfolding is very small. In addition it has been found experimentally that the variation in volume during the denaturation of lysozyme by a strong denaturant is very close to zero [
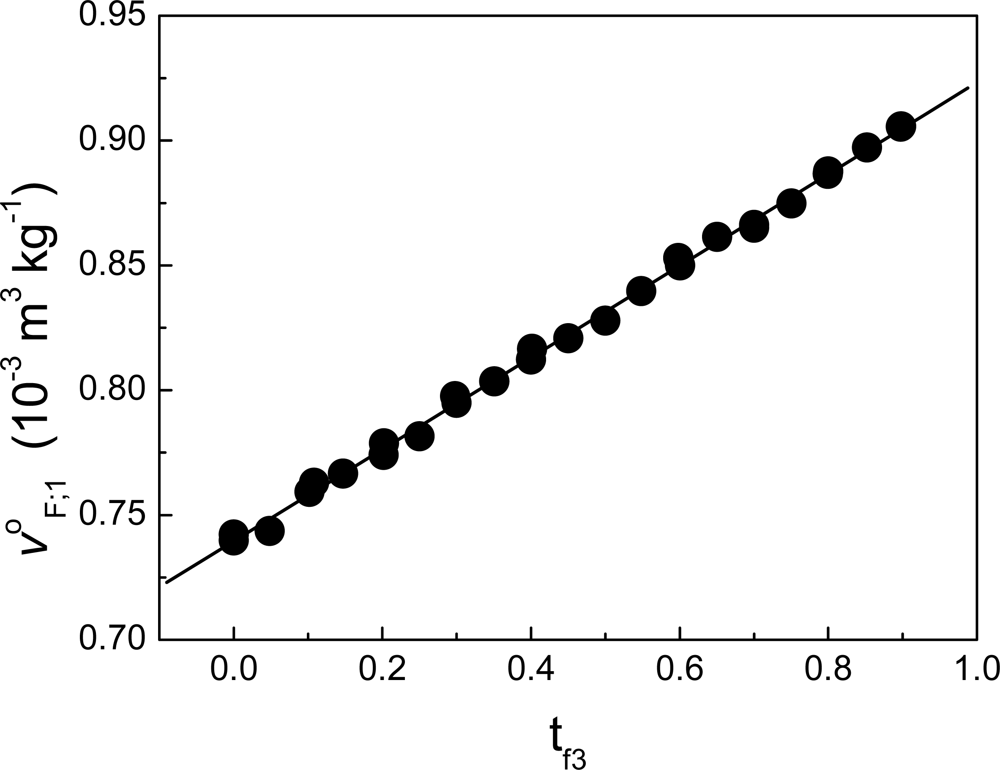
12]. In our case, we have found that Δv
ΔF;1 can be neglected in the process of binding deciltrimethylammonium bromide to lysozyme [
5] (see
Figure 8). Supposing Δv
ΔF;1 ≈ 0 in
Equation (125) (in
Appendix 1: “Limits at infinite dilution in multicomponent systems”), then:
Considering that
Equation (99) holds in general for a process involving protein unfolding, substituting this result into the equation of dq
3;1,2/dns
3 (
Equation (86)) yields for this type of processes:
Another possibility is that for processes of biophysical interest, the approximation |ρ1h1ΔvΔ3;1,2|≪ |ΔhΔ3;1,2| holds.