Next Article in Journal
Application of ‘Inductive’ QSAR Descriptors for Quantification of Antibacterial Activity of Cationic Polypeptides
Previous Article in Journal
Giving Molecules an Identity. On the Interplay Between QSARs and Partial Order Ranking
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Molecules
Volume 9
Issue 12
10.3390/91201019
molecules-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

QSPR Calculation of Normal Boiling Points of Organic Molecules Based on the Use of Correlation Weighting of Atomic Orbitals with Extended Connectivity of Zero- and First-Order Graphs of Atomic Orbitals

by
Maykel Pérez González
1,
Andrey A. Toropov
2,
Pablo R. Duchowicz
3 and
Eduardo A. Castro
3,*
1
Department of Drug Design, Experimental Sugar Cane Station “Villa Clara-Cienfuegos”, Ranchuelo, Villa Clara, C.P. 53100, Cuba
2
Vostok Holding Innovation Company, Sadik Azimov 4th Street, 15, Tashkent 700000, Uzbekistan
3
INIFTA, Suc.4, C.C. 16, La Plata 1900, Argentina
*
Author to whom correspondence should be addressed.
Molecules 2004, 9(12), 1019-1033; https://doi.org/10.3390/91201019
Submission received: 8 July 2004 / Accepted: 4 August 2004 / Published: 31 December 2004
Browse Figure
Versions Notes

Abstract

:
We report the results of a calculation of the normal boiling points of a representative set of 200 organic molecules through the application of QSPR theory. For this purpose we have used a particular set of flexible molecular descriptors, the so called Correlation Weighting of Atomic Orbitals with Extended Connectivity of Zero- and First-Order Graphs of Atomic Orbitals. Although in general the results show suitable behavior to predict this physical chemistry property, the existence of some deviant behaviors points to a need to complement this index with some other sort of molecular descriptors. Some possible extensions of this study are discussed.

Introduction

One of the topics of continuing interest in structure-property studies is to arrive at simple correlations between the selected properties and the molecular structure. For such considerations the molecular structure is often represented as a simple mathematical object, such as a number, sequence, or a set of selected invariants of matrices, generally referred to as molecular descriptors. Multiple regression analysis is usually used in such studies in the hope that it might point to structural factors that influence a particular property. Of course, regression analysis does not establish a causal relationship between structural components and molecular properties. Nevertheless, it may help one in model building and assist in the design of molecules with prescribed desirable properties, which is an important goal in drug research. In chemistry, anything that can be said about the magnitude of the property and its dependence upon changes in the molecular structure depends on the chemist’s capability to establish valid relationships between structure and property. In many physical-chemistry, organic, biochemical and biological areas, it is increasingly necessary to translate those general relations into quantitative associations expressed in useful algebraic equations known as Quantitative Structure-Activity (-Property) Relationships (QSAR/QSPR). To obtain a significant correlation, it is crucial that appropriate descriptors be employed, whether they be theoretical, empirical or derived from readily available experimental features of the molecular structures. Many descriptors reflect simple molecular properties and thus they can provide some meaningful insights into the physical-chemistry nature of the activity/property under consideration.
Chemical graph theory [1] advocates an alternative approach to QSAR/QSPR studies based on mathematically derived molecular descriptors. Such descriptors, often referred to as topological indices [2], include the well-known Wiener index W [3], the Hosoya index Z [4], and the connectivity index χ [5]. The last three decades have witnessed an upsurge of interest in applications of graph theory in chemistry. Constitutional formulae of molecules are chemical graphs where vertices represent the set of atoms and edges represent chemical bonds [6]. The pattern of connectedness of atoms in a molecule is preserved by constitutional graphs. A graph G = [V,E] consists of a finite nonempty set V of points together with a prescribed set E of unordered pairs of distinct points of V [7].
The correlation and prediction of physical-chemistry properties of pure liquids and of mixtures, such as boiling point, density, viscosity, static dielectric constant, and refractive index, is of practical (process design and control) and theoretical (role of the molecular structure in determining the macroscopic properties of the solvent) relevance to both chemists and engineers. Traditionally, procedures for estimating these properties have been based either on theoretical relationships often making use of empirical parameters that have to be fitted or on empirical relationships derived from additive-constitutive schemes based on atomic groups or bonds contribution within the molecule [8,9,10,11,12]. More recently, the QSPR approach has been applied especially to predict boiling points (BPs), partition coefficients, chromatographic retention indexes, surface tension, critical temperatures, viscosity, refractive index, thermodynamic state functions and static dielectric constant, among other properties. The use of calculated molecular descriptors in QSPR analysis has two main advantages: (a) the descriptors can be univocally defined for any molecular structure or fragment; (b) thanks to the high and well-defined physical information content encoded in many theoretical descriptors, they can clarify the mechanism relating the studied property with the chemical structure. Furthermore, QSPR models based on calculated descriptors help understanding of the inter- and intramolecular interactions that are mainly responsible for the behavior of complex chemical systems and processes.
The normal BP (i.e. the boiling point at 1 atm) is one of the major physical-chemistry properties used to characterize and identify a compound. Besides being an indicator for the physical state (liquid or gas) of a compound, the BP also provides an indication of its volatility. In addition, the BPs can be used to predict or estimate other physical properties, such as critical temperatures, flash points, enthalpies of vaporization, etc. [13,14,15]. The BP is often the first property measured for a new compound and one of the few parameters known for almost every volatile compound. Normal BPs are easy to determine, but when a chemical is unavailable, as yet unknown, or hazardous to handle, a reliable procedure for estimating its BP is required. Furthermore, the rapid and nearly explosive growth of combinatorial chemistry, where literally millions of new compounds are synthesized and tested without isolation, could render such a procedure very useful.
A large number of methods for estimating BPs have been devised and numerous QSPR correlations of normal BPs have been reported and detailed reviews have been given elsewhere [15,16,17,18,19,20,21,22]. The aim of this study is to present the results derived from the use of a particular sort of flexible molecular descriptors to estimate the BPs of a representative set of organic molecules, in order to seek better ways of calculating physical-chemistry properties. Some previous experience with this issue has shown the convenience of resorting to this special sort of molecular descriptor.
The paper is organized in the following way: the next section deals with the basic methodology, presenting some general properties of flexible molecular descriptors and some previous uses of the same. Then, we describe the calculation strategy, after which we give and discuss the results. Finally, our conclusions are presented together with some possible future further extensions of the method.

Molecular Descriptors

The basic algebraic expression of the fundamental principle governing the QSAR/QSPR, i.e. the quantitative formula representing the structure-activity/property relationship, is
P = f({d})
where P stands for the activity/property, {d} is a set of molecular descriptors and f is an arbitrary function. The commonest and simplest cases are those where {d} is reduced just to one variable and f is a linear function, i..e.
P = a + bd
with a,b ∈ ℛ, and real numbers a, b are determined by a standard least squares procedure.
Since there are too many possibilities to choose the set of molecular descriptors and besides they can be highly interrelated, this leads to a nasty situation which is termed the nightmare of the regression analysis. Some of these drawbacks include how to make the selection of descriptors, as well as ambiguities of the criteria used to select optimal descriptors and uncertainties when choosing the order in which descriptors are to be orthogonalized. Naturally, none of these difficulties exists for simple regression based on a single molecular descriptor, particularly if the regression is linear. This is one of the major reasons why researchers are striving to find or to design novel descriptors that would produce good correlation for a single molecular property of a set of compounds. However, not many molecular properties can be sufficiently well described by a single descriptor [23].
A quite interesting alternative to surmount these difficulties was proposed long ago by Randic [24] and it consists on defining {d} as a function of one or several variables that are determined during the search for the best correlation. Thus, in contrast to the traditional topological indices, which one can calculate after selecting a set of compounds to be studied and then proceed with statistical analysis, the variable indices are initially non-numerical. Hence, they cannot be calculated in advance for the set of compounds. Instead, one starts with an arbitrary set of values for the yet undetermined variables and, through an iterative procedure, one varies these initial values seeking optimal values that will produce the smallest standard error for the property under consideration. It is clear that the use of variable descriptors (also called flexible descriptors) can only improve correlations over the use of simple indices because if all variables take on a zero value (which is very unlikely), we would obtain the results that coincide with the results based on he traditional rigid molecular descriptors. Current literature shows that the use of variable molecular descriptors dramatically improved regression statistics [23].
Among the different alternatives of choosing flexible molecular descriptors, one of us (A.A.T.) has presented the so called Optimization of Correlation Weights of Local Graph Invariants (OCWLGI) procedure which has proved to be a rather suitable way to apply the method to calculate several biological activities and physical-chemistry properties [25,26,27,28,29,30,31,32,33,34]. The OCWLI may be based on the labeled hydrogen filled graph (LHFG) [35] and the graph of atomic orbitals (GAO) [36]. The OCWLI based upon the LHFGs yield reasonable good models of enthalpies of formation from elements of coordination compounds [37]. Besides, OCWLI based on LHFG have been used to model the Flory-Huggins polymer-solvent interaction parameters [26]. The OCWLI based upon the GAOs give rather good results to predict stability constants of amino acids complexes [36].
Molecular descriptors DCW are calculated by means of the following relationship
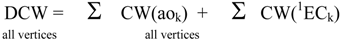
Molecules 09 01019 i001
where CW(aok) and CW(1ECk) are correlation weights of the atomic orbitals that are image of the k-th vertex in the GAO and correlation weights of Morgan extended connectivity of first order that have a k-th vertex in the GAO. The Monte Carlo method is then applied to determine optimum correlation weight values which produce the largest possible values of the correlation coefficient between the physical property as a function of the descriptor computed via Eq. (3). Numerical data of the GAO local invariants are listed in Table 1 and an illustrative example is reproduced in Table 2.
Table 1. Correlation weights for calculating DCW0 and DCW1
Table
DCW0 
DCW0 
1s1 -0.246
1s2 0.165
2s2 -0.556
2p2 1.780
2p3 3.738
2p4 2.722
2p5 -4.591
2p6 -0.726
3s2 -0.437
3p2 1.760
3p3 -2.030
3p4 5.491
3p5 4.532
3p6 0.093
3d10 0.551
4s2 2.873
4p5 0.193
0003 0.626
0004 1.648
0005 0.475
0006 0.175
0007 1.159
0008 0.623
0009 1.758
0010 0.546
0011 1.198
0012 0.463
0013 1.247
0014 3.437
0015 1.877
0016 -0.404
Table
DCW1 
DCW1 
1s1 0.939
1s2 0.155
2s2 0.104
2p2 0.704
2p3 4.943
2p4 0.748
2p5 -2.191
2p6 0.222
3s2 -0.183
3p2 0.827
3p3 4.546
3p4 5.322
3p5 0.939
3p6 8.663
3d10 9.470
4s2 8.444
4p5 8.422
0012 5.903
0015 -2.827
0018 0.150
0020 0.376
0021 1.669
0024 -0.381
0027 2.112
0030 1.574
0033 2.507
0035 0.685
0036 1.462
0038 1.577
0039 0.219
0042 0.224
0045 0.033
0048 1.204
0050 0.071
0051 1.528
0053 1.086
0054 1.323
00571.983
0059 0.574
0060 0.469
0062 0.669
0063-0.236
0066-0.161
0069 0.737
0070-2.190
0075 3.355
0078 3.944
0079 0.582
0080 0.582
0081 2.970
0082 0.904
0084 0.646
0086-0.466
0087 -0.007
0089 0.376
0090 2.254
0091 4.903
0094 -0.955
0096 2.028
0097 -1.506
0098 4.564
0099 1.506
0100 5.589
0101 3.285
0102 -5.967
0103 1.738
0105 1.969
0108 0.273
0109 4.121
0110 2.223
0111 2.796
0112 1.653
0116 4.641
0120 -2.254
0122 0.616
0124 1.832
0134 1.828
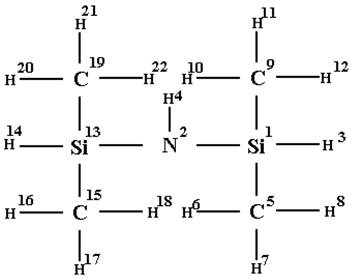
Molecules 09 01019 i002
Table
Table 2. Calculation of the DCW1 for 1,1,3,3-tetramethyldisilazane (DCW1 = 8.39793)
Table 2. Calculation of the DCW1 for 1,1,3,3-tetramethyldisilazane (DCW1 = 8.39793)
atom Nat EC1ao Nao EC1 CW(V) CW(LI)
Si 1 121s2 1 86 0.155 -0.466
2s2 2 86 0.104 -0.466
2p6 3 86 0.222 -0.466
3s2 4 86 -0.183 -0.466
3p2 5 86 0.827 -0.466
N 2 91s2 6 103 0.155 1.738
2s2 7 103 0.104 1.738
2p3 8 103 4.943 1.738
H 3 41s1 9 50 0.939 0.071
H 4 31s1 10 33 0.939 2.507
C 5 71s2 11 59 0.155 0.574
2s2 12 59 0.104 0.574
2p2 13 59 0.704 0.574
H 6 41s1 14 24 0.939 -0.381
H 7 41s1 15 24 0.939 -0.381
H 8 41s1 16 24 0.939 -0.381
C 9 71s2 17 59 0.155 0.574
2s2 18 59 0.104 0.574
2p2 19 59 0.704 0.574
H 10 41s1 20 24 0.939 -0.381
H 11 41s1 21 24 0.939 -0.381
H 12 41s1 22 24 0.939 -0.381
Si 13 121s2 23 86 0.155 -0.466
2s2 24 86 0.104 -0.466
2p6 25 86 0.222 -0.466
3s2 26 86 -0.183 -0.466
3p2 27 86 0.827 -0.466
H 14 41s1 28 50 0.939 0.071
C 15 71s2 29 59 0.155 0.574
2s2 30 59 0.104 0.574
2p2 31 59 0.704 0.574
H 16 41s1 32 24 0.939 -0.381
H 17 41s1 33 24 0.939 -0.381
H 18 41s1 34 24 0.939 -0.381
C 19 71s2 35 59 0.155 0.574
2s2 36 59 0.104 0.574
2p2 37 59 0.704 0.574
H 20 41s1 38 24 0.939 -0.381
H 21 41s1 39 24 0.939 -0.381
H 22 41s1 40 24 0.939 -0.381
Since the complete and detailed description of these flexible descriptors has been given before, we refer the reader interested in further minutiae to the specific papers where these details were largely reported [25,26,27,28,29,30,31,32,33,34].

Results and Discussion

We have chosen a representative set of 200 organic molecules of varied composition to study their normal boiling points (NBPs). These molecules, with both linear and cyclic structures, comprise ketones, acids, esters, aldehydes, nitriles, amines, alcohols, and hydrocarbons and a wide variety of atoms, such as C, H, O, N, Si, Cl, Br, F, P, S. The list of molecules is given in Table 3, together with their NBPs and the extended connectivity of zero- and first-order descriptors in the GAOs (DCW0 and DCW1, respectively).
Table
Table 3. Organic molecules, experimental NBPs (Celsius degrees) and DCWs.
Table 3. Organic molecules, experimental NBPs (Celsius degrees) and DCWs.
n CAS Molecule DCW0DCW1NBPexp
115933-59-21,1,3,3-Tetramethyldisilalazane 5.4608.39899.000
2105-54-4Butanoic acid, ethyl ester 5.54311.949120.000
3623-27-81,4-Benzenedicarboxaldehyde 16.53718.618245.000
47212-44-41,6,10-Dodecatrien-3-ol, 3,7,11-trimethyl 14.38917.08468.000
5705-86-25-Hydroxydecanoic acid lactone 8.59613.405117.000
6620-22-4Benzonitrile, 3-methyl- 12.82616.07599.000
7621-33-03-Ethoxyaniline 12.73525.122248.000
8150-76-5Mequinol 14.58423.498243.000
9109-52-4Pentanoic acid 9.04214.320185.000
1075-55-8Aziridine, 2-methyl- 1.5299.32566.000
11586-39-03-Nitrosostyrene 21.31714.38556.000
12224-41-9Dibenz[a,j]anthracene 39.91753.421531.000
13105-05-5Benzene, 1,4-diethyl- 11.38419.030184.000
14110-42-9Decanoic acid, methyl ester 8.33013.914108.000
15111-69-3Hexanedinitrile 6.9068.394295.000
161112-55-6Silane , tetraethyl- 10.65411.853130.000
171719-57-9Silane, chloro(chloromethyl)dimethyl- 5.12910.177115.000
18123-31-9Hydroquinoline 18.08228.959285.000
19100-02-7Phenol, 4-nitro- 23.19725.692279.000
202548-87-02-Octenal, (E)- 7.83715.14184.000
216166-86-52,4,6,8,10-Pentamethylcyclopentasiloxane 10.19115.986168.000
222031-79-01,1,3,3,5,5-Hexaethylcyclotrisiloxane 5.49310.852117.000
233862-73-5Trifluoroaniline 4.6052.79692.000
2415980-15-11,4-Oxathiane 3.11211.780147.000
25108-41-8Benzene, 1-chloro-3-methyl- 11.57516.747160.000
2678-81-91-Propanamine, 2-methyl 2.0066.15264.000
277087-68-5Diisopropylethylamine 6.55612.133127.000
2817477-29-1Propyldimethylchlorosilane 3.7189.954113.000
2975-35-4Ethylene, 1,1-dichloro- 5.812-4.70430.000
3091-64-5Coumarin 17.92820.526298.000
31328-87-04-Chloro-3-cyanobenzotrifluoride 6.40511.573210.000
32616-25-11-Penten-3-ol 6.43812.844114.000
3375-85-42-Butanol, 2-methyl- 4.2319.165102.000
34138-86-3Limonene 10.36710.009170.000
35333-41-5Diazinon 4.4866.70883.000
3615570-12-4meta-Methoxybenzenethiol 16.49022.256223.000
37198-55-0Perylene 37.00550.768495.000
38192-97-2Benzo[e]pyrene 37.00550.768492.000
39205-99-2Benzo[b]fluoranthene 37.00552.659481.000
40218-01-9Chrysene 32.12145.048448.000
41217-59-4Triphenylene 32.12147.211425.000
42611-32-5Quinoline, 8-methyl- 16.42722.665143.000
4376783-59-0Ethyl-3-trifluoromethylbenzoate 6.64115.738101.000
4476-86-8Triphenylchlorosilane 28.95339.379378.000
451241-94-7Phosphoric acid, 2-ethylhexyldiphenylester 26.20033.929375.000
462943-75-1N-octyltriethoxysilane 9.04315.45898.000
47594-72-9Ethane,1,1-dichloro-1-nitro- 11.75111.958124.000
4862-73-7Dimethyl-2,2-dichlorovinyl phosphate 10.28320.471140.000
49123-15-9Pentanol, 2-methyl- 4.1968.437119.000
506640-27-3Phenol, 2-chloro-4- methyl- 16.24819.546195.000
51537-92-8N-(3-tolyl)acetic acid amide 17.89630.207303.000
52105-99-7Hexanedioic acid, dibutyl ester 13.75422.346305.000
5377-35-2Phenanthrene, 9,10-dihydro- 22.52927.241168.000
542713-33-93,4-Difluorophenol 9.14313.61585.000
55111-83-1Octane, 1-bromo- 5.89914.924201.000
56101-68-8Benzene, 1,1'-methylene bis(4-isocyanato)- 26.54829.352200.000
57597-49-93-Ethyl-3-pentanol 5.34614.104141.000
5818395-90-9di-tert-Butyldichlorosilane 10.98018.381190.000
59107-12-0Propanenitrile 2.6775.53197.000
601825-62-3Silane, ethoxytrimethyl 3.0965.12275.000
6156-55-3Benz[a]anthracene 32.12140.882438.000
62243-17-42,3-Benzofluorene 30.66638.282402.000
6357-11-4Octadecanoic acid 16.28721.581183.000
6498-03-3Thiophenecarboxaldehyde 10.46815.608198.000
65605-39-02,2'-Dimethylbiphenyl 20.97628.363258.000
66831-91-4Benzene, [(phenylmethyl)thio] 19.80423.867197.000
67761-65-9Formamide, N,N-dibutyl- 11.70517.359120.000
68348-54-9Benzeneamine, 2-fluoro- 8.87014.610182.000
69136-77-6Hexylresorcinol 21.63631.606333.000
70100-53-8Benzenemethanethiol 16.54318.999194.000
71191-30-01,2,9,10-Dibenzopyrene 44.80159.414595.000
72109-73-91-Butanamine 3.2926.59378.000
73100-69-6Pyridine, 2-ethenyl- 10.65913.05879.000
741712-70-51-Chloro-4-isopropenylbenzene 14.36818.139214.500
7595-56-7Phenol, 2-bromo- 18.07625.834195.000
762984-50-1Oxirane, hexyl- 4.1378.77163.000
77100-43-6Pyridine, 4-ethenyl- 10.6598.90562.000
78919-31-3Propanenitrile, 3-(triethoxysilyl)- 8.81313.961224.000
79874-60-24-Methylbenzoic acid chloride 15.47624.765225.000
8080-62-62-Propenoic acid, 2-methyl-, methyl ester 6.6655.278100.000
81645-49-8(Z)-Stilbene 22.35427.371307.000
82103-84-4Acetamide, N-phenyl- 17.12827.646304.000
83106-49-0para-Toluidine 11.77024.079200.000
8490-90-4Methanone, (4-bromophenyl)phenyl- 28.01130.846350.000
85519-73-3Triphenylmethane 29.76834.483359.000
86832-69-9Phenanthrene, 1-methyl- 25.09335.107359.000
8760-29-7Ethoxyethane 1.0855.88635.000
88539-74-2Propanoic acid, 3-bromo-ethyl ester 7.97816.094135.000
89598-31-22-Propanone, 1-bromo- 6.45613.853137.000
90571-61-9Naphthalene, 1,5-dimethyl- 18.06525.165265.000
911885-14-9Carbonochloridic acid, phenyl ester 15.11717.64074.000
92754-05-2Silane, ethenyltrimethyl- 3.9453.49055.000
93238-84-61,2-Benzofluorene 30.66642.448407.000
9499-08-1Benzene, 1-methyl-3-nitro- 11.77023.077230.000
957209-38-31,4-bis(3-Aminopropyl)piperazine 19.90511.808150.000
961558-33-4Silane, dichloro(chloromethyl)methyl- 5.34910.947121.000
9765-85-0Benzoic acid 17.31021.998249.000
98132-64-9Dibenzofuran 21.82226.034154.000
99213-46-7Picene (benzo[a]chrysene) 39.91757.587525.000
100191-07-1Coronene 46.77357.883525.000
101287-92-3Cyclopentane 2.7872.79350.000
1022782-91-4Thiourea, tetramethyl- 15.02129.789245.000
103109-07-9Piperazine, 2-methyl- 5.61211.565155.000
1047005-72-3Benzene, 1-chloro-4-phenoxy- 21.92331.152284.000
105532-27-4Ethanone, 2-chloro-1-phenyl- 15.93719.618244.000
10691-57-6Naphthalene, 2-methyl- 17.29822.531241.000
107109-01-3Piperazine, 1-methyl- 5.46112.701138.000
108591-35-5Phenol, 3,5-dichloro- 17.55323.380233.000
109454-89-7Benzaldehyde, 3-(trifluoromethyl)- 4.90910.98383.000
11099-04-7Benzoic acid, 3-methyl- 18.07724.559263.000
111120-72-9Indole 14.20520.915253.000
112109-86-4Ethanol, 2-methoxy- 4.99110.296125.000
113617-84-5N,N-Diethylformamide 9.47614.478176.000
114129-00-0Pyrene 29.21036.066360.000
11586-74-8Carbazole 22.00031.584355.000
11679-06-1Acrylamide 6.9908.215125.000
117589-18-4Benzene methanol, 4-methyl- 14.73321.268217.000
118123-07-9Phenol, 4-ethyl- 14.73323.994218.000
11975-78-5Silane, dichlorodimethyl- 3.5535.15270.000
120120-80-91,2-Benzenediol 18.08224.434245.000
121123-92-21-Butanol, 3-methyl-, acetate 5.3718.225142.000
122626-39-1Benzene, 1,3,5-tribromo- 22.73927.936271.000
12389-99-6Benzenemethanamine, 2-fluoro- 9.42810.34773.000
124366-18-72,2'-Dipyridine 17.70228.255273.000
12575-05-8Acetonitrile 2.1195.27181.000
12677-81-6Tabun 7.77124.781246.000
1277691-02-3CH2CHOS(CH3)(CH3)NS(CH3)(CH3)CHCH2 12.36614.725160.000
128615-67-81,4-Benzenediol, 2-chloro- 20.15525.666263.000
129591-93-51,4-Pentadiene 4.173-2.54126.000
130350-46-9Benzene, 1-fluoro-4-nitro- 16.39114.681205.000
131108-90-7Benzene, chloro- 10.80716.761132.000
13295-78-3Benzenamine, 2,5-dimethyl- 12.53721.017218.000
133557-11-9Urea, allyl- 8.10511.476163.000
134557-17-5Methyl propyl ether 1.0856.40739.000
135110-06-5di-tert-Butyldisulfide 13.14019.686200.000
136594-70-7Propane, 2-methyl-2-nitro- 8.78915.359127.000
1375582-62-7(Propargyloxy)trimethylsilane 5.69310.843110.000
1381072-43-1Thiirane, methyl- 1.4106.65872.000
139124-07-2Octanoic acid 10.71415.996237.000
140919-30-21-Propanamine, 3-(triethoxysilyl)- 8.31412.139122.000
141623-00-74-Bromobenzoic acid nitrile 16.72719.293235.000
142100-44-7Benzyl chloride 12.03616.857177.000
143109-55-71,3-Propanediamine, N,N-dimethyl- 8.40010.048133.000
144598-72-12-Bromopropanoic acid 11.17311.912203.000
145822-86-6Cyclohexane, 1,2-dichloro-(trans) 6.93613.335193.000
14667-71-0Dimethylsulfone 4.84422.383238.000
14756-33-71,1,3,3-Tetramethyl-1,3-diphenyldisiloxane 20.96414.576155.000
148112-57-2Tetraethylenepentamine 18.19837.473340.000
1494333-56-6Cyclopropyl bromide 4.9189.45769.000
15080-10-4Diphenyldichlorosilane 20.63331.348305.000
15196-23-12-Propanol, 1,3-dichloro- 8.92125.525174.000
152110-89-4Piperidine 3.3738.827106.000
15395-77-2Phenol, 3,4-dichloro- 17.55323.879145.000
154123-54-6Acetylacetone 7.92210.594140.000
15591-01-0Benzenemethanol, α-phenyl- 23.73431.844297.000
156115-19-53-Butyn-2-ol, 2-methyl- 6.27114.827104.000
15778-84-2Propanal, 2-methyl- 3.0826.66063.000
158104-54-12-Propen-1-ol, 3-phenyl- 16.87823.577250.000
159420-56-4Silane, fluorothiomethyl- -1.061-2.00557.000
16098-02-22-Furanmethanethiol 14.03916.547155.000
1613970-62-53-Pentanol, 2,2-dimethyl- 4.61718.157132.000
16292-84-2Phenothiazine 21.13332.840371.000
16393-99-2Benzoic acid, phenyl ester 23.75127.643298.000
164109-67-11-Pentene 2.7033.24430.000
165451-40-1Ethanone, 1,2-diphenyl- 23.90124.618320.000
166625-30-92-Pentanamine 2.5637.87691.000
1672051-60-71,1'-Biphenyl, 2-chloro- 21.51527.031274.000
1682425-79-8Oxirane,2,2'[1,4-butanediylbis(oximethylene)]bis- 7.29913.704155.000
169623-73-4Ethyldiazoacetate 8.78418.857140.000
170103-11-72-Propenoic acid, 2-ethylhexyl ester 9.07015.387215.000
171107-05-11-Propene, 3-chloro- 4.1224.57044.000
172108-31-62,5-Furandione 11.12213.982200.000
17357-06-7Allylisothiocyanate 6.2814.360150.000
17477-75-8Meparfynol (1-pentyne-3-ol, 3-methyl) 6.82817.020121.000
175229-87-8Phenanthridine 23.45634.557349.000
1765510-99-6Phenol, 2,6-bis(1-methylpropyl)- 16.82933.099255.000
1773544-25-04-Aminophenylacetic acid nitrile 14.88525.592312.000
178501-65-5Diphenylethylene 19.92822.715170.000
179994-49-0Hexaethyldisiloxane 2.85217.928129.000
180189-64-0Dibenzo[a,h]pyrene 44.80159.141596.000
181127-19-5Acetamide, N,N-dimethyl- 9.1287.664165.000
18214548-46-0Phenyl, 4-pyridyl ketone 22.47325.002315.000
1831897-45-6Tetrachloroisophthalonitrile 23.67328.057350.000
184135-01-3Benzene, 1,2-diethyl- 11.38416.301183.000
185109-77-3Malononitrile 5.2345.889220.000
1861008-88-4Pyridine, 3-phenyl- 18.57222.606269.000
1873741-00-2Cyclopentane, pentyl- 4.8449.432181.000
188109-92-2Ethene, ethoxy- 2.5542.07033.000
189636-30-6Benzenamine, 2,4,5-trichloro- 17.22022.555270.000
1902916-68-9Trimethyl-2-hydroxyethylsilane 6.0015.43790.000
191126-73-8Tri-n-butylphosphate 8.16415.583180.000
19269-72-7Benzoic acid, 2-hydroxy- 21.98330.500211.000
193771-51-71H-indole-3-acetonitrile 21.22629.641157.000
194624-83-9Methane, isocyanato- 2.31213.65537.000
195191-24-2Benzo[ghi]perylene 41.88954.326542.000
196107-02-82-Propenal 3.2536.80953.000
197622-97-9Benzene, 1-ethenyl-4-methyl- 12.29612.533175.000
198762-49-2Ethane, 1-bromo-2-fluoro- 0.21210.71071.000
1995263-87-6Quinoline, 6-methoxy- 16.83525.734193.000
200108-01-0Ethanol, 2-(dimethylamino)- 10.24814.465133.000
First we have calculated the complete set via zero- and first-order descriptors, thus obtaining the following linear relationships:
NBP = 50.24 + 10.91 DCW0
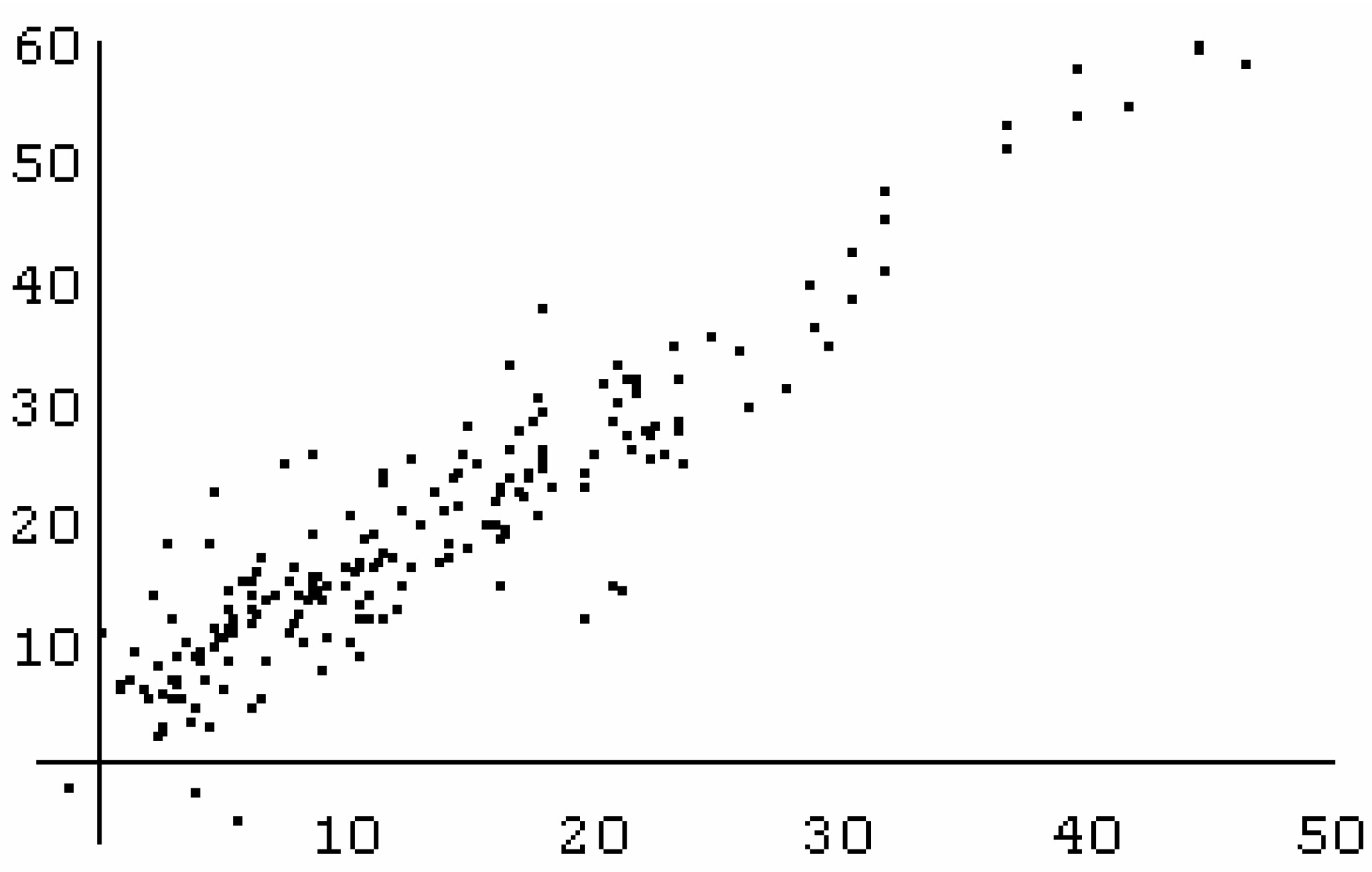
n = 200, r = 0.8910, S = 53.7, F = 763
NBP = 25.83 + 8.87 DCW1
n = 200, r = 0.892, S = 56.0, F = 783
where the statistical parameters have the usual meanings.
The statistical data is moderately satisfactory and when Eqs.(4) and (5) are used to predict NBPs there are relatively large deviations for a significant number of molecules.
We then proceed to a more usual calculation procedure when dealing with a large number of molecules, which consists of defining two disjoint sets: a training set to determine the regression equation and a test set to perform true predictions. Results are as follows:
NBP = 49.16 + 10.89 DCW0
n = 150, r = 0.8841, S = 55.1, F = 530 (training set)
n = 50, r = 0.9120, S = 49.3, F = 237 (test set)
NBP = 23.72 + 8.96 DCW1
n = 150, r = 0.9328, S = 42.5, F = 530 (training set)
n = 50, r = 0.8766, S = 57.6, F = 237 (test set)
These results are somewhat better than the previous ones and large deviations occur for a smaller number of molecules. Since the choice of the molecules comprising the training and test sets are somewhat arbitrary, we have tested several partitions of the compounds, but final results are not markedly dependent on the way used to choose the molecules in both sets.
Since there are some large deviant behaviors, we have resorted to removing these molecules (just five, from the total 200 molecules: numbers 11, 15, 56, 98 and 146 according to the identification number n from Table 3). Results are the following ones:
NBP = 43.25 + 11.41 DCW0
n = 145, r = 0.9199, S = 46.8, F = 787 (training set)
n = 50, r = 0.9120, S = 46.6, F = 237 (test set)
If molecules 4, 15, 53, 91 and 98 are removed, statistical results are
NBP = 22.50 + 9.10 DCW1
n = 145, r = 0.9530, S = 36.1, F = 1414 (training set)
n = 50, r = 0.8765, S = 53.9, F = 159 (test set)
These results show that by taking out some deviant molecules, the results improve remarkably and somewhat better predictions can be obtained.
A final numerical test was made to define training and test sets based on the clustering approach [38]. The k-Means Cluster Analysis (k-MCA) may be used in training and testing (or predictive) series design [39,40]. The idea consists of carrying out a partition of the series of compounds into several statistically representative classes of chemicals. Thence, one may select from the number of all these classes of training and predicting series. This procedure ensures that any chemical classes (as determined by the clusters derived form the k-MCA will be represented in both series of compounds (i.e. training and test sets). It permits the design of both training and predicting series, which are representative of the entire experimental universe.
NBP = 53.09 + 11.39DCW0
n = 158, r = 0.9586, S = 34.8, F = 1770 (complete set)
NBP = 54.28 + 11.45 DCW0
n = 126, r = 0.9633, S = 33.3, F = 1599 (training set)
n = 32, r = 0.9391, S = 39.1, F = 224 (test set)
NBP = 23.50 + 9.119 DCW1
n = 144, r = 0.9592, S = 33.9, F = 1633 (training set)
n = 37, r = 0.9564, S = 34.8, F = 376 (test set)
These last results are the best ones among the different equations presented before and they represent a suitable improvement with respect to the first ones defined by Equations (4-9). An additional possibility for doing these calculations would be to employ both descriptors together, but this is not possible since they are strongly correlated, as shown in Figure 1.
We cannot make any direct comparison with other theoretical results since, to the best of our knowledge, the standard literature does not register any calculation for this particular molecular set. This is quite sensible, since the molecules are quite diverse and it is well known that working with molecular sets comprising similar molecules gives results that are better than those derived from a quite dissimilar set of molecules, as it is the present case. However, our aim has been precisely this: to make a regression approach for quite different molecules via quite simple linear equations based on a single molecular descriptor to predict NBPs. A complete listing of NBP results derived from using Eqs. (4-12) is available upon request from the corresponding author.
Molecules 09 01019 g001 550
Figure 1. DCW1 (vertical axis) versus DCW0 (horizontal axis). Regression equation: DCW1 = 2.978 + 1.222 DCW0.
Figure 1. DCW1 (vertical axis) versus DCW0 (horizontal axis). Regression equation: DCW1 = 2.978 + 1.222 DCW0.
Molecules 09 01019 g001

Conclusions

We have presented results on NBPs for a quite diverse molecular set based upon simple linear regression equations depending on a single molecular descriptor in order to test the capability of a special kind of such parameter: a flexible molecular descriptor. Results are very encouraging and they show the power of such types of topological variables. In fact, although there are some large deviations when employing the complete initial molecular set comprising very diverse organic molecules, the average deviations are quite sensible ones. In order to judge the relative merits of the present approach one must take into consideration that a single figure is representing a physical-chemistry property (i.e. NBPs), which evidently depends on many molecular features which cannot be encoded in a single topological descriptor. In order to reproduce a given property, it is necessary to resort to a many variables regression equation, each of them taking into account a different molecular feature. Furthermore, usually one employs a set comprising similar molecules, but our main purpose has not been to make exact numerical predictions, but rather to show the real possibilities of a particular kind of flexible topological descriptor. We consider this objective has been fully met. The next step is to complement these calculations using a several variables approach, based on choosing other molecular descriptors in order to add other physical molecular features which are not included into the OCWLI. Work along this line of research is under way and results will be presented elsewhere very soon.

References

  1. King R., B. (Ed.) Chemical Applications of Topology and Graph Theory; Elsevier: Amsterdam, 1983.
  2. Diudea, M. V. (Ed.) QSPR/QSAR Studies by Molecular Descriptors; Nova Science Publishers, Inc.: Huntington, New York, 2001.
  3. Wiener, H. Structural Determination of Paraffin Boiling Points. J. Am. Chem. Soc. 1947, 56, 17–20. [Google Scholar]
  4. Hosoya, H. Topological Index. A Newly Proposed Quantity Characterizing the Topological Nature of Structural Isomers of Saturated Hydrocarbons. Bull. Chem. Soc. Jpn. 1971, 44, 2332–2339. [Google Scholar]
  5. Randic, M. On Characterization of Molecular Branching. J. Am. Chem. Soc. 1975, 97, 6609–6615. [Google Scholar]
  6. Trinajstic, N. Graph Theory; CRC Press: Boca Raton, FL, 1983. [Google Scholar]
  7. Harary, F. Graph Theory; Addison-Wesley: Reading, MA, 1969. [Google Scholar]
  8. Cramer, R. D. BC(DEF) Parameters. 2. An Empirical structure-Based Scheme for the Prediction of Some Physical Properties. J. Am. Chem. Soc. 1979, 102, 1849–1859. [Google Scholar]
  9. Monnery, W. D.; Svreck, W. Y.; Mehrota, A. K. Voscicity: A Critical Review of Practical Predictive and Correlative Methods. Can. J. Chem. Eng. 1995, 73, 3–40. [Google Scholar]
  10. Stein, S. E.; Brown, R. L. Estimation of Normal Boiling Points from Group Contributions. J. Chem. Inf. Comput. Sci. 1994, 34, 581–587. [Google Scholar]
  11. Pouchly, J.; Quin, A.; Munk, P. Excess Volume of Mixing and Equation of State Theory. J. Solution Chem. 1993, 22, 399–418. [Google Scholar]
  12. Elbro, H. S.; Fredenslund, A.; Rasmussen, P. Group Contribution Meted for the Prediction of Liquid Densities as a Function of Temperatures for Solvents, Oligomers and Polymers. Ind. Eng. Chem. Res. 1991, 30, 2576–2593. [Google Scholar]
  13. Fisher, C. H. Boiling Point Gives Critical Temperatures. Chem. Eng. 1989, 96, 157–158. [Google Scholar]
  14. Satyanarayana, K.; Kakati, M. C. Note: Correlation of Flash Points. FIRE Mater. 1991, 15, 97–100. [Google Scholar]
  15. Rechsteiner, C. E. Handbook of Chemical Property Estimation Methods; Lyman, W. J., Reehl, W. F., Rosenblatt, D. H., Eds.; McGraw-Hill: New York, 1982; Chapter 12. [Google Scholar]
  16. Katritzky, A.R.; Mu, L.; Lobanov, V. S.; Karelson, M. Correlation of Boiling Points with Molecular Structure. 1. A Training Set of 298 Diverse Organics and a Test Set of 9 Simple Inorganics. J. Phys. Chem. 1996, 100, 10400–10407. [Google Scholar]
  17. Horvath, A.L. Molecular Design: Chemical Structure Generation from the Properties of Pure Organic Compounds; Elsevier: Amsterdam, 1992. [Google Scholar]
  18. Wessel, M. D.; Jurs, P. C. Prediction of Normal Boiling Points for a Diverse Set of Industrially Important Organic Compounds from Molecular Structure. J. Chem. Inf. Comput. Sci. 1995, 35, 841–850. [Google Scholar]
  19. Lee, T. D.; Weers, J. G. QSPR and GCA Models for Predicting the Normal Boiling Points of Fluorocarbons. J. Phys. Chem. 1995, 99, 6739–6747. [Google Scholar]
  20. Komasa, A. Prediction of Boiling Points of Ketones Using a Quantitative Structure-Property Relationships Treatment. Polish J. Chem. 2003, 77, 1491–1499. [Google Scholar]
  21. Kompany-Zareh, M. A QSPR Study of Boiling Point of Saturated Alcohols Using Genetic Algorithm. Acta Chim. Slov. 2003, 50, 259–273. [Google Scholar]
  22. Öberg, T. Boiling Points of Halogenated Aliphatic Compounds: A Quantitative Structure-Property Relationship for Prediction and Validation. J. Chem. Inf. Comput. Sci. 2004, 44, 187–192. [Google Scholar]
  23. Randic, M.; Basak, S. C. Variable Molecular Descriptors, in Some Aspects of Mathematical Chemistry; Sinha, D. K., Basak, S. C., Mohanty, R. K., Busamallick, I. N., Eds.; Visva-Bharati University Press: Santiniketan (India), 1999. [Google Scholar]
  24. Randic, M. Novel Graph Theoretical Approach to Heteroatoms in QSAR. Chemom. Intel. Labl. Syst. 1991, 10, 213–223. [Google Scholar]
  25. Toropova, A.P.; Toropov, A. A.; Ishankhodzhaeva, M. M.; Parpiev, N. A. QSPR Modeling of Stability Constants of Coordination Compounds by Optimization Weights of Local Graph Invariants. Russ. J. Inorg. Chem. 2000, 45, 1057–1059. [Google Scholar]
  26. Toropov, A. A.; Voropaeva, N. L.; Ruban, I. N.; Rashidova, S. Sh. Quantitative Structure-Property Relationships for Binary Polymer-Solvent Systems: Correlation Weighting of the Local Invariants of Molecular Graphs. Polymer Science Ser. A 1999, 41, 975–985. [Google Scholar]
  27. Toropov, A.; Toropova, A.; Ismailov, T.; Bonchev, D. 3D Weighting of Molecular Descriptors for QSPR/QSAR by the Method of Ideal Symmetry (MIS). 1. Application to Boiling Points of Alkanes. J. Mol. Struct. THEOCHEM 1998, 424, 237–247. [Google Scholar]
  28. Krenkel, G.; Castro, E. A.; Toropov, A. A. Improved Molecular Descriptors Based on the Optimization of Correlation Weights of Local Graphs. Int. J. Molec. Sci. 2001, 2, 57–65. [Google Scholar]
  29. Toropov, A. A.; Toropova, A. A. Prediction of Heteroatomic Amine Mutagenicity by Means of Correlation Weighting of Atomic Orbital Graphs of Local Invariants. J. Mol. Struct. THEOCHEM 2001, 538, 287–293. [Google Scholar]
  30. Toropov, A. A.; Toropova, A. P. Modeling the Lipophilicity by Means of Correlation Weighting of Local Graph Invariants. J. Mol. Struct. THEOCHEM 2001, 538, 197–199. [Google Scholar]
  31. Mercader, A.; Castro, E. A.; Toropov, A. A. QSPR Modeling the Enthalpy of Formation from Elements by Means of Correlation Weighting of Local Invariants of Atomic Orbital Molecular Graphs. Chem. Phys. Lett. 2000, 330, 612–623. [Google Scholar]
  32. Toropov, A. A. A. P. Toropova, QSAR Modeling of Toxicity on Optimization of Correlation Weights of Morgan Extended Connectivity. J. Mol. Struct. THEOCHEM 2002, 578, 129–134. [Google Scholar]
  33. Toropov, A. A.; Toropova, A. P. QSPR Modeling of Alkanes Properties Based on Graph of Atomic Orbitals. J. Mol. Struct. THEOCHEM 2003, 637, 1–10. [Google Scholar]
  34. Toropov, A. A.; Nesterov, I. V.; Nabiev, O. M. QSPR Modeling of Cycloalkanes Properties by Correlation Weighting of Extended Graph Valence Shells. J. Mol. Struct. THEOCHEM 2003, 637, 37–42. [Google Scholar]
  35. Basak, S. C.; Grunwald, G. D. Predicting mutagenicity of chemicals using topological and quantum chemical parameters: A similarity based study. Chemosphere 1995, 31, 2529. [Google Scholar]
  36. Toropov, A. A.; Toropova, A. P. QSPR modeling of the formation constants for complexes using Atomic Orbital Graphs. Russ. J. Coord. Chem. 2000, 26, 398. [Google Scholar]
  37. Toropov, A. A. A. P. Toropova, Optimization of correlation weights of the local graph invariants: use of the enthalpies of formation of complexes compounds for the QSPR modeling. Russ. J. Coord. Chem. 1998, 24, 81. [Google Scholar]
  38. Pérez-González, M.; González Díaz, H.; Molina Ruiz, R.; Cabrera, M. A.; Ramos de Armas, R. TOPS-MODE Based QSARs Derived from Heterogeneous Series of Compounds. Applications to the Design of New Herbicides. J. Chem. Inf. Comput. Sci. 2003, 43, 1192–1199. [Google Scholar]
  39. Kowalski, R. B.; Wold, S. Pattern Recognition in Chemistry. In Handbook of Statistics; Krishnaiah, P. R., Kanal, L. N., Eds.; North Holland Publishing Company: Amsterdam, 1982; pp. 673–697. [Google Scholar]
  40. McFarland, J. W.; Gans, D. J. Cluster Significance Analysis. In Methods and Principles in Medicinal Chemistry; Manhnhold, R., Krgsgaard, L., Timmerman, H., Eds.; VCH: Weinheim, 1995; Vol. 2 , (Chemometric Methods in Molecular Design, van Waterbeemd, H. ed.); pp. 295–307. [Google Scholar]

Share and Cite

MDPI and ACS Style

González, M.P.; Toropov, A.A.; Duchowicz, P.R.; Castro, E.A. QSPR Calculation of Normal Boiling Points of Organic Molecules Based on the Use of Correlation Weighting of Atomic Orbitals with Extended Connectivity of Zero- and First-Order Graphs of Atomic Orbitals. Molecules 2004, 9, 1019-1033. https://doi.org/10.3390/91201019

AMA Style

González MP, Toropov AA, Duchowicz PR, Castro EA. QSPR Calculation of Normal Boiling Points of Organic Molecules Based on the Use of Correlation Weighting of Atomic Orbitals with Extended Connectivity of Zero- and First-Order Graphs of Atomic Orbitals. Molecules. 2004; 9(12):1019-1033. https://doi.org/10.3390/91201019

Chicago/Turabian Style

González, Maykel Pérez, Andrey A. Toropov, Pablo R. Duchowicz, and Eduardo A. Castro. 2004. "QSPR Calculation of Normal Boiling Points of Organic Molecules Based on the Use of Correlation Weighting of Atomic Orbitals with Extended Connectivity of Zero- and First-Order Graphs of Atomic Orbitals" Molecules 9, no. 12: 1019-1033. https://doi.org/10.3390/91201019

Article Metrics

Back to TopTop