Total and Local Quadratic Indices of the Molecular Pseudograph's Atom Adjacency Matrix: Applications to the Prediction of Physical Properties of Organic Compounds

Ponce, Yovani Marrero

doi:10.3390/80900687

Open AccessArticle

Total and Local Quadratic Indices of the Molecular Pseudograph's Atom Adjacency Matrix: Applications to the Prediction of Physical Properties of Organic Compounds

by

Yovani Marrero Ponce

Department of Pharmacy, Faculty of Chemical-Pharmacy and Department of Drug Design, Bioactive Chemical Center. Central University of Las Villas, Santa Clara, 54830, Villa Clara, Cuba

Molecules 2003, 8(9), 687-726; https://doi.org/10.3390/80900687

Submission received: 17 June 2003 / Revised: 29 July 2003 / Accepted: 3 August 2003 / Published: 15 August 2003

Download

Browse Figure

Versions Notes

Abstract

:

A novel topological approach for obtaining a family of new molecular descriptors is proposed. In this connection, a vector space E (molecular vector space), whose elements are organic molecules, is defined as a “direct sum” of different ℜⁱ spaces. In this way we can represent molecules having a total of i atoms as elements (vectors) of the vector spaces ℜⁱ (i=1, 2, 3,..., n; where n is number of atoms in the molecule). In these spaces the components of the vectors are atomic properties that characterize each kind of atom in particular. The total quadratic indices are based on the calculation of mathematical quadratic forms. These forms are functions of the k-th power of the molecular pseudograph’s atom adjacency matrix (M). For simplicity, canonical bases are selected as the quadratic forms’ bases. These indices were generalized to “higher analogues” as number sequences. In addition, this paper also introduces a local approach (local invariant) for molecular quadratic indices. This approach is based mainly on the use of a local matrix [M^k(G, F_R)]. This local matrix is obtained from the k-th power (M^k(G)) of the atom adjacency matrix M. M^k(G, F_R) includes the elements of the fragment of interest and those that are connected with it, through paths of length k. Finally, total (and local) quadratic indices have been used in QSPR studies of four series of organic compounds. The quantitative models found are significant from a statistical point of view and permit a clear interpretation of the studied properties in terms of the structural features of molecules. External prediction series and cross-validation procedures (leave-one-out and leave-group-out) assessed model predictability. The reported method has shown similar results, compared with other topological approaches. The results obtained were the following: a) Seven physical properties of 74 normal and branched alkanes (boiling points, molar volumes, molar refractions, heats of vaporization, critical temperatures, critical pressures and surface tensions) were well modeled (R>0.98, q²>0.95) by the total quadratic indices. The overall MAE of 5-fold cross-validation were of 2.11 ^oC, 0.53 cm³, 0.032 cm³, 0.32 KJ/mol, 5.34 ^oC, 0.64 atm, 0.23 dyn/cm for each property, respectively; b) boiling points of 58 alkyl alcohols also were well described by the present approach; in this sense, two QSPR models were obtained; the first one was developed using the complete set of 58 alcohols [R=0.9938, q²=0.986, s=4.006^oC, overall MAE of 5-fold cross-validation=3.824 ^oC] and the second one was developed using 29 compounds as a training set [R=0.9979, q²=0.992, s=2.97 ^oC, overall MAE of 5-fold cross-validation=2.580 ^oC] and 29 compounds as a test set [R=0.9938, s=3.17 ^oC]; c) good relationships were obtained for the boiling points property (using 80 and 26 cycloalkanes in the training and test sets, respectively) using 2 and 5 total quadratic indices: [Training set: R=0.9823 (q²=0.961 and overall MAE of 5-fold cross-validation=6.429 ^oC) and R=0.9927 (q²=0.977 and overall MAE of 5-fold cross-validation=4.801 ^oC); Test set: R=0.9726 and R=0.9927] and d) the linear model developed to describe the boiling points of 70 organic compounds containing aromatic rings has shown good statistical features, with a squared correlation coefficient (R²) of 0.981 (s=7.61 ^oC). Internal validation procedures (q²=0.9763 and overall MAE of 5-fold cross-validation=7.34 ^oC) allowed the predictability and robustness of the model found to be assessed. The predictive performance of the obtained QSPR model also was tested on an extra set of 20 aromatic organic compounds (R=0.9930 and s=7.8280 ^oC). The results obtained are valid to establish that these new indices fulfill some of the ideal requirements proposed by Randić for a new molecular descriptor.

Keywords:

Molecular Vector Space; Total and Local Quadratic Index; QSPR; Physical Property; Organic Compound

Introduction

The last decade has witnessed much progress in how chemical structures are characterized and described, how large sets of compounds are synthesized via a combinatorial chemistry approach and how simple and fast in-vitro assays are carried out. In this sense, the method most used for drug discovery is high-throughput screening (HTS), where massive screening of chemicals on a robot-assisted battery of biological assays is carried out [1,2]. Lately, virtual screening has emerged as an interesting alternative to the handling and screening of large databases in order to find a reduced set of potential new drug candidates [3,4,5]. This methodology and in general, molecular biology and drug design, are centered on the relationships between the chemical structures and measured properties of polymers and organic compounds.

In order to obtain structure-property (activity) relationships, henceforth-abbreviated SPR and SAR and quantitative SPR and SAR relationships (abbreviated QSPR and QSAR, respectively), it is necessary to have a structure parameterization. The structure parameterization includes the use of molecular descriptors. Molecular descriptors are “numbers that characterize a specific aspect of the molecule structure” [6]. At present, there are a great number of molecular descriptors that can be used in QSAR and QSPR studies [7]. Among them, the so-called topological indices (TIs) have found major application in medicinal chemistry and molecular modeling [8,9,10,11]. TIs are molecular descriptors derived from graph-theoretical invariants; i.e. they do not depend on the labeling of the vertices or edges on the “molecular graph” [12,13,14,15,16,17,18,19,20,21,22,23,24]. These indices codify structural information contained in ‘molecular connectivities’ and can be considered as structure cryptic descriptors [15,16,17].

The first TI capable of characterizing the ramification of a “graph” was proposed by Wiener [18]. This index was based on the topological concept of distance, understood as the number of bonds between two atoms by the shortest path. Other authors have defined various indices; prominent among them are the Balaban’s J index [19], Randić’s molecular connectivity [20], Kier and Hall’s electrotopological state (E-state) index [21], the Harary number [22], and Estrada’s spectral moments [23,24,25], among others. The latter are related with the bond adjacency matrix, while the majority of the remainder are derived from the vertex adjacency or distance matrices.

The proliferation of topological indices can be compared with the effect produced on quantum chemical parameters by changes in the molecular orbital. In this connection, TIs have been classified according to their nature as first, second and third generation [17]. In a recent paper, Randić [26] has proposed a list of desirable attributes for a topological descriptor. Therefore, this list can be considered as a methodological guide for the development of new TIs. One of the most important criteria is the possibility of defining the descriptors locally. This attribute refers to the fact that the index could be calculated for the molecule as a whole but also over certain fragments of the structure itself.

At times, the properties of a group of molecules are more related to a certain zone or fragment, rather than to the molecule as a whole. Thereinafter, the global definition never satisfies the structural requirements needed to obtain a good correlation in QSAR and QSPR studies. The local indices can be used in certain problems such as:

Research on drugs, toxics or generally any organic molecules with a common skeleton, which is responsible for the activity or property under study.
Study of the reactivity of specific sites of a series of molecules, which can undergo a chemical reaction or enzymatic metabolism.
In the study of molecular properties such as spectroscopic measurements, which are calculated experimentally in a local fashion
In any general case where it is necessary to study not the molecule as a whole, but rather some local properties of certain fragments, then the definition of local descriptors could be necessary.

Another of Randić’s attributes refers to the generalization of the indices. The description of the molecular structure by a simple number can bring about loss of information. For this reason, in most cases the use of a family of different simple descriptors for obtaining the algebraic models that relate the structure with its physical, chemical and biological properties is needed [27]. The two possibilities to solve the loss of information in the graph theoretical descriptors are: (1) the generalization of a simple descriptor to “higher” analogues or (2) the generation of graph theoretical invariants as a sequence of numbers [26].

Chemical graph theory is continuously evolving, and novel approaches have appeared as solutions to those difficulties. Recently, several molecular descriptors based on the two–dimensional topological structure of molecules have been defined and tested in QSAR models [28,29,30,31,32,33,34,35], showing that definition of novel molecular descriptors is a promising field in medicinal chemistry (see Todeschini, Karelson, Devillers and Estrada [15,16,17] for an exhaustive compilation). In this sense, the author has developed a novel method called TOMO-COMD (acronym of TOpological MOlecular COMputer Design) [36]. It calculates several families of topological molecular descriptors. One of these families has been defined as quadratic indices by analogy with the quadratic mathematical forms.

The main aim of this paper is to propose a total and local definition of quadratic indices of the “molecular pseudograph’s atom adjacency matrix”. In order to test the QSPR applicability of the present approach, we will develop quantitative models towards the prediction of several physical properties from the molecular structure of diverse organic compounds, combining quadratic indices and a multiple linear regression method. Finally, predicting series and a (leave-one-out and leave-group-out) cross-validation procedure will be used to corroborate the predictive power of the models.

Results and Discussion

Computational methods. Mathematical definition of the molecular descriptor

Molecular vector space

Each element of the periodic table has inherent atomic properties, such as electronegativity, density, atomic radius and so on. Each one of these properties numerically characterizes each kind of atom taking values in the real set (ℜ). For example, the Mulliken electronegativity (X_A) [37] of the atom A take the values X_H = 2.2 for Hydrogen, X_C = 2.63 for Carbon, X_N = 2.33 for Nitrogen, X_O = 3.17 for Oxygen, X_Cl = 3.0 for Chlorine and so on.

Let there be a molecular vector whose elements are the atomic properties of the atoms in the molecule, for instance X_A. Thus, a molecule having 2, 3, 4,…, n atoms can be “represented” by means of vectors, with 2, 3, 4,...., n components, belonging to the spaces ℜ², ℜ³, ℜ⁴,..., ℜⁿ, respectively. Where n is the dimension of these real subsets (ℜⁿ).

This approach allows us to express compounds such as benzene, cyclohexane, hexane and all the constitutional and geometric isomers of hexane through a general kind of vector X= (X_C, X_C, X_C, X_C, X_C, X_C). On the other hand, n-propanol, iso-propanol, propanal, and acetone may be represented by (X_C, X_C, X_C, X_O) or any permutation of the components of this vector. All these vectors belong to the product space ℜ⁶ and ℜ⁴, respectively. It must be noted that the order of the vector components is meaningless here. This fact, not common in classical vector spaces, will be explained elsewhere. In this example the hydrogen atoms were not considered.

By taking into consideration all the universe of organic molecules, a molecular vector space (E) could be defined:

E = ℜ \oplus ℜ^{2} \oplus ℜ^{3} \oplus ... \oplus ℜ^{n} = \oplus_{i = 1}^{n} ℜ^{i}

(1)

where, i=1, 2, 3,…n; ℜ^k ⌒ ℜ^l = {0}: k ≠ l [38,39] and the dimension of E is the sum of the dimensions of each one of the ℜⁱ spaces. Therefore, this dimension is n(n+1)/2.

This space includes all possible molecules having n atoms as vectors of the ℜⁿ spaces. This mathematical formalism makes it possible to represent any drug or organic molecule as a vector space and then, to use the well-known applications of this algebraic construction to codify molecular structure in a timely but mathematically rigorous way.

Total quadratic indices; [q_k(x)].

Mathematically, a quadratic form is defined as follows [39,40,41]: Let H be a K-space of a finite dimension n. Then the application q: H→ K is a quadratic form (q(x)) if for X=x₁a₁+...+x_na_n, where (a_i)_1≤i≤n is a base of H, it satisfies that:

q (x) = \sum_{i = 1}^{n} \sum_{j = 1}^{n} a_{i j} X_{i} Y_{j}

(2)

Therefore, the quadratic indices are calculated based on an equation analogue to Eq. 2 as an application in the ℜⁱ, vector space of finite dimension i: q: ℜⁱ→ K. If a molecule is considered with n atoms (vector of ℜⁿ), the k-th quadratic indices q_k(x) are defined as q application (q: ℜⁿ→ℜ) if the molecular vector (X) can be expressed by a linear combination with a base belonging to the vector space ℜⁿ (X=x₁a₁+...+x_na_n, where (a_i)_1≤i≤n is a base of ℜⁿ). Taking into consideration the above mentioned conditions q is a quadratic form if Eq. 3 is considered. In this way, the whole form q_k(x), is written as a sum of all the possible terms a_ijx_ix_j, of "i" and "j", independently one of the other, taking values from 1 to n.

q_{k} (x) = \sum_{i = 1}^{n} \sum_{j = 1}^{n}^{k} a_{i j} X_{i} Y_{j}

(3)

where ^ka_ij = ^ka_ji and n is the number of atoms of the molecule. The coefficients ^ka_ij are the elements of the k-th power of the “molecular pseudograph’s atom adjacency matrix” (G). Here, M (G) = M = [a_ij], where n is the number of vertices and the elements a_ij are defined as follows:

a_{i j} = P_{i j} if i≠j and \exists e_{k} \in E / e_{k} ~ v_{i}, v_{j} = L_{i i} if i = j = 0 otherwise

(4)

where, P_ij is the number of edges that comply with e_k ~ v_i,v_j among the vertices (atoms) v_i and v_j and L_ii is the number of loops in v_i. Thus, mathematically a pseudograph can be defined in the following way [38,39]: Let V be a finite not empty set and E an unordered finite set of pairs of elements in V (with equal pairs in E inclusive): the pairs G=<V,E >, are called graphs with loops and multiple edges or pseudograph.

The elements a_ij (if a_ij = P_ij) of this matrix represent the bonds between an atom v_i and an other v_j. The matrix M^k provides the number of walks of length k that links the vertices v_i and v_j. For this reason each edge represents 2 electrons of a covalent bond between atoms v_i and v_j, and it is appreciated in the M (k=1) matrix input that v_ij and v_ji is equal to 1. In this way, the benzene molecule can be represented by two different multigraphs, where each multigraph is related with one of the Kekulé structures. Taking this into consideration, it is necessary the use of a pseudograph to avoid this situation in compounds with more than one canonical structure. This happens for substituted aromatic compounds such as pyridine, naphthalene, quinoline, etc., where the electrons of PI(π)-orbitals are represented as loops of all-ring atoms.

Aromatic rings with only one canonical structure, such as furan, thiophene, pyrrole etc. are represented as a multigraph. This explanation is represented, in an easy way, in Scheme 1 and in Table 1. As can be observed, for the benzene molecule, the total quadratic indices (without considering hydrogen atoms) calculated using the multigraph matrices (connectivity matrices) have the same values. However, some molecules such as acetylsalicylic acid show differences in the total and local (heteroatoms and H-bonding heteroatoms) quadratic indices obtained from each multigraph (Scheme 1, MKA and MKB). The representation number, like a multigraph, is higher when the number of rings with more than one canonical structure is increased.

On the other hand, from the expression of q_k(x) the following considerations arise in a natural way: 1) With the coefficients a_ij, evidently, the square matrix M=[a_ij] of order n can be formed, and 2) let X = [x₁, x₂, x₃,...., x_n], the vector of coordinates of X in the base {a₁,...,a_i}, a matrix of n-row and a single columns; transposing this matrix, X^t= [X₁ X₂,........,X_n] is obtained; which is the row vector of the coordinates of X in the base {a₁,...,a_i}. Then q(x) can be written in the form of a matrix product q(x) =X^tMX. Recently, other descriptors have been expressed through the vector-matrix-vector multiplication procedure [42]. The result of the matrix multiplication is a matrix formed by a row and a column that is a number. Therefore, if we use the canonical bases, the coordinates of any molecular vector (X) coincide with the components of that vector. For that reason, those coordinates can be considered as weights (atom labels) of the vertices of the molecular pseudograph, due to the fact that components of the vector are values of some atomic property, which characterizes each kind of atom.

Scheme 1. Graphical representation of some molecules using “multigraphs” and “pseudographs”.

Table 1. Total and Local Quadratic Indices Calculated for Multigraphs (MKA, MKB) and Pseudographs (P).

**Table 1.** Total and Local Quadratic Indices Calculated for Multigraphs (MKA, MKB) and Pseudographs (P).
Benzene
	q₀(x)	q₁(x)	q₂(x)	q₃(x)	q₄(x)	q₅(x)	q₆(x)	q₇(x)
P	41.5014	124.5042	373.5126	1120.5378	3361.6134	10084.8402	30254.5206	90763.5618
MKA	41.5014	124.5042	373.5126	1120.5378	3361.6134	10084.8402	30254.5206	90763.5618
MKB	41.5014	124.5042	373.5126	1120.5378	3361.6134	10084.8402	30254.5206	90763.5618
Acetylsalicylic acid
	q₀(x)	q₁(x)	q₂(x)	q₃(x)	q₄(x)	q₅(x)	q₆(x)	q₇(x)
P	102.4477	268.8912	873.5982	2566.8034	8381.4114	25593.6122	83330.7872	260026.931
MKA	102.4477	268.8912	873.5982	2549.8376	8284.7898	25063.374	81351.7828	250745.988
MKB	102.4477	268.8912	873.5982	2566.5118	8389.425	25513.2092	83389.772	258104.308
	^Eq₀(x)	^Eq₁(x)	^Eq₂(x)	^Eq₃(x)	^Eq₄(x)	^Eq₅(x)	^Eq₆(x)	^Eq₇(x)
P	40.1956	58.3597	265.963	510.2749	2171.4817	4947.1654	19328.9482	49869.8377
MKA	40.1956	58.3597	265.963	500.226	2133.2198	4618.7534	18773.2472	44486.7656
MKB	40.1956	58.3597	265.963	508.5631	2201.8503	4802.1696	19870.6695	47162.9747
	^Hq₀(x)	^Hq₁(x)	^Hq₂(x)	^Hq₃(x)	^Hq₄(x)	^Hq₅(x)	^Hq₆(x)	^Hq₇(x)
P	4.84	6.974	10.626	33.682	67.54	270.578	670.604	2600.972
MKA	4.84	6.974	10.626	33.682	67.54	269.632	647.306	2589.686
MKB	4.84	6.974	10.626	33.682	67.54	271.766	653.092	2639.868
Metolazone
	q₀(x)	q₁(x)	q₂(x)	q₃(x)	q₄(x)	q₅(x)	q₆(x)	q₇(x)
P	171.9119	485.942	1711.0469	5439.1693	19235.232	62338.8312	220106.56	721470.089
MKAA	171.9119	485.942	1711.0469	5424.1812	19161.672	61839.7906	218582.941	710431.996
MKAB	171.9119	485.942	1711.0469	5411.9254	19107.9148	61560.958	217543.348	706114.062
MKBA	171.9119	485.942	1711.0469	5426.3854	19199.863	61837.827	219141.462	710613.352
MKBB	171.9119	485.942	1711.0469	5414.1296	19146.1058	61558.9944	218101.869	706307.674
	^Eq₀(x)	^Eq₁(x)	^Eq₂(x)	^Eq₃(x)	^Eq₄(x)	^Eq₅(x)	^Eq₆(x)	^Eq₇(x)
P	61.2415	133.8902	554.1099	1558.9199	6272.0672	18784.7951	73539.8425	228597.096
MKAA	61.2415	133.8902	554.1099	1545.5098	6202.9256	18310.0294	72577.097	218343.795
MKAB	61.2415	133.8902	554.1099	1539.3819	6196.7977	18225.9483	72439.9618	217339.95
MKBA	61.2415	133.8902	554.1099	1553.8419	6260.6838	18444.8521	73549.9487	220551.513
MKBB	61.2415	133.8902	554.1099	1547.714	6254.5559	18360.771	73412.8135	219553.796
	^Hq₀(x)	^Hq₁(x)	^Hq₂(x)	^Hq₃(x)	^Hq₄(x)	^Hq₅(x)	^Hq₆(x)	^Hq₇(x)
P	14.52	15.378	46.376	146.608	380.556	1654.686	4353.734	19526.76
MKAA	14.52	15.378	46.376	146.608	381.216	1662.65	4285.534	19850.446
MKAB	14.52	15.378	46.376	146.608	381.216	1662.65	4284.588	19835.926
MKBA	14.52	15.378	46.376	146.608	380.27	1647.096	4238.41	19605.3
MKBB	14.52	15.378	46.376	146.608	380.27	1647.096	4237.464	19590.78
Prazocin
	q₀(x)	q₁(x)	q₂(x)	q₃(x)	q₄(x)	q₅(x)	q₆(x)	q₇(x)
P	198.7612	541.9074	1696.6156	5358.4782	17314.5582	56186.8214	183864.863	603661.363
MKAA	198.7612	541.7274	1694.1796	5323.0646	17197.7804	55637.9444	181811.302	595116.828
MKAB	198.7612	541.7274	1694.3596	5327.7986	17244.174	55914.3384	183221.047	601548.719
MKBB	198.7612	541.7274	1694.3596	5335.6406	17224.5402	55735.215	181942.392	595274.105
	^Eq₀(x)	^Eq₁(x)	^Eq₂(x)	^Eq₃(x)	^Eq₄(x)	^Eq₅(x)	^Eq₆(x)	^Eq₇(x)
P	67.3401	144.9615	468.8527	1384.3378	4526.6829	14281.5586	46761.2533	151360.249
MKAA	67.3401	146.3595	475.5165	1381.8781	4632.9291	14424.8713	48134.0569	153961.075
MKAB	67.3401	146.3595	474.1185	1363.4944	4559.3158	14146.1775	47209.3348	151083.318
MKBB	67.3401	146.3595	474.1185	1377.4643	4553.9629	14140.7919	46743.0601	149152.807
	^Hq₀(x)	^Hq₁(x)	^Hq₂(x)	^Hq₃(x)	^Hq₄(x)	^Hq₅(x)	^Hq₆(x)	^Hq₇(x)
P	9.68	10.252	30.932	64.152	216.128	645.392	2236.476	7512.296
MKAA	9.68	10.252	30.932	64.152	220.088	668.8	2359.72	7965.76
MKAB	9.68	10.252	30.932	62.832	208.516	616.484	2135.1	7120.168
MKBB	9.68	10.252	30.932	62.832	208.516	615.912	2111.956	7031.288

If we make M the matrix of paths of length k (M^k) among n vertices of the molecular pseudograph and we multiply it by the coordinates of molecular vector (X) in the canonical basis of ℜⁿ, we obtain k values that constitute numeric descriptors of the molecular structure. Therefore we can “define” a molecule as quadratic indices (q(x)’s) in the matrix form X^tM^kX = q_k(x), k ≥ 10.

From the given definitions of M and q_k(x) it can be observed that the total quadratic indices are positive integers. The data presented in Table 2 exemplifies the calculation of five quadratic indices for isonicotinic acid.

In any case, if a complete series of indices is considered, a specific characterization of the chemical structure is obtained, which is not repeated in any other molecule. The generalization of the matrices and descriptors to “superior analogues” is necessary for the evaluation of situations where one descriptor is unable to bring a good structural characterization [26].

Table 2. Definition and Calculation of Five (k=0-4) Quadratic Indices of the Molecular Pseudograph’s Atom Adjacency Matrix of the Isonicotinic Acid Molecule.

**Table 2.** Definition and Calculation of Five (k=0-4) Quadratic Indices of the Molecular Pseudograph’s Atom Adjacency Matrix of the Isonicotinic Acid Molecule.
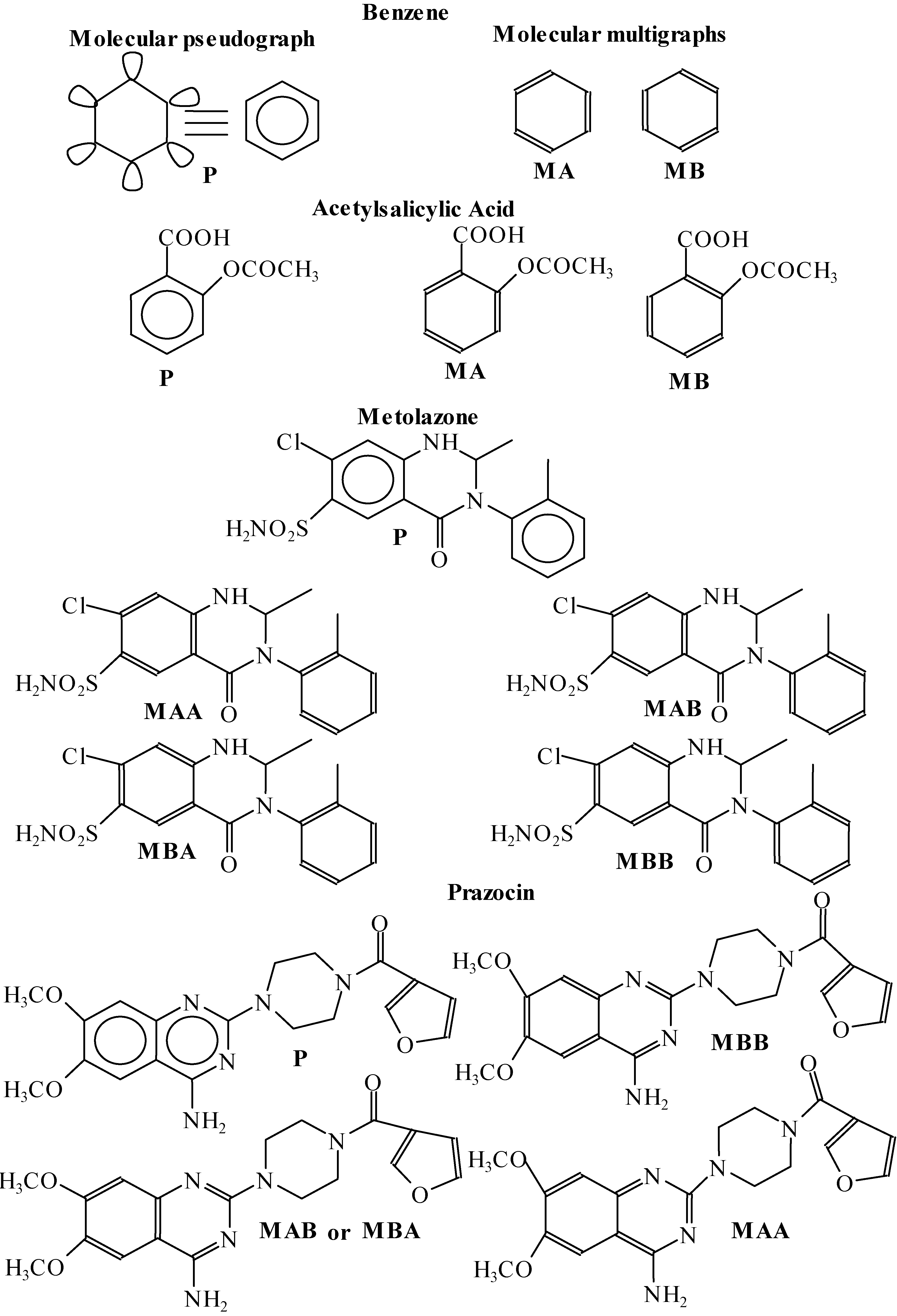
Isonicotinic acid Molecular Structure	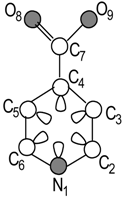Molecular Pseudograph (G) (Hydrogen Suppressed-pseudograph)		X=[N1 C2 C3 C4 C5 C6 C7 O8 O9] Molecular Vector: X∊ℜ⁹ and ℜ⁹∊E; E: Molecular Vector Space In the definition of the X, as molecular vector, the chemical symbol of the element is used to indicate the corresponding electronegativity value. That is: if we write O it means χ(O), oxygen Mulliken electronegativity or some atomic property, which characterizes each atom in the molecule. Therefore, if we use the canonical bases of R⁹, the coordinates of any vector X coincide with the components of that molecular vector X^t =[233 263 263 263 263 263 263 3.17 3.17] X^t = transposed of X and it means the vector of the coordinates of X in the Canonical basis of R⁹ (a row vector) X: vector of coordinates of X in the Canonical basis of R⁹ (a column vector)
$q_{0} (x) = \sum_{i = 1}^{n} \sum_{j = 1}^{n}_{0} a_{i j} X_{i} X_{j}$		= X^tM⁰X=67.0281
$q_{1} (x) = \sum_{i = 1}^{n} \sum_{j = 1}^{n}_{1} a_{i j} X_{i} X_{j}$		= X^tM¹X=183.7166
$q_{2} (x) = \sum_{i = 1}^{n} \sum_{j = 1}^{n}_{2} a_{i j} X_{i} X_{j}$		= X^tM²X=589.963	$M (G) = \begin{matrix} N 1 & C 2 & C 3 & C 5 & 1 & C 6 & C 7 & C 8 & C 9 \\ N 1 & 1 & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ C 2 & 1 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ C 3 & 0 & 1 & 1 & 1 & 0 & 0 & 0 & 0 & 0 \\ C 4 & 0 & 0 & 1 & 1 & 1 & 0 & 1 & 0 & 0 \\ C 5 & 0 & 0 & 0 & 1 & 1 & 1 & 0 & 0 & 0 \\ C 6 & 1 & 0 & 0 & 0 & 1 & 1 & 0 & 0 & 0 \\ C 7 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 2 & 1 \\ C 8 & 0 & 0 & 0 & 0 & 0 & 0 & 2 & 0 & 0 \\ C 9 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \end{matrix}$ M(G): Adjacency Matrix Among Vertices of the Molecular Pseudograph (G)
$q_{3} (x) = \sum_{i = 1}^{n} \sum_{j = 1}^{n}_{3} a_{i j} X_{i} X_{j}$		= X^tM³X=1784.6905
$q_{4} (x) = \sum_{i = 1}^{n} \sum_{j = 1}^{n}_{4} a_{i j} X_{i} X_{j}$		= X^tM⁴X=5707.7232

Local quadratic indices; [q_kL(x)]

In the case of quadratic indices it is possible to define analogues to total quadratic indices that possess similar properties and which are defined as local quadratic indices of the “molecular pseudograph`s atoms adjacency matrix”. The definition of this descriptor, graph theoretical invariant for a given fragment F_R (connected subgraph), within a specific pseudograph (G) is the following:

q_{k L} (x) = \sum_{i = 1}^{m} \sum_{j = 1}^{m}_{k} a_{i j L} X_{i} X_{j}

(5)

where m is the number of atoms of the fragment of interest and ^ka_ijL is the element of the file “i” and column “j” of the matrix M^k_L=M^k(G, F_R) [q_kL(x) = q_k(x, F_R)]. This matrix is extracted from the M^k matrix and it contains the information referred to the vertices of the specific fragments (F_R) and also of the molecular environment.

The matrix M^k_L=[^ka_ijL] with elements ^ka_ijL is defined as follows:

^ka_ijL = ^ka_ij if both v_i and v_j are vertices contained in the specific fragment.
=1/2 ^ka_ij either v_i or v_j is contained in the specific fragment but not both
at the same time
=0 otherwise

(6)

with ^ka_ij being the elements of the k-th power of M. These local analogues can also be expressed in matrix form by the expression:

q_kL(x) =X^t M^k_L X: M^k_L:it is extract from M^k

(7)

As can be seen. if a molecule is partitioned in Z molecular fragments, the matrix M^k can be partitioned in Z local matrices M^k_L, L=1,... Z. The k-th power of matrix M is exactly the sum of the k-th power of local Z matrices:

M^{k} = \sum_{L = 1}^{Z} M_{\underset{L}{}}^{\underset{k}{}}

(8)

or in the same way as M^k=[^ka_ij], where:

^{k} a_{i j} = \sum_{L = 1}^{Z}^{k} a_{i j L}

(9)

and consequently, the total quadratic indices of order k can be expressed as the sum of the local quadratic indices of the Z fragments of the same order: F_R

q_{k} (x) = \sum_{L = 1}^{Z} q_{k L} (x)

(10)

Any local quadratic index has a particular meaning, especially for the first values of k, where the information about the structure of the fragment F_R is contained. High values of k are in relation to the environment information of the fragment F_R considered inside the molecular pseudograph (G). A general equation for k order is described as follows:

q_{k L} (x) = {\sum_{i}}^{k} a_{i i L} {X_{i}}^{2} + 2 {\sum_{(i, j)}}^{k} a_{i j L} X_{i} X_{j}

(11)

In a similar way to total analogues, the complete series of indices brings gives a unique characterization of the chemical structure fragment, which not only has information about the fragment under study, but also on the molecular environment. These local indices can also be used together with total indices as variables of QSAR and QSPR models for properties or activities that depend more on a region or fragment than on the whole molecule.

Calculation of total and local quadratic indices

Let us now consider the molecule of 1-methylallyl alcohol (but-3-en-2-ol) and its labelled molecular “pseudograph” and atom adjacency matrix as a simple example. The zero, first and second powers of this matrix and local matrices of these orders of each one of the three fragments shown in the molecule are given in Table 3.

The quadratic indices of the “molecular pseudograph’s atoms adjacency matrix” are calculated in the following way:

1): Total and Local indices of zero order [q₀(x) and q_0L(x)]. These indices are obtained when the matrix M is raised to the power 0 (k=0). A matrix raised to the power 0 is the identity matrix (I); which is constituted by the elements a_ii=1 [M⁰(i, i)=1]. Since the zero order matrix is diagonal, its quadratic form contains only the terms with the squares of the coordinates (an atomic property) of the X vector in canonical bases. Generally, we can establish that.

$q_{0} (x) = \sum_{i = 1}^{n} X i^{2}$

(12)

and

$q_{0 L} (x) = \sum_{i = 1}^{m} X i^{2}$

(13)

where n and m are the number of atoms in the molecule or in the fragment F_R under study, respectively.

The total quadratic indices of zero order are obtained by the matrix product, q₀(x)=X^tM⁰X and local quadratic indices of zero order for each one of the three represented fragments are calculated using the three local matrices as the matrix of the quadratic form. Making the matrix product by the row matrix (X^t) and by the column matrix (X), the three local molecular quadratic indices (one for each fragment) are obtained (see Table 3): q₀(x, F₁)=1^.(X_O4)²=1^.(3.17)²=10.0489; q₀(x, F₂)= 1^.(X_C3)² + 1^.(X_C5)²=1^.(2.63)²+1^.(2.63)²=13.8338 and q₀(x, F₃)= 1^.(X_C1)² + 1^.(X_C2)²=1^.(2.63)²+1^.(2.63)²=13.8338. It should be noted that q₀(x, G)= q₀(x, F₁)+q₀(x, F₂)+q₀(x, F₃)= 1^.(X_C1)² +1^.(X_C2)² +1^.(X_C3)² +1^.(X_O4)² +1^.(X_C5)² =1^.(2.63)²+1^.(2.63)²+1^.(2.63)²+ 1^.(3.17)²+ 1^.(2.63)²=37.7165 and that M⁰(G)=M⁰(G, F₁)+M⁰(G, F₂)+M⁰(G, F₃).

The local quadratic index, q_0L(x) contains information about the fragment under study, without regard to which atom(s) it is bonded to, since the ones in the main diagonal express that paths of length 0 is the succession of a single vertex. That is to say, those sub-graphs of zero order consist of isolated vertices. This index has information about the molecular size of the fragment and it depends on the number and type of atoms that are contained in the fragment under study.

2): Total and local quadratic indices of first order [q₁(x) and q_1L(x)]. These indices are obtained when the matrix M is raised to the unit power (M¹= M) and multiplied by the matrices X^t and X. We can write the expression for q₁(x) and q_1L(x) in the forms:

$q_{1} (x) = \sum_{i} a_{i i} {X_{i}}^{2} + 2 \sum_{(i, j)} a_{i j} X_{i} X_{j}$

(14)

and

$q_{1 L} (x) = \sum_{i} a_{i i L} {X_{i}}^{2} + 2 \sum_{(i, j)} a_{i j L} X_{i} X_{j}$

(15)

The total quadratic index of first order is: q₁(x)= 4^.(X_C₁^.X_C₂) + 2^.(X_C₂^.X_C₃) + 2^.(X_C₃^.X_O₄) + 2^.(X_C₃^.X_C₅) = 4^.(2.63^.2.63) +2^.(2.63^.2.63) +2^.(2.63^.3.17) +2^.(2.63^.2.63) = 72.0094. To obtain the local analogues for each fragment we proceed to the extract of the matrices “partitioned” for each one of the fragments (see Table 3). Making the matrix product we get: q₁(x,F₁) = 1^.(X_C₃^.X_O₄) = 1^.(2.63^.3.17) = 8.3371; q₁(x,F₂) = 1^.(X_C₂^.X_C₃) +1^.(X_C₃^.X_O₄)+2^.(X_C₃^.X_C₅) = 1^.(2.63^.2.63) +1^.(2.63^.3.17) +2^.(2.63^.2.63) = 29.0878 and q₁(x, F₃) = 4^.(X_C₁^.X_C2) +1^.(X_C₂^.X_C₃) = 4^.(2.63^.2.63) +1^.(2.63^.2.63) = 34.5845. It should be observed that q₁(x, G)= q₁(x, F₁)+ q₁(x, F₂) +q₁(x, F₃) and that M¹(G)=

\sum_{R = 1}^{3}

M¹(G, F_R).

As can be seen, this index not only has information about the fragment F_R of interest, but also has information about the atoms to which this fragment is connected to by a step (by means of a walk of length 1). As it is appreciated from its formulation that this index is capable of differentiating between saturated and unsaturated sub-structures (fragments) inside a molecular pseudograph (molecule). Two sub-graphs will only have the same value, if and only if, both fragments present the same composition, equal topological arrangements among the atoms that constitute them and, the fragments are connected to the same atoms that are not part of the fragment by a path of length 1 (in a step).

3): Total and local quadratic indices of second order [q₂(x) and q_2L(x)]. In general, these indices are calculated as:

$q_{2} (x) = \sum_{i = 1}^{n} \sum_{j = 1}^{n}^{2} a_{i j} X_{i} X_{j}$

(16)

and

$q_{2 L} (x) = \sum_{i = 1}^{m} \sum_{j = 1}^{m}^{2} a_{i j L} X_{i} X_{j}$

(17)

As it can be observed, to obtain this index it is necessary to obtain the matrices M², which are given in Table 3. If in the four cases (total and three local ones) we carry out the matrix product we obtain:

q₂(x,G)=4^.(X_C₁)²+5^.(X_C₂)²+3^.(X_C₃)²+1^.(X_O₄)²+1^.(X_C₅)²+4^.(X_C₁^.X_C₃)+2^.(X_C₂^.X_O₄)+2^.(X_C₂^.X_C₅)+2^.(X_O₄^.X_C₅)=4^.(2.63)² +5^.(2.63)² +3^.(2.63)² +1^.(3.17)² +1^.(2.63)² +4^.(2.63^.2.63) +2^.(2.63^.3.17) +2^.(2.63^.2.63) +2^.(3.17^.2.63)=174.8184;
q₂(x, F₁)=1^.(X_C₂^.X_O₄)+1^.(X_O₄^.X_C₅)+1^.(X_O₄)²=1^.(2.63^.3.17) +1^.(3.17^.2.63)
+1^.(3.17)²=26.7231;
q₂(x, F₂)=2^.(X_C₁^.X_C₃) +1^.(X_C₂^.X_C₅) +1^.(X_C₄^.X_C₅) +3^.(X_C₃)² +1^.(X_C₅)²=2^.(2.63^.2.63)
+1^.(2.63^.2.63) +1^.(3.17^.2.63) +3^.(2.63)²+ 1^.(2.63)²=56.7554, and
q₂(x, F₃)=2^.(X_C₁^.X_C₃) +1^.(X_C₂^.X_C₄) +1^.(X_C₂^.X_C₅) +4^.(X_C₁)² +5^.(X_C₂)²=2^.(2.63^.2.63)
+1^.(2.63^.3.17) +1^.(2.63^.2.63) +4^.(2.63)² +5^.(2.63)²=91.3399.

It is easy to prove that q₂(x, G) = q₂(x, F₁)+q₂(x, F₂)+q₂(x, F₃) and that M²(G)=

\sum_{R = 1}^{3}

M²(G, F_R).

Table 3. The Zero, First and Second Powers of the Molecular “pseudograph’s” Atom Adjacency Matrix and Local Matrices for These Order of Each One of 3 Fragments Shown in the Molecule of 1-methylallyl alcohol (but-3-en-2-ol).

**Table 3.** The Zero, First and Second Powers of the Molecular “pseudograph’s” Atom Adjacency Matrix and Local Matrices for These Order of Each One of 3 Fragments Shown in the Molecule of 1-methylallyl alcohol (but-3-en-2-ol).
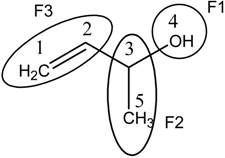Molecular Structure of 1-methylallyl alchohol (But-3-en-2-ol)	X=[C₁ C₂ C₃ O₄ C₅] Molecular Vector: X∊ℜ⁵ and ⁵∊ℜE; E: Molecular Vector Space In the definition of the X, as molecular vector, the chemical symbol of the element is used to indicate the corresponding electronegativity value. That is: if we write O it means χ(O), oxygen Mulliken electronegativity or some atomic property, which characterizes each atom in the molecule. Therefore, if we use the canonical bases of ℜ⁵, the coordinates of any molecular vector X coincide with the components of that molecular vector. X^t = [2.63 2.63 2.63 3.17 2.63] X^t = transposed of X and it means the vector of the coordinates of X in the Canonical basis of ℜ⁵ (a row vector) X: vector of coordinates of X in the Canonical basis of ℜ⁵ (a column vector)
The zero, first and second powers of the molecular “pseudograph’s” total atom adjacency matrix.
$M^{0} (G) = I (G) = \begin{matrix} 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \end{matrix}$	$M^{1} (G) = \begin{matrix} 0 & 2 & 0 & 0 & 0 \\ 2 & 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 1 & 1 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \end{matrix}$	$M^{2} (G) = \begin{matrix} 4 & 0 & 2 & 0 & 0 \\ 0 & 5 & 0 & 1 & 1 \\ 2 & 0 & 3 & 0 & 0 \\ 0 & 1 & 0 & 1 & 1 \\ 0 & 1 & 0 & 1 & 1 \end{matrix}$
The zero, first and second powers of the molecular “pseudograph’s” local atom adjacency matrix of each one of 3 fragments shown in the molecule of 1-methylallyl alcohol
$M^{0} (G, F_{1}) = \begin{matrix} 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{matrix}$	$M^{1} (G, F_{1}) = \begin{matrix} 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 / 2 & 0 \\ 0 & 0 & 1 / 2 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{matrix}$	$M^{2} (G, F_{1}) = \begin{matrix} 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 / 2 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 1 / 2 & 0 & 1 & 1 / 2 \\ 0 & 0 & 0 & 1 / 2 & 0 \end{matrix}$
$M^{0} (G, F_{2}) = \begin{matrix} 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 \end{matrix}$	$M^{1} (G, F_{2}) = \begin{matrix} 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 / 2 & 0 & 0 \\ 0 & 1 / 2 & 0 & 1 / 2 & 1 \\ 0 & 0 & 1 / 2 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \end{matrix}$	$M^{2} (G, F_{2}) = \begin{matrix} 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 / 2 \\ 1 & 0 & 3 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 / 2 \\ 0 & 1 / 2 & 0 & 1 / 2 & 1 \end{matrix}$
$M^{0} (G, F_{3}) = \begin{matrix} 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{matrix}$	$M^{1} (G, F_{3}) = \begin{matrix} 0 & 2 & 0 & 0 & 0 \\ 2 & 0 & 1 / 2 & 0 & 0 \\ 0 & 1 / 2 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{matrix}$	$M^{2} (G, F_{3}) = \begin{matrix} 4 & 0 & 1 & 0 & 0 \\ 0 & 5 & 0 & 1 / 2 & 1 / 2 \\ 1 & 0 & 0 & 0 & 0 \\ 0 & 1 / 2 & 0 & 0 & 0 \\ 0 & 1 / 2 & 0 & 0 & 0 \end{matrix}$

The TOMO-COMD software

The calculation of total and local quadratic indices for any organic molecule was implemented with the TOMO-COMD software [36]. This software has a graphical interface that makes it user friendly for medicinal chemists. The input of the chemical structure is by directly drawing the molecular pseudograph using the software’s drawing mode. This procedure is carried out by a selection of the active atom symbols belonging to different groups of the periodic table. The multiple edges and loops are edited with a right mouse click. Afterwards, in the calculation mode, one should select the atomic property and the family descriptor before calculating the molecular indices. In this work, we used the Mulliken electronegativity as an example of an atomic property [37]. The descriptors calculated were the following:

(1): q_k(x) and q_k^H(x) are the k-th total quadratic indices calculated using the k-th power of the matrices [M^k(G) or M^k(G^H)] of the molecular pseudograph (G) considering and not considering hydrogen atoms, respectively.
(2): ^Eq_k_L(x) [or ^Eq_k_L^H(x)] and ^H q_k_L(x) are the k-th local quadratic indices calculated using a k-th power of the local matrices [M^k_L(G, F_R)] of the molecular pseudograph (G) not considering (or considering) hydrogen atoms for heteroatoms (S,N,O) and hydrogen bonding heteroatoms, respectively.

Physical properties data sets for QSPR studies

To test the ability of the set of the total and local quadratic indices to predict molecular physical properties, the following four series have been investigated (three of which have been previously investigated by other “topological” procedures):

a): 74 alkanes (Table 4) with seven representative physical properties: Boiling point (Bp), molar volume at 20 ^oC (MV), molar refraction at 20 ^oC (MR), heat of vaporization at 25 ^oC (HV), critical temperature (TC), critical pressure (PC), and surface tension at 20 ^oC (ST) [43];
b): 58 alkyl alcohols with Bp data (Table 8, Table 9 and Table 10) [44];
c): 106 cycloalkanes, including polycycles and spiroalkanes with Bp data (Table 12 and Table 13) [25];
d): Bp data of 95 structurally diverse compounds belonging to several chemical groups, but all containing in their structure some aromatic rings (Table 14 and Table 15) [45,46].

Table 4. Quadratic Indices of the “Molecular Pseudograph’s Atom Adjacency Matrix” for C3-C9 Alkanes.

**Table 4.** Quadratic Indices of the “Molecular Pseudograph’s Atom Adjacency Matrix” for C3-C9 Alkanes.
no.	Alkane	q₀^H(x)	q₁^H(x)	q₂^H(x)	q₃^H(x)	q₄^H(x)	q₀(x)	q₂(x)	q₃(x)	q₅(x)
1	2	42.8738	83.2658	211.8872	461.6846	1097.3462	13.8338	13.8338	13.8338	13.8338
2	3	59.4707	120.2436	319.0366	749.5692	1876.432	20.7507	41.5014	55.3352	110.6704
3	4	76.0676	157.2214	426.186	1037.8236	2666.8698	27.6676	69.169	110.6704	290.5098
4	2M3	76.0676	157.2214	426.5558	1048.8058	2757.6878	27.6676	83.0028	124.5042	373.5126
5	5	92.6645	194.1992	533.3354	1326.078	3457.6774	34.5845	96.8366	166.0056	498.0168
6	2M4	92.6645	194.1992	533.7052	1337.43	3559.4776	34.5845	110.6704	193.6732	664.0224
7	22MM3	92.6645	194.1992	534.4448	1359.3944	3741.1136	34.5845	138.338	221.3408	885.3632
8	6	109.2614	231.177	640.4848	1614.3324	4248.485	41.5014	124.5042	221.3408	719.3576
9	2M5	109.2614	231.177	640.8546	1625.6844	4350.655	41.5014	138.338	249.0084	899.197
10	3M5	109.2614	231.177	640.8546	1626.0542	4361.6372	41.5014	138.338	262.8422	982.1998
11	22MM4	109.2614	231.177	641.5942	1648.3884	4554.2554	41.5014	166.0056	304.3436	1314.211
12	23MM4	109.2614	231.177	641.2244	1637.4062	4463.4374	41.5014	152.1718	290.5098	1175.873
13	7	125.8583	268.1548	747.6342	1902.5868	5039.2926	48.4183	152.1718	276.676	940.6984
14	2M6	125.8583	268.1548	748.004	1913.9388	5141.4626	48.4183	166.0056	304.3436	1134.3716
15	3M6	125.8583	268.1548	748.004	1914.3086	5152.8146	48.4183	166.0056	318.1774	1231.2082
16	3E.5	125.8583	268.1548	748.004	1914.6784	5164.1666	48.4183	166.0056	332.0112	1328.0448
17	22MM5	125.8583	268.1548	748.7436	1936.6428	5345.8026	48.4183	193.6732	359.6788	1577.0532
18	23MM5	125.8583	268.1548	748.3738	1926.0304	5265.9668	48.4183	179.8394	359.6788	1521.718
19	24MM5	125.8583	268.1548	748.3738	1925.2908	5244.0024	48.4183	179.8394	332.0112	1328.0448
20	33MM5	125.8583	268.1548	748.7436	1937.3824	5367.767	48.4183	193.6732	387.3464	1770.7264
21	223MMM4	125.8583	268.1548	749.1134	1948.7344	5469.5672	48.4183	207.507	415.014	1992.0672
22	8	142.4552	305.1326	854.7836	2190.8412	5830.1002	55.3352	179.8394	332.0112	1162.0392
23	2M7	142.4552	305.1326	855.1534	2202.1932	5932.2702	55.3352	193.6732	359.6788	1355.7124
24	3M7	142.4552	305.1326	855.1534	2202.563	5943.6222	55.3352	193.6732	373.5126	1466.3828
25	4M7	142.4552	305.1326	855.1534	2202.563	5943.992	55.3352	193.6732	373.5126	1480.2166
26	3E.6	142.4552	305.1326	855.1534	2202.9328	5955.344	55.3352	193.6732	387.3464	1590.887
27	22MM6	142.4552	305.1326	855.893	2224.8972	6136.6102	55.3352	221.3408	415.014	1826.0616
28	23MM6	142.4552	305.1326	855.5232	2214.2848	6057.1442	55.3352	207.507	415.014	1784.5602
29	24MM6	142.4552	305.1326	855.5232	2213.915	6046.162	55.3352	207.507	401.1802	1673.8898
30	25MM6	142.4552	305.1326	855.5232	2213.5452	6034.4402	55.3352	207.507	387.3464	1563.2194
31	33MM6	142.4552	305.1326	855.893	2225.6368	6159.3142	55.3352	221.3408	442.6816	2047.4024
32	34MM6	142.4552	305.1326	855.5232	2214.6546	6068.4962	55.3352	207.507	428.8478	1881.3968
33	23ME5	142.4552	305.1326	855.5232	2214.6546	6068.866	55.3352	207.507	428.8478	1895.2306
34	33ME5	142.4552	305.1326	855.893	2226.3764	6181.6484	55.3352	221.3408	470.3492	2254.9094
35	223MMM5	142.4552	305.1326	856.2628	2237.3586	6272.4664	55.3352	235.1746	484.183	2365.5798
36	224MMM5	142.4552	305.1326	856.2628	2236.2492	6239.5198	55.3352	235.1746	442.6816	2033.5686
37	233MMM5	142.4552	305.1326	856.2628	2237.7284	6283.4486	55.3352	235.1746	498.0168	2476.2502
38	234MMM5	142.4552	305.1326	855.893	2226.0066	6170.6662	55.3352	221.3408	456.5154	2088.9038
39	2233MMMM4	147.2952	305.1326	857.0024	2260.4324	6487.049	55.3352	262.8422	553.352	3001.9346
40	9	159.0521	342.1104	961.933	2479.0956	6620.9078	62.2521	207.507	387.3464	1383.38
41	2M8	159.0521	342.1104	962.3028	2490.4476	6723.0778	62.2521	221.3408	415.014	1577.0532
42	3M8	159.0521	342.1104	962.3028	2490.8174	6734.4298	62.2521	221.3408	428.8478	1687.7236
43	4M8	159.0521	342.1104	962.3028	2490.8174	6734.7996	62.2521	221.3408	428.8478	1715.3912
44	3E.7	159.0521	342.1104	962.3028	2491.1872	6746.1516	62.2521	221.3408	442.6816	1826.0616
45	4E.7	159.0521	342.1104	962.3028	2491.1872	6746.5214	62.2521	221.3408	442.6816	1853.7292
46	22MM7	159.0521	342.1104	963.0424	2513.1516	6927.4178	62.2521	249.0084	470.3492	2047.4024
47	23MM7	159.0521	342.1104	962.6726	2502.5392	6847.9518	62.2521	235.1746	470.3492	2019.7348
48	24MM7	159.0521	342.1104	962.6726	2502.1694	6837.3394	62.2521	235.1746	456.5154	1922.8982
49	25MM7	159.0521	342.1104	962.6726	2502.1694	6836.5998	62.2521	235.1746	456.5154	1895.2306
50	26MM7	159.0521	342.1104	962.6726	2501.7996	6825.2478	62.2521	235.1746	442.6816	1770.7264
51	33MM7	159.0521	342.1104	963.0424	2513.8912	6950.1218	62.2521	249.0084	498.0168	2296.4108
52	34MM7	159.0521	342.1104	962.6726	2502.909	6859.6736	62.2521	235.1746	484.183	2144.239
53	35MM7	159.0521	342.1104	962.6726	2502.5392	6848.3216	62.2521	235.1746	470.3492	2019.7348
54	44MM7	159.0521	342.1104	963.0424	2513.8912	6950.8614	62.2521	249.0084	498.0168	2324.0784
55	23ME6	159.0521	342.1104	962.6726	2502.909	6860.0434	62.2521	235.1746	484.183	2171.9066
56	24ME6	159.0521	342.1104	962.6726	2502.5392	6848.6914	62.2521	235.1746	470.3492	2047.4024
57	33ME6	159.0521	342.1104	963.0424	2514.6308	6973.1956	62.2521	249.0084	525.6844	2545.4192
58	34ME6	159.0521	342.1104	962.6726	2503.2788	6871.3954	62.2521	235.1746	498.0168	2268.7432
59	223MMM6	159.0521	342.1104	963.4122	2525.613	7063.6438	62.2521	262.8422	539.5182	2642.2558
60	224MMM6	159.0521	342.1104	963.4122	2524.8734	7041.6794	62.2521	262.8422	511.8506	2393.2474
61	225MMM6	159.0521	342.1104	963.4122	2524.5036	7029.5878	62.2521	262.8422	498.0168	2268.7432
62	233MMM6	159.0521	342.1104	963.4122	2525.9828	7074.9958	62.2521	262.8422	553.352	2766.76
63	234MMM6	159.0521	342.1104	963.0424	2514.6308	6973.1956	62.2521	249.0084	525.6844	2462.4164
64	235MMM6	159.0521	342.1104	963.0424	2513.8912	6950.4916	62.2521	249.0084	498.0168	2241.0756
65	244MMM6	159.0521	342.1104	963.4122	2525.2432	7053.0314	62.2521	262.8422	525.6844	2517.7516
66	334MMM6	159.0521	342.1104	963.4122	2526.3526	7086.3478	62.2521	262.8422	567.1858	2863.5966
67	33EE5	159.0521	342.1104	963.0424	2515.3704	6995.8996	62.2521	249.0084	553.352	2766.76
68	223MME5	159.0521	342.1104	963.4122	2525.9828	7075.7354	62.2521	262.8422	553.352	2766.76
69	233MME5	159.0521	342.1104	963.4122	2526.7224	7097.6998	62.2521	262.8422	581.0196	2988.1008
70	234MEM5	159.0521	342.1104	963.0424	2514.6308	6973.9352	62.2521	249.0084	525.6844	2490.084
71	2233(M)5	159.0521	342.1104	964.1518	2549.4264	7301.3002	62.2521	290.5098	636.3548	3513.7852
72	2234(M)5	159.0521	342.1104	963.782	2537.3348	7177.5356	62.2521	276.676	581.0196	2960.4332
73	2244(M)5	159.0521	342.1104	964.1518	2547.2076	7235.407	62.2521	290.5098	553.352	2766.76
74	2334(M)5	159.0521	342.1104	963.782	2538.0744	7199.5	62.2521	276.676	608.6872	3209.4416
no.	q₇(x)	q₁₁(x)	q₁₃(x)	q₁₅(x)	no.	q₇(x)	q₁₁(x)	q₁₃(x)	q₁₅(x)
1	13.8338	13.8338	13.8338	13.8338	38	9531.4882	198335.19	904716.69	4126913
2	221.3408	885.3632	1770.7264	3541.4528	39	16033.374	452213.09	2398545.7	12719902
3	760.859	5215.3426	13653.9606	35746.539	40	4980.168	65018.86	235174.6	850778.7
4	1120.5378	10084.84	30254.5206	90763.562	41	6031.5368	88812.996	341252.18	1311776.3
5	1494.0504	13446.454	40339.3608	121018.08	42	6695.5592	106326.59	424531.65	1696120.7
6	2268.7432	26450.226	90307.0464	308327.73	43	6930.7338	114032.01	463003.45	1880234.8
7	3541.4528	56663.245	226652.979	906611.92	44	7580.9224	131365.76	547431.13	2281968.3
8	2337.9122	24665.665	80097.702	260089.27	45	7802.2632	138504.01	583675.69	2459760.3
9	3250.943	42538.935	153901.025	556810.45	46	9019.6376	178179.34	795498.84	3556836
10	3665.957	51060.556	190560.595	711181.82	47	8715.294	163432.51	708926.91	3076720.1
11	5658.0242	104763.37	450774.373	1939581.8	48	8148.1082	146859.62	623696.87	2648840.7
12	4717.3258	75546.382	302199.361	1208811.3	49	7871.4322	135571.24	562274.8	2331382.6
13	3209.4416	37406.595	127713.642	436041.38	50	7082.9056	113326.49	453305.96	1813223.8
14	4233.1428	58959.656	220040.423	821202.04	51	10679.694	233182.53	1091597.5	5112419.1
15	4772.661	71797.422	278515.895	1080447.4	52	9545.322	189772.07	846421.05	3775354.7
16	5312.1792	84994.867	339979.469	1359917.9	53	8687.6264	160831.76	692022.01	2977614.8
17	6944.5676	135156.23	596541.124	2633153.2	54	10956.37	245024.27	1159383.1	5486153.1
18	6418.8832	114045.85	480641.547	2025600.3	55	9752.829	196688.97	883301.96	3966786.8
19	5312.1792	84994.867	339979.469	1359917.9	56	8908.9672	168329.68	731310	3176683.2
20	8078.9392	168108.34	766835.202	3497959.3	57	12367.417	292640.21	1423940.7	6928990.7
21	9462.3192	212155.16	1004001.87	4751080.3	58	10347.682	215309.26	982144.46	4480103.8
22	4094.8048	51060.556	180365.084	637115.66	59	12962.271	312505.54	1534901.6	7539338
23	5132.3398	73886.326	280632.467	1066267.8	60	11219.212	247237.67	1161361.3	5456410.4
24	5782.5284	90279.379	356995.043	1411988.3	61	10347.682	215309.26	982144.46	4480103.8
25	5907.0326	94443.353	377759.577	1511024.5	62	13833.8	345845	1729225	8646125
26	6543.3874	110767.24	455782.209	1875475.9	63	11537.389	253324.55	1186995.4	5561796.3
27	8092.773	160236.91	714156.091	3184194.9	64	10071.006	202803.51	909378.68	4076654.9
28	7677.759	142142.3	611606.132	2631603.8	65	12090.741	279636.43	1345613.7	6476127.5
29	6986.069	121585.27	507105.607	2114869.8	66	14456.321	368504.76	1860549.3	9393758.9
30	6294.379	101443.26	406533.881	1628127.6	67	13833.8	345845	1729225	8646125
31	9503.8206	205390.43	955196.222	4442545	68	13833.8	345845	1729225	8646125
32	8258.7786	159185.54	698869.742	3068226.2	69	15327.85	402729.59	2064003	10577877
33	8369.449	163114.34	720035.456	3178412.4	70	11786.398	263948.9	1249026.1	5910463.4
34	10804.198	248026.2	1188364.92	5693798.4	71	19228.982	572193.64	3118774.9	16996954
35	11523.555	273010.04	1328584.32	6465267.9	72	15051.174	389172.46	1979229.4	10066248
36	9365.4826	199303.56	920044.537	4247972.6	73	13833.8	345845	1729225	8646125
37	12242.913	298408.9	1472843.18	7269219.2	74	16821.901	461274.23	2415270.8	12646528

Data analysis

The statistical analyses were carried out with the STATISTICA software package [47]. Linear multiple regression analysis (LMR) was used to obtain quantitative models that relate the structures and physical properties of organic compounds. The quality of the models was determined examining the statistic parameters of multivariable comparison of regression and cross-validation procedures [leave-one-out and leave-group (5-fold)-out]. In recent years, the leave-one-out (LOO) press statistics (e.g., q²) have been used as a means of indicating predictive ability. Many authors consider high q² values (for instance, q²> 0.5) as indicator or even as the ultimate proof of the high predictive power of a QSAR model. In a recent paper, Golbraikh and Tropsha demonstrated that high values of LOO q² appears to be a necessary but not the sufficient condition for the model to have a high predictive power [48]. A more exhaustive cross-validation method can be used in which a fraction of the data (10-20%) is left out and predicted from a model based on the remaining data. This process (leave-group-out, LGO) is repeated until each observation has been left out at least once [49,50]. For this present paper, each investigated data set was splited randomly into five groups of approximately the same size (20%). Each group was left out (LGO) and that group was then predicted by a model developed from the remaining observations (80% of the data). This process was carried out five times on five unique subsets. In this way, every observation was left out once, in groups of 20%, and its value predicted. The mean absolute errors (MAE) for the five groups will be used as the significant criterion for assessing model quality. The level of overall (average) MAE (for a 20% full leave-out) of 5-fold cross-validation procedure can be taken as good confirmation of the predictive quality of the model. In addition, to assess the robustness and predictive power of the found models, external prediction (test) sets also were used. This type of model validation is very important, if we take into consideration that the predictive ability of a QSAR model can only be estimated using an external test set of compounds that was not used for building the model [48].

QSPR applications

The objective will be to show, in as direct a manner as possible, that the total and local quadratic indices delineated in the previous section yield predictive molecular physical properties in a QSPR analysis. In this sense, we can find a quantitative relation between a property P and the quadratic indices of M having, for instance, the following appearance:

P=a₀q₀(x) + a₁q₁(x) + a₂q₂(x) +….+ a_kq_k(x) + c

(18)

where P is the measurement of the property, q_k(x) [or q_kL(x)] is the kth total [or local] quadratic indices, and the a_k’s are the coefficients obtained by the linear regression analysis.

Taking into consideration another of Randić’s attributes, it is convenient that candidates for molecular descriptors have good correlations with at least one physical property [26]. In the present work we have selected physical properties of several data sets of organic compounds. The first data set is formed by 74 alkanes. The values of the total quadratic indices for such molecules are presented in Table 4. The alkanes represent an especially attractive class of compounds as a starting point for the application of molecular modeling techniques, because many alkane properties vary in a regular manner according to molecular mass and extent of branching. Besides, the alkanes are nonpolar and a number of complexities that arise with more polar compounds are thus avoided [43].

The best linear regression models for seven representative physical properties of alkanes were obtained by a forward stepwise procedure; the equation and the statistical parameters are presented in Table 5. In this Table, R is the multiple correlation coefficient, s is the standard deviation of the regression, q² is the square multiple correlation coefficient of the LOO cross-validation procedure; MAE is the (average) mean absolute error of the LGO cross-validation procedure; F is the Fisher ratio at the 95% confidence level, and the p-value is the significance level.

Table 5. Multiple Regression Equation for Physical Properties Using the Quadratic Indices of the Molecular Pseudograph’s Atom Adjacency Matrix.

**Table 5.** Multiple Regression Equation for Physical Properties Using the Quadratic Indices of the Molecular Pseudograph’s Atom Adjacency Matrix.
B.p. (^oC)=-204.184(±3.262) +1.44048(±0.026)^.q₁^H(x) -9.29x10^-3(±0.427x10^-3)^.q₀(x)^.q₂(x) +2.91x10^-7 (±1.75x10^-8)^.q₀(x)^.q₁₃(x) -0.11678(±0.028)^.q₂(x) (19) N=74 R=0.9988 q²=0.9970 F(4.69)=7068.1 s=2.35 MAE=2.11 p<0.0000 MV (cm³)=39.72(±2.441) +0.7651(±0.031)^.q₀^H(x) -4.4x10^-7(±1.08x10^-7)^.q₁₅(x) +4.634x10^-3(±0.214 x10^-3)^.q₀(x)^.q₂(x) -1.74x10^-3(±0.132x10^-3)^.q₀(x)^.q₃(x) (20) N=69 R=0.9991 q²=0.9973 F(4.69)=8916.5 s= 0.75 MAE=0.53 p<0.0000 MR (cm³)=3.2327(±0.048) +1.734x10^-2(±4.71x10^-5)^. q₃^H(x) -0.01012(±0.302x10^-3)^.q₃(x) +7.486x10^-3 (±0.836x10^-3)^.q₂(x) (21) N= 69 R=0.9999 q²=0.9999 F(3.65)= 2.52x10⁵ s= 0.049 MAE=0.0322 p<0.00 HV (KJ/mol)=-1.35607(±0.327) +0.07648(±0.001)^.q₂^H(x) -0.1309(±0.004)^.q₂(x) +1.19x10^-5(±9.3x10^-7) ^.q₁₁(x) (22) N=69 R=0.998 q²= 0.9955 F(3.65)=5469.5 s= 0.34 MAE=0.32 p<0.0000 TC (^oC)=-71.6809(±6.373) +0.2399(±0.007)^.q₃^H(x) -0.02165(±0.001)^.q₀(x)^.q₂(x) +0.83x10^-3(±6.01x10^-5) ^.q₀(x)^. q₅(x) (23) N=74 R=0.9953 q²= 0.9892 F(3.70)=2460.1 s=5.66 MAE=5.34 p<0.0000 PC (atm)=54.7074(±0.786) -6.998x10^-3(±0.265x10^-3)^.q₄^H(x)+5.95x10^-4(±3.72x10^-5)^.q₀(x)^.q₃(x) (24) N=74 R=0.9803 q²=0.9575 F(2.71)= 878.64 s= 0.86 MAE=0.64 p<0.0000 ST (dyn/cm)=-3.49402(±1.097) +0.04848(±0.001)^.q₂^H(x) -0.00163(±0.122x10^-3)^.q₀(x)^.q₂(x) +1.21x10^-5(±5.15x10^-7)^.q₀(x)^.q₇(x) -0.01617(±0.006)^.q₂(x) (25) N=68 R=0.9892 q²= 0.9734 F(4.63)=722.14 s= 0.29 MAE=0.23 p<0.0000

Table 6. Statistical Parameters for the Models Describing Physical Properties of Alkanes by Using Conectivity Indices, ad hoc Descriptors, Spectral Moments of Edge-Adjacency Matrix and Quadratic Indices of the Molecular Pseudograph’s Atom.Adjacency Matrix.

**Table 6.** Statistical Parameters for the Models Describing Physical Properties of Alkanes by Using Conectivity Indices, ad hoc Descriptors, Spectral Moments of Edge-Adjacency Matrix and Quadratic Indices of the Molecular Pseudograph’s Atom.Adjacency Matrix.
	Connectivity Indices			ad hoc Descriptors			Moments of E Matrix			Quadratic Indices of M Matrix
Prop.	n^a	R	s	n^a	R	s	n^a	R	s	n^a	R	s
Bp	5	0.9995	1.86	5	0.9989	2.0	4	0.9984	2.48	4	0.9988	2.35
MV	5	0.9995	0.5	5	0.9995	0.4	5	0.9993	0.6	4	0.9991	0.75
MR	5	0.9999	0.05	5	0.9999	0.05	4	0.9999	0.05	3	0.9999	0.05
HV	5	0.9989	0.2	5	0.9969	0.4	3	0.9988	0.2	3	0.9980	0.34
TC	5	0.9975	4.1	5	0.9970	4.8	5	0.9944	5.4	3	0.9953	5.66
PC	5	0.9904	0.6	5	0.9889	0.7	5	0.9854	0.6	2	0.9803	0.86
ST	5	0.9929	0.2	5	0.9945	0.2	6	0.9869	0.3	4	0.9892	0.29

^a Number of Variables in QSPR Models.

As can be observed from the statistical parameters of the regression equations in Table 5, most of the physical properties are well accounted for by quadratic indices of the “molecular pseudograph’s atom adjacency matrix”. In Table 6 we show the statistical parameters of the best regression equations obtained by Needham et al. [43] using connectivity indices and ad hoc descriptors and by Estrada [23] using spectral moments of edge-adjacency matrix in a molecular graph.

In this sense, the QSPR models obtained by using quadratic indices present less variables (parsimony principle) that the equation obtained by Needham et al. and Estrada with molecular modeling techniques. Nevertheless, in this Table it can be well appreciated that the statistical parameters of the equation obtained with quadratic indices are similar to those obtained in previous studies [23,43]. For most properties, the accuracies of the models are sufficient for many practical purposes.

In second place, we have chosen a group of molecules used by Randić and Basak [51] and later on by Krenkel et. al. [44] from which the Bp of the 58 alkyl alcohols have been computed, which have been used in several QSAR/QSAR studies [52,53,54,55,56].

Using the RLM analysis two QSPR equations have been obtained. Eq. 26 was obtained using the complete set just like Randić and Basak and the Eq. 27 was obtained using as a training set, the same 29 compounds that Krenkel et. al. used. Therefore, in the second case the data of compounds were split into two equivalent sub-sets: 1) a training set, which is constituted by the molecules 1, 2, 3, 4, 6, 8, 9, 11, 14, 16, 18, 20, 22, 26, 27, 29, 34, 35, 37, 39, 41, 44, 45, 48, 49, 52, 53, 56 and 58 of the Table 9 and 2) a test set which includes the remaining molecules (5, 7, 10, 12, 13, 15, 17, 19, 21, 23, 24, 25, 28, 30, 31, 32, 33, 36, 38, 40, 42, 43, 46, 47, 50, 51, 54, 55 and 57). The obtained models are given as follows and the corresponding statistical parameters to the regression equations (Eq. 26-27) are depicted in Table 7. These values have also been included for the equations reported by Randić-Basak and Krenkel et al. (see Table 7 in reference 48 and Table 2 in reference 44). The observed Bp, those calculated for Eq. 26 and 27 and their residuals values as well as those obtained in previous studies is depicted in the Table 8, Table 9 and Table 10.

Bp (^oC) =34.16625(±2.696) +0.26497(±0.0111)^.q₂^H(x) -0.29237(±0.045)^.q₂(x)
-78.0818x10 ^–5(±9.932x10^-5)^.Eq_9L^H(x)

(26)

Bp (^oC) =461.7348(±30.20806) +0.092098(±0.002)^.q₃^H(x) -0.0175226(±0.001)^.q₆(x)
-10.266162(±0.707)^.Eq_2L^H(x) +10.956280x10^-5(±1.32x10^-5)^.E q_14L(x)

(27)

The correlation coefficient (R²) for equations 26 and 27 were 0.9877 and 0.9977, respectively. Therefore, these models explained more than 98% and 99% of the variance for the experimental values of Bp [57,58].

Table 7. Statistical Parameters Corresponding to the Regression Equations.

**Table 7.** Statistical Parameters Corresponding to the Regression Equations.
Equation	Set	Correlation Coefficient (R)	Standard Error (S)	Fischer ratio (F)	Average Deviation
Eq. 26	Complete	0.9938	4.006	1446.9	2.82
Randić and Basak /48/	Complete	0.9938	4.039	2193	2.90
Eq. 27	Training Test	0.9979 0.9938	2.97 3.17	1390.7 2177.9	2.13 2.15
Eq. 11 /44/	Training Test	0.9953 0.9948	2.903 3.025	5733 2529	2.20 2.50
Eq. 12 /44/	Training Test	0.9953 0.9948	3.008 2.833	2764 1296	2.20 2.48
Eq. 13 /44/	Training Test	0.9954 0.9949	2.874 2.871	2018 841	2.03 2.63

In order to assess the predictability of the model found, a LOO cross-validation was carried out. Using this approach, the models 26 and 27 had a cross-validation square correlation coefficient (q²) of 0.986 and 0.992, respectively.

In the LGO cross-validation procedure carried out for a more exhustive validation of Eq. 26 (Eq. 27), the mean absolute errors for the five groups (used in each case) were as follows: MAE=3.202, 3.053, 3.461, 4.849 and 4.555 ^oC (MAE=1.579, 1.728, 2.674, 3.546 and 3.375 ^oC). The overall MAE were 3.824 ^oC and 2.580 ^oC for the models 26 and 27, respectively. For a 20% full leave-out cross-validation procedure, this level of MAE is good confirmation of the predictive quality of the models developed.

On the other hand, the statistical parameters represented in Table 7, demonstrates the statistical quality of the obtained models (Eq. 26 and 27), which are similar to those obtained previously. This way, for example, for the complete series the coefficients of multivariable correlation (R) are similar in Eq. 26 to the one obtained in the paper of Randić and Basak [48]. However, the standard error (s) and the average of the deviation obtained by us are smaller.

Similarly, there were no significant differences between model (Eq. 27) obtained using the other alternative (starting from the training set) and the results obtained from previous theoretical results. In this sense, not statistical difference was evidenced using a t-Student test procedure for both models and for those reported previously.

In addition, to assess the utility of quadratic indices to describe in an adequate form the chemical structure of molecules that contain cycles, we have selected from the literature the Bp of 106 cycloalkanes [25]. The same training and prediction sets were taken into consideration as were used in the original study, to make the study comparative.

Table 8. Experimental and Calculated Bp of Alkyl Alcohols in full Set.

**Table 8.** Experimental and Calculated Bp of Alkyl Alcohols in full Set.
Alkyl alcohol	Bp exp (^oC)	Bp calc. (Eq.26)	∆^*	% ∆	Bp cal. Ref./48/
1. methanol	64.70	65.50	-0.80	-1.24	65.24 (-0.54)
2. ethanol	78.30	78.43	-0.13	-0.17	77.69 (0.61)
3. 1-propanol	97.20	95.63	1.57	1.62	96.42 (0.77)
4. 2. propanol	82.30	85.83	-3.53	-4.28	84.11 (-1.81)
5. 1-butanol	117.70	113.40	4.30	3.65	115.67 (2.03)
6. 2-butanol	99.60	102.87	-3.27	-3.28	102.43 (-2.83)
7. 2-methyl-1-propanol	107.90	108.66	-0.76	-0.71	109.15 (-1.25)
8. 2-methyl-2-propanol	82.40	87.68	-5.28	-6.41	84.52 (-2.12)
9. 1-pentanol	137.80	133.16	4.64	3.36	134.92 (2.88)
10. 2-pentanol	119.00	120.59	-1.59	-1.34	121.68 (-2.68)
11. 3-pentanol	115.30	119.90	-4.60	-3.99	120.75 (-5.45)
12. 2-methyl-1-butanol	128.70	126.39	2.31	1.80	127.97 (0.73)
13. 3-methyl-1-butanol	131.20	127.13	4.07	3.10	128.90 (2.30)
14. 2.methyl-2-butanol	102.00	104.57	-2.57	-2.52	102.41 (-0.41)
15. 3-methyl-2-butanol	111.50	115.75	-4.25	-3.81	114.72 (-3.22)
16. 2,2-dimethyl-1-propanol	113.10	117.54	-4.44	-3.93	115.84 (-2.74)
17. 1-hexanol	157.13	153.12	4.01	2.55	154.17 (2.83)
18. 2-hexanol	139.90	140.35	-0.45	-0.32	140.92 (-1.02)
19. 3-hexanol	135.40	137.63	-2.23	-1.64	139.99 (-4.59)
20. 2-methyl-1-pentanol	148.00	146.14	1.86	1.25	147.22 (0.78)
21.3-methyl-1-pentanol	152.40	146.89	5.51	3.61	147.72 (4.8)
22. 4-methyl-1-pentanol	151.80	148.97	2.83	1.86	148.15 (3.65)
23. 2-methyl-2-pentanol	121.40	122.25	-0.85	-0.70	121.66 (-0.25)
24. 3-methyl-2-pentanol	134.20	133.42	0.78	0.58	133.55 (0.65)
25. 4-methyl-2-pentanol	131.70	134.27	-2.57	-1.95	134.90 (-3.20)
26. 2-methyl-3-pentanol	126.50	132.77	-6.27	-4.96	134.31 (-7.81)
27. 3-methyl-3-pentanol	122.40	121.45	0.95	0.78	120.30 (2.10)
28. 2-ethyl-1-butanol	146.50	144.11	2.39	1.63	146.79 (-0.29)
29. 2,2-dimethyl-1-butanol	136.80	135.21	1.59	1.16	134.37 (2.43)
30. 2,3-dimethyl-1-butanol	149.00	140.07	8.93	6.00	140.77 (8.23)
31. 3.3-dimethyl-1-butanol	143.00	136.82	6.18	4.32	136.11 (6.89)
32. 2,3-dimethyl-2-butanol	118.60	117.30	1.30	1.10	114.28 (4.32)
33. 3,3-dimethyl-2-butanol	120.00	124.47	-4.47	-3.72	121.00 (-1.00)
34. 1-heptanol	176.30	173.38	2.92	1.66	173.41 (2.87)
35. 3-heptanol	156.80	157.38	-0.58	-0.37	159.24 (-2.44)
36. 4-heptanol	155.00	155.35	-0.35	-0.23	159.24 (-4.24)
37. 2-methyl-2-hexanol	142.50	142.00	0.50	0.35	140.90 (1.60)
38. 3-methyl-3-hexanol	142.40	139.13	3.27	2.30	139.55 (2.85)
39. 3-ethyl-3-pentanol	142.50	138.32	4.18	2.93	138.37 (4.13)
40. 2,3-dimethyl-2-pentanol	139.70	134.92	4.78	3.42	133.11 (6.59)
41.3,3-dimethyl-2-pentanol	133.00	142.09	-9.09	-6.83	139.67 (-6.57)
42. 2.2-dimethyl-3-pentanol	136.00	141.49	-5.49	-4.04	139.32 (-3.32)
43. 2,3-dimethyl-3-pentanol	139.00	134.17	4.83	3.48	132.18 (6.82)
44. 2,4-dimethyl-3-pentanol	138.80	145.64	-6.84	-4.93	145.34 (-6.54)
45. 1-octanol	195.20	193.67	1.53	0.78	192.58 (2.62)
46. 2-octanol	179.80	180.57	-0.77	-0.43	179.33 (0.47)
47. 2-ethyl-1-hexanol	184.60	183.82	0.78	0.42	185.29 (-0.69)
48. 2,2,3trimethyl-3-pentanol	152.20	142.73	9.47	6.22	152.78 (-0.57)
49. 1-nonanol	213.10	213.97	-0.87	-0.41	211.91 (1.19)
50. 2-nonanol	198.50	200.85	-2.35	-1.19	198.66 (-0.16)
51. 3-nonanol	194.70	197.60	-2.90	-1.49	197.73 (-3.03)
52. 4-nonanol	193.00	195.07	-2.07	-1.07	197.73 (-4.73)
53. 5-nonanol	195.10	194.87	0.23	0.12	197.73 (-2.63)
54. 7-methyl-1-octanol	206.00	210.01	-4.01	-1.95	205.46 (0.54)
55. 2,6-dimethyl-4-heptanol	178.00	182.72	-4.72	-2.65	185.69 (-7.69)
56. 3,5-dimethyl-4-hexanol	187.00	180.99	6.01	3.21	183.83 (3.17)
57. 3,3,5-trimethyl-1-hexanol	193.00	192.54	0.46	0.24	186.98 (6.02)
58. 1-decanol	230.20	234.27	-4.07	-1.77	231.15 (-0.95)

^*Residual, defined as [Bp exp.– Bp calc], given in brackets for Ref. /48/.

Table 9. Experimental and Calculated Bp of Alkyl Alcohols in Training Set.

**Table 9.** Experimental and Calculated Bp of Alkyl Alcohols in Training Set.
Alkyl alcohol	Bp exp (^oC)	Bp calc. (Eq. 27)	∆*	% ∆	Bp calc. (Eq. 11)
1. methanol	64.70	66.03	-1.33	-2.06	64.68 (0.02)
2. ethanol	78.30	75.96	2.34	2.99	77.36 (0.94)
3. 1-propanol	97.20	97.44	-0.24	-0.24	96.80 (0.40)
4. 2. propanol	82.30	80.69	1.61	1.96	78.24 (4.06)
6.2-butanol	99.60	100.08	-0.48	-0.48	97.68 (1.92)
8. 2-methyl-2-propanol	82.40	81.63	0.77	0.93	84.97 (-2.57)
9. 1-pentanol	137.80	137.06	0.74	0.54	135.69 (2.11)
11. 3-pentanol	115.30	118.40	-3.10	-2.69	117.13 (-1.83)
14. 2.methyl-2-butanol	102.00	101.74	0.26	0.26	104.41 (-2.41)
16. 2,2-dimethyl-1-propanol	113.10	116.94	-3.84	-3.40	117.11 (4.01)
18. 2-hexanol	139.90	138.73	1.17	0.83	136.57 (3.33)
20. 2-methyl-1-pentanol	148.00	147.82	0.18	0.12	148.68 (-0.68)
22. 4-methyl-1-pentanol	151.80	149.11	2.69	1.77	148.68 (3.12)
26. 2-methyl-3-pentanol	126.50	131.41	-4.91	-3.88	130.11 (-3.61)
27. 3-methyl-3-pentanol	122.40	121.41	0.99	0.81	123.86 (-1.46)
29. 2,2-dimethyl-1-butanol	136.80	132.03	4.77	3.49	136.55 (0.25)
34. 1-heptanol	176.30	175.42	0.88	0.50	174.57 (1.73)
35. 3-heptanol	156.80	156.88	-0.08	-0.05	156.01 (0.79)
37. 2-methyl-2-hexanol	142.50	140.89	1.61	1.13	143.30 (-0.80)
39. 3-ethyl-3-pentanol	142.50	140.75	1.75	1.23	143.30 (-0.80)
41.3,3-dimethyl-2-pentanol	133.00	136.16	-3.16	-2.37	137.43 (-4.43)
44. 2,4-dimethyl-3-pentanol	138.80	143.48	-4.68	-3.37	143.10 (-4.30)
45. 1-octanol	195.20	194.46	0.74	0.38	194.01 (1.19)
48. 2,2,3trimethyl-3-pentanol	152.20	154.18	-1.98	-1.30	144.16 (8.04)
49. 1-nonanol	213.10	213.32	-0.22	-0.10	213.45 (-0.35)
52. 4-nonanol	193.00	195.49	-2.49	-1.29	194.89 (-1.89)
53. 5-nonanol	195.10	195.34	-0.24	-0.12	194.89 (0.21)
56. 3,5-dimethyl-4-hexanol	187.00	178.80	8.20	4.39	181.99 (5.01)
58. 1-decanol	230.20	232.18	-1.98	-0.86	232.86 (-2.66)

^*Residual, defined as [Bp exp. – Bp calc] given in brackets for Eq. 11. Ref. [44].

Table 10. Experimental and Calculated Bp of Alkyl alcohols in Test Set.

**Table 10.** Experimental and Calculated Bp of Alkyl alcohols in Test Set.
Alkyl alcohol	Bp exp. (^oC)	Bp calc. (Eq. 27)	∆^*	% ∆	Bp calc.(Eq. 11)
5. 1-butanol	117.70	117.50	0.20	0.17	116.25 (1.45)
7. 2-methyl-1-propanol	107.90	112.68	-4.78	-4.43	109.79 (-1.89)
10. 2-pentanol	119.00	119.23	-0.23	-0.20	117.13 (1.87)
12. 2-methyl-1-butanol	128.70	130.00	-1.30	-1.01	129.34 (-0.64)
13. 3-methyl-1-butanol	131.20	131.11	0.09	0.07	129.23 (1.97)
15. 3-methyl-2-butanol	111.50	114.17	-2.67	-2.39	110.67 (0.83)
17. 1-hexanol	157.13	156.38	0.75	0.48	155.13 (1.87)
19. 3-hexanol	135.40	137.52	-2.12	-1.57	136.57 (-1.17)
21.3-methyl-1-pentanol	152.40	147.35	5.05	3.31	148.68 (3.72)
23. 2-methyl-2-pentanol	121.40	121.16	0.24	0.20	123.86 (-2.46)
24. 3-methyl-2-pentanol	134.20	131.27	2.93	2.18	130.11 (4.09)
25. 4-methyl-2-pentanol	131.70	132.55	-0.85	-0.65	130.11 (1.59)
28. 2-ethyl-1-butanol	146.50	146.12	0.38	0.26	148.68 (-2.18)
30. 2,3-dimethyl-1-butanol	149.00	141.00	8.00	5.37	142.22 (6.78)
31. 3.3-dimethyl-1-butanol	143.00	133.59	9.41	6.58	136.55 (6.45)
32. 2,3-dimethyl-2-butanol	118.60	119.44	-0.84	-0.71	117.40 (1.20)
33. 3,3-dimethyl-2-butanol	120.00	120.08	-0.08	-0.06	117.99 (2.01)
36. 4-heptanol	155.00	156.58	-1.58	-1.02	156.01 (-1.01)
38. 3-methyl-3-hexanol	142.40	141.12	1.28	0.90	143.30 (-0.90)
40. 2,3-dimethyl-2-pentanol	139.70	138.02	1.68	1.20	136.84 (2.86)
42. 2.2-dimethyl-3-pentanol	136.00	136.45	-0.45	-0.33	137.43 (-1.43)
43. 2,3-dimethyl-3-pentanol	139.00	138.90	0.10	0.07	136.84 (2.16)
46. 2-octanol	179.80	177.28	2.52	1.40	175.45 (4.35)
47. 2-ethyl-1-hexanol	184.60	182.69	1.91	1.03	187.56 (-2.96)
50. 2-nonanol	198.50	196.41	2.09	1.05	194.89 (3.61)
51. 3-nonanol	194.70	195.53	-0.83	-0.43	194.89 (-0.19)
54. 7-methyl-1-octanol	206.00	205.50	0.50	0.24	207.00 (1.00)
55. 2,6-dimethyl-4-heptanol	178.00	183.63	-5.63	-3.16	181.99 (-3.99)
57. 3,3,5-trimethyl-1-hexanol	193.00	190.45	2.55	1.32	188.43 (4.57)

^*Residual, defined as [Bp exp.– Bp calc], given in brackets for Eq. 11. Ref. [44].

This data contains cyclic, mono, poly-substituted alkanes, as well as spiroalkanes. Using a stepwise procedure, two MLR models that describe the Bp of compounds in the training and prediction sets, using the quadratic indices as independent variables, were obtained:

Bp (^oC)=-105.146(±4.718) +3.1629(±0.118)^.q₁(x) -0.4933(±0.045)^.q₂(x)

(28)

Bp (^oC)=-108.197(±3.635) +1.6358(±0.361)^.q₀(x) +2.038(±0.103)^.q₁(x)
-0.3016(±4.718)^.q₂(x) -1.75x10^-5(±3.75x10^-6)^.q₁₄(x)
+6.42x10^-6(±1.34x10^-6) ^.q₁₅(x)

(29)

The statistical parameters of these two QSPR equations and the values reported by Estrada [25] are presented in Table 11.

Table 11. Statistical Parameters Corresponding to the Regression Equations for 80 Compounds Present in the Training Data Set.

**Table 11.** Statistical Parameters Corresponding to the Regression Equations for 80 Compounds Present in the Training Data Set.
Equation	Set	Correlation Coefficient (R)	Standard Error (S)	Fischer ratio (F)
Eq. (28) two descriptors	Training Test	0.9823 0.9726	7.8211 10.245	1058.2 421.21
Eq. (29) Five descriptors	Training Test	0.9927 0.9938	5.0145 4.7865	5257.9 2025.4
Eq. (1)/(25). Six descriptors	Training Test	0.9937 0.9943	4.800 4.696	960 2094.8

The statistical parameters show a high statistical quality of the developed models. For example, the correlation coefficient of model 28 with two single variables is bigger than 0.98 and the standard deviation represents less than 8% of the variance of the experimental property. Nevertheless, the statistical parameters of this equation are inferior to those obtained by Estrada [25], although its model includes 6 molecular descriptors. Furthermore, models with more statistical quality were obtained (Eq. 29), with a lineal correlation coefficient of 0.9927 and the standard deviation represented less than 5% of the variance in the experimental property.

These statistical parameters are accepted for the Bp description of molecules that contain cycles, if we take into consideration that the generation of good equations for the description of the Bp of these compounds is not the principal objective of this work. Nevertheless, our model with less variables (parsimony principle) and including single linear terms presents statistical parameters comparable to that of the original paper [25], which use 6 variables (spectral moments of different order) and non-linear dependence between the physical property and the spectral moments. The use of non-linear terms influence significantly in the multivariable equations. In this case, the statistical parameters of the equations obtained for the description of physical properties of alkanes using the spectral moments improved with the introduction of the square root of variables [23]. In this role, the improvements were significant, especially for the Bp, when including in the model the square root of the spectral moment of order zero, reducing the value of the standard deviation in half and R and F increased from 0.9949 to 0.9984 and from 1650 to 5194, respectively. In the case of the description of the critical pressure (PC, atm) using spectral moments, R had a significant increase from 0.9756 to 0.9854, because of the inclusion of non-linear terms [23].

In Table 12, the experimental and calculated values of the Bp are given for compounds in the training set, for the two equations obtained in this study and for the models obtained by Estrada [25].

Table 12. Experimental and Calculated Bp of Cycloalkanes of the Training Set.

**Table 12.** Experimental and Calculated Bp of Cycloalkanes of the Training Set.
no	Cycloalkane	Obsd (^oC)	Cald [Eq. 28]	Res.	Cald [Eq. 29]	Res.	Cald [Eq. 1 /25 ]	Res.
1	cyclopropane	-32.8	-14.82	-17.98	-16.07	-16.73	-36.99	4.19
2	cyclobutane	12.51	15.29	-2.78	14.64	-2.13	1.77	10.74
3	spiropentane	40.6	48.20	-7.60	43.20	-2.60	49.42	-8.82
4	methylcyclobutane	36.3	38.57	-2.27	38.83	-2.53	33.49	2.81
5	cyclopentane	49.262	48.20	1.06	43.20	6.06	52.5	-3.24
6	1,1-dimethylcyclopropane	20.63	24.92	-4.29	26.19	-5.56	23.95	-3.32
7	cis-1,2-dimethylcyclopropane	37.03	31.74	5.29	31.66	5.37	30.15	6.88
8	ethylcyclopropane	36	38.57	-2.57	37.95	-1.95	37.46	-1.46
9	bicyclo[3.1.0]hexane	79.2	85.14	-5.94	73.57	5.63	85.82	-6.62
10	1,1-dimethylcyclobutane	56	55.03	0.97	53.43	2.57	54.31	1.69
11	cis-1,2-dimethylcyclobutane	68	61.85	6.15	62.67	5.33	62.41	5.59
12	tras-1,2-dimethylcyclobutane	60	61.85	-1.85	62.67	-2.67	62.41	-2.41
13	cis-1,3-dimethylcyclobutane	60.5	61.85	-1.35	61.01	-0.51	59.56	0.94
14	tras-1,3-dimethylcyclobutane	57.5	61.85	-4.35	61.01	-3.51	59.56	-2.06
15	cyclohexane	80.738	75.50	5.24	76.05	4.68	84.36	-3.62
16	methylcyclopentane	71.812	68.68	3.14	69.84	1.98	75.98	-4.17
17	1,1,2-trimethylcyclopropane	52.48	48.20	4.28	50.35	2.13	54.66	-2.18
18	cis,cis-1,2,3,-trimethylcyclopropane	71	55.03	15.97	71.01	-0.01	61.37	9.63
19	cis,trans-1,2,3,-trimethylcyclopropane	66	55.03	10.97	55.10	10.90	61.37	4.63
20	cis-1-ethyl-2-ethylcyclopropane	70	91.96	-21.96	70.495	-0.495	64.86	5.14
21	propylcyclopropane	68.5	68.68	-0.18	68.11	0.39	72.82	-4.32
22	isopropylcyclopropane	58.34	61.85	-3.51	62.15	-3.81	63.18	-4.84
23	bicyclo[3.2.0]heptane	109.3	115.24	-5.94	103.51	5.79	112.2	-2.9
24	bicyclo[4.1.0]heptane	111.5	115.24	-3.74	103.60	7.90	111.69	-0.19
25	2-cyclopropylbutane	90.98	91.96	-0.98	91.89	-0.91	94.75	-3.77
26	propylcyclobutane	100.6	115.24	-14.64	103.52	-2.92	100.42	0.18
27	isopropylcyclobutane	92.7	91.96	0.74	93.02	-0.32	91.13	1.57
28	methylcyclohexane	100.93	98.78	2.15	100.42	0.52	104.36	-3.43
29	1,1-dimethylcyclopentane	87.846	85.14	2.71	86.44	1.40	90.62	-2.77
30	trans-1,2-dimethylcyclopentane	91.869	91.96	-0.09	93.48	-1.61	98.15	-6.28
31	cis-1,3-dimethylcyclopentane	91.725	91.96	-0.24	93.68	-1.95	95.52	-3.79
32	trans-1,3-dimethylcyclopentane	90.773	91.96	-1.19	93.68	-2.90	95.52	-4.75
33	1,1,2,2-tetramethylcyclopropane	75.6	64.66	10.94	75.64	-0.04	74.28	1.32
34	1,1,2,3-tetramethylcyclopropane	78.5	71.49	7.01	78.08	0.42	84.01	-5.51
35	1-methyl-1-isopropylcyclopropane	82.1	78.31	3.79	80.28	1.82	84.83	-2.73
36	1,1-dimethylcyclopropane	88.67	85.14	3.53	84.92	3.75	92.95	-4.28
37	2-methylbicyclo[2.2.1]heptane	125.8	138.53	-12.73	127.90	-2.10	130.33	-4.53
38	3,3-dimethylbicyclo[3.1.0]hexane	115.3	124.88	-9.58	119.06	-3.76	110.49	4.81
39	1,1,3,3-tetramethylcyclobutane	78.2	94.77	-16.57	75.30	2.90	86.57	-8.37
40	trans-1,2-diethylcyclobutane	115.5	122.07	-6.57	121.40	-5.90	122.24	-6.74
41	methylcycloheptane	134	128.89	5.11	131.20	2.80	133.38	0.62
42	1,1-dimethylcyclohexane	119.54	115.24	4.30	116.01	3.53	116.49	3.05
43	trans-1,2-imethylcyclohexane	123.42	122.07	1.35	124.23	-0.81	123.9	-0.48
44	cis-1,3-dimethylcyclohexane	120.09	122.07	-1.98	123.67	-3.59	121.28	-1.19
45	trans-1,3-dimethylcyclohexane	124.45	122.07	2.38	123.67	0.78	121.28	3.17
46	cis-1,4-dimethylcyclohexane	124.32	122.07	2.25	124.90	-0.58	121.51	2.81
47	ethylcyclohexane	131.78	128.89	2.89	130.24	1.54	133.19	-1.41
48	cyclooctane	151.14	135.72	15.42	137.47	13.67	145.2	5.89
49	1,1,2-trimethylcyclopentane	113.73	108.42	5.31	110.08	3.65	112.39	1.34
50	cis,cis-1,1,3-trimethylcyclopentane	123	115.24	7.76	116.71	6.29	117	6
51	cis,trans-1,1,3-trimethylcyclopentane	117.5	115.24	2.26	116.71	0.79	117	0.5
52	trans,cis-1,1,3-trimethylcyclopentane	110.2	115.24	-5.04	116.71	-6.51	117	-6.8
53	1-ethyl-1-methylcyclopentane	121.52	115.24	6.28	115.75	5.77	121.05	0.47
54	isopropylcyclopentane	126.42	122.07	4.35	123.75	2.67	127.4	-0.98
55	1,1,2-trimethyl-2-ethylcyclopropane	104	94.77	9.23	108.34	-4.34	103.22	0.78
56	1-methyl-1,2-diethylcyclopropane	108.5	108.42	0.08	110.79	-2.29	114.83	-6.83
57	7,7-bicycloylbicyclo[2.2.1]heptane	143.5	124.88	18.62	141.78	1.72	143.2	0.3
58	2-ethylbicyclo[2.2.1]heptane	146.5	168.64	-22.14	157.75	-11.25	154.66	-8.16
59	4-methylspiro[5.2]octane	149	161.81	-12.81	155.20	-6.20	151.49	-2.49
60	1,2-dimethylcycloheptane	153	152.18	0.82	154.91	-1.91	150.71	2.29
61	1,1,2-trimethylcyclohexane	145.2	138.53	6.67	140.19	5.01	136.28	8.92
62	1,1,3-trimethylcyclohexane	136.63	138.53	-1.90	137.22	-0.59	130.74	5.88
63	1,1,4-trimethylcyclohexane	135	138.53	-3.53	141.47	-6.47	131.32	3.68
64	1-ethyl-1-methylcyclohexane	152.16	145.35	6.81	145.61	6.55	144.59	7.57
65	propylcyclohexane	156.72	159.00	-2.28	160.30	-3.58	159.77	-3.06
66	isopropylcyclohexane	154.76	152.18	2.59	154.45	0.31	150.6	4.16
67	cyclononane	178.4	165.82	12.58	168.18	10.22	171.95	6.45
68	1,1,2,2-tetramethylcyclopentane	135	124.88	10.12	129.67	5.33	124.67	10.36
69	1,1,3,3--tetramethylcyclopentane	117.96	124.88	-6.92	125.09	-7.13	115.29	2.67
70	cis-1,2-dimethyl-1-ethylcyclopentane	143	138.53	4.47	139.53	3.47	140.15	3.15
71	trans-1,2-dimethyl-1-ethylcyclopentane	142	138.53	3.47	139.53	2.47	140.15	2.15
72	1-methyl-1-propylcyclopentane	146	145.35	0.65	145.04	0.96	147.4	-1.4
73	1,1-diethylcyclopentane	151	145.35	5.65	145.05	5.95	148.92	2.08
74	trans-1,3-dietjhylcyclopentane	150	152.18	-2.18	152.91	-2.91	150.87	-0.87
75	cis-1-methyl-3-isopropylcyclopentane	142	145.35	-3.35	147.58	-5.58	141.76	1.76
76	trans-1-methyl-3-isopropylcyclopentane	143	145.35	-2.35	147.58	-4.58	141.76	2.76
77	isobutylcyclopentane	147.95	152.18	-4.23	154.29	-6.34	151.47	-3.52
78	sec-butylcyclopentane	154.35	152.18	2.17	153.42	0.93	153.79	0.56
79	2-cyclopropylhexane	142.95	152.18	-9.23	152.67	-9.72	150.35	-7.4
80	3-cyclobutylpentane	151.5	152.18	-0.68	152.06	-0.56	146.12	5.38

Using the LOO cross-validation procedure, the models 28 and 29 had a q² of 0.961 and 0.977, respectively. Using the LGO cross-validation method, the Eqs 28 and 29 had a overall MAE of 6.429 ^oC (7.452, 5.766, 7.070, 7.321 and 4.536 ^oC) and 4.801 ^oC (5.472, 5.159, 3.539, 5.426 and 4.41 ^oC), respectively.

Table 13. Experimental and Calculated Bp of Cycloalkanes of the Test Set.

**Table 13.** Experimental and Calculated Bp of Cycloalkanes of the Test Set.
no	Cycloalkane	Obsd (^oC)	Cald [Eq. 28]	Res.	Cald [Eq. 29]	Res.	Cald [Eq. 1 /25 ]	Res.
1	methylcyclopropane	0.73	8.46	-7.73	8.35	-7.62	-2.34	3.07
2	trans-1,2-dimethylcyclopropane	28.21	31.74	-3.53	31.66	-3.45	30.15	-1.94
3	bicyclo[2.2.0]hexane	80.2	85.14	-4.94	73.41	6.79	78.97	1.23
4	ethylcyclobutane	70.6	68.68	1.92	68.71	1.89	68.66	1.94
5	1-ethyl-1-methylcyclopropane	56.77	55.03	1.74	55.46	1.31	60.36	-3.59
6	trans-1,2-diethylcyclopropane	65	91.96	-26.96	64.80	0.2	64.86	0.14
7	cycloheptane	118.79	105.61	13.18	106.76	12.03	116.11	2.68
8	cis-1,2-dymethylcyclopentane	99.532	91.96	7.57	93.48	6.05	98.15	1.382
9	ethylcyclopentane	103.46	98.78	4.68	99.56	3.90	107.67	-4.204
10	spiro[5.2]octane	125.5	138.53	-13.03	128.38	-2.88	135.02	-9.52
11	cis-1,2-dimethylcyclohexane	129.72	122.07	7.65	124.23	5.49	123.9	5.828
12	trans-1,4-dimethylcyclohexane	119.35	122.07	-2.72	124.90	-5.55	121.51	-2.159
13	1,1,2-trimethylcyclopentane	104.89	108.42	-3.53	110.08	-5.18	106.86	-1.967
14	propylcyclopentane	130.95	128.89	2.06	129.68	1.27	136.57	-5.621
15	2-cyclopropylpentane	117.74	122.07	-4.33	122.09	-4.35	123.66	-5.92
16	cis-bicyclo[4.3.0]nonane	166	175.46	-9.46	164.38	1.62	164.59	1.41
17	1,1-dimethyl-2-ethylcyclopentane	138	138.53	-0.53	138.78	-0.78	138.33	-0.33
18	1,1-dimethylcyclopentane	133	138.53	-5.53	139.46	-6.46	133.37	-0.37
19	cis-1,3-diethylcyclopentane	150	152.18	-2.18	152.91	-2.91	150.87	-0.87
20	butylcyclopentane	156.6	159.00	-2.40	160.22	-3.62	163.27	-6.67
21	tert-butylcyclopentane	144.85	138.53	6.32	140.05	4.80	138.18	6.67
22	dicyclobutylmethane	161.8	175.46	-13.66	164.47	-2.67	152.11	9.69
23	1,5-dimethylspiro[3.3]heptane	132.2	154.99	-22.79	135.25	-3.05	142.44	-10.24
24	4-methylspiro[5.2]octane	149	161.81	-12.81	155.20	-6.20	151.49	-2.49
25	2,6-dimethylbicyclo[3.2.1]octane	164.5	191.92	-27.42	165.4	-0.90	165.41	-0.91
26	3,7-dimethylbicyclo[3.3.0]octane	166	191.92	-25.92	166.03	-0.03	165.6	0.4

In addition, as a second corroboration of the predictive power of the model, an external prediction set of twenty-six cyclic alkanes was used (external validation). The Bp of the compounds included in the external test set was predicted with the same accuracy as the compounds in the data set. The linear relationship in this series can be supported by the statistical parameters for this set depicted in Table 11.

In Table 13, the experimental and calculated Bp for both equations and for the model obtained by Estrada [25] are depicted. These statistical parameters are adequate for the description of physical properties and are comparable with those obtained by Estrada for the same series. Considering the whole set (Training and test set), the correlation coefficient and standard deviation were 0.9931 and 4.94 ^oC, respectively. As it can be observe, in both series, the predictability and robustness of the theoretical model was demonstrated.

Finally, in order to test the applicability of quadratic indices on structure-property correlations, and with the aim of extending the approach to molecules that contain aromatic cycles in their structure, 95 structurally diverse organic compounds, were selected. They were randomly splitted into two subsets; one contained 75 compounds that were used as a training set, and the other 20 compounds were used as a test set. Using a series of 75 compounds as training set, a quantitative model as a function of total and local quadratic indices, was developed. The Bp values were described by multivariate linear regression analysis using a stepwise procedure. The best QSPR model obtained, together with its statistical parameter, are given below:

Bp (^oC) = -21.10996(±5.894) +0.352115(±0.084)^.q₀^H(x) +0.2756648(±0.012)^.q₂(x) +5.420964(±0.218)^.Hq_1L(x) +1.644634(±0.347)^.Eq_1L(x) +0.041902(±0.012)^.Eq_4L^H(x) -0.025834(±0.004)^.Eq_5L(x)

(30)

N=70 R=0.9905 q²=0.9763 F(6.63)=539.43 s=7.6115 MAE=7.34 p<0.0001

In the development of the quantitative model for the Bp description of the calibration data set, five compounds were detected as statistical outliers. Outlier detection was carried out using the following standard statistical test: residual, standardized residuals, Studentized residual and Cooks’ distance [55]. The five compounds were m-bromophenol, o-anisidine, p-nitroaniline, hexamethylbenzene and furan cycle. As can be observed there are no distinctive structural relationships among these compounds.

In Table 14 are listed the experimental and calculated Bp values of the training set. Statistical parameters in Eq. 30 suggest a high quality of the found model. The correlation coefficient R is over 0.99 and standard deviation is only 7.61^oC. The squared correlation coefficient (R²) for Eq. 30 was 0.981, so this model explained more than 98% of the variance for the experimental Bp values.

In order to assess the predictability and robustness of the found model, internal and external validation procedures were carried out. Using LOO cross-validation procedure, the Eq. 30 had a cross-validation squre correlation coefficient of 0.976. In LGO cross-validation approach, the model 30 had the following mean absolute errors for the five groups (20%, 14 compounds): MAE=9.679, 6.788, 4.262, 7.727 and 8.250 ^oC. The overall MAE was 7.342. Like a more exhaustive corroboration of the predictive power of the model, an external prediction set of 20 aromatic organic compounds was used. The Bp of the compounds included in the external test set was predicted with the same accuracy as compounds in the data set. The statistical parameters for this series were: R= 0.9930, F(1.18)=1274.4 and s=7.8280 ^oC. These results evidence the good predictive power of the model found. Experimental and calculated Bp of the 20 aromatic compounds is given in Table 15. Considering the full set (training and test set) the correlation coefficients were 0.9884, F(1.88)=3717.5 and s=8.43 ^oC.

Table 14. Experimental and Calculated Values of the Bp of Molecules Included in the Training Set, that Contain Aromatic Cycles in Their Molecular Structure, as Well as Residual of Regression and Cross-Validation.

**Table 14.** Experimental and Calculated Values of the Bp of Molecules Included in the Training Set, that Contain Aromatic Cycles in Their Molecular Structure, as Well as Residual of Regression and Cross-Validation.
Compound	Obs. (^oC)	Calc.	Res.	R-_CV	Compound	Obs. (^oC)	Calc.	Res.	R-_CV
Chlorobenzene	132.00	130.79	1.21	1.34	Mesitylene	165.00	169.99	-4.99	-5.24
m-Nitrochlorobenzene	236.00	235.11	0.89	1.25	Prehnitene	205.00	191.08	13.92	15.14
p-Nitrochlorobenzene	239.00	237.21	1.79	2.48	Isodurene	197.00	191.08	5.92	6.44
Aniline	184.00	187.35	-3.35	-3.57	Durene	195.00	191.08	3.92	4.26
Phenol	181.00	174.56	6.44	6.78	Pentamethylbenzene	231.00	212.18	18.82	21.97
o-Cresol	191.00	193.84	-2.84	-2.95	Ethylbenzene	136.00	141.26	-5.26	-5.54
m-Cresol	201.00	194.85	6.15	6.34	n-Propylbenzene	152.00	158.55	-6.55	-7.01
p-Cresol	201.00	195.22	5.78	5.95	tert-Butylbenzene	169.00	179.64	-10.64	-11.92
o-Toluic Acid	259.00	265.28	-6.28	-6.68	p-Cymene	177.00	179.64	-2.64	-2.96
m- Toluic Acid	263.00	266.40	-3.40	-3.63	Biphenyl	255.00	257.78	-2.78	-3.20
p- Toluic Acid	275.00	267.05	7.95	8.52	Diphenylmethane	263.00	271.25	-8.25	-9.32
o-Tolualdehyde	196.00	197.50	-1.50	-1.56	Styrene	145.00	153.11	-8.11	-8.65
m-Tolualdehyde	199.00	198.25	0.75	0.78	Phenylacetaldehyde	193.00	200.62	-7.62	-8.65
p-Tolualdehyde	205.00	198.68	6.32	6.61	Diphenylether	259.00	281.11	-22.11	-24.23
o-Bromophenol	194.00	191.36	2.64	2.82	Benzyl Alcohol	205.00	194.72	10.28	10.72
p-Fluorophenol	185.00	189.05	-4.05	-6.64	α-Phenylethyl Alcohol	205.00	212.19	-7.19	-7.54
o-Phenylenediamine	252.00	265.08	-13.08	-15.96	β-Phenylethyl Alcohol	221.00	211.43	9.57	10.37
p-Phenylenediamine	267.00	267.44	-0.44	-0.53	α-Picoline	128.00	136.75	-8.75	-9.50
o-Toluidine	200.00	207.11	-7.11	-7.48	β-Picoline	143.00	139.17	3.83	4.10
m-Toluidine	203.00	207.85	-4.85	-5.08	γ-Picoline	144.00	139.75	4.25	4.53
p-Toluidine	200.00	208.13	-8.13	-8.51	Phthalyc Anhydride	284.00	280.66	3.34	4.85
Benzoic Acid	250.00	245.95	4.05	4.28	Naphthalene	218.00	215.18	2.82	3.23
Benzaldehyde	178.00	177.58	0.42	0.45	1-Methylnaphthalene	241.00	236.28	4.72	5.23
m-Anisidine	251.00	244.98	6.02	6.52	2-Methylnaphthalene	240.00	236.28	3.72	4.12
p-Anisidine	244.00	245.78	-1.78	-1.93	1-Naphtylamine	301.00	292.10	8.90	9.90
o-Nitroaniline	284.00	287.79	-3.79	-5.32	2-Naphtylamine	294.00	294.61	-0.61	-0.69
N-Methylaniline	196.00	184.00	12.00	12.38	1-Naphthol	280.00	277.96	2.04	2.20
Acetophenone	202.00	196.57	5.43	5.65	2-Naphthol	286.00	281.38	4.62	5.04
Benzophenone	308.00	310.04	-2.04	-2.33	Phenylthiol	169.50	157.48	12.02	12.85
Benzoyl Chloride	197.00	200.84	-3.84	-4.08	9,10-Anthraquinone	380.00	374.99	5.01	9.29
o-Xylene	144.00	148.89	-4.89	-5.12	Pyrrole	130.00	120.91	9.09	10.14
m-Xylene	139.00	148.89	-9.89	-10.35	Pyridine	115.00	120.15	-5.15	-5.75
p-Xylene	138.00	148.89	-10.89	-11.40	Furfuryl Alcohol	171.00	175.81	-4.81	-5.42
1, 2, 3-Trimethyl benzene	176.00	169.99	6.01	6.32	Phenylacetic Acid	266.00	275.84	-9.84	-12.57
Pseudocumene	169.00	169.99	-0.99	-1.04	Cathechol	245.00	237.21	7.79	8.70

Colinearity between variables and redundancy of information

One on the main problems concerning the application of TIs to QSPR/QSAR studies is that many descriptors are colinear and that there will be much redundancy of information. Problems with redundancy of information, and collinearity, have been illustrated with the use of TIs, such as the molecular connectivities [59,60].

Table 15. Experimental and Calculated Values of the Bp of Molecules, Included in the Test Set, that Contain Aromatic Cycles in their Molecular Structure as Well as Residual of Regression.

**Table 15.** Experimental and Calculated Values of the Bp of Molecules, Included in the Test Set, that Contain Aromatic Cycles in their Molecular Structure as Well as Residual of Regression.
Compound	Obs. (^oC)	Cal.	Res.	Compound	Obs. (^oC)	Cal.	Res.
o-Chlorotoluene	159.00	150.17	8.83	sec-butylbenzene	173.50	172.02	1.48
m-Chlorotoluene	162.00	151.12	10.88	tert-butylbenzene	284.00	284.72	-0.72
p-Chlorotoluene	162.00	151.48	10.52	Cinnamylic Alcohol	257.50	239.34	18.16
o-Nitrobenzene	245.00	229.54	15.46	1,4-Dihidronaphthalene	212.00	199.52	12.48
m-Chlorophenol	214.00	196.98	17.02	Isoquinoline	243.00	222.61	20.39
m-Phenylendiamine	287.00	266.86	20.14	Phenanthrene	340.00	323.67	16.33
o-Chloroaniline	209.00	207.48	1.52	Thiophene	84.00	90.31	-6.31
m-Nitroaniline	307.00	292.21	14.79	m-Bromophenol*	236.00	194.79	41.21
N,N-Dimethylaniline	194.00	182.57	11.43	o-Anisidine*	225.00	241.99	-16.99
Diphenylaniline	302.00	301.00	1.00	p-Nitroaniline*	232.00	293.93	-61.93
n-Propylbenzene	159.00	154.73	4.27	Hexamethylbenzene*	264.00	233.28	30.72
n-Butylbenzene	183.00	168.20	14.80	Furan*	32.00	105.28	-73.28
Isobutylbenzene	171.00	173.72	-2.72

^*Compound detected as an outlier in the training set.

For a better statistical interpretation of the QSPR/QSAR models (in order to understand which effects cannot be separated), where inter-related indices are considered (such as topologic or topographic indices based on the same graph-theoretical invariant), the inclusion in the model of strongly interrelated variables should be avoided. It is necessary to consider the above-mentioned criterion because an interrelation among different descriptors produces a highly unstable correlation coefficient and makes it difficult to know the real contribution of each variable included in the model [58]. An unfortunate illustration of this phenomenon was described recently by Romanelli et al. [61] who reported a QSAR for the toxicity of twelve aliphatic alcohols, using nine collinear variables, achieving an R² of 0.9932. To solve this problem Randić proposed a procedure of orthogonalization of molecular descriptors that have been applied with much success to QSPR and QSAR studies [62,63,64,65,66]. The orthogonalization of molecular descriptors is an approach in which molecular descriptors are transformed in such a way that they do not mutually correlate. The nonorthogonal descriptors and the derived orthogonal descriptors both contain the same information, which results in the same statistical parameters of the QSAR models [62,63,64,65,66]. However, the coefficient of the QSAR model based on orthogonal descriptors are stable to the inclusion of novel descriptors, which permits to interpret the regression terms and evaluate the role of individual descriptors to the QSAR model.

For the present paper, to alleviate the colinearity between variables in each investigated data set, an interrelation study among the quadratic indices used in the obtained equations were carried out, using correlation matrices of the molecular descriptors used in QSPRs. The acceptable level of colinearity to avoid is a more subjective issue. In this sense, reports of acceptable correlation coefficients between variables have range from less than 0.4 to 0.9 in the literature. In the view of the Cronin and Schultz, the collinearity of the variables should be as low as possible, but must be significantly lower that the statistical fit of the QSPR/QSAR itself [67]. In order to shown the procedure above mentioned, the inter-correlation study between total and local quadratic indices used in the development of the Eq. 30 was considered. In Table 16, the correlation matrix for this equation shows that there is low colinearity among these variables. In Table 17, other useful parameters to detect the existence of multicolinear variables (partial correlation and tolerance) are given. In this sense, the tolerance represents the unexplained variability for the other variables, and the partial correlation coefficient explains the correlation between the property and a specific variable, when the linear effects of other independent variables have been eliminated.

Table 16. The squared correlation matrix showing covariance (r²) among the topological descriptors (Total and local quadratic indices) used in the regression analysis for 70 compounds.

**Table 16.** The squared correlation matrix showing covariance (r²) among the topological descriptors (Total and local quadratic indices) used in the regression analysis for 70 compounds.
^eq₂(x)	^Heq_1L(x)	^Eeq_1L(x)	^Eeq_5L(x)	^eq₀^H(x)	^Eeq_4L^H(x)
1.0000	0.1824	0.4142	-0.3593	-0.8106	-0.1738
	1.0000	0.3980	0.1503	-0.0116	-0.4667
		1.0000	-0.2225	-0.2098	-0.6433
			1.0000	0.1378	-0.5776
				1.0000	0.1826
					1.0000

Table 17. “Redundancy” of total and local quadratic indices used as independent variables.

**Table 17.** “Redundancy” of total and local quadratic indices used as independent variables.
Descriptors	Multiple R	Multiple R-square	R-square change	Partial Correlation.	Tolernce	R-square
^eq₂(x)	0.8063	0.6501	0.6501	0.9421	0.2060	0.7940
^Heq_1L(x)	0.9653	0.9317	0.2817	0.9527	0.6936	0.3064
^Eeq_1L(x)	0.9775	0.9555	0.0238	0.5129	0.0366	0.9634
^Eeq_5L(x)	0.9865	0.9732	0.0176	-0.6647	0.0346	0.9654
^eq₀^H(x)	0.9885	0.9772	0.0040	0.4687	0.2657	0.7343
^Eeq_4L^H(x)	0.9904	0.9809	0.0037	0.4046	0.0221	0.9779

Interpretation of QSPR models

At present, it is known that properties are influenced by different kinds of interactions. In Eq. 31, the Bp is represented as a function of several interaction properties.

Bp = f (Molecular Weight, H-Bonding Capacity, Dipole Moment,
Molecular Branching)

(31)

Several approaches can be used to extract a structural interpretation of an obtained model using quadratic indices. We used two different ways that permit an easy interpretation of the Bp in terms of molecular structure. The first one is the “classical” way in which we do a direct analysis of the structural information presented by each molecular descriptor and how this contributes to the property under study. The second one the way that is how the total contribution of different atoms in a specific molecule is expressed. In the second approach, a more compact additive scheme is obtained [68]. The first approach permits estimating the relative contribution of different molecular factors (mass, branching, electronic and steric factor) to the physical properties. As can be observed in the obtained regression models, the included variables are related with the factors that influence on the Bp values and these ones with the structural features of molecules. Taken into consideration the structurally diverse organic compounds included in the fourth QSPR example, this dataset was selected to develop a simple analysis. For example, in Eq. 31, the variables ^Hq_1L(x) and ^Eq_1L(x), ^Eq_5L(x), ^Eq_4L^H(x) are in relation with the H-bonding capacity (hydrogen atoms as donors and acceptors, respectively). The coefficients of these variables in the Eq. 31 are positive; only local “heteroatoms” quadratic indices of fifth order [^Eq_5L(x)] have a negative contribution to the property. This is a logical result because when the number of hydrogen atoms bonded to heteroatoms in molecules is increased then the Bp increases also, because the possibility of intermolecular H-bonding increases with the increase of H-X groups (O, N and S) in molecules. In this sense, the “protonic” quadratic indices of first order [^Hq_1L(x)] are the sum of all possible products of electronegativity of the hydrogen atoms and heteroatoms bonded to them. If X is O, N or S atom, then values of this index increase in the same order, because the electronegativity of these atoms decreases from oxygen atom until the sulfur atom. For this reason, this index is an indicative of the number and type of hydrogen atom linked to heteroatoms.

On the other hand, the ^Eq_1L(x), ^Eq_5L(x) and ^Eq_4L^H(x) also are in relation with molecular charge, that is to say, these indices are variables that parameterize to the molecular dipole moment. Finally, molecular weight is described for total quadratic indices [q₂(x) and q₀^H(x)], suppressing and including hydrogen atoms in molecular pseudograph, respectively. For example, the q₀^H(x) possesses positive contribution to the Bp due to this molecular descriptor is the sum of the squared of all posible products of the electronegativity of all atoms in the molecule, which is an indicative of the molecular size that increase with the number (n) of atoms in the molecule. The other molecular descriptor [q₂(x)] is related with the possible effect of this variable on molecular weight, size and molecular branching. That is, this variable is a good choice to describe the Bp defined by the combination of molecular weight and branching. This influence is demonstrated by the positive contribution of this index to the studied property.

The second approach permits to obtain the contribution of atoms in a specific molecule allowing the comparison among them in a more effective way. In these sense, we can substitute expression (Eq.10) into QSPR model (Eq. 18) to obtain the total contribution of the different atoms in a specific molecule. The atoms’ contribution is calculated from this procedure as shown in Eq. 32,

P = b_{0} + \sum_{k} a_{k} q_{k} (x) = b_{0} + \sum_{k} \sum_{L} a_{k} q_{k L} (x)

(32)

where _L stands for the corresponding atom.

Considering the QSPR models obtained for describing the Bp of cycloalkenes (Eq. 28 and Eq. 29) and the molecule of 1-methyl-1,2-diethylcyclopropane, a simple example is given here for calculation of these atoms contributions to Bp. This molecule with its atom numbering and the total and local (atom) quadratic indices are depicted in Table 18.

Table 18. Molecule of 1-methyl-1,2-diethylcyclopropane with the Following Atom Numbering and Their Total and Local (Atom) Quadratic Indices.

**Table 18.** Molecule of 1-methyl-1,2-diethylcyclopropane with the Following Atom Numbering and Their Total and Local (Atom) Quadratic Indices.

Atom (f)	q_0L(x, f)	q_1L(x, f)	q_2L(x, f)	q_14L(x, f)	q_15L(x, f)	BpA [0C; (Eq. 28)]	Bp_B [^oC; (Eq. 29)
a	6.9169	27.6676	55.3352	3605884	9077470	47.07	34.90
b	6.9169	20.7507	55.3352	3153885	7816879	25.19	20.34
c	6.9169	13.8338	48.4183	2717007	6759769	6.73	8.92
e	6.9169	13.8338	34.5845	1744048	4293673	13.55	13.68
f	6.9169	6.9169	13.8338	687788.9	1744048	1.91	7.30
d	6.9169	6.9169	27.6676	1462530	3605884	-4.91	2.01
g	6.9169	13.8338	27.6676	1493988	3759467	16.96	16.56
h	6.9169	6.9169	13.8338	605581.5	1493988	1.91	7.09
Total	55.3352	110.6704	276.676	15470712	38551176	108.42	110.79

Now, if we divide the intercept values of the QSPR models by the number of atoms in the molecule (n=8) and we using the atom quadratic indices as molecular descriptors into models A (Eq. 28) and B (Eq. 29), then the atom contribution for each specific atom is obtained:

Bp_A (a)= (-105.146/8) +3.1629^.q_1L(x, a)–0.4933^.q_2L(x, a)=47.07 ^oC
Bp_B (a)=(-108.197/8) +1.6358^.q_0L(x, a) +2.038^.q_1L(x, a)–0.3016^.q_2L(x, a)
-1.75x10^-5.q_14L(x, a) +6.42x10^-6. q_15L(x, a)=34.90 ^oC
Bp_A (b)= (-105.146/8) +3.1629^.q_1L(x, b)–0.4933^.q_2L(x, b)=25.19 ^oC
Bp_B (b)= (-108.197/8) +1.6358^.q_0L(x, b)+2.038^.q_1L(x, b)–0.3016^.q_2L(x, b)
-1.75x10^-5.q_14L(x, b) +6.42x10^-6. q_15L(x, b)=20.34 ^oC
Bp_A (c)= (-105.146/8) +3.1629^.q_1L(x, c)–0.4933^.q_2L(x, c)=6.73 ^oC
Bp_B (c)= (-108.197/8) +1.6358^.q_0L(x, c)+2.038^.q_1L(x, c)–0.3016^.q_2L(x, c)
-1.75x10^-5.q_14L(x, c) +6.42x10^-6. q_15L(x, c)=8.92 ^oC
Bp_A (d)= (-105.146/8) +3.1629^.q_1L(x, d)–0.4933^.q_2L(x, d)=-4.91 ^oC
Bp_B (d)= (-108.197/8) +1.6358^.q_0L(x, d)+2.038^.q_1L(x, d)–0.3016^.q_2L(x, d)
-1.75x10^-5.q_14L(x, d) +6.42x10^-6. q_15L(x, d)=13.68 ^oC
Bp_A (e)= (-105.146/8) +3.1629^.q_1L(x, e)–0.4933^.q_2L(x, e)=13.55 ^oC
Bp_B (e)= (-108.197/8) +1.6358^.q_0L(x, e) +2.038^.q_1L(x, e)–0.3016^.q_2L(x, e)
-1.75x10^-5.q_14L(x, e) +6.42x10^-6. q_15L(x, e)=13.68 ^oC
Bp_A (f)= (-105.146/8) +3.1629^.q_1L(x, f)–0.4933^.q_2L(x, f)=1.91 ^oC
Bp_B (f)= (-108.197/8) +1.6358^.q_0L(x, f)+2.038^.q_1L(x, f)–0.3016^.q_2L(x, f)
-1.75x10^-5.q_14L(x, f) +6.42x10^-6. q_15L(x, f)=7.30 ^oC
Bp_A (g)= (-105.146/8) +3.1629^.q_1L(x, g)–0.4933^.q_2L(x, g)=16.96 ^oC
Bp_B (g)= (-108.197/8) +1.6358^.q_0L(x, g)+2.038^.q_1L(x, g)–0.3016^.q_2L(x, g)
-1.75x10^-5.q_14L(x, g) +6.42x10^-6. q_15L(x, g)=16.56 ^oC
Bp_A (h)= (-105.146/8) +3.1629^.q_1L(x, h)–0.4933^.q_2L(x, h)=1.91 ^oC
Bp_B (h)= (-108.197/8) +1.6358^.q_0L(x, h)+2.038^.q_1L(x, h)–0.3016^.q_2L(x, h)
-1.75x10^-5.q_14L(x, h) +6.42x10^-6. q_15L(x, h)=7.09 ^oC

Now, we can calculate the Bp of the 1-methyl-1,2-diethylcyclopropane molecule using two approaches. The first one is using the atom’s quadratic indices, because it is clear that the sum of these atom contributions gives the value of the Bp of the molecule (see right hand column in Table 18) and the second one is using the total quadratic indices (considering the whole molecule). The Bp of the molecule as a function of total quadratic indices can be obtained as follows:

Bp_A (Molecule)=-105.146+3.1629^.q₁(x)–0.4933^.q₂(x)=108.42^oC
Bp_B (Molecule)=-108.197+1.6358^.q₀(x)+2.038^.q₁(x)–0.3016^.q₂(x)-1.75x10^-5.q₁₄(x)
+6.42x10^-6. q₁₅(x)=110.79 ^oC

This approach allows building of topological chemical representations of molecules (using a pseudograph) by combining molecular fragments. In this sense, k-th total quadratic indices can be expressed as a “linear combination” of k-th fragment (local) quadratic indices (subgraph). This way, the calculation of several molecules properties by combining distributions (atom contributions) of smaller fragments present in the molecule is carried out. This method is based on the assumption that contribution of a given molecular fragment to the complete molecular property should be quite similar in different molecules or in different locations of the same molecule, provided that the molecular environments are similar. That is to say, the atom or fragment contribution of several properties of molecular fragments is approximately “transferable”. Now consider two the ethyl fragments present (e-f and g-h) in the 1-methyl-1,2-diethylcyclopropane molecule as in the example given above. These fragments had similar contributions but not the same. This is a logical result because the molecular enviroment is similar but not the identical. For example q_0L(x, f) [q_0L(x, e-f)=6.9169+0.9169 and q_0L(x, g-h)=6.9169+0.9169] and q₁_L(x, f) [q_1L(x, e-f)=13.8338+6.9169 and q_1L(x, g-h)=13.8338+6.9169] had the same value for both ethyl fragments; but the values of the other molecular descriptors included in the obtained models (Eq. 28 and Eq. 29) are not the same; for example: q_2L(x, f) [q_2L(x, e-f)=34.5845+13.8338 and q_2L(x, g-h)=27.6676+13.8338]. In this case, the difference is in relation with the different values of the local qudratic indices of e and g atom, which is logic because the topologic enviroment (in two steps) is not the same for both atoms. Notice that the f and h atoms have the same value for local qudratic indices and their atom contribution in the ethyl fragment is the same [q_2L(x, f)= q_2L(x, h)=13.8338].The magnitude of the local quadratic indices increases as the order of the index increases as a consequence of the greater amount of structural information contained in higher order local quadratic indices. For intance, q_{14; 15L}(x, e-f) and q_{14; 15L}(x, g-h) contain more information about both ethyl fragment (on the atom that constitute the fragment and on theirs molecular enviroment), than the previous one.

Conclusions

A promising topological approach to obtain a family of new molecular descriptors has been proposed. In this connection, a vector space E (molecular vector space), whose elements are organic molecules, was defined as a “direct sum” of different ℜⁱ spaces.

The descriptors were denominated, in general, as quadratic indices, in analogy to the mathematical quadratic forms. The k-th power of the atom adjacency matrix (M) of the molecular pseudograph and canonical bases are selected as the quadratic forms’ matrices and bases, respectively. This molecular TIs has been implemented in computer in the TOMO-COMD software, with the aim of creating a new calculation method. Specifically, the electronegativities of the atoms were used as atomic property. These indices were generalized to “higher analogues (higher order)” as number sequences, with the aim of creating a family of descriptors that constitute a tool of great utility for drug design and bioinformatic studies. In addition, this paper introduces a local approach for molecular quadratic indices. The local definition of these indices allows obtaining these descriptors for an atom or a fragment in study, which can be used in the description of molecular properties that are greatly related with the contribution of this portion. This way, for example, these local indices are of great importance in the modeling of properties of molecules that contain heteroatoms in their structure.

Finally, total and local quadratic indices and MLR have been used in QSPR studies of organic compounds. The resulting quantitative models are significant from a statistical point of view and permit a clear interpretation of the studied properties in terms of the structural features of molecules. A LOO and LGO cross-validation procedure (internal validation) and external predicting series (external validation) revealed that the regression models had a fairly good predictability. The physical properties of the test set compounds were predicted with the same accuracy as the compounds of the training set. The comparison with other approaches reveals a good behavior of the proposed method. The obtained results are valid to establish that these new indices fulfill several desirable attributes for a new molecular descriptor.

The approach described in this paper appears to be a very promising structural invariant, useful for QSPR/QSAR studies and showed to providing an excellent alternative or guides for discovery and optimization of new lead compounds, reducing the time and cost of traditional procedure.

Acknowledgements

The author thanks Dr. Ernesto Estrada for sending me several reprints of his papers about Chemical Graph Theory. Also, the author thanks the anonymous referees for their useful comments, which contributed to an improved presentation of these results.

References

Devlin, J. P. (Ed.) High Throughput Screening; Marcel Dekker: New York, 2000.
Broach, J. R.; Thorner, J. High-Throughput Screening for Drug Discovery. Nature 1996, 384 Suppl., 14–16. [Google Scholar]
Walters, W. P.; Stahl, M. T.; Murcko, M. A. Virtual Screening-an Overview. Drug Disc Today. 1998, 3, 160–178. [Google Scholar]
Drie, J. H. V.; Lajinees, M. S. Approaches to Virtual Library Design. Drug Disc Today. 1998, 3, 274–283. [Google Scholar]
de Julián-Ortiz, J. V.; Gálvez, J.; Muñoz-Collado, C.; García- Domenech, R.; Gimeno-Cardona, C. Virtual Combinatorial Synthesis and Computational Screening of New Potential Anti-Herpes Compounds. J Med Chem. 1999, 42, 3308–3314. [Google Scholar]
Van de Waterbeemd, H.; Carter, R. E.; Grassy, G.; Kubinyi, H.; Martin, Y. C.; Tute, M. S.; Willett, P. Annu. Rep. Med. Chem. 1998, 33, 397.
Karelson, M. Molecular Descriptors in QSAR/ QSPR; John Wiley & Sons: New York, 2000. [Google Scholar]
Katritzky, A. R.; Gordeeva, E. V. Traditional Topological Indexes vs Electronic, Geometrical, and Combined Molecular Descriptors in QSAR/QSPR Research. J. Chem. Inf. Comput. Sci. 1993, 33, 835. [Google Scholar]
Kier, L. B.; Hall, L. H. Molecular Structure Description. The Electrotopological State; Academic Press: New York, 1999. [Google Scholar]
Balaban, A. Topological and Stereochemical Molecular Descriptors for Databases Useful in QSAR, Similarity/Dissimilarity and Drug Design. SAR QSAR Environ. Res. 1998, 8, 1–21. [Google Scholar]
Estrada, E. On the Topological Sub-Structural Molecular Design (TOSS-MODE) in QSPR/QSAR and Drug Design Research. SAR QSAR Environ. Res. 2000, 11, 55–73. [Google Scholar]
Randić, M. Encyclopedia of Computational Chemistry; Schleyer, P. V. R., Ed.; John Wiley & Sons: New York, 1998; Vol. 5, pp. 3018–3032. [Google Scholar]
Rouvray, D. H. Mathematical and Computational Concepts in Chemistry; Trinajstic, N., Ed.; Ellis Horwood: Chichester, 1986; pp. 295–306. [Google Scholar]
Balaban, A. T. (Ed.) From Chemical Graphs to Three-Dimensional Geometry; Plenum Press: New York, 1997.
Todeschini, R.; Consoni, V. Handbook of molecular descriptors; Wiley VCH, Weinheim: Germany, 2000. [Google Scholar]
Topological Indices and Related Descriptors in QSAR and QSPR; Devillers, J.; Balaban, A. T. (Eds.) Gordon and Breach: Amsterdam, the Netherlands, 1999.
Estrada, E.; Uriarte, E. Recent Advances on the Role of Topological Indices in Drug Discovery Research. Curr. Med. Chem. 2001, 8, 1699–1714. [Google Scholar]
Wiener, H. Structural Determination of Paraffin Boiling Point. J. Am. Chem. Soc. 1947, 69, 17–20. [Google Scholar]
Balaban, A. T. Highly Discriminant Distance-Based Topological Index. Chem. Phys. Lett. 1982, 89, 399–404. [Google Scholar]
Randić, M. Characterization of Molecular Branching. J. Am. Chem. Soc. 1975, 69, 6609–6615. [Google Scholar]
Kier, L. B.; Hall, L. H. Molecular Structure Description. The Electrotopological State; Academic Press: New York, 1999. [Google Scholar]
Plavšić, D.; Nikolić, S.; Trinajstić, N.; Mihalić, Z. On the Harary Index for the Characterization of Chemical Graphs. J. Math. Chem. 1993, 12, 235–250. [Google Scholar]
Estrada, E. Spectral Moment of Edge Adjacency Matrix in Molecular Graphs.1. Definition and Application to the Prediction of Physical Properties of Alkanes. J. Chem. Inf. Comp. Sci. 1996, 36, 846–849. [Google Scholar]
Estrada, E. Spectral Moment of Edge Adjacency Matrix in Molecular Graphs. 2. Molecules Containing Heteroatom and QSAR Applications. J. Chem. Inf. Comp. Sci. 1997, 37, 320–328. [Google Scholar]
Estrada, E. Spectral Moment of Edge Adjacency Matrix in Molecular Graphs 3. Molecules Containing Cycles. J. Chem. Inf. Comp. Sci. 1998, 38, 123–27. [Google Scholar]
Randić, M. Generalized Molecular Descriptors. J. Math. Chem. 1991, 7, 155–168. [Google Scholar]
Mihalic, Z.; Trinajstić, N. A Graph-Theoretical Approach to Structure-Property Relationships. J. Chem. Educ. 1992, 69, 701–712. [Google Scholar]
Diudea, M. V. (Ed.) QSPR/QSAR Studies by Molecular Descriptors; Nova Science, Huntington: New York, 2001.
Ivanciuc, O.; Ivanciuc, T.; Cabrol–Bass, D.; Balaban, A. T. Evaluation in Quantitative Structure–Property Relationship Models of Structural Descriptors Derived from Information–Theory Operators. J. Chem. Inf. Comput. Sci. 2000, 40, 631–643. [Google Scholar]
Balaban, T.; Mills, D.; Ivanciuc, O.; Basak, S. C. Reverse Wiener Indices. Croat. Chem. Acta. 2000, 73, 923. [Google Scholar]
Ivanciuc, O.; Ivanciuc, T.; Klein, D. J.; Seitz, W. A.; Balaban, A. T. Wiener Index Extension by Counting Even/Odd Graph Distances. J. Chem. Inf. Comput. Sci. 2001, 41, 536–549. [Google Scholar]
Torrens, F. Valence Topological Charge-Transfer Indices for Dipole Moments. Molecules 2003, 8, 169–185. [Google Scholar]
Rios–Santamarina, I.; García–Domenech, R.; Cortijo, J.; Santamaria, P.; Morcillo, E. J.; Gálvez, J. Natural Compounds with Bronchodilator Activity Selected by Molecular Topology. Internet Electron. J. Mol. Des. 2002, 1, 70–79. http://www.biochempress.com. [Google Scholar]
Marino, D. J. G.; Peruzzo, P. J.; Castro, E. A.; Toropov, A. A. QSAR Carcinogenic Study of Methylated Polycyclic Aromatic Hydrocarbons Based on Topological Descriptors Derived from Distance Matrices and Correlation Weights of Local Graph Invariants. Internet Electron. J. Mol. Des. 2002, 1, 115–133. http://www.biochempress.com. [Google Scholar]
Ivanciuc, O. QSAR Comparative Study of Wiener Descriptors for Weighted Molecular Graphs. J. Chem. Inf. Comput. Sci. 2000, 40, 1412–1422. [Google Scholar]
Marrero, Y.; Romero, V. TOMO-COMD software. Central University of Las Villas, 2002; TOMO-COMD (TOpological MOlecular COMputer Design) for Windows, version 1.0 is a preliminary experimental version; in the future a professional version may be obtained upon request to Y. Marrero: [email protected]; [email protected]. [Google Scholar]
Cotton, F. A. Advanced Inorganic Chemistry; Revolucionaria: Havana; p. 103.
Ross, K. A.; Wright, C.R.B. Matemáticas Discretas; Prentice Hall Hispanoamericana: México, 1990. [Google Scholar]
Noriega, T. Álgebra; Revolucionaria: Havana, Cuba, 1990; pp. 2-10, 43-49. [Google Scholar]
Maltsev, A. I. Fundamentos del álgebra lineal; Mir: Moscow, 1976; pp. 68, 262. [Google Scholar]
Garrido, L. G. Introduccion a la Matemáticas Discretas; Revolucionaria: Havana, Cuba, 1990; pp. 237–298. [Google Scholar]
Estrada, E.; Rodriguez, L. Matrix Algebraic Manipulation of Molecular Graphs. 2. Harary- and MTI-like Molecular Descriptors. Match 1997, 35, 157–167. [Google Scholar]
Needham, D. E.; Wei, I-C.; Seybold, P. G. Molecular Modeling of the Physical Properties of the Alkanes. J. Am. Chem. Soc. 1998, 110, 4186–4194. [Google Scholar]
Krenkel, G.; Castro, E. A.; Toropov, A. A. Improved Molecular Descriptors Based on the Optimization of Correlation Weights of local Graph Invariants. Int. J. Mol. Sci. 2001, 2, 57–65. http://www.mdpi.org.ijms. [Google Scholar]
Morrison, R. T.; Boyd, R. N. Organic Chemistry; Revolucionaria: Havana, Cuba, 1970. [Google Scholar]
Solomon, J. W. G. Química Orgánica; Limusa: Mexico, 1987. [Google Scholar]
STATISTICA ver. 5.5. Statsoft, Inc., 1999.
Golbraikh, A.; Tropsha, A. Beware of q²! J. Mol. Graph. Modell. 2002, 20, 269–276. [Google Scholar]
Rose, K.; Hall, L. H.; Kier, L. B. Modeling Blood-Brain Barrier Partitioning Using the Electrotopological State. J. Chem. Inf. Comput. Sci. 2002, 42, 651–666. [Google Scholar]
Wold, S.; Erikson, L. Statistical Validation of QSAR Results. Validation Tools. In Chemometric Methods in Molecular Design; van de Waterbeemd, H., Ed.; VCH Publishers: New York, 1995; pp. 309–318. [Google Scholar]
Randić, M.; Basak, S. Optimal Molecular Descriptors Based on Weighted Path Numbers. J. Chem. Inf. Comput. Sci. 1999, 39, 261–266. [Google Scholar]
Chenzhong, C.; Zhiliang, L. Molecular Polarizability. 1. Relationship to Water Solubility of Alkanes and Alcohols. J. Chem. Inf. Comput. Sci. 1998, 38, 1–7. [Google Scholar]
Katritzky, A. R.; Lobanov, V. S.; Karelson, M. Normal Boiling Points for Organic Compounds: Correlation and Prediction by a Quantitative Structure-Property Relationship. J. Chem. Inf. Comput. Sci. 1998, 38, 28–41. [Google Scholar]
Estrada, E.; Ivanciuc, O.; Gutman, I.; Gutiérrez, A.; Rodríguez, L. Extended Wiener Indices. A New Set of Descriptors for Quantitative Structure-Property Studies. New J. Chem. 1998, 22, 819–822. [Google Scholar]
Katrizky, A.; Maran, U.; Lobanov, V. S.; Karelson, M. Structurally Diverse Quantitative Structure-Property Relationship Correlations of Technologically Relevant Physical Properties. J. Chem. Inf. Comput. Sci. 2000, 40, 1–18. [Google Scholar]
Stanton, D. T. Development of a Quantitative Structure-Property Relationship Model for Estimating Normal Boiling Points of Small Multifunctional Organic Molecules. J. Chem. Inf. Comput. Sci. 2000, 40, 81–90. [Google Scholar]
Belsey, D. A.; Kuh, E.; Welsch, R. E. Regression Diagnostics; Wiley: New York, 1980. [Google Scholar]
Alzina, R. B. Introduccion conceptual al análisis multivariable. Un enfoque informatico con los paquetes SPSS-X, BMDP, LISREL Y SPAD; PPU, SA: Barcelona, 1989; Chapter 8; Vol. 1, p. 202. [Google Scholar]
Basak, S. C.; Balaban, A. T.; Grunwald, G. D.; Gute, B. D. Topological Indices: Their Nature and Mutual Relatedness. J. Chem. Inf. Comput. Sci. 2000, 40, 891–898. [Google Scholar]
Patel, H.; Cronin, M. T. D. A Novel Index for the Description of Molecular Linearity. J. Chem. Inf. Comput. Sci. 2001, 41, 1228–1236. [Google Scholar]
Romanelli, G. P.; Cafferata, L. F. R.; Castro, E. A. An improved QSAR study of toxicity of saturated alcohols. J. Mol. Struct. (Theochem). 2000, 504, 261–265. [Google Scholar]
Randić, M. Orthogonal Molecular Descriptors. New J. Chem. 1991, 15, 517–525. [Google Scholar]
Randić, M. Fitting of Nonlinear Regression by Orthogonalized Power Series. J. Comput. Chem. 1993, 14, 363–370. [Google Scholar]
Randić, M. Resolution of Ambiguities in Structure-Property Studies by us of Orthogonal Descriptors. J. Chem. Inf. Comput. Sci. 1991, 31, 311–320. [Google Scholar]
Randić, M. Correlation of Enthalpy of Octanes with Orthogonal Connectivities indices. J. Mol. Struct. (Theochem). 1991, 233, 45–59. [Google Scholar]
Lučić, B.; Nikolić, S.; Trinajstić, N.; Jurić, D. The Structure-Property Models can be Improbad Using the Orthogonalized Descriptors. J. Chem. Inf. Comput. Sci. 1995, 35, 532–538. [Google Scholar]
Cronin, M. T. D.; Schultz, T. W. Pitfalls in QSAR. J. Mol. Struct. (Theochem). 2003, 622, 39–51. [Google Scholar]
Estrada, E.; Gonzáles, H. What Are the Limits of Applicability for Graph Theoretic Descriptors in QSPR/QSAR? Modeling Dipole Moments of Aromatic Compounds with TOPS-MODE Descriptors. J. Chem. Inf. Comput. Sci. 2003, 43, 75–84. [Google Scholar]

Sample Availability: Not applicable.

Share and Cite

MDPI and ACS Style

Ponce, Y.M. Total and Local Quadratic Indices of the Molecular Pseudograph's Atom Adjacency Matrix: Applications to the Prediction of Physical Properties of Organic Compounds. Molecules 2003, 8, 687-726. https://doi.org/10.3390/80900687

AMA Style

Ponce YM. Total and Local Quadratic Indices of the Molecular Pseudograph's Atom Adjacency Matrix: Applications to the Prediction of Physical Properties of Organic Compounds. Molecules. 2003; 8(9):687-726. https://doi.org/10.3390/80900687

Chicago/Turabian Style

Ponce, Yovani Marrero. 2003. "Total and Local Quadratic Indices of the Molecular Pseudograph's Atom Adjacency Matrix: Applications to the Prediction of Physical Properties of Organic Compounds" Molecules 8, no. 9: 687-726. https://doi.org/10.3390/80900687

Article Menu

Total and Local Quadratic Indices of the Molecular Pseudograph's Atom Adjacency Matrix: Applications to the Prediction of Physical Properties of Organic Compounds

Abstract

Introduction

Results and Discussion

Computational methods. Mathematical definition of the molecular descriptor

Molecular vector space

Total quadratic indices; [q_k(x)].

Local quadratic indices; [q_kL(x)]

Calculation of total and local quadratic indices

The TOMO-COMD software

Physical properties data sets for QSPR studies

Data analysis

QSPR applications

Colinearity between variables and redundancy of information

Interpretation of QSPR models

Conclusions

Acknowledgements

References

Share and Cite

Article Metrics

Article Access Statistics

Further Information

Guidelines

MDPI Initiatives

Follow MDPI

Article Menu

Total and Local Quadratic Indices of the Molecular Pseudograph's Atom Adjacency Matrix: Applications to the Prediction of Physical Properties of Organic Compounds

Abstract

Introduction

Results and Discussion

Computational methods. Mathematical definition of the molecular descriptorMolecular vector space

Total quadratic indices; [qk(x)].

Local quadratic indices; [qkL(x)]

Calculation of total and local quadratic indices

The TOMO-COMD software

Physical properties data sets for QSPR studies

Data analysis

QSPR applications

Colinearity between variables and redundancy of information

Interpretation of QSPR models

Conclusions

Acknowledgements

References

Share and Cite

Article Metrics

Article Access Statistics

Further Information

Guidelines

MDPI Initiatives

Follow MDPI

Computational methods. Mathematical definition of the molecular descriptor

Molecular vector space

Total quadratic indices; [q_k(x)].

Local quadratic indices; [q_kL(x)]