Production of Ultracold XOH (X = Ca, Sr, Ba) Molecules by Direct Laser Cooling: A Theoretical Study Based on Accurate Ab Initio Calculations
Abstract
1. Introduction
2. Results
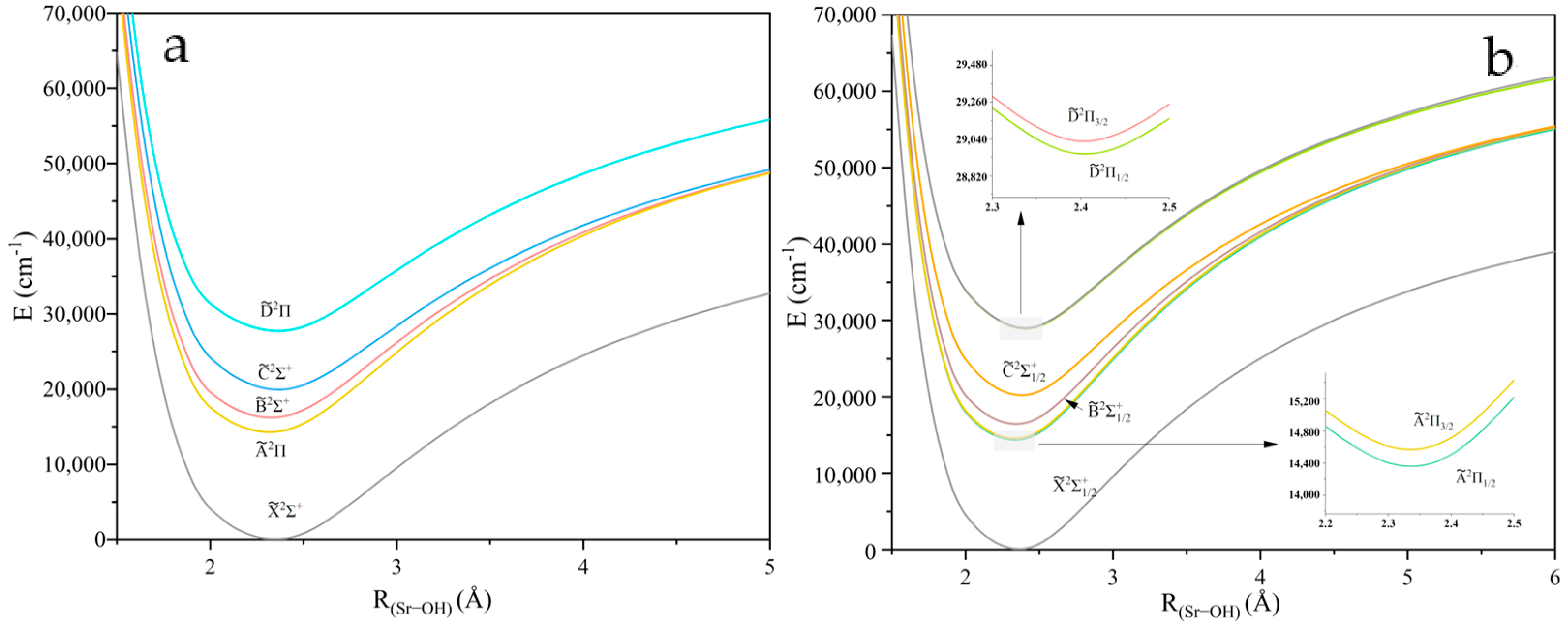
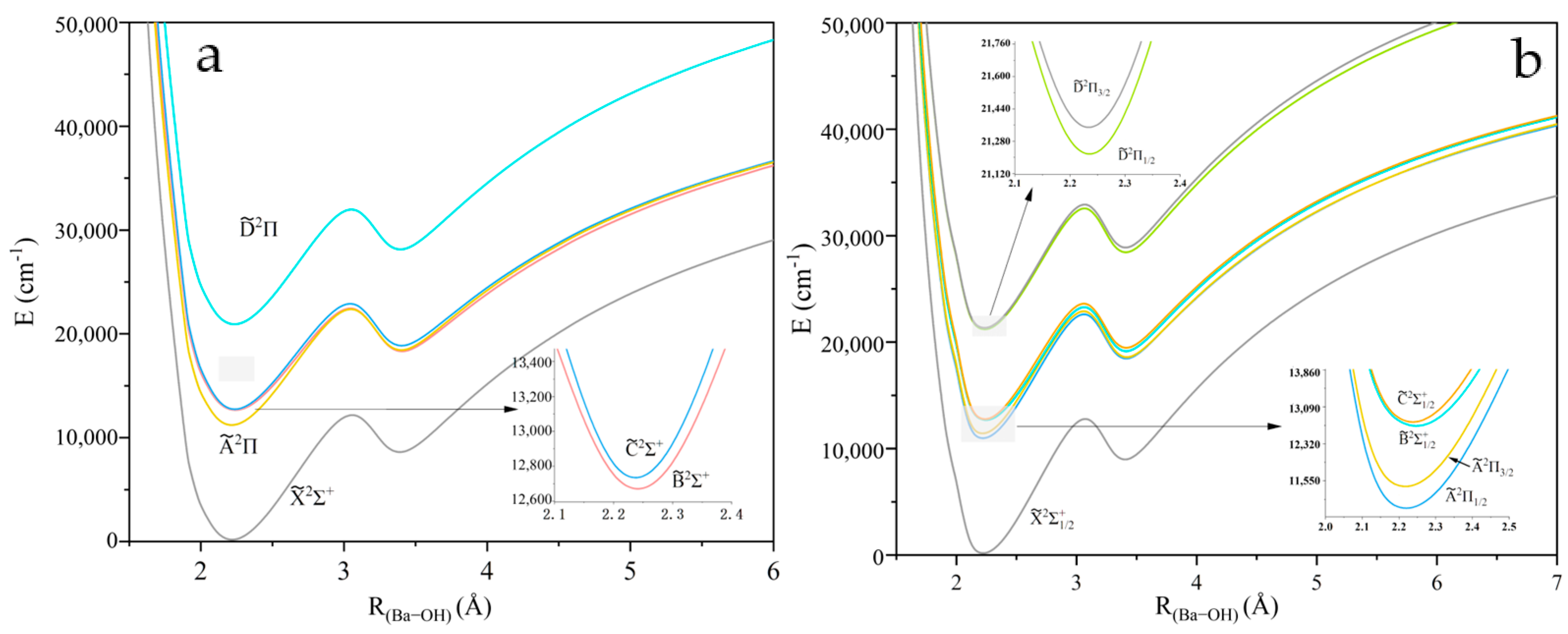
2.1. Potential Energy Curves
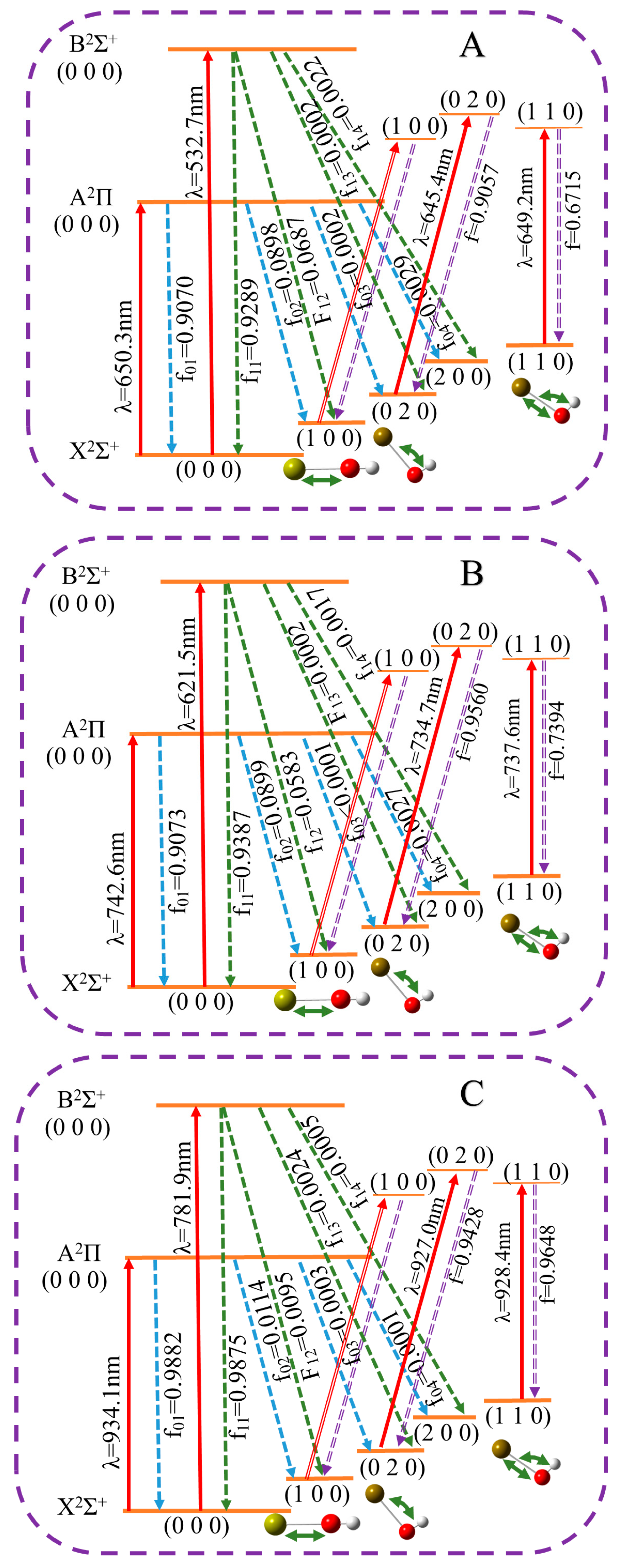
2.2. Laser Cooling Scheme
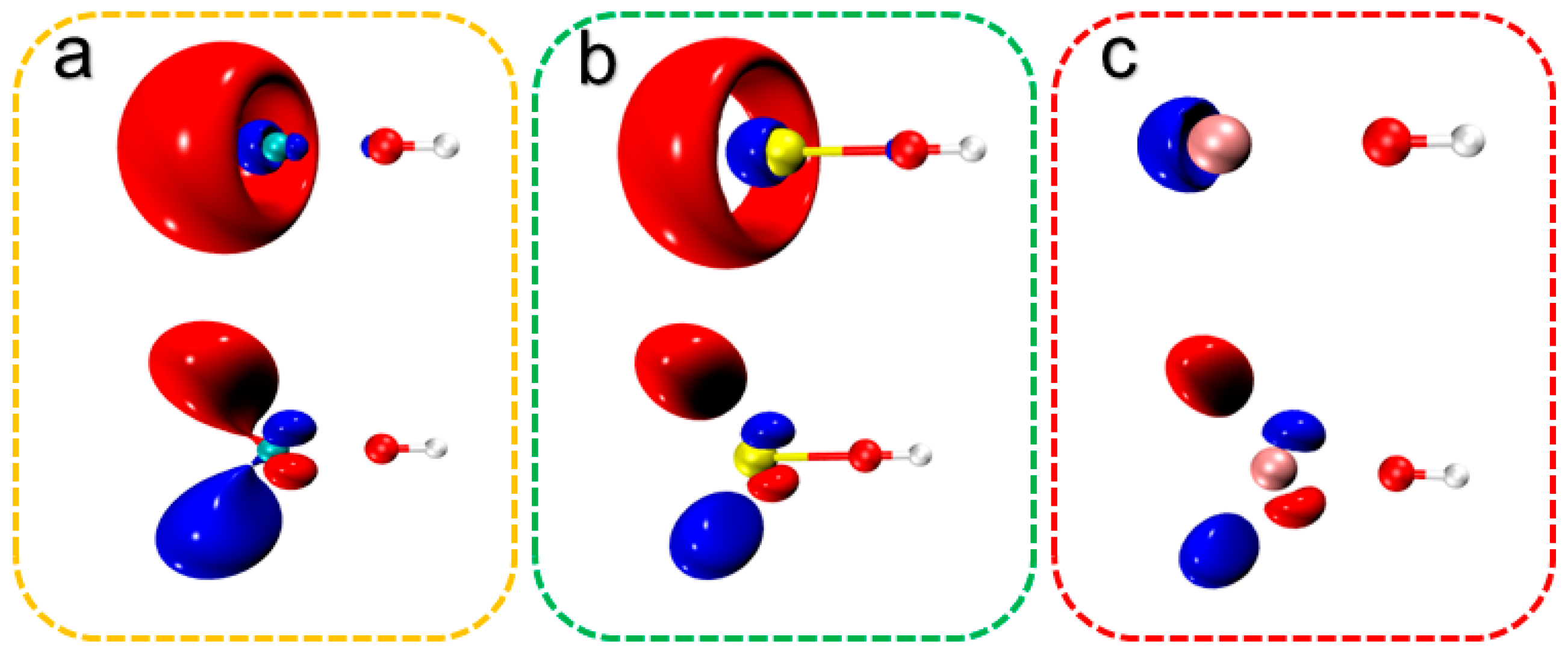
2.3. Laser Cooling Feasibility Assessment
3. Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yu, P.; Cheuk, L.W.; Kozyryev, I.; Doyle, J.M. A scalable quantum computing platform using symmetric-top molecules. New J. Phys. 2019, 21, 093049. [Google Scholar] [CrossRef]
- Wall, M.L.; Maeda, K.; Carr, L.D. Realizing unconventional quantum magnetism with symmetric top molecules. New J. Phys. 2015, 17, 025001. [Google Scholar] [CrossRef]
- Augustovičová, L.D.; Bohn, J.L. Ultracold collisions of polyatomic molecules: CaOH. New J. Phys. 2019, 21, 103022. [Google Scholar] [CrossRef]
- Heazlewood, B.R.; Softley, T.P. Towards chemistry at absolute zero. Nat. Rev. Chem. 2021, 5, 125–140. [Google Scholar] [CrossRef] [PubMed]
- Kozyryev, I.; Hutzler, N.R. Precision measurement of time-reversal symmetry violation with laser-cooled polyatomic molecules. Phys. Rev. Lett. 2017, 119, 133002. [Google Scholar] [CrossRef] [PubMed]
- Isaev, T.A.; Berger, R. Polyatomic candidates for cooling of molecules with lasers from simple theoretical concepts. Phys. Rev. Lett. 2016, 116, 063006. [Google Scholar] [CrossRef]
- Isaev, T.A.; Zaitsevskii, A.V.; Eliav, E. Laser-coolable polyatomic molecules with heavy nuclei. J. Phys. B At. Mol. Opt. Phys. 2017, 50, 225101. [Google Scholar] [CrossRef]
- O’Rourke, M.J.; Hutzler, N.R. Hypermetallic polar molecules for precision measurements. Phys. Rev. A 2019, 100, 022502. [Google Scholar] [CrossRef]
- Augenbraun, B.L.; Doyle, J.M.; Zelevinsky, T.; Kozyryev, I. Molecular asymmetry and optical cycling: Laser cooling asymmetric top molecules. Phys. Rev. X 2020, 10, 031022. [Google Scholar] [CrossRef]
- Kłos, J.; Kotochigova, S. Prospects for laser cooling of polyatomic molecules with increasing complexity. Phys. Rev. Res. 2020, 2, 013384. [Google Scholar] [CrossRef]
- Ivanov, M.V.; Bangerter, F.H.; Wójcik, P.; Krylov, A.I. Toward ultracold organic chemistry: Prospects of laser cooling large organic molecules. J. Phys. Chem. Lett. 2020, 11, 6670–6676. [Google Scholar] [CrossRef]
- Dickerson, C.E.; Guo, H.; Shin, A.J.; Augenbraun, B.L.; Caram, J.R.; Campbell, W.C.; Alexandrova, A.N. Franck-Condon tuning of optical cycling centers by organic functionalization. Phys. Rev. Lett. 2021, 126, 123002. [Google Scholar] [CrossRef] [PubMed]
- Dickerson, C.E.; Guo, H.; Zhu, G.Z.; Hudson, E.R.; Caram, J.R.; Campbell, W.C.; Alexandrova, A.N. Optical cycling functionalization of arenes. J. Phys. Chem. Lett. 2021, 12, 3989–3995. [Google Scholar] [CrossRef] [PubMed]
- Bauschlicher, C.W., Jr.; Langhoff, S.R.; Steimle, T.C.; Shirley, J.E. The permanent electric dipole moment of CaOH. J. Chem. Phys. 1990, 93, 4179–4186. [Google Scholar] [CrossRef]
- Owens, A.; Clark, V.H.; Mitrushchenkov, A.; Yurchenko, S.N.; Tennyson, J. Theoretical rovibronic spectroscopy of the calcium monohydroxide radical (CaOH). J. Chem. Phys. 2021, 154, 234302. [Google Scholar] [CrossRef]
- Zhang, C.; Augenbraun, B.L.; Lasner, Z.D.; Vilas, N.B.; Doyle, J.M.; Cheng, L. Accurate prediction and measurement of vibronic branching ratios for laser cooling linear polyatomic molecules. J. Chem. Phys. 2021, 155, 091101. [Google Scholar] [CrossRef]
- Koput, J.; Peterson, K.A. Ab initio potential energy surface and vibrational—Rotational energy levels of X2σ + CaOH. J. Phys. Chem. A 2002, 106, 9595–9599. [Google Scholar] [CrossRef]
- Baum, L.; Vilas, N.B.; Hallas, C.; Augenbraun, B.L.; Raval, S.; Mitra, D.; Doyle, J.M. Establishing a nearly closed cycling transition in a polyatomic molecule. Phys. Rev. A 2021, 103, 043111. [Google Scholar] [CrossRef]
- Kozyryev, I.; Baum, L.; Matsuda, K.; Augenbraun, B.L.; Anderegg, L.; Sedlack, A.P.; Doyle, J.M. Sisyphus laser cooling of a polyatomic molecule. Phys. Rev. Lett. 2017, 118, 173201. [Google Scholar] [CrossRef]
- Lasner, Z.; Lunstad, A.; Zhang, C.; Cheng, L.; Doyle, J.M. Vibronic branching ratios for nearly closed rapid photon cycling of SrOH. Phys. Rev. A 2022, 106, L020801. [Google Scholar] [CrossRef]
- Lasner, Z.D.; Frenett, A.; Sawaoka, H.; Anderegg, L.; Augenbraun, B.; Lampson, H.; Li, M.; Lunstad, A.; Mango, J.; Nasir, A.; et al. Magneto-optical trapping of a heavy polyatomic molecule for precision measurement. Phys. Rev. Lett. 2025, 134, 083401. [Google Scholar] [CrossRef] [PubMed]
- Baum, L.; Vilas, N.B.; Hallas, C.; Augenbraun, B.L.; Raval, S.; Mitra, D.; Doyle, J.M. 1D magneto-optical trap of polyatomic molecules. Phys. Rev. Lett. 2020, 124, 133201. [Google Scholar] [CrossRef]
- Vilas, N.B.; Hallas, C.; Anderegg, L.; Robichaud, P.; Winnicki, A.; Mitra, D.; Doyle, J.M. Magneto-optical trapping and sub-Doppler cooling of a polyatomic molecule. Nature 2022, 606, 70–74. [Google Scholar] [CrossRef]
- Augenbraun, B.L.; Lasner, Z.D.; Frenett, A.; Sawaoka, H.; Miller, C.; Steimle, T.C.; Doyle, J.M. Laser-cooled polyatomic molecules for improved electron electric dipole moment searches. New J. Phys. 2020, 22, 022003. [Google Scholar] [CrossRef]
- Mitra, D.; Vilas, N.B.; Hallas, C.; Anderegg, L.; Augenbraun, B.L.; Baum, L.; Miller, C.; Raval, S.; Doyle, J.M. Direct laser cooling of a symmetric top molecule. Science 2020, 369, 1366–1369. [Google Scholar] [CrossRef]
- Augenbraun, B.L.; Lasner, Z.D.; Frenett, A.; Sawaoka, H.; Le, A.T.; Doyle, J.M.; Steimle, T.C. Observation and laser spectroscopy of ytterbium monomethoxide, YbOCH 3. Phys. Rev. A 2021, 103, 022814. [Google Scholar] [CrossRef]
- Titov, A.V.; Mosyagin, N.S.; Petrov, A.N.; Isaev, T.A.; DeMille, D.P. P,T-PARITYVIOLATIONEFFECTS INPOLARHEAVY-ATOM MOLECULES. In Recent Advances in the Theory of Chemical and Physical Systems; Springer: Dordrecht, The Netherlands, 2006; pp. 253–283. [Google Scholar]
- Klemperer, W.; Lehmann, K.K.; Watson, J.K.G.; Wofsy, S.C. Can molecules have permanent electric dipole moments? J. Phys. Chem. 1993, 97, 2413–2416. [Google Scholar] [CrossRef]
- Isaev, T.A.; Hoekstra, S.; Berger, R. Laser-cooled RaF as a promising candidate to measure molecular parity violation. Phys. Rev. A 2010, 82, 052521. [Google Scholar] [CrossRef]
- Theodorakopoulos, G.; Petsalakis, I.D.; Liebermann, H.P.; Buenker, R.J.; Koput, J. Ab initio calculations on electronic states of CaOH. J. Chem. Phys. 2002, 117, 4810–4819. [Google Scholar] [CrossRef]
- Bernath, P.F.; Brazier, C.R. Spectroscopy of CaOH. Astrophys. J. 1985, 288, 373–376. [Google Scholar] [CrossRef]
- Li, M.; Coxon, J.A. Dye laser excitation studies of the (100)/(020)– (020)/(000) bands of CaOD: Analysis of the (100)∼(020) Fermi resonance. J. Chem. Phys. 1996, 104, 4961–4977. [Google Scholar] [CrossRef]
- Kozyryev, I.; Steimle, T.C.; Yu, P.; Nguyen, D.T.; Doyle, J.M. Determination of CaOH and CaOCH3 vibrational branching ratios for direct laser cooling and trapping. New J. Phys. 2019, 21, 052002. [Google Scholar] [CrossRef]
- Tandy, J.D.; Wang, J.G.; Bernath, P.F. High-resolution laser spectroscopy of BaOH and BaOD: Anomalous spin-orbit coupling in the state. J. Mol. Spectrosc. 2009, 255, 63–67. [Google Scholar] [CrossRef]
- Presunka, P.I.; Coxon, J.A. Laser excitation and dispersed fluorescence investigations of the – system of SrOH. Chem. Phys. 1995, 190, 97–111. [Google Scholar] [CrossRef]
- Wang, J.G.; Dick, M.J.; Sheridan, P.M.; Yu, S.; Bernath, P.F. Further spectroscopic investigations of the high energy electronic states of SrOH: The (000)– (000) and the 2Σ+ (000)– (000) transitions. J. Mol. Spectrosc. 2007, 245, 26–33. [Google Scholar] [CrossRef]
- Zhang, C.; Korslund, H.; Wu, Y.; Ding, S.; Cheng, L. Towards accurate prediction for laser-coolable molecules: Relativistic coupled-cluster calculations for yttrium monoxide and prospects for improving its laser cooling efficiencies. Phys. Chem. Chem. Phys. 2020, 22, 26167–26177. [Google Scholar] [CrossRef] [PubMed]
- Tarbutt, M.R.; Sauer, B.E.; Hudson, J.J.; Hinds, E.A. Design for a fountain of YbF molecules to measure the electron’s electric dipole moment. New J. Phys. 2013, 15, 053034. [Google Scholar] [CrossRef]
- Williams, H.J.; Truppe, S.; Hambach, M.; Caldwell, L.; Fitch, N.J.; Hinds, E.A.; Sauer, B.E.; Tarbutt, M.R. Characteristics of a magneto-optical trap of molecules. New J. Phys. 2017, 19, 113035. [Google Scholar] [CrossRef]
- Werner, H.J.; Knowles, P.J. A second order multiconfiguration SCF procedure with optimum convergence. J. Chem. Phys. 1985, 82, 5053–5063. [Google Scholar] [CrossRef]
- Werner, H.J.; Knowles, P.J. An efficient internally contracted multiconfiguration–reference configuration interaction method. J. Chem. Phys. 1988, 89, 5803–5814. [Google Scholar] [CrossRef]
- Langhoff, S.R.; Davidson, E.R. Configuration interaction calculations on the nitrogen molecule. Int. J. Quantum Chem. 1974, 8, 61–72. [Google Scholar] [CrossRef]
- Van Mourik, T.; Dunning, T.H.; Peterson, K.A. Ab Initio Characterization of the HCOx (x = −1, 0, +1) Species: Structures, Vibrational Frequencies, CH Bond Dissociation Energies, and HCO Ionization Potential and Electron Affinity. J. Phys. Chem. A 2000, 104, 2287–2293. [Google Scholar] [CrossRef]
- Hao, Y.; Pašteka, L.F.; Visscher, L.; Aggarwal, P.; Bethlem, H.L.; Boeschoten, A.; Borschevsky, A.; Denis, M.; Esajas, K.; Hoekstra, S.; et al. High accuracy theoretical investigations of CaF, SrF, and BaF and implications for laser-cooling. J. Chem. Phys. 2019, 151, 034302. [Google Scholar] [CrossRef]
- Schuchardt, K.L.; Didier, B.T.; Elsethagen, T.; Sun, L.; Gurumoorthi, V.; Chase, J.; Li, J.; Windus, T.L. Basis set exchange: A community database for computational sciences. J. Chem. Inf. Model. 2007, 47, 1045–1052. [Google Scholar] [CrossRef] [PubMed]
- Feller, D. The role of databases in support of computational chemistry calculations. J. Comput. Chem. 1996, 17, 1571–1586. [Google Scholar] [CrossRef]
- Berning, A.; Schweizer, M.; Werner, H.J.; Knowles, P.J.; Palmieri, P. Spin-orbit matrix elements for internally contracted multireference configuration interaction wavefunctions. Mol. Phys. 2000, 98, 1823–1833. [Google Scholar] [CrossRef]
- Werner, H.J.; Knowles, P.J.; Manby, F.R.; Black, J.A.; Doll, K.; Heßelmann, A.; Kats, D.; Köhn, A.; Korona, T.; Kreplin, D.A.; et al. The Molpro quantum chemistry package. J. Chem. Phys. 2020, 152, 144107. [Google Scholar] [CrossRef] [PubMed]
- Gozem, S.; Krylov, A.I. The ezSpectra suite: An easy-to-use toolkit for spectroscopy modeling. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2022, 12, e1546. [Google Scholar] [CrossRef]
- Duschinsky, F. The importance of the electron spectrum in multi atomic molecules concerning the Franck-Condon principle. Acta Physicochim. URSS 1937, 7, 551–566. [Google Scholar]

| State | Coordinate | T1 [31] | TD [32] | Measured [33] | CASSCF (Def2-qzvppd) |
|---|---|---|---|---|---|
| Ca-O | 1.9698 | 1.9656 | 1.9746 | 2.004 | |
| O-H | 0.9644 | 0.9646 | 0.9562 | 0.9517 | |
| ∠Ca-O-H | 180 | 180 | 180 | 179.97 | |
| Ca-O | 1.9698 | 1.9652 | 1.9532 | 1.9803 | |
| O-H | 0.9648 | 0.9646 | 0.9572 | 0.9514 | |
| ∠Ca-O-H | 180 | 180 | 179.97 | ||
| Mode (symmetry) | |||||
| Bend (Π) | 356.72 | 344.89/345.29 | 352.93 | 400.7 | |
| Ca–O stretch (Σ) | 625.22 | 603.84 | 609.02 | 625.59 | |
| O–H stretch (Σ) | 3816.28 | 3819.96 | 3778 | 3933.55 | |
| Bend (Π) | 368.41 | 370.37/371.13 | 361.36 | 370.45 | |
| Ca–O stretch (Σ) | 625.18 | 603.84 | 630.68 | 642.44 | |
| O–H stretch (Σ) | 3816.06 | 3819.96 | 3960.06 | ||
| Ba | Sr | ||||
|---|---|---|---|---|---|
| State | Coordinate | Measured [34] | CASSCF (Def2-qzvppd) | Measured [35,36] | CASSCF (Def2-qzvppd) |
| X-O | 2.201 | 2.2539 | 2.111 | 2.17875 | |
| O-H | 0.927 | 0.9592 | 0.922 | 0.95134 | |
| X-O-H | 179.71 | 179.997 | |||
| X-O | 2.237 | 2.3171 | 2.091 | 2.12221 | |
| O-H | 0.758 | 0.9352 | 0.922 | 0.95047 | |
| X-O-H | 180 | 179.996 | |||
| X-O | 2.231 | 2.3171 | 2.098 | 2.12221 | |
| O-H | 0.909 | 0.9352 | 0.921 | 0.95047 | |
| X-O-H | 180 | ||||
| Mode (symmetry) | |||||
| Bend (Π) | 341.6 | 355.44 | 387.6/387.6 | ||
| X–O stretch (Σ) | 492.4 | 471.77 | 463.88 | ||
| O–H stretch (Σ) | 3894.54 | 3935.41 | |||
| Bend (Π) | 381.69 | 399 | |||
| X–O stretch (Σ) | 468.3 | 540.72 | |||
| O–H stretch (Σ) | 3897.64 | 3960.14 | |||
| Bend (Π) | 399.63 | 421.17 | |||
| X–O stretch (Σ) | 467.59 | 540.72 | |||
| O–H stretch (Σ) | 3897.3 | 3960.14 | |||
| FCF | Sum | FCF | Sum | ||
|---|---|---|---|---|---|
| CaOH | |||||
| 0.9070 | 0.9289 | ||||
| 0.9968 | 0.9976 | ||||
| 0.9970 | 0.9978 | ||||
| 0.9999 | 0.9998 | ||||
| SrOH | |||||
| 0.9073 | 0.9387 | ||||
| 0.9972 | 0.9970 | ||||
| 0.9673 | 0.9972 | ||||
| 0.9999 | 0.9999 | ||||
| BaOH | |||||
| 0.9882 | 0.9875 | ||||
| 0.9996 | 0.9970 | ||||
| 0.9999 | 0.9994 | ||||
| 0.9999 | 0.9999 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, J.; Li, P.; Wu, J.; Li, Y.; Liu, W.; Fu, Y.; Ma, J. Production of Ultracold XOH (X = Ca, Sr, Ba) Molecules by Direct Laser Cooling: A Theoretical Study Based on Accurate Ab Initio Calculations. Molecules 2025, 30, 1950. https://doi.org/10.3390/molecules30091950
Wei J, Li P, Wu J, Li Y, Liu W, Fu Y, Ma J. Production of Ultracold XOH (X = Ca, Sr, Ba) Molecules by Direct Laser Cooling: A Theoretical Study Based on Accurate Ab Initio Calculations. Molecules. 2025; 30(9):1950. https://doi.org/10.3390/molecules30091950
Chicago/Turabian StyleWei, Jingbo, Peng Li, Jizhou Wu, Yuqing Li, Wenliang Liu, Yongming Fu, and Jie Ma. 2025. "Production of Ultracold XOH (X = Ca, Sr, Ba) Molecules by Direct Laser Cooling: A Theoretical Study Based on Accurate Ab Initio Calculations" Molecules 30, no. 9: 1950. https://doi.org/10.3390/molecules30091950
APA StyleWei, J., Li, P., Wu, J., Li, Y., Liu, W., Fu, Y., & Ma, J. (2025). Production of Ultracold XOH (X = Ca, Sr, Ba) Molecules by Direct Laser Cooling: A Theoretical Study Based on Accurate Ab Initio Calculations. Molecules, 30(9), 1950. https://doi.org/10.3390/molecules30091950









