Performance Optimization of SiO2f/SiO2 Composites Derived from Polysiloxane Ceramic Precursors
Abstract
1. Introduction
2. Experimental
2.1. Raw Materials
2.2. Preparation of Materials
2.2.1. Preparation of PESO
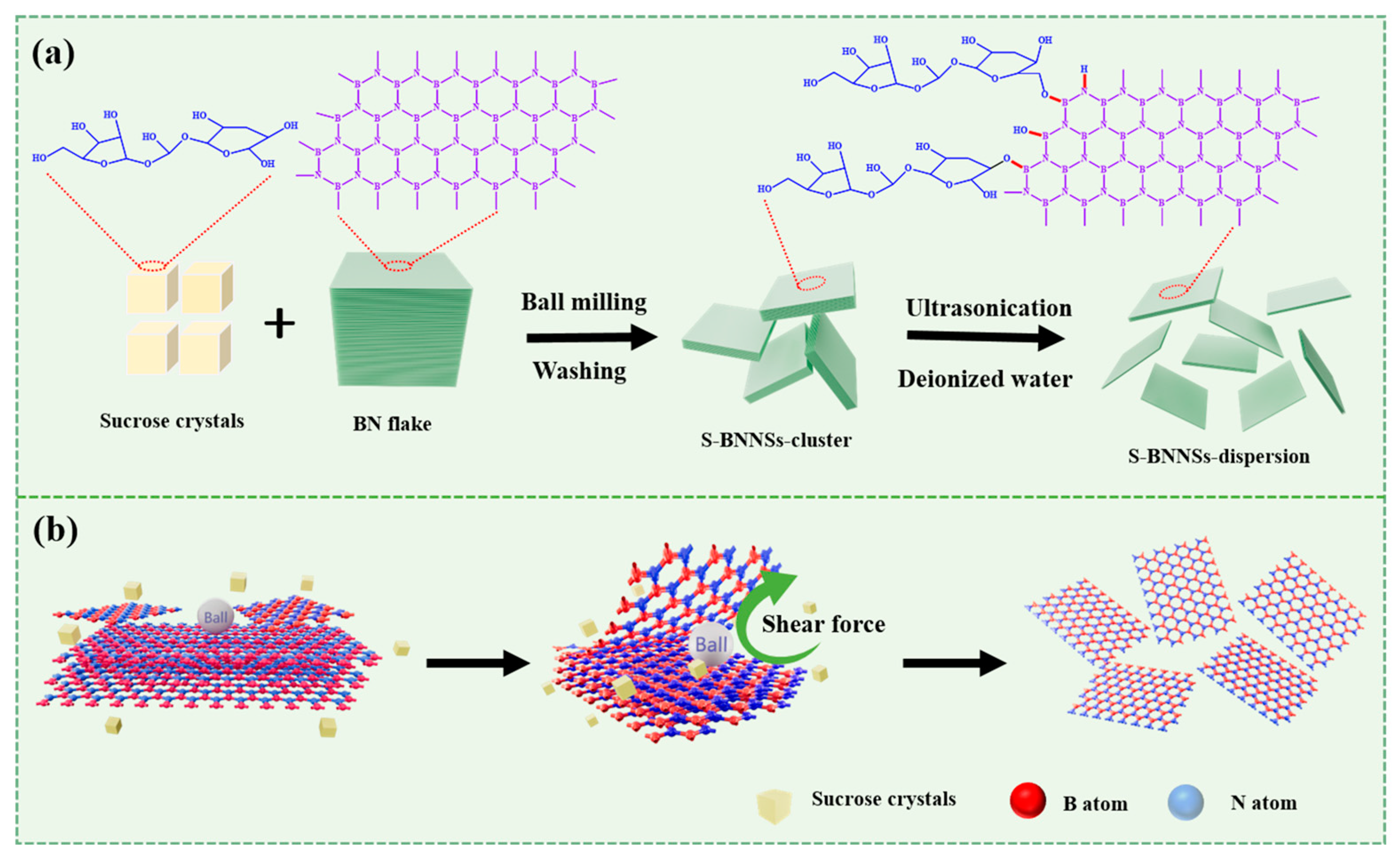
2.2.2. Preparation of BNNSs Using the SAMCE Method
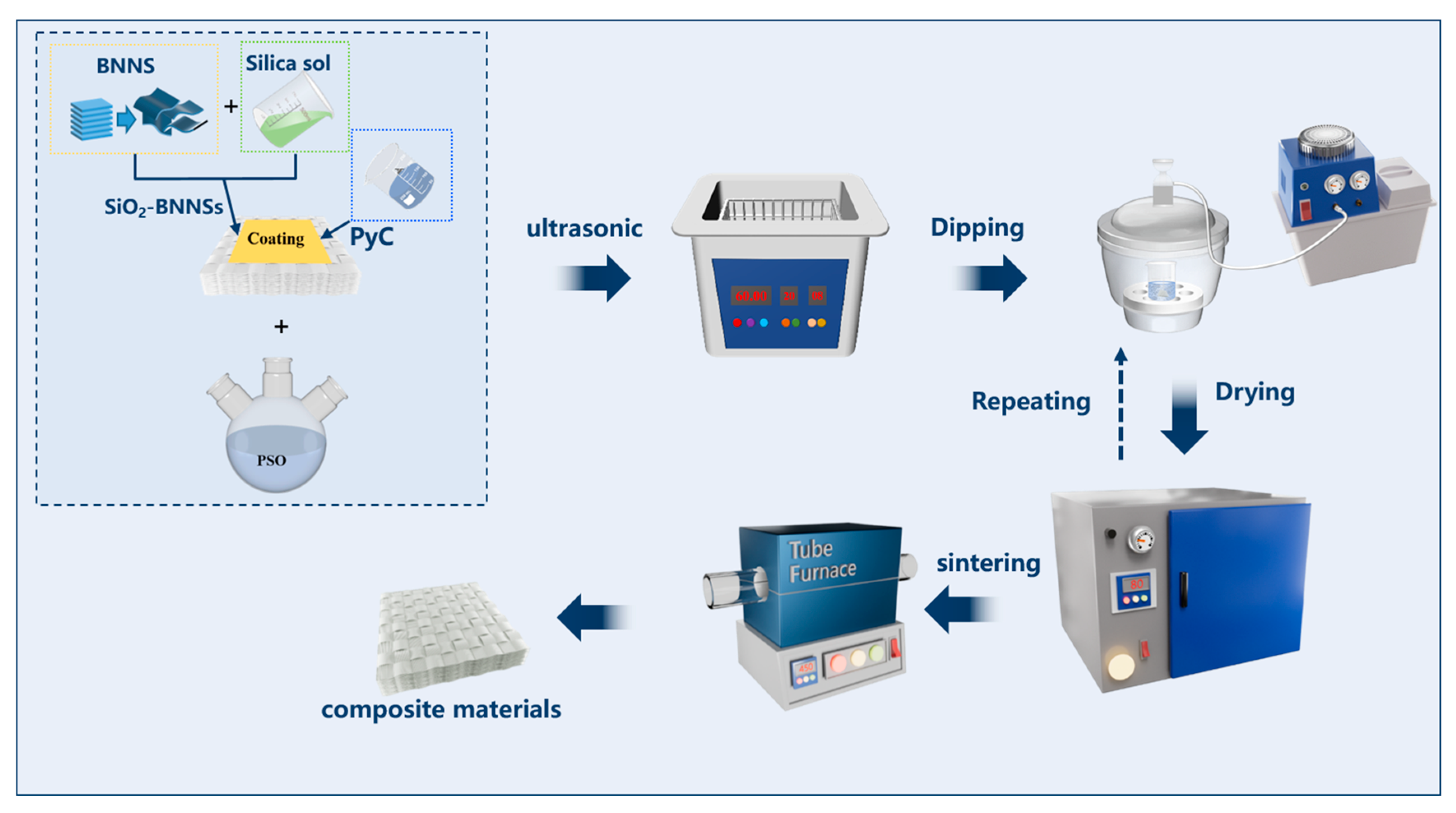
2.2.3. Preparation of PyC-SiO2/BNNSs Double-Interface Coating on the Surface of Quartz Fiber Preform
2.2.4. Preparation of SiO2f/SiO2 Composites
2.2.5. Preparation of Quartz Fiber-Reinforced Composites
2.3. Characterization
3. Results and Discussion
3.1. Characterization of PESO
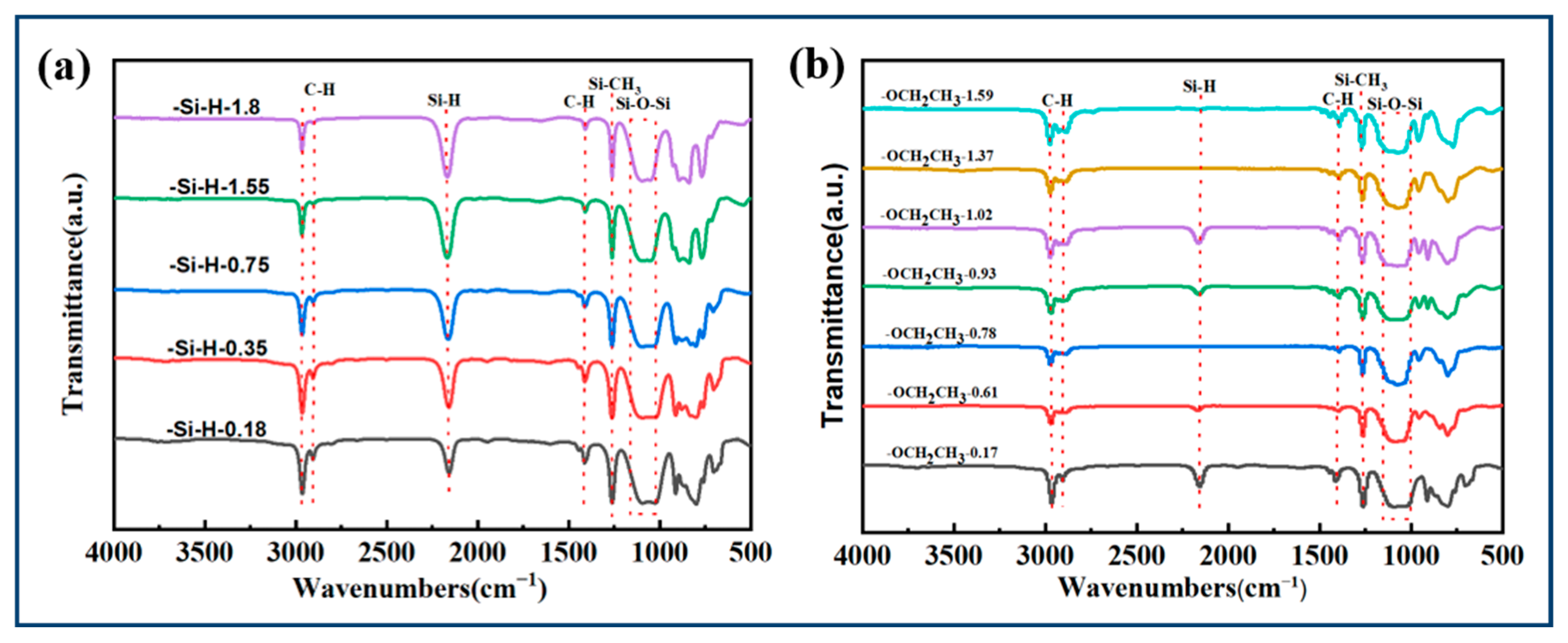
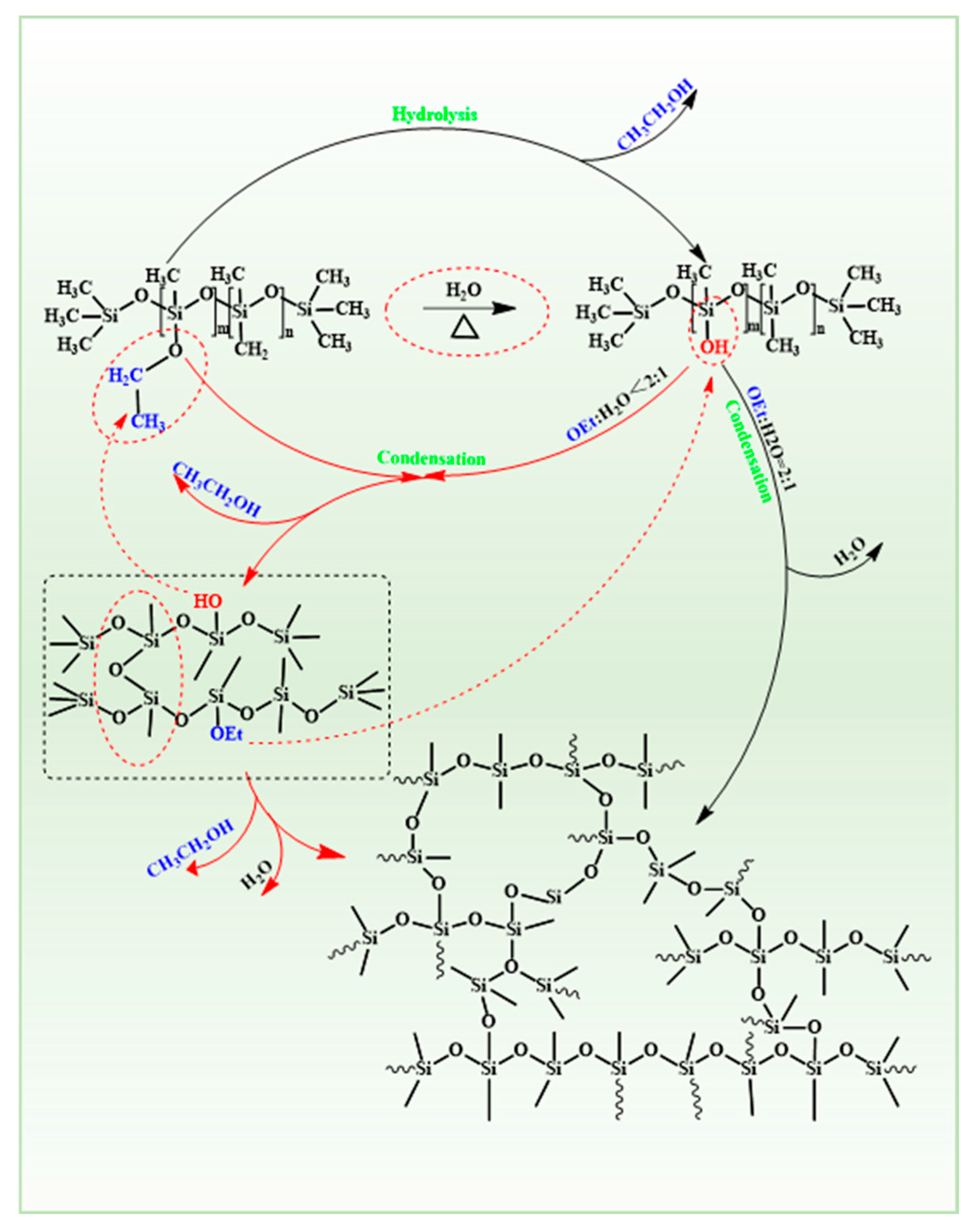
3.1.1. Synthesis of PESO
3.1.2. Curing of PESO
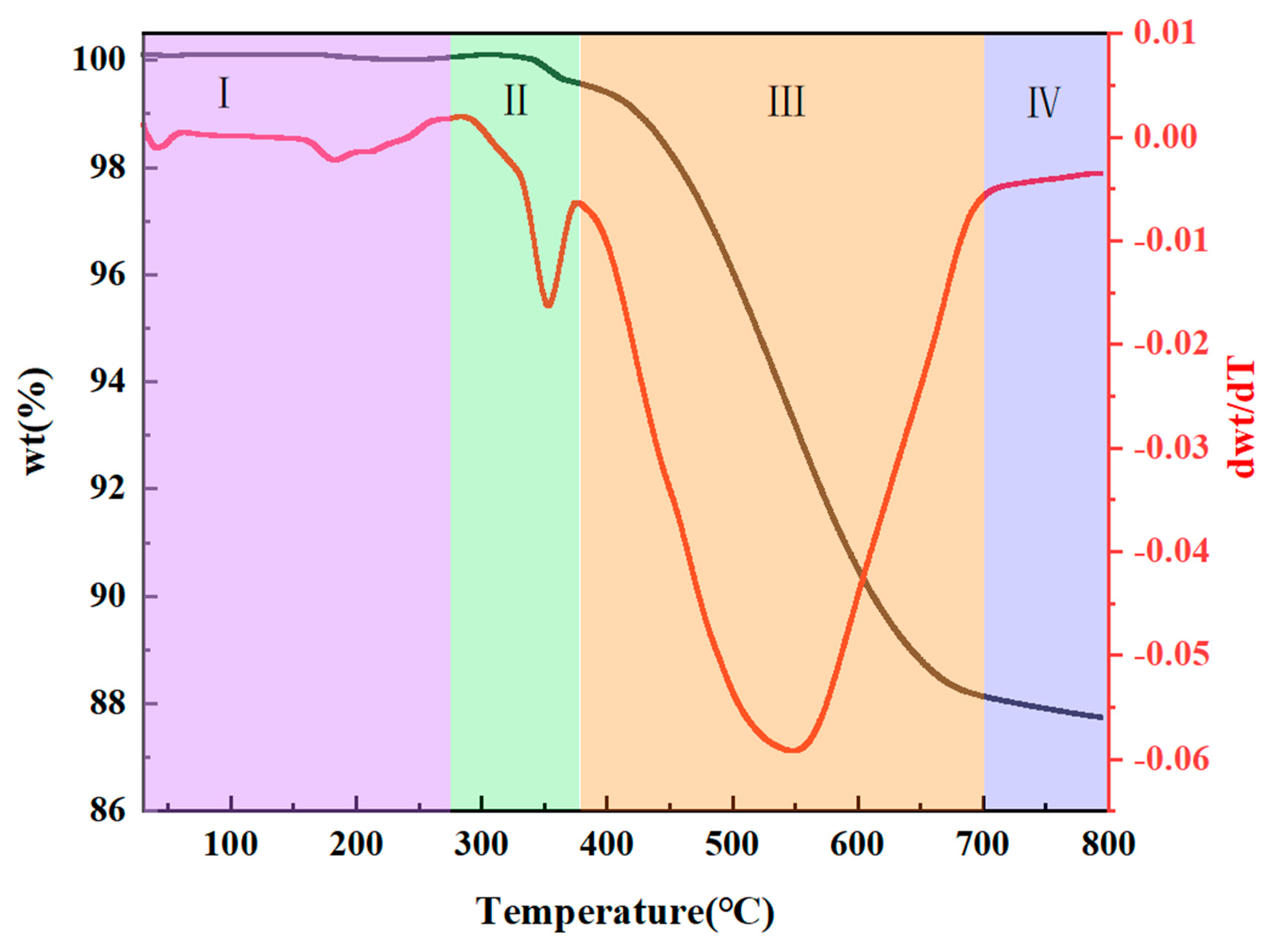
3.1.3. Pyrolysis of PESO
- (1)
- RT~275 °C: A slight weight loss is observed during this stage, which can be attributed to the release of unreacted small molecules from PESO that has not fully cross-linked during the curing process. Additionally, Si–H groups react with O2 in the air.
- (2)
- 275~375 °C: During this stage, PESO experiences a gradual weight loss, likely due to further curing and cross-linking, which involves dehydration and alcohol elimination reactions. This leads to the formation of a three-dimensional network structure, reducing the release of small molecules and enhancing the yield of the resulting ceramic.
- (3)
- 375~700 °C: In this stage, PESO undergoes rapid weight loss, primarily attributed to the complete decomposition of the polymer network and the removal of residual organic groups. This stage marks the thermal decomposition of PESO, where the material transitions from an organic to an inorganic phase. The Si–O–Si bonds break, and exchange reactions occur between Si–O and Si–H or Si–C, resulting in the generation of gases such as methane.
- (4)
- 700~800 °C: In this final stage, PESO experiences minimal weight loss as the inorganic conversion is nearly complete. The thermal decomposition process concludes, and the material fully transitions from organic to inorganic, forming SiO ceramic. Ultimately, the ceramic yield of the SiO precursor reaches 87.15%.
- Initiation:
- Propagation:
- Termination:
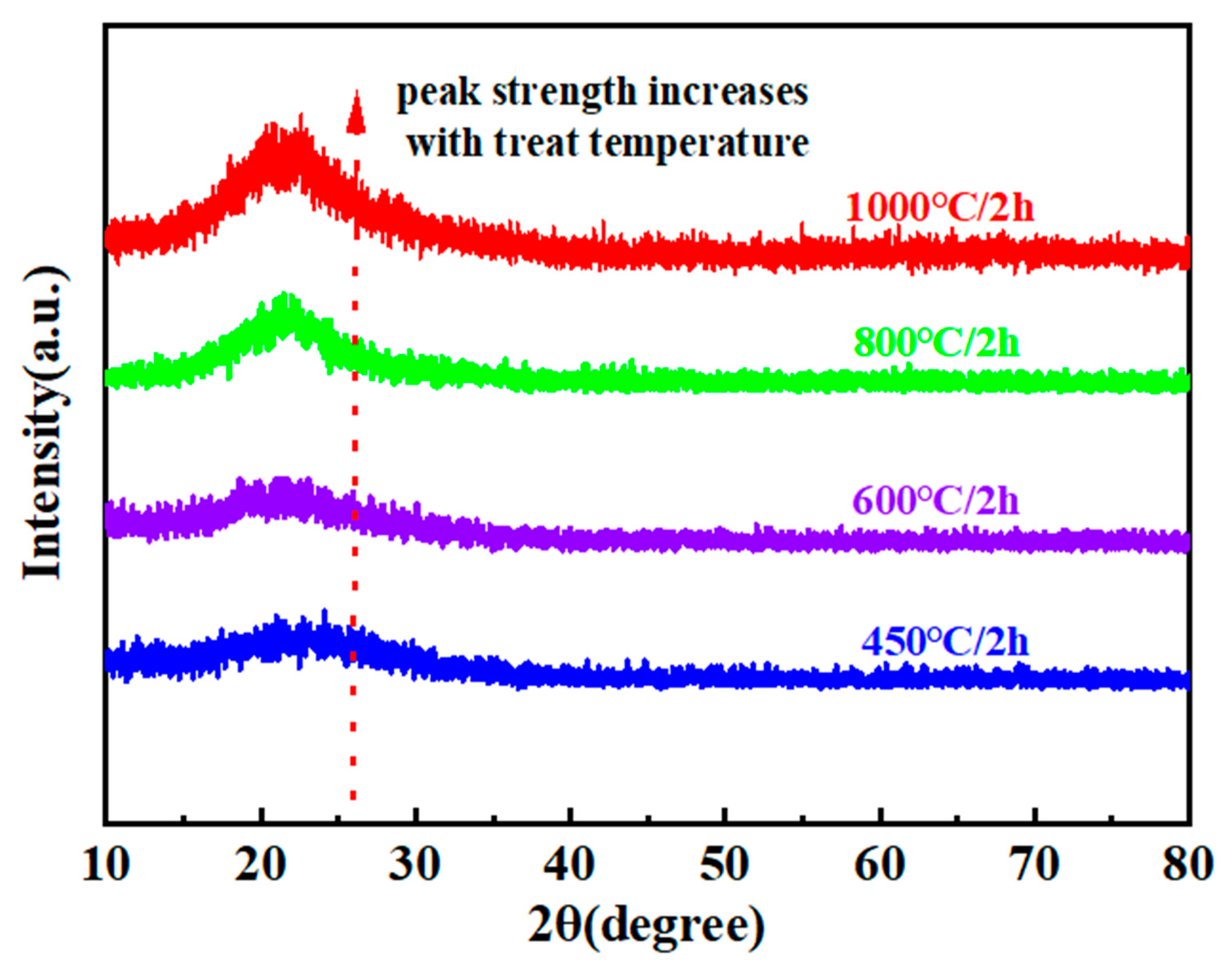
3.2. Interface Characterization
3.3. Composite Material Characterization
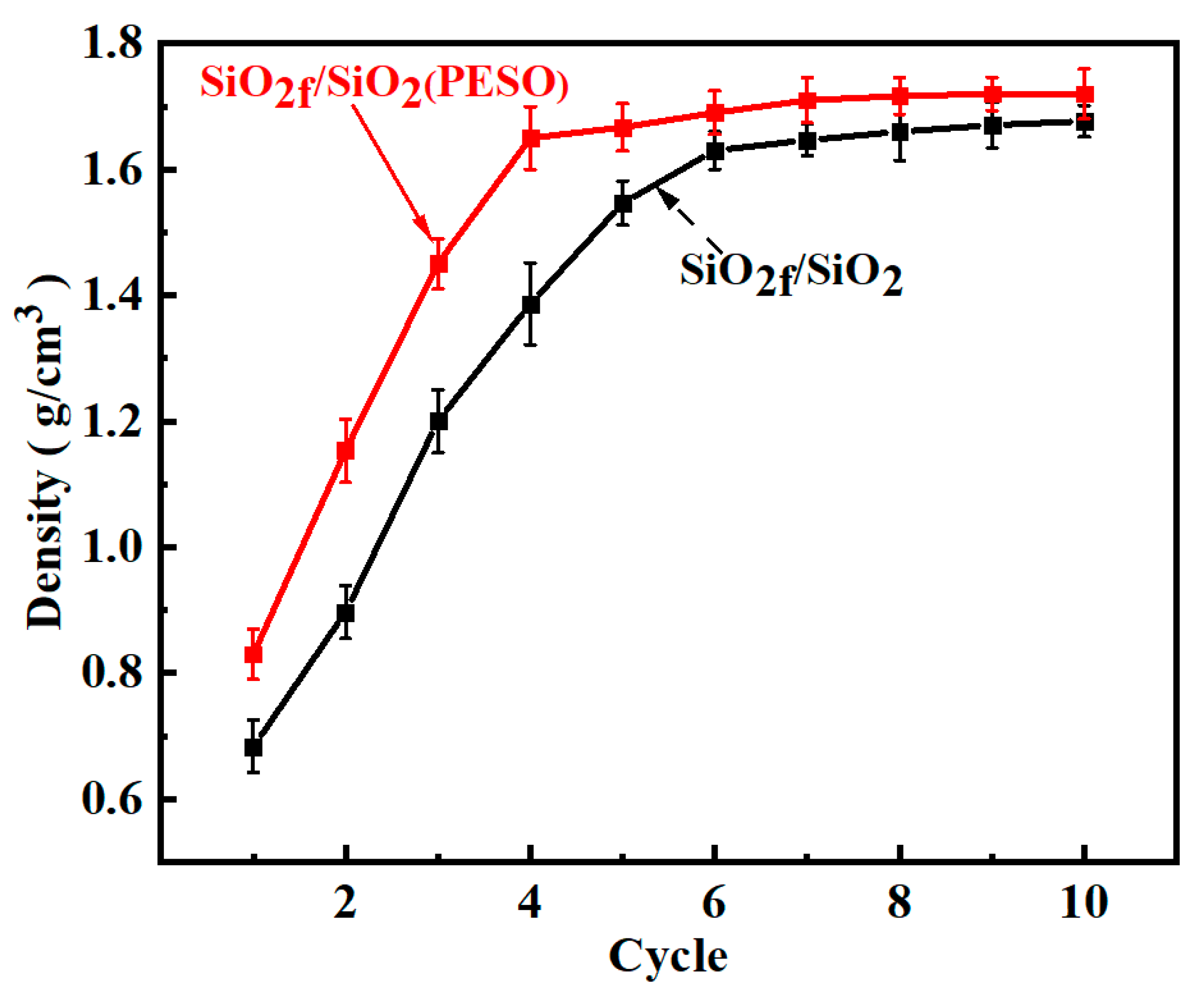
3.3.1. Density and Porosity
3.3.2. Microstructure
3.3.3. Mechanical Properties
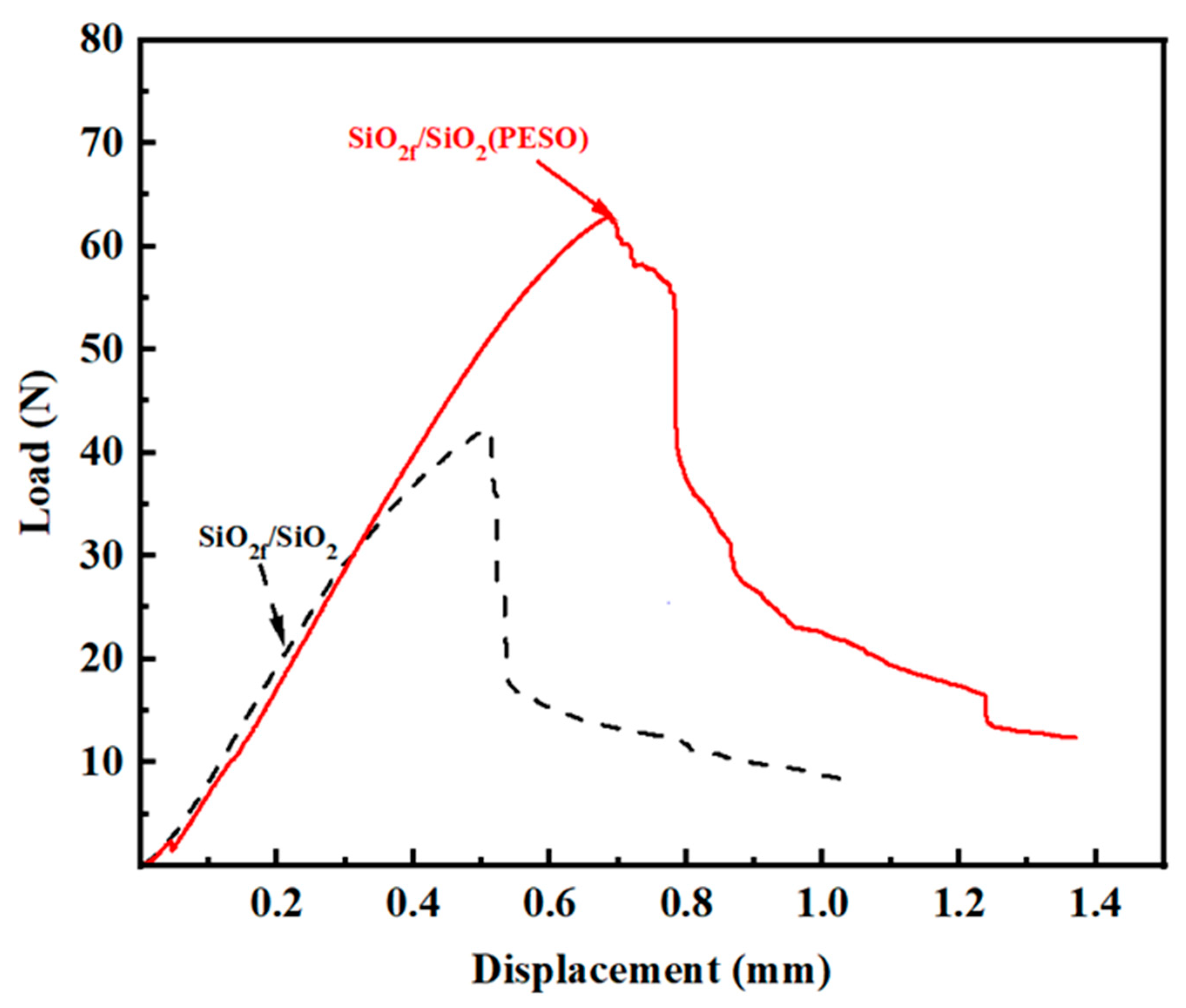
3.3.4. Interface and Strengthening Mechanism of the Quartz Fiber-Reinforced Composite
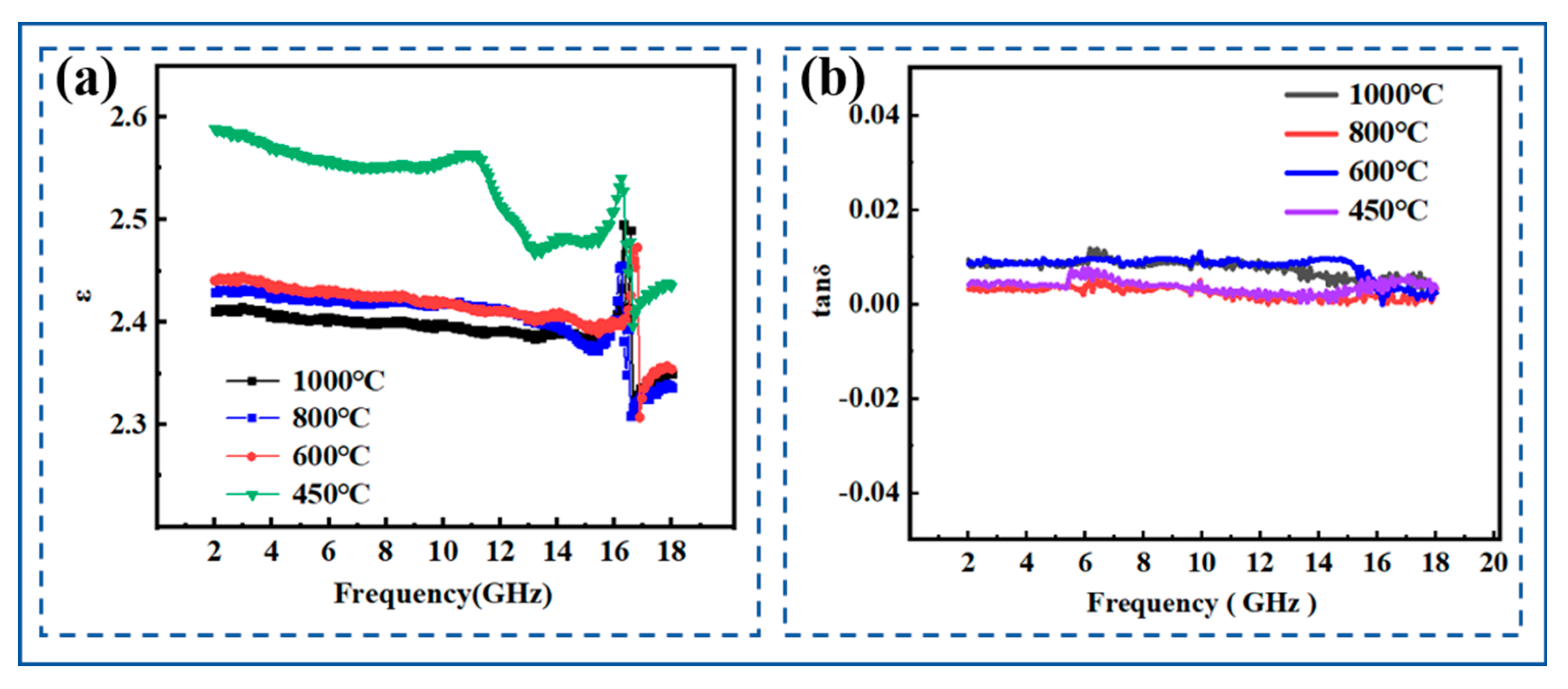
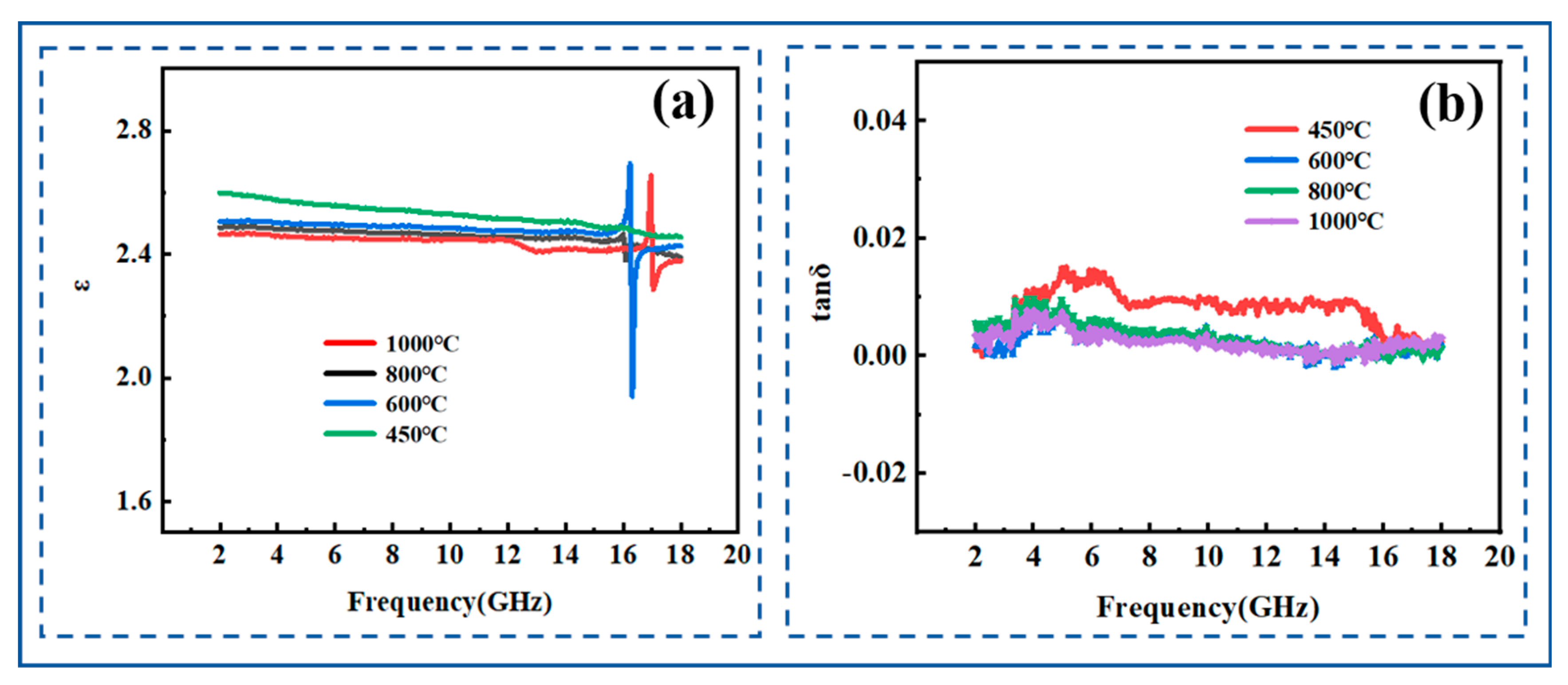
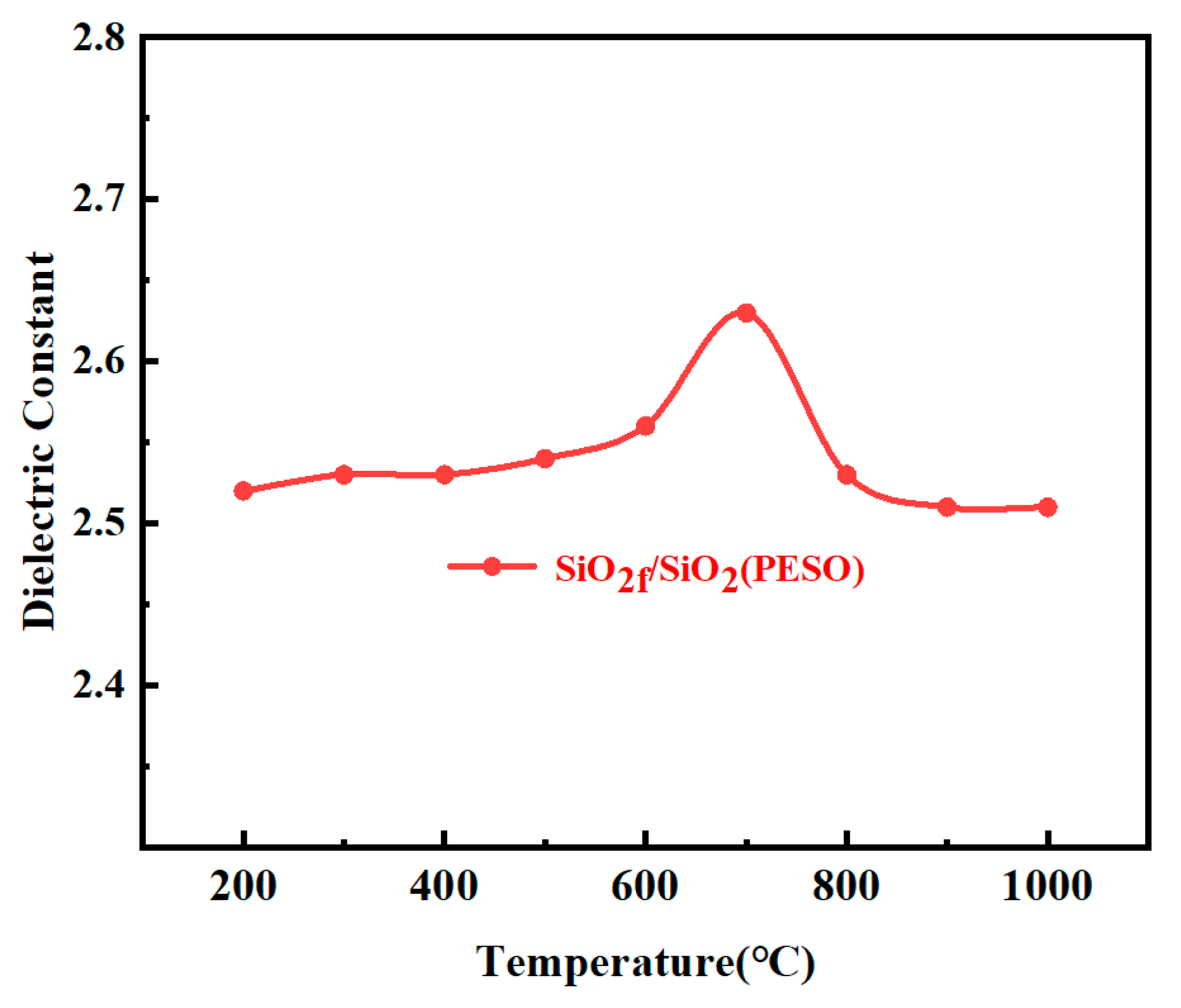
3.3.5. Dielectric Properties
3.3.6. Thermophysical Properties
3.3.7. Moisture Resistance
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xia, X.; Duan, J.; Mao, B.; Wang, D.; Gao, G. Effect of Sintering Temperature on Microstructure and Flexural Strength of 2.5D SiO2f/SiO2 Composites. Silicon 2024, 16, 1847–1856. [Google Scholar] [CrossRef]
- Li, J.; Wang, Y.; Zhao, W.; Xu, P.; Wang, T.; Kong, J. High-performance quartz fiber/polysilazane and epoxy-modified cyanate ester microwave-transparent composites. Adv. Compos. Hybrid. Mater. 2022, 5, 1830–1840. [Google Scholar] [CrossRef]
- Liu, Z.; Zhao, W.; Yu, G.; Wu, L. Fabrication and mechanical behaviors of quartz fiber composite honeycomb with extremely low permittivity. Compos. Struct. 2021, 271, 114129. [Google Scholar] [CrossRef]
- Vukovic, A.; Sewell, P.; Benson, T.M. Impact of In Situ Radome Lightning Diverter Strips on Antenna Performance. IEEE Trans. Antennas Propag. 2020, 68, 7287–7296. [Google Scholar] [CrossRef]
- Zhang, F.; Xu, J.; Xu, G.; Zu, L. The buckling behavior of radome with different braided angles based on CFRP. Compos. Struct. 2017, 176, 597–607. [Google Scholar] [CrossRef]
- Zhou, J.; Ye, F.; Cheng, L.; Zhao, K.; Wei, Y.; Li, M.; Meng, N. Development of high-temperature wave-transparent nitride-based CFCMCs for aircraft radomes. Compos. Part. A Appl. Sci. Manuf. 2023, 167, 107444. [Google Scholar] [CrossRef]
- Li, H.-Y.; Li, C.-M.; Gao, J.-G.; Sun, W.-F. Ameliorated Mechanical and Dielectric Properties of Heat-Resistant Radome Cyanate Composites. Molecules 2020, 25, 3117. [Google Scholar] [CrossRef]
- Han, D.; You, G.; Zhang, Y.; Tian, H.; He, J.; Liang, J.; Wang, H.; Wang, C.-A.; Zhang, R.; Shao, G. Increased microwave absorption property of porous Si3 N4 ceramics by loading polymer-derived SiCN for a multifunctional design. J. Mater. Chem. C 2023, 11, 6130–6137. [Google Scholar] [CrossRef]
- Haider, I.; Gul, I.H.; Faraz, M.I.; Aziz, S.; Jaffery, S.H.I.; Khan, M.A.; Jung, D.-W. Investigation of Dielectric, Mechanical, and Thermal Properties of Epoxy Composites Embedded with Quartz Fibers. Polymers 2023, 15, 4133. [Google Scholar] [CrossRef]
- Zhou, L.; Liu, Z.; Tang, L.; Pei, Y. Design and characterization for a high-temperature dual-band radome wall structure for airborne applications. Mater. Des. 2017, 114, 264–270. [Google Scholar] [CrossRef]
- Saliha Fidan, Ş.; Ünal, R. A survey on ceramic radome failure types and the importance of defect determination. Eng. Fail. Anal. 2023, 149, 107234. [Google Scholar] [CrossRef]
- Wang, C.; Wang, Y.; Chen, Y.; Gao, W.; Xu, Q.; Wang, Z.; Liu, J.; Zhou, C.; Xu, W.; Zhong, J. Coupling Model and Electronic Compensation of Antenna-Radome System for Hypersonic Vehicle With Effect of High-Temperature Ablation. IEEE Trans. Antennas Propag. 2020, 68, 2340–2355. [Google Scholar] [CrossRef]
- Dan, Y.; Yang, J. Electromagnetic Performance Analysis of Inhomogeneous Radome Walls Considering Temperature and Ablation. Aerospace 2023, 10, 927. [Google Scholar] [CrossRef]
- Wang, G.; Fu, G.; Gao, T.; Kuang, H.; Wang, R.; Yang, F.; Jiao, W.; Hao, L.; Liu, W. Preparation and characterization of novel film adhesives based on cyanate ester resin for bonding advanced radome. Int. J. Adhes. Adhes. 2016, 68, 80–86. [Google Scholar] [CrossRef]
- Lee, C.; Kim, I.-S.; Lee, B. Slow crack growth in a cordierite-based glass–ceramic missile radome due to stress corrosion. Eng. Fail. Anal. 2018, 93, 76–86. [Google Scholar] [CrossRef]
- Iqbal, Z.; Umer, M.A.; Khan, H.A.; Asim, K. Multi-functional hybrid sandwich composite structures: Evaluating damage mechanics and tolerance using compression after impacts. J. Reinf. Plast. Compos. 2024, 1, 1–17. [Google Scholar] [CrossRef]
- Kandi, K.K.; Thallapalli, N.; Chilakalapalli, S.P.R. Development of Silicon Nitride-Based Ceramic Radomes—A Review. Int. J. Appl. Ceram. Tech. 2015, 12, 909–920. [Google Scholar] [CrossRef]
- Jang, J.H.; Ahn, S.H. Bird-Strike Damage Analysis and Preliminary Design of Composite Radome Structure Using Smoothed Particle Hydrodynamics. Appl. Compos. Mater. 2019, 26, 763–782. [Google Scholar] [CrossRef]
- Wang, W.; Gao, X.; Li, Z.; Shen, C.; Wang, G.; He, R. Fiber-laying-assisted material extrusion additive manufacturing of continuous carbon fiber reinforced SiC ceramic matrix composites. Mater. Sci. Eng. A 2024, 890, 145944. [Google Scholar] [CrossRef]
- Xu, Q.; Xiao, S.; Wang, Y.-Q.; Gao, H. A review on the grinding of SiC-based ceramic matrix composites reinforced by continuous fibre: Damage mechanisms and evaluations. J. Manuf. Process. 2024, 132, 261–295. [Google Scholar] [CrossRef]
- Xiangping, L.; Xi, C.; Hong, Z.; Guangcheng, L. Effect of the distribution of lip-shaped matrix cracks in continuous fibre reinforced ceramic matrix composites on failure progress under transverse tension. Adv. Appl. Ceram. 2021, 120, 32–46. [Google Scholar] [CrossRef]
- Baxevanis, T.; Plexousakis, M. On the effect of fiber creep-compliance in the high-temperature deformation of continuous fiber-reinforced ceramic matrix composites. Int. J. Solids Struct. 2010, 47, 2487–2497. [Google Scholar] [CrossRef]
- Tong, Y.; Bai, S.; Chen, K. A low cost fabrication route for continuous carbon fiber reinforced TiC based ceramic matrix composite. Mater. Sci. Eng. A 2012, 556, 980–983. [Google Scholar] [CrossRef]
- Chen, M.; Qiu, H.; Xie, W.; Zhang, B.; Liu, S.; Luo, W.; Ma, X. Research Progress of Continuous Fiber Reinforced Ceramic Matrix Composite in Hot Section Components of Aero engine. IOP Conf. Ser. Mater. Sci. Eng. 2019, 678, 012043. [Google Scholar] [CrossRef]
- Powell, K.L.; Smith, P.A.; Yeomans, J.A. Aspects of residual thermal stresses in continuous-fibre-reinforced ceramic matrix composites. Compos. Sci. Technol. 1993, 47, 359–367. [Google Scholar] [CrossRef]
- Jessen, T.L.; Greenhut, V.A.; Ii Lewis, D.; Friel, J.J. Effect of Microstructure on the Mechanical Behavior of Continuous-Fiber-Reinforced Ceramic-Matrix Composites. J. Am. Ceram. Soc. 1999, 82, 2753–2761. [Google Scholar] [CrossRef]
- Hu, J.; Hu, Y.; Deng, S.F.; Zhou, J.L.; Jiang, N.; Zhu, Y.; Sun, M. Synthesis and properties of a novel silicon-containing phthalonitrile resin and its quartz-fiber-reinforced composites. High Perform. Polym. 2020, 32, 1112–1121. [Google Scholar] [CrossRef]
- Tao, X.; Wan, Y.; Zhang, R.; Zhang, Y.; Wang, Y.; Yu, X.; Wang, M. Facile Synthesis and Properties of Highly Porous Quartz Fiber-Reinforced Phenolic Resin Composites with High Strength. Materials 2024, 17, 2486. [Google Scholar] [CrossRef]
- Yan, X.; Jin, X.; Pan, Y.; Wang, H.; Fan, Z.; Hong, C.; Zhang, X. Assessment of continuous laser ablation model for lightweight quartz fiber reinforced phenolic composite. Polym. Compos. 2024, 45, 6549–6563. [Google Scholar] [CrossRef]
- Meireman, T.; Daelemans, L.; Van Verre, E.; Van Paepegem, W.; De Clerck, K. Nanofibre toughening of dissimilar interfaces in composites. Mater. Des. 2020, 195, 109050. [Google Scholar] [CrossRef]
- Zhang, Q.; Hu, Y.; Kong, D.; Chen, H.; Duan, J.; Sun, X. Preparation of fused silica glass micropatterns via gel method using quartz fiber as reinforcer. Ceram. Int. 2024, 50, 33666–33676. [Google Scholar] [CrossRef]
- Zou, Y.; Jiang, J.; Yang, J.; Zhang, Z.; Guo, J. Enhancing the toughness of bonding interface in steel-UHPC composite structure through fiber bridging. Cem. Concr. Compos. 2023, 137, 104947. [Google Scholar] [CrossRef]
- Zou, Y.; Zhou, X.; Jiang, J.; Yang, J.; Zhang, Z.; Liu, L. Tensile performance of toughness enhanced interfaces for steel-UHPC composite bridge decks. Constr. Build. Mater. 2024, 449, 138355. [Google Scholar] [CrossRef]
- Deriabin, K.V.; Islamova, R.M. Ferrocenyl-Containing Oligosiloxanes and Polysiloxanes: Synthesis, Properties, and Application. Polym. Sci. Ser. C 2022, 64, 95–109. [Google Scholar] [CrossRef]
- Du, Y.; Bai, T.; Ding, F.; Yan, H.; Zhao, Y.; Feng, W. The inherent blue luminescence from oligomeric siloxanes. Polym. J. 2019, 51, 869–882. [Google Scholar] [CrossRef]
- Mehta, G.K.; Nguyen, T.T.; Flores, M.; Trovitch, R.J. Manganese catalysed dehydrocoupling of silanes and siloxanes with ammonia to prepare oligosilazanes and polysiloxazanes. Dalton Trans. 2024, 53, 14272–14277. [Google Scholar] [CrossRef]
- Mizerska, U.; Rubinsztajn, S.; Chojnowski, J.; Cypryk, M.; Uznanski, P.; Walkiewicz-Pietrzykowska, A.; Fortuniak, W. Self-Restructuring of Polyhydromethylsiloxanes by the Hydride Transfer Process: A New Approach to the Cross-Linking of Polysiloxanes and to the Fabrication of Thin Polysiloxane Coatings. Materials 2022, 15, 6981. [Google Scholar] [CrossRef]
- Yu, J.; Liu, Y. Cyclic Polysiloxanes with Linked Cyclotetrasiloxane Subunits. Angew. Chem. Int. Ed. 2017, 56, 8706–8710. [Google Scholar] [CrossRef]
- Sodkhomkhum, R.; Ervithayasuporn, V. Synthesis of poly(siloxane/double-decker silsesquioxane) via dehydrocarbonative condensation reaction and its functionalization. Polymer 2016, 86, 113–119. [Google Scholar] [CrossRef]
- Wang, S.; Peng, Z.; Huang, Y.; Zhu, M.; Liu, Y.; Zhang, Y. Synthesis, characterization and properties of vinyl-terminated poly[dimethylsiloxane-co-methyl(phenyl)siloxane]. Polymer 2024, 311, 127554. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, J.; Xu, T.; Sima, H.; Hou, J. Effects of Polyhedral Oligomeric Silsesquioxane (POSS) on Thermal and Mechanical Properties of Polysiloxane Foam. Materials 2020, 13, 4570. [Google Scholar] [CrossRef] [PubMed]
- Ren, Z.; Yan, S. Polysiloxanes for optoelectronic applications. Prog. Mater. Sci. 2016, 83, 383–416. [Google Scholar] [CrossRef]
- Chen, M.; Zhang, G.; Liang, X.; Zhang, W.; Zhou, L.; He, B.; Song, P.; Yuan, X.; Zhang, C.; Zhang, L.; et al. Thermally stable transparent sol–gel based active siloxane–oligomer materials with tunable high refractive index and dual reactive groups. RSC Adv. 2016, 6, 70825–70831. [Google Scholar] [CrossRef]
- Mizerska, U.; Halasa, R.; Turecka, K.; Chojnowski, J.; Pospiech, P.; Fortuniak, W.; Slomkowski, S.; Makowski, T.; Machnowski, W.; Sowinski, P. Bacterial cell killing properties of silver-loaded polysiloxane microspheres. J. Mater. Sci. 2018, 53, 7125–7137. [Google Scholar] [CrossRef]
- Xu, J.; Teng, H.; Hou, Z.; Gu, C.; Zhu, L. Comb-like polysiloxanes with oligo(oxyethylene) and sulfonate groups in side chains for solvent-free dimethoxysilyl-terminated polypropylene oxide waterborne emulsions. Colloid. Polym. Sci. 2018, 296, 157–163. [Google Scholar] [CrossRef]
- Stochmal, E.; Strzezik, J.; Krowiak, A. Physicochemical and catalytic properties of polysiloxane network–Pt systems. RSC Adv. 2017, 7, 26342–26360. [Google Scholar] [CrossRef]
- Xing, B.; Ding, D.; Xiao, G.; Yang, N.; Lei, C.; Luo, J.; Mu, Y.; Chong, X.; Jing, C.; Luo, X.; et al. Preparation of SiCf/Si–O–C composites by impregnation pyrolysis of polysiloxane and its electromagnetic wave absorption properties. Int. J. Appl. Ceram. Tech. 2023, 20, 1681–1691. [Google Scholar] [CrossRef]
- Suttor, D.; Erny, T.; Greil, P.; Goedecke, H.; Haug, T. Fiber-Reinforced Ceramic-Matrix Composites with a Polysiloxane/Boron-Derived Matrix. J. Am. Ceram. Soc. 1997, 80, 1831–1840. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, S.; Xu, Q.; Wang, K.; Yu, Y.; Zhao, Q.; Jiang, M.; Liu, P. Molecular dynamics simulation: The roles of silane coupling agent structural configurations on quartz fiber-epoxy interface. Comput. Mater. Sci. 2024, 235, 112833. [Google Scholar] [CrossRef]
- Zhang, J.; Zhou, Z.; Zhang, C.; Fu, Z.; Zhou, S.; Shao, J.; Xia, L.; Liu, X.; Xu, W. Carbon nanotubes-intervened interface design of quartz fiber/polyurethane composite fibers towards improved mechanical properties. Compos. Sci. Technol. 2025, 262, 111065. [Google Scholar] [CrossRef]
- Wang, S.; Zheng, Y. Effect of different thickness h-BN coatings on interface shear strength of quartz fiber reinforced SiOCN composite. Appl. Surf. Sci. 2014, 292, 876–879. [Google Scholar] [CrossRef]
- Du, Z.; Zeng, X.; Zhu, M.; Kanta, A.; Liu, Q.; Li, J.; Kong, L.B. Alkyl ethoxylate assisted liquid phase exfoliation of BN nanosheet and its application as interphase for oxide/oxide composites. Ceram. Int. 2018, 44, 21461–21469. [Google Scholar] [CrossRef]
- Yi, S.; Li, J.; Zuo, Z.; Fu, J.; Chen, H.; Yang, L.; Xu, Y.; Qian, L.; Chen, L.; Ding, S. Mechanochemical exfoliation of sugar-assisted boron nitride nanosheets for achieving superlubricity and wear distinction. Wear 2024, 554–555, 205482. [Google Scholar] [CrossRef]
- GB/T 23806-2009; Fine Ceramics (Advanced Ceramics, Advanced Technical Ceramics)—Test Method for Fracture Toughness of Monolithic Ceramics at Room Temperature by Single Edge Precracked Beam (SEPB) Method. ISO: Beijing, China, 2009; p. 32.
- Schellenberger, A.; Belli, R.; Karsten, J.; Lohbauer, U. On the robustness of the Single-Edge-Precracked-Beam (SEPB) method for fracture toughness testing of ceramic materials. Eng. Fract. Mech. 2023, 291, 109527–109547. [Google Scholar] [CrossRef]
- Ciancio, V. On the Generalized Debye Equation for Media with Dielectric Relaxation Phenomena Described by Vectorial Internal Thermodynamic Variables. J. Non-Equilib. Thermodyn. 1989, 14, 239–250. [Google Scholar] [CrossRef]
- Yu, Y.; Zhao, Y.; Huang, B.; Ji, Y.; Zhao, Y.; Zhang, Z.; Fei, H.-F. Effect of phenyl side groups on the dielectric properties and dielectric behavior of polysiloxane. Polymer 2022, 249, 124865. [Google Scholar] [CrossRef]
- Yang, T.; Hu, Y.; Deng, S.; Du, L.; Zhou, J.; Hu, J.; Jian, X. Synthesis and thermal stability of a novel acetylene end-capped silicon-containing polyimide coupling agent with a silane pendant group. High Perform. Polym. 2019, 31, 1259–1271. [Google Scholar] [CrossRef]
- Kumar, A.; Malik, G.; Sharma, S.; Chandra, R.; Mulik, R.S. Precursors controlled morphologies of nanocrystalline h-BN and its growth mechanism. Ceram. Int. 2021, 47, 30985–30992. [Google Scholar] [CrossRef]






| Si (wt%) | C (wt%) | H (wt%) | O (wt%) | |
|---|---|---|---|---|
| Before cracking | 37.1 | 25.9 | 6.4 | 30.6 |
| 450 °C | 37.23 | 0.28 | 1.7 | 60.79 |
| 600 °C | 37.17 | 0.471 | 1.436 | 60.923 |
| 800 °C | 37.35 | 0.107 | 0.822 | 61.721 |
| 1000 °C | 37.42 | 0.035 | 0.536 | 62.009 |
| Coating Type | Temperature (°C) | Tensile Strength (GPa) | Tensile Strength Retention (%) |
|---|---|---|---|
| Original quartz fibers | RT | 2.77 ± 0.03 | |
| 450 | 1.74 ± 0.02 | 63.12 | |
| 600 | 1.31 ± 0.02 | 47.33 | |
| 700 | 1.07 ± 0.03 | 38.75 | |
| 800 | 0.55 ± 0.02 | 20.15 | |
| 900 | 0.09 ± 0.03 | 3.31 | |
| SiO2-BN | RT | 3.35 ± 0.02 | |
| 450 | 2.23 ± 0.02 | 66.56 | |
| 600 | 1.75 ± 0.03 | 52.23 | |
| 700 | 1.35 ± 0.02 | 40.29 | |
| 800 | 0.75 ± 0.03 | 22.38 | |
| 900 | 0.13 ± 0.03 | 3.83 | |
| PI-SiO2-BN | RT | 3.73 ± 0.03 | |
| 450 | 2.81 ± 0.02 | 75.39 | |
| 600 | 2.16 ± 0.02 | 57.95 | |
| 700 | 1.79 ± 0.03 | 48 | |
| 800 | 1.17 ± 0.02 | 31.51 | |
| 900 | 0.14 ± 0.03 | 3.81 |
| Sample | Fabrication Temperature (°C) | Density (g/cm3) | Open Porosity (%) |
|---|---|---|---|
| SiO2f/SiO2 | 400 | 1.61 ± 0.03 | 18.5 ± 0.2 |
| 600 | 1.63 ± 0.02 | 17.1 ± 0.3 | |
| 800 | 1.61 ± 0.02 | 17.5 ± 0.2 | |
| 1000 | 1.59 ± 0.02 | 17.9 ± 0.3 | |
| SiO2f/SiO2 (PESO) | 400 | 1.68 ± 0.03 | 17.2 ± 0.2 |
| 600 | 1.69 ± 0.02 | 15.1 ± 0.3 | |
| 800 | 1.70 ± 0.02 | 16.8 ± 0.2 | |
| 1000 | 1.70 ± 0.02 | 17.7 ± 0.3 |
| Sample | Sintering Temperature (°C) | Bending Strength (MPa) | Fracture Toughness (MPa·m1/2) |
|---|---|---|---|
| SiO2f/SiO2 | 450 | 51 | 2.42 |
| 600 | 41.1 | 2.36 | |
| 800 | 11 | / | |
| 1000 | 3.1 | / | |
| SiO2f/SiO2 (PESO) | 450 | 65.7 | 2.54 |
| 600 | 63.3 | 2.52 | |
| 800 | 25.1 | / | |
| 1000 | 3.7 | / |
| Sample | Treatment Temperature (°C) | Thermal Conductivity (W·m−1·K−1) |
|---|---|---|
| SiO2f/SiO2 (PESO) | 200 | 0.446 |
| 400 | 0.317 | |
| 600 | 0.350 |
| Sample | Density Before Coating | Density After Coating | Water Absorption | Dielectric Constant |
|---|---|---|---|---|
| Contrast | 1.65 | / | 10.52 | 2.38 |
| SiO2f/SiO2 (PESO) | 1.67 | 1.71 | 0.4 | 2.5 |
| Sample | Treatment Temperature (°C) | Water Absorption (%) |
|---|---|---|
| 200 | 0.4 | |
| 400 | 0.61 | |
| SiO2f/SiO2 (PESO) | 600 | 1.21 |
| 800 | 8.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Xiao, B.; Hou, Y.; Wen, G. Performance Optimization of SiO2f/SiO2 Composites Derived from Polysiloxane Ceramic Precursors. Molecules 2025, 30, 1385. https://doi.org/10.3390/molecules30061385
Zhang X, Xiao B, Hou Y, Wen G. Performance Optimization of SiO2f/SiO2 Composites Derived from Polysiloxane Ceramic Precursors. Molecules. 2025; 30(6):1385. https://doi.org/10.3390/molecules30061385
Chicago/Turabian StyleZhang, Xia, Bo Xiao, Yongzhao Hou, and Guangwu Wen. 2025. "Performance Optimization of SiO2f/SiO2 Composites Derived from Polysiloxane Ceramic Precursors" Molecules 30, no. 6: 1385. https://doi.org/10.3390/molecules30061385
APA StyleZhang, X., Xiao, B., Hou, Y., & Wen, G. (2025). Performance Optimization of SiO2f/SiO2 Composites Derived from Polysiloxane Ceramic Precursors. Molecules, 30(6), 1385. https://doi.org/10.3390/molecules30061385






