The High-Pressure Response of 9,9′-Spirobifluorene Studied by Raman Spectroscopy
Abstract
1. Introduction
2. Results and Discussion
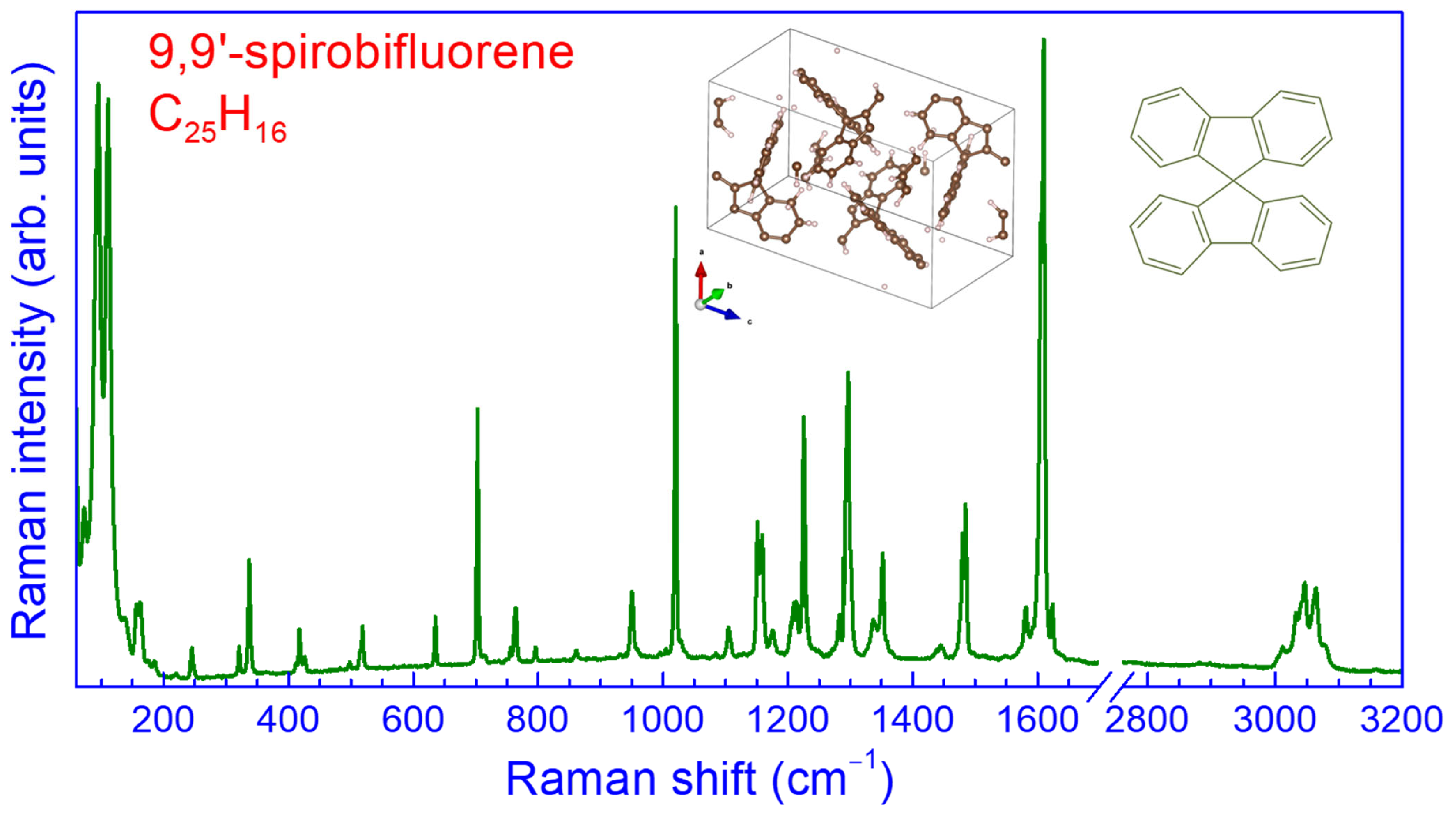
2.1. Raman Spectrum of SBF at Ambient Pressure
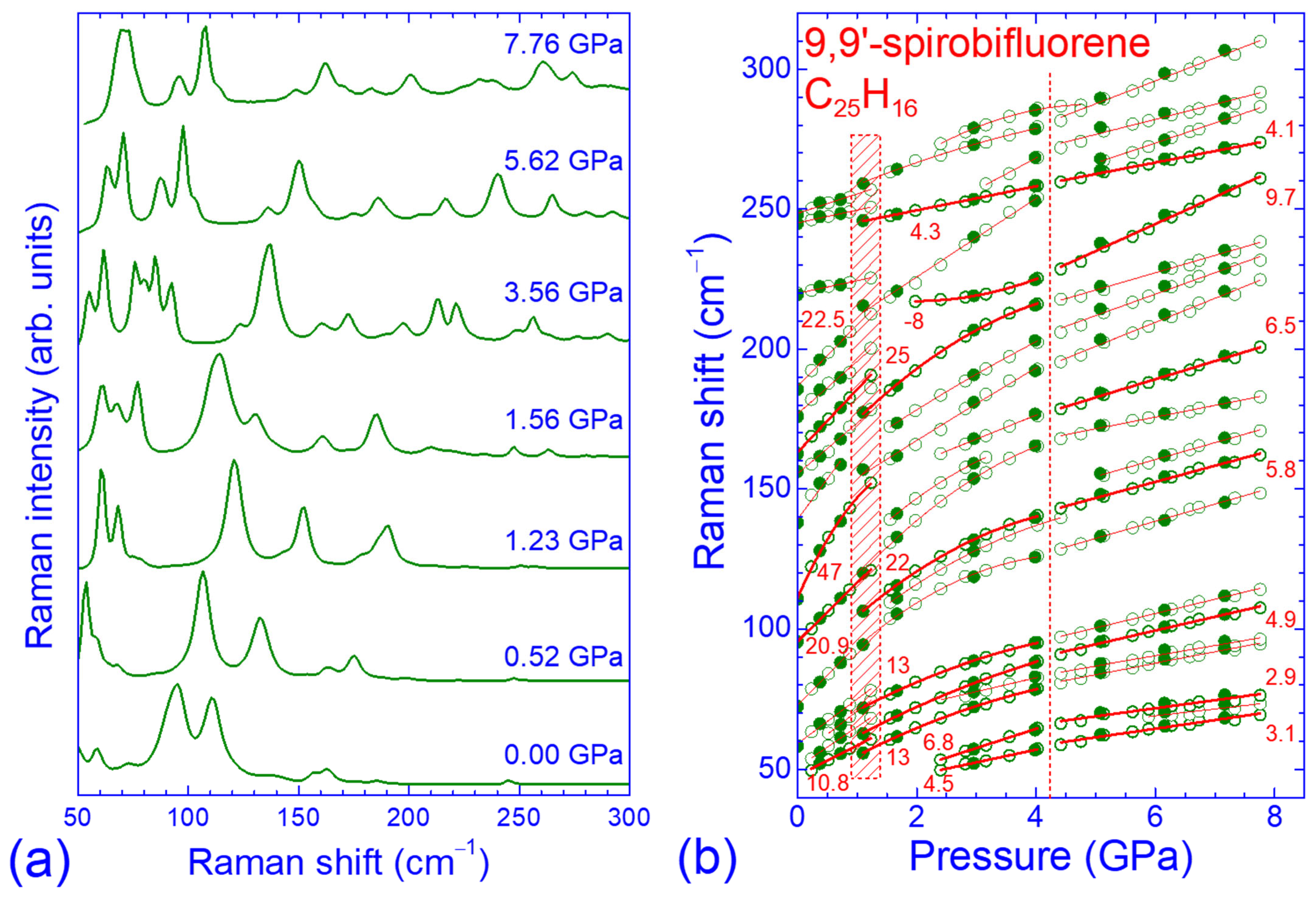
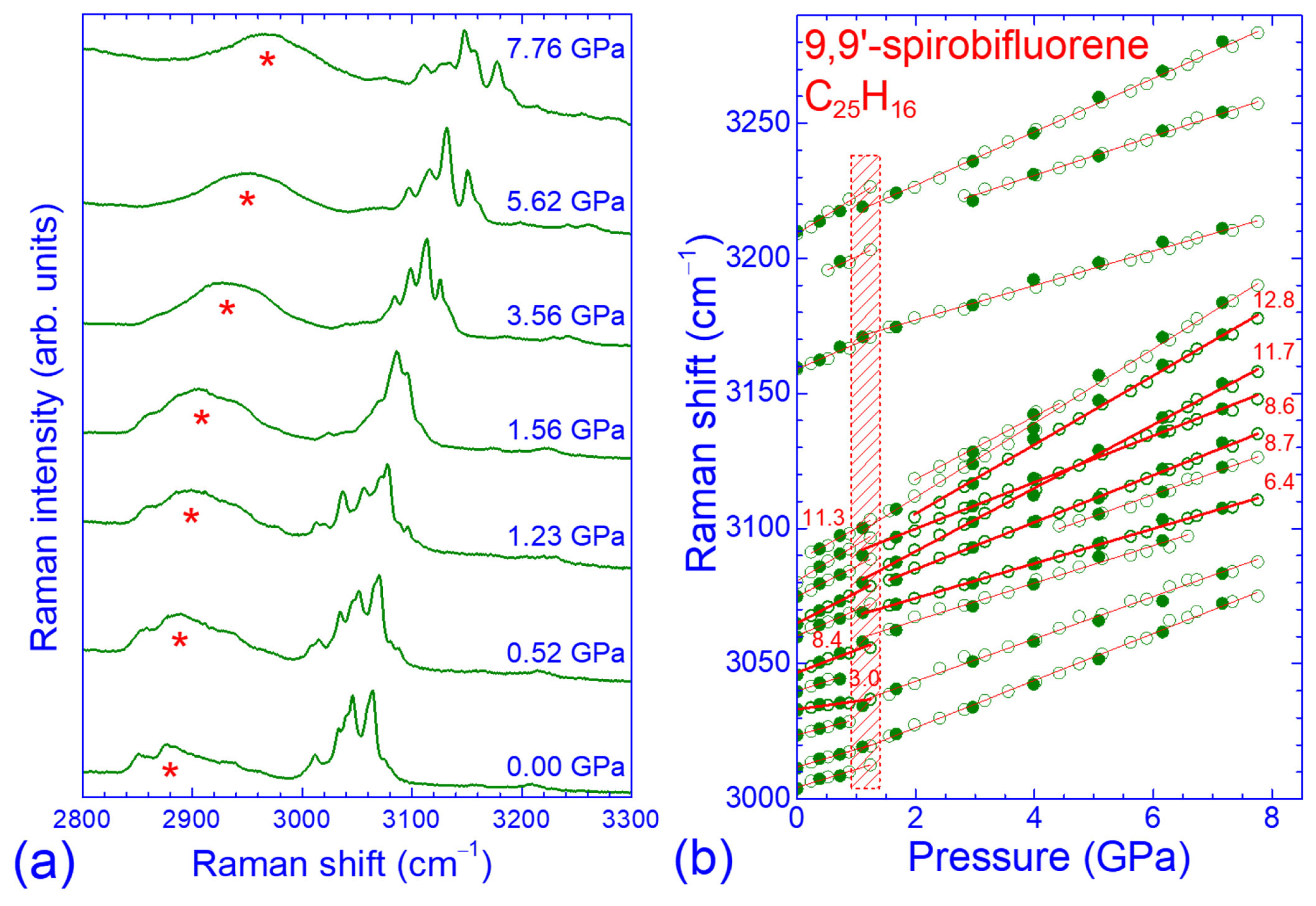
2.2. Pressure Dependence of the Raman Spectrum in the Low- and High-Frequency Regions
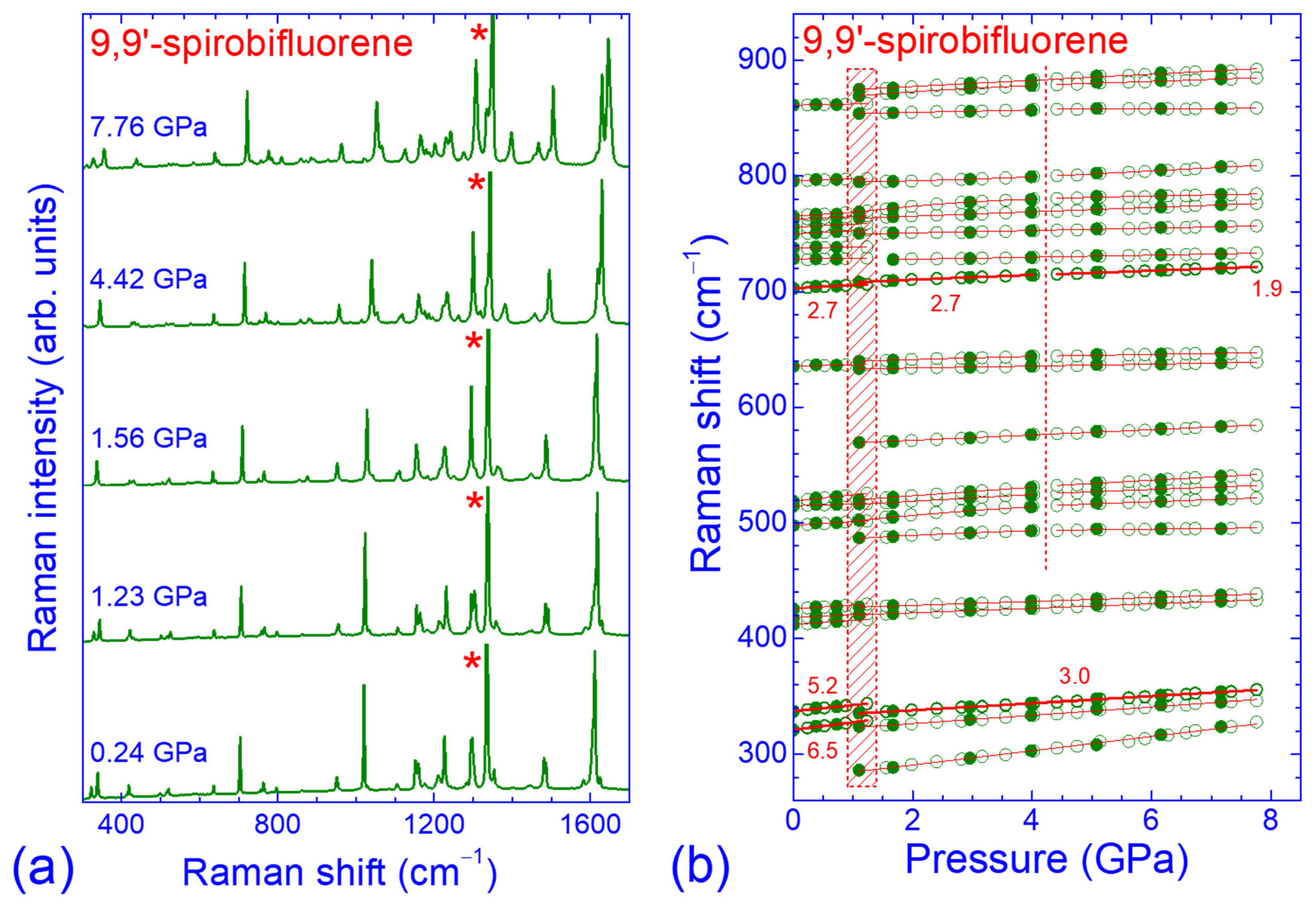
2.3. Pressure Dependence of the Raman Spectrum in the Intermediate-Frequency Region
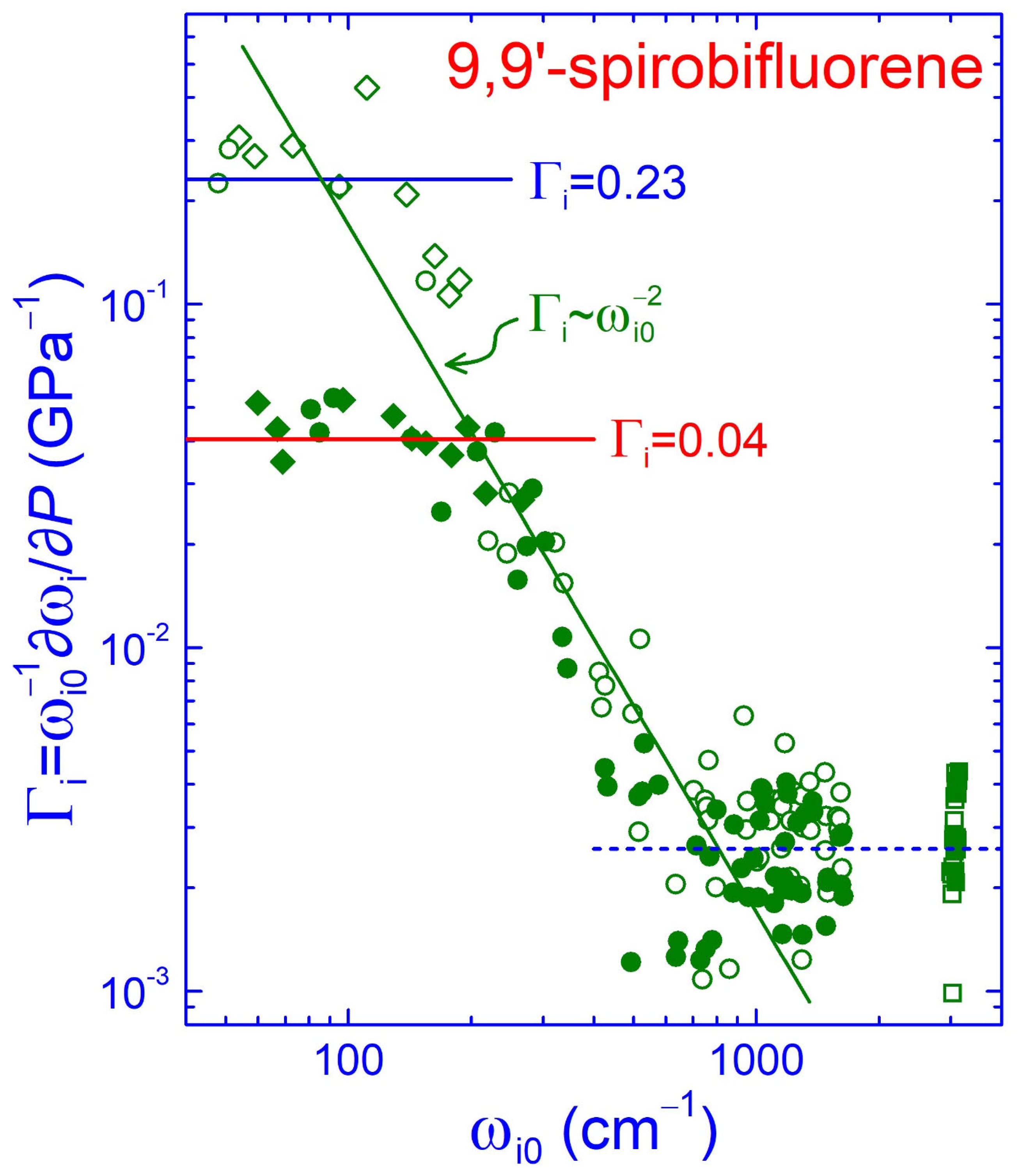
2.4. Force Hierarchy and Elastic Properties of SBF
3. Materials and Methods
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Peak | Sym.* | Approx. Mode Description * | ωcalc * | ωexp ** | P < 1.3 GPa | 1.1 < P < 4.1 GPa | P > 4.2 GPa | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ωi0 | b1 | b2 | ωj0 | b1 | b2 | ωk0 | b1 | |||||
| ω1 | 50 | 4.5 | 60 | 3.1 | ||||||||
| ω2 | 69 | 2.4 | ||||||||||
| ω3 | 54 | 6.8 | 67 | 2.9 | ||||||||
| ω4 | B1 | ring tor | 47 | 48 | 48 | 10.8 | 56 | 12.6 | −0.95 | 81 | 4.0 | |
| ω5 | 75 | 4.9 | 85 | 3.6 | ||||||||
| ω6 | E | ring tor and defm | 46 | 51 | 14.4 | 63 | 12.6 | −0.77 | 92 | 4.9 | ||
| ω7 | external | 54 | 16.5 | |||||||||
| ω8 | external | 59 | 15.9 | 72 | 13.1 | −1.03 | 97 | 5.1 | ||||
| ω9 | external | 73 | 21.1 | 95 | 23.3 | −2.53 | 129 | 6.1 | ||||
| ω10 | 110 | 20.4 | −1.64 | |||||||||
| ω11 | E | ring tor and defm or external | 92 | 95 | 20.9 | 106 | 22.1 | −2.06 | 143 | 5.8 | ||
| ω12 | 155 | 6.1 | ||||||||||
| ω13 | 121 | 27.5 | −2.38 | 169 | 4.2 | |||||||
| ω14 | 139 | 25.5 | −2.50 | |||||||||
| ω15 | external | 111 | 47.4 | −11.60 | 163 | 8.6 | 179 | 6.5 | ||||
| ω16 | 155 | 13.9 | −0.15 | 196 | 8.6 | |||||||
| ω17 | external | 139 | 29.0 | |||||||||
| ω18 | B1 | ring tor | 156 | 156 | 155 | 18.1 | 172 | 15.7 | −0.59 | 207 | 7.7 | |
| ω19 | external | 163 | 22.5 | 177 | 24.8 | −2.20 | 217 | 6.1 | ||||
| ω20 | external | 177 | 18.8 | |||||||||
| ω21 | external | 187 | 22.0 | 213 | 14.0 | 267 | 7.2 | |||||
| ω22 | B2 | ring defm | 216 | 220 | 4.5 | 217 | −7.8 | 1.95 | 229 | 9.7 | ||
| ω23 | E | ring tor, ip (CH + CCC) bend | 240 | 245 | 4.6 | 246 | 4.3 | 260 | 4.1 | |||
| ω24 | 259 | 11.3 | 274 | 5.4 | ||||||||
| ω25 | E | ring tor, ip (CH + CCC) bend | 240 | 248 | 7.0 | 260 | 9.8 | −0.62 | 283 | 8.2 | ||
| ω26 | 273 | 21.5 | −2.17 | |||||||||
| ω27 | 285 | 6.2 | 6.2 | |||||||||
| ω28 | B1 | ring tor | 319 | 320 | 321 | 6.5 | 323 | 3.6 | 3.6 | |||
| ω29 | A1 | ip CH and CCC bend | 331 | 336 | 337 | 5.2 | 335 | 3.0 | 3.0 | |||
| ω30 | B2 | ring defm | 407 | 412 | 412 | 3.5 | ||||||
| ω31 | E | ring tor | 424 | 419 | 418 | 2.8 | 420 | 1.9 | 1.9 | |||
| ω32 | A1 | ring defm | 420 | 424 | 426 | 3.3 | 427 | 1.7 | 1.7 | |||
| ω33 | 487 | 3.5 | −0.25 | 494 | 0.6 | |||||||
| ω34 | B1 | oop CH and CCC bend | 501 | 498 | 3.2 | 502 | 6.3 | 515 | 1.9 | |||
| ω35 | E | ring tor, ip (CH + CCC) bend | 513 | 514 | 515 | 1.5 | 516 | 2.9 | 526 | 2.0 | ||
| ω36 | E | ring tor, ip (CH + CCC) bend | 513 | 519 | 5.5 | 520 | 3.7 | 532 | 2.8 | |||
| ω37 | 569 | 2.3 | 2.3 | |||||||||
| ω38 | E | ring tor, ip (CH + CCC) bend | 644 | 636 | 635 | 1.3 | 633 | 0.8 | 0.8 | |||
| ω39 | 640 | 1.9 | −0.10 | 644 | 0.9 | |||||||
| ω40 | A1 | ip CH and CCC bend | 705 | 704 | 703 | 2.7 | 708 | 2.7 | −0.12 | 715 | 1.9 | |
| ω41 | E | oop CH and CCC bend | 735 | 727 | 728 | 0.2 | 728 | 0.9 | 0.9 | |||
| ω42 | E | oop CH and CCC bend | 735 | 738 | 0.8 | |||||||
| ω43 | E | oop CH bend | 752 | 750 | 750 | 2.7 | 750 | 1.0 | 1.0 | |||
| ω44 | E | oop CH bend | 752 | 756 | 2.6 | |||||||
| ω45 | A1 | ip CH and CCC bend | 766 | 760 | 763 | 2.4 | 764 | 1.9 | 1.9 | |||
| ω46 | B1 | oop CH bend | 762 | 765 | 3.6 | 769 | 7.8 | −0.79 | 781 | 1.1 | ||
| ω47 | B1 | oop CH and CCC bend | 800 | 796 | 796 | 1.6 | 795 | 0.3 | 0.25 | 800 | 2.7 | |
| ω48 | E | oop CH bend | 864 | 861 | 1.0 | 854 | 1.1 | 858 | 0.2 | |||
| ω49 | 869 | 5.3 | −0.44 | 879 | 1.7 | |||||||
| ω50 | 875 | 2.7 | 2.7 | |||||||||
| ω51 | 915 | 2.1 | 2.1 | |||||||||
| ω52 | B1 | oop CH and CCC bend | 943 | 932 | 5.9 | |||||||
| ω53 | E | oop CH and CCC bend | 947 | 946 | 948 | 2.8 | 951 | 1.8 | 1.8 | |||
| ω54 | B2 | ip CH and CCC bend | 948 | 948 | 951 | 3.4 | ||||||
| ω55 | E | oop CH and CCC bend | 947 | 959 | 0.4 | |||||||
| ω56 | 980 | 2.4 | 2.4 | |||||||||
| ω57 | B1, E | oop CH and CCC bend, ip CH and CCC bend | 984, 1005 | 1004 | 1005 | 2.4 | 1008 | 1.9 | 1.9 | |||
| ω58 | 1020 | 3.2 | ||||||||||
| ω59 | A1, B2 | ip CH and CCC bend | 1020 | 1020, 1021 | 1020 | 2.5 | 1026 | 4.0 | 4.0 | |||
| ω60 | E | ip CH and CCC bend | 1035 | 1031 | 1029 | 4.0 | 1041 | 3.7 | 3.7 | |||
| ω61 | A1 | ip CH and CCC bend | 1083 | 1088 | 1084 | 3.4 | ||||||
| ω62 | B2 | ip CH and CCC bend | 1105 | 1104 | 1105 | 0.7 | 1102 | 2.0 | 2.0 | |||
| ω63 | E | ip CH and CCC bend | 1103 | 1110 | 4.0 | 1105 | 2.4 | 2.4 | ||||
| ω64 | 1111 | 2.4 | 2.4 | |||||||||
| ω65 | A1 | ip CH and CCC bend | 1148 | 1152 | 1152 | 3.0 | 1155 | 1.7 | 1.7 | |||
| ω66 | E | ip CH and CCC bend | 1155 | 1157 | 4.2 | 1158 | 2.3 | 2.3 | ||||
| ω67 | E | ip CH and CCC bend | 1155 | 1164 | 1160 | 4.0 | 1163 | 2.5 | 2.5 | |||
| ω68 | 1170 | 3.2 | 3.2 | |||||||||
| ω69 | 1171 | 4.8 | 4.8 | |||||||||
| ω70 | A1, E | ip CH and CCC bend | 1178, 1179 | 1176 | 1175 | 6.2 | 1182 | 4.5 | 4.5 | |||
| ω71 | B2 | C(sp3)—C str, ip CH and CCC bend | 1206 | 1208 | 1210 | 2.6 | ||||||
| ω72 | B2 | ip CH and CCC bend | 1222 | 1214 | 3.8 | 1215 | 2.4 | 2.4 | ||||
| ω73 | A1 | ring str, ip CH bend | 1221 | 1224 | 1226 | 4.6 | 1226 | 2.5 | 2.5 | |||
| ω74 | 1232 | 4.7 | ||||||||||
| ω75 | 1249 | 3.9 | 3.9 | |||||||||
| ω76 | E | ip CH and CCC bend | 1288 | 1282 | 1282 | 2.6 | 1286 | 2.5 | 2.5 | |||
| ω77 | B2 | ip CH and CCC bend | 1299 | 1295 | 1294 | 1.6 | 1294 | 1.9 | 1.9 | |||
| ω78 | A1 | ip CH and CCC bend | 1298 | 1297 | 1297 | 4.8 | ||||||
| ω79 | E | ip CH and CCC bend | 1305 | 1301 | 3.9 | 1304 | 4.3 | 4.3 | ||||
| ω80 | B2 | ip CH and CCC bend | 1352 | 1351 | 1352 | 5.5 | 1360 | 4.9 | 4.9 | |||
| ω81 | A1 | ip CH and CCC bend | 1354 | 1352 | 1359 | 4.0 | 1368 | 4.6 | 4.6 | |||
| ω82 | 1477 | 2.3 | 2.3 | |||||||||
| ω83 | E | ip CH and CCC bend | 1473 | 1474 | 1476 | 6.4 | ||||||
| ω84 | A1 | ip CH and CCC bend | 1471 | 1480 | 1480 | 3.8 | 1485 | 3.1 | 3.1 | |||
| ω85 | B2 | ip CH and CCC bend | 1474 | 1480 | 1485 | 4.8 | 1488 | 3.2 | 3.2 | |||
| ω86 | 1498 | 2.9 | ||||||||||
| ω87 | A1, B2 | ip CH and CCC bend | 1573, 1572 | 1580, 1581 | 1581 | 5.1 | 1587 | 4.5 | 4.5 | |||
| ω88 | 1591 | 4.7 | ||||||||||
| ω89 | 1609 | 3.3 | 3.3 | |||||||||
| ω90 | E | ip CH and CCC bend | 1594 | 1601 | 3.3 | |||||||
| ω91 | E | ip CH and CCC bend | 1594 | 1604 | 1605 | 5.1 | 1609 | 4.6 | 4.6 | |||
| ω92 | A1 | ip CH and CCC bend | 1596 | 1608 | 1610 | 6.1 | 1614 | 4.7 | 4.7 | |||
| ω93 | B2 | ip CH and CCC bend | 1591 | 1628 | 1624 | 3.7 | 1630 | 3.1 | 3.1 | |||
| ω94 | 2nd order | 3004 | 6.7 | |||||||||
| ω95 | 2nd order | 3012 | 6.6 | 3019 | 8.7 | 8.7 | ||||||
| ω96 | E | CH str | 3047 | 3024 | 5.8 | |||||||
| ω97 | E | CH str | 3047 | 3033 | 3.0 | 3036 | 7.8 | 7.8 | ||||
| ω98 | B2 | CH str | 3048 | 3040 | 7.0 | |||||||
| ω99 | A1 | CH str | 3048 | 3047 | 8.4 | 3060 | 6.9 | 6.9 | ||||
| ω100 | A1 | CH str | 3058 | 3060 | 9.6 | 3068 | 6.4 | 6.4 | ||||
| ω101 | 3100 | 8.0 | ||||||||||
| ω102 | A1 | CH str | 3068 | 3065 | 11.3 | 3081 | 8.7 | 8.7 | ||||
| ω103 | E | CH str | 3067 | 3075 | 11.1 | 3081 | 11.7 | 11.7 | ||||
| ω104 | A1 | totally sym CH str | 3080 | 3081 | 13.3 | 3092 | 8.6 | 8.6 | ||||
| ω105 | 3105 | 12.8 | 12.8 | |||||||||
| ω106 | B2 | CH str | 3080 | 3088 | 12.3 | 3099 | 13.7 | 13.7 | ||||
| ω107 | 3118 | 11.7 | 11.7 | |||||||||
| ω108 | 2nd order | 3159 | 9.4 | 3171 | 6.4 | 6.4 | ||||||
| ω109 | 2nd order | 3196 | 10.1 | 3222 | 7.2 | 7.2 | ||||||
| ω110 | 2nd order | 3209 | 13.8 | 3218 | 9.9 | 9.9 | ||||||

References
- Harvey, R.G. Polycyclic Aromatic Hydrocarbons; Wiley-VCH: New York, NY, USA, 1997. [Google Scholar]
- Neilson, A.H. (Ed.) PAHs and Related Compounds, Chemistry; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1998. [Google Scholar]
- Skupińska, K.; Misiewicz, I.; Kasprzycka-Guttman, T. Polycyclic aromatic hydrocarbons: Physicochemical properties, environmental appearance and impact on living organisms. Acta Pol. Pharm. 2004, 61, 233–240. [Google Scholar] [PubMed]
- Bandeira, G.C.; Meneses, H.E. (Eds.) Handbook of Polycyclic Aromatic Hydrocarbons: Chemistry, Occurrence and Health Issues; Nova Science Publishers: Hauppauge, NY, USA, 2012. [Google Scholar]
- Lawal, A.T. Polycyclic aromatic hydrocarbons. A review. Cogent Environ. Sci. 2017, 3, 1339841. [Google Scholar] [CrossRef]
- Ahn, T.K.; Kim, K.S.; Kim, D.Y.; Noh, S.B.; Aratani, N.; Ikeda, C.; Osuka, A.; Kim, D. Relationship between two-photon absorption and the π-conjugation pathway in porphyrin arrays through dihedral angle control. J. Am. Chem. Soc. 2006, 128, 1700–1704. [Google Scholar] [CrossRef] [PubMed]
- Anthony, J.E. Functionalized acenes and heteroacenes for organic electronics. Chem. Rev. 2006, 106, 5028–5048. [Google Scholar] [CrossRef] [PubMed]
- Ye, Q.; Chi, C. Recent highlights and perspectives on acene based molecules and Materials. Chem. Mater. 2014, 26, 4046–4056. [Google Scholar] [CrossRef]
- Delouche, T.; Hissler, M.; Pierre-Antoine Bouit, P.-A. Polycyclic aromatic hydrocarbons containing heavy group 14 elements: From synthetic challenges to optoelectronic devices. Coord. Chem. Rev. 2022, 464, 214553. [Google Scholar] [CrossRef]
- Ma, L.; Han, Y.; Shi, O.; Huang, H. The design, synthesis and application of rubicene based polycyclic aromatic hydrocarbons (PAHs). J. Mater. Chem. C 2023, 11, 16429–16438. [Google Scholar] [CrossRef]
- Mathur, C.; Gupta, R.; Bansal, R.K. Organic donor-acceptor complexes as potential semiconducting materials. Chem. Eur. J. 2024, 30, e202304139. [Google Scholar] [CrossRef]
- Yadav, B.; Ravikanth, M. Porphyrinoid framework embedded with polycyclic aromatic hydrocarbons: New synthetic marvels. Org. Biomol. Chem. 2024, 22, 1932–1960. [Google Scholar] [CrossRef]
- Salbeck, J. New low molecular organic compounds with high glass transition temperature as materials for blue electroluminescence. In Inorganic and Organic Electroluminescence; Mauch, R.H., Gumlich, H.-E., Eds.; Wissenschaft & Technik: Berlin, Germany, 1996; pp. 243–246. [Google Scholar]
- Salbeck, J.; Yu, N.; Bauer, J.; Weissörtel, F.; Bestgen, H. Low molecular organic glasses for blue electroluminescence. Synth. Met. 1997, 91, 209–215. [Google Scholar] [CrossRef]
- Pudzich, R.; Fuhrmann-Lieker, T.; Salbeck, J. Spiro compounds for organic electroluminescence and related applications. Adv. Polym. Sci. 2006, 199, 83–142. [Google Scholar]
- Saragi, T.P.I.; Spehr, T.; Siebert, A.; Fuhrmann-Lieker, T.; Salbeck, J. Spiro compounds for organic optoelectronics. Chem. Rev. 2007, 107, 1011–1065. [Google Scholar] [CrossRef] [PubMed]
- Clarkson, R.G.; Gomberg, M. Spirans with four aromatic radicals on the spiro carbon atom. J. Am. Chem. Soc. 1930, 52, 2881–2896. [Google Scholar] [CrossRef]
- Alcazar, V.; Diederich, F. Enantioselective complexation of chiral dicarboxylic acids in clefts of functionalized 9,9′-spirobifluorenes. Angew. Chem. Int. Ed. 1992, 31, 1521–1523. [Google Scholar] [CrossRef]
- Poriel, C.; Ferrand, Y.; le Maux, P.; Paul, C.; Rault-Berthelot, J.; Simonneaux, G. Poly(ruthenium carbonyl spirobifluorenylporphyrin): A new polymer used as a catalytic device for carbene transfer. Chem. Commun. 2003, 2308–2309. [Google Scholar] [CrossRef]
- Wong, K.T.; Chien, Y.Y.; Chen, R.T.; Wang, C.F.; Lin, Y.T.; Chiang, H.H.; Hsieh, P.Y.; Wu, C.C.; Chou, C.H.; Su, Y.O.; et al. Ter(9,9-diarylfluorene)s: Highly efficient blue emitter with promising electrochemical and thermal stability. J. Am. Chem. Soc. 2002, 124, 11576–11577. [Google Scholar] [CrossRef]
- Schenk, H. Crystal and molecular structure of Bis-(2,2′-biphenylene)methane. Acta Cryst. B 1972, 28, 625–628. [Google Scholar] [CrossRef]
- Douthwaite, R.E.; Taylor, A.; Whitwood, A.C. A new polymorph and two inclusion compounds of 9,9′-spirobifluorene. Acta Cryst. C 2005, 61, o328–o331. [Google Scholar] [CrossRef]
- Zallen, R. Pressure-Raman effects and vibrational scaling laws in molecular crystals: S8 and As2S3. Phys. Rev. B 1974, 9, 4485–4496. [Google Scholar] [CrossRef]
- Zallen, R.; Slade, M.L. Influence of pressure and temperature on phonons in molecular chalcogenides: Crystalline As4S4 and S4N4. Phys. Rev. B 1978, 18, 5775–5798. [Google Scholar] [CrossRef]
- Marinopoulou, A.; Christopoulou, V.; Karabinaki, O.; Christofilos, D.; Arvanitidis, J. The high-pressure response of trans-cinnamic acid crystals studied by Raman spectroscopy. Appl. Res. 2024, 3, e202300129. [Google Scholar] [CrossRef]
- Zallen, R.; Griffiths, C.H.; Slade, M.L.; Hayek, M.; Brafman, O. The solid state transition in Pyrene. Chem. Phys. Lett. 1976, 39, 85–89. [Google Scholar] [CrossRef]
- Adams, D.M.; Appleby, R. Vibrational spectroscopy at very high pressures: Part 18.-Three solid phases of benzene. J. Chem. Soc. Faraday Trans. 1977, 73, 1896–1905. [Google Scholar] [CrossRef]
- Thiéry, M.M.; Léger, J.M. High pressure solid phases of benzene. I. Raman and x-ray studies of C6H6 at 294 K up to 25 GPa. J. Chem. Phys. 1988, 89, 4255–4271. [Google Scholar] [CrossRef]
- Zhao, L.; Baer, B.J.; Chronister, E.L. High-pressure Raman study of anthracene. J. Phys. Chem. A 1999, 103, 1728–1733. [Google Scholar] [CrossRef]
- Venuti, E.; Guido Della Valle, R.; Farina, L.; Brillante, A. Phonons and structures of tetracene polymorphs at low temperature and high pressure. Phys. Rev. B 2004, 70, 104106. [Google Scholar] [CrossRef]
- Sun, B.; Dreger, Z.A.; Gupta, Y.M. High-pressure effects in pyrene crystals: Vibrational spectroscopy. J. Phys. Chem. A 2008, 112, 10546–10551. [Google Scholar] [CrossRef]
- Zhou, M.; Wang, K.; Mena, Z.; Gao, S.; Li, Z.; Sun, C. Study of high-pressure Raman intensity behavior of aromatic hydrocarbons: Benzene, biphenyl and naphthalene. Spectrochim. Acta A 2012, 97, 526–531. [Google Scholar] [CrossRef]
- Meletov, K.P. Phonon spectrum of a naphthalene crystal at a high pressure: Influence of shortened distances on the lattice and intramolecular vibrations. Phys. Solid State 2013, 55, 581–588. [Google Scholar] [CrossRef]
- O’Bannon III, E.; Williams, Q. Vibrational spectra of four polycyclic aromatic hydrocarbons under high pressure: Implications for stabilities of PAHs during accretion. Phys. Chem. Miner. 2016, 43, 181–208. [Google Scholar] [CrossRef]
- Zhao, X.-M.; Zhong, G.-H.; Zhang, J.; Huang, Q.-W.; Goncharov, A.F.; Lin, H.Q.; Chen, X.J. Combined experimental and computational study of high pressure behavior of triphenylene. Sci. Rep. 2016, 6, 25600. [Google Scholar] [CrossRef] [PubMed]
- Capitani, F.; Höppner, M.; Malavasi, L.; Marini, C.; Dore, P.; Boeri, L.; Postorino, P. The effect of high pressure on the lattice structure and dynamics of phenacenes. J. Phys. Conf. Ser. 2017, 950, 042017. [Google Scholar] [CrossRef]
- Terzidou, A.G.V.; Sorogas, N.; Pinakidou, F.; Paloura, E.C.; Arvanitidis, J. The pressure-induced structural phase transition of fluorene studied by Raman spectroscopy. Vib. Spectrosc. 2021, 115, 103272. [Google Scholar] [CrossRef]
- Yuan, C.; Wang, J.; Yang, Q.; Feng, S.; Zhu, X.; Yang, K.; Su, L. Phase transition behavior of benzene under dynamic compression: A stable precocious phase. J. Mol. Liq. 2024, 411, 125706. [Google Scholar] [CrossRef]
- Zhao, X.; Suo, T.; Mao, Q.; Zhao, Z.; Wang, S.; Wan, B.; Liu, J.; Zhang, L.; Liang, X.; Xu, A.; et al. Structure and piezochromism of chrysene at high pressures. Dyes Pigments 2024, 227, 112161. [Google Scholar] [CrossRef]
- Decker, C. Laser-Raman spectroscopy of disubstituted spiro-cyclopropane-1,9′-fluorene stereoisomers. Spectrochim. Acta A 1979, 35, 1303–1306. [Google Scholar] [CrossRef]
- Lee, S.Y.; Boo, B.H. Density functional theory study of vibrational spectra of fluorene. J. Phys. Chem. 1996, 100, 8782–8785. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Boo, B.H.; Park, J.; Yeo, H.G.; Lee, S.Y.; Park, C.J.; Kim, J.H. Infrared and Raman spectroscopy of 9,9′-spirobifluorene, bis(2,2′-biphenylene)silane, and bis(2,2′-biphenylene)germane. Vibrational assignment by depolarization measurement and HF and density functional theory studies. J. Phys. Chem. A 1998, 102, 1139–1145. [Google Scholar] [CrossRef]
- Bree, A.; Zwarich, R. Vibrational assignment of fluorene from the infrared and Raman spectra. J. Chem. Phys. 1969, 51, 912–920. [Google Scholar] [CrossRef]
- Cuff, L.; Kertesz, M. Theoretical prediction of the vibrational spectrum of fluorene and planarized poly(p-phenylene). J. Phys. Chem. 1994, 98, 12223–12231. [Google Scholar] [CrossRef]
- Heimel, G.; Hummer, K.; Ambrosh-Draxl, C.; Chunwachirasiri, W.; Winokur, M.J.; Hanfland, M.; Oehzelt, M.; Aichholzer, A.; Resel, R. Phase transition and electronic properties of fluorene: A joint experimental and theoretical high-pressure study. Phys. Rev. B 2006, 73, 024109. [Google Scholar] [CrossRef]
- Grüneisen, E. Handbuch der Physik; Springer: Berlin, Germany, 1926; Volume 10. [Google Scholar]
- Bridgman, P.W. Further rough compressions to 40,000 kg/cm2, especially certain liquids. Proc. Am. Acad. Arts Sci. 1949, 77, 129–146. [Google Scholar] [CrossRef]
- Jayaraman, A. Ultrahigh pressures. Rev. Sci. Instrum. 1986, 57, 1013–1031. [Google Scholar] [CrossRef]
- Sasaki, S.; Kato, S.; Kume, T.; Shimizu, H.; Okada, T.; Aoyama, S.; Kusuyama, F.; Murata, K. Elastic properties of new-pressure transmitting medium Daphne 7474 under high pressure. J. Appl. Phys. 2010, 49, 106702. [Google Scholar] [CrossRef]
- Murata, K.; Yokogawa, K.; Yoshino, H.; Klotz, S.; Munsch, P.; Irizawa, A.; Nishiyama, M.; Iizuka, K.; Nanba, T.; Okada, T.; et al. Pressure transmitting medium Daphne 7474 solidifying at 3.7 GPa at room temperature. Rev. Sci. Instrum. 2008, 79, 085101. [Google Scholar] [CrossRef]
- Barnett, J.D.; Block, S.; Piermarini, G.J. An optical fluorescence system for quantitative pressure measurement in the diamond-anvil cell. Rev. Sci. Instrum. 1973, 44, 1–9. [Google Scholar] [CrossRef]
- Mao, H.K.; Xu, J.; Bell, P.M. Calibration of the ruby pressure gauge to 800 kbar under quasi-hydrostatic conditions. J. Geophys. Res. 1986, 91, 4673–4676. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Siavou, M.-T.; Siapaka, K.; Karabinaki, O.; Christofilos, D.; Arvanitidis, J. The High-Pressure Response of 9,9′-Spirobifluorene Studied by Raman Spectroscopy. Molecules 2025, 30, 638. https://doi.org/10.3390/molecules30030638
Siavou M-T, Siapaka K, Karabinaki O, Christofilos D, Arvanitidis J. The High-Pressure Response of 9,9′-Spirobifluorene Studied by Raman Spectroscopy. Molecules. 2025; 30(3):638. https://doi.org/10.3390/molecules30030638
Chicago/Turabian StyleSiavou, Maria-Tereza, Konstantina Siapaka, Olga Karabinaki, Dimitrios Christofilos, and John Arvanitidis. 2025. "The High-Pressure Response of 9,9′-Spirobifluorene Studied by Raman Spectroscopy" Molecules 30, no. 3: 638. https://doi.org/10.3390/molecules30030638
APA StyleSiavou, M.-T., Siapaka, K., Karabinaki, O., Christofilos, D., & Arvanitidis, J. (2025). The High-Pressure Response of 9,9′-Spirobifluorene Studied by Raman Spectroscopy. Molecules, 30(3), 638. https://doi.org/10.3390/molecules30030638






