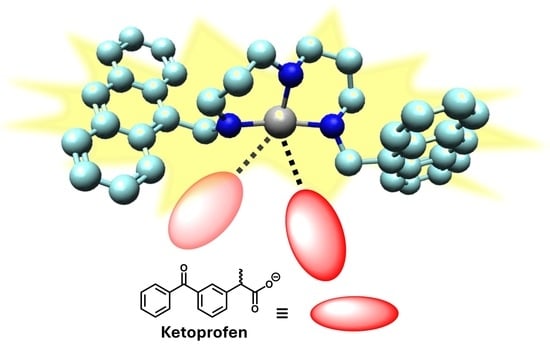
Ketoprofen Recognition and Sensing by Zn(II) Complexes with Fluorogenic Triamine Receptors
Abstract
1. Introduction
2. Results
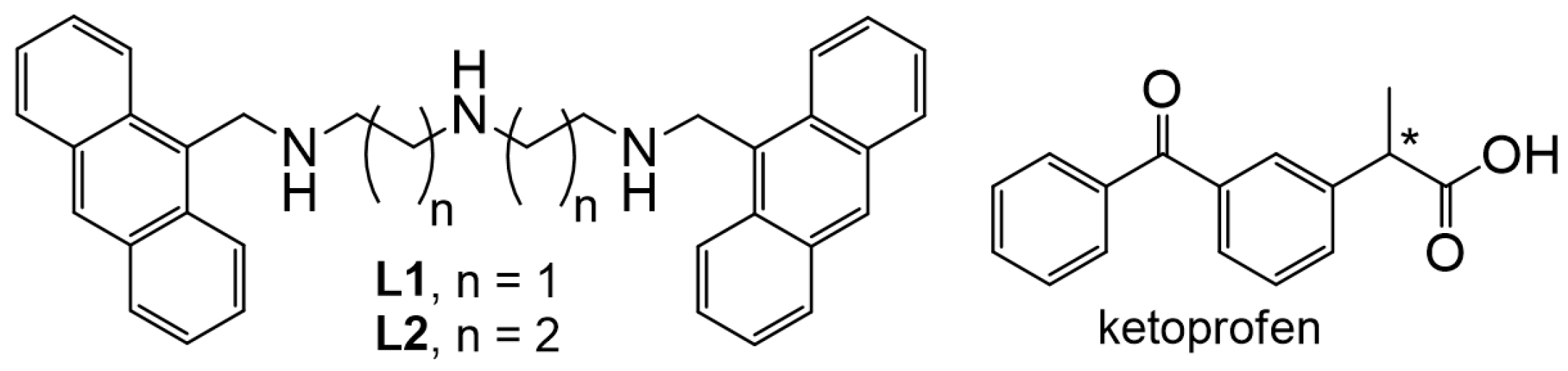
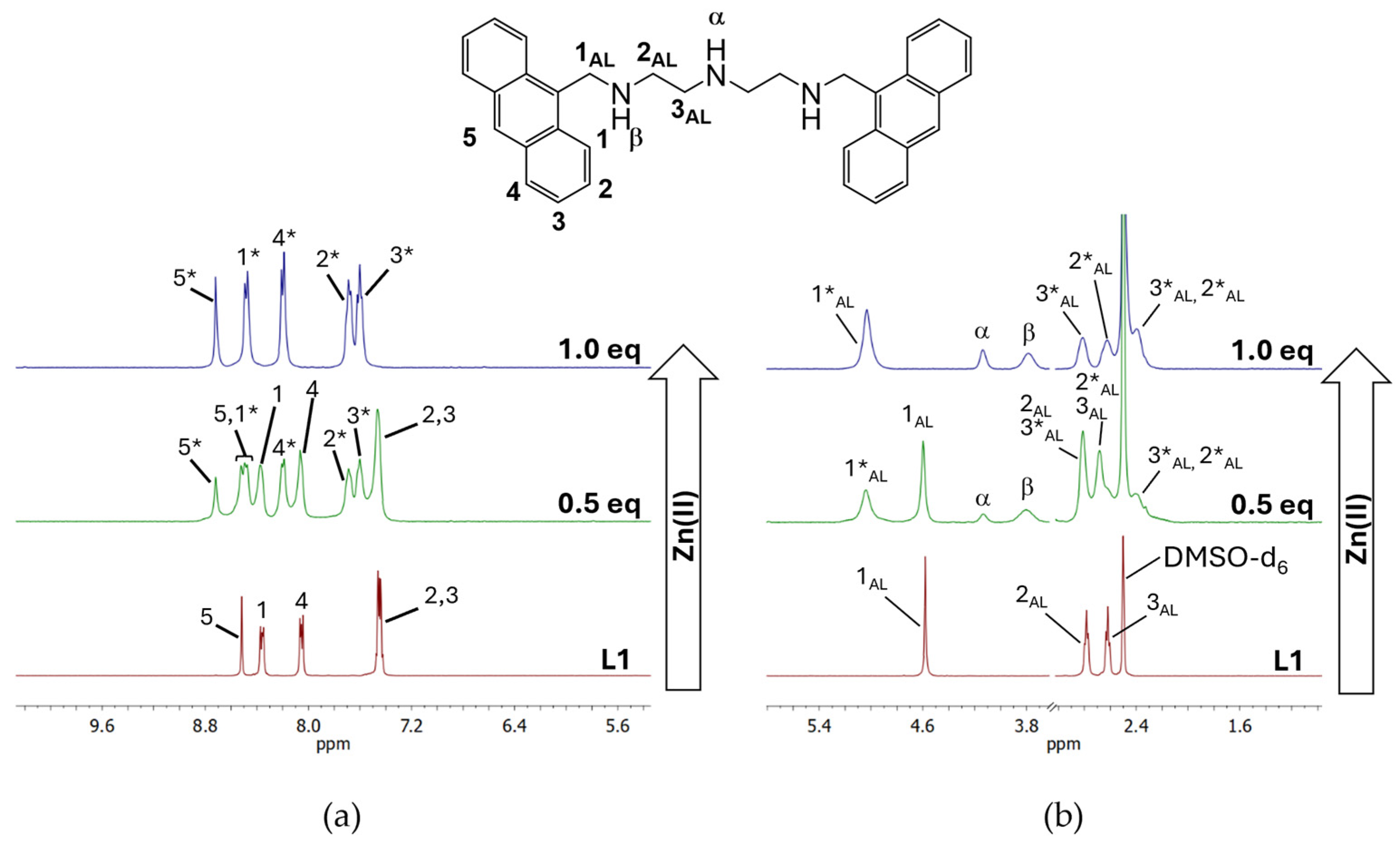
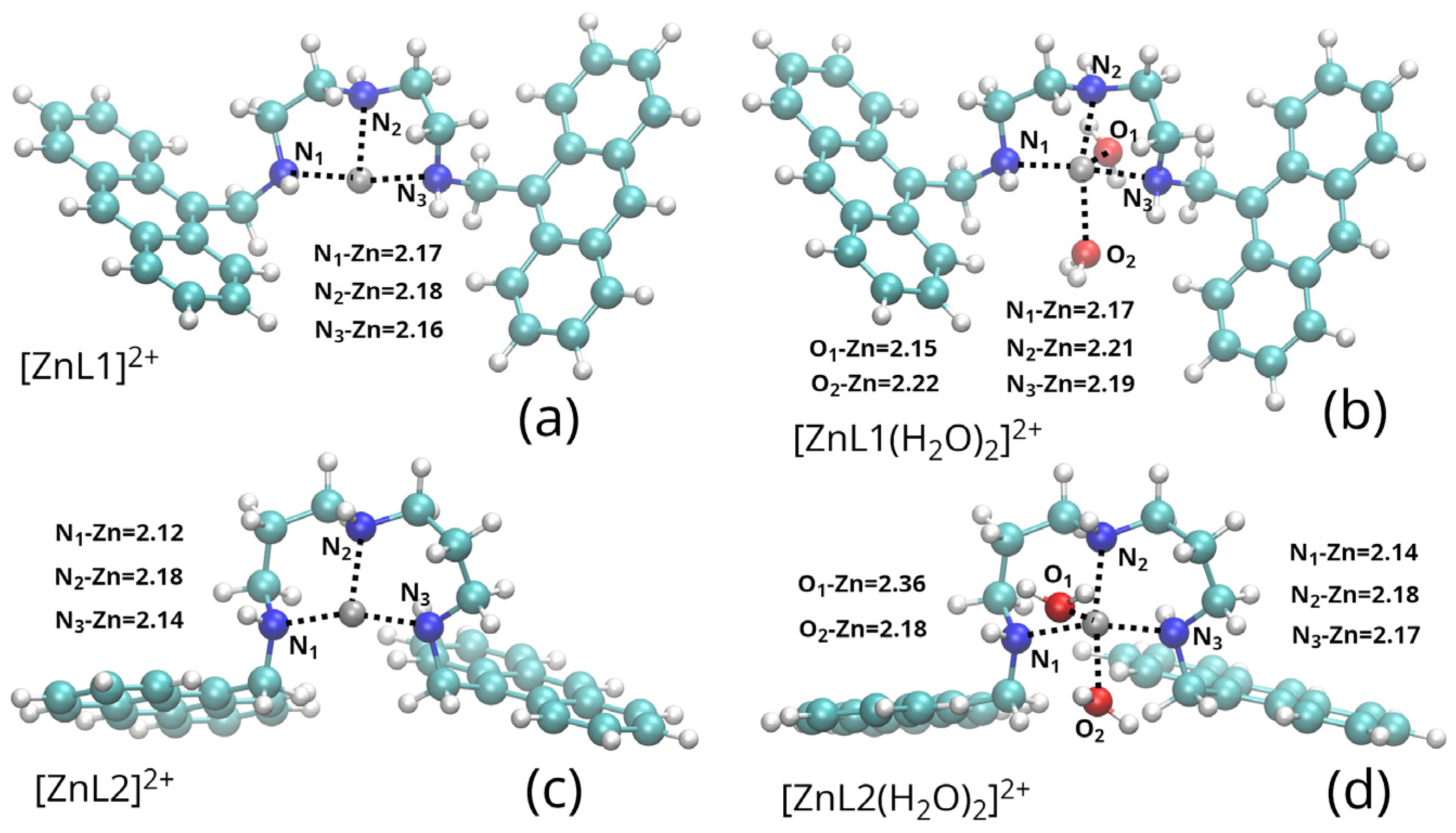
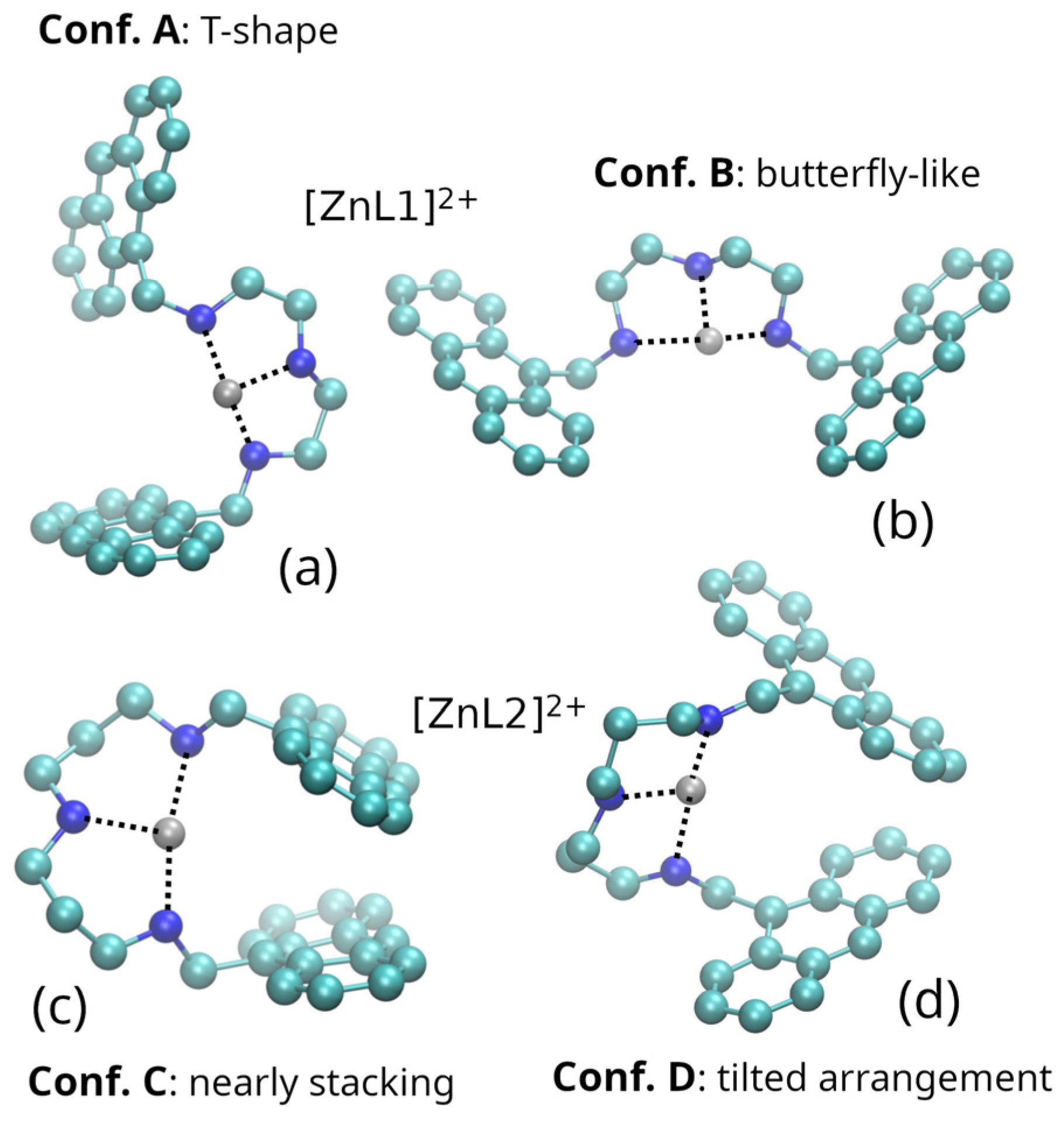
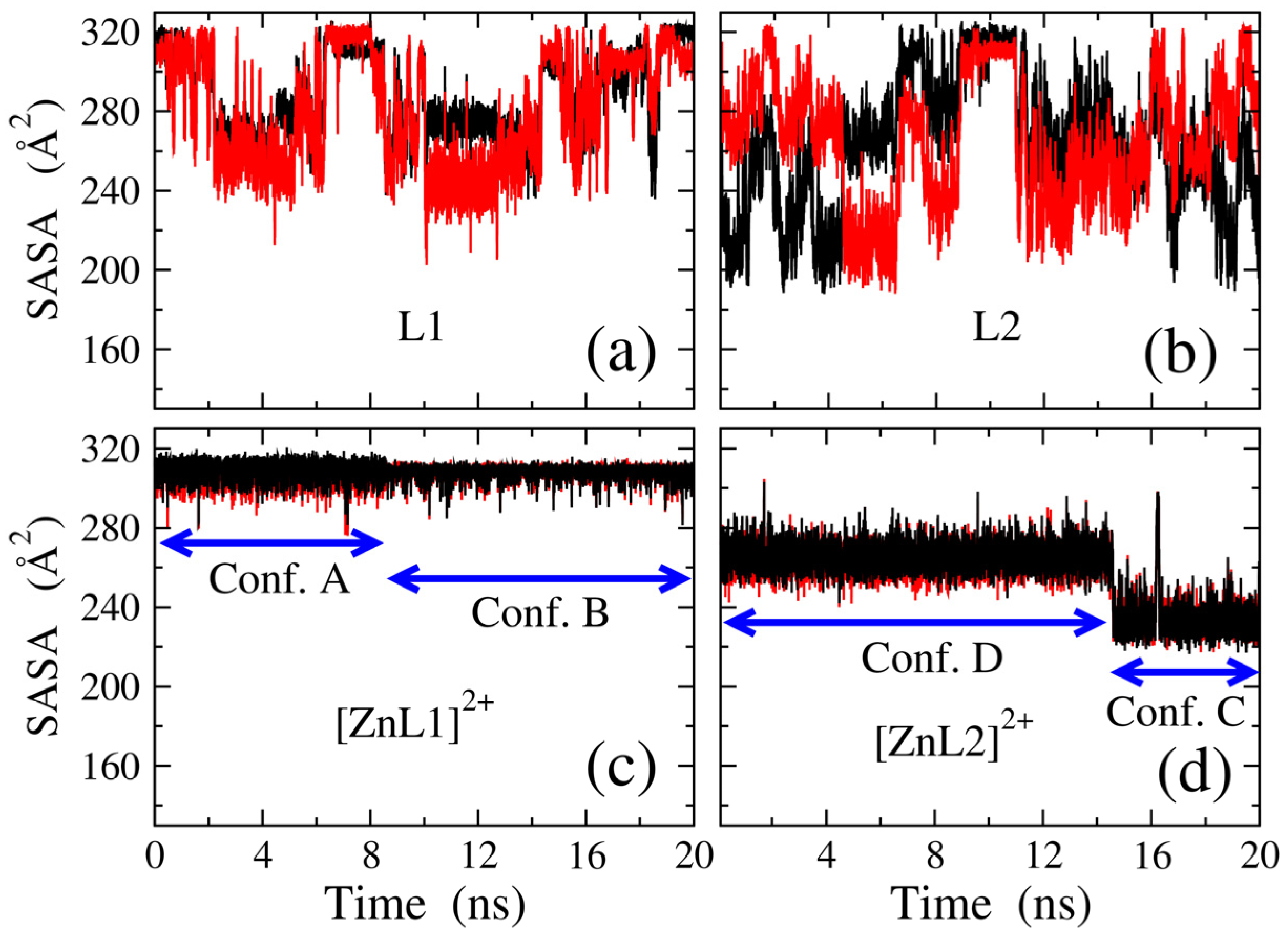
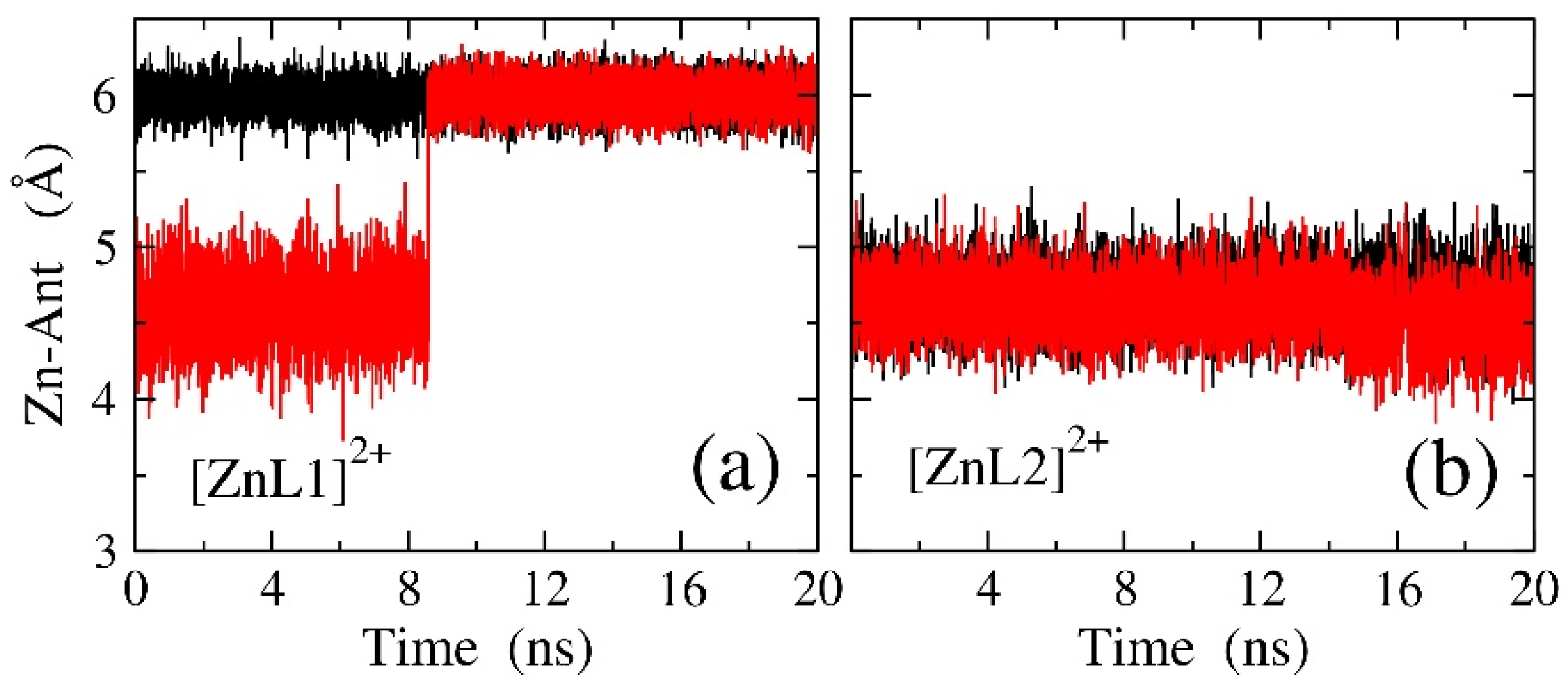
2.1. Zn(II) Coordination with L1 and L2
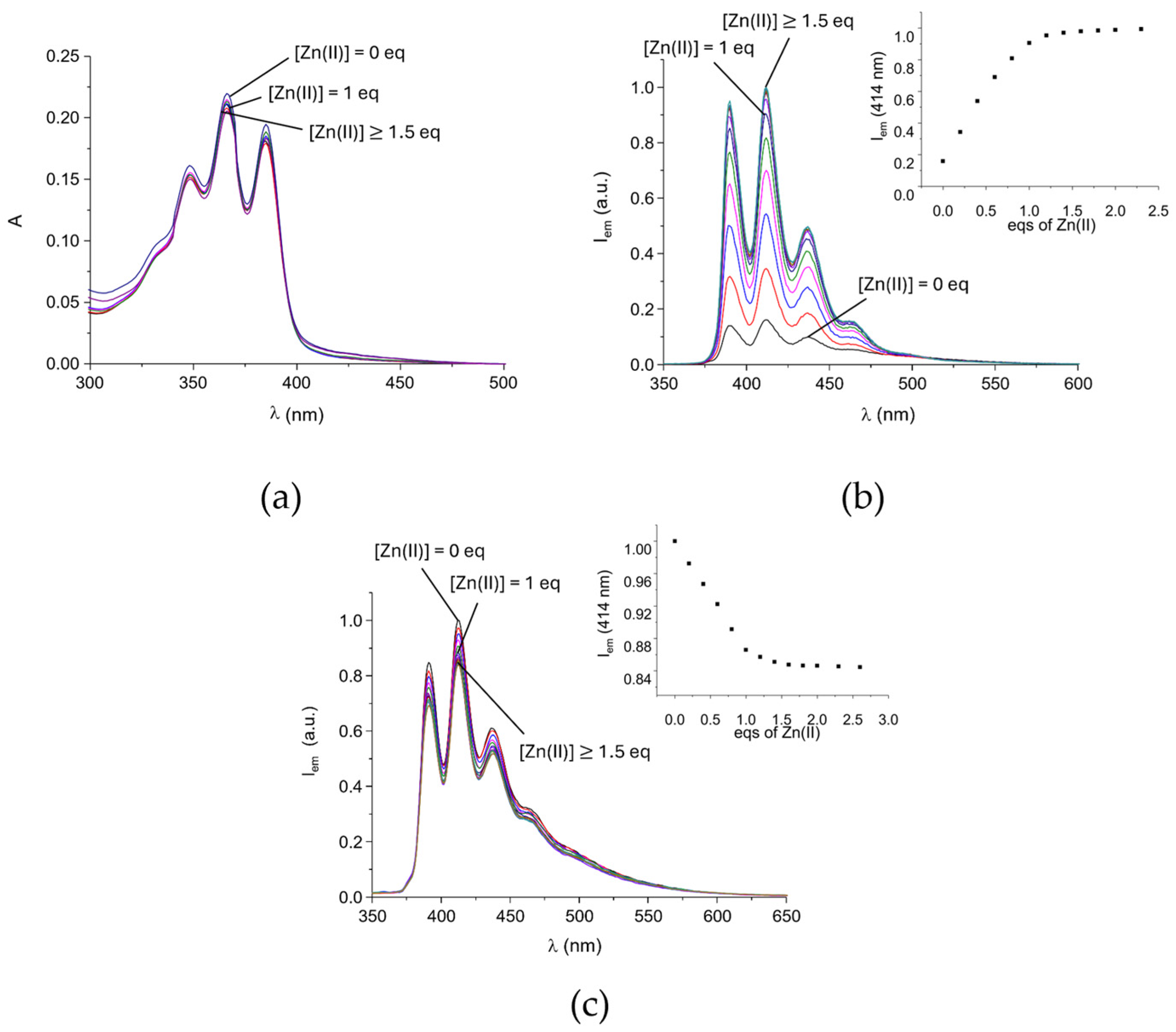
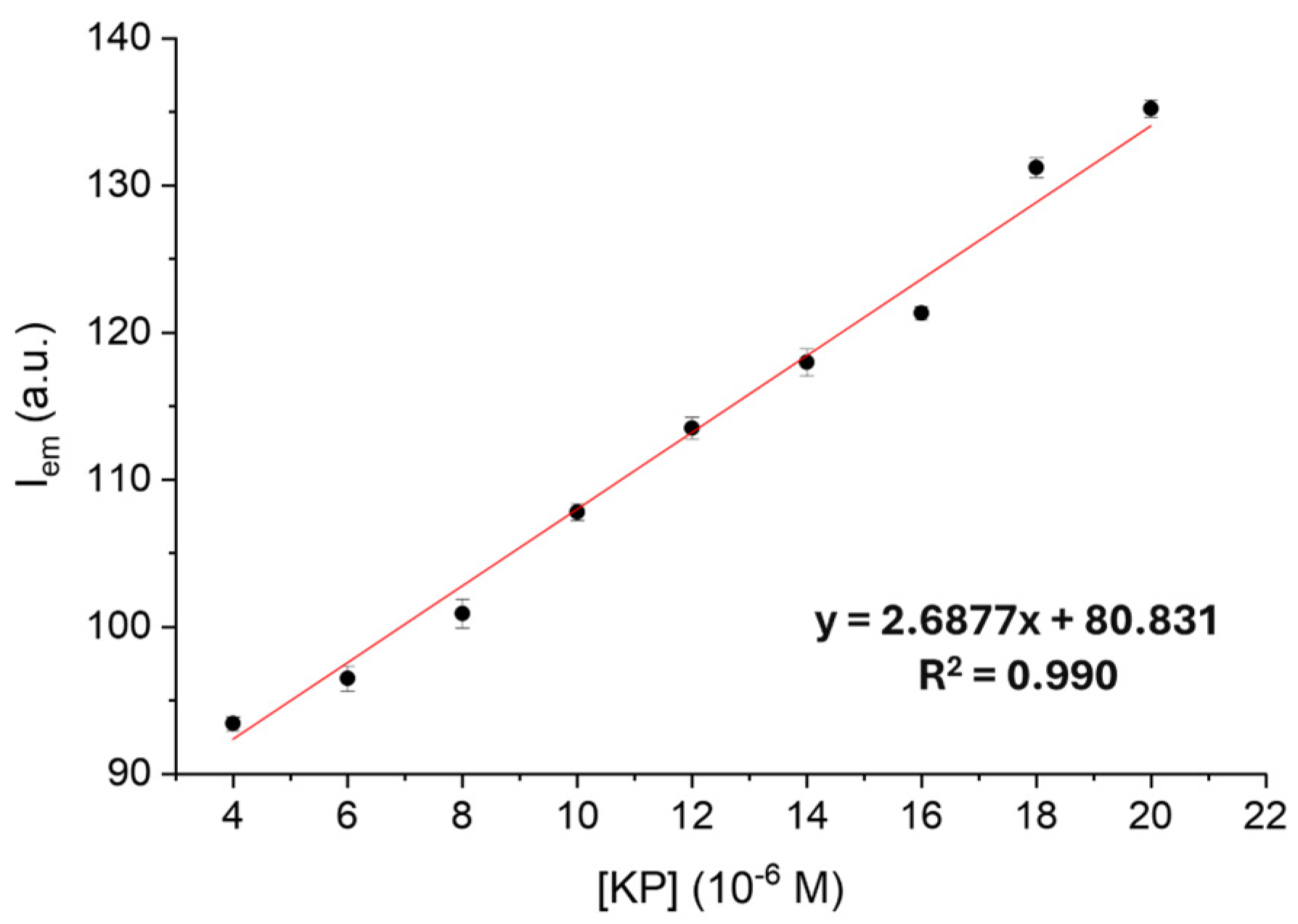
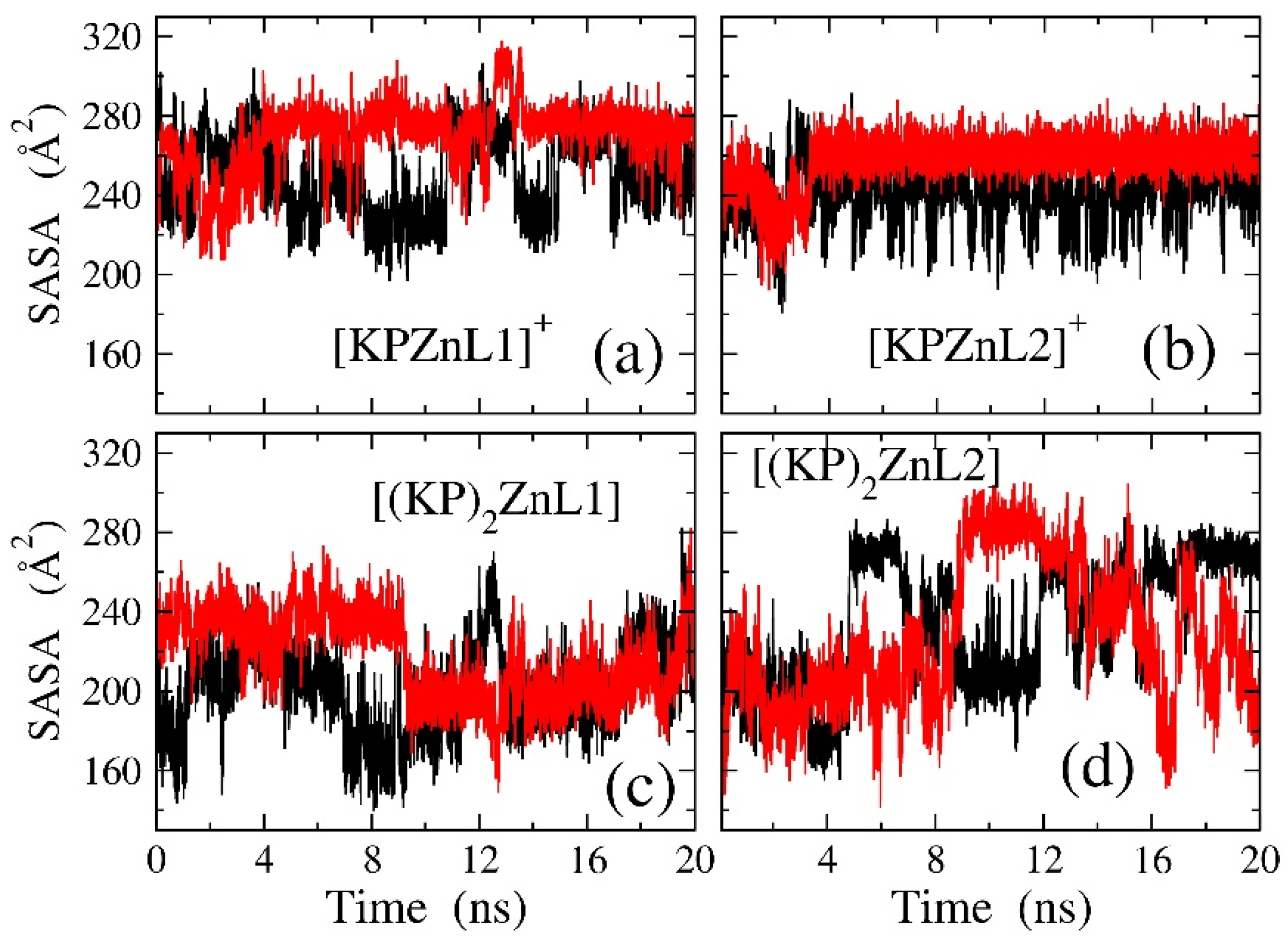
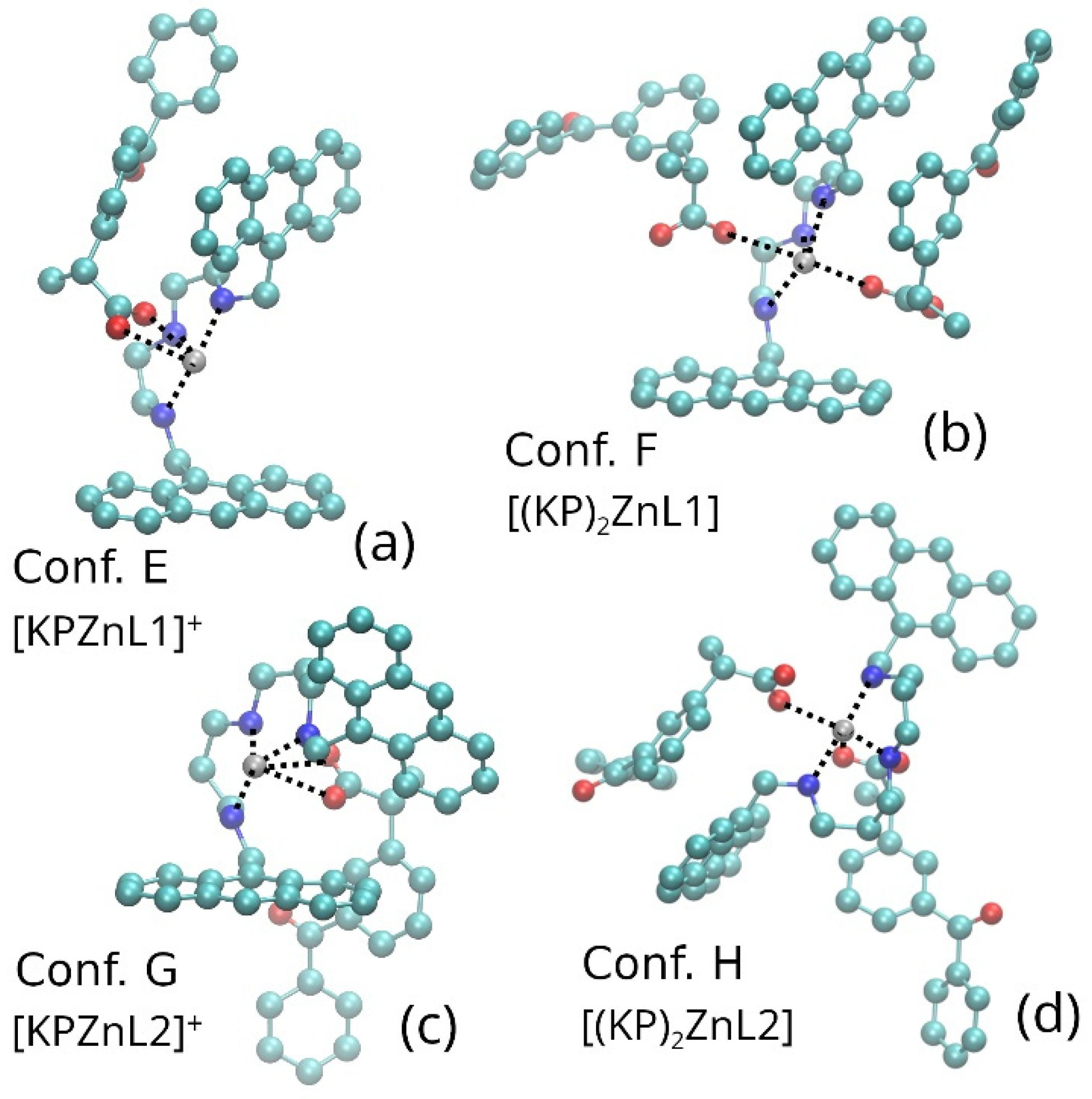
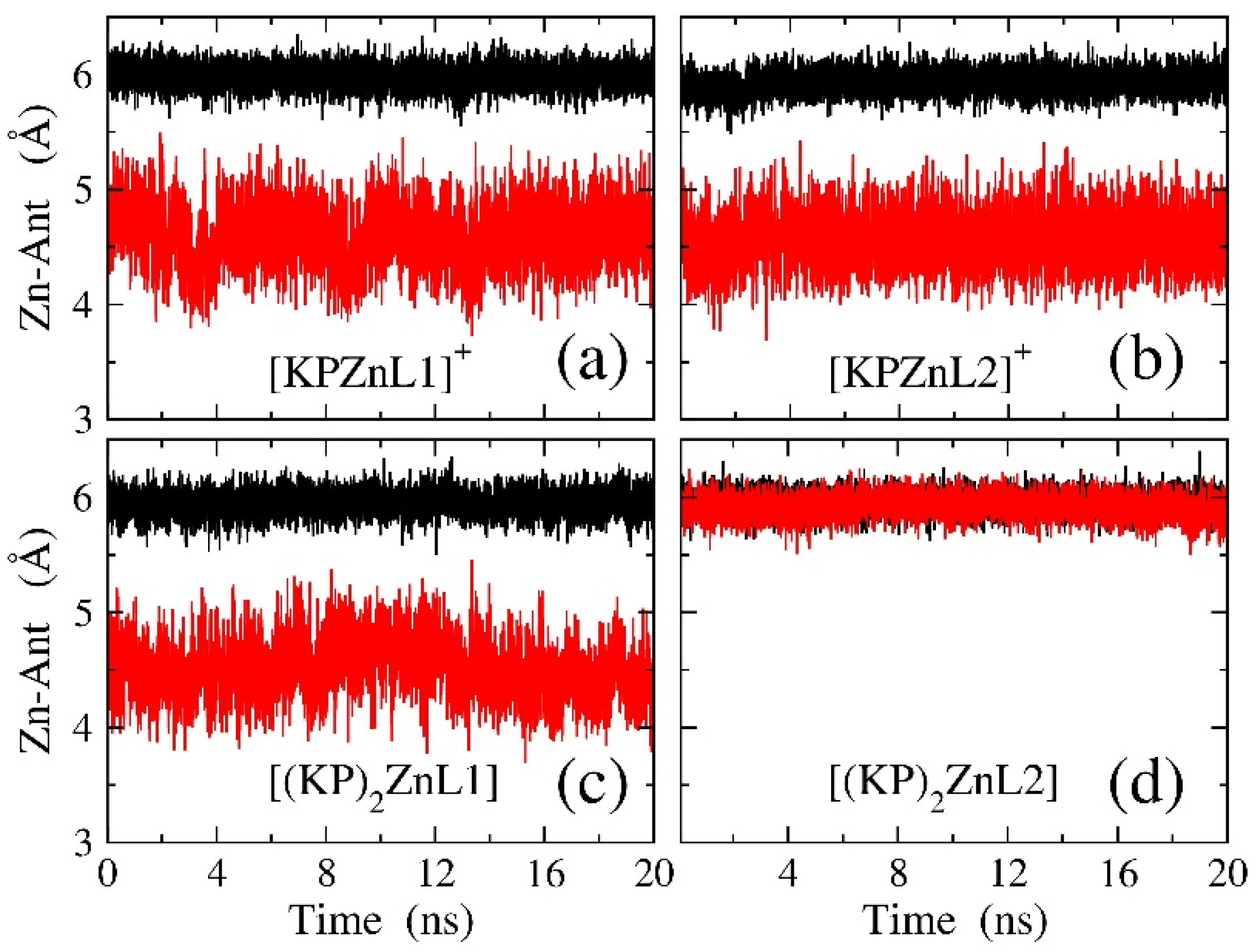
2.2. Ketoprofen Binding by the Zn(II) Complexes with L1 and L2
3. Materials and Methods
3.1. Synthesis of [(ZnL1)(ClO4)2]·2 H2O
3.2. Synthesis of [(ZnL2)(ClO4)2]·2 H2O
3.3. Electronic Absorption and Fluorescence Measurements
3.4. NMR Measurements
3.5. Molecular Dynamic Simulations
3.6. Ab Initio Calculations
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| PET | Photoinduced Electron Transfer |
| KP | Ketoprofen |
| NSAIDs | Non-Steroidal Anti-Inflammatory Drugs |
| QDs | Quantum Dots |
| CDs | Carbon Dots |
| EtOH | Ethanol |
| TRIS | Tris(hydroxymethyl)aminomethane |
| NMR | Nuclear Magnetic Resonance |
| MD | Molecular Dynamics |
| SASA | Solvent Accessible Surface Area |
| LOD | Limit Of Detection |
| MeOH | Methanol |
| BuOH | Butanol |
References
- Wongrakpanich, S.; Wongrakpanich, A.; Melhado, K.; Rangaswami, J. A Comprehensive Review of Non-Steroidal Anti-Inflammatory Drug Use in The Elderly. Aging Dis. 2018, 9, 143–150. [Google Scholar] [CrossRef]
- Jahnavi, K.; Pavani Reddy, P.; Vasudha, B.; Narender, B. Non-Steroidal Anti-Inflammatory Drugs: An Overview. J. Drug Delivery Ther. 2019, 9, 442–448. [Google Scholar] [CrossRef]
- Vishwakarma, R.K.; Negi, D.S. The development of cox-1 and cox-2 inhibitors: A review. Int. J. Pharm. Sci. Res. 2020, 11, 3544–3555. [Google Scholar]
- Huynh, N.C.; Nguyen, T.T.T.; Nguyen, D.T.C.; Tran, T.V. Occurrence, toxicity, impact and removal of selected non-steroidal anti-inflammatory drugs (NSAIDs): A review. Sci. Total Environ. 2023, 898, 165317. [Google Scholar] [CrossRef] [PubMed]
- Brennan, R.; Shawabkeh, H.; Wazaify, M.; Boardley, I.; McVeigh, J.; Van Hout, M.C. A scoping review of non-medical and extra-medical use of non-steroidal anti-inflammatory drugs (NSAIDs). Drug Saf. 2021, 44, 917–928. [Google Scholar] [CrossRef]
- Browne, N.; Conneely, M.; Hudson, C. Use of Non-Steroidal Anti-Inflammatory Drugs and Attitudes to Pain in Pasture-Based Dairy Cows: A Comparative Study of Farmers and Veterinarians. Front. Vet. Sci. 2022, 9, 912564. [Google Scholar] [CrossRef] [PubMed]
- Tsekouras, N.; Christodoulopoulos, M.A.B.; Meletis, E.; Kousoulis, C.; Kostoulas, P.; Pantazis, V.; Papatsiros, V.G.; Dimoveli, K.; Gougoulis, D. Associations Between Non-Steroidal and Steroidal Anti-Inflammatory Drug Use, Welfare, and Milk Production in Dairy Sheep: A Multivariate Study. Animals 2025, 15, 1104. [Google Scholar] [CrossRef]
- Izadi, P.; Izadi, P.; Salem, R.; Papry, S.A.; Magdouli, S.; Pulicharla, R.; Brar, S.K. Non-steroidal anti-inflammatory drugs in the environment: Where were we and how far we have come? Environ. Pollut. 2020, 267, 115370. [Google Scholar] [CrossRef]
- Jurado, A.; Vázquez-Suñé, E.; Pujades, E. Urban Groundwater Contamination by Non-Steroidal Anti-Inflammatory Drugs. Water 2021, 13, 720. [Google Scholar] [CrossRef]
- Aranda-Lara, L. Non-Steroidal Anti-Inflammatory Drugs in Water: Emerging Contaminants and Ecological Impact; Gomez-Olivan, L.M., Ed.; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Patel, N.; Khan, M.D.; Shahane, S.; Rai, D.; Chauhan, D.; Kant, C.; Chaudhary, V.K. Emerging Pollutants in Aquatic Environment: Source, Effect, and Challenges in Biomonitoring and Bioremediation—A Review. Pollution 2020, 6, 99–113. [Google Scholar]
- Wilkinson, J.; Hooda, P.S.; Barker, J.; Barton, S.; Swinden, J. Occurrence, fate and transformation of emerging contaminants in water: An overarching review of the field. Environ. Pollut. 2017, 231, 954–970. [Google Scholar] [CrossRef]
- Gale, P.A.; Caltagirone, C. Fluorescent and colorimetric sensors for anionic species. Coord. Chem. Rev. 2018, 354, 2–27. [Google Scholar] [CrossRef]
- Laxman, W.; Anushree, T.; Pawan, K.; Yong, S.; Samandhan, P.; Akash, D.; Ki, H. Functionalized fluorescent nanomaterials for sensing pollutants in the environment: A critical review. Trends Anal. Chem. 2017, 97, 458–467. [Google Scholar]
- Das, A.K. Advances in detecting non-steroidal anti-inflammatory drugs (NSAIDs) using molecular receptors and nanostructured assemblies. RSC Med. Chem. 2025, 16, 511–524. [Google Scholar] [CrossRef]
- Chen, S.; Zhou, S.; Fu, J.; Tang, S.; Wu, X.; Zhao, P.; Zhang, Z. A near infrared fluorescence imprinted sensor based on zinc oxide nanorods for rapid determination of ketoprofen. Anal. Methods 2021, 13, 2836–2846. [Google Scholar] [CrossRef]
- Delgado-Pérez, T.; Bouchet, L.M.; de la Guardia, M.; Galian, R.E.; Pérez-Prieto, J. Sensing chiral drugs by using CdSe/ZnS nanoparticles capped with N-acetyl-L-cysteine methyl ester. Chem. Eur. J. 2013, 19, 11068–11076. [Google Scholar] [CrossRef]
- Molina-García, L.; Santos, J.L.M.; Ruiz-Medina, A.; Llorent-Martínez, E.J. Determination of ketoprofen based on its quenching effect in the fluorescence of quantum dots. J. Food Drug Anal. 2013, 21, 426–431. [Google Scholar] [CrossRef]
- Bhogal, S.; Kaur, K.; Maheshwari, S.; Malik, A.K. Surface Molecularly Imprinted Carbon Dots Based Core-Shell Material for Selective Fluorescence Sensing of Ketoprofen. J. Fluoresc. 2019, 29, 145–154. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.; Li, Q.; Wang, M.; Xu, J.; Li, J.; Wang, F. Synthesis of fluorescent artificial receptors with high specificity for simultaneous detection of non-steroidal anti-inflammatory drugs. Food Chem. 2023, 410, 135419. [Google Scholar] [CrossRef] [PubMed]
- Mabrouk, M.; Hammad, S.F.; Abdella, A.A.; Mansour, F.R. A novel strategy for ketorolac detection based on turn-on plasmonic enhanced FRET synchronous fluorometric sensor employing micellized chitosan/AgNPs nanocomposites: Preparation and mechanism investigation. Colloids Surf. A 2021, 614, 126182. [Google Scholar] [CrossRef]
- Saini, A.; Kaur, M.; Mayank, S.; Kuwar, A.; Kaur, N.; Singh, N. Hybrid nanoparticle based fluorescence switch for recognition of ketoprofen in aqueous media. Mol. Syst. Des. Eng. 2020, 5, 1428–1436. [Google Scholar] [CrossRef]
- Jouyban, A.; Rahimpour, E. Optical sensors based on silver nanoparticles for determination of pharmaceuticals: An overview of advances in the last decade. Talanta 2020, 217, 121071. [Google Scholar] [CrossRef]
- Sun, X.; Liu, P.; Mancin, F. Sensor arrays made by self-organized nanoreceptors for detection and discrimination of carboxylate drugs. Analyst 2018, 143, 5754–5763. [Google Scholar] [CrossRef]
- Liu, Y.; Minami, T.; Nishiyabu, R.; Wang, Z.; Anzenbacher, P., Jr. Sensing of carboxylate drugs in urine by a supramolecular sensor array. J. Am. Chem. Soc. 2013, 135, 7705–7712. [Google Scholar] [CrossRef]
- Akdeniz, A.; Mosca, L.; Minami, T.; Anzenbacher, P. Sensing of enantiomeric excess in chiral carboxylic acids. Chem. Commun. 2015, 51, 5770–5773. [Google Scholar] [CrossRef] [PubMed]
- Pushina, M.; Koutnik, P.; Nishiyabu, R.; Minami, T.; Savechenkov, P.; Anzenbacher, P., Jr. Anion Sensing by Fluorescent Expanded Calixpyrroles. Chem. Eur. J. 2018, 24, 4879–4884. [Google Scholar] [CrossRef] [PubMed]
- Akdeniz, A.; Minami, T.; Watanabe, S.; Yokoyama, M.; Ema, T.; Anzenbacher, P., Jr. Determination of enantiomeric excess of carboxylates by fluorescent macrocyclic sensors. Chem. Sci. 2016, 7, 2016–2022. [Google Scholar] [CrossRef]
- Picci, G.; Aragoni, M.C.; Arca, M.; Caltagirone, C.; Formica, M.; Fusi, V.; Giorgi, L.; Ingargiola, F.; Lippolis, V.; Macedi, E.; et al. Fluorescent sensing of non-steroidal anti-inflammatory drugs naproxen and ketoprofen by dansylated squaramide-based receptors. Org. Biomol. Chem. 2023, 21, 2968–2975. [Google Scholar] [CrossRef] [PubMed]
- Romano, G.M.; Mummolo, L.; Savastano, M.; Paoli, P.; Rossi, P.; Prodi, L.; Bencini, A. Polyamine receptors containing anthracene as fluorescent probes for ketoprofen in H2O/EtOH solution. Chem. Commun. 2022, 58, 7022–7025. [Google Scholar] [CrossRef]
- Paderni, D.; Macedi, E.; Giacomazzo, G.E.; Formica, M.; Giorgi, L.; Valtancoli, B.; Rossi, P.; Paoli, P.; Conti, L.; Fusi, V.; et al. A new biphenol-dipicolylamine based ligand and its dinuclear Zn2+ complex as fluorescent sensors for ibuprofen and ketoprofen in aqueous solution. Dalton Trans. 2024, 53, 9495–9509. [Google Scholar] [CrossRef]
- Martell, E.; Smith, R.M.; Motekaitis, R.J. NIST Standard Reference Database 46. In NIST Critically Selected Stability Constants of Metal Complexes Database, Version 8.0; Texas A&M University: College Station, TX, USA, 2004. [Google Scholar]
- Alarcón, J.; Aucejo, R.; Albelda, M.T.; Alves, S.; Clares, M.P.; García-España, E.; Lodeiro, C.; Marchin, K.L.; Parola, A.J.; Pina, F.; et al. Fluorescent type II materials from naphthylmethyl polyamine precursor. Supramol. Chem. 2004, 16, 573–580. [Google Scholar] [CrossRef]
- Valeur, B. Molecular Fluorescence Principles and Applications; Wiley-VCH: Weinheim, Germany, 2001. [Google Scholar]
- Alves, S.; Pina, F.; Albelda, M.; García-España, E.; Soriano, C.; Luis, S.V. Open-Chain Polyamine Ligands Bearing an Anthracene Unit–Chemosensors for Logic Operations at the Molecular Level. Eur. J. Inorg. Chem. 2001, 2001, 405–412. [Google Scholar] [CrossRef]
- Bazzicalupi, C.; Bencini, A.; Bianchi, A.; Giorgi, C.; Fusi, V.; Valtancoli, B.; Bernardo, M.A.; Pina, F. Effect of protonation and Zn(II) coordination on the fluorescence emission of a phenanthroline-containing macrocycle. An unusual case of “nonemissive” Zn(II) complex. Inorg. Chem. 1999, 38, 3806–3813. [Google Scholar] [CrossRef]
- Gans, P.; Sabatini, A.; Vacca, A. Investigation of equilibria in solution. Determination of equilibrium constants with the HYPERQUAD suite of programs. Talanta 1996, 43, 1739–1753. [Google Scholar] [CrossRef]
- Irving, H.; Williams, R.J.P.; Ferrett, D.J.; Williams, A.E. The influence of ring size upon the stability of metal chelates. J. Chem. Soc. 1954, 3494–3504. [Google Scholar] [CrossRef]
- Cukrowski, I.; Cukrowska, E.; Hancock, R.D.; Anderegg, G. The effect of chelate ring size on metal ion size-based selectivity in polyamine ligands containing pyridyl and saturated nitrogen donor groups. Anal. Chim. Acta 1995, 312, 307–321. [Google Scholar] [CrossRef]
- Lee, B.; Richards, F.M. The interpretation of protein structures: Estimation of static accessibility. J. Mol. Biol. 1971, 55, 379–400. [Google Scholar] [CrossRef]
- Mitternacht, S. FreeSASA: An open-source C library for solvent accessible surface area calculations. F1000Research 2016, 5, 189. [Google Scholar] [CrossRef]
- Tan, S.S.; Kim, S.J.; Kool, E.T. Differentiating between fluorescence-quenching metal ions with polyfluorophore sensors built on a DNA backbone. J. Am. Chem. Soc. 2011, 133, 2664–2671. [Google Scholar] [CrossRef]
- Nugent, J.W.; Lee, H.; Lee, H.S.; Reibenspies, J.H.; Hancock, R.D. The effect of π contacts between metal ions and fluorophores on the fluorescence of PET sensors: Implications for sensor design for cations and anions. Inorg. Chem. 2014, 53, 9014–9026. [Google Scholar] [CrossRef]
- Romano, G.M.; Simonini Steiner, Y.T.; Bartoli, F.; Conti, L.; Macedi, E.; Bazzicalupi, C.; Rossi, P.; Paoli, P.; Innocenti, M.; Bencini, A.; et al. Selective binding and fluorescence sensing of Zn(II)/Cd(II) using macrocyclic tetra-amines with different fluorophores: Insights into the design of selective chemosensors for transition metals. Dalton Trans. 2025, 54, 1689–1702. [Google Scholar] [CrossRef]
- Bartoli, F.; Bencini, A.; Conti, L.; Giorgi, C.; Valtancoli, B.; Paoli, P.; Rossi, P.; Le Bris, N.; Tripier, R. Catching anions with coloured assemblies: Binding of pH indicators by a giant-size polyammonium macrocycle for anion naked-eye recognition. Org. Biomol. Chem. 2016, 14, 8309–8321. [Google Scholar] [CrossRef]
- Adams, M.J.; Highfield, J.C.; Kirkbright, G.F. Determination of absolute fluorescence quantum efficiency of quinine bisulfate in aqueous medium by optoacoustic spectrometry. Anal. Chem. 1997, 49, 1850–1852. [Google Scholar] [CrossRef]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695–1697. [Google Scholar] [CrossRef]
- Hoover, W.G. Constant-pressure equations of motion. Phys. Rev. A 1986, 34, 2499–2500. [Google Scholar] [CrossRef]
- Parrinello, M.; Rahman, A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar] [CrossRef]
- Hornak, V.; Abel, R.; Okur, A.; Strockbine, B.; Roitberg, A.; Simmerling, C. Comparison of multiple amber force fields and development of improved protein backbone parameters. Proteins 2006, 65, 712–725. [Google Scholar] [CrossRef] [PubMed]
- Bayly, C.I.; Cieplak, P.; Cornell, W.D.; Kollman, P.A. A wellbehaved electrostatic potential based method using charge restraints for deriving atomic charges: The RESP model. J. Phys. Chem. 1993, 97, 10269–10280. [Google Scholar] [CrossRef]
- Li, P.; Roberts, B.P.; Chakravorty, D.K.; Merz, K.M., Jr. Rational Design of Particle Mesh Ewald Compatible Lennard-Jones. Parameters for +2 Metal Cations in Explicit Solvent. J. Chem. Theory Comput. 2013, 9, 2733–2748. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- de Oliveira Cavalcante, A.; Chelli, R. Polarizability relaxation in water/ethanol mixtures. J. Mol. Liq. 2021, 332, 115839. [Google Scholar] [CrossRef]
- Essmann, U.; Perera, M.L.; Berkowitz, M.L.; Darden, T.; Lee, H.; Pedersen, G.L. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577–8593. [Google Scholar] [CrossRef]
- Tuckerman, M.E.; Berne, B.; Martyna, G. Reversible multiple time scale molecular dynamics. J. Chem. Phys. 1992, 97, 1990–2001. [Google Scholar] [CrossRef]
- Marsili, S.; Signorini, G.; Chelli, R.; Marchi, M.; Procacci, P. ORAC: A molecular dynamics simulation program to explore free energy surfaces in biomolecular systems at the atomistic level. J. Comput. Chem. 2010, 31, 1106–1116. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Vosko, H.; Wilk, L.; Nusair, M. Accurate spin-dependent electron liquid correlation energies for local spin density calculations: A critical analysis. Can. J. Phys. 1980, 58, 1200–1211. [Google Scholar] [CrossRef]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comp. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
- Dunning, T.H., Jr.; Hay, P.J. Methods of electronic structure theory. In Modern Theoretical Chemistry; Schaefer, H.F., III, Ed.; Plenum: New York, NY, USA, 1977; Volume 3, pp. 1–28. [Google Scholar]
- Tomasi, J.; Mennucci, B.; Cammi, R. Quantum mechanical continuum solvation models. Chem. Rev. 2005, 105, 2999–3094. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision B.01; Gaussian, Inc.: Wallingford, CT, USA, 2016.


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Simonini Steiner, Y.T.; Mummolo, L.; Zartit, R.; Innocenti, M.; Bonechi, M.; Savastano, M.; Prodi, L.; Bencini, A.; Chelli, R.; Romano, G.M. Ketoprofen Recognition and Sensing by Zn(II) Complexes with Fluorogenic Triamine Receptors. Molecules 2025, 30, 4556. https://doi.org/10.3390/molecules30234556
Simonini Steiner YT, Mummolo L, Zartit R, Innocenti M, Bonechi M, Savastano M, Prodi L, Bencini A, Chelli R, Romano GM. Ketoprofen Recognition and Sensing by Zn(II) Complexes with Fluorogenic Triamine Receptors. Molecules. 2025; 30(23):4556. https://doi.org/10.3390/molecules30234556
Chicago/Turabian StyleSimonini Steiner, Yschtar Tecla, Liviana Mummolo, Rania Zartit, Massimo Innocenti, Marco Bonechi, Matteo Savastano, Luca Prodi, Andrea Bencini, Riccardo Chelli, and Giammarco Maria Romano. 2025. "Ketoprofen Recognition and Sensing by Zn(II) Complexes with Fluorogenic Triamine Receptors" Molecules 30, no. 23: 4556. https://doi.org/10.3390/molecules30234556
APA StyleSimonini Steiner, Y. T., Mummolo, L., Zartit, R., Innocenti, M., Bonechi, M., Savastano, M., Prodi, L., Bencini, A., Chelli, R., & Romano, G. M. (2025). Ketoprofen Recognition and Sensing by Zn(II) Complexes with Fluorogenic Triamine Receptors. Molecules, 30(23), 4556. https://doi.org/10.3390/molecules30234556