DFT Calculations of Structure and IR Spectra of M@C60 and M2@C60 Endofullerenes (M=Sc and Y)
Abstract
1. Introduction
2. Results and Discussion
2.1. Structure of M@C60 and M2@C60 Endofullerenes
2.2. Energy Stability and Availability of M@C60 and M2@C60 Structures
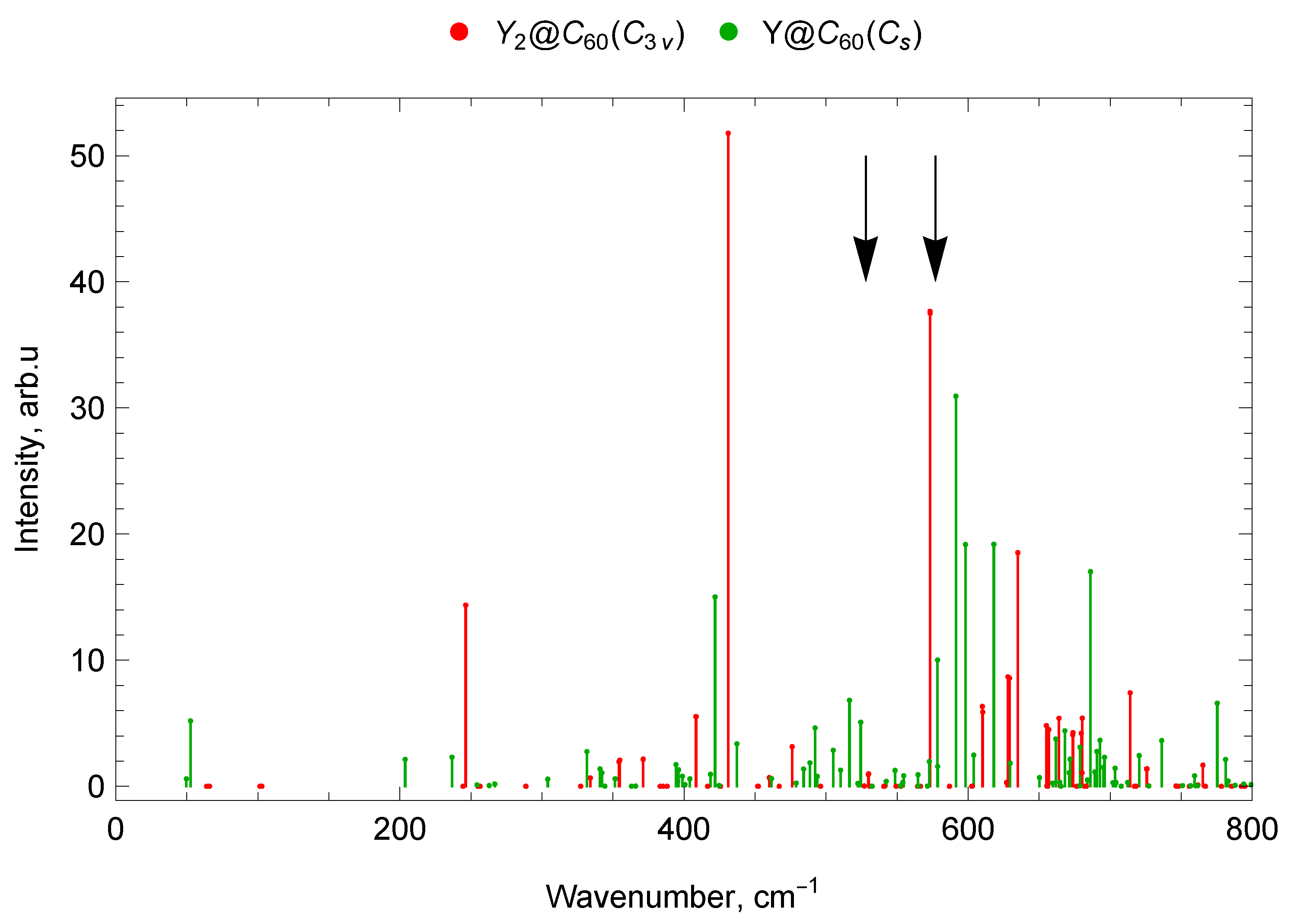
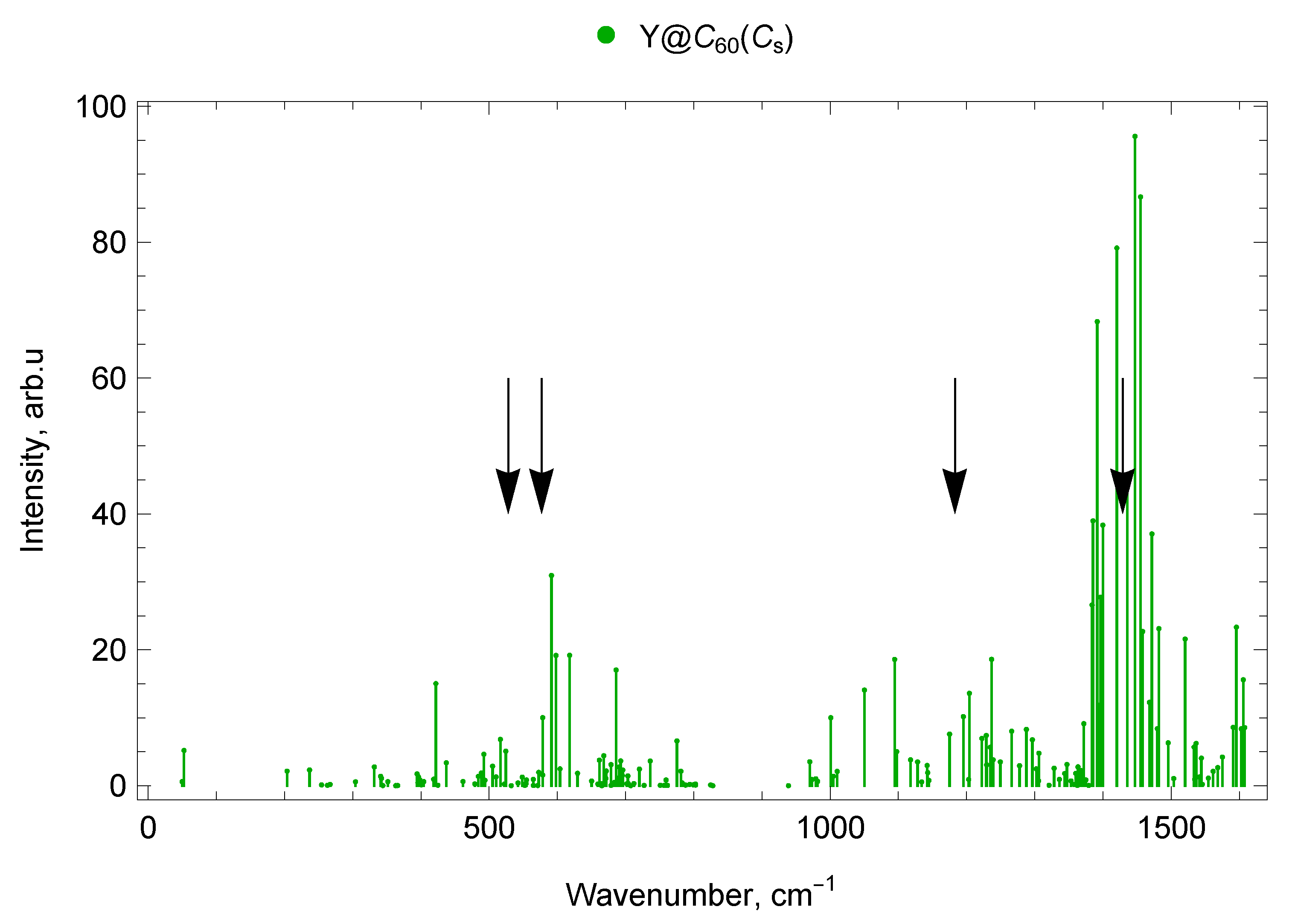
2.3. Vibrational Spectra of the M@C60 and M2@C60 Endofullerenes
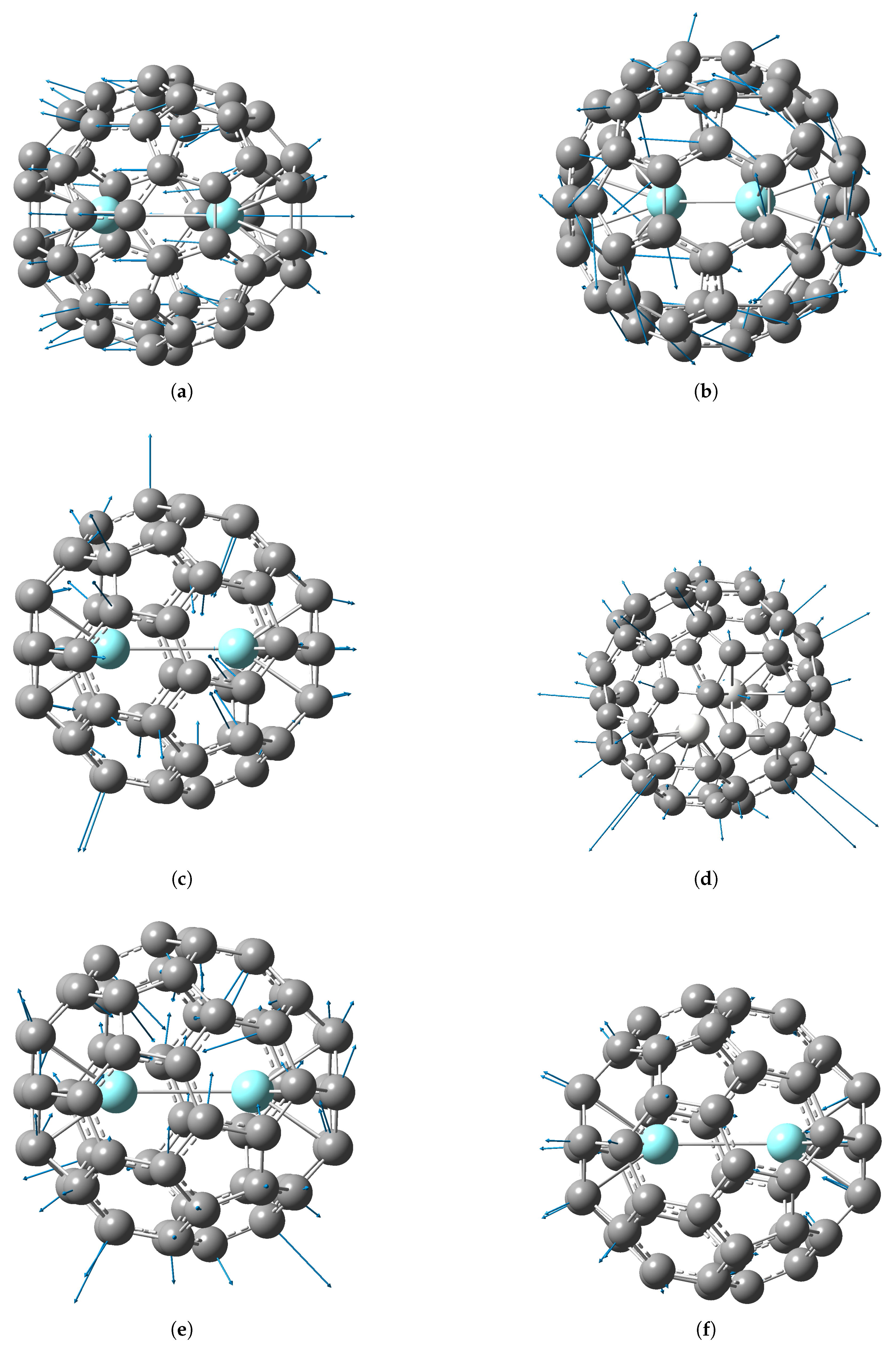
2.4. M–Cage Modes in Mono- and di-EMFs
2.5. Spectra of Mono-EMFs of Sc and Y
2.5.1. Sc@C60 ()
2.5.2. Y@C60 ()
2.6. Spectra of di-EMFs of Sc and Y
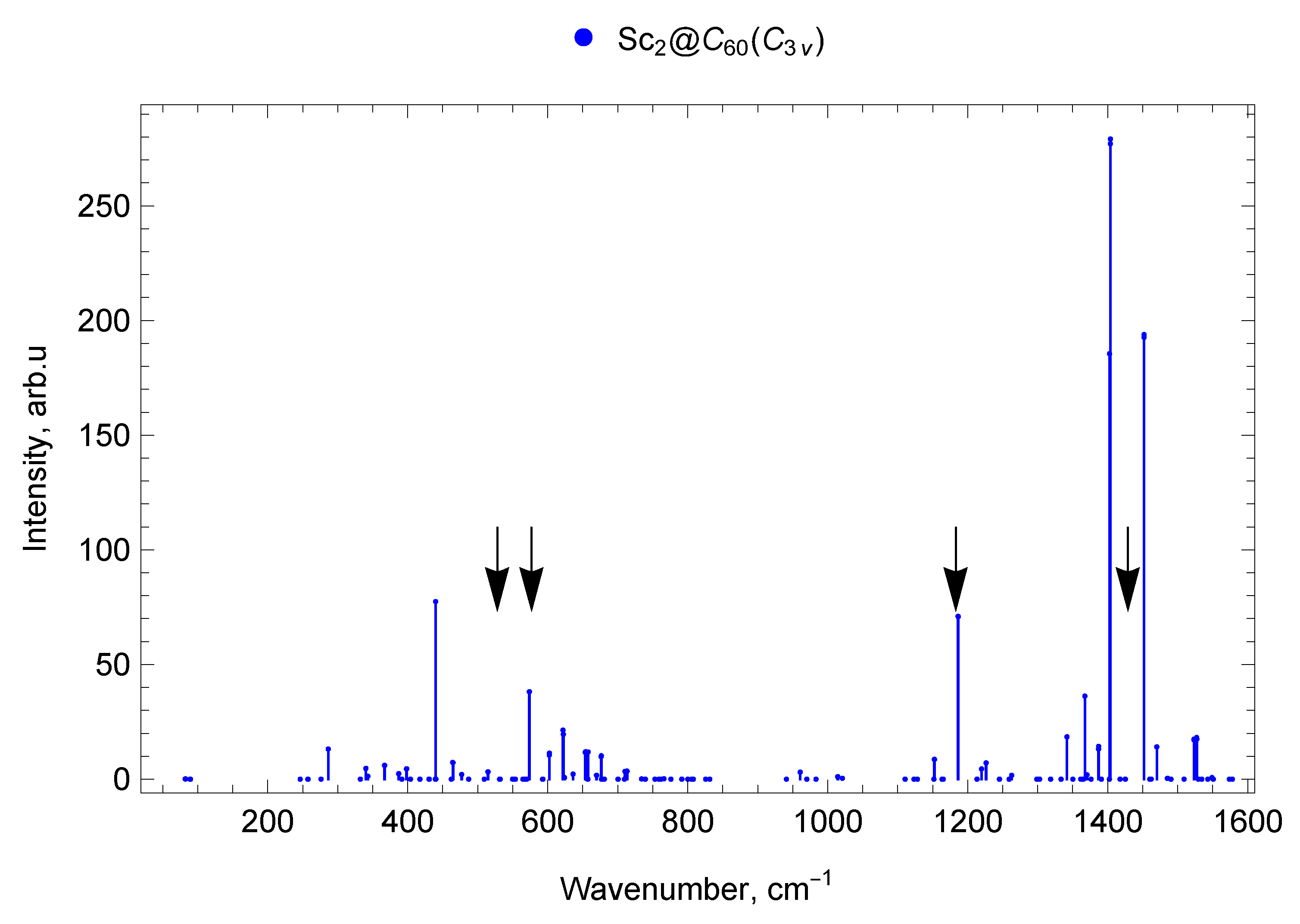
2.6.1. Sc2@C60 ()
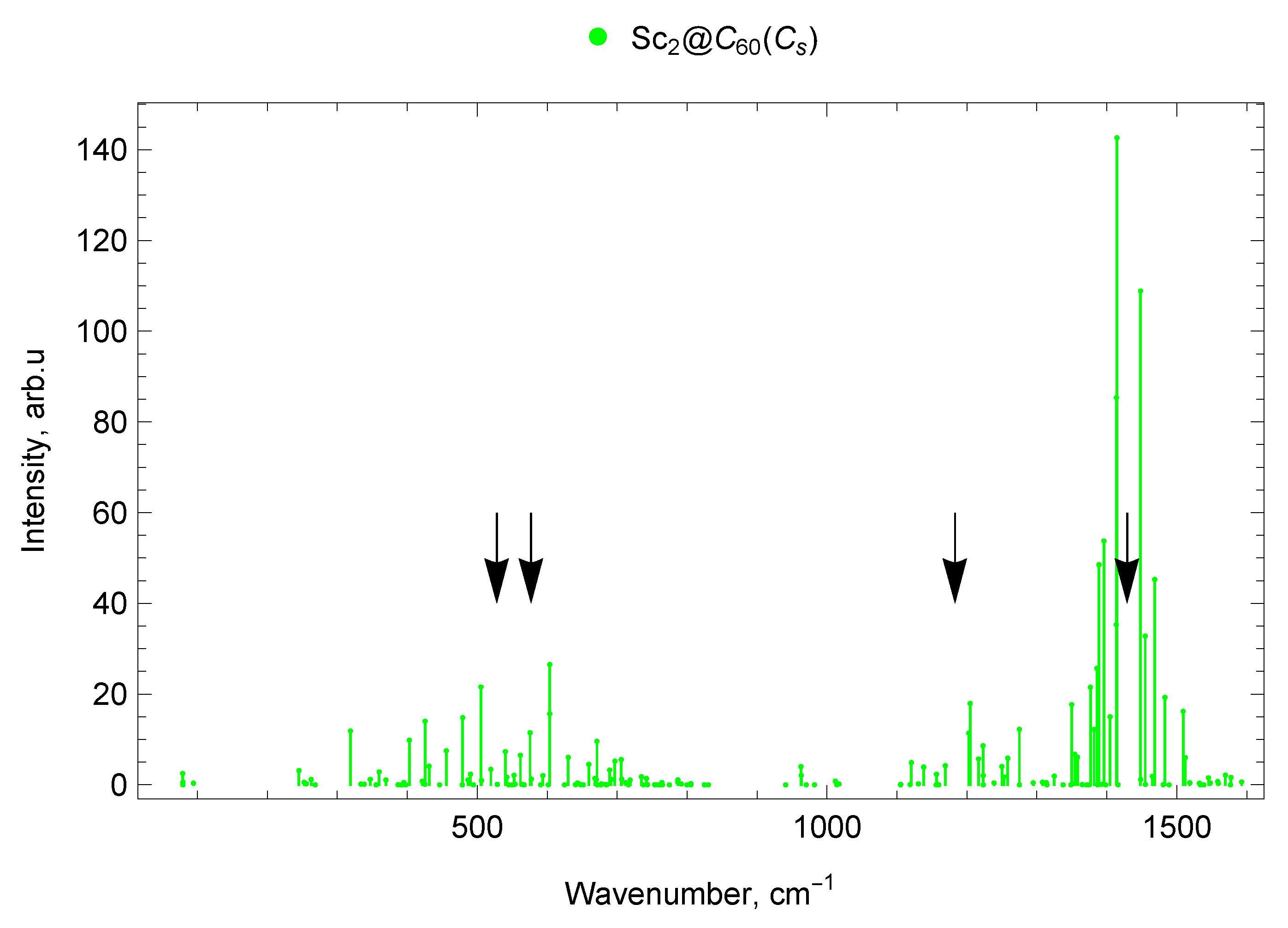
2.6.2. Sc2@C60 ()
2.6.3. Y2@C60 ()
2.7. Comparison of the Calculated Spectra
2.7.1. Spectra of Scandium Mono- and di-EMFs
2.7.2. Spectra of Yttrium Mono- and di-EMFs
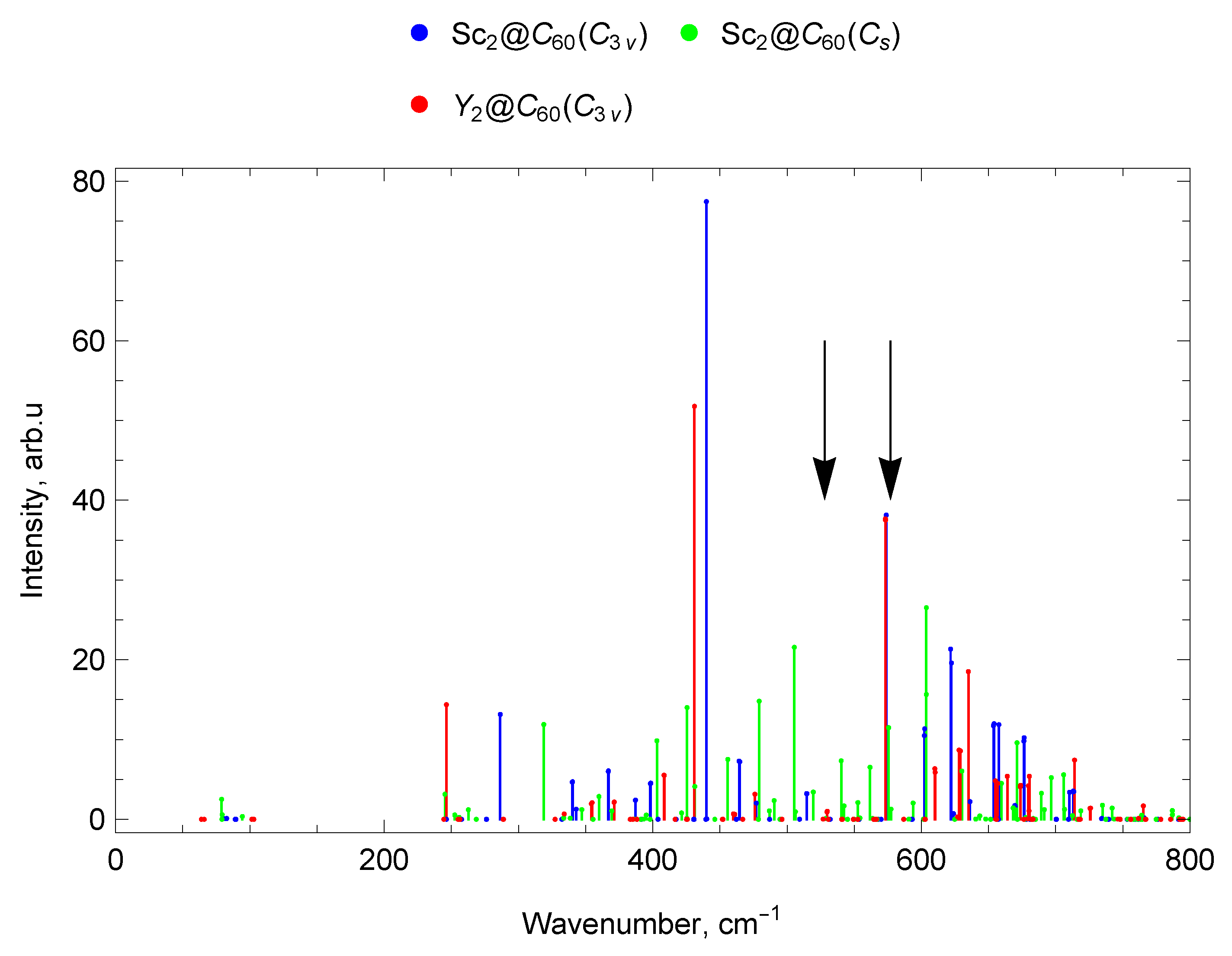
2.7.3. Spectra of Sc and Y di-EMFs
3. Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| No. | () | () | ||
|---|---|---|---|---|
| 1 | 54.9188 | 10.5034 | 49.762 | 0.5939 |
| 2 | 84.3682 | 1.3061 | 52.622 | 5.1854 |
| 3 | 231.9072 | 2.1295 | 203.7065 | 2.1403 |
| 4 | 245.2244 | 1.8977 | 236.669 | 2.3121 |
| 5 | 254.8434 | 0.275 | 254.2988 | 0.1129 |
| 6 | 265.6296 | 0.036 | 262.8707 | 0.0603 |
| 7 | 269.5616 | 0.37 | 266.813 | 0.1857 |
| 8 | 319.6795 | 1.2952 | 304.1148 | 0.5722 |
| 9 | 335.255 | 1.2511 | 331.6442 | 2.7561 |
| 10 | 338.5788 | 0.9032 | 340.8941 | 1.3791 |
| 11 | 344.0158 | 1.3401 | 342.1575 | 1.0795 |
| 12 | 345.6743 | 0.0243 | 344.2537 | 0.0151 |
| 13 | 354.3939 | 1.5238 | 351.5146 | 0.5949 |
| 14 | 364.2819 | 0.1483 | 363.0392 | 0.0128 |
| 15 | 378.7477 | 0.8108 | 365.9182 | 0.0229 |
| 16 | 398.3175 | 0.78 | 394.3682 | 1.7211 |
| 17 | 399.396 | 0.0095 | 395.6482 | 0.4245 |
| 18 | 399.772 | 0.6038 | 396.2064 | 1.315 |
| 19 | 401.7526 | 0.2977 | 398.8513 | 0.7967 |
| 20 | 404.719 | 0.3872 | 400.7425 | 0.1307 |
| 21 | 416.5978 | 2.3301 | 404.1454 | 0.5953 |
| 22 | 422.8969 | 1.1861 | 418.6619 | 0.9549 |
| 23 | 426.2233 | 11.2429 | 421.8858 | 15.0228 |
| 24 | 426.9951 | 2.4991 | 424.7635 | 0.0654 |
| 25 | 442.7812 | 3.82 | 437.2006 | 3.3695 |
| 26 | 463.2727 | 2.3697 | 461.6701 | 0.6099 |
| 27 | 479.0408 | 0.0182 | 478.956 | 0.2597 |
| 28 | 484.8858 | 2.7619 | 484.2166 | 1.3652 |
| 29 | 493.4576 | 0.8953 | 488.6431 | 1.863 |
| 30 | 500.0551 | 0.0035 | 492.2553 | 4.6305 |
| 31 | 500.9249 | 1.8808 | 493.8308 | 0.786 |
| 32 | 506.4679 | 3.1632 | 505.055 | 2.8607 |
| 33 | 511.6815 | 1.0673 | 510.2221 | 1.2842 |
| 34 | 519.3214 | 10.2078 | 516.4876 | 6.8183 |
| 35 | 523.8925 | 0.8604 | 522.3363 | 0.2304 |
| 36 | 529.5547 | 10.6873 | 524.3846 | 5.0813 |
| 37 | 538.0455 | 0.0683 | 532.4612 | 0.0058 |
| 38 | 543.0311 | 0.5084 | 542.3137 | 0.3999 |
| 39 | 552.3908 | 1.145 | 548.5767 | 1.2618 |
| 40 | 553.0114 | 0.0223 | 552.3477 | 0.0395 |
| 41 | 555.042 | 0.3994 | 554.0949 | 0.3178 |
| 42 | 557.2458 | 2.8281 | 554.637 | 0.8385 |
| 43 | 563.5956 | 2.3317 | 564.7591 | 0.9204 |
| 44 | 565.9737 | 0.1446 | 564.9387 | 0.03 |
| 45 | 571.9696 | 0.0044 | 571.3255 | 0.02 |
| 46 | 575.3572 | 4.6815 | 572.7128 | 1.9636 |
| 47 | 578.9891 | 2.1215 | 578.4874 | 10.0132 |
| 48 | 583.4793 | 15.3897 | 578.5398 | 1.5721 |
| 49 | 592.3889 | 26.0894 | 591.3812 | 30.938 |
| 50 | 606.2789 | 12.8187 | 598.0936 | 19.172 |
| 51 | 609.53 | 0.7846 | 603.9177 | 2.4704 |
| 52 | 637.2138 | 2.3095 | 618.081 | 19.1911 |
| 53 | 640.9119 | 1.9561 | 629.5912 | 1.8307 |
| 54 | 651.6078 | 1.1549 | 650.2402 | 0.6928 |
| 55 | 662.381 | 0.0207 | 659.5293 | 0.256 |
| 56 | 663.3835 | 1.9392 | 661.6663 | 3.7551 |
| 57 | 666.241 | 0.1712 | 664.5723 | 0.3112 |
| 58 | 667.1808 | 0.3004 | 665.2914 | 0.004 |
| 59 | 668.799 | 3.6108 | 668.0754 | 4.4051 |
| 60 | 670.3037 | 2.6129 | 671.0978 | 1.0753 |
| 61 | 674.1803 | 0.0278 | 671.7388 | 2.1576 |
| 62 | 676.6796 | 4.4683 | 678.7048 | 0.0388 |
| 63 | 677.0959 | 1.0939 | 678.7211 | 3.099 |
| 64 | 683.0884 | 1.2403 | 683.9271 | 0.5006 |
| 65 | 687.6209 | 11.1933 | 686.1794 | 17.0234 |
| 66 | 688.7571 | 0.8989 | 689.2218 | 1.1416 |
| 67 | 691.4907 | 4.1649 | 690.6114 | 2.7627 |
| 68 | 693.3245 | 1.6307 | 692.8733 | 3.6523 |
| 69 | 694.0059 | 1.4743 | 695.2835 | 1.5051 |
| 70 | 695.173 | 2.2695 | 695.9895 | 2.2944 |
| 71 | 704.101 | 0.0227 | 701.9196 | 0.2835 |
| 72 | 704.7625 | 0.494 | 703.439 | 1.4335 |
| 73 | 705.0558 | 0.3317 | 703.9615 | 0.2426 |
| 74 | 705.0664 | 0.0904 | 703.9766 | 0.3184 |
| 75 | 709.009 | 0.1873 | 707.747 | 0.011 |
| 76 | 711.8809 | 0.087 | 712.2943 | 0.3092 |
| 77 | 722.2866 | 3.2397 | 720.3689 | 2.4373 |
| 78 | 727.7552 | 0.1452 | 727.1894 | 0.031 |
| 79 | 736.5369 | 1.9579 | 736.1791 | 3.6256 |
| 80 | 738.2888 | 0.1788 | 750.9225 | 0.0559 |
| 81 | 755.761 | 0.0073 | 756.5885 | 0.0462 |
| 82 | 758.2315 | 0.0831 | 759.3982 | 0.835 |
| 83 | 760.5557 | 0.3114 | 760.0718 | 0.0453 |
| 84 | 762.3751 | 0.0989 | 761.4314 | 0.0444 |
| 85 | 778.562 | 4.9404 | 775.3487 | 6.5901 |
| 86 | 783.8644 | 1.1869 | 781.1952 | 2.1291 |
| 87 | 788.0201 | 0.1788 | 782.9962 | 0.4141 |
| 88 | 788.6326 | 0.0309 | 787.9893 | 0.0814 |
| 89 | 799.8413 | 0.168 | 793.9862 | 0.1776 |
| 90 | 801.5983 | 0.2498 | 799.1997 | 0.1369 |
| 91 | 803.2158 | 0.239 | 802.6487 | 0.2448 |
| 92 | 803.2443 | 0.3458 | 802.6651 | 0.0862 |
| 93 | 825.739 | 0.1767 | 824.7525 | 0.1069 |
| 94 | 826.8086 | 0.1544 | 826.1007 | 0.0672 |
| 95 | 829.581 | 0.0003 | 827.9333 | 0.0032 |
| 96 | 941.4669 | 0 | 938.9152 | 0.0013 |
| 97 | 973.1506 | 1.3964 | 970.1702 | 3.52 |
| 98 | 975.1995 | 1.242 | 973.309 | 0.9045 |
| 99 | 982.0183 | 1.0759 | 978.9959 | 1.0072 |
| 100 | 984.5874 | 0.6413 | 981.6339 | 0.6234 |
| 101 | 1001.0734 | 6.3485 | 1000.9679 | 10.0023 |
| 102 | 1005.9538 | 0.6753 | 1004.6588 | 1.3841 |
| 103 | 1010.1159 | 2.2504 | 1010.3693 | 2.1099 |
| 104 | 1069.2678 | 19.8583 | 1050.2398 | 14.0723 |
| 105 | 1104.8915 | 8.3598 | 1094.5464 | 18.5848 |
| 106 | 1106.6563 | 3.6433 | 1097.6029 | 5.0212 |
| 107 | 1121.624 | 4.2392 | 1117.9292 | 3.8061 |
| 108 | 1131.0334 | 2.6283 | 1128.2198 | 3.4907 |
| 109 | 1134.3259 | 0.0941 | 1134.1728 | 0.55 |
| 110 | 1144.1817 | 1.6187 | 1142.0874 | 2.9744 |
| 111 | 1144.2033 | 3.6899 | 1143.1169 | 1.9164 |
| 112 | 1144.889 | 0.3629 | 1144.7654 | 0.7733 |
| 113 | 1181.7175 | 9.4999 | 1175.1109 | 7.5938 |
| 114 | 1203.9204 | 6.4762 | 1195.3264 | 10.1651 |
| 115 | 1211.0441 | 2.7927 | 1203.1612 | 0.911 |
| 116 | 1212.4373 | 11.7736 | 1204.1803 | 13.5954 |
| 117 | 1224.9623 | 6.3276 | 1222.5103 | 6.9472 |
| 118 | 1231.1092 | 0.4618 | 1228.9144 | 7.3897 |
| 119 | 1233.9767 | 0.9676 | 1229.4857 | 3.0721 |
| 120 | 1236.8193 | 7.9966 | 1234.8869 | 5.6621 |
| 121 | 1240.1197 | 14.7899 | 1236.7402 | 18.5959 |
| 122 | 1241.8546 | 1.1859 | 1238.9986 | 3.7997 |
| 123 | 1252.3547 | 1.0543 | 1249.4936 | 3.4864 |
| 124 | 1275.8072 | 3.3947 | 1266.1577 | 8.0192 |
| 125 | 1285.4383 | 0.7219 | 1277.75 | 2.9424 |
| 126 | 1293.4739 | 5.8009 | 1287.7458 | 8.2785 |
| 127 | 1298.0086 | 5.622 | 1296.5271 | 6.7523 |
| 128 | 1306.0515 | 1.0948 | 1302.3494 | 2.4795 |
| 129 | 1307.2429 | 0.6915 | 1305.7566 | 0.7031 |
| 130 | 1309.6005 | 3.1042 | 1306.104 | 4.7755 |
| 131 | 1322.3785 | 0.0002 | 1321.0631 | 0.0612 |
| 132 | 1331.2151 | 3.0344 | 1328.4262 | 2.5652 |
| 133 | 1341.777 | 0.2741 | 1336.0932 | 0.9261 |
| 134 | 1345.581 | 1.5801 | 1343.9778 | 1.7768 |
| 135 | 1355.2006 | 0.3488 | 1347.2503 | 3.1169 |
| 136 | 1356.7307 | 1.1597 | 1353.1607 | 0.6969 |
| 137 | 1359.6725 | 0.1918 | 1357.4534 | 0.1664 |
| 138 | 1362.4249 | 1.3346 | 1360.0586 | 1.8072 |
| 139 | 1365.4416 | 0.1414 | 1362.5424 | 0.0419 |
| 140 | 1365.9558 | 0.2896 | 1363.3912 | 2.7744 |
| 141 | 1373.0613 | 3.5375 | 1367.8749 | 2.2178 |
| 142 | 1373.8142 | 0.7722 | 1371.9478 | 9.1227 |
| 143 | 1379.0199 | 1.5245 | 1375.033 | 0.845 |
| 144 | 1386.1731 | 0.0147 | 1379.1069 | 0.0336 |
| 145 | 1388.7594 | 6.1198 | 1384.0419 | 26.5846 |
| 146 | 1389.8179 | 20.8553 | 1385.4215 | 38.9756 |
| 147 | 1396.4684 | 1.0623 | 1391.6847 | 68.3 |
| 148 | 1398.8875 | 11.5202 | 1395.6489 | 11.8558 |
| 149 | 1402.7378 | 22.337 | 1396.4134 | 27.749 |
| 150 | 1411.8222 | 74.3599 | 1399.8106 | 38.3463 |
| 151 | 1433.885 | 74.3562 | 1420.3688 | 79.1329 |
| 152 | 1449.0511 | 28.2437 | 1435.8272 | 44.7941 |
| 153 | 1456.4103 | 11.3805 | 1447.0131 | 95.5718 |
| 154 | 1458.6693 | 68.3782 | 1455.2032 | 86.6558 |
| 155 | 1467.1926 | 47.612 | 1458.1421 | 22.6936 |
| 156 | 1468.3445 | 1.7234 | 1468.2107 | 12.2601 |
| 157 | 1474.4349 | 27.5706 | 1471.7573 | 37.0593 |
| 158 | 1482.7782 | 8.8604 | 1479.7459 | 8.3834 |
| 159 | 1484.6975 | 27.6066 | 1482.0358 | 23.1165 |
| 160 | 1501.0501 | 6.3663 | 1495.6085 | 6.3091 |
| 161 | 1508.524 | 0.9038 | 1503.7295 | 1.0529 |
| 162 | 1519.3326 | 27.1187 | 1520.5333 | 21.5776 |
| 163 | 1539.6454 | 0.0009 | 1533.5779 | 5.6703 |
| 164 | 1542.481 | 5.6754 | 1534.495 | 0.9343 |
| 165 | 1544.5977 | 6.4449 | 1536.6477 | 6.2245 |
| 166 | 1549.4958 | 0.4941 | 1541.3156 | 1.2692 |
| 167 | 1551.6914 | 1.0817 | 1544.3037 | 4.0452 |
| 168 | 1553.4086 | 0.4043 | 1545.6009 | 0.2033 |
| 169 | 1563.0796 | 2.8773 | 1554.5661 | 1.1125 |
| 170 | 1571.1412 | 2.4778 | 1561.5705 | 2.1147 |
| 171 | 1572.8589 | 2.5782 | 1568.3456 | 2.6574 |
| 172 | 1583.0124 | 4.0122 | 1575.1561 | 4.2037 |
| 173 | 1598.0393 | 5.2015 | 1590.9557 | 8.5787 |
| 174 | 1601.3145 | 14.1149 | 1595.6297 | 23.3172 |
| 175 | 1604.6917 | 9.0311 | 1602.8863 | 8.3741 |
| 176 | 1611.2009 | 8.6319 | 1605.774 | 15.5851 |
| 177 | 1612.355 | 5.146 | 1607.8493 | 8.5419 |
| No. | () | () | () | |||
|---|---|---|---|---|---|---|
| 1 | 81.95 | 0.0891 | 78.95 | 2.5033 | 63.95 | 0.0000 |
| 2 | 82.6828 | 0.0991 | 79.24 | 0.0050 | 65.99 | 0.0000 |
| 3 | 89.0201 | 0 | 79.39 | 0.5868 | 101.49 | 0.0028 |
| 4 | 89.6563 | 0 | 94.37 | 0.3545 | 102.91 | 0.0038 |
| 5 | 246.3521 | 0 | 245.22 | 3.1424 | 244.43 | 0.0001 |
| 6 | 257.2319 | 0 | 252.59 | 0.5416 | 246.34 | 14.3723 |
| 7 | 257.6413 | 0 | 255.78 | 0.2414 | 254.99 | 0.0000 |
| 8 | 276.0961 | 0.0002 | 262.64 | 1.1927 | 256.45 | 0.0000 |
| 9 | 276.2172 | 0.0001 | 268.56 | 0.0000 | 288.63 | 0.0001 |
| 10 | 286.4063 | 13.1518 | 318.83 | 11.8847 | 288.83 | 0.0000 |
| 11 | 332.2817 | 0.0017 | 333.69 | 0.1506 | 327.27 | 0.0005 |
| 12 | 340.0485 | 4.6591 | 338.53 | 0.1369 | 334.06 | 0.6695 |
| 13 | 340.2518 | 4.7108 | 347.14 | 1.2174 | 354.24 | 1.9465 |
| 14 | 342.9838 | 1.2709 | 355.53 | 0.0000 | 354.80 | 2.0762 |
| 15 | 366.8752 | 5.9916 | 359.91 | 2.8679 | 371.23 | 2.1276 |
| 16 | 366.971 | 6.0703 | 369.47 | 1.0545 | 371.30 | 2.1624 |
| 17 | 386.998 | 2.3818 | 386.84 | 0.0332 | 383.21 | 0.0017 |
| 18 | 387.1514 | 2.4051 | 390.96 | 0.0000 | 383.34 | 0.0003 |
| 19 | 391.5877 | 0.0028 | 393.21 | 0.0315 | 385.23 | 0.0000 |
| 20 | 398.1662 | 4.4883 | 395.12 | 0.5279 | 388.18 | 0.0001 |
| 21 | 398.5032 | 4.5393 | 398.01 | 0.0000 | 408.35 | 5.5303 |
| 22 | 403.912 | 0.0002 | 403.06 | 9.8448 | 408.56 | 5.5210 |
| 23 | 417.3545 | 0 | 421.45 | 0.8017 | 416.58 | 0.0001 |
| 24 | 430.3878 | 0 | 425.30 | 0.1248 | 425.18 | 0.0004 |
| 25 | 430.7603 | 0 | 425.52 | 14.0096 | 425.68 | 0.0000 |
| 26 | 439.518 | 0.0001 | 431.30 | 4.1123 | 431.05 | 51.7812 |
| 27 | 439.882 | 77.4321 | 446.19 | 0.0000 | 451.87 | 0.0000 |
| 28 | 440.1611 | 0.0555 | 455.84 | 7.5080 | 452.28 | 0.0001 |
| 29 | 462.2293 | 0.0002 | 478.68 | 0.0031 | 460.01 | 0.6850 |
| 30 | 464.2559 | 7.295 | 479.20 | 14.8063 | 460.99 | 0.6246 |
| 31 | 464.7875 | 7.2196 | 486.83 | 1.0518 | 466.97 | 0.0000 |
| 32 | 477.0306 | 2.0317 | 490.38 | 2.3426 | 476.07 | 3.1430 |
| 33 | 486.9704 | 0 | 494.67 | 0.0000 | 496.17 | 0.0000 |
| 34 | 509.3085 | 0.0074 | 505.36 | 21.5666 | 526.88 | 0.0260 |
| 35 | 514.5194 | 3.2183 | 506.19 | 0.9547 | 529.70 | 0.9291 |
| 36 | 514.787 | 3.2154 | 519.52 | 3.4110 | 529.94 | 0.9939 |
| 37 | 531.1489 | 0 | 528.75 | 0.0927 | 530.64 | 0.0078 |
| 38 | 531.4358 | 0 | 540.27 | 7.3260 | 540.64 | 0.0000 |
| 39 | 532.068 | 0 | 542.38 | 1.6787 | 541.14 | 0.0000 |
| 40 | 549.7759 | 0 | 545.00 | 0.0000 | 549.30 | 0.0000 |
| 41 | 553.6764 | 0 | 549.92 | 0.0000 | 552.54 | 0.0001 |
| 42 | 553.7494 | 0 | 552.69 | 2.0966 | 552.64 | 0.0000 |
| 43 | 564.5495 | 0 | 554.21 | 0.1566 | 564.45 | 0.0002 |
| 44 | 564.6892 | 0 | 561.76 | 6.5229 | 565.45 | 0.0000 |
| 45 | 568.1453 | 0 | 563.62 | 0.1104 | 566.35 | 0.0003 |
| 46 | 570.0265 | 0.0015 | 567.02 | 0.0000 | 566.44 | 0.0002 |
| 47 | 573.756 | 38.1059 | 575.60 | 11.4872 | 573.18 | 37.6595 |
| 48 | 573.8159 | 38.1402 | 577.37 | 1.2664 | 573.28 | 37.5027 |
| 49 | 592.5356 | 0.0002 | 590.65 | 0.0219 | 586.86 | 0.0002 |
| 50 | 592.7212 | 0.0001 | 593.83 | 2.0420 | 602.52 | 0.0014 |
| 51 | 593.1775 | 0.0008 | 601.53 | 0.0107 | 602.90 | 0.0000 |
| 52 | 602.234 | 10.492 | 603.66 | 15.6539 | 609.98 | 6.3385 |
| 53 | 602.4031 | 11.3363 | 603.69 | 26.5221 | 610.24 | 5.8881 |
| 54 | 621.7374 | 21.346 | 624.80 | 0.0000 | 627.05 | 0.3042 |
| 55 | 622.3506 | 19.5939 | 630.13 | 6.0526 | 628.03 | 8.6707 |
| 56 | 623.9753 | 0.7065 | 640.48 | 0.0340 | 629.03 | 8.5735 |
| 57 | 636.1944 | 2.2156 | 643.48 | 0.4214 | 634.98 | 18.5265 |
| 58 | 653.6652 | 11.7356 | 647.90 | 0.0361 | 655.08 | 4.8152 |
| 59 | 654.105 | 11.9753 | 651.53 | 0.0000 | 655.41 | 0.0195 |
| 60 | 656.8444 | 0.0006 | 659.55 | 4.5040 | 655.95 | 0.0007 |
| 61 | 657.3784 | 0.0061 | 668.31 | 1.4273 | 656.75 | 4.4998 |
| 62 | 657.6973 | 11.8607 | 670.18 | 1.1774 | 663.97 | 5.3958 |
| 63 | 669.6253 | 1.7236 | 671.20 | 9.5921 | 673.65 | 4.0864 |
| 64 | 669.8302 | 1.6076 | 671.53 | 0.0003 | 673.81 | 4.2600 |
| 65 | 676.2943 | 9.7942 | 676.35 | 0.0295 | 676.38 | 0.0002 |
| 66 | 676.5571 | 10.223 | 676.94 | 0.0000 | 679.32 | 0.0718 |
| 67 | 676.7821 | 0.0021 | 677.70 | 0.2084 | 679.65 | 4.2042 |
| 68 | 677.3025 | 0.0013 | 683.31 | 0.0944 | 680.12 | 1.0623 |
| 69 | 677.6551 | 0.0271 | 684.95 | 0.0000 | 680.39 | 5.4029 |
| 70 | 678.2954 | 0.0001 | 689.37 | 3.2574 | 681.99 | 0.0059 |
| 71 | 680.814 | 0 | 691.51 | 1.2116 | 683.15 | 0.0003 |
| 72 | 700.2868 | 0 | 696.74 | 5.2250 | 714.04 | 7.4142 |
| 73 | 700.5939 | 0 | 705.86 | 5.5792 | 717.12 | 0.0017 |
| 74 | 709.5648 | 0.0001 | 706.51 | 1.2426 | 717.52 | 0.0024 |
| 75 | 710.3009 | 3.3806 | 712.45 | 0.4658 | 718.24 | 0.0002 |
| 76 | 713.0645 | 3.5423 | 716.04 | 0.0000 | 725.54 | 1.3798 |
| 77 | 713.4601 | 3.4636 | 718.69 | 1.0675 | 725.91 | 1.3945 |
| 78 | 734.1041 | 0.094 | 734.82 | 1.7653 | 746.32 | 0.0250 |
| 79 | 734.3033 | 0.1076 | 737.29 | 0.0000 | 746.41 | 0.0203 |
| 80 | 739.3554 | 0 | 742.02 | 1.3988 | 748.03 | 0.0002 |
| 81 | 739.498 | 0 | 743.59 | 0.0334 | 755.77 | 0.0000 |
| 82 | 753.1752 | 0.0003 | 753.61 | 0.0246 | 755.97 | 0.0000 |
| 83 | 753.2007 | 0 | 758.02 | 0.0011 | 761.56 | 0.0931 |
| 84 | 758.9885 | 0 | 760.67 | 0.0000 | 761.76 | 0.0957 |
| 85 | 761.4512 | 0.0005 | 763.46 | 0.0000 | 765.27 | 1.6817 |
| 86 | 761.5185 | 0.0006 | 764.00 | 0.5207 | 766.74 | 0.0008 |
| 87 | 766.0023 | 0.1636 | 764.66 | 0.0055 | 767.10 | 0.0001 |
| 88 | 775.852 | 0 | 774.78 | 0.0000 | 778.28 | 0.0004 |
| 89 | 776.0167 | 0 | 786.86 | 1.0939 | 785.52 | 0.0000 |
| 90 | 791.457 | 0 | 786.91 | 0.5732 | 792.36 | 0.0000 |
| 91 | 791.6218 | 0 | 791.72 | 0.1765 | 792.47 | 0.0000 |
| 92 | 800.0554 | 0 | 799.88 | 0.0000 | 794.11 | 0.0001 |
| 93 | 805.6614 | 0 | 804.42 | 0.1150 | 794.86 | 0.0000 |
| 94 | 805.8526 | 0 | 805.47 | 0.2774 | 802.17 | 0.0000 |
| 95 | 808.051 | 0 | 805.49 | 0.0256 | 802.24 | 0.0000 |
| 96 | 825.6711 | 0 | 824.75 | 0.0196 | 824.02 | 0.0000 |
| 97 | 825.7765 | 0 | 824.97 | 0.0000 | 824.13 | 0.0001 |
| 98 | 831.5413 | 0 | 830.38 | 0.0145 | 826.71 | 0.0000 |
| 99 | 940.985 | 0.0001 | 940.96 | 0.0000 | 935.18 | 0.0055 |
| 100 | 960.6919 | 3.0671 | 962.80 | 4.0195 | 938.13 | 7.5552 |
| 101 | 970.0638 | 0.0169 | 963.32 | 2.0807 | 956.24 | 0.2956 |
| 102 | 970.1174 | 0.015 | 970.33 | 0.0000 | 956.56 | 0.2961 |
| 103 | 983.2568 | 0.0001 | 982.16 | 0.0141 | 981.95 | 0.0001 |
| 104 | 1014.251 | 1.0647 | 1011.96 | 0.8107 | 1001.44 | 0.0430 |
| 105 | 1014.487 | 1.0751 | 1013.89 | 0.0286 | 1001.55 | 0.0417 |
| 106 | 1020.997 | 0.3986 | 1017.28 | 0.1740 | 1015.30 | 0.0021 |
| 107 | 1110.588 | 0 | 1105.21 | 0.0000 | 1093.94 | 0.0000 |
| 108 | 1110.621 | 0 | 1105.31 | 0.1068 | 1094.02 | 0.0001 |
| 109 | 1123.244 | 0 | 1118.83 | 0.0550 | 1100.79 | 0.0000 |
| 110 | 1123.404 | 0 | 1120.57 | 4.9126 | 1100.90 | 0.0002 |
| 111 | 1128.135 | 0 | 1130.58 | 0.2243 | 1103.17 | 0.0000 |
| 112 | 1151.748 | 0.0002 | 1138.20 | 3.9136 | 1108.10 | 0.0970 |
| 113 | 1152.372 | 8.6974 | 1156.04 | 0.0000 | 1108.66 | 0.0907 |
| 114 | 1152.537 | 8.6067 | 1156.62 | 2.3323 | 1137.65 | 0.0003 |
| 115 | 1163.412 | 0 | 1157.63 | 0.1048 | 1155.21 | 0.0002 |
| 116 | 1163.468 | 0 | 1159.73 | 0.0000 | 1155.31 | 0.0001 |
| 117 | 1165.1 | 0 | 1169.09 | 4.2220 | 1156.67 | 0.0000 |
| 118 | 1186.293 | 71.0026 | 1202.70 | 11.4163 | 1177.45 | 26.9316 |
| 119 | 1186.438 | 70.8642 | 1204.63 | 17.9355 | 1177.51 | 27.1322 |
| 120 | 1213.316 | 0.0012 | 1216.64 | 5.7063 | 1198.44 | 0.5152 |
| 121 | 1219.581 | 4.42 | 1223.06 | 8.6008 | 1198.57 | 0.3940 |
| 122 | 1219.821 | 4.4907 | 1223.33 | 2.0393 | 1201.28 | 8.2368 |
| 123 | 1226.307 | 7.0833 | 1223.39 | 0.0003 | 1206.87 | 0.0006 |
| 124 | 1245.295 | 0.0011 | 1238.88 | 0.4244 | 1225.29 | 0.0001 |
| 125 | 1245.421 | 0.0013 | 1250.03 | 4.0419 | 1225.48 | 0.0004 |
| 126 | 1259.181 | 0.0001 | 1253.01 | 1.7399 | 1243.67 | 0.6242 |
| 127 | 1259.237 | 0 | 1258.45 | 5.8822 | 1243.73 | 0.6234 |
| 128 | 1262.828 | 1.6848 | 1275.01 | 12.2292 | 1247.57 | 5.8973 |
| 129 | 1298.759 | 0 | 1275.16 | 0.0000 | 1277.21 | 0.0002 |
| 130 | 1298.822 | 0 | 1294.82 | 0.4487 | 1277.34 | 0.0009 |
| 131 | 1302.634 | 0 | 1307.98 | 0.5697 | 1284.88 | 0.0011 |
| 132 | 1318.451 | 0 | 1313.54 | 0.5133 | 1305.02 | 0.0027 |
| 133 | 1318.577 | 0 | 1314.33 | 0.0000 | 1312.35 | 0.0058 |
| 134 | 1333.39 | 0 | 1324.82 | 1.9123 | 1312.68 | 0.0077 |
| 135 | 1341.82 | 18.4106 | 1337.41 | 0.0000 | 1315.44 | 177.9984 |
| 136 | 1341.877 | 18.4887 | 1348.65 | 0.0000 | 1317.54 | 23.9301 |
| 137 | 1350.26 | 0 | 1349.83 | 17.6868 | 1317.92 | 25.0840 |
| 138 | 1361.42 | 0.0045 | 1354.19 | 6.7394 | 1331.82 | 0.0089 |
| 139 | 1363.96 | 0 | 1355.74 | 0.4737 | 1340.77 | 0.0082 |
| 140 | 1363.971 | 0 | 1358.22 | 6.1220 | 1346.10 | 0.0121 |
| 141 | 1365.289 | 0.0001 | 1364.80 | 0.0434 | 1346.79 | 81.2490 |
| 142 | 1367.395 | 36.2336 | 1370.87 | 0.0010 | 1347.23 | 82.6081 |
| 143 | 1370.049 | 1.8206 | 1374.98 | 0.0000 | 1349.60 | 0.0025 |
| 144 | 1370.413 | 1.9469 | 1376.59 | 21.4997 | 1349.86 | 0.0208 |
| 145 | 1376.264 | 0.0023 | 1381.82 | 12.2208 | 1364.25 | 10.6934 |
| 146 | 1386.941 | 13.1141 | 1385.77 | 25.6910 | 1364.41 | 10.9053 |
| 147 | 1387.036 | 14.325 | 1387.02 | 0.0046 | 1365.19 | 0.0058 |
| 148 | 1390.861 | 0.0002 | 1388.85 | 48.5261 | 1365.28 | 0.0138 |
| 149 | 1390.993 | 0.0001 | 1392.17 | 0.0763 | 1371.40 | 0.0078 |
| 150 | 1402.414 | 0.0007 | 1395.89 | 53.7825 | 1372.93 | 22.0939 |
| 151 | 1402.654 | 185.532 | 1398.46 | 0.0000 | 1373.17 | 84.6566 |
| 152 | 1403.807 | 277.0629 | 1404.65 | 15.0140 | 1384.21 | 53.7793 |
| 153 | 1403.904 | 279.1288 | 1413.42 | 35.3228 | 1384.33 | 54.4713 |
| 154 | 1417.706 | 0.0051 | 1413.73 | 85.3519 | 1393.55 | 0.0000 |
| 155 | 1425.242 | 0.0004 | 1414.49 | 142.6477 | 1397.62 | 0.0007 |
| 156 | 1425.284 | 0.0009 | 1416.01 | 0.0136 | 1397.80 | 0.0010 |
| 157 | 1451.926 | 192.5961 | 1448.29 | 108.8656 | 1428.93 | 326.6849 |
| 158 | 1452.03 | 193.8582 | 1448.37 | 1.1858 | 1428.99 | 325.9180 |
| 159 | 1460.183 | 0 | 1454.97 | 32.7941 | 1446.09 | 0.0006 |
| 160 | 1460.246 | 0 | 1455.17 | 0.0850 | 1446.11 | 0.0003 |
| 161 | 1462.182 | 0.0292 | 1465.19 | 1.8584 | 1451.21 | 0.0085 |
| 162 | 1470.152 | 14.083 | 1468.47 | 45.2911 | 1455.82 | 31.2813 |
| 163 | 1485.167 | 0.3396 | 1480.60 | 0.0367 | 1466.23 | 0.0005 |
| 164 | 1485.246 | 0.3957 | 1483.05 | 19.2811 | 1466.46 | 0.0005 |
| 165 | 1490.299 | 0 | 1488.98 | 0.0000 | 1476.84 | 0.2428 |
| 166 | 1490.433 | 0.0001 | 1509.09 | 16.2044 | 1476.98 | 0.2008 |
| 167 | 1509.153 | 0 | 1512.26 | 6.0089 | 1502.95 | 0.0001 |
| 168 | 1523.09 | 17.2113 | 1518.62 | 0.4619 | 1505.30 | 16.6201 |
| 169 | 1523.397 | 17.4556 | 1532.34 | 0.3468 | 1505.51 | 16.4199 |
| 170 | 1527.187 | 18.1574 | 1533.65 | 0.0000 | 1515.71 | 0.0000 |
| 171 | 1527.337 | 17.4534 | 1534.18 | 0.0326 | 1521.41 | 5.8033 |
| 172 | 1529.74 | 0.0003 | 1538.52 | 0.0000 | 1521.60 | 5.8307 |
| 173 | 1534.508 | 0 | 1545.24 | 1.5445 | 1521.65 | 0.0559 |
| 174 | 1542.936 | 0.0014 | 1547.81 | 0.4148 | 1526.44 | 1.9181 |
| 175 | 1548.994 | 0.6798 | 1558.62 | 0.7472 | 1536.47 | 0.0000 |
| 176 | 1550.791 | 0 | 1559.33 | 0.3628 | 1536.72 | 0.0000 |
| 177 | 1550.89 | 0 | 1569.51 | 2.1475 | 1538.09 | 0.0005 |
| 178 | 1573.825 | 0 | 1576.79 | 0.0001 | 1559.16 | 0.0000 |
| 179 | 1573.97 | 0 | 1577.46 | 1.6381 | 1559.34 | 0.0000 |
| 180 | 1578.164 | 0 | 1592.76 | 0.6369 | 1576.68 | 0.0001 |
References
- Nie, H.; Zhao, C.; Shi, Z.; Jia, C.; Guo, X. Single-Molecule Fullerenes: Current Stage and Perspective. ACS Mater. Lett. 2022, 4, 1037–1052. [Google Scholar] [CrossRef]
- Shinohara, H. Endohedral metallofullerenes. Rep. Prog. Phys. 2000, 63, 843–892. [Google Scholar] [CrossRef]
- Rodríguez-Fortea, A.; Balch, A.L.; Poblet, J.M. Endohedral metallofullerenes: A unique host–guest association. Chem. Soc. Rev. 2011, 40, 3551–3563. [Google Scholar] [CrossRef]
- Stevenson, S.; Fowler, P.W.; Heine, T.; Duchamp, J.C.; Rice, G.; Glass, T.; Harich, K.; Hajdu, E.; Bible, R.; Dorn, H.C. A stable non-classical metallofullerene family. Nature 2000, 408, 427–428. [Google Scholar] [CrossRef]
- Kako, M.; Nagase, S.; Akasaka, T. Functionalization of Endohedral Metallofullerenes with Reactive Silicon and Germanium Compounds. Molecules 2017, 22, 1179. [Google Scholar] [CrossRef]
- Jin, P.; Li, Y.; Magagula, S.; Chen, Z. Exohedral functionalization of endohedral metallofullerenes: Interplay between inside and outside. Coord. Chem. Rev. 2019, 388, 406–439. [Google Scholar] [CrossRef]
- Yamada, M.; Liu, M.T.H.; Nagase, S.; Akasaka, T. New Horizons in Chemical Functionalization of Endohedral Metallofullerenes. Molecules 2020, 25, 3626. [Google Scholar] [CrossRef] [PubMed]
- Dubrovin, V.; Avdoshenko, S.M. Conformational preferences of endohedral metallofullerenes on Ag, Au, and MgO surfaces: Theoretical studies. J. Comput. Chem. 2022, 43, 1614–1620. [Google Scholar] [CrossRef]
- Zhukov, V.V.; Erohin, S.V.; Churkin, V.D.; Vnukova, N.G.; Antipina, L.Y.; Elesina, V.I.; Visotin, M.A.; Tomashevich, Y.V.; Popov, M.Y.; Churilov, G.N.; et al. Feature of the Endohedral Metallofullerene Y@C82 and Gd@C82 Polymerization under High Pressure. J. Phys. Chem. C 2022, 126, 17366–17373. [Google Scholar] [CrossRef]
- Cioslowski, J. Electronic Structure Calculations on Endohedral Complexes of Fullerenes: Reminiscences and Prospects. Molecules 2023, 28, 1384. [Google Scholar] [CrossRef]
- Cai, W.; Zhang, M.; Echegoyen, L.; Lu, X. Recent advances in endohedral metallofullerenes. Fundam. Res. 2023, 5, 767–781. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Zhang, X.; Tan, X.; Li, H.; Dai, S.; Yao, B.; Liu, X.; He, Y.; Jin, F. Recent Progress on the Functionalization of Endohedral Metallofullerenes. Inorganics 2023, 11, 346. [Google Scholar] [CrossRef]
- Lu, X.; Feng, L.; Akasaka, T.; Nagase, S. Current status and future developments of endohedral metallofullerenes. Chem. Soc. Rev. 2012, 41, 7723–7760. [Google Scholar] [CrossRef]
- Yang, S.; Wang, X.; Chu, H.; Liu, W. Electrode-Supported Endohedral Metallofullerenes: Insights into the Confined Internal Dynamics. Inorg. Chem. 2024, 63, 6836–6844. [Google Scholar] [CrossRef] [PubMed]
- Amerikheirabadi, F.; Diaz, C.; Mohan, N.; Zope, R.R.; Baruah, T. A DFT analysis of the ground and charge-transfer excited states of Sc3N@Ih–C80 fullerene coupled with metal-free and zinc-phthalocyanine. Phys. Chem. Chem. Phys. 2018, 20, 25841–25848. [Google Scholar] [CrossRef]
- Trukhina, O.; Rudolf, M.; Bottari, G.; Akasaka, T.; Echegoyen, L.; Torres, T.; Guldi, D.M. Bidirectional Electron Transfer Capability in Phthalocyanine–Sc3N@Ih–C80 Complexes. J. Am. Chem. Soc. 2015, 137, 12914–12922. [Google Scholar] [CrossRef]
- Liang, Y.; Feng, L. Dual Electron Acceptor/Electron Donor Character of Endohedral Nitride Clusterfullerenes. Fullerenes Nanotub. Carbon Nanostruct. 2014, 22, 227–234. [Google Scholar] [CrossRef]
- Jones, L.O.; Mosquera, M.A.; Fu, B.; Schatz, G.C.; Ratner, M.A.; Marks, T.J. Germanium Fluoride Nanocages as Optically Transparent n-Type Materials and Their Endohedral Metallofullerene Derivatives. J. Am. Chem. Soc. 2019, 141, 1672–1684. [Google Scholar] [CrossRef] [PubMed]
- Okamura, N.; Yoshida, K.; Sakata, S.; Hirakawa, K. Electron transport in endohedral metallofullerene Ce@C82 single-molecule transistors. Appl. Phys. Lett. 2015, 106, 043108. [Google Scholar] [CrossRef]
- Xu, T.; Yin, H.; Yu, P.; He, Z.; Chen, N.; Shen, W.; Zhu, M.; Akasaka, T.; Lu, X. Ultraviolet Photodetectors Based on Dimetallofullerene Lu2@Cs(6)-C82 Nanorods. ACS Appl. Nano Mater. 2022, 5, 1683–1689. [Google Scholar] [CrossRef]
- Nam, J.S.; Seo, Y.; Han, J.; Lee, J.W.; Kim, K.; Rane, T.; Kim, H.D.; Jeon, I. Exploring Endohedral Metallofullerenes for Advanced Thin-Film Device Applications toward Next-Generation Electronics. Chem. Mater. 2023, 35, 8323–8337. [Google Scholar] [CrossRef]
- Sinitsa, A.S.; Chamberlain, T.W.; Zoberbier, T.; Lebedeva, I.V.; Popov, A.M.; Knizhnik, A.A.; McSweeney, R.L.; Biskupek, J.; Kaiser, U.; Khlobystov, A.N. Formation of Nickel Clusters Wrapped in Carbon Cages: Toward New Endohedral Metallofullerene Synthesis. Nano Lett. 2017, 17, 1082–1089. [Google Scholar] [CrossRef]
- Shui, Y.; Liu, D.; Zhao, P.; Zhao, X.; Ehara, M.; Lu, X.; Akasaka, T.; Yang, T. Element effects in endohedral metal–metal-bonding fullerenes M2@C82 (M = Sc, Y, La, Lu). J. Chem. Phys. 2023, 159, 244302. [Google Scholar] [CrossRef]
- Kandrashkin, Y.E.; Zaripov, R.B. Low-temperature motion of the scandium bimetal in endofullerene Sc2@C80(CH2Ph). Phys. Chem. Chem. Phys. 2023, 25, 31493–31499. [Google Scholar] [CrossRef]
- Wu, Y.; Zhou, Z.; Wang, Z. Stability and Electronic Properties of Mixed Rare-Earth Tri-Metallofullerenes YxDy3−x@C80 (x = 1 or 2). Molecules 2024, 29, 447. [Google Scholar] [CrossRef]
- Westerström, R.; Dreiser, J.; Piamonteze, C.; Muntwiler, M.; Weyeneth, S.; Brune, H.; Rusponi, S.; Nolting, F.; Popov, A.; Yang, S.; et al. An Endohedral Single-Molecule Magnet with Long Relaxation Times: DySc2N@C80. J. Am. Chem. Soc. 2012, 134, 9840–9843. [Google Scholar] [CrossRef]
- Hu, Z.; Yang, S. Endohedral metallofullerene molecular nanomagnets. Chem. Soc. Rev. 2024, 53, 2863–2897. [Google Scholar] [CrossRef]
- Wu, B.; Hu, J.; Cui, P.; Jiang, L.; Chen, Z.; Zhang, Q.; Wang, C.; Luo, Y. Visible-Light Photoexcited Electron Dynamics of Scandium Endohedral Metallofullerenes: The Cage Symmetry and Substituent Effects. J. Am. Chem. Soc. 2015, 137, 8769–8774. [Google Scholar] [CrossRef] [PubMed]
- Su, M.; Hu, Y.; Yang, S.; Yu, A.; Peng, P.; Yang, L.; Jin, P.; Su, B.; Li, F.F. Large-Area Endohedral Metallofullerene Single-Crystal Arrays for High-Performance Field-Effect Transistors and Photodetectors. Adv. Electron. Mater. 2022, 8, 2100753. [Google Scholar] [CrossRef]
- Chen, W.; Huang, M.; Wu, M.; Lei, Y. Endohedral Metallofullerenes: Unveiling Synthesis Mechanisms and Advancing Photoelectric Energy Conversion Applications. Top. Curr. Chem. 2025, 383, 14. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Flores, C.; Basiuk, V.A. Ln@C60 endohedral fullerenes: A DFT analysis for the complete series from lanthanum to lutetium. Comput. Theor. Chem. 2022, 1217, 113878. [Google Scholar] [CrossRef]
- Putaud, T.; Chartrand, J.C.; Kalugina, Y.; Michaut, X.; Roy, P.N.; Ayotte, P. A simple confined rotor model to describe the ro-translational dynamics of water endofullerenes and to assign the ro-vibrational spectra of solid H2O@C60. J. Chem. Phys. 2025, 162, 144313. [Google Scholar] [CrossRef]
- Krisilov, A.; Nechaev, I.; Kotova, A.; Shikhaliev, K.; Chernov, V.; Zon, B. The role of the encapsulated atom in the vibrational spectra of La@C60–Lu@C60 lanthanide endofullerenes. Comput. Theor. Chem. 2015, 1054, 100–108. [Google Scholar] [CrossRef]
- Civiš, S.; Krisilov, A.V.; Ferus, M.; Nechaev, I.V.; Kubelík, P.; Chernov, V.E.; Zon, B.A. Vibrational spectra of La@C60 and Ce@C60 endohedral fullerenes: Influence of spin state multiplicity. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2021, 254, 119593. [Google Scholar] [CrossRef] [PubMed]
- Nakagawa, A.; Nishino, M.; Niwa, H.; Ishino, K.; Wang, Z.; Omachi, H.; Furukawa, K.; Yamaguchi, T.; Kato, T.; Bandow, S.; et al. Crystalline functionalized endohedral C60 metallofullerides. Nat. Commun. 2018, 9, 3073. [Google Scholar] [CrossRef] [PubMed]
- Matsuo, Y.; Okada, H.; Ueno, H. Endohedral Lithium-Containing Fullerenes: Preparation, Derivatization, and Application; Springer: Singapore, 2017. [Google Scholar] [CrossRef]
- Ogawa, T.; Sugai, T.; Shinohara, H. Isolation and Characterization of Er@C60. J. Am. Chem. Soc. 2000, 122, 3538–3539. [Google Scholar] [CrossRef]
- Kanbara, T.; Kubozono, Y.; Takabayashi, Y.; Fujiki, S.; Iida, S.; Haruyama, Y.; Kashino, S.; Emura, S.; Akasaka, T. Dy@C60: Evidence for endohedral structure and electron transfer. Phys. Rev. B 2001, 64, 113403. [Google Scholar] [CrossRef]
- Kubozono, Y.; Maeda, H.; Takabayashi, Y.; Hiraoka, K.; Nakai, T.; Kashino, S.; Emura, S.; Ukita, S.; Sogabe, T. Extractions of Y@C60, Ba@C60, La@C60, Ce@C60, Pr@C60, Nd@C60, and Gd@C60 with Aniline. J. Am. Chem. Soc. 1996, 118, 6998–6999. [Google Scholar] [CrossRef]
- Wang, Z.; Omachi, H.; Shinohara, H. Non-Chromatographic Purification of Endohedral Metallofullerenes. Molecules 2017, 22, 718. [Google Scholar] [CrossRef]
- Wang, C.R.; Kai, T.; Tomiyama, T.; Yoshida, T.; Kobayashi, Y.; Nishibori, E.; Takata, M.; Sakata, M.; Shinohara, H. A Scandium Carbide Endohedral Metallofullerene: (Sc2C2)@C84. Angew. Chem. 2001, 40, 397–399. [Google Scholar] [CrossRef]
- Inoue, T.; Tomiyama, T.; Sugai, T.; Okazaki, T.; Suematsu, T.; Fujii, N.; Utsumi, H.; Nojima, K.; Shinohara, H. Trapping a C2 Radical in Endohedral Metallofullerenes: Synthesis and Structures of (Y2C2)@C82 (Isomers I, II, and III). J. Phys. Chem. B 2004, 108, 7573–7579. [Google Scholar] [CrossRef]
- Zheng, H.; Zhao, X.; Wang, W.W.; Yang, T.; Nagase, S. Sc2@C70 rather than Sc2C2@C68: Density functional theory characterization of metallofullerene Sc2@C70. J. Chem. Phys. 2012, 137, 014308. [Google Scholar] [CrossRef] [PubMed]
- Kurihara, H.; Lu, X.; Iiduka, Y.; Mizorogi, N.; Slanina, Z.; Tsuchiya, T.; Akasaka, T.; Nagase, S. Sc2C2@C80 Rather than Sc2@C82: Templated Formation of Unexpected C2v(5)−C80 and Temperature-Dependent Dynamic Motion of Internal Sc2C2 Cluster. J. Am. Chem. Soc. 2011, 133, 2382–2385. [Google Scholar] [CrossRef]
- Han, Y.; Zheng, H.; He, J.; Li, M.; Ehara, M.; Zhao, X. Stabilities Referring to the f Electron Effect in Erbium-Based Endohedral Metallofullerenes: Revisiting Er2@C80 and the Missing Er2C2@C78. Inorg. Chem. 2025, 64, 8302–8312. [Google Scholar] [CrossRef]
- Shen, Y.; Roselló, Y.; Abella, L.; Qiu, J.; Du, X.; Meng, Q.; Zheng, L.; Cao, Z.; He, Z.; Poblet, J.M.; et al. Fluoride Clusterfullerenes: Tuning Metal–Metal Bonding and Magnetic Properties via Single Fluorine Atom Doping. J. Am. Chem. Soc. 2024, 146, 34924–34933. [Google Scholar] [CrossRef]
- Yao, Y.R.; Shi, X.M.; Zheng, S.Y.; Chen, Z.C.; Xie, S.Y.; Huang, R.B.; Zheng, L.S. Atomically Precise Insights into Metal–Metal Bonds Using Comparable Endo-Units of Sc2 and Sc2C2. Chin. Chem. Soc. Chem. 2021, 3, 294–302. [Google Scholar] [CrossRef]
- Pan, C.; Shen, W.; Yang, L.; Bao, L.; Wei, Z.; Jin, P.; Fang, H.; Xie, Y.; Akasaka, T.; Lu, X. Crystallographic characterization of Y2C2n (2n = 82, 88–94): Direct Y–Y bonding and cage-dependent cluster evolution. Chem. Sci. 2019, 10, 4707–4713. [Google Scholar] [CrossRef]
- Inoue, T.; Kubozono, Y.; Kashino, S.; Takabayashi, Y.; Fujitaka, K.; Hida, M.; Inoue, M.; Kanbara, T.; Emura, S.; Uruga, T. Electronic structure of Eu@C60 studied by XANES and UV–VIS absorption spectra. Chem. Phys. Lett. 2000, 316, 381–386. [Google Scholar] [CrossRef]
- Yang, W.; Barbosa, M.F.d.S.; Alfonsov, A.; Rosenkranz, M.; Israel, N.; Büchner, B.; Avdoshenko, S.M.; Liu, F.; Popov, A.A. Thirty Years of Hide-and-Seek: Capturing Abundant but Elusive MIII@C3v(8)-C82 Isomer, and the Study of Magnetic Anisotropy Induced in Dy3+ Ion by the Fullerene π-Ligand. J. Am. Chem. Soc. 2024, 146, 25328–25342. [Google Scholar] [CrossRef] [PubMed]
- Kwok, S. Complex Organics in Space: A Changing View of the Cosmos. Galaxies 2023, 11, 104. [Google Scholar] [CrossRef]
- El-Barbary, A. IR spectroscopic analysis of heterohedral metallofullerenes. Diam. Relat. Mater. 2023, 136, 110082. [Google Scholar] [CrossRef]
- Jiang, Y.; Li, Z.; Zhang, J.; Wang, Z. Endohedral Metallofullerene M2@C80: A New Class of Magnetic Superhalogen. J. Phys. Chem. C 2020, 124, 2131–2136. [Google Scholar] [CrossRef]
- Popov, A.A.; Avdoshenko, S.M.; Pendás, A.M.; Dunsch, L. Bonding between strongly repulsive metal atoms: An oxymoron made real in a confined space of endohedral metallofullerenes. Chem. Commun. 2012, 48, 8031–8050. [Google Scholar] [CrossRef]
- Zuo, T.; Xu, L.; Beavers, C.M.; Olmstead, M.M.; Fu, W.; Crawford, T.D.; Balch, A.L.; Dorn, H.C. M2@C79N (M = Y, Tb): Isolation and Characterization of Stable Endohedral Metallofullerenes Exhibiting M−M Bonding Interactions inside Aza[80]fullerene Cages. J. Am. Chem. Soc. 2008, 130, 12992–12997. [Google Scholar] [CrossRef]
- Slanina, Z.; Uhlík, F.; Lee, S.L.; Adamowicz, L.; Nagase, S. Lix@C60: Calculations of the Encapsulation Energetics and Thermodynamics. Int. J. Mol. Sci. 2008, 9, 1841–1850. [Google Scholar] [CrossRef]
- Hu, Y.H.; Ruckenstein, E. Endohedral Chemistry of C60-Based Fullerene Cages. J. Am. Chem. Soc. 2005, 127, 11277–11282. [Google Scholar] [CrossRef] [PubMed]
- Kobayashi, K.; Nagase, S. Structures and electronic states of endohedral dimetallofullerenes: M2@C80 (M = Sc, Y, La, Ce, Pr, Eu, Gd, Yb and Lu). Chem. Phys. Lett. 1996, 262, 227–232. [Google Scholar] [CrossRef]
- Kobayashi, K.; Nagase, S. Theoretical calculations of vibrational modes in endohedral metallofullerenes: La@C82 and Sc2@C84. Mol. Phys. 2003, 101, 249–254. [Google Scholar] [CrossRef]
- Inakuma, M.; Shinohara, H. Temperature-Dependent EPR Studies on Isolated Scandium Metallofullerenes: Sc@C82(I, II) and Sc@C84. J. Phys. Chem. B 2000, 104, 7595–7599. [Google Scholar] [CrossRef]
- Schettino, V.; Pagliai, M.; Ciabini, L.; Cardini, G. The Vibrational Spectrum of Fullerene C60. J. Phys. Chem. A 2001, 105, 11192–11196. [Google Scholar] [CrossRef]
- Bethune, D.S.; Meijer, G.; Tang, W.C.; Rosen, H.J.; Golden, W.G.; Seki, H.; Brown, C.A.; de Vries, M.S. Vibrational Raman and infrared spectra of chromatographically separated C60 and C70 fullerene clusters. Chem. Phys. Lett. 1991, 179, 181–186. [Google Scholar] [CrossRef]
- Krause, M.; Popov, V.N.; Inakuma, M.; Tagmatarchis, N.; Shinohara, H.; Georgi, P.; Dunsch, L.; Kuzmany, H. Multipole induced splitting of metal-cage vibrations in crystalline endohedral D2d−M2@C84 dimetallofullerenes. J. Chem. Phys. 2004, 120, 1873–1880. [Google Scholar] [CrossRef]
- Schettino, V.; Remigio Salvi, P.; Bini, R.; Cardini, G. On the vibrational assignment of fullerene C60. J. Chem. Phys. 1994, 101, 11079–11081. [Google Scholar] [CrossRef]
- Iglesias-Groth, S.; Cataldo, F.; Manchado, A. Infrared spectroscopy and integrated molar absorptivity of C60 and C60 fullerenes at extreme temperatures. Mon. Not. R. Astron. Soc. 2011, 413, 213–222. [Google Scholar] [CrossRef]
- Tamuliene, J. Electronic and Vibrational Spectra of C60 and Its Ions. Fuller. Nanotub. Carbon Nanostructures 2015, 23, 187–195. [Google Scholar] [CrossRef]
- Menéndez, J.; Page, J.B. Vibrational spectroscopy of C60. In Light Scattering in Solids VIII: Fullerenes, Semiconductor Surfaces, Coherent Phonons; Cardona, M., Güntherodt, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2000; pp. 27–95. [Google Scholar] [CrossRef]
- Tuchin, A.V. A realignment and activation of vibrational modes of the fullerene C60 and C70 in the electric field. Condens. Matter Interphases 2014, 16, 323–336. [Google Scholar]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09 Revision D.1; Gaussian Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Adamo, C.; Barone, V. Exchange functionals with improved long-range behavior and adiabatic connection methods without adjustable parameters: The mPW and mPW1PW models. J. Chem. Phys. 1998, 108, 664–675. [Google Scholar] [CrossRef]
- Pritchard, B.P.; Altarawy, D.; Didier, B.; Gibson, T.D.; Windus, T.L. New Basis Set Exchange: An Open, Up-to-Date Resource for the Molecular Sciences Community. J. Chem. Inf. Model. 2019, 59, 4814–4820. [Google Scholar] [CrossRef]
- Chandrasekharaiah, M.; Gingerich, K. Chapter 86 Thermodynamic properties of gaseous species. In Handbook on the Physics and Chemistry of Rare Earths; Karl, A., Gschneidner, J., Eyring, L., Eds.; Elsevier: Amsterdam, The Netherlands, 1989; Volume 12, pp. 409–431. [Google Scholar] [CrossRef]
- Kohl, F.J.; Stearns, C.A. Vaporization Thermodynamics of Yttrium Dicarbide–Carbon System and Dissociation Energy of Yttrium Dicarbide and Tetracarbide. J. Chem. Phys. 1970, 52, 6310–6315. [Google Scholar] [CrossRef]
- Min, J.; Halfen, D.; Ziurys, L. Fourier transform microwave/millimeter-wave spectroscopy of the ScC2 (2A1) radical: A model system for endohedral metallofullerenes. Chem. Phys. Lett. 2014, 609, 70–75. [Google Scholar] [CrossRef]
- Halfen, D.; Min, J.; Ziurys, L. The Fourier transform microwave spectrum of YC2 (2A1) and its 13C isotopologues: Chemical insight into metal dicarbides. Chem. Phys. Lett. 2013, 555, 31–37. [Google Scholar] [CrossRef]
- Burton, M.A.; Cheng, Q.; Halfen, D.T.; Lane, J.H.; DeYonker, N.J.; Ziurys, L.M. The structure of ScC2 (2A1): A combined Fourier transform microwave/millimeter-wave spectroscopic and computational study. J. Chem. Phys. 2020, 153, 034304. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Wang, M.; Yang, C.; Ma, X.; Li, J. DFT calculations for anharmonic force field and spectroscopic constants of YC2 and its 13C isotopologues. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2018, 191, 382–388. [Google Scholar] [CrossRef] [PubMed]
- Standard Thermodynamic Properties of Chemical Substances. In CRC Handbook of Chemistry and Physics, 97th ed.; Haynes, W.M., Lide, D.R., Bruno, T.J., Eds.; CRC Press/Taylor and Francis: Boca Raton, FL, USA, 2017; pp. 5–9. [Google Scholar]
- Hedberg, K.; Hedberg, L.; Bethune, D.S.; Brown, C.A.; Dorn, H.C.; Johnson, R.D.; Vries, M.D. Bond Lengths in Free Molecules of Buckminsterfullerene, C60 from Gas-Phase Electron Diffraction. Science 1991, 254, 410–412. [Google Scholar] [CrossRef]
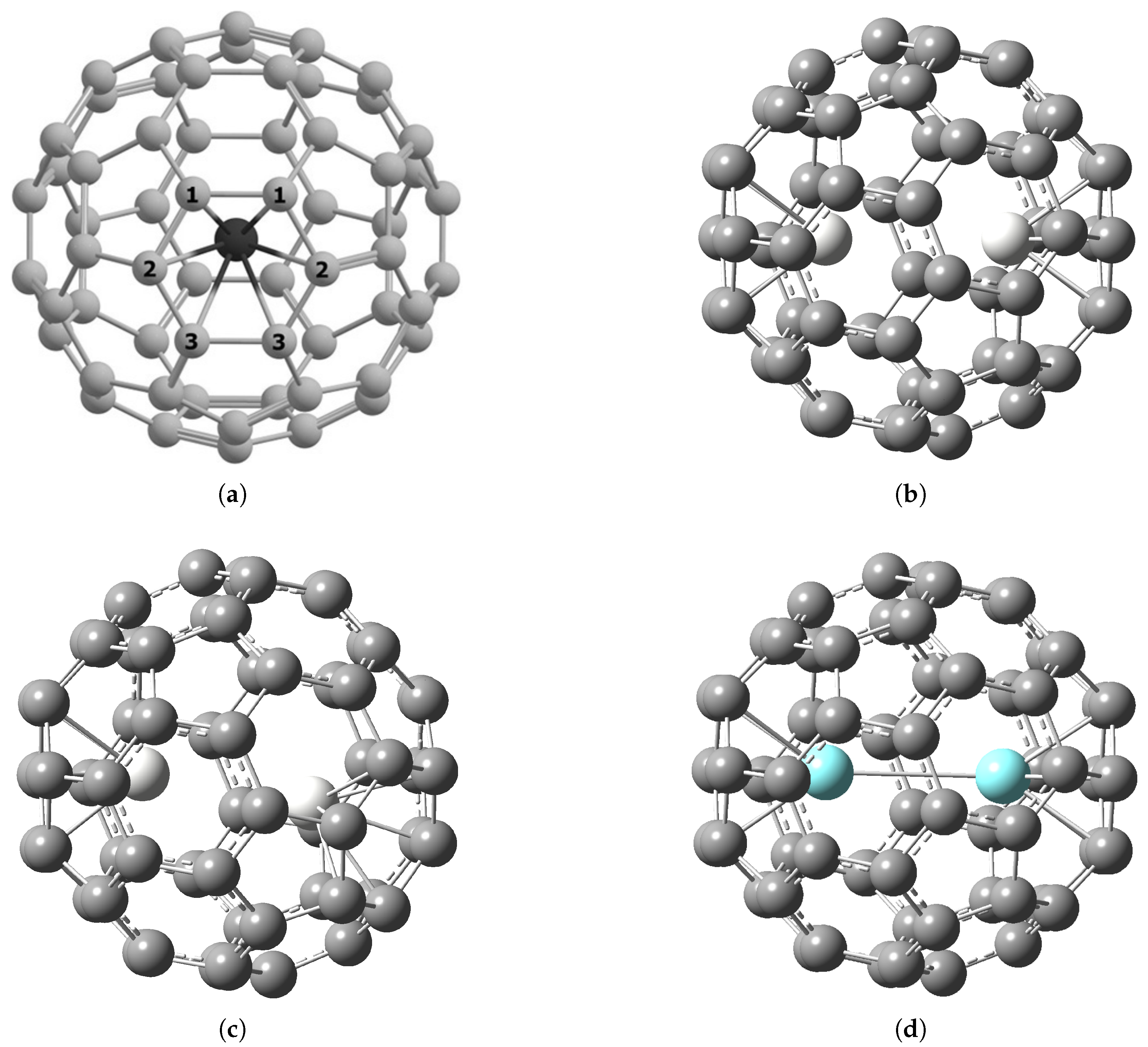




| () | () | () | () | () | |
|---|---|---|---|---|---|
| r(M–C1), Å | 2.17 | 2.34 | 2.26 | 2.24 | 2.36 |
| r(M–C2), Å | 2.24 | 2.40 | 2.26 | 2.24 | 2.36 |
| r(M–C3), Å | 2.33 | 2.48 | 2.26 | 2.25 | 2.36 |
| r(M–M), Å | – | – | 3.25 | 3.11 | 3.13 |
| calc. | expt. | calc. | expt. | |
|---|---|---|---|---|
| , kJ/mol | 1183 | 1182 | 1239 | 1254 |
| r(M–C), Å | 2.046 | 2.057 | 2.191 | 2.187 |
| r(C–C), Å | 1.278 | 1.259 | 1.277 | 1.270 |
| , cm−1 | 335 | 330.0 | 337 | 342.0 |
| , cm−1 | 662 | 634.6 | 604 | 581.1 |
| , cm−1 | 1816 | 1767.9 | 1826 | 1839.7 |
| calc. | expt. | diff. | |
|---|---|---|---|
| , kJ/mol | 2405 | 2502 | 4.2% |
| , Å | 1.451 | 1.452 | 0.1% |
| , Å | 1.397 | 1.397 | <0.1% |
| , cm−1 | 523 | 527 | 0.76% |
| , cm−1 | 595 | 576 | 3.2% |
| , cm−1 | 1233 | 1182 | 4.1% |
| , cm−1 | 1497 | 1429 | 4.6% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krisilov, A.V.; Nechaev, I.V.; Chernov, V.E.; Kallu, G.E. DFT Calculations of Structure and IR Spectra of M@C60 and M2@C60 Endofullerenes (M=Sc and Y). Molecules 2025, 30, 3421. https://doi.org/10.3390/molecules30163421
Krisilov AV, Nechaev IV, Chernov VE, Kallu GE. DFT Calculations of Structure and IR Spectra of M@C60 and M2@C60 Endofullerenes (M=Sc and Y). Molecules. 2025; 30(16):3421. https://doi.org/10.3390/molecules30163421
Chicago/Turabian StyleKrisilov, Alexey V., Igor V. Nechaev, Vladislav E. Chernov, and Gie Eli Kallu. 2025. "DFT Calculations of Structure and IR Spectra of M@C60 and M2@C60 Endofullerenes (M=Sc and Y)" Molecules 30, no. 16: 3421. https://doi.org/10.3390/molecules30163421
APA StyleKrisilov, A. V., Nechaev, I. V., Chernov, V. E., & Kallu, G. E. (2025). DFT Calculations of Structure and IR Spectra of M@C60 and M2@C60 Endofullerenes (M=Sc and Y). Molecules, 30(16), 3421. https://doi.org/10.3390/molecules30163421






