The g-Strained EPR Line Shape of Transition-Ion Complexes and Metalloproteins: Four Decades of Misunderstanding and Its Consequences
Abstract
1. Introduction

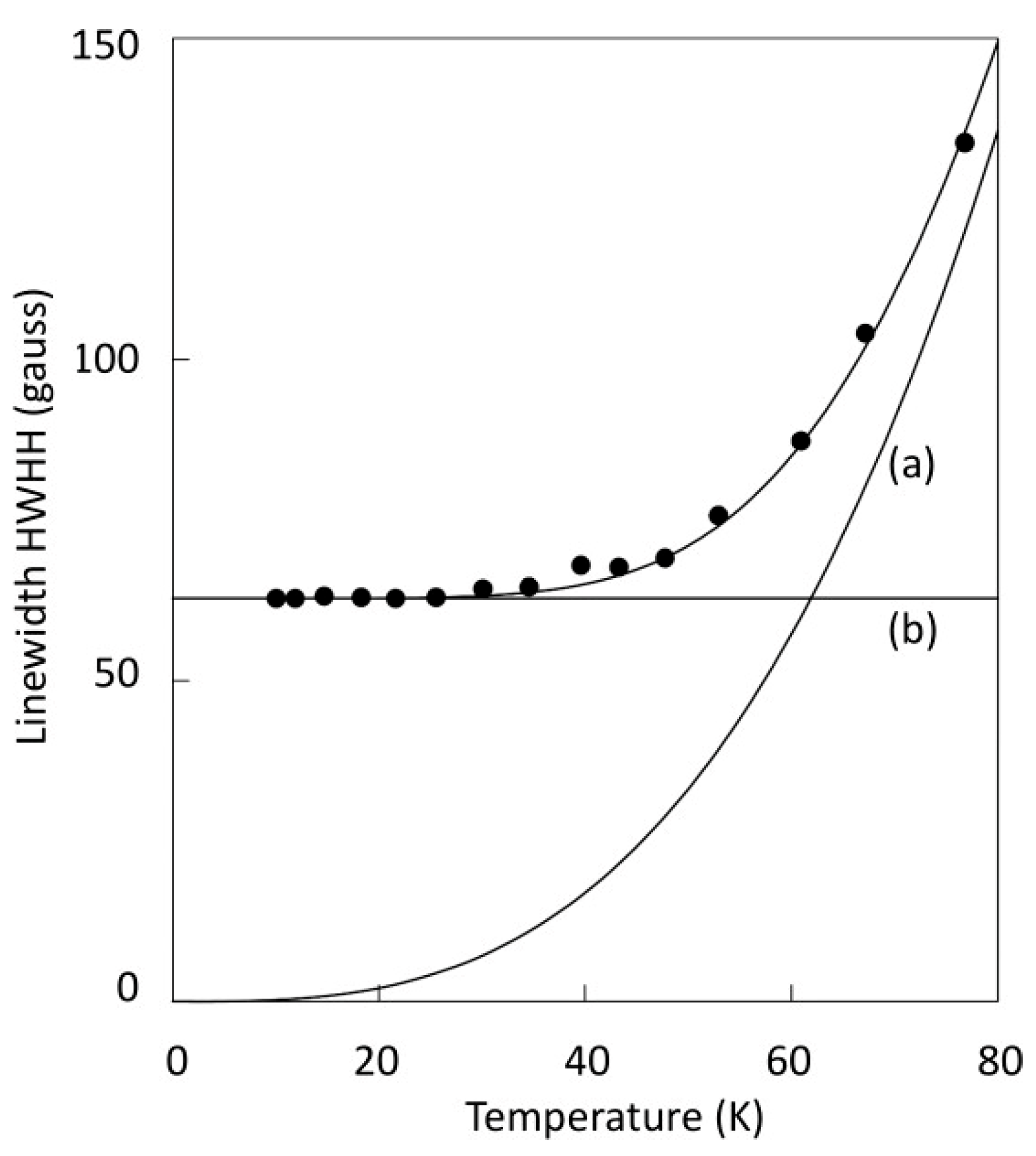

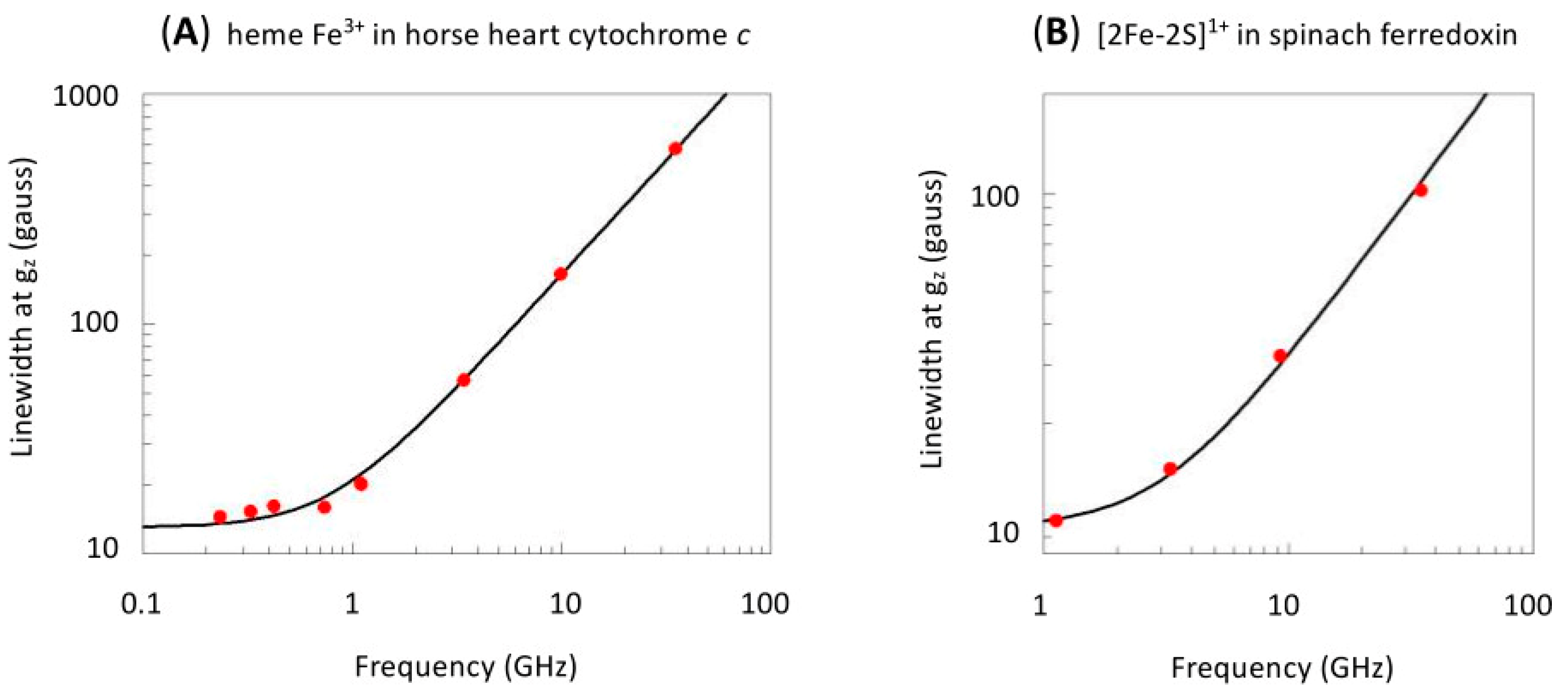
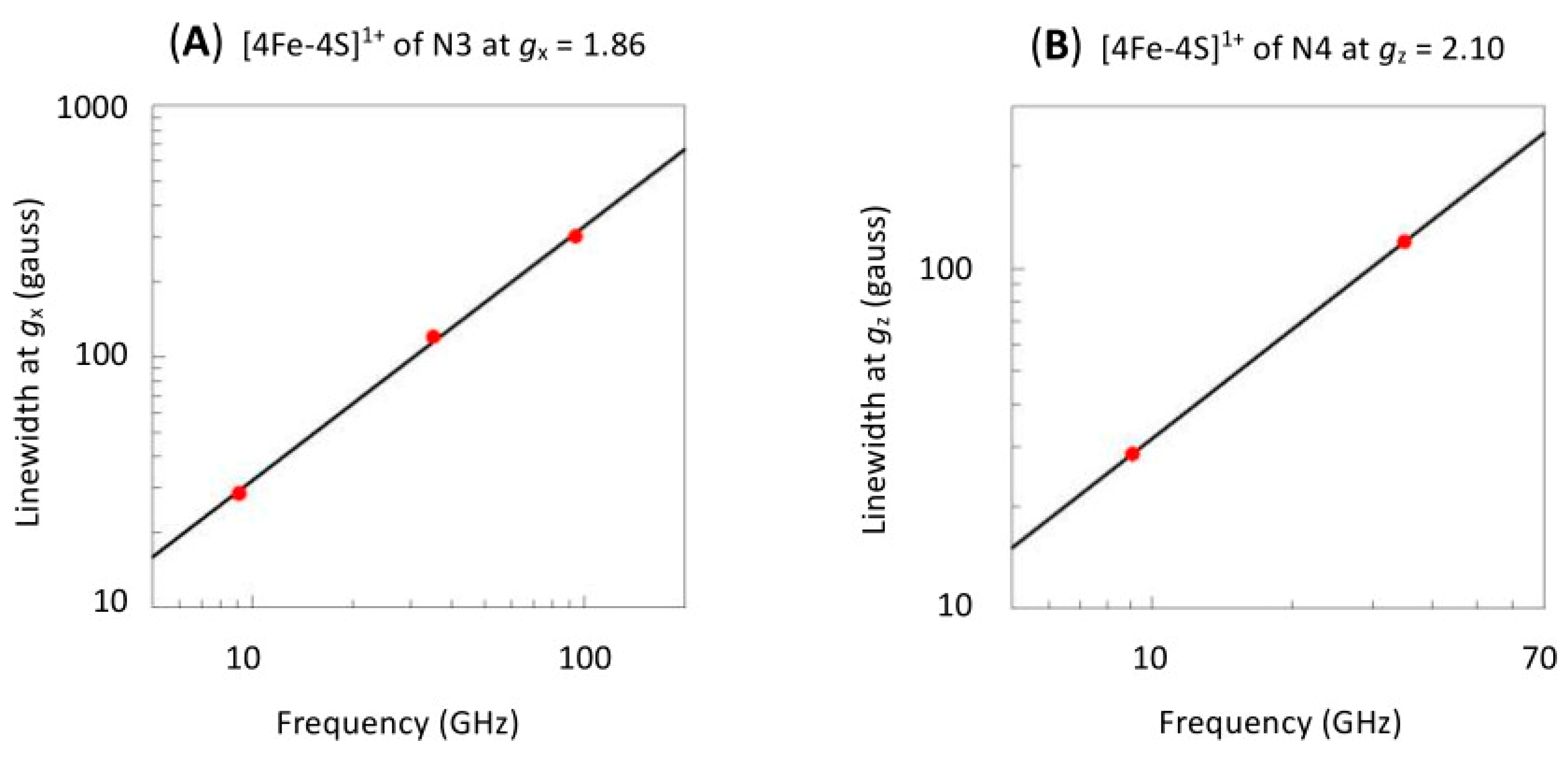
2. Linewidth Frequency Dependence
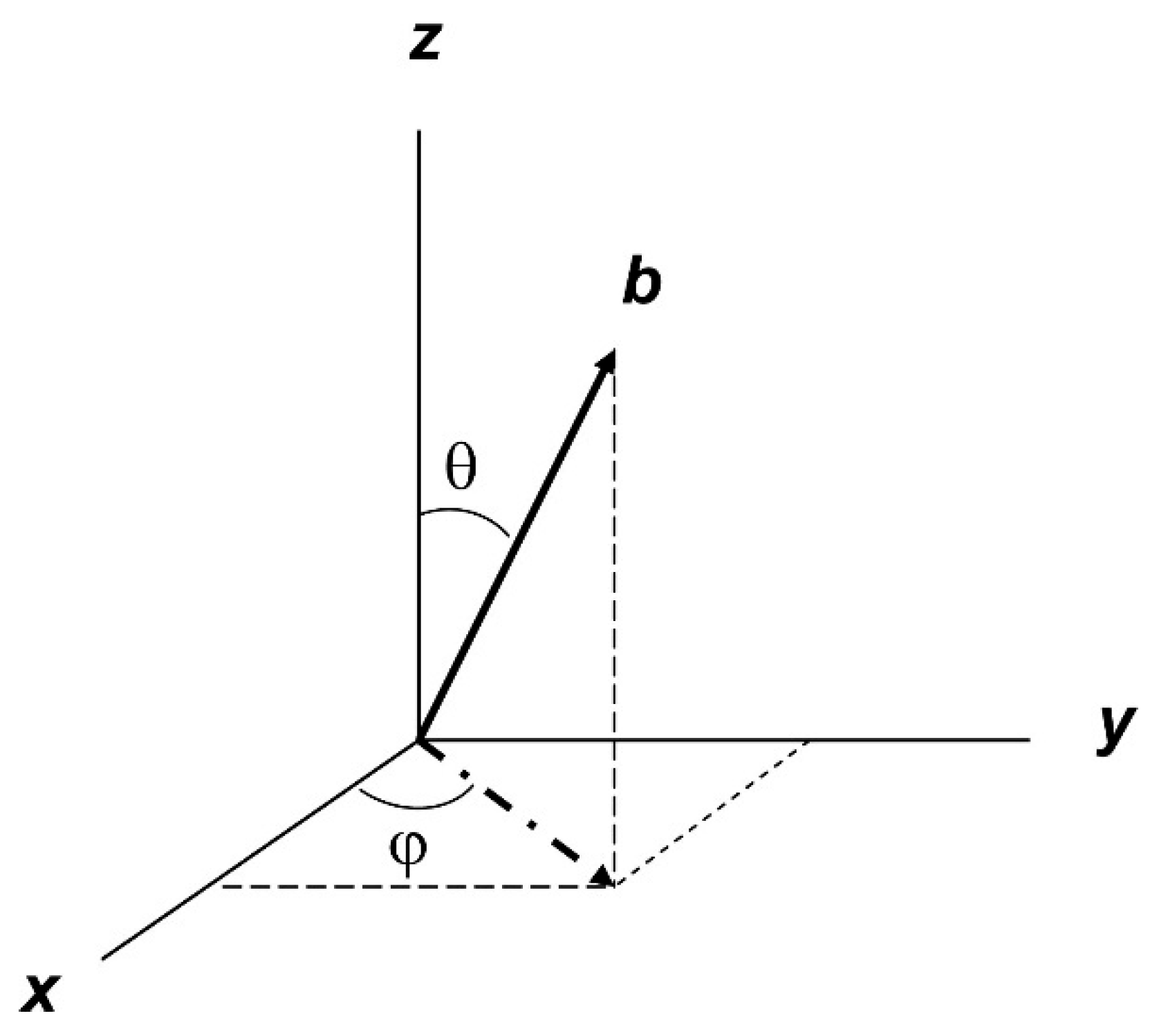
3. Linewidth (Non-)Colinearity
4. Key Consequences of g-Strain
- (1)
- The inhomogeneous line shape is a normal distribution in g-space; in B-space, the line shape is slightly skewed, and the peak does not correspond exactly with the average g-value (cf Figure 6C’).
- (2)
- The three main features in the powder pattern are generally asymmetric: the low-field absorption-shaped peak skews towards low field; the lobes of the derivative-shaped peak have unequal amplitudes and different widths; the high-field absorption-shaped negative peak skews towards high field (cf Figure 6E).
- (3)
- The possibility of full negative correlation implies that the linewidth may change sign (that is, go through zero) for a particular intermediate (θ, φ) orientation of the field vector in the molecular axes system; as a consequence, the number of orientations required to numerically generate a smooth powder pattern with no microcrystallinity artifacts may increase by a few orders of magnitude.
- (4)
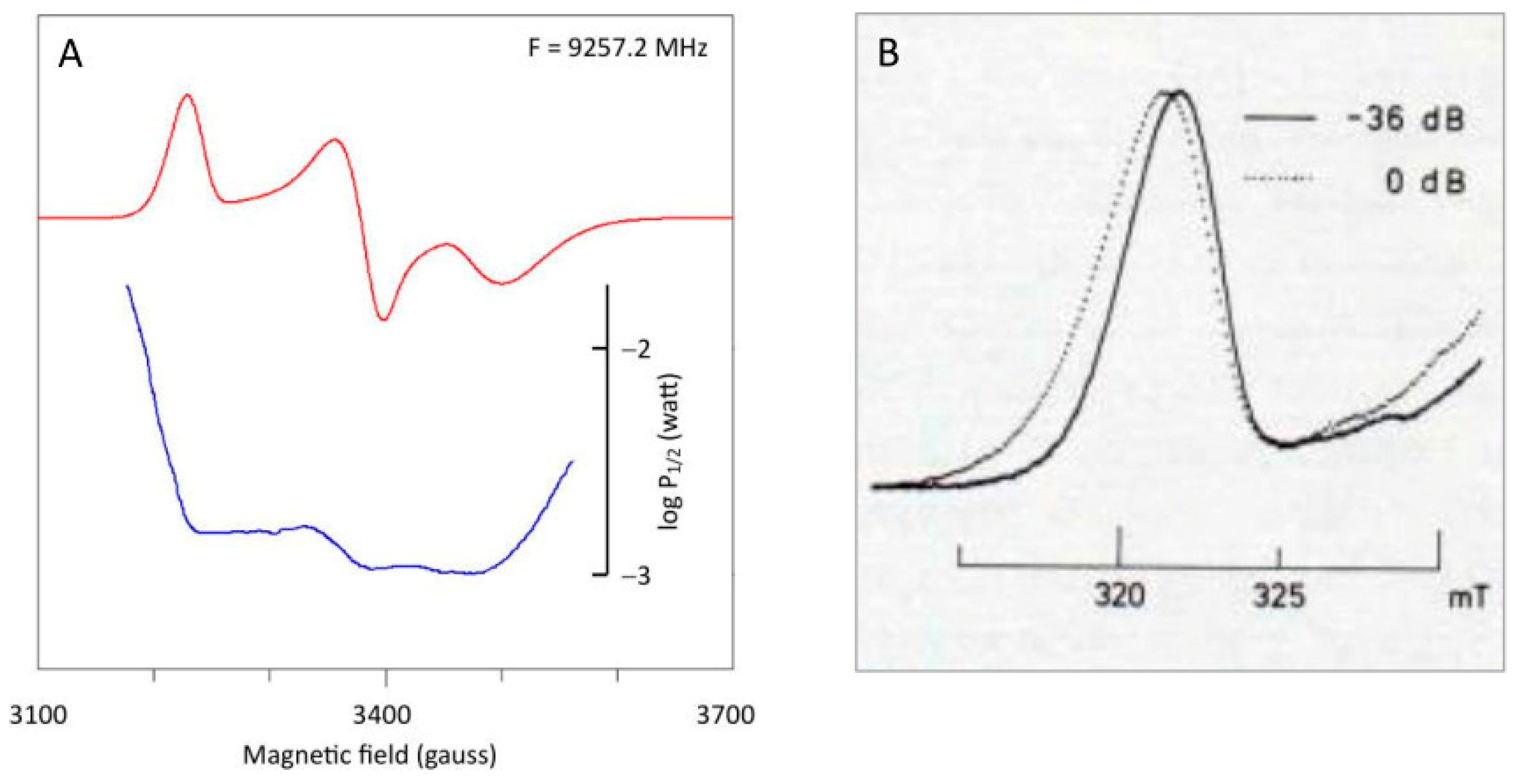
- Microwave power saturation over the powder pattern is not a constant. In particular, the low-field wing of the absorption peak and the high-field wing of the negative absorption peak are increasingly difficult to saturate towards extreme field, as illustrated for spinach ferredoxin in Figure 7, in which half-saturation values were determined with Equation (19).in which S is the signal amplitude, P is the microwave power, and P1/2 is the power for which the signal is half-saturated.Figure 7. Differential saturation over the powder pattern of spinach ferredoxin. (A) the microwave power level required for half saturation was determined at every point of the digital spectrum. Note the particularly pronounced decrease in saturation into the extreme wings of the spectrum. Data taken from ref. [10]. (B) The gz peak was taken at non-saturating versus saturating power at a temperature of 24 K, a frequency of 9236 MHz, and with a low modulation frequency of 1 kHz to avoid deformation (partial integration) by passage effects (reprinted from [13]).Figure 7. Differential saturation over the powder pattern of spinach ferredoxin. (A) the microwave power level required for half saturation was determined at every point of the digital spectrum. Note the particularly pronounced decrease in saturation into the extreme wings of the spectrum. Data taken from ref. [10]. (B) The gz peak was taken at non-saturating versus saturating power at a temperature of 24 K, a frequency of 9236 MHz, and with a low modulation frequency of 1 kHz to avoid deformation (partial integration) by passage effects (reprinted from [13]).Clearly, attempts to saturate the low− and high-field peaks will lead to strong deformation of shape with apparent increase in intensity towards extreme fields. In other words, differential saturation is inherent in g-strain.Note, in passing, that in the iron–sulfur protein literature (specifically in the literature on Complex I, which is the subject of the next sections), a variant of Equation (19) has been usedin which b is an ‘inhomogeneity parameter’ that is usually taken to run from b = 1 (inhomogeneous broadening) to b = 2 (homogeneous broadening). A justification for this form was never given. For example, Equation (20) was used in refs. [19,20,21] with reference to previous papers [22,23] that simply pose the equation without explanation or reference to any original source. The equation originates from a 1953 paper by Portis, who, however, deduced it for—long extinct—spectrometers with a modulated microwave source [24]. Its use on data from field-modulated spectrometers has no theoretical basis but is supported by the good fits it gives to experimental data. Thus, the parameter P1/2 effectively characterizes saturation, hopefully, in a semi-quantitative manner. Furthermore, I have made the point that for lines that are inhomogeneously broadened by g-strain, an adjustable inhomogeneity parameter, b, has no meaning beyond that of a fudge factor [10].
- (5)
- Methods have been described in the literature to determine spin concentration on the basis of the first integral of one of the peaks in the powder pattern [6]. If these peaks are asymmetric due to non-colinear g-strain, then the method may lead to an underestimation of the spin concentration of the order of some 25% [8]. In cases in which the peak is poorly separated from the derivative feature, quantifications have been based on the surface under one-half of the peak (the half on the extreme-field side) [25]. For g-strained systems, this may well lead to an additional error in spin count.
5. Forty Years of Misinterpretations of the Key Consequences of g-Strain
6. Complex-I: Stoichiometry of Signals N1b-N4
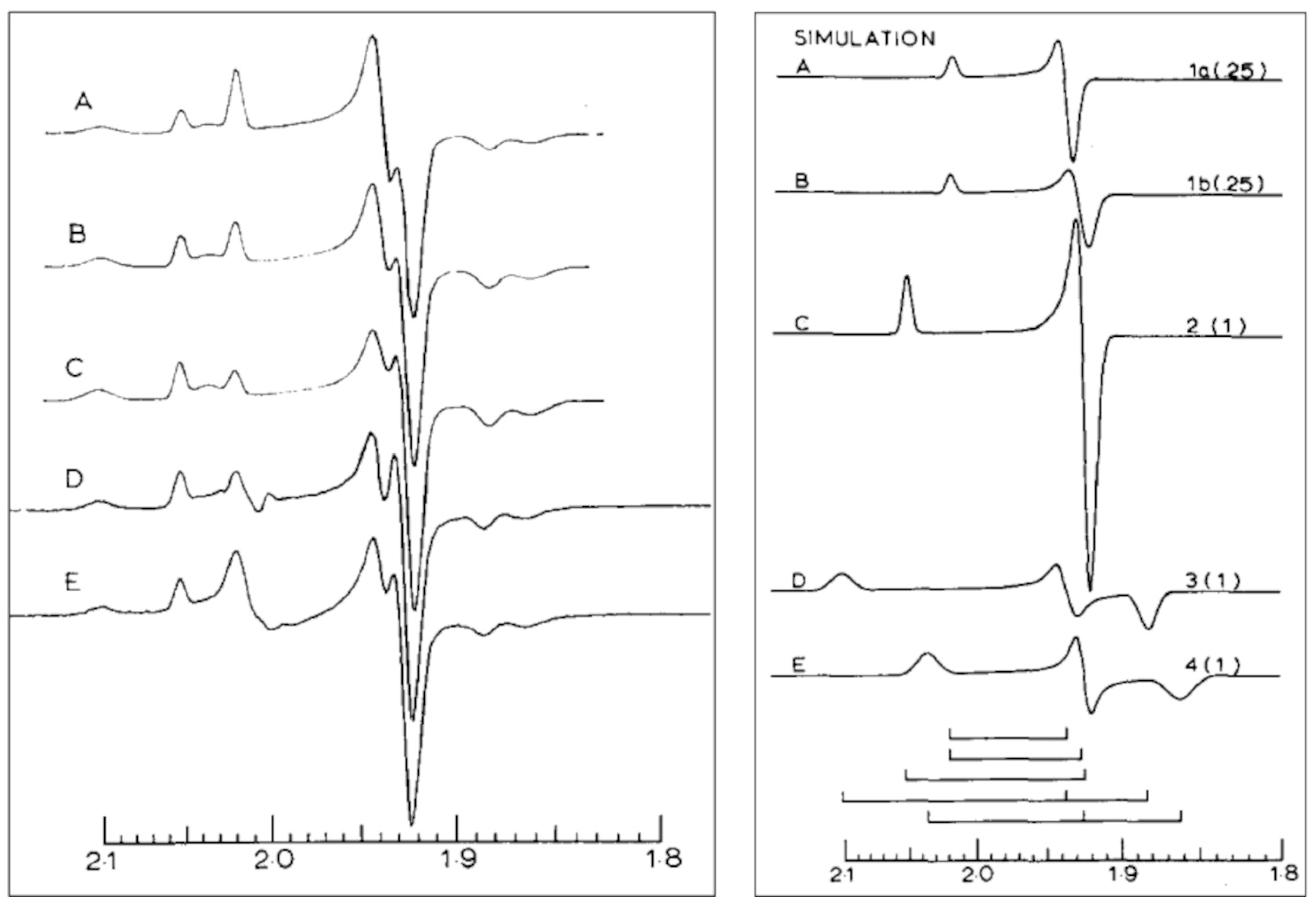
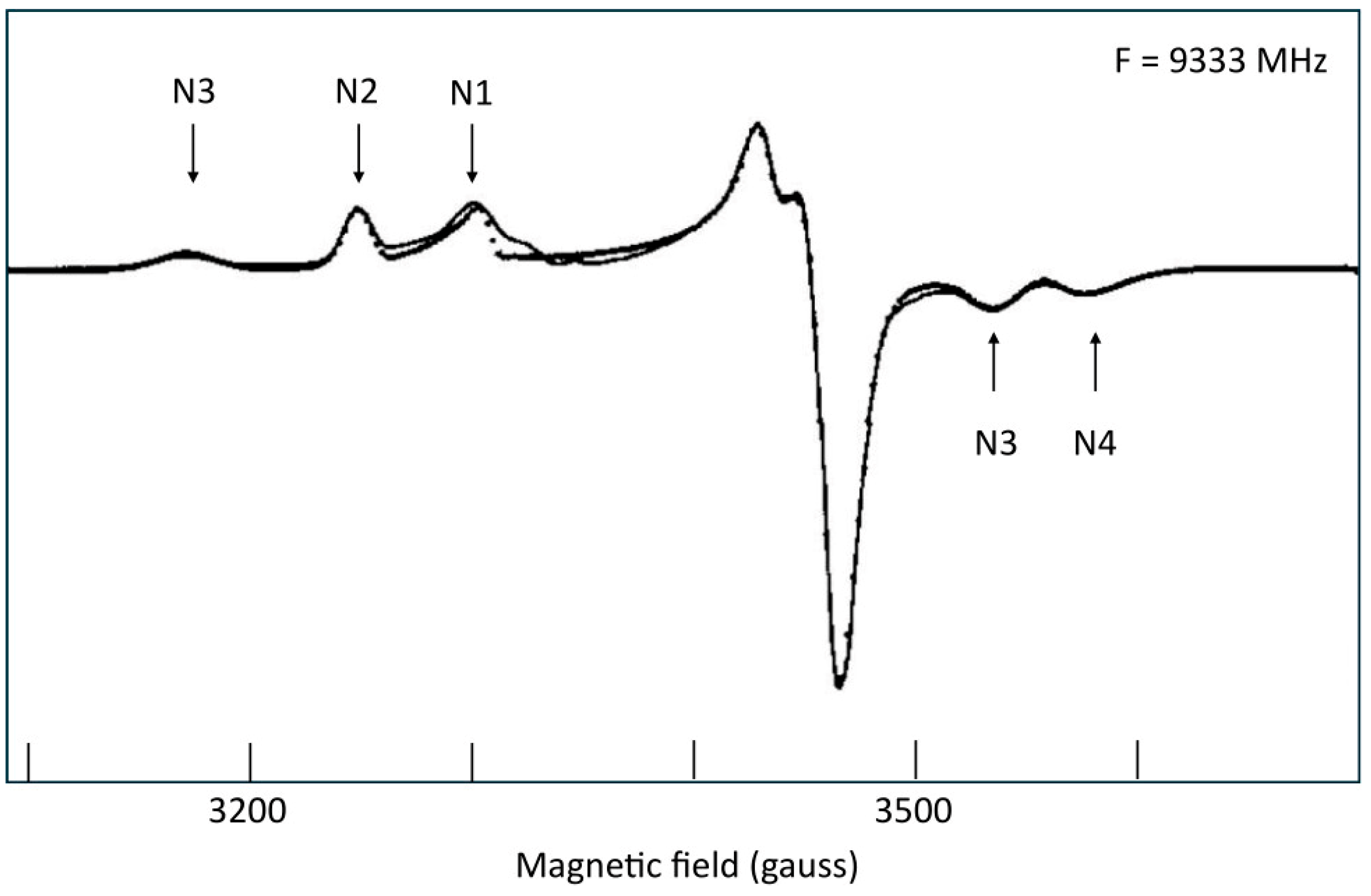
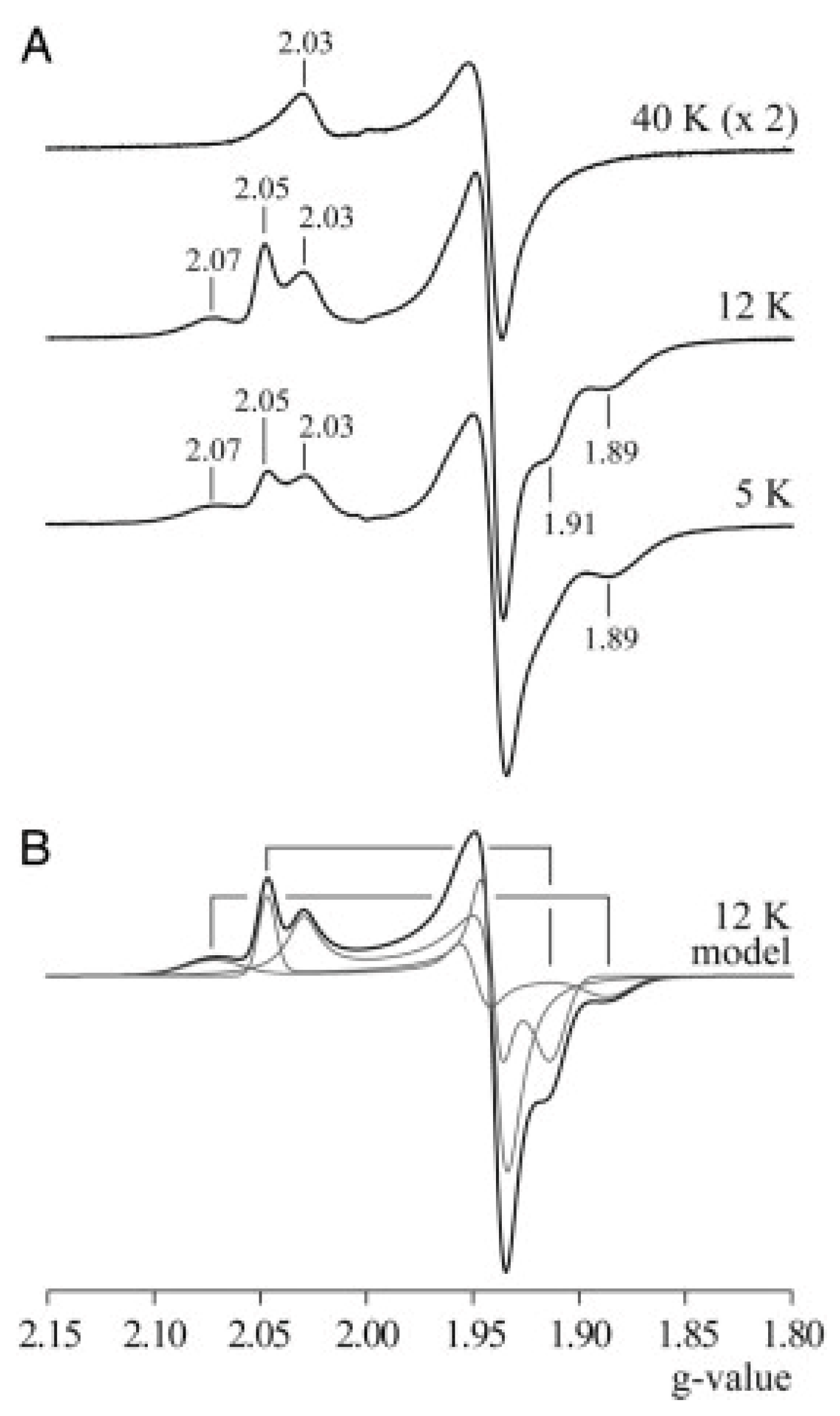
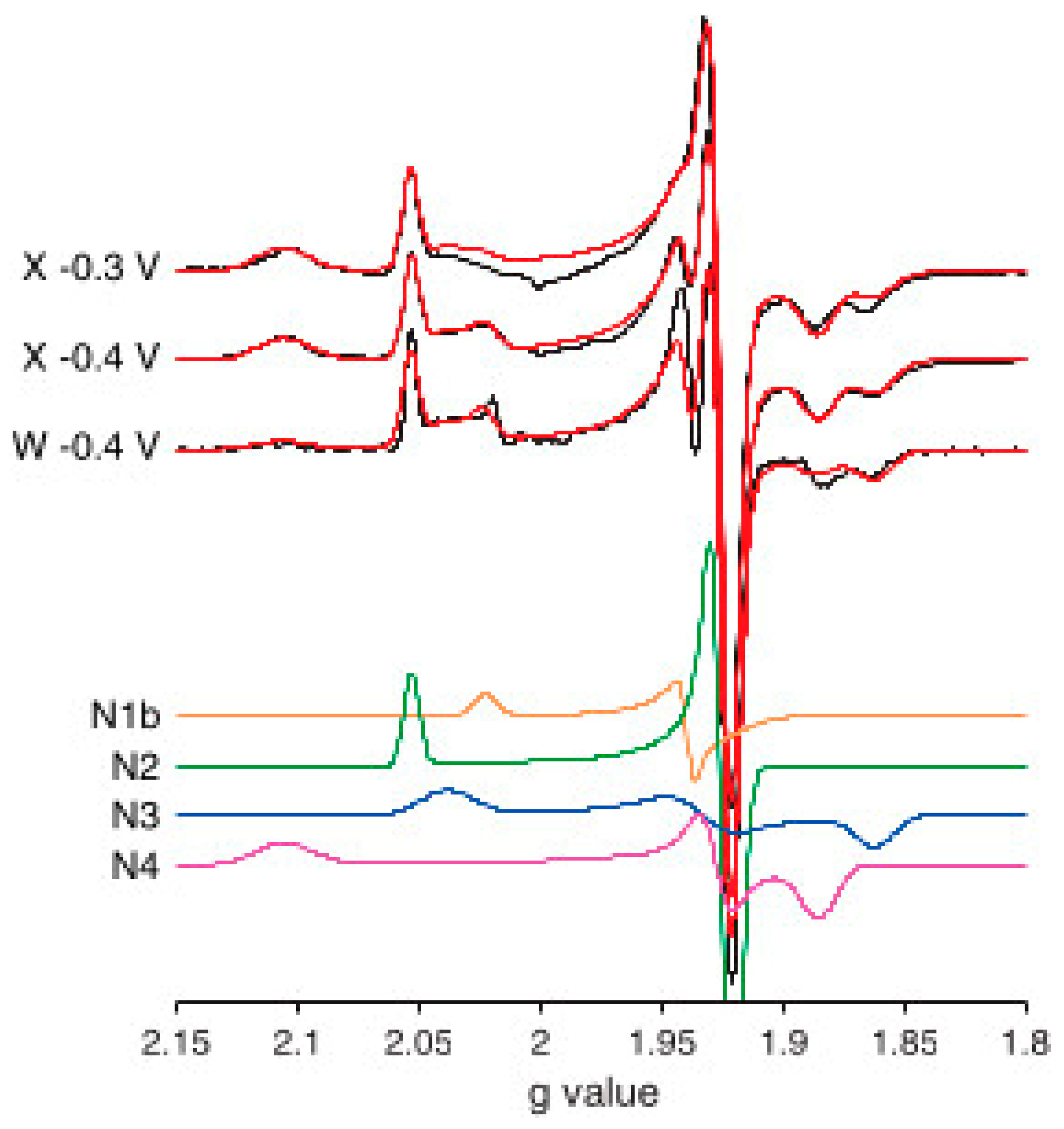
7. Complex-I: Differential Saturation of Other Clusters

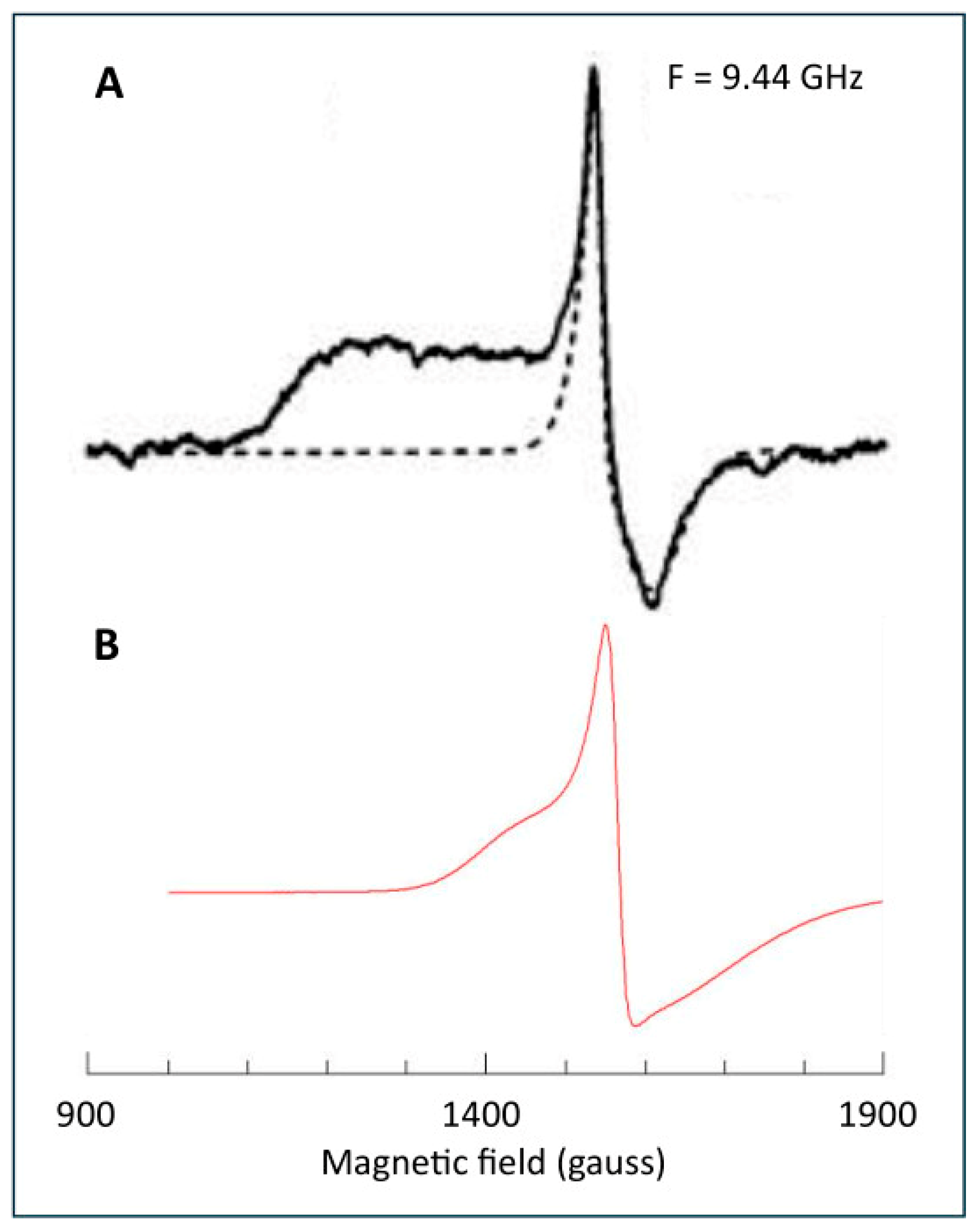

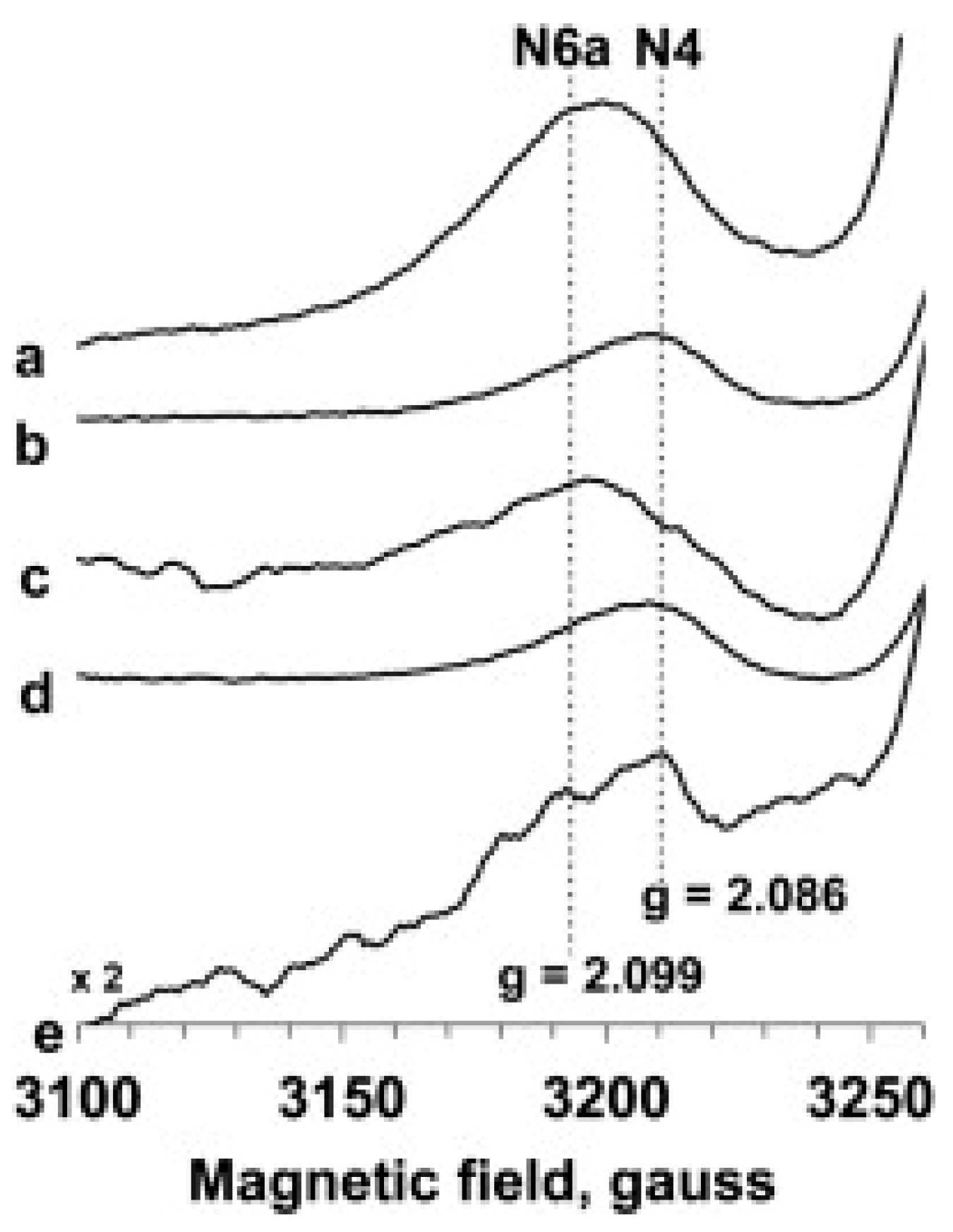
8. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ponti, A. Simulation of magnetic resonance static powder lineshapes: A quantitative assessment of spherical codes. J. Magn. Reson. 1999, 138, 288–297. [Google Scholar] [CrossRef]
- Hagen, W.R. Very low-frequency broadband electron paramagnetic resonance spectroscopy of metalloproteins. J. Phys. Chem. A 2021, 125, 3208–3218. [Google Scholar] [CrossRef]
- Hagen, W.R. Een Onderzoek Naar de Electron Paramagnetische Resonantie Eigenschappen van Cytochroom c Oxidase. Master’s Thesis, University of Amsterdam, Amsterdam, The Netherlands, 1976. [Google Scholar]
- Johnston, T.S.; Hecht, H.G. An automated fitting procedure for the determination of anisotropic g-tensors from EPR studies of powder samples. J. Mol. Spectrosc. 1965, 17, 98–107. [Google Scholar] [CrossRef]
- Venable, J.H., Jr. Electron paramagnetic resonance spectroscopy of protein single crystals: II Computational methods. In Magnetic Resonance in Biological Systems, Proceedings of the Second International Conference Held at the Wenner-Gren Center Stockholm, Stockholm, Sweden, 9–15 June 1966; Ehrenberg, A., Malmström, B.G., Vänngård, T., Eds.; Pergamon: Oxford, UK, 1967. [Google Scholar]
- Aasa, R.; Vänngård, T. EPR signal intensity and powder shapes: A reexamination. J. Magn. Reson. 1975, 19, 308–315. [Google Scholar] [CrossRef]
- Aasa, R.; Albracht, S.P.J.; Falk, K.-E.; Lanne, B.; Vänngård, T. EPR signals from cytochrome c oxidase. Biochim. Biophys. Acta 1976, 422, 260–272. [Google Scholar] [CrossRef] [PubMed]
- Hagen, W.R. Dislocation strain broadening as a source of anisotropic linewidth and asymmetrical lineshape in the electron paramagnetic resonance spectrum of metalloproteins and related systems. J. Magn. Reson. 1981, 44, 447–469. [Google Scholar] [CrossRef]
- Hagen, W.R. g-Strain: Inhomogeneous broadening in metalloprotein EPR. In Advanced EPR; Applications in Biology and, Biochemistry; Hoff, A.J., Ed.; Elsevier: Amsterdam, The Netherlands, 1989. [Google Scholar]
- Hagen, W.R.; Albracht, S.P.J. Analysis of strain-induced EPR-line shapes and anisotropic spin-lattice relaxation in a [2Fe-2S] ferredoxin. Biochim. Biophys. Acta 1982, 702, 61–71. [Google Scholar] [CrossRef]
- Hagen, W.R.; Hearshen, D.O.; Harding, L.J.; Dunham, W.R. Quantitative numerical analysis of g strain in the EPR of distributed systems and its importance for multicenter metalloproteins. J. Magn. Reson. 1985, 61, 233–244. [Google Scholar] [CrossRef]
- Pilbrow, J.R. Lineshapes in frequency-swept and field-swept EPR for spin 1/2. J. Magn. Reson. 1984, 58, 186–203. [Google Scholar] [CrossRef]
- Hagen, W.R. Electron Paramagnetic Resonance of Metalloproteins; with Emphasis on Components of the Respiratory Chain. Ph.D. Thesis, University of Amsterdam, Amsterdam, The Netherlands, 1982. [Google Scholar]
- Pake, G.E.; Estle, T.L. The Physical Principles of Electron Paramagnetic Resonance; Benjamin: Reading, MA, USA, 1973. [Google Scholar]
- Hagen, W.R.; Hearshen, D.O.; Sands, R.H.; Dunham, W.R. A statistical theory for powder EPR in distributed systems. J. Magn. Reson. 1985, 61, 220–232. [Google Scholar] [CrossRef]
- Hearshen, D.O.; Hagen, W.R.; Sands, R.H.; Grande, H.J.; Crespi, H.L.; Gunsalus, I.C.; Dunham, W.R. An analysis of g strain in the EPR of two [2Fe-2S] ferredoxins. Evidence for a protein rigidity model. J. Magn. Reson. 1986, 69, 440–459. [Google Scholar] [CrossRef]
- Wiertz, F.G.M.; Richter, O.-M.H.; Cheropanov, A.V.; MacMillan, F.; Ludwig, B.; de Vries, S. An oxo-ferryl tryptophan radical catalytic intermediate in cytochrome c and quinol oxidases trapped by microsecond freeze-hyperquenching (MHQ). FEBS Lett. 2004, 575, 127–130. [Google Scholar] [CrossRef] [PubMed]
- Srour, B.; Strampraad, M.J.F.; Hagen, W.R.; Hagedoorn, P.-L. Refolding kinetics of cytochrome c studied with microsecond timescale continuous-flow UV-vis spectroscopy and rapid freeze-quench EPR. J. Inorg. Biochem. 2018, 184, 42–49. [Google Scholar] [CrossRef]
- Vinogradov, A.D.; Sled, V.D.; Burbaev, D.S.; Grivennikova, V.G.; Moroz, I.A.; Ohnishi, T. Energy-dependent complex I-associated ubisemiquinones in submitochondrial particles. FEBS Lett. 1995, 370, 83–87. [Google Scholar] [CrossRef]
- Roessler, M.M.; King, M.S.; Robinson, A.J.; Armstrong, F.A.; Harmer, J.; Hirst, J. Direct assignment of EPR spectra to structurally defined iron-sulfur clusters in complex I by double electron-electron resonance. Proc. Natl. Acad. Sci. USA 2010, 107, 1930–1935. [Google Scholar] [CrossRef]
- Narayanan, M.; Leung, S.A.; Inaba, Y.; Elguindy, M.M.; Nakamaru-Ogiso, E. Semiquinone intermediates are involved in the energy coupling mechanism of E coli complex I. Biochim. Biophys. Acta 2015, 1847, 681–689. [Google Scholar] [CrossRef]
- Beinert, H.; Orme-Johnson, W.H. Electron spin relaxation as a probe for active centers of paramagnetic enzyme species. In Magnetic Resonance in Biological Systems, Proceedings of the Second International Conference Held at the Wenner-Gren Center Stockholm, Stockholm, Sweden, 9–15 June 1966; Ehrenberg, A., Malmström, B.G., Vänngård, T., Eds.; Pergamon: Oxford, UK, 1967. [Google Scholar]
- Rupp, H.; Rao, K.K.; Hall, D.O.; Cammack, R. Electron spin relaxation of iron-sulphur proteins studied by microwave power saturation. Biochim. Biophys. Acta 1978, 537, 255–269. [Google Scholar] [CrossRef]
- Portis, A.M. Electronic structure of F centers: Saturation of the electron spin. Phys. Rev. 1953, 91, 1071–1078. [Google Scholar] [CrossRef]
- Albracht, S.P.J.; Leeuwerik, F.J.; van Swol, B. The stoichiometry of the iorn-sulphur clusters 1a, 1b and 2 of NADH:Q oxidoreductase as present in beef-heart submitochondrial particles. FEBS Lett. 1979, 104, 197–200. [Google Scholar] [CrossRef] [PubMed]
- Petrovich, R.M.; Ruzicka, F.J.; Reed, G.H.; Frey, P.A. Characterization of iron-sulfur clusters in lysine 2,3-aminomutase by electron paramagnetic resonance spectroscopy. Biochemistry 1992, 31, 10774–10781. [Google Scholar] [CrossRef]
- Kjaer, B.; Jung, Y.-S.; Yu, L.; Golbeck, J.H.; Scheller, H.V. Iron-sulfur centers in the photosynthetic reaction center complex from Chloronium vibrioforme. Differences from and similarities to the iron-sulfur centers in photosystem I. Photosys. Res. 1994, 41, 105–114. [Google Scholar] [CrossRef]
- Broderick, J.B.; Duderstadt, R.E.; Fernandez, D.C.; Wojtuszewski, K.; Henshaw, T.F.; Johnson, M.K. Pyruvate formate-lyase activating enzyme is an iron-sulfur protein. J. Am. Chem. Soc. 1997, 119, 7396–7397. [Google Scholar] [CrossRef]
- Vassiliev, I.R.; Antonkine, M.L.; Golbeck, J.H. Iron-sulfur clusters in type I reaction centers. Biochim. Biophys. Acta 2001, 1507, 139–160. [Google Scholar] [CrossRef]
- Madadi-Kahkesk, S.; Duin, E.C.; Heim, S.; Albracht, S.P.J.; Johnson, M.K.; Hedderich, R. A paramagnetic species with unique EPR characteristics in the active site of heterodisulfide reductase from methanogenic archaea. Eur. J. Biochem. 2001, 268, 2566–2577. [Google Scholar] [CrossRef] [PubMed]
- Duin, E.C.; Bauer, C.; Jaun, B.; Hedderich, R. Coenzyme M binds to a [4Fe-4S] cluster in the active site of heterodisulfide reductase as deduced from EPR studies with the [33S]coenzyme M-treated enzyme. FEBS Lett. 2003, 538, 81–84. [Google Scholar] [CrossRef] [PubMed]
- Agarwalla, S.; Stroud, R.M.; Gaffney, B.J. Redox reactions of the iron-sulfur cluster in a ribosomal RNA methyltransferase, RumA. J. Biol. Chem. 2004, 279, 34123–34129. [Google Scholar] [CrossRef]
- Yakovlev, G.; Reda, T.; Hirst, J. Reevaluating the relationship between EPR spectra and enzyme structure for the iron-sulfur clusters in NADH:quinone oxidoreductase. Proc. Natl. Acad. Sci. USA 2007, 104, 12720–12725. [Google Scholar] [CrossRef]
- Reda, T.; Barker, C.D.; Hirst, J. Reduction of the iron-sulfur clusters in mitochondrial NADH:ubiquinone oxidoreductase (Complex I) by EuII-DTPA, a very low potential reductant. Biochemistry 2008, 47, 8885–8893. [Google Scholar] [CrossRef]
- Kondo, T.; Nomata, J.; Fujita, Y.; Itoh, S. EPR study of 1Asp-3Cys ligated 4Fe-4S iron-sulfur cluster in NB-protein (BchN-BchB) of a dark-operative protochlorophyllide reductase complex. FEBS Lett. 2011, 585, 214–218. [Google Scholar] [CrossRef] [PubMed]
- Stich, T.A. Characterization of paramagnetic iron-sulfur clusters using electron paramagnetic resonance spectroscopy. In Fe-S Proteins; Methods and Protocols; Dos Santos, P.C., Ed.; Humana Press: Totowa, NJ, USA; Springer Nature: New York, NY, USA, 2021. [Google Scholar]
- Priem, A.H.; Klaassen, A.A.K.; Reijerse, E.J.; Meyer, T.E.; Luchinat, C.; Capozzi, F.; Dunham, W.R.; Hagen, W.R. EPR analysis of multiple forms of [4Fe-4S]3+ clusters in HiPIPs. J. Biol. Inorg. Chem. 2005, 10, 417–424. [Google Scholar] [CrossRef]
- Blaszczyk, A.J.; Silakov, A.; Zhang, B.; Mailcco, S.J.; Lanz, N.D.; Kelly, W.L.; Elliott, S.J.; Krebs, C.; Booker, S.J. Spectroscopic and electrochemical characterization of the iron-sulfur and cobalamin cofactors of TsrM, and unusual radical s-adenosylmethionine methylase. J. Am. Chem. Soc. 2016, 138, 3416–3426. [Google Scholar] [CrossRef]
- Barr, I.; Stich, T.A.; Gizzi, A.S.; Grove, T.L.; Bonanno, J.B.; Latham, J.A.; Chung, T.; Wilmot, C.M.; Britt, C.D.; Almo, S.C.; et al. X-ray and EPR characterization of the auxiliary Fe-S clusters in the radical SAM enzyme PqqE. Biochemistry 2018, 57, 1306–1315. [Google Scholar] [CrossRef]
- Heghmanns, M.; Günzel, A.; Brandis, D.; Kutin, Y.; Engelbrecht, V.; Wikler, M.; Happe, T.; Kasanmascheff, M. Fine-tuning of FeS proteins monitored via pulsed EPR redox potentiometry at Q-band. Biophys. Rep. 2021, 1, 100016. [Google Scholar] [CrossRef] [PubMed]
- Laurikenas, A.; Sakalauskas, D.; Marsalka, A.; Raudonis, R.; Antuzevics, A.; Balevidus, V.; Zarkov, A.; Karelva, A. Investigation of lanthanum substitution effects in yttrium aluminium garnet: Importance of solid state NMR and EPR methods. J. Sol-Gel Sci. Technol. 2021, 97, 479–487. [Google Scholar] [CrossRef]
- Paulin, J.V.; Batagin-Neto, A.; Naydenov, B.; Lips, K.; Graeff, C.F.O. High-field/high frequency EPR spectroscopy on synthetic melanin: On the origin of carbon-centered radicals. Mater. Adv. 2021, 2, 6297–6305. [Google Scholar] [CrossRef]
- Dubroca, T.; Wang, X.; Mentink-Vigier, F.; Trociewitz, B.; Starck, M.; Parker, D.; Sherwin, M.S.; Hill, S.; Krzystek, J. Terahertz EPR spectroscopy using a 36-tesla high-homogeneity series-connected hybrid magnet. J. Magn. Reson. 2023, 353, 107480. [Google Scholar] [CrossRef]
- Tran, V.A.; Teucher, M.; Galazzo, L.; Sharma, B.; Pongratz, T.; Kast, S.M.; Marx, D.; Bordignon, E.; Schnegg, A.; Neese, F. Dissecting the molecular origin of g-tensor heterogeneity and strain in nitroxide radicals in water: Electron paramagnetic resonance experiment versus theory. J. Phys. Chem. A 2023, 127, 6447–6466. [Google Scholar] [CrossRef]
- Maio, N.; Raza, M.K.; Li, Y.; Zhang, D.-L.; Bollinger, J.M., Jr.; Krebs, C.; Rouault, T.A. An iron-sulfur cluster in the zink-binding domain of the SARS-CoV-2 helicase modulates its RNA-binding and -unwinding activities. Proc. Natl. Acad. Sci. USA 2023, 120, e2303860120. [Google Scholar] [CrossRef]
- Santanni, F.; Little, E.; Lockyer, S.J.; Whitehead, G.F.S.; McInnes, E.J.L.; Timco, G.A.; Bowen, A.M.; Sessoli, R.; Winpenny, R.E.P. Weak exchange interactions in multispin systems: EPR studies of metalloporphyrins decorated with {Cr7Ni} rings. Inorg. Chem. 2024, 63, 15460–15466. [Google Scholar] [CrossRef]
- Kultaeva, A.; Biktagirov, T.; Sperlich, A.; Dörfinger, P.; Calvo, M.E.; Otal, E.; Dyakonov, V. Photoinduced spin centers in photocatalytic metal-organic framework UiO-66. Adv. Funct. Mater. 2025, 35, 2413297. [Google Scholar] [CrossRef]
- Stoll, S.; Schweiger, A. EasySpin, a comprehensive software package for spectral simulation and analysis in EPR. J. Magn. Reson. 2006, 178, 42–55. [Google Scholar] [CrossRef]
- Stoll, S. CW-EPR spectral simulations: Solid state. Methods Enzymol. 2015, 563, 121–142. [Google Scholar]
- Beinert, H.; Sands, R.H. Studies on succinic and DPNH dehydrogenase preparations by paramagnetic resonance (EPR) spectroscopy. Biochem. Biophys. Res. Commun. 1960, 3, 41–46. [Google Scholar] [CrossRef]
- Ohnishi, T.; Asakura, T.; Wohlrab, H.; Yonetani, T.; Chance, B. Electron paramagnetic resonance studies on iron-sulfur proteins of submitochondrial particles from Candida utilis cells. J. Biol. Chem. 1970, 245, 901–902. [Google Scholar] [CrossRef]
- Albracht, S.P.J.; Slater, E.C. EPR studies at 200 K on the mitochondrial respiratory chain. Biochim. Biophys. Acta 1971, 245, 503–507. [Google Scholar] [CrossRef] [PubMed]
- Orme-Johnson, N.R.; Orme-Jonson, W.H.; Hansen, R.E.; Beinert, H. EPR detectable electron acceptors in submitochondrial particles from beef heart with special reference to the iron-sulfur components of DPNH-ubiquinone reductase. Biochem. Biophys. Res. Commun. 1971, 44, 446–452. [Google Scholar] [CrossRef] [PubMed]
- Ohnishi, T.; Asakura, T.; Yonetani, T.; Chance, B. Electron paramagnetic resonance studies at temperatures below 77 °K on iron-sulfur proteins of yeast and bovine heart submitochondrial particles. J. Biol. Chem. 1971, 246, 5960–5964. [Google Scholar] [CrossRef]
- Ohnishi, T.; Wilson, D.F.; Asakura, T.; Chance, B. Studies on iron-sulfur proteins in the site I region of the respiratory chain in pigeon heart mitochondria and submitochondrial particles. Biochem. Biophys. Res. Commun. 1974, 46, 1631–1638. [Google Scholar] [CrossRef]
- Albracht, S.P.J. Some new paramagnetic centers in submitochondrial particles detectable by EPR spectroscopy. Biochim. Biophys. Acta 1974, 347, 183–192. [Google Scholar] [CrossRef]
- Orme-Johnson, N.R.; Hansen, R.E.; Beinert, H. Electron paramagnetic resonance-detectable electron acceptors in beef heart mitochondria. Reduced diphosphopyridine nucleotide ubiquinone reductase segment of the electron transfer system. J. Biol. Chem. 1974, 249, 1922–1927. [Google Scholar] [CrossRef]
- Ohnishi, T. Thermodynamic and EPR characterization of iron-sulfur centers in the NADH-ubiquinone segment of the mitochondrial respiratory chain in pigeon heart. Biochim. Biophys. Acta 1975, 387, 475–490. [Google Scholar] [CrossRef]
- Albracht, S.P.J.; Dooijewaard, G.; Leeuwerik, F.J.; van Swol, B. EPR signals of NADH:Q oxidoreductase. Shape and intensity. Biochim. Biophys. Acta 1977, 459, 300–317. [Google Scholar] [CrossRef]
- Clifford, E.R.; Wright, J.J.; Collauto, A.; Hirst, J.; Roessler, M.M. Characterization of a semiquinone radical bound in the active site of respiratory complex I by hyperfine spectroscopy. ChemRxiv 2025. [Google Scholar] [CrossRef]
- Hearshen, D.O.; Dunham, W.R.; Albracht, S.P.J.; Ohnishi, T.; Beinert, H. EPR spectral simulation on cluster N-1b in NADH-ubiquinone oxidoreductase of bovine heart mitochondria. FEBS Lett. 1981, 133, 287–290. [Google Scholar] [CrossRef]
- Kowal, A.T.; Morningstar, J.E.; Johnson, M.K.; Ramsay, R.R.; Singer, T.P. Spectroscopic characterization of the number and type of iron-sulfur clusters in NADH:ubiquinone oxidoreductase. J. Biol. Chem. 1986, 261, 9239–9245. [Google Scholar] [CrossRef]
- Ohnishi, T.; Nakamaru-Ogiso, E. Were there any “misassignments” among iron-sulfur clusters N4, N5 and N6b in NADH-quinone oxidoreductase (complex I)? Biochim. Biophys. Acta 2008, 1777, 703–710. [Google Scholar] [CrossRef]
- Ohnishi, T.; Ohnishi, S.T.; Salerno, J.C. Five decades of research on mitochondrial NADH-quinone oxidoreductase (complex I). Biol. Chem. 2018, 399, 1249–1264. [Google Scholar] [CrossRef] [PubMed]
- Jarman, O.D.; Biner, O.; Wright, J.J.; Hirst, J. Paracoccus denitrificans: A genetically tractable model system for studying respiratory complex I. Sci. Rep. 2021, 11, 10143. [Google Scholar] [CrossRef] [PubMed]
- Bridges, H.R.; Bill, E.; Hirst, J. Mössbauer spectroscopy of respiratory complex I: The iron-sulfur cluster ensemble in the NADH-reduced enzyme is partially oxidized. Biochemistry 2012, 51, 149–158. [Google Scholar] [CrossRef] [PubMed]
- van Belsen, R.; Mariette, A.; Albracht, S.P.J. On the stoichiometry of the iron-sulphur clusters in mitochondrial NADH: Ubiquinone oxidoreductase. Eur. J. Biochem. 1992, 209, 1019–1022. [Google Scholar] [CrossRef]
- Albracht, S.P.J.; Mariette, A. Bovine -heart NADH:ubiquinone oxidoreductase is a monomer with 8 Fe-S clusters and 2 FMN groups. Biochim. Biophys. Acta 1997, 1318, 92–106. [Google Scholar] [CrossRef] [PubMed]
- Leif, H.; Sled, V.D.; Ohnishi, T.; Weiss, H.; Friedrich, T. Isolation and characterization of the proton-translocating NADH: Ubiquinone oxidoreductase from Escherichia coli. Eur. J Biochem. 1995, 230, 538–548. [Google Scholar] [CrossRef]
- Ohnishi, T. Iron-sulfur clusters/semiquinones in Complex I. Biochim. Biophys. Acta 1998, 1364, 186–206. [Google Scholar] [CrossRef]
- Uhlmann, M.; Friedrich, T. EPR signals assigned to Fe/S cluster N1c of the Escherichia coli NADH:ubiquinone oxidoreductase (complex I) derive from cluster N1a. Biochemistry 2005, 44, 1653–1658. [Google Scholar] [CrossRef]
- Wang, D.-C.; Meinhardt, S.; Sackmann, U.; Weiss, H.; Ohnishi, T. The iron-sulfur clusters in two related forms of mitochondrial NADH:ubiquinone oxidoreductase made by Neurospora crassa. Eur. J. Biochem. 1991, 197, 257–264. [Google Scholar] [CrossRef]
- Lin, T.-I.; Sled, V.D.; Ohnishi, T.; Brennicke, A.; Grohmann, L. Analysis of the iron-sulfur clusters within comple I (NADH:ubiquinone oxidoreductase) isolated from potato tuber mitochondria. Eur. J. Biochem. 1995, 230, 1032–1036. [Google Scholar] [PubMed]
- Hinchliffe, P.; Sazanov, L.A. Organization of iron-sulfur clusters in respiratory complex I. Science 2005, 309, 771–774. [Google Scholar] [CrossRef]
- Sazanov, L.A.; Hinchliffe, P. Structure of the hydrophilic domain of respiratory complex I from Thermus thermophilus. Science 2006, 311, 1430–1436. [Google Scholar] [CrossRef]
- Berrisford, J.M.; Sazanov, L.A. Structural basis for the mechanism of respiratory complex I. J. Biol. Chem. 2009, 284, 29773–29783. [Google Scholar] [CrossRef]
- Efremov, R.G.; Baradaran, R.; Sazanov, L.A. The architecture of respiratory complex I. Nature 2010, 465, 441–445. [Google Scholar] [CrossRef] [PubMed]
- Vinothkumar, K.R.; Zhu, J.; Hirst, J. Archirecture of mammalian respiratory complex I. Nature 2014, 515, 80–84. [Google Scholar] [CrossRef]
- Zhu, J.; Vinothkumar, K.R.; Hirst, J. Structure of mammalian respiratory complex I. Nature 2016, 536, 354–358. [Google Scholar] [CrossRef] [PubMed]
- Feidorczuk, K.; Letts, J.A.; Degliesposti, G.; Kaszuba, K.; Skehel, M.; Sazanov, L.A. Atomic structure of the entire mammalian mitochondrial complex I. Nature 2016, 538, 406–410. [Google Scholar] [CrossRef]
- Letts, J.A.; Fiedorczuk, K.; Degliesposti, G.; Skehel, M.; Sazanov, L.A. Structures of respiratory supercomplex I+III2 reveal functional and conformational crosstalk. Mol. Cell 2019, 75, 1131–1146. [Google Scholar] [CrossRef]
- Soufari, H.; Parrot, C.; Kuhn, L.; Waltz, F.; Hashem, Y. Specific features and assembly of the plant mitochondrial complex I revealed by cryo-EM. Nat. Commun. 2020, 11, 5195. [Google Scholar] [CrossRef]
- Parey, K.; Lasham, J.; Mills, D.J.; Djurabekova, A.; Haapanen, O.; Galemou Yoga, E.; Xie, H.; Kühlbrandt, W.; Sharma, V.; Vonck, J.; et al. High-resolution structure and dynamics of mitochondrial complex I—Insights into the proton pumping mechanism. Sci. Adv. 2021, 7, eab3221. [Google Scholar] [CrossRef]
- Gu, J.; Liu, T.; Guo, R.; Zhang, L.; Yang, M. The coupling mechanism of mammalian mitochondrial complex I. Nat. Struct. Mol. Biol. 2022, 29, 172–182. [Google Scholar] [CrossRef]
- Schimpf, J.; Oppermann, S.; Gerasimova, T.; Santos Seica, A.F.; Hellwig, P.; Grishkovskaya, I.; Wohlwend, D.; Haselbach, D.; Friedrich, T. Structure of the peripheral arm of a minimalistic respiratory complex I. Structure 2022, 30, 80–94. [Google Scholar] [CrossRef]
- Ohnishi, T. NADH-quinone oxidoreductase, the most complex complex. J. Bioenerg. Biomembr. 1993, 25, 325–330. [Google Scholar] [CrossRef] [PubMed]
- Yano, T.; Sklar, J.; Nakamuru-Ogiso, E.; Takahashi, Y.; Yagi, T.; Ohnishi, T. Characterization of cluster N5 as a fast-relaxing [4Fe-4S] cluster in the Nqo3 subunit of the proton-translocating NADH-ubiquinone oxidoreductase from Paracoccus denitrificans. J. Biol. Chem. 2003, 278, 15514–15522. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Troup, G.J.; Hutton, D.R. Paramagnetic resonance of Fe3+ in kyanite. Brit. J. Appl. Phys. 1964, 15, 1493–1499. [Google Scholar] [CrossRef]
- Hagen, W.R. EPR spectroscopy of iron-sulfur proteins. Adv. Inorg. Chem. 1992, 38, 165–222. [Google Scholar]
- Hagen, W.R. Wide zero field interaction distributions in the high-spin EPR of metalloproteins. Mol. Phys. 2007, 105, 2031–2039. [Google Scholar] [CrossRef]
- Nakamaru-Ogiso, E.; Yano, T.; Yagi, T.; Ohnishi, T. Characterization of the iron-sulfur cluster N7 (N1c) in the subunit NuoG of the proton translocating NADH-quinone oxidoreductase from Escherichia coli. J. Biol. Chem. 2005, 280, 301–307. [Google Scholar] [CrossRef]
- Sled, V.D.; Friedrich, T.; Leif, H.; Weiss, H.; Meinhardt, S.W.; Fukumori, Y.; Calhoun, M.W.; Gennis, R.B.; Ohnishi, T. Bacterial NADH-quinone oxidoreductases: Iron-sulfur clusters and related problems. J. Bioenerg. Biomenbr. 1993, 25, 347–356. [Google Scholar] [CrossRef] [PubMed]
- Djafarzadeh, R.; Kerscher, S.; Zwicker, K.; Radermacher, M.; Lindahl, M.; Schägger, H.; Brandt, U. Biophysical and structural characterization of proton-translocating NADH-dehydrogenase (complexI) from the strictly aerobic yeast Yarrowia lipolytica. Biochim. Biophys. Acta 2000, 1459, 230–238. [Google Scholar] [CrossRef]
- Kerscher, S.; Kashani-Poor, N.; Zwicker, K.; Zickermann, V.; Brandt, U. Exploring the catalytic core of complex I by Yarrowia lipolytica yeast genetics. J. Bioenerg. Biomembr. 2001, 33, 187–196. [Google Scholar] [CrossRef]
- Waletko, A.; Zwicker, K.; Abdrakhmanova, A.; Zickermann, V.; Brandt, U. Histidine 129 in the 75-kDa subunit of mitochondrial complex I from Yarrowia lipolytica is not a ligand for [Fe4S4] cluster N5 but is required for catalytic activity. J. Biol. Chem. 2005, 280, 5622–5625. [Google Scholar] [CrossRef]
- Sinha, P.K.; Nakamaru-Ogiso, E.; Torres-Bacete, J.; Sato, M.; Castro-Guerrero, N.; Ohnishi, T.; Matsuno-Yagi, A.; Yagi, T. Electron transfer in subunit NuoI (TYKY) of Escherichia coli NADH:quinone oxidoreductase (NDH-1). J. Biol. Chem. 2012, 287, 17363–17373. [Google Scholar] [CrossRef]
- Wright, J.J.; Salvadori, E.; Bridges, H.R.; Hirst, J.; Roessner, M.M. Small-volume potentiometric titrations: EPR investigations of Fe-S cluster N2 in mitochondrial complex I. J. Inorg. Biochem. 2016, 162, 201–206. [Google Scholar] [CrossRef]
- Belevich, G.; Euro, L.; Wikström, M.; Verkhovskaya, M. Role of the conserved arginine 274 and histidine 224 and 228 residues in the NuoCD subunit of complex I from Escherichia coli. Biochemistry 2007, 46, 526–533. [Google Scholar] [CrossRef] [PubMed]
- Narayanan, M.; Gabrieli, D.; Leung, S.A.; Elguindy, M.M.; Glaser, C.A.; Saju, N.; Sinha, S.C.; Nakamaru-Ogiso, E. Semiquinone and cluster N6 signals in his-tagged proton-translocating NADH:ubiquinone oxidoreductase (complex I) from Escherichia coli. J. Biol. Chem. 2013, 288, 14310–14319. [Google Scholar] [CrossRef] [PubMed]
- Zu, Y.; Di Bernardo, S.; Yagi, T.; Hirst, J. Redox properties of the [2Fe-2S] center in the 24 kDa (NQO2) subunit of NADH:ubiquinone oxidoreductase (complex I). Biochemistry 2002, 41, 10056–10069. [Google Scholar] [CrossRef] [PubMed]
- Nakamaru-Ogiso, E.; Yano, T.; Ohnishi, T.; Yagi, T. Characterization of the iron-sulfur cluster coordinated by a cycteine cluster motif (CXXCXXXCX27C) in the Nqo3 subunit in the proton-translocating NADH:quinone oxidoreductase (NDH-1) of Thermus thermophilus HB-8. J. Biol. Chem. 2002, 277, 1680–1688. [Google Scholar] [CrossRef] [PubMed]

| Center (a) | gx | gy | gz | Author |
|---|---|---|---|---|
| N1b | 1.9278–1.9381 | 2.0213 | (Albracht et al. [59]) | |
| 1.925 | 1.937 | 2.019 | (Hagen et al. [11]) | |
| 1.923 | 1.941 | 2.022 | (Clifford et al. [60]) | |
| N2 | 1.925 | 1.925 | 2.0538 | [59] |
| 1.925 | 1.925 | 2.053 | [11] | |
| 1.922 | 1.928 | 2.055 | [60] | |
| N3 | 1.884 | 1.938 | 2.103 | [59] |
| 1.887 | 1.941 | 2.104 | [11] | |
| 1.883 | 1.929 | 2.102 | [60] | |
| N4 | 1.863 | 1.9263 | 2.037 | [59] |
| 1.862 | 1.921 | 2.034 | [11] | |
| 1.864 | 1.928 | 2.039 | [60] | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hagen, W.R. The g-Strained EPR Line Shape of Transition-Ion Complexes and Metalloproteins: Four Decades of Misunderstanding and Its Consequences. Molecules 2025, 30, 3299. https://doi.org/10.3390/molecules30153299
Hagen WR. The g-Strained EPR Line Shape of Transition-Ion Complexes and Metalloproteins: Four Decades of Misunderstanding and Its Consequences. Molecules. 2025; 30(15):3299. https://doi.org/10.3390/molecules30153299
Chicago/Turabian StyleHagen, Wilfred R. 2025. "The g-Strained EPR Line Shape of Transition-Ion Complexes and Metalloproteins: Four Decades of Misunderstanding and Its Consequences" Molecules 30, no. 15: 3299. https://doi.org/10.3390/molecules30153299
APA StyleHagen, W. R. (2025). The g-Strained EPR Line Shape of Transition-Ion Complexes and Metalloproteins: Four Decades of Misunderstanding and Its Consequences. Molecules, 30(15), 3299. https://doi.org/10.3390/molecules30153299