Photophysical Properties of 1,3-Diphenylisobenzofuran as a Sensitizer and Its Reaction with O2
Abstract
1. Introduction
2. Results and Discussions
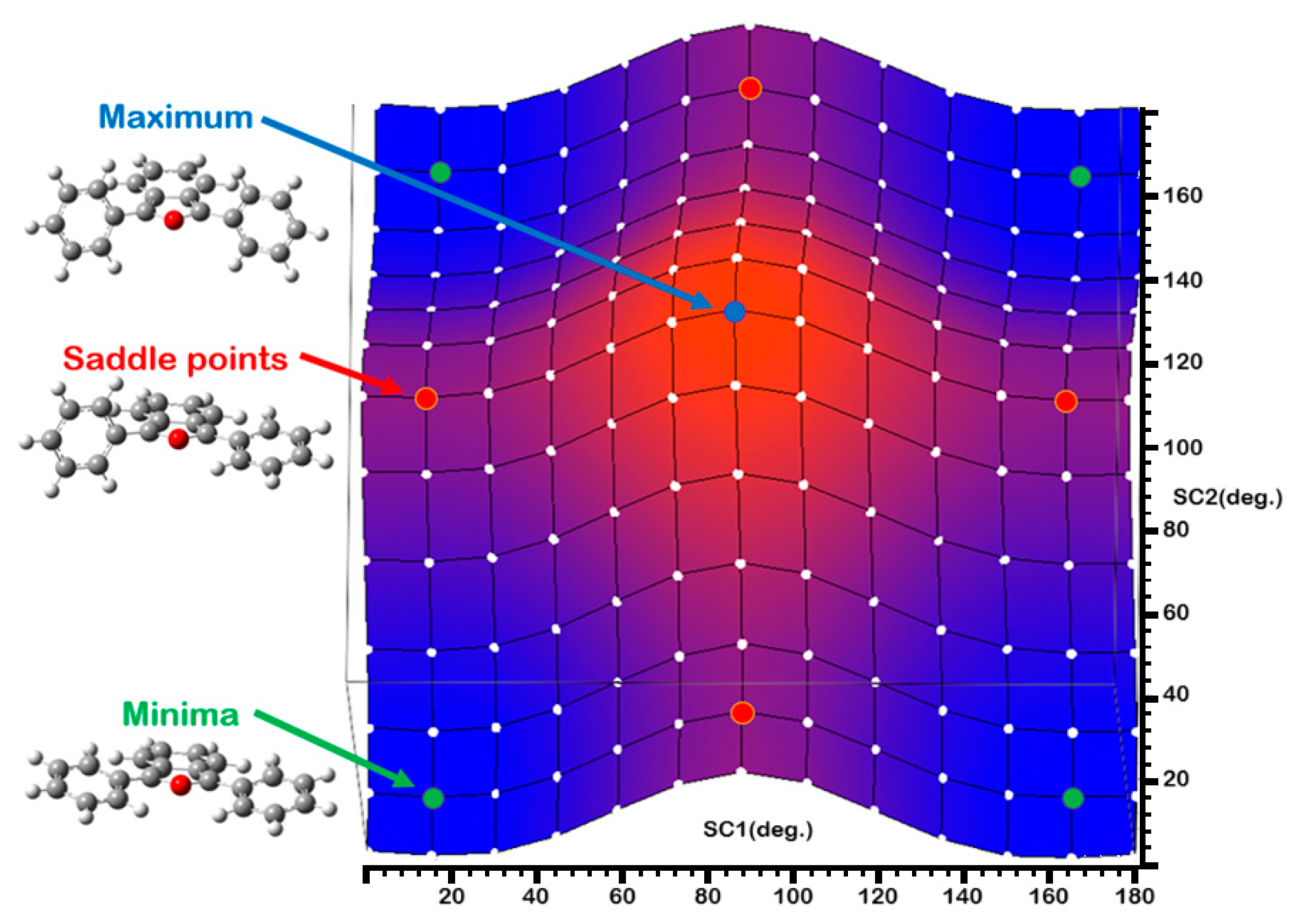
2.1. Conformers and Boltzmann Population Analysis
2.2. Conformational Analysis of the DPBF Molecule
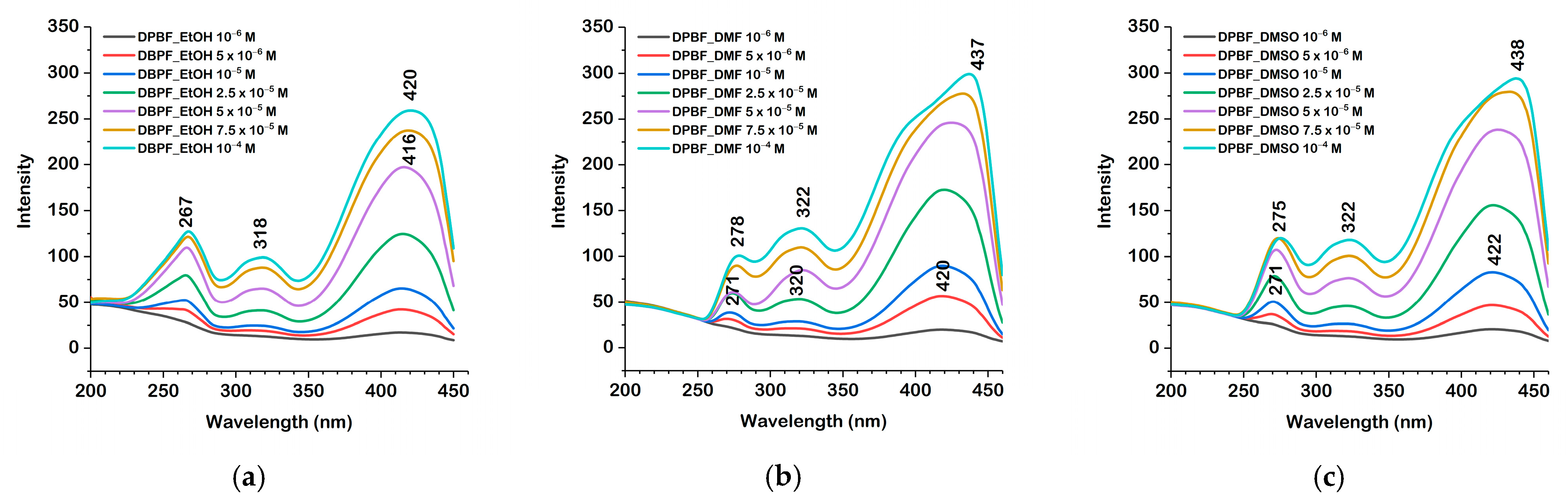
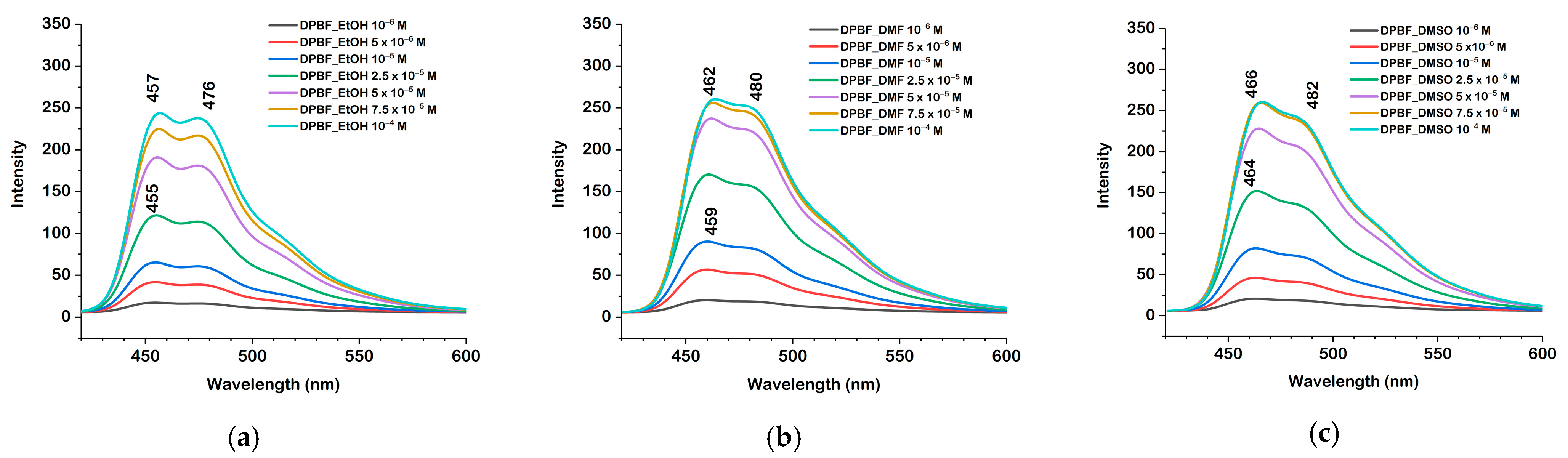
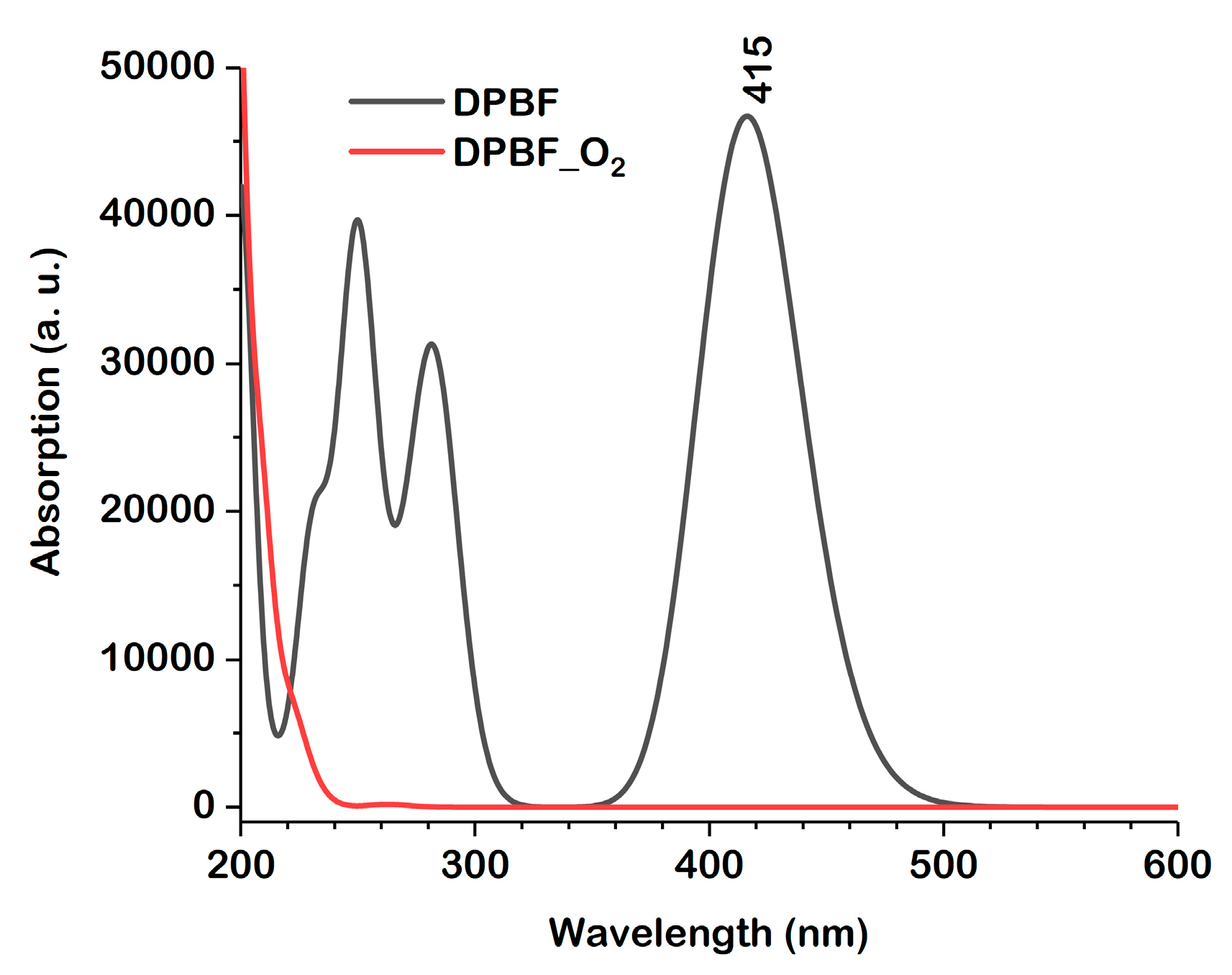
2.3. Absorption and Fluorescence Spectra
2.4. Photophysical Parameters of the DPBF Molecule
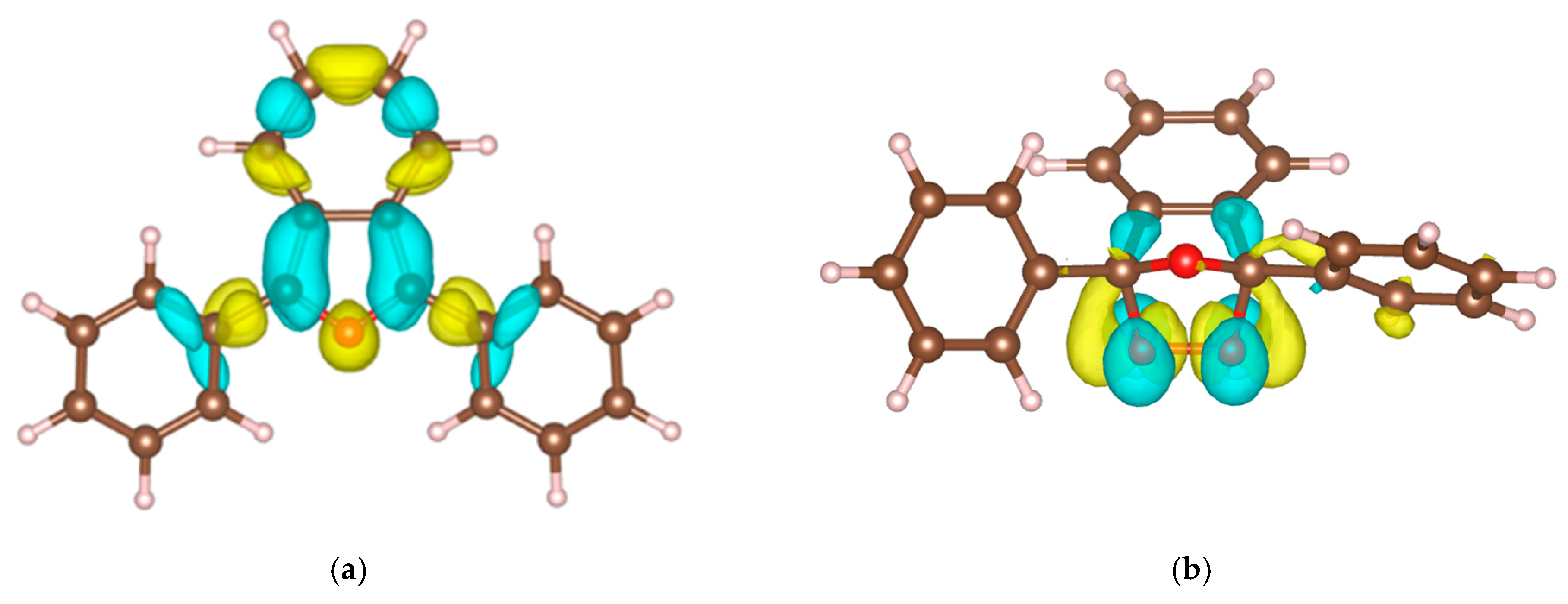
2.5. Electronic Structure and Nature of the Transition
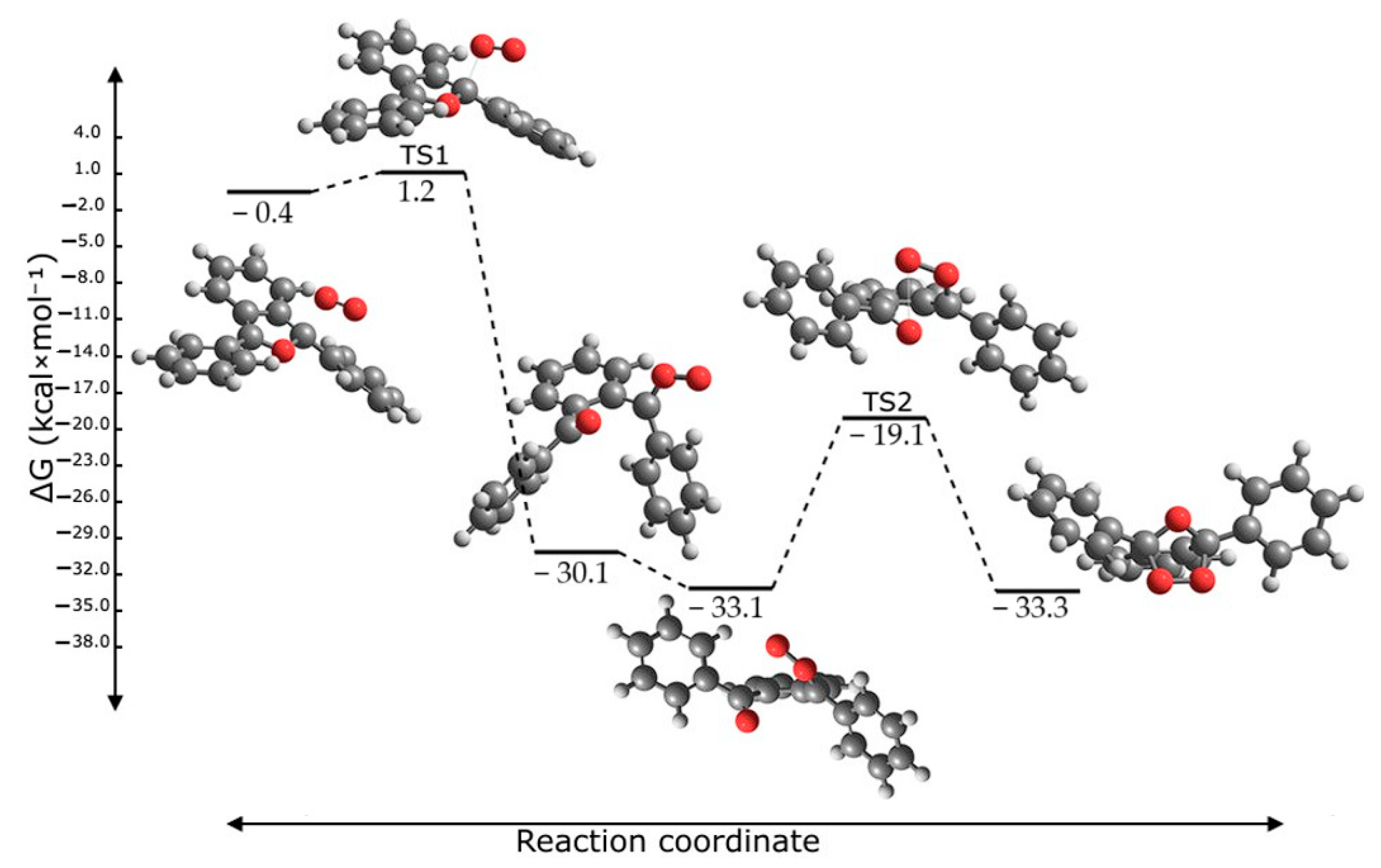
2.6. Reaction Mechanism
| DPBF in DMF | |||
| State | λ (nm) | f | Major MO → MO Contributions |
| S1 | 415.9 | 0.6445 | HOMO → LUMO (98%) |
| S2 | 282.6 | 0.2454 | HOMO → L + 1 (89%) |
| S3 | 282.3 | 0.1528 | HOMO → L + 3 (86%), HOMO → L + 2 (6%), HOMO → L + 5 (2%) |
| 2,5-endoperoxide in DMF | |||
| State | λ (nm) | f | Major MO → MO contributions |
| S1 | 262.3 | 0.0026 | H-6 → LUMO (18%), H-6 → L + 13 (19%), H-1 → LUMO (14%) H-6 → L + 4 (3%), H-4 → LUMO (2%), H-3 → LUMO (2%), H-2 → LUMO (3%), H-1 → L + 13 (8%) |
| S2 | 234.1 | 0.0004 | H-1 → LUMO (16%), HOMO → L + 2 (31%), H-6 → LUMO (7%), H-5 → L + 2 (2%), H-4 → L + 2 (3%), H-1 → L + 1 (3%), H-1 → L + 3 (2%), H-1 → L + 4 (3%), H-1 → L + 6 (5%), HOMO → L + 1 (4%), HOMO → L + 4 (2%) |
| S3 | 230.1 | 0.0084 | H-3 → L + 1 (12%), H-2 → L + 1 (18%), H-5 → L + 2 (2%), H-5 → L + 5 (6%), H-5 → L + 6 (5%), H-4 → LUMO (4%), H-4 → L + 1 (7%), H-4 → L + 2 (6%), H-4 → L + 5 (4%), H-4 → L + 6 (4%), H-3 → L + 5 (6%), H-3 → L + 6 (2%), H-2 → LUMO (7%), H-1 → L + 1 (2%) |
| S6 | 208.1 | 0.1825 | H-5 → L + 1 (11%), H-4 → LUMO (13%), H-3 → LUMO (11%), H-1 → LUMO (14%), H-5 → LUMO (5%), H-3 → L + 4 (3%), H-3 → L + 6 (5%), H-2 → L + 2 (3%), H-2 → L + 4 (3%), HOMO → LUMO (3%), HOMO → L + 5 (4%) |
3. Experimental Details
4. Computational Methods
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Entradas, T.; Waldron, S.; Volk, M. The detection sensitivity of commonly used singlet oxygen probes in aqueous environments. J. Photochem. Photobiol. B Biol. 2020, 204, 111787. [Google Scholar] [CrossRef] [PubMed]
- Carloni, P.; Damiani, E.; Greci, L.; Stipa, P.; Tanfani, F.; Tartaglini, E.; Wozniak, M.J.R.O.C.I. On the use of 1,3-diphenylisobenzofuran (DPBF). Reactions with carbon and oxygen centered radicals in model and natural systems. Res. Chem. Intermed. 1993, 19, 395–405. [Google Scholar] [CrossRef]
- Zhang, X.-F.; Li, X. The photostability and fluorescence properties of diphenylisobenzofuran. J. Lumin. 2011, 131, 2263–2266. [Google Scholar] [CrossRef]
- Żamojć, K.; Zdrowowicz, M.; Rudnicki-Velasquez, P.B.; Krzymiński, K.; Zaborowski, B.; Niedziałkowski, P.; Jacewicz, D.; Chmurzyński, L. The development of 1,3-diphenylisobenzofuran as a highly selective probe for the detection and quantitative determination of hydrogen peroxide. Free Radic. Res. 2017, 51, 38–46. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.H.; Wei, X.F.; Liu, J.H.; Yang, W.; Liu, Y.A.; Cheng, K.; He, X.Y.; Fu, X.L.; Zhang, Y.; Zhang, H.X. Chlorin e6-1,3-diphenylisobenzofuran polymer hybrid nanoparticles for singlet oxygen-detection photodynamic ablation. Methods Appl. Fluoresc. 2021, 9, 025003. [Google Scholar] [CrossRef]
- Foresman, J.B.; Frisch, A. Exploring Chemistry with Electronic Structure Methods, 3rd ed.; Gaussian, Inc.: Wallingford, CT, USA, 2015. [Google Scholar]
- Udofia, I.A.; Oloba-Whenu, O.A.; Ogunbayo, T.B.; Isanbor, C. Theoretical Study of the Photophysical and Photochemical Properties of 1H-Benzimidazole and 2-Ethyl-7-nitro-5-Substituted 1H-Benzimidazoles. ChemistrySelect 2023, 8, e202302135. [Google Scholar] [CrossRef]
- Chávez, B.Y.; Paz, J.L.; Gonzalez-Paz, L.A.; Alvarado, Y.J.; Contreras, J.S.; Loroño-González, M.A. Theoretical Study of Cyanidin-Resveratrol Copigmentation by the Functional Density Theory. Molecules 2024, 29, 2064. [Google Scholar] [CrossRef] [PubMed]
- Ali, A.; Farid, T.; Rafiq, M.I.; Zhoub, B.; Tang, W. Evaluating the impact of Hartree–Fock exact exchange on the performance of global hybrid functionals for the vertical excited-state energies of fused-ring electron acceptors using TD-DFT. Phys. Chem. Chem. Phys. 2022, 24, 21270–21282. [Google Scholar] [CrossRef] [PubMed]
- Fedorowicz, J.; Sączewski, J.; Drażba, Z.; Wiśniewska, P.; Gdaniec, M.; Wicher, B.; Suwiński, G.; Jalińska, A. Synthesis and fluorescence of dihydro-[1,2,4]triazolo[4,3-a]pyridin-2-ium-carboxylates: An experimental and TD-DFT comparative study. Dye. Pigment. 2019, 161, 347–359. [Google Scholar] [CrossRef]
- Charaf-Eddin, A.; Planchat, A.; Mennucci, B.; Adamo, C.; Jacquemin, D. Choosing a Functional for Computing Absorption and Fluorescence Band Shapes with TD-DFT. J. Chem. Theory Comput. 2013, 9, 2749–2760. [Google Scholar] [CrossRef] [PubMed]
- Okuno, K.; Shigeta, Y.; Kishi, R.; Nakano, M. Non-empirical tuning of CAM-B3LYP functional in time-dependent density functional theory for excitation energies of diarylethene derivatives. Chem. Phys. Lett. 2013, 585, 201–206. [Google Scholar] [CrossRef]
- Vinţeler, E.; Stan, N.-F.; Luchian, R.; Căinap, C.; Prates-Ramalho, J.P.; Chiș, V. Conformational landscape and low lying excited states of imatinib. J. Mol. Model. 2015, 21, 84. [Google Scholar] [CrossRef] [PubMed]
- Frau, J.; Glossman-Mitnik, D. Molecular Reactivity and Absorption Properties of Melanoidin Blue-G1 through Conceptual DFT. Molecules 2018, 23, 559. [Google Scholar] [CrossRef] [PubMed]
- Andrzejak, M.; Zams, J.; Goclon, J.; Kolek, P. Symmetry Breaking of Electronic Structure upon the π→π* Excitation in Anthranilic Acid Homodimer. Molecules 2024, 29, 5562. [Google Scholar] [CrossRef] [PubMed]
- Širůček, J.; Le Guennic, B.; Damour, Y.; Loos, P.-F.; Jacquemin, D. Excited-State Absorption: Reference Oscillator Strengths, Wave Function, and TDDFT Benchmarks. J. Chem. Theory Comput. 2025, 21, 4688–4703. [Google Scholar] [CrossRef] [PubMed]
- Grabarz, A.M.; Ośmiałowski, B. Benchmarking Density Functional Approximations for Excited-State Properties of Fluorescent Dyes. Molecules 2021, 26, 7434. [Google Scholar] [CrossRef]
- Martin, R.L. Natural transition orbitals. J. Chem. Phys. 2003, 118, 4775–4777. [Google Scholar] [CrossRef]
- Casida, M.E.; Jamorski, C.; Casida, K.C.; Salahub, D.R. Molecular excitation energies to high-lying bound states from time-dependent density-functional response theory: Characterization and correction of the time-dependent local density approximation ionization threshold. J. Chem. Phys. 1998, 108, 4439–4449. [Google Scholar] [CrossRef]
- Austin, A.; Petersson, G.A.; Frisch, M.J.; Dobek, F.J.; Scalmani, G.; Throssell, K. A density functional with spherical atom dispersion terms. J. Chem. Theory Comput. 2012, 8, 4989–5007. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Cole-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef] [PubMed]
- Vosko, S.H.; Wilk, L.; Nusair, M. Accurate spin-dependent electron liquid correlation energies for local spin density calculations: A critical analysis. Can. J. Phys. 1980, 58, 1200–1211. [Google Scholar] [CrossRef]
- Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab initio calculation of vibrational absorption and circular dichroism spectra using density functional force fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
- Yanai, T.; Tew, D.P.; Handy, N.C. A new hybrid exchange-correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Henderson, T.M.; Izmaylov, A.F.; Scalmani, G.; Scuseria, G.E. Can short-range hybrids describe long-range-dependent properties? J. Chem. Phys. 2009, 131, 044108. [Google Scholar] [CrossRef] [PubMed]
- Chai, J.-D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom-atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef] [PubMed]
- Tomasi, J.; Mennucci, B.; Cammi, R. Quantum mechanical continuum solvation models. Chem. Rev. 2005, 105, 2999–3094. [Google Scholar] [CrossRef] [PubMed]
- Ducasse, L.; Castet, F.; Fritsch, A.; Huc, I.; Buffeteau, T. Density functional theory calculations and vibrational circular dichroism of aromatic foldamers. J. Phys. Chem. A 2007, 111, 5092–5098. [Google Scholar] [CrossRef] [PubMed]
- Willoughby, P.H.; Jansma, M.J.; Hoye, T.R. A guide to small-molecule structure assignment through computation of (1H and 13C) NMR chemical shifts. Nat. Protoc. 2014, 9, 643–660. [Google Scholar] [CrossRef] [PubMed]
- Lopes Jesus, A.J.; Jarmelo, S.; Fausto, R.; Reva, I. Conformational preferences of 3,4-dihydroxyphenylacetic acid (DOPAC). Spectrochim. Acta A Mol. Biomol. Spectrosc. 2015, 140, 54–64. [Google Scholar] [CrossRef] [PubMed]
- Breneman, C.M.; Wiberg, K.B. Determining atom-centered monopoles from molecular electrostatic potentials. The need for high sampling density in formamide conformational analysis. J. Comput. Chem. 1990, 11, 361–373. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian, version 16, revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2019.
- Dennington, R.; Keith, T.; Millam, J. GaussView, Version 6.1.1; Semichem Inc.: Shawnee Mission, KS, USA, 2019.



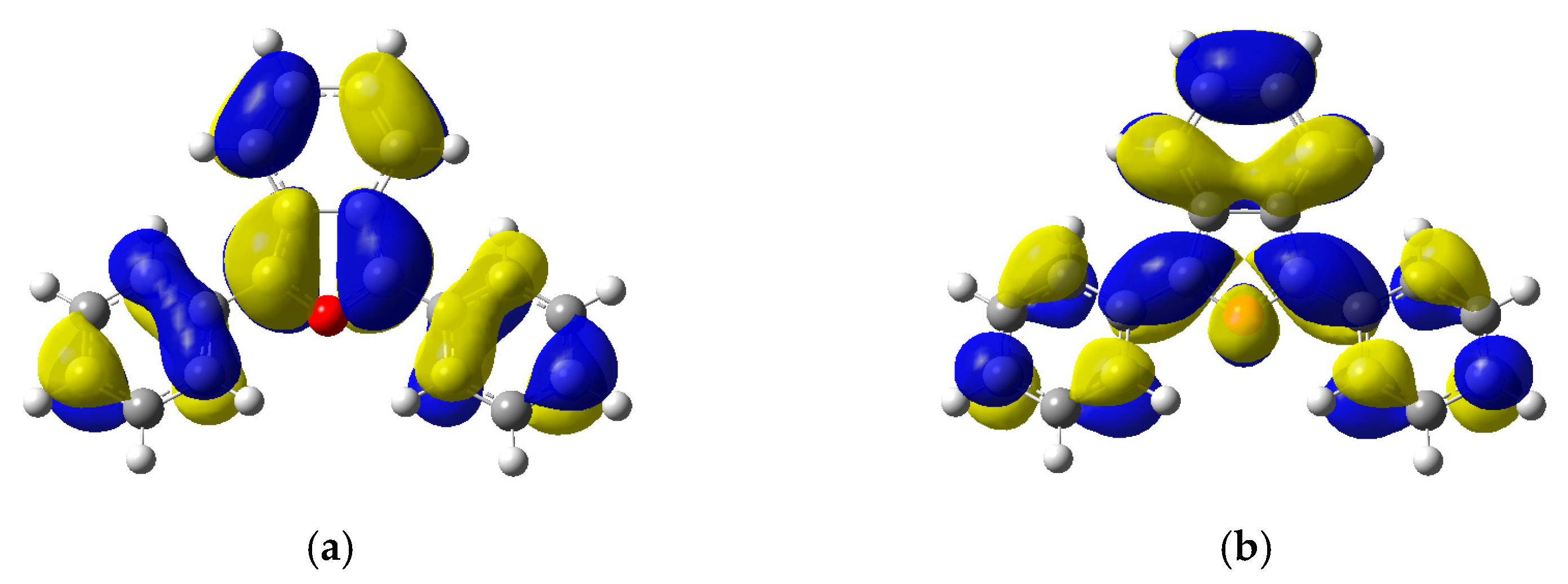
| Conformer | ΔG (kcal/mol) | The Boltzmann Factor | Relative Boltzmann Population (%) |
|---|---|---|---|
| DPBF in gas phase | |||
| C2 | 0.33 | 0.573 | 36.42 |
| Cs | 0.00 | 1.000 | 63.58 |
| DPBF in ethanol | |||
| C2 | 0.40 | 0.509 | 33.74 |
| Cs | 0.00 | 1.000 | 66.26 |
| DPBF in DMSO | |||
| C2 | 0.40 | 0.509 | 33.74 |
| Cs | 0.00 | 1.000 | 66.26 |
| DPBF with an ethanol molecule in ethanol | |||
| c1 | 0.00 | 1.000 | 60.40 |
| c2 | 0.25 | 0.656 | 39.60 |
| Conformer | ΔG (kcal/mol) | The Boltzmann Factor | Relative Boltzmann Population (%) |
|---|---|---|---|
| DPBF in DMSO | |||
| C2 | 0.58 | 0.376 | 27.31 |
| Cs | 0.00 | 1.000 | 72.69 |
| Basis Set | Functional | Solvent | λabs (nm) | f (a.u.) | λem (nm) Vertical/Adiabatic | |μ10|2 (a.u.) | τr (ns) |
|---|---|---|---|---|---|---|---|
| 6-311+G(2d,p) | APFD | EtOH | 440.1 | 0.5735 | 568.6/516.5 | 13.7952 | 6.58 |
| DMF | 441.9 | 0.5882 | 570.3/517.8 | 13.9729 | 6.55 | ||
| DMSO | 441.5 | 0.5856 | 571.0/518.3 | 14.0475 | 6.55 | ||
| B3LYP | EtOH | 451.1 | 0.5652 | 583.6/530.6 | 13.9355 | 7.04 | |
| DMF | 452.8 | 0.5778 | 585.4/532.0 | 14.1166 | 7.01 | ||
| DMSO | 452.4 | 0.5752 | 586.1/532.5 | 14.1926 | 7.00 | ||
| cam-B3LYP | EtOH | 397.0 | 0.6101 | 544.2/478.7 | 14.0328 | 5.67 | |
| DMF | 398.3 | 0.6229 | 545.9/480.0 | 14.1974 | 5.66 | ||
| DMSO | 398.2 | 0.6214 | 546.7/480.4 | 14.2664 | 5.65 | ||
| PBE0 | EtOH | 436.4 | 0.5807 | 564.5/512.5 | 13.8025 | 6.43 | |
| DMF | 439.4 | 0.5935 | 566.2/515.8 | 13.9781 | 6.41 | ||
| DMSO | 438.5 | 0.5911 | 566.9/514.4 | 14.0517 | 6.40 | ||
| ωB97X-D | EtOH | 389.2 | 0.6050 | 536.8/470.1 | 13.9017 | 5.49 | |
| DMF | 390.5 | 0.6188 | 538.5/471.2 | 14.0644 | 5.48 | ||
| DMSO | 390.1 | 0.6149 | 539.3/471.8 | 14.1327 | 5.48 | ||
| LC-ωHPBE | EtOH | 351.7 | 0.6338 | 508.0/431.8 | 13.6037 | 4.76 | |
| DMF | 352.8 | 0.6472 | 509.7/432.8 | 13.7533 | 4.75 | ||
| DMSO | 352.6 | 0.6448 | 510.4/433.2 | 13.8161 | 4.75 |
| Functional | Δλ (nm) EtOH | Δλ (nm) DMF | Δλ (nm) DMSO | MAE (nm) | RMSE (nm) |
|---|---|---|---|---|---|
| cam-B3LYP | 13.0 | 15.7 | 17.8 | 15.50 | 15.62 |
| ωB97X-D | 20.8 | 23.5 | 25.9 | 23.40 | 23.49 |
| PBE0 | 26.4 | 25.4 | 22.5 | 24.77 | 24.82 |
| APFD | 30.1 | 27.9 | 25.5 | 27.83 | 27.90 |
| B3LYP | 41.1 | 38.8 | 36.4 | 38.77 | 38.81 |
| LC-ωHPBE | 58.3 | 61.2 | 63.4 | 60.97 | 61.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stan, Ș.; Ramalho, J.P.P.; Holca, A.; Chiș, V. Photophysical Properties of 1,3-Diphenylisobenzofuran as a Sensitizer and Its Reaction with O2. Molecules 2025, 30, 3021. https://doi.org/10.3390/molecules30143021
Stan Ș, Ramalho JPP, Holca A, Chiș V. Photophysical Properties of 1,3-Diphenylisobenzofuran as a Sensitizer and Its Reaction with O2. Molecules. 2025; 30(14):3021. https://doi.org/10.3390/molecules30143021
Chicago/Turabian StyleStan, Ștefan, João P. Prates Ramalho, Alexandru Holca, and Vasile Chiș. 2025. "Photophysical Properties of 1,3-Diphenylisobenzofuran as a Sensitizer and Its Reaction with O2" Molecules 30, no. 14: 3021. https://doi.org/10.3390/molecules30143021
APA StyleStan, Ș., Ramalho, J. P. P., Holca, A., & Chiș, V. (2025). Photophysical Properties of 1,3-Diphenylisobenzofuran as a Sensitizer and Its Reaction with O2. Molecules, 30(14), 3021. https://doi.org/10.3390/molecules30143021








