Mechanistic Insights into the Hot-Spot Formation and Pyrolysis of LLM-105 with Different Void Defects: A ReaxFF Molecular Dynamics Study
Abstract
1. Introduction
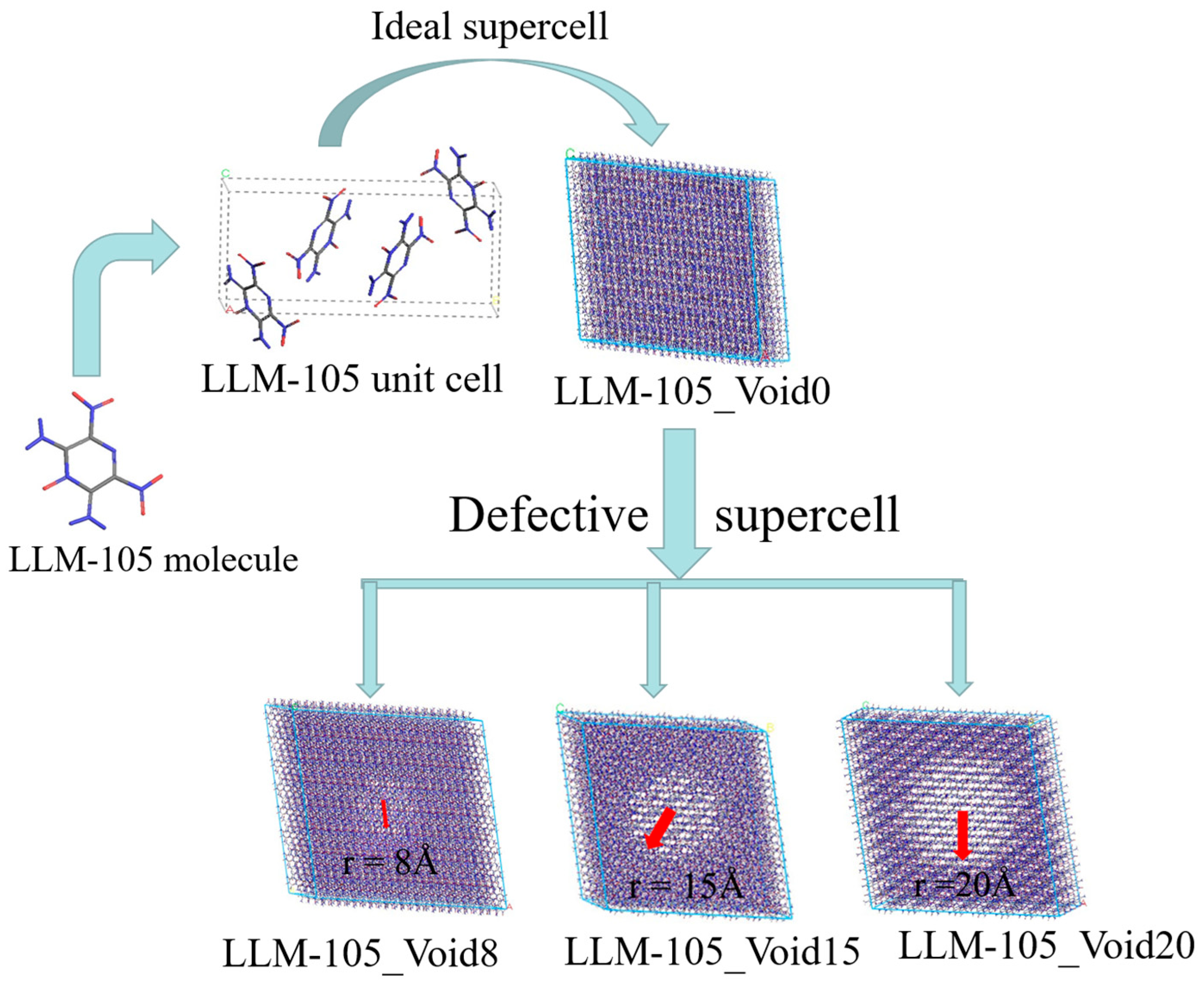
2. Results
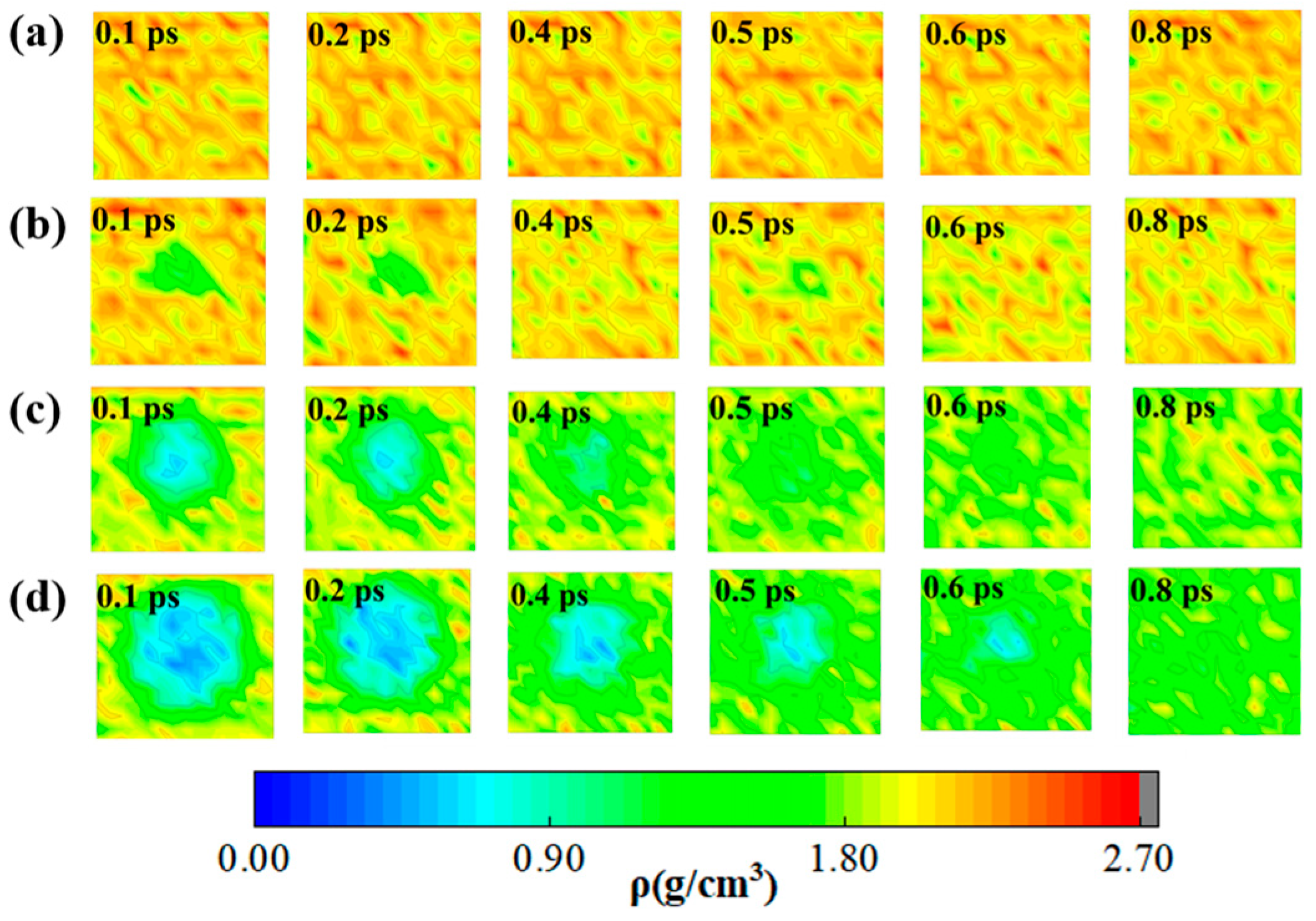
2.1. Density Evolution
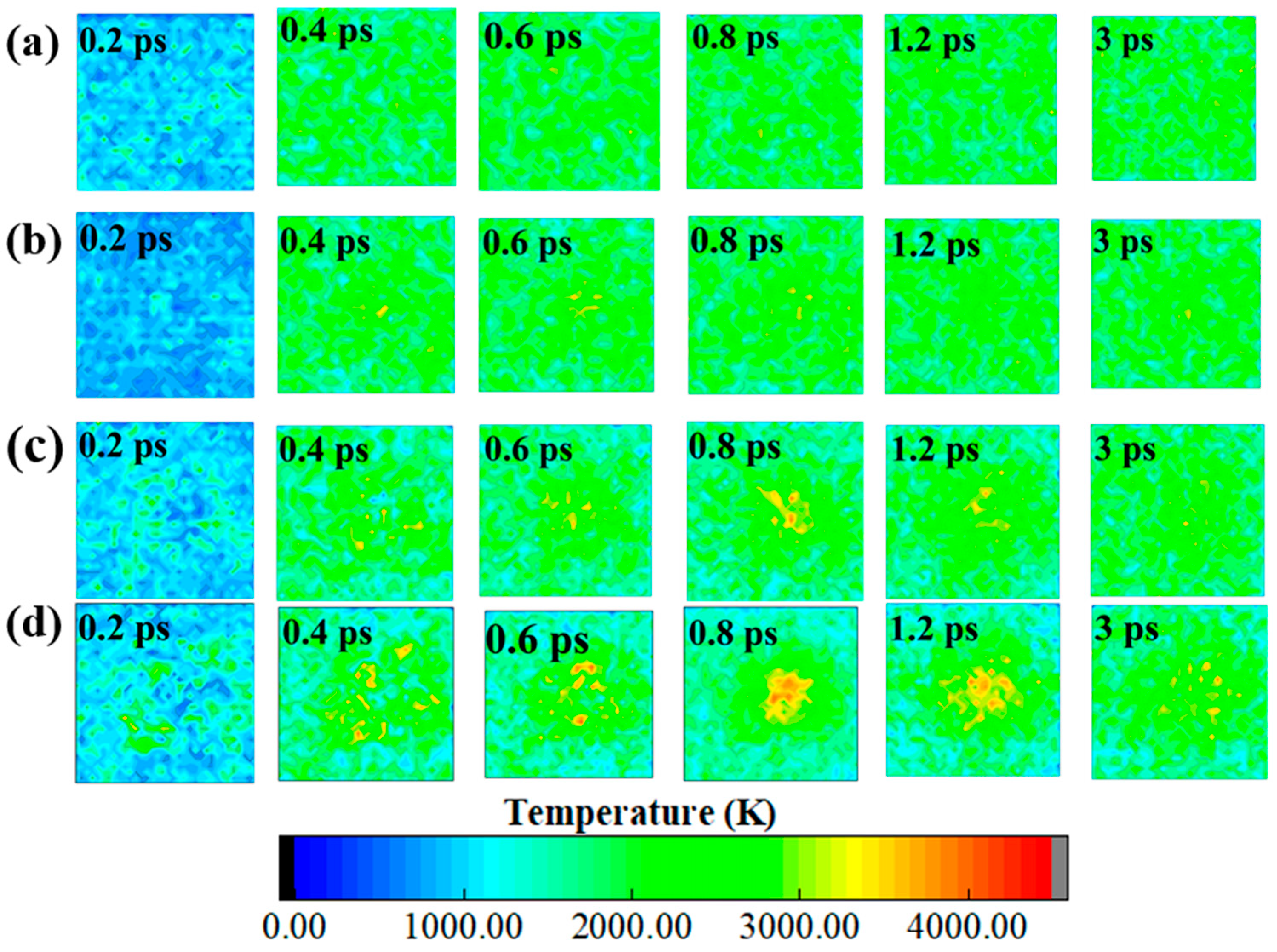
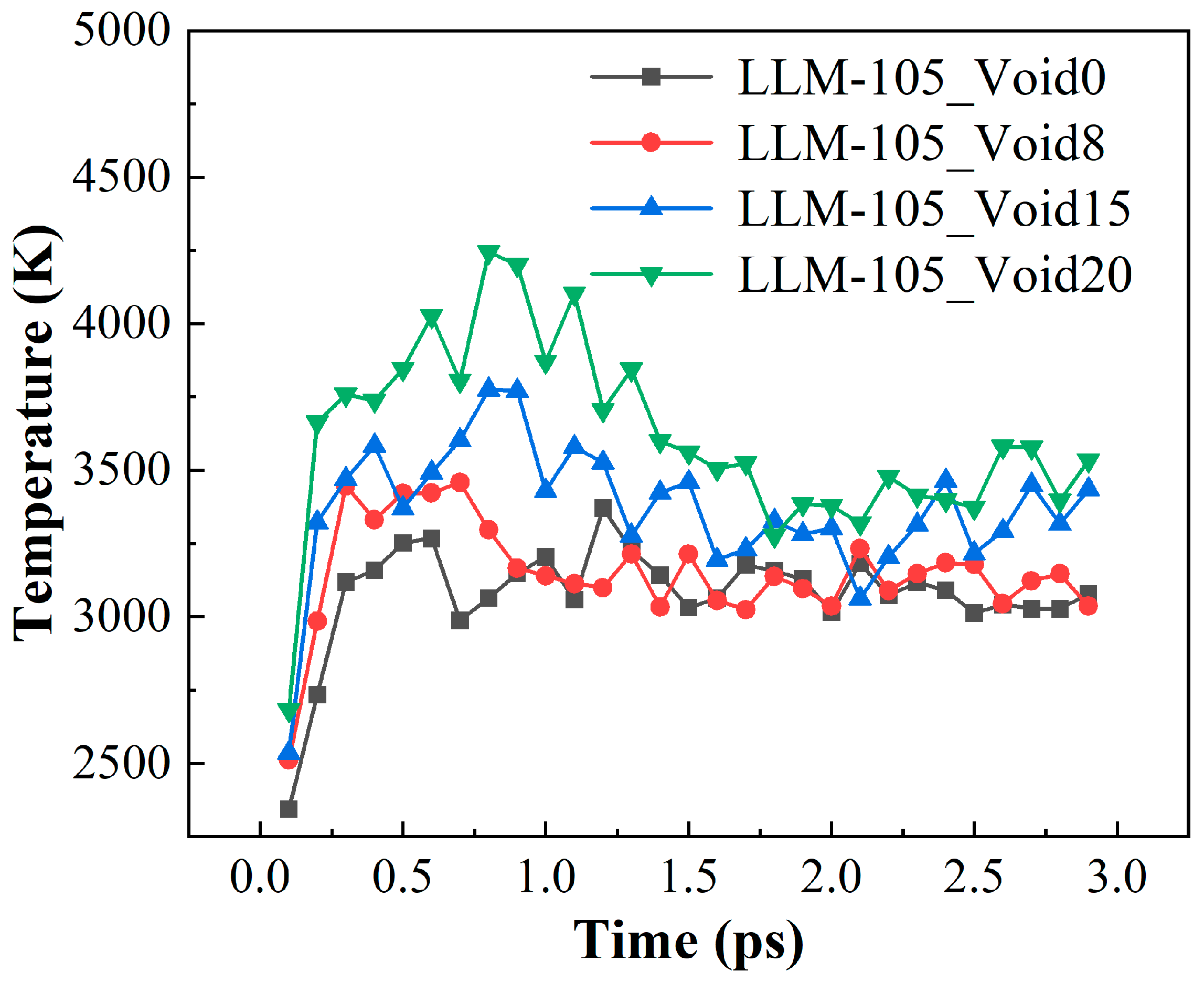
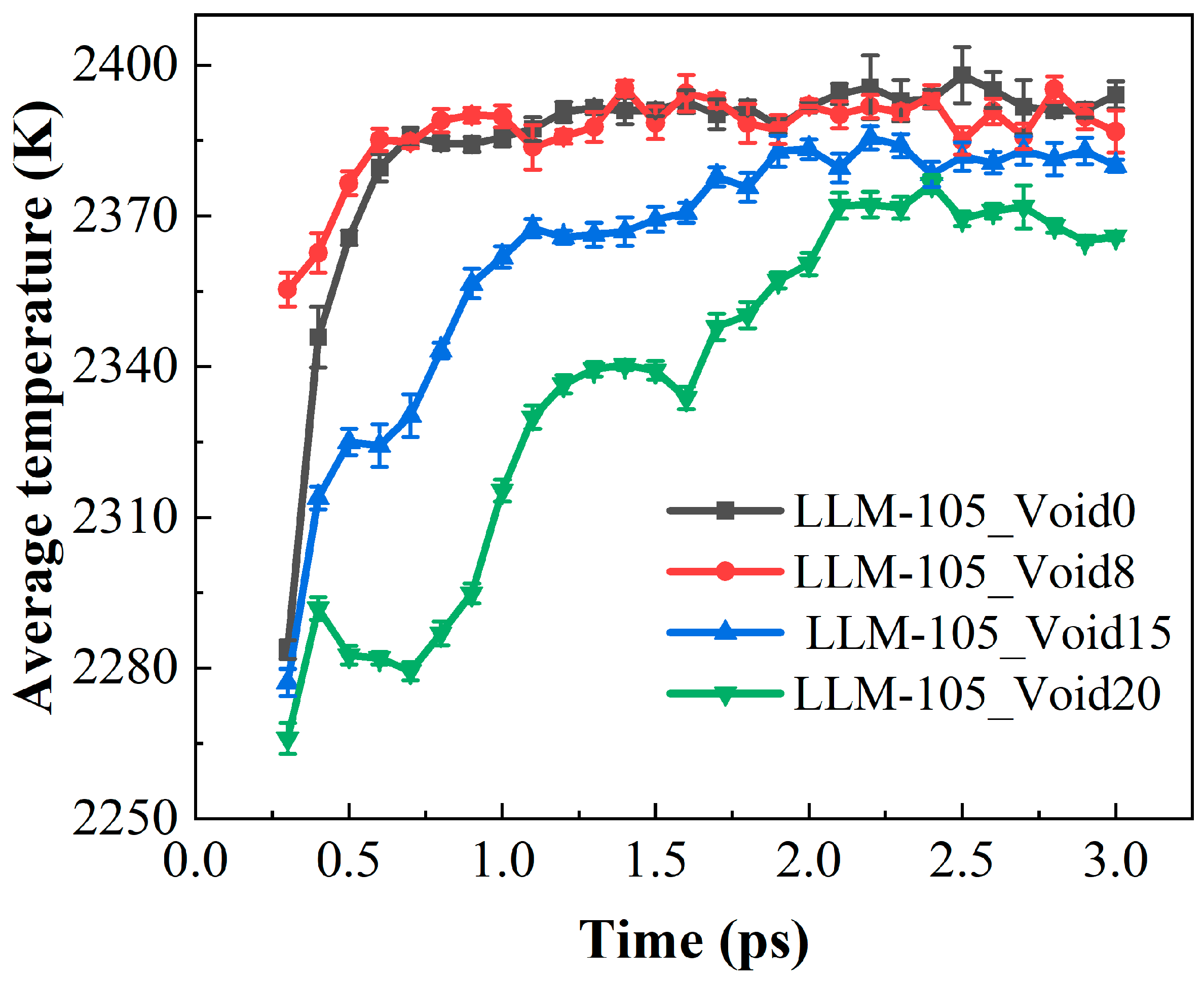
2.2. Evolution of Hotspots and Maximum Temperature
2.3. Early Evolution of Kinetic Energy
2.4. Early Evolution of LLM-105 Molecules
2.5. Evolution of Potential Energy and Number of Species
2.6. Pyrolysis Mechanisms and Chemical Species
2.7. Diffusion Behavior
3. Computational Details
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Crawford, M.-J.; Klapötke, T.M.; Welch, J. Energetic Materials: Particle Processing and Characterization; Teipel, U., Ed.; Wiley-VCH: Hoboken, NJ, USA, 2005; Volume 44, p. 1909. [Google Scholar]
- Fried, L.E.; Manaa, M.R.; Pagoria, P.F.; Simpson, R.L. Design and Synthesis of Energetic Materials. Annu. Rev. Mater. Res. 2001, 31, 291–321. [Google Scholar] [CrossRef]
- Mei, X.; Yang, H.; Li, X.; Li, Y.; Cheng, Y. Study of Some Low Temperature Gas-Generating Compositions. Propellants Explos. Pyrotech. 2015, 40, 526–553. [Google Scholar] [CrossRef]
- Tang, J.; Cheng, G.; Feng, S.; Zhao, X.; Zhang, Z.; Ju, X.; Yang, H. Boosting Performance and Safety of Energetic Materials by Polymorphic Transition. Cryst. Growth Des. 2019, 19, 4822–4828. [Google Scholar] [CrossRef]
- Xiao, T.; Chen, J.; Xu, J.; Ma, P.; Ma, C. Theoretical Insight into Different Energetic Groups on the Performance of Energetic Materials 2,5,7,9-Tetranitro-2,5,7,9-Tetraazabicyclo[4,3,0]Nonane-8-One. J. Mol. Model. 2023, 29, 231. [Google Scholar] [CrossRef] [PubMed]
- Patwardhan, W.D. Explosives, Chemistry and Technology. Nature 1965, 205, 432. [Google Scholar] [CrossRef]
- Badgujar, D.M.; Talawar, M.B.; Asthana, S.N.; Mahulikar, P.P. Advances in Science and Technology of Modern Energetic Materials: An Overview. J. Hazard. Mater. 2008, 151, 289–305. [Google Scholar] [CrossRef] [PubMed]
- Peng, D.-J.; Chang, C.-M.; Chiu, M. Thermal Reactive Hazards of HMX with Contaminants. J. Hazard. Mater. 2004, 114, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Bennion, J.C.; McBain, A.; Son, S.F.; Matzger, A.J. Design and Synthesis of a Series of Nitrogen-Rich Energetic Cocrystals of 5,5′-Dinitro-2H,2H′-3,3′-Bi-1,2,4-Triazole (DNBT). Cryst. Growth Des. 2015, 15, 2545–2549. [Google Scholar] [CrossRef]
- Patil, V.B.; Zeman, S. Progress in Energy−Safety Balanced Cocrystallization of Four Commercially Attractive Nitramines. Cryst. Growth Des. 2024, 24, 7361–7388. [Google Scholar] [CrossRef]
- Liu, W.-H.; Liu, Q.-J.; Zhong, M.; Gan, Y.-D.; Liu, F.-S.; Li, X.-H.; Tang, B. Predicting Impact Sensitivity of Energetic Materials: Insights from Energy Transfer of Carriers. Acta Mater. 2022, 236, 118137. [Google Scholar] [CrossRef]
- Liu, R.; Chen, P.W. Modeling Ignition Prediction of HMX-Based Polymer Bonded Explosives under Low Velocity Impact. Mech. Mater. 2018, 124, 106–117. [Google Scholar] [CrossRef]
- Yang, P.; Yang, H.; Yang, W.; Tang, J.; Zhang, G.; Hu, W.; Cheng, G. Studies on the Synthesis and Properties of High-Energy Low-Sensitivity Compounds Based on 3-Amino-1,2,4-Triazole. Cryst. Growth Des. 2022, 22, 4221–4227. [Google Scholar] [CrossRef]
- Ferdowsi, M.; Yazdani, F.; Omidkhah, M.R.; Keshavarz, M.H. Reliable Prediction of Shock Sensitivity of Energetic Compounds Based on Small-scale Gap Test through Their Electric Spark Sensitivity. Z. Anorg Allge Chem. 2018, 644, 888–889. [Google Scholar] [CrossRef]
- Xiong, X.; He, X.; Xiong, Y.; Xue, X.; Yang, H.; Zhang, C. Correlation between the Self-Sustaining Ignition Ability and the Impact Sensitivity of Energetic Materials. Energetic Mater. Front. 2020, 1, 40–49. [Google Scholar] [CrossRef]
- Xue, Z.-H.; Xu, R.; Wang, Z.; Yu, M.; Zhao, X.; Yan, Q.-L. Interfacial Self-Assembling of Nano-TATB@PDA Embedded Football-like CL-20 Co-Particles with Reduced Sensitivity. Chem. Eng. J. 2024, 488, 151010. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, X.; Huang, H. π-Stacked Interactions in Explosive Crystals: Buffers against External Mechanical Stimuli. J. Am. Chem. Soc. 2008, 130, 8359–8365. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Cao, X.; Xiang, B. Sandwich Complex of TATB/Graphene: An Approach to Molecular Monolayers of Explosives. J. Phys. Chem. C 2010, 114, 22684–22687. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, A.; Zhang, C.; Jiang, D.; Zhu, Y.; Zhang, C. Crystal Packing of Low-Sensitivity and High-Energy Explosives. Cryst. Growth Des. 2014, 14, 4703–4713. [Google Scholar] [CrossRef]
- Kuklja, M.M.; Rashkeev, S.N. Shear-Strain-Induced Chemical Reactivity of Layered Molecular Crystals. Appl. Phys. Lett. 2007, 90, 151913. [Google Scholar] [CrossRef]
- Kuklja, M.M.; Rashkeev, S.N. Shear-Strain-Induced Structural and Electronic Modifications of the Molecular Crystal 1,1-Diamino-2,2-Dinitroethylene: Slip-Plane Flow and Band Gap Relaxation. Phys. Rev. B 2007, 75, 104111. [Google Scholar] [CrossRef]
- Xue, X.; Wen, Y.; Long, X.; Li, J.; Zhang, C. Influence of Dislocations on the Shock Sensitivity of RDX: Molecular Dynamics Simulations by Reactive Force Field. J. Phys. Chem. C 2015, 119, 13735–13742. [Google Scholar] [CrossRef]
- Van der Heijden, A.E.D.M.; Bouma, R.H.B. Crystallization and Characterization of RDX, HMX, and CL-20. Cryst. Growth Des. 2004, 4, 999–1007. [Google Scholar] [CrossRef]
- Zhang, M.; Tan, Y.; Zhao, X.; Zhang, J.; Huang, S.; Zhai, Z.; Liu, Y.; Yang, Z. Seeking a Novel Energetic Co-Crystal Strategy through the Interfacial Self-Assembly of CL-20 and HMX Nanocrystals. CrystEngComm 2019, 22, 61–67. [Google Scholar] [CrossRef]
- Klapwijk, A.R.; Simone, E.; Nagy, Z.K.; Wilson, C.C. Tuning Crystal Morphology of Succinic Acid Using a Polymer Additive. Cryst. Growth Des. 2016, 16, 4349–4359. [Google Scholar] [CrossRef]
- Yan, P.; Zhao, X.; Rui, J.; Zhao, J.; Xu, M.; Zhai, L. Molecular Dynamics Simulation of the Influence of RDX Internal Defects on Sensitivity. Crystals 2021, 11, 329. [Google Scholar] [CrossRef]
- Katritzky, A.R.; Rachwal, S.; Smith, T.P.; Steel, P.J. Synthesis and Reactivity of 2,6-Diamino-4-Methyl-3-Pyridinecarbonitrile. J. Heterocycl. Chem. 1995, 32, 979–984. [Google Scholar] [CrossRef]
- Xu, W.; An, C.; Wang, J.; Dong, J.; Geng, X. Preparation and Properties of An Insensitive Booster Explosive Based on LLM-105. Propellants Explos. Pyrotech. 2013, 38, 136–141. [Google Scholar] [CrossRef]
- Pagoria, P.; Zhang, M.; Zuckerman, N.; Lee, G.; Mitchell, A.; DeHope, A.; Gash, A.; Coon, C.; Gallagher, P. Synthetic Studies of 2,6-Diamino-3,5-Dinitropyrazine- 1-Oxide (LLM-105) from Discovery to Multi-Kilogram Scale. Propellants Explos. Pyrotech. 2018, 43, 15–27. [Google Scholar] [CrossRef]
- Yuan, W.-S.; Gan, Y.-D.; Jiang, C.-L.; Zhu, S.-H.; Zhang, M.-J.; Liu, F.-S.; Tang, B.; Hong, D.; Liu, Q.-J. First-Principles Calculations of the Electronic, Vibrational, and Thermodynamic Properties of 2,6-Diamino-3,5-Dinitropyrazine-1-Oxide (LLM-105). Chem. Phys. 2021, 548, 111232. [Google Scholar] [CrossRef]
- Yu, Q.; Zhao, C.; Chen, J.; Liao, L.; Yang, F.; Zhang, H.; Duan, Y.; Li, J. Turn a Weakness into a Strength: Performance Enhancement of 2,6-Diamino-3,5-Dinitropyrazine-1-Oxide (LLM-105) via Defect Engineering. J. Phys. Chem. C 2021, 125, 2739–2747. [Google Scholar] [CrossRef]
- Xing, J.; Zhang, H.; Bai, L.; Zhu, G.; Yu, Q.; Huang, B.; Liu, Y.; Wang, W.; Li, S.; Liu, Y. Nano-Voids in Ultrafine Explosive Particles: Characterization and Effects on Thermal Stability. Langmuir 2023, 39, 3391–3399. [Google Scholar] [CrossRef] [PubMed]
- Mei, M.; Sun, Z.; Ji, J.; Zhu, W. Stability, Electronic Properties, and Decomposition Mechanisms of 2,6-Diamino-3,5-Dinitropyrazine-1-Oxide Crystals with Different Vacancy Defects. CrystEngComm 2024, 26, 3643–3652. [Google Scholar] [CrossRef]
- Guo, Z.; Wang, X.; Hao, G.; Xiao, L.; Feng, X.; Yang, J.; Jiang, W. Structural and Decomposition Analysis of TKX-50 with Vacancy Defects: Insights from DFT and AIMD Simulations. Phys. Chem. Chem. Phys. 2024, 26, 9665–9674. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Jin, S.; Lan, G.; Chen, S.; Shu, Q.; Li, L.; Chen, K. Reactive Molecular Dynamics Simulations on the Thermal Decompositions and Oxidations of TKX-50 and Twinned TKX-50. CrystEngComm 2020, 22, 2593–2600. [Google Scholar] [CrossRef]
- Hang, G.-Y.; Yu, W.-L.; Wang, T.; Wang, J.-T. Theoretical Investigations into Effects of Adulteration Crystal Defect on Properties of HMX by Molecular Dynamics Method. Theor. Chem. Acc. 2019, 138, 33. [Google Scholar] [CrossRef]
- Yang, J.; Guo, Z.; Wang, X.; Hao, G.; Hu, Y.; Feng, X.; Guo, R.; Jiang, W. A Theoretical Study on the Decomposition of TKX-50 with Different Vacancy Defect Concentrations under Shock Wave Loading. Energetic Mater. Front. 2025, 6, 24–34. [Google Scholar] [CrossRef]
- Hang, G.; Yu, W.; Wang, T.; Wang, J. Theoretical Investigations into Effects of Adulteration Crystal Defect on Properties of CL-20/TNT Cocrystal Explosive. Comput. Mater. Sci. 2019, 156, 77–83. [Google Scholar] [CrossRef]
- Hang, G.-Y.; Wang, J.-T.; Xue, H.-J.; Wang, T.; Yu, W.-L.; Shen, H.-M. Theoretical Investigation to Predict Properties of CL-20/HMX Cocrystal Explosive with Adulteration Crystal Defect: A Molecular Dynamics (MD) Study. Theor. Chem. Acc. 2024, 143, 47. [Google Scholar] [CrossRef]
- Ji, J.; Wang, K.; Zhu, S.; Zhu, W. Structure, Intermolecular Interactions, and Dynamic Properties of NTO Crystals with Impurity Defects: A Computational Study. CrystEngComm 2021, 23, 2455–2468. [Google Scholar] [CrossRef]
- Wang, T.B.; Li, L.J.; Tao, Y.T.; Ning, L.Y.; Jin, S.H.; Cen, K.; Lu, Z.Y. Influence of Cavity Crystal Defects on the Thermal Ecomposition Mechanism of NTO. J. Phys. Conf. Ser. 2024, 2891, 022032. [Google Scholar] [CrossRef]
- Tan, K.; Liu, R.; Deng, C.; Guo, F.; Huang, X.; Han, Y.; Wen, Y.; Dai, X.; Huang, F.; Li, M. Impacts of Defect Distribution on the Ignition of Crystalline Explosives: An Insight from the Overlapping Effect. Energetic Mater. Front. 2022, 3, 53–60. [Google Scholar] [CrossRef]
- Sun, Z.; Ji, J.; Zhu, W. Reactive Molecular Dynamics Simulations on the Hotspot Formation and Pyrolysis Mechanisms of the TNBI/TANPDO Cocrystal: Effects of Defects with Different Nano-Void Sizes. CrystEngComm 2024, 26, 5941–5952. [Google Scholar] [CrossRef]
- Zhou, T.; Lou, J.; Zhang, Y.; Song, H.; Huang, F. Hot Spot Formation and Chemical Reaction Initiation in Shocked HMX Crystals with Nanovoids: A Large-Scale Reactive Molecular Dynamics Study. Phys. Chem. Chem. Phys. 2016, 18, 17627–17645. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Kiziltas, A.; Blanchard, P.; Walsh, T.R. Calculation of 1D and 2D Densities in VMD: A Flexible and Easy-to-Use Code. Comput. Phys. Commun. 2021, 266, 108032. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual Molecular Dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef] [PubMed]
- Tyrrell, H.J.V. The Origin and Present Status of Fick’s Diffusion Law. J. Chem. Educ. 1964, 41, 397. [Google Scholar] [CrossRef]
- Dayananda, M.A. A Direct Derivation of Fick’s Law from Continuity Equation for Interdiffusion in Multicomponent Systems. Scr. Mater. 2022, 210, 114430. [Google Scholar] [CrossRef]
- Hamilton, B.W.; Kroonblawd, M.P.; Strachan, A. The Potential Energy Hotspot: Effects of Impact Velocity, Defect Geometry, and Crystallographic Orientation. J. Phys. Chem. C 2022, 126, 3743–3755. [Google Scholar] [CrossRef]
- Xue, H.; Wu, Y.; Yang, K.; Wu, Y. Microcrack- and Microvoid-Related Impact Damage and Ignition Responses for HMX-Based Polymer-Bonded Explosives at High Temperature. Def. Technol. 2022, 18, 1602–1621. [Google Scholar] [CrossRef]
- Johnson, B.P.; Zhou, X.; Ihara, H.; Dlott, D.D. Observing Hot Spot Formation in Individual Explosive Crystals Under Shock Compression. J. Phys. Chem. A 2020, 124, 4646–4653. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Wang, T.; He, Y. Hot Spot Formation and Initial Chemical Reaction of PETN Containing Nanoscale Spherical Voids under High Shock Loading. RSC Adv. 2022, 12, 11060–11074. [Google Scholar] [CrossRef] [PubMed]
- Lan, Q.; Zhang, H.; Ni, Y.; Chen, J.; Wang, H. Thermal Decomposition Mechanisms of LLM-105/HTPB Plastic-Bonded Explosive: ReaxFF-Lg Molecular Dynamics Simulations. J. Energetic Mater. 2023, 41, 269–290. [Google Scholar] [CrossRef]
- Jiang, J.; Qiu-li, J.; Chen, Y.; Hao, W.; Liu, Y.; Zhang, S.-H. ReaxFF MD Simulations of Thermolysis Mechanism of 2, 6-Diamino-3, 5-Dinitropyrazine-1-Oxidated. Comput. Theor. Chem. 2020, 1185, 112891. [Google Scholar] [CrossRef]
- Zhou, T.-T.; Huang, F.-L. Effects of Defects on Thermal Decomposition of HMX via ReaxFF Molecular Dynamics Simulations. J. Phys. Chem. B 2011, 115, 278–287. [Google Scholar] [CrossRef]
- Yuan, X.; Huang, Y.; Zhang, S.; Gou, R.; Zhu, S.; Guo, Q. Multi-Aspect Simulation Insight on Thermolysis Mechanism and Interaction of NTO/HMX-Based Plastic-Bonded Explosives: A New Conception of the Mixed Explosive Model. Phys. Chem. Chem. Phys. 2023, 25, 20951–20968. [Google Scholar] [CrossRef] [PubMed]
- Cheng, N.; Gan, Q.; Yu, Q.; Zhang, X.; Li, R.; Qian, S.; Feng, C. Initial Mechanisms for the Unimolecular Thermal Decomposition of 2,6-Diamino-3,5-Dinitropyrazine-1-Oxide. Molecules 2018, 24, 125. [Google Scholar] [CrossRef] [PubMed]
- Thompson, A.P.; Aktulga, H.M.; Berger, R.; Bolintineanu, D.S.; Brown, W.M.; Crozier, P.S.; in ’t Veld, P.J.; Kohlmeyer, A.; Moore, S.G.; Nguyen, T.D.; et al. LAMMPS-a Flexible Simulation Tool for Particle-Based Materials Modeling at the Atomic, Meso, and Continuum Scales. Comput. Phys. Commun. 2022, 271, 10817. [Google Scholar] [CrossRef]
- Liu, L.; Liu, Y.; Zybin, S.V.; Sun, H.; Goddard, W.A.I. ReaxFF-Lg: Correction of the ReaxFF Reactive Force Field for London Dispersion, with Applications to the Equations of State for Energetic Materials. J. Phys. Chem. A 2011, 115, 11016–11022. [Google Scholar] [CrossRef] [PubMed]
- Van Duin, A.C.T.; Dasgupta, S.; Lorant, F.; Goddard, W.A. ReaxFF: A Reactive Force Field for Hydrocarbons. J. Phys. Chem. A 2001, 105, 9396–9409. [Google Scholar] [CrossRef]
- Hu, Z.; Wei, L. Review on Characterization of Biochar Derived from Biomass Pyrolysis via Reactive Molecular Dynamics Simulations. J. Compos. Sci. 2023, 7, 354. [Google Scholar] [CrossRef]
- Ermakov, V.A.; Alaferdov, A.V.; Vaz, A.R.; Perim, E.; Autreto, P.A.S.; Paupitz, R.; Galvao, D.S.; Moshkalev, S.A. Burning Graphene Layer-by-Layer. Sci. Rep. 2015, 5, 11546. [Google Scholar] [CrossRef] [PubMed]
- Zheng, M.; Wang, Z.; Li, X.; Qiao, X.; Song, W.; Guo, L. Initial Reaction Mechanisms of Cellulose Pyrolysis Revealed by ReaxFF Molecular Dynamics. Fuel 2016, 177, 130–141. [Google Scholar] [CrossRef]
- Zhang, L.; Zybin, S.V.; van Duin, A.C.T.; Dasgupta, S.; Goddard, W.A.I.; Kober, E.M. Carbon Cluster Formation during Thermal Decomposition of Octahydro-1,3,5,7-Tetranitro-1,3,5,7-Tetrazocine and 1,3,5-Triamino-2,4,6-Trinitrobenzene High Explosives from ReaxFF Reactive Molecular Dynamics Simulations. J. Phys. Chem. A 2009, 113, 10619–10640. [Google Scholar] [CrossRef] [PubMed]
- Zeng, J.; Cao, L.; Chin, H.; Ren, H.; Zhu, T. ReacNetGenerator: An Automatic Reaction Network Generator for Reactive Molecular Dynamics Simulations. Phys. Chem. Chem. Phys. 2020, 22, 683–691. [Google Scholar] [CrossRef] [PubMed]






| Primary Reactions | Occurrence Frequencies | ||||
|---|---|---|---|---|---|
| LLM-105_Void0 | LLM-105_Void8 | LLM-105_Void15 | LLM-105_Void20 | ||
| A | C4H4O5N6 → C4H2O5N5 + NH2 | 19 | 21 | 33 | 27 |
| B | C4H4O5N6 → C4H4O4N5 + NO | 24 | 36 | 44 | 48 |
| C | C4H4O5N6 → C4H3O5N6 + H | 63 | 76 | 71 | 110 |
| D | C4H4O5N6 → C4H4O3N5 + NO2 | 134 | 143 | 179 | 203 |
| E | C4H4O5N6 → C4H4O4N6 + O | 94 | 86 | 86 | 75 |
| Primary Reactions | Occurrence Frequencies | |||
|---|---|---|---|---|
| LLM-105_Void0 | LLM-105_Void8 | LLM-105_Void15 | LLM-105_Void20 | |
| HNO → H + NO | 109 | 133 | 142 | 229 |
| HNO2 → OH + NO | 65 | 67 | 88 | 160 |
| H + N2H → N2 + H2 | 397 | 426 | 463 | 565 |
| OH + HNO → H2O + NO | 307 | 327 | 381 | 410 |
| HN2O → OH + N2 | 244 | 246 | 206 | 148 |
| H + OH → H2O | 88 | 79 | 72 | 48 |
| HNO3 → OH + NO2 | 55 | 63 | 57 | 69 |
| LLM-105_Void0 | LLM-105_Void8 | LLM-105_Void15 | LLM-105_Void20 | |
|---|---|---|---|---|
| slope | ||||
| C | 2.52 | 2.76 | 4.26 | 6.78 |
| O | 3.72 | 4.14 | 5.94 | 8.88 |
| N | 5.88 | 6.24 | 8.16 | 11.22 |
| H | 8.16 | 8.82 | 11.28 | 15.54 |
| Diffusion coefficients | ||||
| C | 0.42 | 0.46 | 0.71 | 1.13 |
| O | 0.62 | 0.69 | 0.99 | 1.48 |
| N | 0.98 | 1.04 | 1.36 | 1.87 |
| H | 1.36 | 1.47 | 1.88 | 2.59 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mei, M.; Sun, Z.; Ye, L.; Zhu, W. Mechanistic Insights into the Hot-Spot Formation and Pyrolysis of LLM-105 with Different Void Defects: A ReaxFF Molecular Dynamics Study. Molecules 2025, 30, 3016. https://doi.org/10.3390/molecules30143016
Mei M, Sun Z, Ye L, Zhu W. Mechanistic Insights into the Hot-Spot Formation and Pyrolysis of LLM-105 with Different Void Defects: A ReaxFF Molecular Dynamics Study. Molecules. 2025; 30(14):3016. https://doi.org/10.3390/molecules30143016
Chicago/Turabian StyleMei, Mengyun, Zijian Sun, Lixin Ye, and Weihua Zhu. 2025. "Mechanistic Insights into the Hot-Spot Formation and Pyrolysis of LLM-105 with Different Void Defects: A ReaxFF Molecular Dynamics Study" Molecules 30, no. 14: 3016. https://doi.org/10.3390/molecules30143016
APA StyleMei, M., Sun, Z., Ye, L., & Zhu, W. (2025). Mechanistic Insights into the Hot-Spot Formation and Pyrolysis of LLM-105 with Different Void Defects: A ReaxFF Molecular Dynamics Study. Molecules, 30(14), 3016. https://doi.org/10.3390/molecules30143016






