Adsorption of Ciprofloxacin on Clay Minerals in Argentinian Santa Rosa-Corrientes Soils
Abstract
1. Introduction
2. Results and Discussion
2.1. Experiment with the Soil Samples
2.1.1. Physical–Chemical Properties
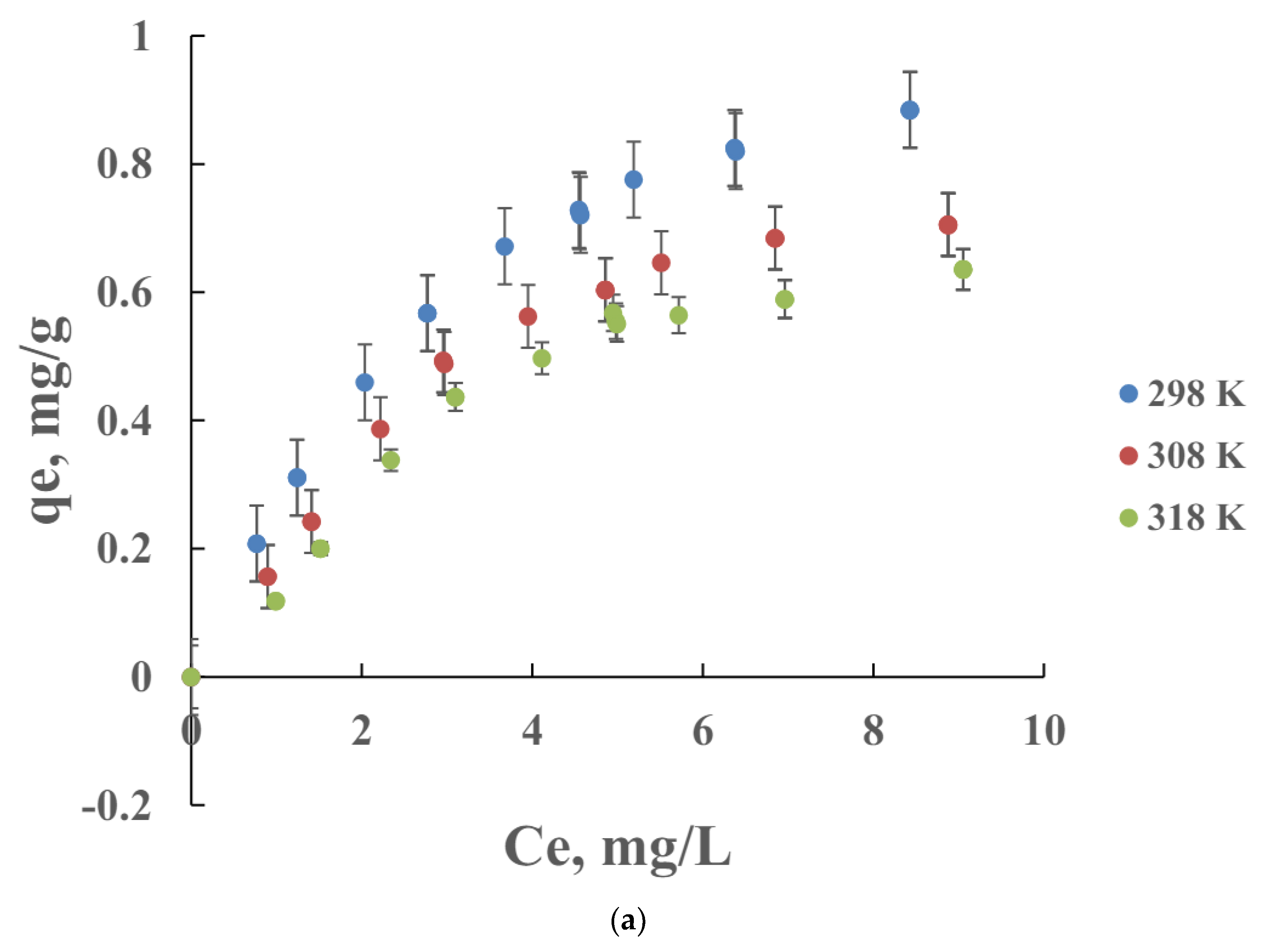
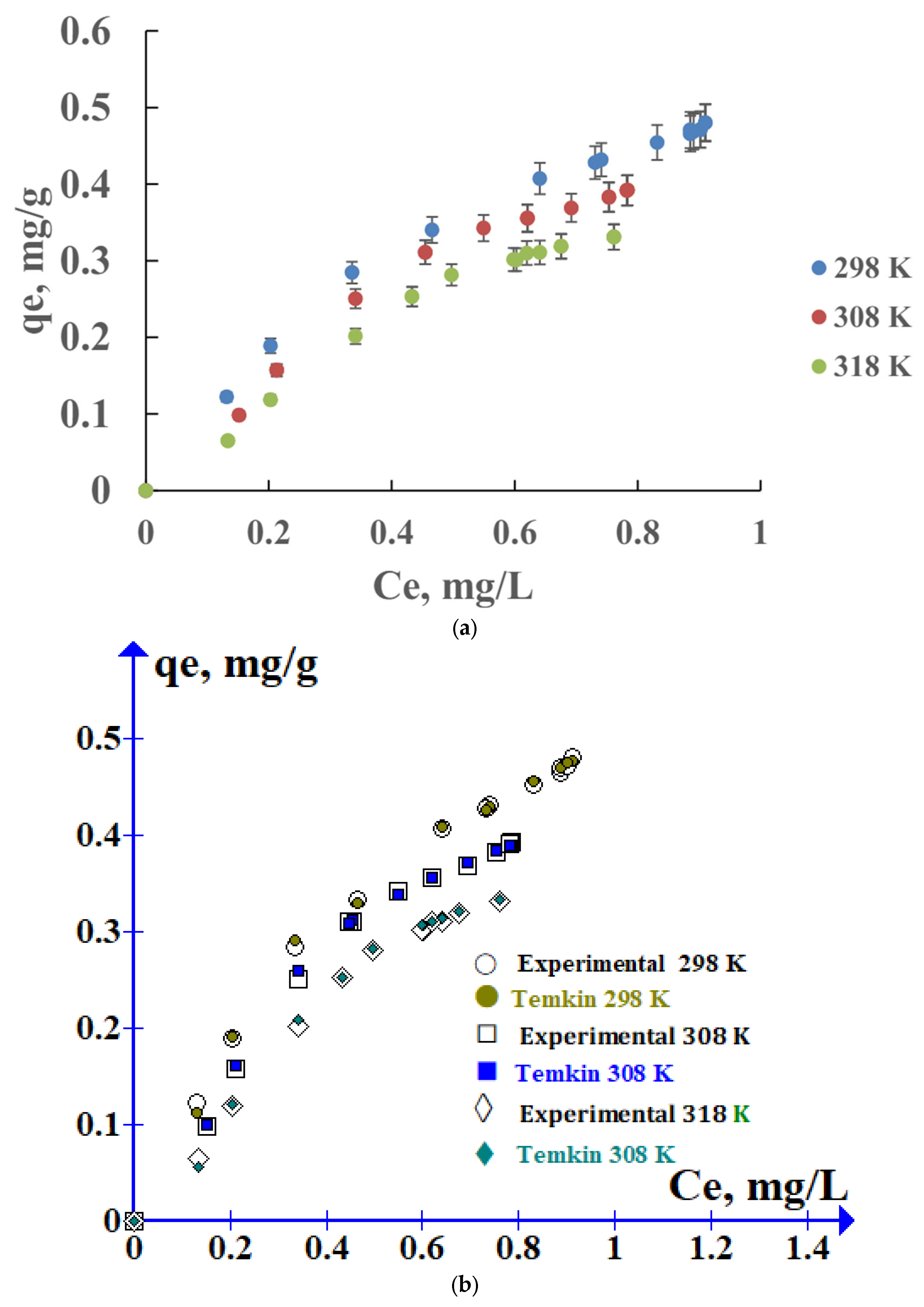
2.1.2. Adsorption Isotherms
2.1.3. Balance Model
2.1.4. Desorption Isotherms
2.1.5. Thermodynamic Study
2.2. Molecular Modeling
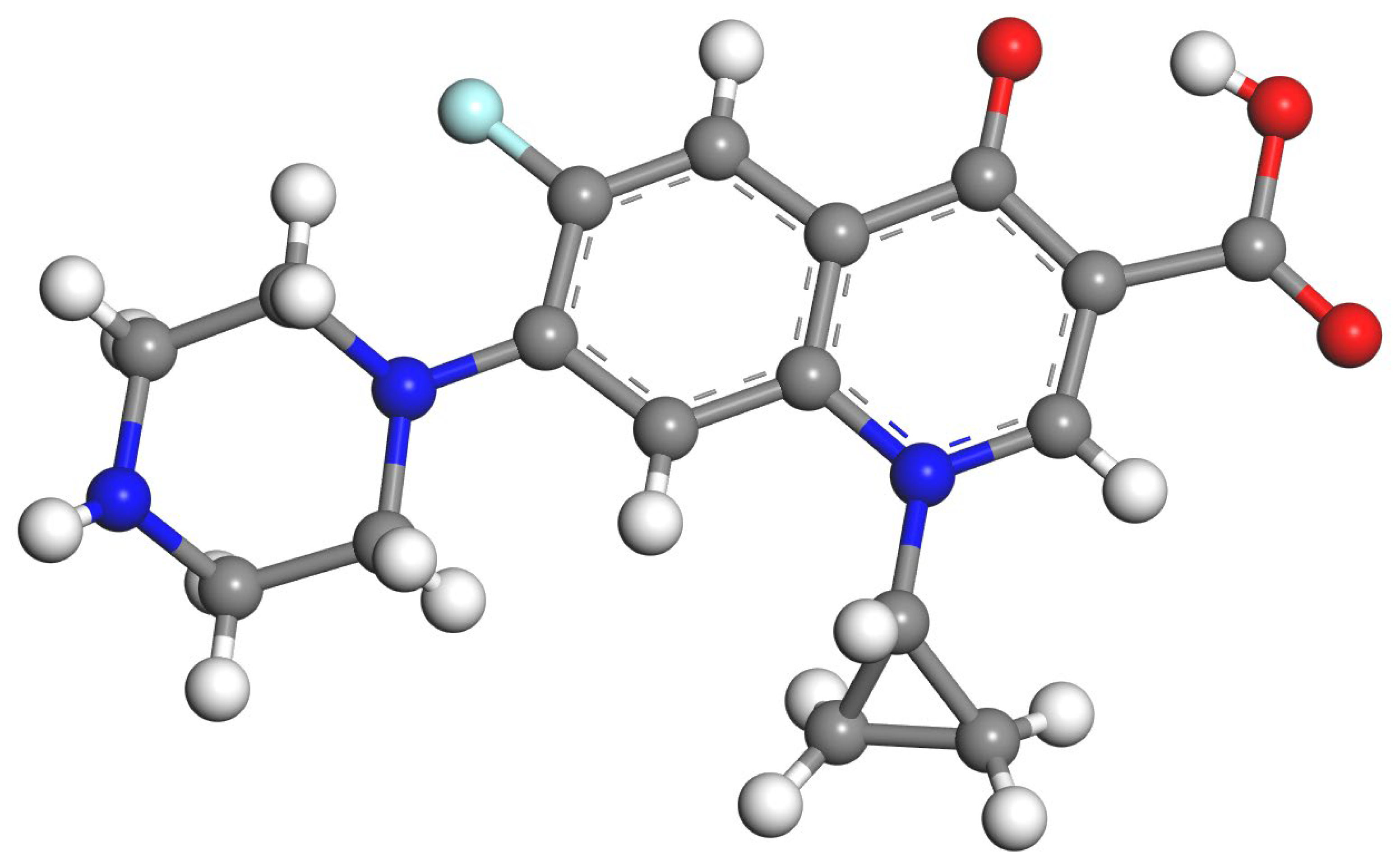
2.2.1. Cipro Structures
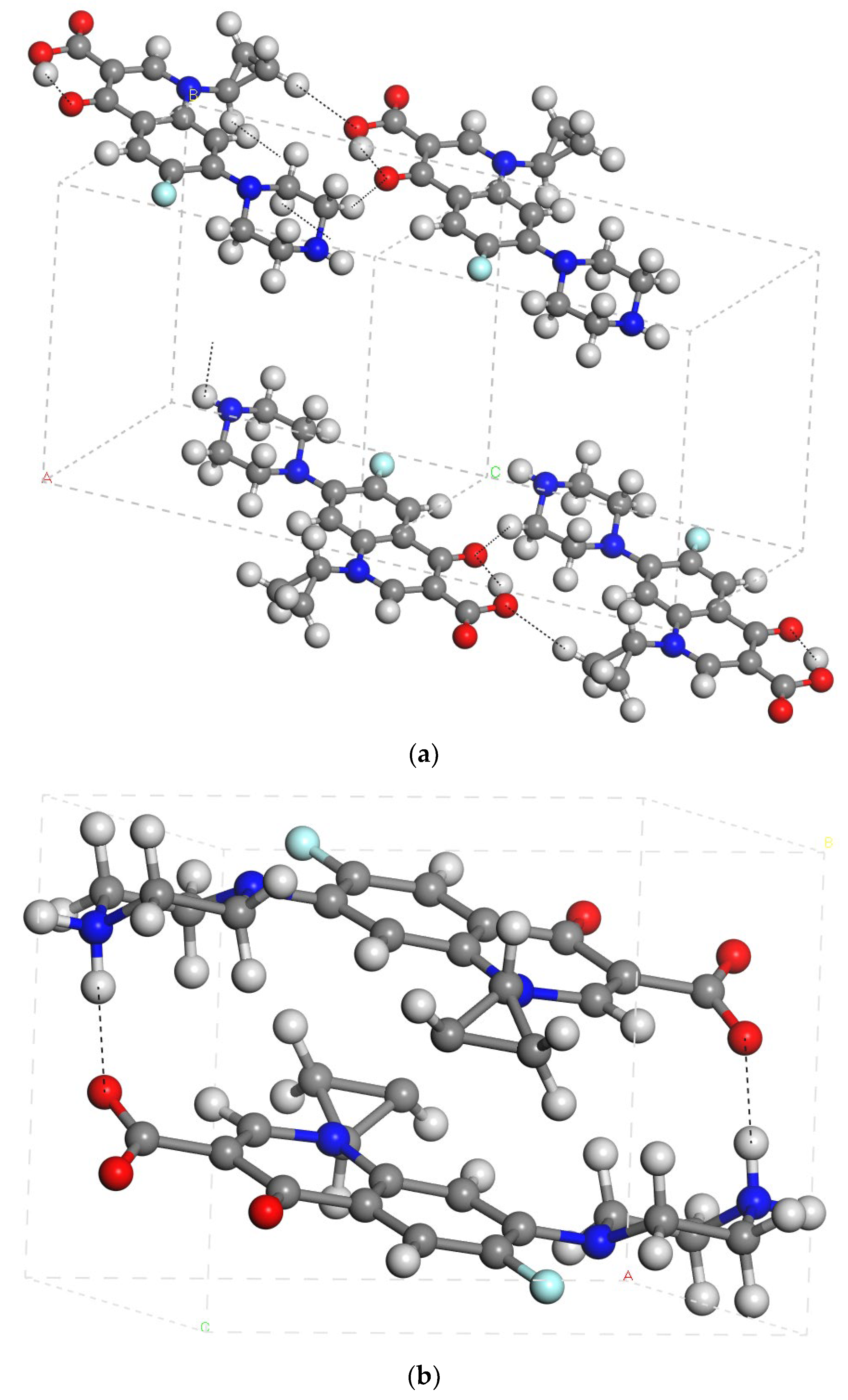
2.2.2. Adsorption of Cipro into Mont
2.2.3. Desorption of Cipro from Mont
2.3. Comparison of Experimental and Molecular Modelling Results
3. Materials and Methodology
3.1. Materials
3.2. Adsorption Experiments
3.3. Desorption Experiments
3.4. Analytical Methods
3.5. Data Analysis
4. Atomistic Modelling Methodology
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Manyi-Loh, C.; Mamphwell, S.; Meyer, E.; Okoh, A. Antibiotic Use in Agriculture and Its Consequential Resistance in Environmental Sources: Potential Public Health Implications. Molecules 2018, 23, 795. [Google Scholar] [CrossRef] [PubMed]
- Moyane, J.N.; Jideani, A.I.O.; Aiyegoro, O.A. Antibiotics usage in food-producing animals in South Africa and impact on human: Antibiotic resistance. Afr. J. Microbiol. Res. 2013, 7, 2990–2997. [Google Scholar]
- Williams-Nguyen, J.; Sallach, J.B.; Bartelt-Hunt, S.; Boxall, A.B.; Durso, L.M.; McLain, J.E.; Singer, R.S.; Snow, D.D.; Zilles, J.L. Antibiotics and Antibiotic Resistance in Agroecosystems: State of the Science. J. Environ. Qual. 2016, 45, 394–406. [Google Scholar] [CrossRef] [PubMed]
- Van Boeckel, T.P.; Brower, C.; Gilbert, M.; Grenfell, B.T.; Levin, S.A.; Robinson, T.P.; Teillant, A.; Laxminarayan, R. Global trends in antimicrobial use in food animals. Proc. Natl. Acad. Sci. USA 2015, 112, 5649–5654. [Google Scholar] [CrossRef] [PubMed]
- Qiao, M.; Ying, G.-G.; Singer, A.C.; Zhu, Y.-G. Review of antibiotic resistance in China and its environment. Environ. Int. 2018, 110, 160–172. [Google Scholar] [CrossRef] [PubMed]
- Tiseo, K.; Huber, L.; Gilbert, M.; Robinson, T.P.; Van Boeckel, T.P. Global Trends in Antimicrobial Use in Food Animals from 2017 to 2030. Antibiotics 2020, 9, 918–933. [Google Scholar] [CrossRef] [PubMed]
- Hernández-Guijarro, K.; Okada, E.; Perez, D.J. Antibióticos derivados de actividades agropecuarias: Presencia ambiental y desarrollo de resistencia bacteriana a antibióticos. Visión Rural 2021, 27, 37–39. [Google Scholar]
- Genç, N.; Dogan, E.C.; Yurtsever, M. Bentonite for ciprofloxacin removal from aqueous solution. Water Sci. Technol. 2013, 68, 848–855. [Google Scholar] [CrossRef]
- Maged, A.; Kharbish, S.; Ismael, I.S.; Bhatnagar, A. Characterization of activated bentonite clay mineral and the mechanisms underlying its sorption for ciprofloxacin from aqueous solution. Environ. Sci. Pollut. Res. 2020, 27, 32980–32997. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.J.; Li, Z.; Jiang, W.T.; Jean, J.S.; Liu, C.C. Cation exchange interaction between antibiotic ciprofloxacin and montmorillonite. J. Hazard. Mater. 2010, 183, 309–314. [Google Scholar] [CrossRef] [PubMed]
- Massaro, M.; Borrego-Sánchez, A.; Sánchez-Espejo, R.; Viseras-Iborra, C.; Cavallaro, G.; García-Villén, F.; Guernelli, S.; Lazzara, G.; Miele, D.; Sainz-Díaz, C.I.; et al. Ciprofloxacin carrier systems based on hectorite/halloysite hybrid hydrogels for potential wound healing applications. Appl. Clay Sci. 2021, 215, 106310. [Google Scholar] [CrossRef]
- Antonelli, R.; Malpass, G.R.P.; da Silva, M.G.C.; Vieira, M.G.A. Hybrid process of adsorption and electrochemically based green regeneration of bentonite clay for ofloxacin and ciprofloxacin removal. Environ. Sci. Pollut. Res. 2023, 30, 53648–53661. [Google Scholar] [CrossRef] [PubMed]
- Nowara, A.; Burhenne, J.; Spiteller, M. Binding of Fluoroquinolone Carboxylic Acid Derivatives to Clay Minerals. J. Agric. Food Chem. 1997, 45, 1459–1463. [Google Scholar] [CrossRef]
- Wu, Q.; Li, Z.; Hong, H.; Ke Yin, K.; Tie, L. Adsorption and intercalation of ciprofloxacin on montmorillonite. Appl. Clay Sci. 2010, 50, 204–211. [Google Scholar] [CrossRef]
- Septian, A.; Shin, W.S. Removal of sulfadiazine and ciprofloxacin by clays and manganese oxides: Coupled sorption-oxidation kinetic model. Chemosphere 2020, 250, 126251. [Google Scholar] [CrossRef] [PubMed]
- Okaikue-Woodi, F.E.K.; Kelch, S.E.; Schmidt, M.P.; Enid Martinez, C.; Youngman, R.E.; Aristilde, L. Structures and mechanisms in clay nanopore trapping of structurally-different fluoroquinolone antimicrobials. J. Colloid Interface Sci. 2018, 513, 367–378. [Google Scholar] [CrossRef] [PubMed]
- Wu, Q.; Li, Z.; Hong, H.; Li, R.; Jiang, W.T. Desorption of ciprofloxacin from clay mineral surfaces. Water Res. 2013, 47, 259–268. [Google Scholar] [CrossRef] [PubMed]
- Septian, A.; Oh, S.; Shin, W.S. Sorption of antibiotics onto montmorillonite and kaolinite: Competition modelling. Environ. Technol. 2019, 40, 2940–2953. [Google Scholar] [CrossRef]
- Borrego-Sánchez, A.; Sánchez-Espejo, R.; García-Guillén, F.; Viseras, C.; Sainz-Díaz, C.I. Praziquantel–Clays as accelerated release systems to enhance the low solubility of the drug. Pharmaceutics 2020, 12, 914. [Google Scholar] [CrossRef] [PubMed]
- Escamilla-Roa, E.; Huertas, F.J.; Hernández-Laguna, A.; Sainz-Díaz, C.I. A DFT study of the adsorption of glycine in the interlayer space of montmorillonite. Phys. Chem. Chem. Phys. 2017, 19, 14961–14971. [Google Scholar] [CrossRef] [PubMed]
- Dos Santos, E.C.; Rozynek, Z.; Hansen, E.L.; Hartmann-Petersen, R.; Klitgaard, R.N.; Løbner-Olesen, A.; Michels, L.; Mikkelsen, A.; Plivelic, T.S.; Bordallo, H.N.; et al. Ciprofloxacin intercalated in fluorohectorite clay: Identical pure drug activity and toxicity with higher adsorption and controlled release rate. RSC Adv. 2017, 7, 26537. [Google Scholar] [CrossRef]
- Day, R.P. Pipette method of particle size analysis. In Methods of Soil Analysis; Agronomy ASA: Madison, WI, USA, 1965; Volume 9, pp. 553–562. [Google Scholar]
- Santa-Cruz, J.N.; Orfeo, O.; Gulisano, F. Geología de la Provincia de Corrientes—Argentina y Cuencas Geotectónicas Relacionadas; Moglia: Corrientes, Argentina, 2019; p. 273. [Google Scholar]
- Afzal, M.Z.; Sun, X.F.; Liu, J.; Song, C.; Wang, S.G.; Javed, A. Enhancement of ciprofloxacin sorption on chitosan/biochar hydrogel beads. Sci. Total Environ. 2018, 639, 560–569. [Google Scholar] [CrossRef] [PubMed]
- Guo, H.; Zhang, S.; Kou, Z.; Zhai, S.; Ma, W.; Yang, Y. Removal of cadmium (II) from aqueous solutions by chemically modified maize straw. Carbohydr. Polym. 2015, 115, 177–185. [Google Scholar] [CrossRef] [PubMed]
- Giles, C.H.; Smith, D.; Huitson, A. A general treatment and classification of the solute adsorption isotherm. I. Theoretical. J. Colloid Interface Sci. 1974, 47, 755–765. [Google Scholar] [CrossRef]
- Chu, K.H. Revisiting the Temkin Isotherm: Dimensional Inconsistency and Approximate Forms. Ind. Eng. Chem. Res. 2021, 60, 13140–13147. [Google Scholar] [CrossRef]
- Liao, P.; Zhan, Z.; Dai, J.; Wu, X.; Zhang, W.; Wang, K.; Yuan, S. Adsorption of tetracycline and chloramphenicol in aqueous solutions by bamboo charcoal: A batch and fixed-bed column study. Chem. Eng. J. 2013, 228, 496–505. [Google Scholar] [CrossRef]
- Yu, F.; Sun, S.; Han, S.; Zheng, J.; Ma, J. Adsorption removal of ciprofloxacin by multi-walled carbon nanotubes with different oxygen contents from aqueous solutions. Chem. Eng. J. 2016, 285, 588–595. [Google Scholar] [CrossRef]
- Araújo, C.S.; Almeida, I.L.; Rezende, H.C.; Marcionilio, S.M.; Léon, J.J.; de Matos, T.N. Elucidation of mechanism involved in adsorption of Pb (II) onto lobeira fruit (Solanum lycocarpum) using Langmuir, Freundlich and Temkin isotherms. Microchem. J. 2018, 137, 348–354. [Google Scholar] [CrossRef]
- Bhadra, B.N.; Seo, P.W.; Jhung, S.H. Adsorption of diclofenac sodium from water using oxidized activated carbon. Chem. Eng. J. 2016, 301, 27–34. [Google Scholar] [CrossRef]
- Ferreira, R.C.; Couto Junior, O.M.; Carvalho, K.Q.; Arroyo, P.A.; Barros, M.A.S.D. Effect of solution pH on the removal of paracetamol by activated carbon of dende coconut mesocarp. Chem. Biochem. Eng. Q. 2015, 29, 47–53. [Google Scholar] [CrossRef]
- Iovino, P.; Canzano, S.; Capasso, S.; Erto, A.; Musmarra, D. A modeling analysis for the assessment of ibuprofen adsorption mechanism onto activated carbons. Chem. Eng. J. 2015, 277, 360–367. [Google Scholar] [CrossRef]
- Song, J.Y.; Bhadra, B.N.; Jhung, S.H. Contribution of H-bond in adsorptive removal of pharmaceutical and personal care products from water using oxidized activated carbon. Micropor. Mesopor. Mater. 2017, 243, 221–228. [Google Scholar] [CrossRef]
- Hines, A.L.; Maddox, R.N. Mass Transfer: Fundamentals and Applications; Prentice-Hall: Englewood-Cliffs, NJ, USA, 1985; p. 151. [Google Scholar]
- Sánchez-Martín, M.J.; Sánchez-Camazano, M. Los Plaguicidas. Adsorción y Evolución en el Suelo; I.O.A.T.O. Excma; Diputación provincial de Salamanca: Salamanca, Spain, 1985. [Google Scholar]
- Lin, H.; Xu, J.; Dong, Y.; Wang, L.; Xu, W.; Zhou, Y. Adsorption of heavy metal cadmium (II) ions using chemically modified corncob: Mechanism, kinetics, and thermodynamics. Desalination Water Treat. 2016, 57, 18537–18550. [Google Scholar] [CrossRef]
- Antunes, M.; Esteves, V.I.; Guégan, R.; Crespo, J.S.; Fernandes, A.N.; Giovanela, M. Removal of diclofenac sodium from aqueous solution by Isabel grape bagasse. Chem. Eng. J. 2012, 192, 114–121. [Google Scholar] [CrossRef]
- Tonucci, M.C.; Gurgel, L.V.A.; de Aquino, S.F. Activated carbons from agricultural byproducts (pine tree and coconut shell), coal, and carbon nanotubes as adsorbents for removal of sulfamethoxazole from spiked aqueous solutions: Kinetic and thermodynamic studies. Ind. Crop. Prod. 2015, 74, 111–121. [Google Scholar] [CrossRef]
- Worch, E. Adsorption Technology in Water Treatment: Fundamentals, Processes, and Modeling; De Gruyter: Berlin, Germany; Boston, MA, USA, 2012. [Google Scholar]
- Suresh, S.; Srivastava, V.C.; Mishra, I.M. Isotherm, thermodynamics, desorption, and disposal study for the adsorption of catechol and resorcinol onto granular activated carbon. J. Chem. Eng. Data 2011, 56, 811–818. [Google Scholar] [CrossRef]
- Heinz, H.; Lin, T.J.; Kishore Mishra, R.; Emami, F.S. Thermodynamically consistent force fields for the assembly of inorganic, organic, and biological nanostructures: The INTERFACE force field. Langmuir 2013, 29, 1754–1765. [Google Scholar] [CrossRef] [PubMed]
- Sun, H. COMPASS: An ab Initio Force-Field Optimized for Condensed-Phase Applications. Overview with Details on Alkane and Benzene Compounds. J. Phys. Chem. B 1998, 102, 7338–7364. [Google Scholar] [CrossRef]
- Rappé, A.K.; Goddard, W.A. Charge equilibration for molecular dynamics simulations. J. Phys. Chem. 1991, 95, 3358–3363. [Google Scholar] [CrossRef]
- Delley, B. Hardness conserving semilocal pseudopotentials. Phys. Rev. B 2002, 66, 155125. [Google Scholar] [CrossRef]
- Besler, B.H.; Merz, K.M., Jr.; Kollman, P.A. Atomic charges derived from semiempirical methods. J. Comput. Chem. 1990, 11, 431–439. [Google Scholar] [CrossRef]
- Mahapatra, S.; Venugopala, K.N.; Guru Row, T.N. A Device to Crystallize Organic Solids: Structure of Ciprofloxacin, Midazolam, and Ofloxacin as Targets. Cryst. Growth Des. 2010, 10, 1866–1870. [Google Scholar] [CrossRef]
- Chrysouli, M.P.; Banti, C.N.; Kourkoumelis, N.; Moushi, E.E.; Tasiopoulos, A.J.; Douvalis, A.; Papachristodoulou, C.; Hatzidimitriou, A.G.; Bakas, T.; Hadjikakou, S.K. Ciprofloxacin conjugated to diphenyltin(IV): A novel formulation with enhanced antimicrobial activity. Dalton Trans. 2020, 49, 11522. [Google Scholar] [CrossRef] [PubMed]
- Fabbiani, F.P.A.; Dittrich, B.; Florence, A.J.; Gelbrich, T.; Hursthouse, M.B.; Kuhs, W.F.; Shankland, N.; Sowa, H. Crystal structures with a challenge: High pressure crystallisation of ciprofloxacin sodium salts and their recovery to ambient pressure. CrystEngComm 2009, 11, 1396–1406. [Google Scholar] [CrossRef]
- Mesallati, H.; Mugheirbi, N.A.; Tajber, L. Two Faces of Ciprofloxacin: Investigation of Proton Transfer in Solid State Transformations. Cryst. Growth Des. 2016, 16, 6574–6585. [Google Scholar] [CrossRef]
- Gournis, D.; Lappas, A.; Karakassides, M.A.; Tobbens, D.; Moukarika, A. A neutron diffraction study of alkali cation migration in montmorillonites. Phys. Chem. Miner. 2008, 35, 49–58. [Google Scholar] [CrossRef]
- Meunier, A. Clays; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Millán, F.; Hétier, J.M. Métodos De Análisis De Suelo. In Apéndice Analítico; Universidad de los Andes: Mérida, Venezuela, 2015; pp. 697–853. [Google Scholar]
- Plasencia, A. Análisis de Suelos; Cátedra de Edafología, Facultad de Agronomía y Zootecnia, Universidad Nacional de Tucumán: Tucumán, Argentina, 2017. [Google Scholar]
- Jackson, M.L. Análisis Químicos de Suelos; Editorial Omega: Barcelona, Spain, 1970. [Google Scholar]
- Dewis, J.; Freitas, F. Métodos Físicos y Químicos de análisis de suelos y aguas. In Boletín Sobre Suelos; FAO: Rome, Italy, 1970; Volume 10, p. 252. [Google Scholar]
- Dada, A.O.; Olalekan, A.P.; Olatunya, A.M.; Dada, O. Langmuir, Freundlich, Temkin and Dubinin–Radushkevich Isotherms Studies of Equilibrium Sorption of Zn2+ Unto Phosphoric Acid Modified Rice Husk. J. Appl. Chem. 2012, 3, 38–45. [Google Scholar]
- Ortega-Castro, J.; Hernández-Haro, N.; Dove, M.T.; Hernández-Laguna, A.; Sainz-Díaz, C.I. Density functional theory and Monte Carlo study of octahedral cation ordering of Al/Fe/Mg cations in dioctahedral 2: 1 phyllosilicates. Am. Mineral. 2010, 95, 209–220. [Google Scholar] [CrossRef]
- Sainz-Díaz, C.I.; Palin, E.J.; Hernández-Laguna, A.; Dove, M.T. Octahedral cation ordering of illite and smectite. Theoretical exchange potential determination and Monte Carlo simulations. Phys. Chem. Miner. 2003, 30, 382–392. [Google Scholar] [CrossRef]
- Biovia, Materials Studio; Dassault Inc.: Waltham, MA, USA, 2020.
- Sainz-Díaz, C.I.; Francisco-Márquez, M.; Vivier-Bunge, A. Adsorption of polyaromatic heterocycles on pyrophyllite surface by means of different theoretical approaches. Environ. Chem. 2011, 8, 429–440. [Google Scholar] [CrossRef]
- Heinz, H.; Pramanik, C.; Heinz, O.; Ding, Y.; Mishra, R.K.; Marchon, D.; Flatt, R.J.; Estrela-Lopis, I.; Llop, J.; Moya, S.; et al. Nanoparticle decoration with surfactants: Molecular interactions, assembly, and applications. Surf. Sci. Rep. 2017, 72, 1–58. [Google Scholar] [CrossRef]
- Fu, Y.T.; Zartman, G.D.; Yoonessi, M.; Drummy, L.F.; Heinz, H. Bending of Layered Silicates on the Nanometer Scale: Mechanism, Stored Energy, and Curvature Limits. J. Phys. Chem. C 2011, 115, 22292–22300. [Google Scholar] [CrossRef]
- Heinz, H.; Koerner, H.; Vaia, R.A.; Anderson, K.L.; Farmer, B.L. Force Field for Phyllosilicates and Dynamics of OctadecylammoniumChains Grafted to Montmorillonite. Chem. Mater. 2005, 17, 5658–5669. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]



| Sample Depth (cm) | Sand % | Clay % | Lime % | Texture |
|---|---|---|---|---|
| 0–10 | 91.65 | 4.18 | 4.17 | sandy |
| 10–20 | 93.74 | 2.08 | 4.18 | sandy |
| 20–30 | 93.74 | 4.17 | 2.09 | sandy |
| 30–40 | 97.91 | 0.00 | 2.09 | sandy |
| Properties | Sample Depth (cm) | |||
|---|---|---|---|---|
| 0–10 | 10–20 | 20–30 | 30–40 | |
| Conductivity (dS·cm−1) | 0.117 | 0.049 | 0.064 | 0.088 |
| pH | 4.89 | 5.06 | 4.99 | 4.98 |
| Organic matter (%) | 0.67 | 0.26 | 0.25 | 0.17 |
| K+ (mEq/100 g) | 0.08 | 0.12 | 0.11 | 0.14 |
| Na+ (mEq/100 g) | 0.03 | 0.1 | 0.06 | 0.09 |
| Ca2+ (mEq/100 g) | 0.65 | 0.45 | 0.55 | 0.25 |
| Mg2+ (mEq/100 g) | 1.75 | 1.1 | 1.3 | 1.15 |
| CEC (mEq/100 g) | 4.5 | 3.90 | 3.57 | 3.25 |
| Freundlich | ||||||
|---|---|---|---|---|---|---|
| T (K) | 1/n | KF (L g−1) | R2 | RMSE | ||
| 298 | 0.649 ± 0.03 | 0.320 ± 0.20 | 0.985 | 0.052 | ||
| 308 | 0.333 ± 0.18 | 0.348 ± 0.15 | 0.963 | 0.065 | ||
| 318 | 0.343 ± 0.13 | 0.307 ± 0.16 | 0.963 | 0.042 | ||
| Langmuir | ||||||
| T (K) | qmax (mg g−1) | KL (L mg−1) | RL | R2 | RMSE | |
| 298 | 1.941 ± 0.07 | 0.077 ± 0.10 | 0.54 | 0.982 | 0.045 | |
| 308 | 0.929 ± 0.05 | 0.363 ± 0.20 | 0.56 | 0.997 | 0.019 | |
| 318 | 0.794 ± 0.08 | 0.428 ± 0.10 | 0.53 | 0.990 | 0.019 | |
| Temkin | ||||||
| T (K) | β (mg g−1) | KT (L mg−1) | b kJmol−1/mg g−1 | R2 | RMSE | |
| 298 | 0.416 ± 0.04 | 1.080 ± 0.12 | 2.99 | 0.998 | 0.007 | |
| 308 | 0.269 ± 0.05 | 1.049 ± 0.14 | 6.47 | 0.993 | 0.014 | |
| 318 | 0.244 ± 0.03 | 1.032 ± 0.11 | 7.51 | 0.992 | 0.018 | |
| Dubinin–Radushkevich | ||||||
| T (K) | qmax (mg g−1) | KDR * 104 (kJ−2 mol2) | E KJmol−1 | R2 | RMSE | |
| 298 | 0.920 ± 0.08 | 8.52 ± 0.07 | 23.70 | 0.983 | 0.029 | |
| 308 | 0.740 ± 0.04 | 8.08 ± 0.05 | 24.72 | 0.983 | 0.038 | |
| 318 | 0.647 ± 0.05 | 7.72 ± 0.06 | 26.24 | 0.991 | 0.013 | |
| T (K) | ΔG° (kJ mol−1) | ΔH° (kJ mol−1) | ΔS° (J mol−1 K−1) | |||
| 298 | −10.40 ± 0.15 | −35.83 ± 0.15 | −85.21 ± 1.01 | |||
| 308 | −9.59 ± 0.15 | |||||
| 318 | −8.73 ± 0.15 | |||||
| Freundlich | |||||
|---|---|---|---|---|---|
| T (K) | 1/n | KF (L g−1) | H | R2 | RMSE |
| 298 | 0.502 ± 0.04 | 0.498 ± 0.18 | 0.150 | 0.990 | 0.0110 |
| 308 | 0.413 ± 0.10 | 0.432 ± 0.09 | 0.160 | 0.996 | 0.0153 |
| 318 | 0.378 ± 0.08 | 0.371 ± 0.08 | 0.180 | 0.969 | 0.0103 |
| Langmuir | |||||
| T (K) | qmax (mg g−1) | KL (L mg−1) | RL | R2 | RMSE |
| 298 | 0.846 ± 0.02 | 1.475 ± 0.20 | 0.54 | 0.989 | 0.0060 |
| 308 | 0.599 ± 0.09 | 2.376 ± 0.10 | 0.56 | 0.997 | 0.0080 |
| 318 | 0.419 ± 0.04 | 4.843 ± 0.14 | 0.53 | 0.993 | 0.0050 |
| Temkin | |||||
| T (K) | β (mg g−1) | KT 103 (L mg−1) | b kJ mol−1/mg g−1 | R2 | RMSE |
| 298 | 0.185 ± 0.01 | 1.094 ± 0.12 | 13.39 | 0.998 | 0.0050 |
| 308 | 0.144 ± 0.09 | 1.063 ± 0.12 | 17.78 | 0.998 | 0.0026 |
| 318 | 0.112 ± 0.02 | 1.041 ± 0.15 | 23.60 | 0.999 | 0.0032 |
| Dubinin–Radushkevich | |||||
| T (K) | qmax (mg g−1) | KDR. 108 (kJ−2 mol2) | E kJ mol−1 | R2 | RMSE |
| 298 | 0.630 ± 0.03 | 8.21 ± 0.022 | 2467.82 | 0.985 | 0.0070 |
| 308 | 0.485 ± 0.04 | 5.37 ± 0.032 | 3051.39 | 0.994 | 0.0036 |
| 318 | 0.409 ± 0.09 | 4.81 ± 0.029 | 3224.12 | 0.956 | 0.0044 |
| Process | Non-Ionic Cipro | Zwitterionic Cipro | ciproH+ |
|---|---|---|---|
| Adsorption by intercalation (5.4% of cipro in mont) | 32.4 | −18.9 | |
| Adsorption by intercalation (10.8% of cipro in mont) | −7.2 | −95.4 | |
| Desorption by cation exchange | −14.0 | ||
| Desorption | −24.6 | −18.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jorge, N.L.; Garrafa, M.V.; Romero, J.M.; Jorge, M.J.; Jorge, L.C.; Delfino, M.R.; Meruvia-Rojas, Y.V.; Hernández-Laguna, A.; Sainz-Díaz, C.I. Adsorption of Ciprofloxacin on Clay Minerals in Argentinian Santa Rosa-Corrientes Soils. Molecules 2024, 29, 1760. https://doi.org/10.3390/molecules29081760
Jorge NL, Garrafa MV, Romero JM, Jorge MJ, Jorge LC, Delfino MR, Meruvia-Rojas YV, Hernández-Laguna A, Sainz-Díaz CI. Adsorption of Ciprofloxacin on Clay Minerals in Argentinian Santa Rosa-Corrientes Soils. Molecules. 2024; 29(8):1760. https://doi.org/10.3390/molecules29081760
Chicago/Turabian StyleJorge, Nelly L., María V. Garrafa, Jorge M. Romero, María J. Jorge, Lilian C. Jorge, Mario R. Delfino, Yumeida V. Meruvia-Rojas, Alfonso Hernández-Laguna, and C. Ignacio Sainz-Díaz. 2024. "Adsorption of Ciprofloxacin on Clay Minerals in Argentinian Santa Rosa-Corrientes Soils" Molecules 29, no. 8: 1760. https://doi.org/10.3390/molecules29081760
APA StyleJorge, N. L., Garrafa, M. V., Romero, J. M., Jorge, M. J., Jorge, L. C., Delfino, M. R., Meruvia-Rojas, Y. V., Hernández-Laguna, A., & Sainz-Díaz, C. I. (2024). Adsorption of Ciprofloxacin on Clay Minerals in Argentinian Santa Rosa-Corrientes Soils. Molecules, 29(8), 1760. https://doi.org/10.3390/molecules29081760




