Chiral Jahn–Teller Distortion in Quasi-Planar Boron Clusters
Abstract
1. Introduction
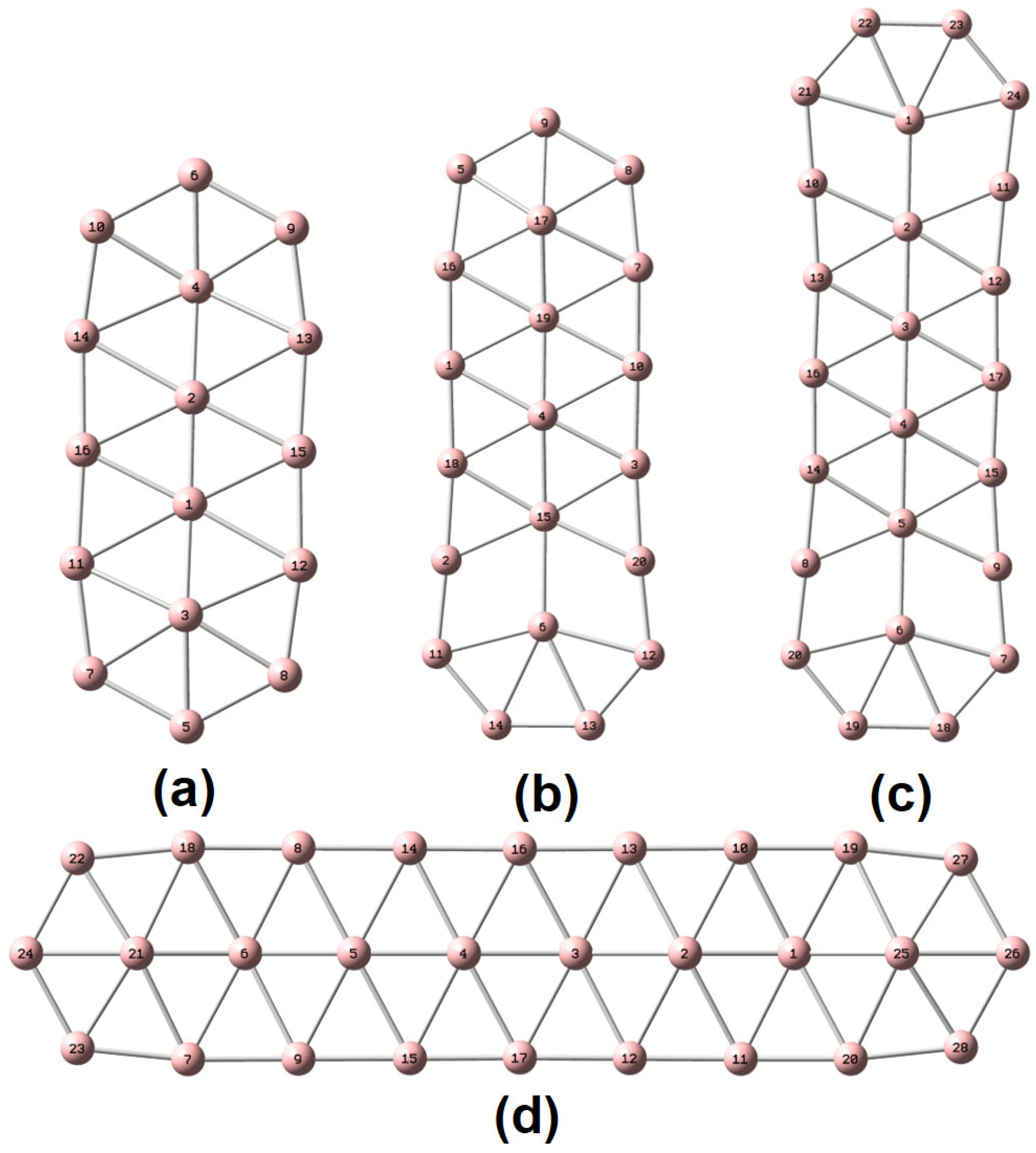
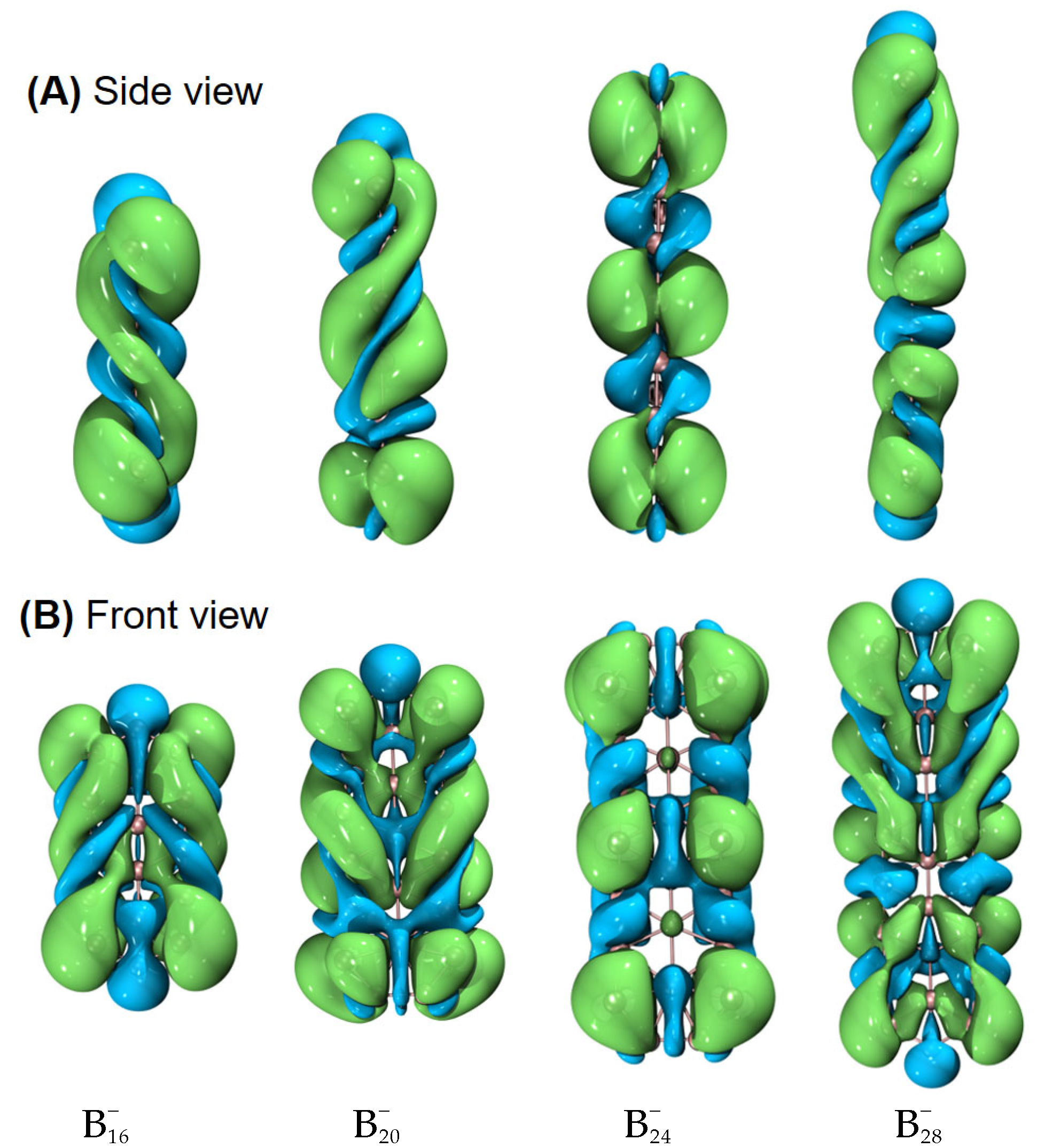
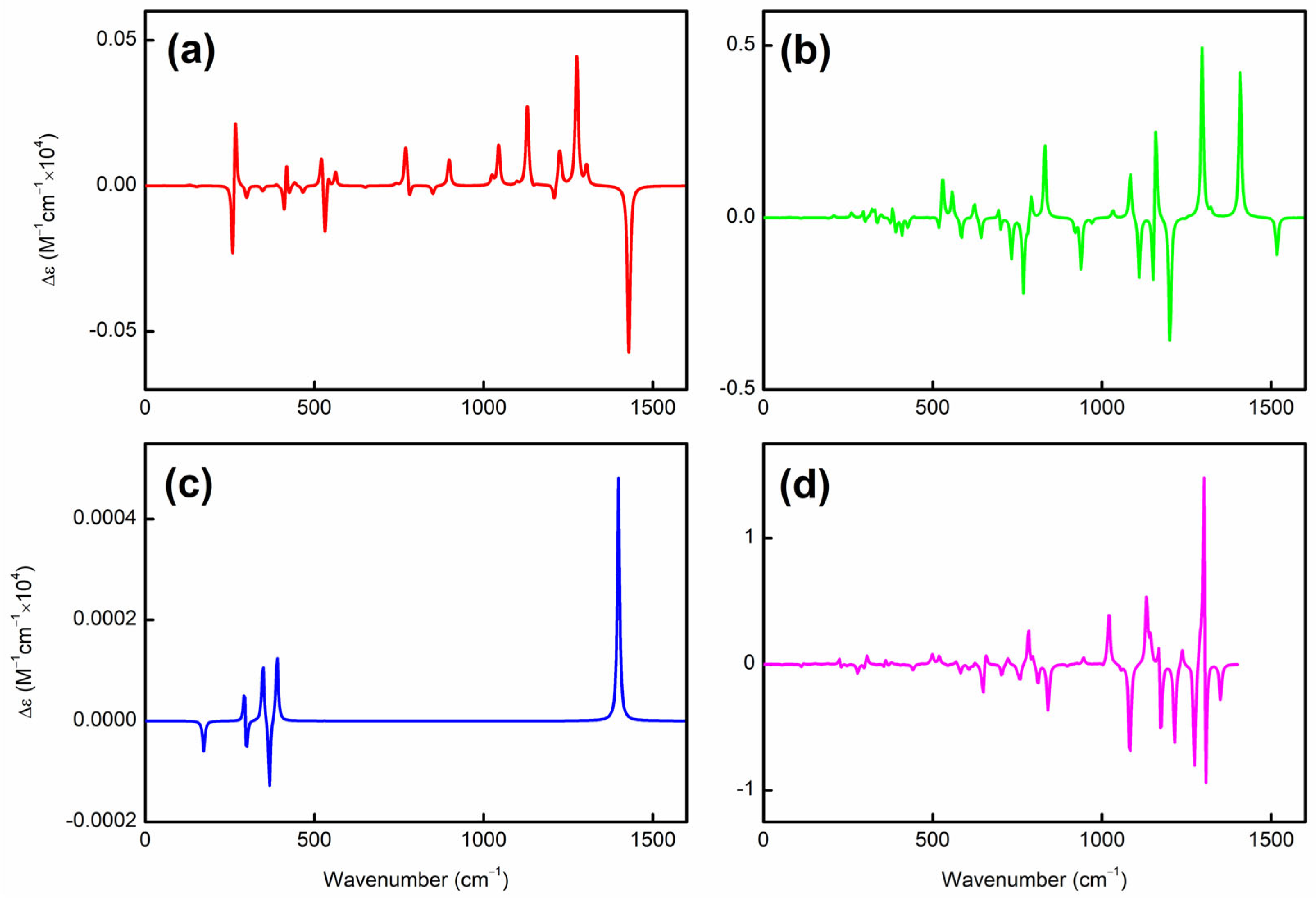
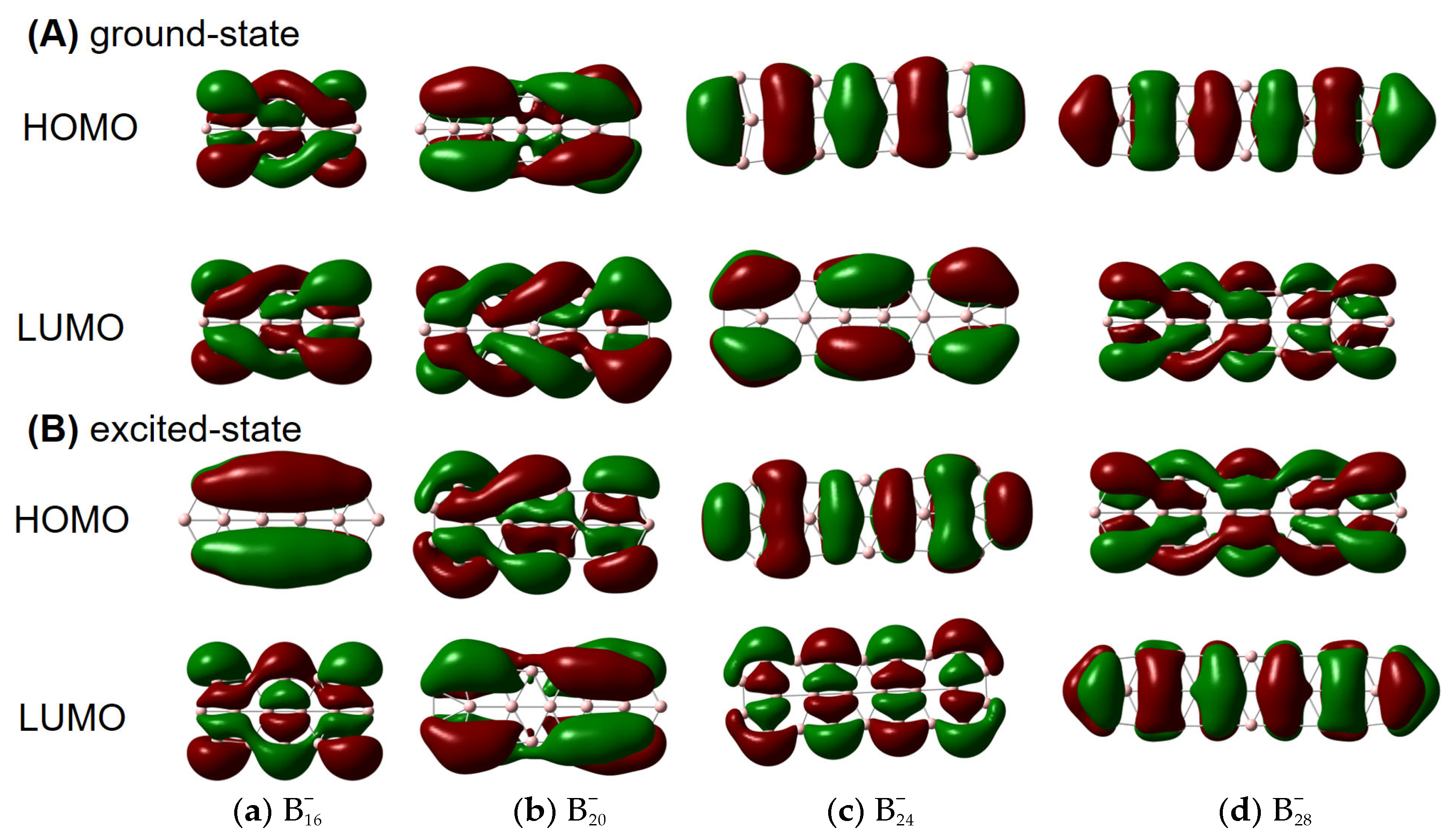
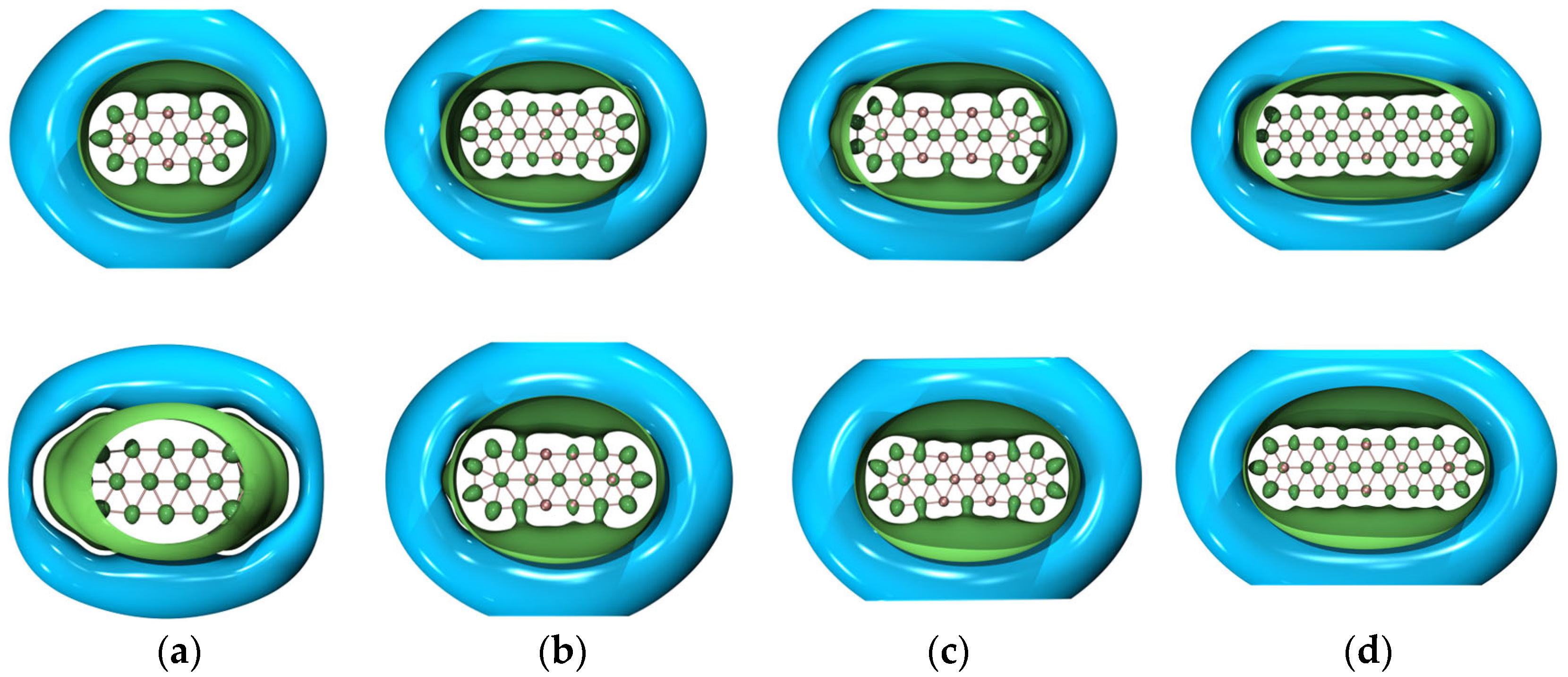
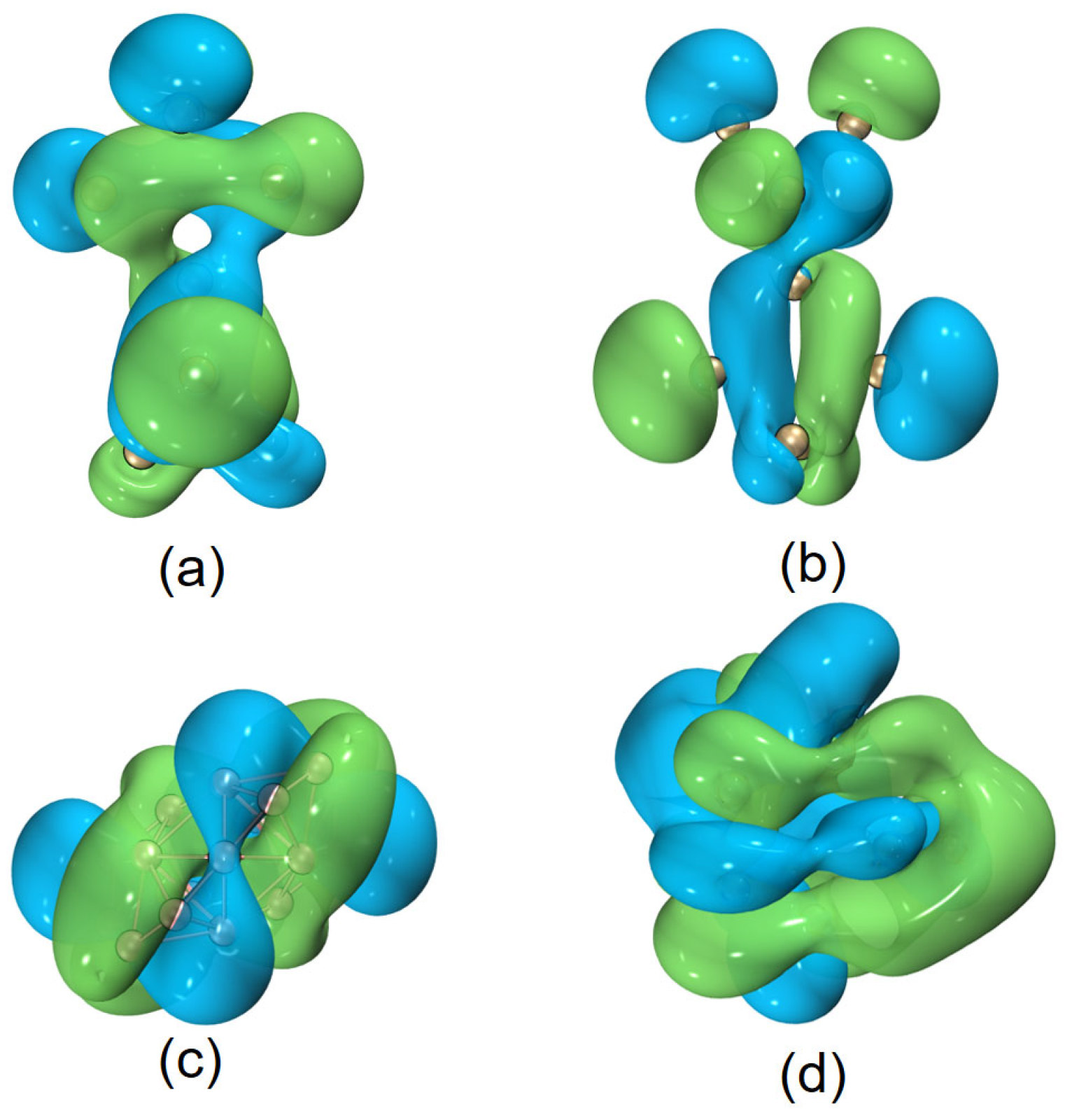
2. Results
3. Discussion
4. Materials and Methods
5. Summary
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Krylov, A.I. From orbitals to observables and back. J. Chem. Phys. 2020, 153, 080901. [Google Scholar] [CrossRef] [PubMed]
- Jin, Z.; Li, Y.; Hu, Z.; Hu, B.; Liu, Y.; Iida, K.; Kamazawa, K.; Stone, M.B.; Kolesnikov, A.I.; Abernathy, D.L.; et al. Magnetic molecular orbitals in MnSi. Sci. Adv. 2023, 9, eadd5239. [Google Scholar] [CrossRef] [PubMed]
- Mazin, I.I.; Jeschke, H.O.; Foyevtsova, K.; Valentí, R.; Khomskii, D.I. Na2IrO3 as a molecular orbital crystal. Phys. Rev. Lett. 2012, 109, 197201. [Google Scholar] [CrossRef]
- Foyevtsova, K.; Jeschke, H.O.; Mazin, I.I.; Khomskii, D.I.; Valentí, R. Ab initio analysis of the tight-binding parameters and magnetic interactions in Na2IrO3. Phys. Rev. B 2013, 88, 035107. [Google Scholar] [CrossRef]
- Streltsov, S.; Mazin, I.I.; Foyevtsova, K. Localized itinerant electrons and unique magnetic properties of SrRu2O6. Phys. Rev. B 2015, 92, 134408. [Google Scholar] [CrossRef]
- Turco, E.; Bernhardt, A.; Krane, N.; Valenta, L.; Fasel, R.; Juríček, M.; Ruffieux, P. Observation of the Magnetic Ground State of the Two Smallest Triangular Nanographenes. ACS Au 2023, 3, 1358–1364. [Google Scholar] [CrossRef] [PubMed]
- Woodward, R.B.; Hoffmann, R. Stereochemistry of Electrocyclic Reactions. J. Am. Chem. Soc. 1965, 87, 395–397. [Google Scholar] [CrossRef]
- Woodward, R.B.; Hoffmann, R. The Conservation of Orbital Symmetry. Angew. Chem. Int. Ed. 1969, 8, 781–853. [Google Scholar] [CrossRef]
- Hoffmann, R.; Woodward, R.B. Conservation of orbital symmetry. Acc. Chem. Res. 1968, 1, 17–22. [Google Scholar] [CrossRef]
- Hendon, C.H.; Tiana, D.; Murray, A.T.; Carbery, D.R.; Walsh, A. Helical frontier orbitals of conjugated linear molecules. Chem. Sci. 2013, 4, 4278–4284. [Google Scholar] [CrossRef]
- Imamura, A.; Aoki, Y. Helical molecular orbitals around straight-chain polyyne oligomers as models for molecular devices. Chem. Phys. Lett. 2013, 590, 136–140. [Google Scholar] [CrossRef]
- Liu, M.; Artyukhov, V.I.; Lee, H.; Xu, F.; Yakobson, B.I. Carbyne from First Principles: Chain of C Atoms, a Nanorod or a Nanorope. ACS Nano 2013, 7, 10075–10082. [Google Scholar] [CrossRef]
- Garner, M.H.; Hoffmann, R.; Rettrup, S.; Solomon, G.C. Coarctate and Möbius: The Helical Orbitals of Allene and Other Cumulenes. ACS Cent. Sci. 2018, 4, 688–700. [Google Scholar] [CrossRef] [PubMed]
- Garner, M.H.; Jensen, A.; Hyllested, L.O.; Solomon, G.C. Helical orbitals and circular currents in linear carbon wires. Chem. Sci. 2019, 10, 4598–4608. [Google Scholar] [CrossRef] [PubMed]
- Orimoto, Y.; Aok, Y.; Imamura, A. Extraction of One-Handed Helical Frontier Orbital in Even [n]Cumulenes by Breaking Mirror Images of Right- and Left-Handed Helical Orbitals: Theoretical Study. J. Phys. Chem. C 2019, 123, 11134–11139. [Google Scholar] [CrossRef]
- Garner, M.H.; Laplaza, R.; Corminboeuf, C. Helical versus linear Jahn–Teller distortions in allene and spiropentadiene radical cations. Phys. Chem. Chem. Phys. 2022, 24, 26134–26143. [Google Scholar] [CrossRef]
- Ozcelik, A.; Aranda, D.; Gil-Guerrero, S.; Pola-Otero, X.A.; Talavera, M.; Wang, L.; Behera, S.K.; Gierschner, J.; Peña-Gallego, Á.; Santoro, F.; et al. Distinct Helical Molecular Orbitals through Conformational Lock. Chem. Eur. J. 2020, 26, 17342–17349. [Google Scholar] [CrossRef] [PubMed]
- Garner, M.H.; Corminboeuf, C. Correlation between Optical Activity and the Helical Molecular Orbitals of Allene and Cumulenes. Org. Lett. 2020, 22, 8028–8033. [Google Scholar] [CrossRef] [PubMed]
- Pinter, P.; Munz, D. Controlling Möbius-Type Helicity and the Excited-State Properties of Cumulenes with Carbenes. J. Phys. Chem. A 2020, 124, 10100–10110. [Google Scholar] [CrossRef]
- Garner, M.H.; Corminboeuf, C. Helical electronic transitions of spiroconjugated molecules. Chem. Commun. 2021, 57, 6408–6411. [Google Scholar] [CrossRef]
- Bro-Jørgensen, W.; Garner, M.H.; Solomon, G.C. Quantification of the Helicality of Helical Molecular Orbitals. J. Phys. Chem. A 2021, 125, 8107–8115. [Google Scholar] [CrossRef] [PubMed]
- Bro-Jørgensen, W.; Solomon, G.C. Understanding Current Density in Molecules Using Molecular Orbitals. J. Phys. Chem. A 2023, 127, 9003–9012. [Google Scholar] [CrossRef] [PubMed]
- Gunasekaran, S.; Venkataraman, L. Tight-binding analysis of helical states in carbyne. J. Chem. Phys. 2020, 153, 124304. [Google Scholar] [CrossRef] [PubMed]
- Aoki, Y.; Orimoto, Y.; Imamura, A. One-Handed Helical Orbitals in Conjugated Molecules. ACS Cent. Sci. 2018, 4, 664–665. [Google Scholar] [CrossRef] [PubMed]
- Gückel, S.; Gluyas, J.B.G.; El-Tarhuni, S.; Sobolev, A.N.; Whiteley, M.W.; Halet, J.-F.; Lapinte, C.; Kaupp, M.; Low, P.J. Iron versus Ruthenium: Clarifying the Electronic Differences between Prototypical Mixed-Valence Organometallic Butadiyndiyl Bridged Molecular Wires. Organometallics 2018, 37, 1432–1445. [Google Scholar] [CrossRef]
- Honda, S.; Sugawara, R.; Ishida, S.; Iwamoto, T. A Spiropentasiladiene Radical Cation: Spin and Positive Charge Delocalization across Two Perpendicular Si=Si Bonds and UV–vis–NIR Absorption in the IR-B Region. J. Am. Chem. Soc. 2021, 143, 2649–2653. [Google Scholar] [CrossRef]
- Barber, J.S.; Yamano, M.M.; Ramirez, M.; Darzi, E.R.; Knapp, R.R.; Liu, F.; Houk, K.N.; Garg, N.K. Diels-Alder cycloadditions of strained azacyclic allenes. Nat. Chem. 2018, 10, 953–960. [Google Scholar] [CrossRef]
- Ramirez, M.; Svatunek, D.; Liu, F.; Garg, N.K.; Houk, K.N. Origins of Endo Selectivity in Diels-Alder Reactions of Cyclic Allene Dienophiles. Angew. Chem. Int. Ed. 2021, 60, 14989–14997. [Google Scholar] [CrossRef]
- Balakrishnan, A.; Vijayakumar, S. Highly delocalised molecular orbitals in boron-, carbon- and nitrogen-based linear chains: A DFT study. Mol. Phys. 2022, 120, e2020923. [Google Scholar] [CrossRef]
- Baronas, P.; Komskis, R.; Tankelevičiu Tė, E.; Adomėnas, P.; Adomėnienė, O.; Juršėnas, S. Helical Molecular Orbitals to Induce Spin–Orbit Coupling in Oligoyne-Bridged Bifluorenes. J. Phys. Chem. Lett. 2021, 12, 6827–6833. [Google Scholar] [CrossRef]
- Albert, B.; Hillebrecht, H. Boron: Elementary Challenge for Experimenters and Theoreticians. Angew. Chem. Int. Ed. 2009, 48, 8640–8668. [Google Scholar] [CrossRef] [PubMed]
- Zhao, D.; He, X.; Li, M.; Wang, B.; Guo, C.; Rong, C.; Chattaraj, P.K.; Liu, S. Density functional theory studies of boron clusters with exotic properties in bonding, aromaticity and reactivity. Phys. Chem. Chem. Phys. 2021, 23, 24118–24124. [Google Scholar] [CrossRef] [PubMed]
- Xu, S.; He, C.; Zhao, Y.; Yang, X.; Xu, H. Generalized Octet Rule with Fractional Occupancies for Boron. J. Am. Chem. Soc. 2023, 145, 25003–25009. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Zhao, Y.; An, X.; Fu, J.; Zhang, J.; Zhao, D.; Liu, S.; Rong, C. Cooperativity and reactivity properties of medium-sized boron clusters: A combined density functional theory and information-theoretic approach study. Mol. Phys. 2022, e2157774. [Google Scholar] [CrossRef]
- Sergeeva, A.P.; Zubarev, D.Y.; Zhai, H.; Boldyrev, A.I.; Wang, L. A Photoelectron Spectroscopic and Theoretical Study of and : An All-Boron Naphthalene. J. Am. Chem. Soc. 2008, 130, 7244–7246. [Google Scholar] [CrossRef]
- Kiran, B.; Bulusu, S.; Zhai, H.; Yoo, S.; Zeng, X.; Wang, L. Planar-to-tubular structural transition in boron clusters: B20 as the embryo of single-walled boron nanotubes. Proc. Natl. Acad. Sci. USA 2005, 102, 961–964. [Google Scholar] [CrossRef] [PubMed]
- Popov, I.A.; Piazza, Z.A.; Li, W.; Wang, L.; Boldyrev, A.I. A combined photoelectron spectroscopy and ab initio study of the quasi-planar cluster. J. Chem. Phys. 2013, 139, 144307. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, Y.; Li, W.; Jian, T.; Chen, Q.; You, X.; Ou, T.; Zhao, X.; Zhai, H.; Li, S.; et al. Observation and characterization of the smallest borospherene, and B28. J. Chem. Phys. 2016, 144, 064307. [Google Scholar] [CrossRef] [PubMed]
- Von Barth, U.; Hedin, L. A Local Exchange-Correlation Potential for the Spin Polarized Case: I. J. Phys. C Solid State Phys. 1972, 5, 1629. [Google Scholar] [CrossRef]
- Gunnarsson, O.; Lundqvist, B.I. Exchange and Correlation in atoms, molecules and solids by the spin-density-functional formalism. Phys. Rev. B 1976, 13, 4274–4298. [Google Scholar] [CrossRef]
- Rajagopal, A.K.; Callaway, J. Inhomogeneous electron gas. Phys. Rev. B 1973, 7, 1912–1919. [Google Scholar] [CrossRef]
- Ayers, P.W.; Yang, W. Legendre-transform functionals for spin-density-functional theory. J. Chem. Phys. 2006, 124, 224108. [Google Scholar] [CrossRef] [PubMed]
- Galván, M.; Vargas, R. Spin Potential in Kohn—Sham Theory. J. Phys. Chem. 1992, 96, 1625–1630. [Google Scholar] [CrossRef]
- Ghanty, T.K.; Ghosh, S.K. Spin-Polarized Generalization of the Concepts of Electronegativity and Hardness and the Description of Chemical Binding. J. Am. Chem. Soc. 1994, 116, 3943–3948. [Google Scholar] [CrossRef]
- Garza, J.; Vargas, R.; Cedillo, A.; Galván, M.; Chattaraj, P.K. Comparison between the frozen core and finite differences approximations for the generalized spin-dependent global and local reactivity descriptors in small molecules. Theor. Chem. Acc. 2006, 115, 257–265. [Google Scholar] [CrossRef]
- Pérez, P.; Chamorro, E.; Ayers, P.W. Universal mathematical identities in density functional theory: Results from three different spin-resolved representations. J. Chem. Phys. 2008, 128, 204108. [Google Scholar] [CrossRef] [PubMed]
- Ayers, P.W.; Fias, S.; Heidar-Zadeh, F. The axiomatic approach to chemical concepts. Comput. Theor. Chem. 2018, 1142, 83–87. [Google Scholar] [CrossRef]
- Liu, S. Conceptual Density Functional Theory and Some Recent Developments. Acta Phys-Chim. Sin. 2009, 25, 590–600. [Google Scholar]
- Johnson, P.A.; Bartolotti, L.J.; Ayers, P.W.; Fievez, T.; Geerlings, P. Charge density and chemical reactivity: A unified view from conceptual DFT. In Modern Charge Density Analysis; Gatti, C., Macchi, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 715–764. [Google Scholar]
- Geerlings, P.; Chamorro, E.; Chattaraj, P.K.; De Proft, F.; Gázquez, J.L.; Liu, S.; Morell, C.; Toro-Labbé, A.; Vela, A.; Ayers, P.W. Conceptual density functional theory: Status, prospects, issues. Theor. Chem. Acc. 2020, 139, 36. [Google Scholar] [CrossRef]
- Jissy, A.K.; Datta, A. What Stabilizes the LinPnInorganic Double Helices? J. Phys. Chem. Lett. 2013, 4, 1018–1022. [Google Scholar] [CrossRef]
- Guo, J.; Feng, L.; Wang, Y.; Jalife, S.; Vásquez-Espinal, A.; Cabellos, J.L.; Pan, S.; Merino, G.; Zhai, H. Coaxial Triple-Layered versus Helical Be6 Clusters: Dual Structural Fluxionality and Multifold Aromaticity. Angew. Chem. Int. Ed. 2017, 56, 10174–10177. [Google Scholar] [CrossRef] [PubMed]
- Reber, A.C.; Ugrinov, A.; Sen, A.; Qian, M.; Khanna, S.N. Helical and linear [K(As11)]2− chains: Role of solvent on the conformation of chains formed by Zintl anions. Chem. Phys. Lett. 2009, 473, 305–311. [Google Scholar] [CrossRef]
- Lu, T. Simple, reliable, and universal metrics of molecular planarity. J. Mol. Model. 2021, 27, 263. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef] [PubMed]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6169. [Google Scholar] [CrossRef]
- McLean, A.D.; Chandler, G.S. Contracted Gaussian-basis sets for molecular calculations. 1. 2nd row atoms, Z=11-18. J. Chem. Phys. 1980, 72, 5639–5648. [Google Scholar] [CrossRef]
- Dennington, R.D., II; Keith, T.A.; Millam, J.M. GaussView 6.0.16; Semichem, Inc.: Shawnee, KS, USA, 2016. [Google Scholar]
- Jusélius, J.; Sundholm, D.; Gauss, J. Calculation of current densities using gauge-including atomic orbitals. J. Chem. Phys. 2004, 121, 3952–3963. [Google Scholar] [CrossRef] [PubMed]
- Fliegl, H.; Taubert, S.; Lehtonen, O.; Sundholm, D. The gauge including magnetically induced current method. Phys. Chem. Chem. Phys. 2011, 13, 20500–20518. [Google Scholar] [CrossRef] [PubMed]
- Schleyer, P.v.R.; Maerker, C.; Dansfeld, A.; Jiao, H.; Hommes, N.J.R.v.E. Nucleus-Independent Chemical Shifts: A Simple and Efficient Aromaticity Probe. J. Am. Chem. Soc. 1996, 118, 6317–6318. [Google Scholar] [CrossRef]
- Kloda, S.; Kleinpeter, E. Ab initio calculation of the anisotropy effect of multiple bonds and the ring current effect of arenes—Application in conformational and configurational analysis. J. Chem. Soc. Perkin Trans. 2001, 2, 1893–1898. [Google Scholar]
- Ahrens, J.; Geveci, B.; Law, C. ParaView: An End-User Tool for Large Data Visualization. In Visualization Handbook; Elesvier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Rega, N.; Cossi, M.; Barone, V. Development and validation of reliable quantum mechanical approaches for the study of free radicals in solution. J. Chem. Phys. 1996, 105, 11060–11067. [Google Scholar] [CrossRef]
- Barone, V. Electronic, vibrational and environmental effects on the hyperfine coupling constants of nitroside radicals. H2NO as a case study. Chem. Phys. Lett. 1996, 262, 201–206. [Google Scholar] [CrossRef]
- Golding, R.M.; Stubbs, L.C. The Evaluation of the Hyperfine Interaction Tensor Components in Molecular Systems. Proc. R. Soc. Lond. A. 1977, 354, 223–244. [Google Scholar]
- Jensen, F. The Basis Set Convergence of Spin−Spin Coupling Constants Calculated by Density Functional Methods. J. Chem. Theory Comput. 2006, 2, 1360–1369. [Google Scholar] [CrossRef] [PubMed]
- Pritchard, B.P.; Altarawy, D.; Didier, B.; Gibson, T.D.; Windus, T.L. A New Basis Set Exchange: An Open, Up-to-date Resource for the Molecular Sciences Community. J. Chem. Inf. Model. 2019, 59, 4814–4820. [Google Scholar] [CrossRef] [PubMed]
- Naaman, R.; Paltiel, Y.; Waldeck, D.H. Chiral Molecules and the Electron Spin. Nat. Rev. Chem. 2019, 3, 250–260. [Google Scholar] [CrossRef]
- Yang, S.-H.; Naaman, R.; Paltiel, Y.; Parkin, S.S.P. Chiral spintronics. Nat. Rev. Phys. 2021, 3, 328–343. [Google Scholar] [CrossRef]
- Liu, Y.; Xiao, J.; Koo, J.; Yan, B. Chirality-driven topological electronic structure of DNA-like materials. Nat. Mater. 2021, 20, 638–644. [Google Scholar] [CrossRef] [PubMed]
- Parr, R.G.; Yang, W. Density Functional Theory of Atoms and Molecules; Oxford University Press: Oxford, UK, 1989. [Google Scholar]
- Teale, A.M.; Helgaker, T.; Savin, A.; Adamo, C.; Aradi, B.; Arbuznikov, A.V.; Ayers, P.W.; Baerends, E.J.; Barone, V.; Calaminici, P.; et al. DFT exchange: Sharing perspectives on the workhorse of quantum chemistry and materials science. Phys. Chem. Chem. Phys. 2022, 24, 28700–28781. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Revision C.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Lee, T.J.; Taylor, P.R. A diagnostic for determining the quality of single-reference electron correlation methods. Int. J. Qunantum Chem. 1989, 36, 199–207. [Google Scholar] [CrossRef]
- Dunning, T.H., Jr. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
- London, F. The quantic theory of inter-atomic currents in aromatic combinations. J. Phys. Radium 1937, 8, 397–409. [Google Scholar] [CrossRef]
- McWeeny, R. Perturbation Theory for Fock-Dirac Density Matrix. Phys. Rev. 1962, 126, 1028–1034. [Google Scholar] [CrossRef]
- Ditchfield, R. Self-consistent perturbation theory of diamagnetism. 1. Gauge-invariant LCAO method for N.M.R. chemical shifts. Mol. Phys. 1974, 27, 789–807. [Google Scholar] [CrossRef]
- Wolinski, K.; Hinton, J.F.; Pulay, P. A Comparison of Models for Calculating Nuclear Magnetic Resonance Shielding Tensors. J. Am. Chem. Soc. 1990, 112, 8251–8260. [Google Scholar] [CrossRef]
- Cheeseman, J.R.; Trucks, G.W.; Keith, T.A.; Frisch, M.J. A comparison of models for calculating nuclear magnetic resonance shielding tensors. J. Chem. Phys. 1996, 104, 5497–5509. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2011, 33, 580–592. [Google Scholar] [CrossRef]


| Species | MPP | SDP | MPD | MND |
|---|---|---|---|---|
| 2 | 0.090 | 0.442 | 0.221 | −0.221 |
| 4 | 0.017 | 0.091 | 0.047 | −0.044 |
| 2 | 0.081 | 0.382 | 0.263 | −0.119 |
| 4 | 0.083 | 0.322 | 0.179 | −0.143 |
| 2 | 0.021 | 0.074 | 0.037 | −0.037 |
| 4 | 0.039 | 0.196 | 0.098 | −0.098 |
| 2 | 0.092 | 0.440 | 0.302 | −0.138 |
| 4 | 0.103 | 0.404 | 0.212 | −0.192 |
| Species | NICS(0) | NICS(0)ZZ | NICS(1) | NICS(1)ZZ | NICS(−1) | NICS(−1)ZZ |
|---|---|---|---|---|---|---|
| 2 | −16.67 | −48.74 | −17.90 | −39.52 | −17.90 | −39.52 |
| 4 | −16.76 | −111.92 | −5.85 | −4.66 | −5.83 | −4.66 |
| 2 | 15.51 | −28.62 | −15.89 | −31.60 | −11.26 | −23.02 |
| 4 | 22.94 | −15.48 | −13.61 | −32.13 | −13.57 | −30.98 |
| 2 | −29.53 | −47.96 | −14.42 | −26.37 | −14.42 | −26.37 |
| 4 | −26.90 | −59.08 | −16.85 | −38.44 | −16.85 | −38.44 |
| 2 | −18.76 | −33.63 | −8.27 | −16.35 | −8.87 | −15.98 |
| 4 | −17.24 | −36.36 | −11.94 | −22.62 | −11.74 | −23.33 |
| no. | 2αiso | 2Aiso | 4αiso | 4Aiso | no. | 2αiso | 2Aiso | 4αiso | 4Aiso |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 77.66 | −2.98 | 78.50 | −1.53 | 9 | 35.33 | 40.64 | 25.78 | 32.87 |
| 2 | 77.66 | −2.98 | 78.50 | −1.56 | 10 | 35.34 | 40.58 | 25.78 | 32.86 |
| 3 | 81.47 | −5.77 | 72.32 | −8.74 | 11 | 69.43 | −11.44 | 82.41 | −10.30 |
| 4 | 81.47 | −5.77 | 72.33 | −8.74 | 12 | 69.42 | −11.46 | 82.41 | −10.30 |
| 5 | 8.77 | −35.62 | 36.11 | −17.18 | 13 | 69.43 | −11.44 | 82.41 | −10.30 |
| 6 | 8.77 | −35.62 | 36.11 | −17.19 | 14 | 69.43 | −11.46 | 82.41 | −10.30 |
| 7 | 35.33 | 40.66 | 25.78 | 32.86 | 15 | 102.86 | −3.11 | 78.37 | 0.72 |
| 8 | 35.34 | 40.60 | 25.78 | 32.85 | 16 | 102.86 | −3.10 | 78.37 | 0.72 |
| no. | 2αiso | 2Aiso | 4αiso | 4Aiso | no. | 2αiso | 2Aiso | 4αiso | 4Aiso |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 82.41 | 0.71 | 92.94 | 1.07 | 11 | 39.89 | 24.08 | 44.65 | 13.31 |
| 2 | 75.99 | −17.57 | 64.17 | −7.19 | 12 | 39.89 | 24.09 | 44.53 | 13.25 |
| 3 | 94.80 | 5.82 | 117.43 | −0.87 | 13 | 26.91 | −9.85 | 30.45 | −7.18 |
| 4 | 82.47 | −15.30 | 78.11 | −12.48 | 14 | 26.91 | −9.86 | 30.46 | −7.30 |
| 5 | 18.41 | 35.48 | 38.64 | 35.92 | 15 | 78.73 | 2.80 | 92.78 | 2.47 |
| 6 | 78.05 | −9.61 | 74.29 | −9.04 | 16 | 81.60 | −10.16 | 69.88 | −8.16 |
| 7 | 81.60 | −10.16 | 69.82 | −8.20 | 17 | 69.79 | −9.31 | 79.02 | −7.43 |
| 8 | 18.42 | 35.48 | 38.84 | 35.95 | 18 | 94.79 | 5.81 | 117.62 | −0.91 |
| 9 | 34.65 | −21.98 | 19.20 | −27.86 | 19 | 77.81 | 4.31 | 86.55 | 0.07 |
| 10 | 82.41 | 0.73 | 93.02 | 1.02 | 20 | 75.99 | −17.58 | 64.29 | −7.26 |
| no. | 2αiso | 2Aiso | 4αiso | 4Aiso | no. | 2αiso | 2Aiso | 4αiso | 4Aiso |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 80.03 | −5.46 | 79.50 | −7.42 | 13 | 118.46 | −9.58 | 120.01 | −3.83 |
| 2 | 78.34 | 1.45 | 79.92 | 5.62 | 14 | 118.46 | −9.58 | 120.01 | −3.83 |
| 3 | 83.41 | −5.35 | 88.96 | −3.69 | 15 | 118.46 | −9.58 | 120.01 | −3.83 |
| 4 | 83.41 | −5.35 | 88.96 | −3.69 | 16 | 68.85 | 12.02 | 70.01 | 4.22 |
| 5 | 78.34 | 1.45 | 79.92 | 5.62 | 17 | 68.85 | 12.02 | 70.01 | 4.22 |
| 6 | 80.03 | −5.46 | 79.50 | −7.42 | 18 | 28.82 | −8.41 | 17.95 | −3.84 |
| 7 | 38.44 | 8.36 | 45.29 | 1.03 | 19 | 28.82 | −8.41 | 17.95 | −3.84 |
| 8 | 66.10 | −7.13 | 64.54 | −4.36 | 20 | 38.44 | 8.36 | 45.29 | 1.03 |
| 9 | 66.10 | −7.13 | 64.54 | −4.36 | 21 | 38.44 | 8.36 | 45.29 | 1.03 |
| 10 | 66.10 | −7.13 | 64.54 | −4.36 | 22 | 28.82 | −8.41 | 17.95 | −3.84 |
| 11 | 66.10 | −7.13 | 64.54 | −4.36 | 23 | 28.82 | −8.41 | 17.95 | −3.84 |
| 12 | 118.46 | −9.58 | 120.01 | −3.83 | 24 | 38.44 | 8.36 | 45.29 | 1.03 |
| no. | 2αiso | 2Aiso | 4αiso | 4Aiso | no. | 2αiso | 2Aiso | 4αiso | 4Aiso |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 79.30 | −7.09 | 70.30 | 5.31 | 15 | 69.93 | −19.78 | 84.30 | 0.54 |
| 2 | 73.04 | −1.60 | 84.98 | −5.58 | 16 | 96.89 | 31.15 | 98.54 | −1.44 |
| 3 | 83.12 | −5.16 | 78.07 | −0.08 | 17 | 96.89 | 31.14 | 98.57 | −1.44 |
| 4 | 84.30 | −6.42 | 78.12 | −0.08 | 18 | 78.19 | −18.49 | 81.49 | −5.32 |
| 5 | 76.95 | −3.58 | 84.99 | −5.61 | 19 | 74.86 | −16.35 | 81.54 | −5.27 |
| 6 | 79.95 | −6.84 | 70.29 | 5.14 | 20 | 74.86 | −16.35 | 81.52 | −5.26 |
| 7 | 78.19 | −18.49 | 81.52 | −5.34 | 21 | 70.58 | −4.58 | 75.02 | −5.81 |
| 8 | 82.74 | 13.22 | 91.03 | −1.62 | 22 | 17.52 | 50.44 | 29.89 | 11.67 |
| 9 | 82.74 | 13.22 | 90.88 | −1.57 | 23 | 17.52 | 50.45 | 29.91 | 11.70 |
| 10 | 77.86 | 17.29 | 90.69 | −1.61 | 24 | 37.06 | −33.92 | 16.67 | −9.92 |
| 11 | 77.87 | 17.30 | 90.80 | −1.66 | 25 | 63.54 | −0.51 | 74.89 | −5.83 |
| 12 | 68.99 | −21.28 | 84.21 | 0.63 | 26 | 42.21 | −19.68 | 16.75 | −9.76 |
| 13 | 68.99 | −21.28 | 84.33 | 0.62 | 27 | 14.01 | 33.86 | 29.71 | 11.46 |
| 14 | 69.93 | −19.77 | 84.19 | 0.55 | 28 | 14.00 | 33.88 | 29.66 | 11.45 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, D.; Zhao, Y.; Xu, T.; He, X.; Hu, S.; Ayers, P.W.; Liu, S. Chiral Jahn–Teller Distortion in Quasi-Planar Boron Clusters. Molecules 2024, 29, 1624. https://doi.org/10.3390/molecules29071624
Zhao D, Zhao Y, Xu T, He X, Hu S, Ayers PW, Liu S. Chiral Jahn–Teller Distortion in Quasi-Planar Boron Clusters. Molecules. 2024; 29(7):1624. https://doi.org/10.3390/molecules29071624
Chicago/Turabian StyleZhao, Dongbo, Yilin Zhao, Tianlv Xu, Xin He, Shankai Hu, Paul W. Ayers, and Shubin Liu. 2024. "Chiral Jahn–Teller Distortion in Quasi-Planar Boron Clusters" Molecules 29, no. 7: 1624. https://doi.org/10.3390/molecules29071624
APA StyleZhao, D., Zhao, Y., Xu, T., He, X., Hu, S., Ayers, P. W., & Liu, S. (2024). Chiral Jahn–Teller Distortion in Quasi-Planar Boron Clusters. Molecules, 29(7), 1624. https://doi.org/10.3390/molecules29071624






