Abstract
Fe-Cr-C-B wear-resistant steels are widely used as wear-resistant alloys in harsh environments. The M3X (M = Fe, Cr; X = C, B) cementite-type material is a commonly used strengthening phase in these alloys. This study investigated the mechanical properties of cementite (Fe, Cr)3(C, B) using the first-principle density functional theory. We constructed crystal structures of (Fe, Cr)3(C, B) with different concentrations of Cr and B. The bulk modulus, shear modulus, Young’s modulus, Poisson’s ratio, and hardness of the material were calculated, and a comprehensive mechanical property database based on CALPHAD modeling of the full composition was established. The optimal concentrations of the (Fe, Cr)3(C, B) phase were systematically evaluated across its entire composition range. The material exhibited the highest hardness, shear modulus, and Young’s modulus at Cr and B concentrations in the range of 70–95 at% and 40 at%, respectively, rendering it difficult to compress and relatively poor in machinability. When the B content exceeded 90 at%, and the Cr content was zero, the shear modulus and hardness were low, resulting in poor resistance to deformation, reduced stiffness, and ease of plastic processing. This study provides an effective alloying strategy for balancing the brittleness and toughness of (Fe, Cr)3(C, B) phases.
1. Introduction
Wear-resistant steel is typically alloyed with elements such as Si, Mn, Cr, Mo, W, V, Nb, Ti, and B [1,2] to improve its overall performance. In general, these alloying elements are introduced through two methods. In the first method, the solid solutions of these elements are incorporated in the steel matrix for solid-solution strengthening. In the second method, these elements are combined with other elements to create compound phases, primarily borides and carbides, which serve as second-phase strengthening agents [3,4,5,6]. Cementite is widely used to strengthen low-, medium-, and high-carbon steels. Specifically, cementite (θ-Fe3C) is the most prevalent and pivotal strengthening phase, which plays a significant role in the heat treatment and processing of steel [7].
In wear-resistant steel materials there are various types of carbides formed, and the carbides exhibit certain metal bonding characteristics resulting in the dissolution of other alloying elements through atomic substitution, forming complex multicomponent solid solutions. This is the main difference between the strengthening phase in steel and traditional compound phases [8]. The solubility of ca rbides is related to atomic radius, the number of outer electrons, and lattice type. Based on experimental statistics, the types of carbide strengthening phases in wear-resistant steel mainly include the following NaCl-type (B1-type) face-centered cubic lattice structure MC phases, such as VC, NbC, TaC, TiC, ZrC, HfC, etc. Non-metallic atoms in these phases often form vacancies, leading to a non-metal to metal ratio of less than 1. For example, the C content in VC ranges from 0.7 to 1, in NbC it ranges from 0.4 to 1, and in TiC it ranges from 0.5 to 1. Therefore, the chemical compositions of commonly existing VC and NbC in steel are VC0.875 (VgC,) and NbC0.875 (NbC,). Metal elements in MC phases can be completely mutually soluble, forming compounds like (V,Ti)C [8,9]. Simple hexagonal lattice MC and M2C phases include MoC, WC, Mo2C, and W2C, while complex hexagonal lattice M7C3 phases include Cr7C3 and Mn7C3. Mo2C and W2C can be completely soluble with each other. Cr7C3 can dissolve a considerable amount of Fe and Mn, and it can also dissolve certain amounts of W, Mo, V, and other elements [10]. Complex cubic lattice M23C6 phases include Cr23C6, Mn23C6, Fe21Mo2C6, and Fe21W2C6, etc. Cr23C6 can dissolve up to 25% Fe, and it can also dissolve some Mn, Mo, W, V, Ni, and other elements [11]. Complex cubic lattice M6C phases include Fe3Mo3C6 and Fe3W3C6, etc. In the M6C phase, W and Mo atoms can infinitely interchange with each other. Complex orthorhombic lattice M3C phases include Fe3C and Mn3C, etc., and they can be completely mutually soluble, forming (Fe,Mn)3C. Fe3C can dissolve a maximum of 28% Cr, 14% Mo, 2% W, or 3% V, forming alloy cementite [12].
It is known that the addition of chromium imparts such valuable properties as strength, hot hardness, and corrosion resistance. By dissolving in iron in the presence of carbon, chromium can form the carbides (FeCr)3C, (CrFe)3C2, (CrFe)7C3, and (CrFe)4C. The strength of the alloys is predominantly determined by the presence of the carbide phase, i.e., the cementite Fe3C, in which the solubility of chromium is as high as 18 at%. A further increase in the chromium content leads to the transformation (Fe,Cr)3C→(Cr,Fe)7C3→Cr7C3 [13]. Steels with an increased chromium content (6–32 at%) have a high wear resistance and the formation of the chromium carbide Cr7C3 plays a significant role in the improvement of their strength. The carbide Cr7C3 is thermodynamically stable. Recently, the metastable carbide Cr3C with a cementite structure (Fe3C-type) has been produced via rapid quenching. It is known that the chromium carbides exhibit unique properties, such as high hardness, chemical stability, and oxidation resistance [14].
White cast iron has been widely used as a wear-resistant material for a long time in many industrial applications. It is well known that the elastic properties of the alloy can be greatly affected by reinforced particles or precipitated phases. For white cast iron, the precipitated carbides usually refer to Fe3C. However, pure Fe3C is thermodynamically unstable. In practice, a small amount of Cr is added into ordinary white cast iron in order to stabilize Fe3C-type carbides, and as a result, the obtained carbides can be finally represented as (Fe, Cr)3C [15]. In current studies on the effect of boron on the wear resistance of Fe-Cr-B alloys containing different boron contents (0 wt%, 5 wt%, 7 wt% and 9 wt%), the boron element greatly improves the wear resistance of specimens as compared with that of an unreinforced specimen.
Cementite precipitates from either austenite or the liquid phase via eutectic reactions. The morphology and kinetics of cementite precipitation significantly affect the mechanical properties of steel. θ-Fe3C is a thermodynamically unstable metastable phase in Fe–C alloys. To obtain stable Fe3C-type carbides, alloying elements such as Cr and B are typically introduced into standard white cast iron. The resulting cementite alloy can be represented as θ-M3X (M = Fe, Cr; X = C, B) [16].
Lv [17,18] employed first-principles calculations to investigate the electronic structure, magnetic properties, and phase stability of Cr and Mn doped cementite alloys. The calculations revealed that the mixing enthalpies of Fe8Cr4C and Fe4Cr8C were negative. Furthermore, the cementite alloys exhibited enhanced chemical and mechanical stability when they were doped with Cr and Mn doping. Compared to θ-Fe3C, these alloys exhibited superior thermodynamic stability. In particular, compared to θ-Fe3C, (Fe,Cr)3C exhibited enhanced elasticity properties.
The inclusion of B as an alloying element in hard-phase tool steels offers several advantages, including enhanced thermal stability, hardness, and modulus of elasticity. Borides are formed through a direct reaction between Fe and B. Owing to the low solubility of B in a Fe lattice (500 ppm), only minimal quantities of B are required to create hard phases within significant bulk contents [19]. Furthermore, B improves the hardenability of the Fe matrix. Incorporating the alloying elements Cr and B further enhances the stability, modulus of elasticity, and hardness of carburizers, achieving a suitable balance between strength and toughness along with improved plasticity and machinability.
Cementite is a complex interstitial compound characterized by an orthorhombic crystal structure (space group Pnma, No. 62). As shown in Figure 1, the crystal cell contains 16 atoms, with metal atoms occupying two Wyckoff positions (4c and 8d) and non-metal atoms occupying one Wyckoff position (4c) [12]. Owing to the complexity of the structure and the inter-element interactions of carburized crystals, few studies have systematically investigated the influence of the composition of alloying elements on the mechanical properties of carburized hard phases. Therefore, this study aimed to quantitatively evaluate the mechanical properties of (Fe,Cr)3(C,B) alloys with respect to their compositional range using the CALPHAD method and first-principle calculations. The structure of θ-M3X (M = Fe, Cr; X = C, B) was constructed for various compositions. The positions of Fe and C atoms were replaced by Cr and B atoms, respectively, as shown in Figure 2.
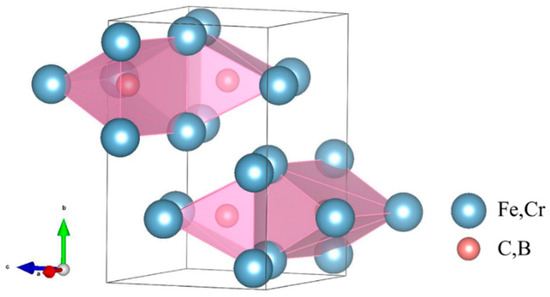
Figure 1.
The crystal structure of cementite-type M3X shows the orthorhombic space lattice, where blue represents the positions of metal atoms and red represents the positions of non-metal atoms.
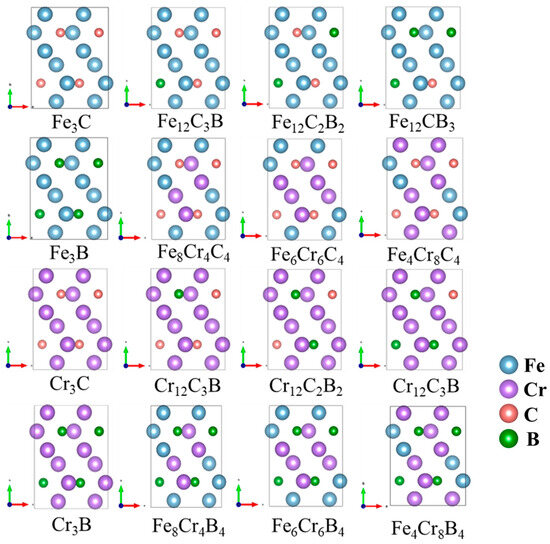
Figure 2.
The atomic configurations of Fe, Cr, B and C in a unit cell of (Fe, Cr)3(C, B), consisting of formula units (16 atoms). The purple and blue spheres correspond to Fe and Cr atoms, while the red and green spheres represent B and C atoms.
2. Computational Methods
We employed first-principle calculations based on the pseudo-potential plane-wave method using the CASTEP quantum mechanics module [20]. The crystal wave functions were expanded using a plane-wave basis set, and the potential was represented using ultrasoft pseudo-potentials in reciprocal space. The exchange-correlation energy was computed within a generalized gradient approximation (GGA) framework using the Perdew–Burke–Ernzerh surface and solid (PBEsol) functional [21]. Fine precision settings were adopted to ensure the accuracy of the computational data and to maintain high efficiency. Periodic boundary conditions were applied and the number of plane waves was determined using the kinetic energy cutoff, which was set as 310 eV for all unit-cell models. The Brillouin zone was discretized using the Monkhorst–Pack method using an 8 × 6 × 9 k-point grid partition [22]. To ensure self-consistent convergence, the convergence thresholds for total energy, maximum stress, and maximum displacement were set as 1.0−5 eV/atom, 0.05 GPa, and 0.001, respectively, and a maximum iteration count of 500 was employed. Before each calculation, the crystal structure was geometrically optimized using the BFGS method to obtain the locally most stable structure. The valence electrons of Cr, Fe, C, and B are 3s23p63d54s14p, 3d64s2, 2s22p2, and 2s22p1, respectively [23].
2.1. Elastic Properties at 0 K
The Birch–Murnaghan equation of state (EOS) [24,25] was adopted to fit the energy vs. volume (E–V) curve from the first-principles calculations at 0 K.
V0 and E0 are the equilibrium volume per atom and the static total energy, respectively. B0 is the bulk modulus and .
The stress–strain method was used to calculate the elastic constants of single crystals and subsequently obtain the matrix of elastic coefficients of θ-M3X (M = Fe, Cr; X = C, B) single crystals. The second-order tensor of the elastic constants was based on the generalized Hooke’s law of elastic deformation [26]. Small strains were applied in different directions to optimize the positions of atoms in the crystal cell, the stress tensor of the deformed crystal cell was analyzed after deformation, and the elastic constants were obtained based on the stress–strain relationship:
where Cij, σj, and εi are the elastic constant, stress tensor, and strain tensor, respectively. An orthorhombic crystal has nine independent crystal elastic constants: C11, C22, C33, C12, C13, C23, C44, C55, and C66. These constants can be determined by applying a small strain to the equilibrium lattice and computing the resultant change in the total energy of the lattice.
By treating polycrystalline materials as aggregates of single crystals with random orientations, the isotropic polycrystalline elastic moduli can be computed as averages of the anisotropic single-crystal elastic constants. The theoretical lower and upper bounds of the true polycrystalline bulk (B) and shear moduli (G) are given by Reuss and Voigt, assuming uniform strain and stress throughout the polycrystal, respectively.
where Sij are the elastic compliances, and their values can be obtained by inverting the elastic constant matrix S = C−1. Based on the Voigt and Reuss models, BV (BR) and GV (GR) are the bulk and shear moduli, respectively [27]. B and G, based on the Hill model, can be calculated using their average values [28].
Young’s modulus (E) and Poisson’s ratio (v) were calculated as follows.
θ-M3X is a highly crucial strengthening component in high boron wear-resistant alloys, characterized by its exceptionally high hardness. Hardness, which is a pivotal parameter for material wear resistance, was a central concern in this study. Hardness indicates the ability of a material to resist plastic deformation and failure. The subscripts V and R represent the Voigt and Reuss limits, respectively, and σ is Poisson’s ratio. In this study, we used the semiempirical equation of hardness proposed by Tian [29]. The following equation was defined to evaluate the hardness.
In Tian’s article [29], a comparison of crystal structures, computed hardness, and experimental hardness for BCX was provided. This comparison encompassed various complex crystal structures, including orthorhombic structures such as BC3 and BC5. Additionally, the calculated hardness for transition metal compounds such as FeC and FeC2 was also presented. These findings suggest that Tian’s computational model is applicable to orthorhombic structures such as (Fe,Cr)3(C,B). In Wang et al.’s research article, they investigated the relationship between the structural characteristics and mechanical behavior of multi-component iron-containing phases using Tian et al.’s proposed model [30]. Furthermore, Zhang et al. also utilized Tian’s model to calculate the hardness of (Fe, Cr)7C [31].
Anisotropic mechanical properties play an important role in material applications. The elastic anisotropy of a crystal can be estimated from independent elastic constants using anisotropic indices. In this study, the universal anisotropic index (AU) and percent anisotropic indices (AB and AG) were calculated using the following equations [32].
Here, BV, BR, GV, and GR are the bulk and shear moduli estimated using the Voigt and Reuss methods, respectively. For isotropic structures, the values of the anisotropic indices are zero. Large discrepancies from zero indicate highly anisotropic mechanical properties. The elastic coefficient matrix of a single crystal of θ-M3X (M = Fe, Cr; X = C, B) phase was obtained using the stress–strain method based on the generalized Hooke’s law. Subsequently, the elastic modulus (Cij), including the bulk modulus (B) of θ-M3X, was obtained using the Voigt–Ruess–Hill approximation. The Born–Huang mechanical stability criterion was satisfied, indicating that the θ-M3X phases are all mechanically stable. For orthorhombic crystal systems, the mechanical stability criterion can be expressed as follows.
2.2. CALPHAD Modeling of Elastic Constants
The CALPHAD method is one of the few approaches capable of directly constructing a component–property relationship model from a multicomponent space. In 2010, Liu [33] modeled the variations in the mechanical properties of (Fe,Cr)3(C,B) solid solutions with concentration using the CALPHAD method. The CALPHAD method establishes a performance model for a multicomponent system. The general form of the model is shown below.
Here, i and j denote pure elements. n is the binary interaction parameter of the elements i and j. n is the order. xi and xj are the molar percentages of elements i and j, respectively. Clm is the elastic stiffness of the alloy. The variation in the elastic constants with concentration calculated by fitting the first-principles calculations was obtained using n.
3. Results and Discussion
The total energies of the substitutional elements M (Fe,Cr) and X (C,B) in their respective ground-state structures were calculated as functions of volume at 0 K and zero pressure unless otherwise stated. The resulting EOS and lattice parameters are listed in Table 1.

Table 1.
Calculated equilibrium lattice parameters (Å3), equilibrium cell volume (Å3) and total cell energy (unit in eV/Cell) of cementite-type M3X (M = Fe, Cr; X = C, B) at 0 K.
Typically, the total energy of the relevant phase is calculated as a function of volume. The energy–volume relationship determines the equilibrium energy E(V0), equilibrium volume (V0), and bulk modulus (B0), as defined in Equation (1). As an example, Figure 3 shows the energy–volume relationship of the cementite M3X (M = Fe, Cr; X = C, B). The lattice parameters (a, b, and c) of the cementite at equilibrium volume were calculated by optimizing the interatomic forces and stresses in the unit cell.
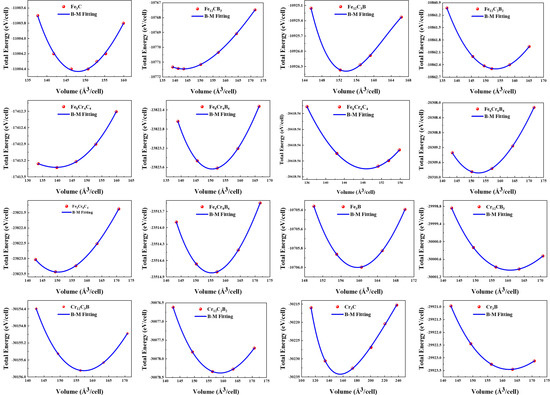
Figure 3.
Calculated total energy at zero temperature and without zero point motion as a function of volume of M3X (M = Fe, Cr; X = C, B). The filled circles represent calculated points, and the line is a fit to EOS in Equation (1).
Table 2 lists the elastic stiffness of M3X (M = Fe, Cr; X = C, B) along with the calculated elastic constants. Among the Fe3X (X = C, B) compounds, Fe3C exhibits the highest C11 value of 543 GPa, indicating the incompressibility of Fe3C. Compressing Fe3C under uniaxial stress along the [001] direction is more difficult. This is because elastic deformation induces a phase transformation from orthorhombic to monoclinic (space group P21/c), reducing its symmetry. Simultaneously, the number of three-dimensional covalent bonds increases which hardens the material. Fe8Cr4C4 exhibits the smallest value of C44 at 68 GPa. This indicates that, compared to other compounds, Fe8Cr4C4 is more susceptible to shear strains at the crystal plane (100). C11, C22, and C33 represent the ability of the crystals to resist axial strain along the [001], [010] and [001] crystallographic directions. C44, C55, and C66 indicate the ability to resist shear strain on the (100), (010) and (001) crystal faces, and C12 denotes resistance of the crystal against shear deformation along the [110] direction.

Table 2.
Elastic constants of Cij from the first principles in the cementite-type M3X (M = Fe, Cr; X = C, B) GPa).
In the field of alloy design, this method has been successfully applied to many metal systems, e.g., the Nb single-bond Zr binary system [39], Ni-based alloys [40], Ti-Nb-Zr [41], the Zr-Nb-Mo ternary system [42], and even and intermetallic compounds. It is found that the crystal structure of Ti(Cu,Pt)2 is of the orthorhombic cell space group Amm2 (No. 38) with the structural prototype of VAu2. The resolved structure of Ti(Cu,Pt)3 is of the tetragonal AlPt3 type, belonging to the space group P4/mmm (No. 123) [43]. Ti(Cu,Pt)3 alloys of full composition were predicted and are in agreement with experimental data.
The recently developed performance-based CALPHAD modeling technique facilitates the rapid design of performance-oriented alloy compositions. This is founded on the ability of the technique to construct data models directly for material composition and properties [44]. Expanding the scope of alloy designing across the entire composition space opens up possibilities for obtaining various desired properties and combinations. Furthermore, it provides a rapid method for designing and optimizing alloys [40,45,46]. Figure 4 shows the elastic constants and CALPHAD model of the binary systems in the M3X (M = Fe, Cr; X = C, B) cementite. Table 3 lists the parameters fitted to the CALPHAD model.
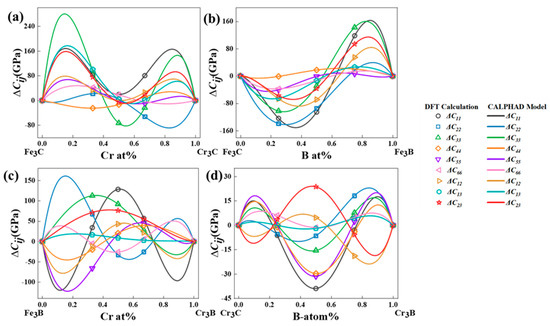
Figure 4.
The elastic constants of cementite-type M3X (M = Fe, Cr; X = C, B) calculated by DFT and fitted by CALPHAD model. (a) (Fe,Cr)3C, (b) Fe3(C,B), (c) (Fe,Cr)3B and (d) Cr3(C,B).

Table 3.
Fitted parameters of the current CALPHAD model in the cementite-type M3X (M = Fe, Cr; X = C, B).
The isotropic bulk modulus (B) and shear modulus (G) were determined. Generally, they cannot be calculated directly from Cij. Nevertheless, the values of the isotropic moduli can be confined within limits assessed in previous studies. Reuss obtained the lower bounds for all lattices, whereas Voigt obtained the upper bounds. Hill demonstrated that the averages proposed by Voigt and Reuss were limited and suggested that the actual effective moduli could be approximated to the arithmetic mean of the two bounds. We also calculated the Young’s modulus (E) and Poisson’s ratio (v) of the materials. These quantities are correlated with the bulk and shear moduli. Table 4 lists the calculated Voigt’s bulk modulus (Bv), Reuss bulk modulus (BR), effective bulk modulus (B), Voigt’s shear modulus (Gv), Reuss shear modulus (GR), effective shear modulus (G), Young’s modulus (E), and Poisson’s ratio (v) of M3X (M = Fe, Cr; X = C, B).

Table 4.
Calculated Voigt’s bulk modulus (Bv), Reuss’s bulk modulus (BR), effective bulk modulus (B), Voigt’s shear modulus (Gv), Reuss’s shear modulus (GR), effective shear modulus (G), Young’s modulus (E in Gpa), Poisson’s ratio (v) and the universal anisotropic index (AU) a for cementite-type M3X (M = Fe, Cr; X = C, B).
The model required for the calculation was generated using the sublattice point model. A finite number of constituent points were selected to construct the model, and the parameters reflecting the mechanical properties of the material, such as elastic constant Cij, bulk modulus B, shear modulus G, Young’s modulus E, Poisson’s ratio v, and hardness, were computed for each of the constituent points. Finally, the variation in the mechanical properties with the chemical composition was assessed across the entire compositional range by fitting the interaction parameters (Figure 5).
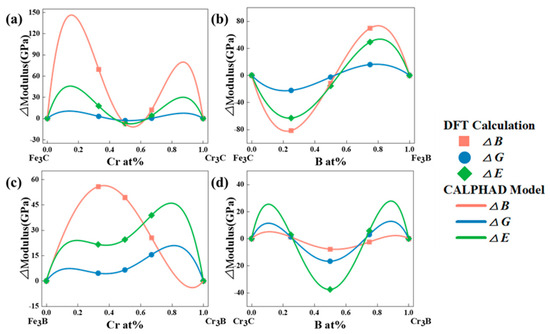
Figure 5.
The elastic of modulus cementite-type M3X (M = Fe, Cr; X = C, B) calculated by DFT and fitted by CALPHAD model. (a) (Fe,Cr)3C, (b) Fe3(C,B), (c) (Fe,Cr)3B and (d) Cr3(C,B).
Parameters such as B, G, E, and Poisson’s ratio are crucial indices for evaluating the mechanical properties of the (Fe,Cr)3(C,B) phase in high boron anti-wear alloys. The bulk modulus characterizes the capacity of a material to resist volume changes. It serves as the evaluation standard for the average valence bond strength of the material. At the macroscopic scale, bulk modulus reflects the external homogeneity of the compression resistance against a hydrostatic pressure. The higher the resistance to deformation, the stronger the material, and consequently, it is more challenging to compress. Fe3C exhibited the largest B value of 320 GPa, while Fe3B has the smallest B value of 120 Gpa. The bulk modulus decreased gradually with increasing concentrations of B and Cr. Therefore, the capacity of the material to resist volumetric deformation decreased gradually with the increase in the concentrations.
The shear modulus is a measure of the ability of a material to resist shear stress. The higher the shear modulus, the stronger the resistance against shear strain. Hence, the modulus is closely related to hardness. The shear modulus G and hardness Hv increased with increasing B and Cr concentrations. That is, the resistance to shear strain increased, indicating that the plastic processing of the material became more difficult. Young’s modulus (E) is expressed as the extent of linear compression of the (Fe,Cr)3(C,B) phase. It reflects the ability of the material to resist positive strain. To a certain extent, it can also reflect the stiffness of the material. The higher the E, the higher the stiffness of the material. Cr3C exhibited the highest Young’s modulus and stiffness of 402 GPa and 18.1 Gpa, respectively (Table 4), indicating that Cr3C may be the stiffest material in the (Fe,Cr)3(C,B) phase. Poisson’s ratio (ν) is an essential parameter in material engineering. It is defined as the ratio of the strain perpendicular to the direction of the applied stress to the strain in the direction of the stress, when a material is subjected to unidirectional stress. Generally, Poisson’s ratio is a measure of both the elastic properties of a material and the stability of the material under the shear stress. It typically ranges between −1 and 0.5. The smaller the Poisson’s ratio, the higher the stability of the material.
The toughness and brittleness of a material can be assessed through the B/G ratio. According to Pugh’s standard, a B/G ratio of 1.75 is the threshold between brittle and ductile materials. A compound can be categorized as tough and brittle when B/G > 1.75 (ν > 0.26) and B/G < 1.75 (ν < 0.26), respectively. The calculated Poisson’s ratios of the materials were below 0.26, except for Fe3B, Cr3C, Fe12C2B2, Cr12CB3, Cr12C3B, and Fe4Cr8B. This indicates that the former materials are brittle and easily deformable under an external force. By contrast, the remaining compounds demonstrate good plasticity.
The elastic anisotropy index (AU) indicates the extent of variations in the mechanical properties of the material in different directions (Table 4). AU = 0 indicates that the material is isotropic. The greater the deviation of AU from 0, the higher the degree of elastic anisotropy in the material. As evident from Table 1, the total anisotropy index of Fe8Cr4C4 has the largest deviation from 0, whereas that of Fe3C has the second largest deviation from 0. This indicates that the mechanical properties of the two compounds are highly anisotropic. The anisotropy index of Cr3B (0.01) has the smallest deviation from zero, indicating that its mechanical anisotropy is the weakest.
Tian et al. proposed a model to predict the hardness of polycrystalline materials and bulk metallic glasses based on the Pugh’s modulus ratio and the shear modulus (G), where Hv denotes the hardness. The results for compounds are presented in Table 4. Umemoto et al. [54] reported that the hardness of cementite Fe3C of 10 GPa (~920 HV) is increased with the addition of Cr to 13.5 GPa (20 atom% Cr) [11]. Lentz et al. provided a comparative and comprehensive study of the indentation hardness and indentation modulus of iron-rich borides and carboborides of types Fe3(C,B). The Fe3(C,B) phase in the Fe-C-B system increased from 11.18 (±0.9) Gpa to 15.94 (±0.72) Gpa. The theoretically predicted hardness values of (Fe,Cr)3C phases are in agreement with the experimental measurements reported in the literature.
Using the CALPHAD method, we meticulously studied the elastic constants and their derived properties across the full compositional space. Figure 6 presents the distribution of elastic constants across the entire composition space. The third-order interaction parameters between the (Fe,Cr)3(C,B) compositions and elastic constants or elastic moduli were obtained by fitting the composition–property relationship using CALPHAD. Subsequently, we modeled the correlation between the elastic constants and elastic moduli of (Fe,Cr)3(C,B) with Cr and B concentrations. This analysis generated a cloud diagram depicting the variations in the mechanical properties of the (Fe,Cr)3(C,B) with respect to the components, as shown in Figure 7. The shear modulus and Young’s modulus exhibited similar trends: they decreased with increasing B content in the range of 30–50 at%. In general, the moduli increased with increasing Cr content in the range of 70–80 at% and decreased in the Cr content range of 80–90 at%. Hardness gradually increased with increasing B content with the Cr content of 0.1–15% and 45–50 at%. The maximum hardness, shear modulus, and Young’s modulus were obtained in the Cr content of 70–95 at% and B content of 0–40 at%. The shear modulus and hardness Hv were significantly low at a B content of 90–100 at% and a Cr content of zero. It can be inferred that the concentration of Cr predominantly influences the mechanical properties of (Fe,Cr)3(C,B). The hardness of the (Fe,Cr)3(C,B) phase increased at Cr contents exceeding 70 at% and B contents below 20 at%. Hence, superior mechanical properties can be obtained.
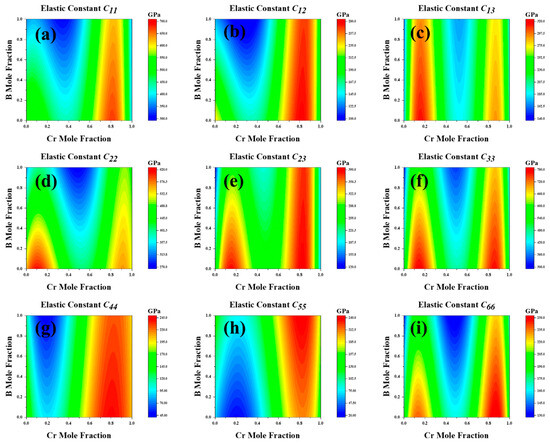
Figure 6.
The elastic constants over the whole composition space of cementite-type M3X (M = Fe, Cr; X = C, B). (a) C11, (b) C12, (c) C13, (d) C22, (e) C23, (f) C33, (g) C44 (h) C55, (i) C66.
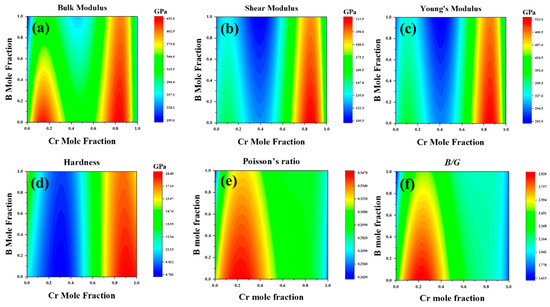
Figure 7.
The elastic modulus over the whole composition space of cementite-type M3X (M = Fe, Cr; X = C, B). (a) the bulk modulus (B), (b) shear modulus (G), (c) Young’s modulus (E), (d) hardness (Hv), (e) Poisson’s ratio (v), (f) B/G.
4. Conclusions
The highest hardness Hv, shear modulus, and Young’s modulus were achieved at Cr and B contents in the range 70–95 at% and 40 at%, respectively. At these concentrations, the material is difficult to compress, resulting in poor machinability. At B contents surpassing 90 at% and at a Cr content of zero, the material exhibited low shear modulus G and hardness, resulting in poor resistance to deformation, reduced stiffness, and the ease of plastic processing. In this study, we systematically investigated the phase formation and linear and nonlinear elastic behaviors of M3X (M = Fe, Cr; X = C, B) across a multicomponent space. We used a combination of first-principle calculations and CALPHAD models. A composition–phase relationship model was constructed for the of the entire multicomponent space, revealing the influence of the elements on the phase composition. Our theoretical study combining the above models can facilitate accelerated alloy design and can be extended to other multicomponent systems. We performed a high-throughput calculation for a cementite-type (M = Fe, Cr; X = C, B) system, providing a set of practical guidelines to facilitate the efficient designing of wear-resistant material compositions.
Author Contributions
Author contributions: Y.H. is an expert in density function theory (DFT) simulation and wrote the original draft. G.W. did the stats and the picture making. X.C. and Y.J. provided funding acquisition, and revised data and the whole paper. Y.L. assisted in analyzing mechanical properties. All authors participated in the analysis of the simulation data, discussions of the results and editing of the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (No. 52001150) and Project Funds of “Xingdian Talent Support Program”.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The authors are willing to provide the supporting data of this study upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Lin, Y.; Chong, X.; Ding, Y. irst-Principles Calculations of Thermal and Electrical Transport Properties of bcc and fcc Dilute Fe–X (X = Al, Co, Cr, Mn, Mo, Nb, Ni, Ti, V, and W) Binary Alloys. Metals 2021, 11, 1988. [Google Scholar] [CrossRef]
- Ande, C.K.; Sluiter, M.H.F. First-principles prediction of partitioning of alloying elements between cementite and ferrite. Acta Mater. 2010, 58, 6276–6281. [Google Scholar] [CrossRef]
- Chong, X.Y.; Jiang, Y.H.; Zhou, R. Elastic properties and electronic structures of CrxBy as superhard compounds. J. Alloys Compd. 2014, 610, 684–694. [Google Scholar] [CrossRef]
- Chong, X.; Jiang, Y.; Feng, J. Exploring the intrinsic ductile metastable Fe-C compounds: Complex chemical bonds, anisotropic elasticity and variable thermal expansion. J. Alloys Compd. 2018, 745, 196–211. [Google Scholar] [CrossRef]
- Chong, X.; Guan, P.-W.; Hu, M. Exploring accurate structure, composition and thermophysical properties of η carbides in 17.90 wt% W-4.15 wt% Cr-1.10 wt% V-0.69 wt% C steel. Scr. Mater. 2018, 154, 149–153. [Google Scholar] [CrossRef]
- Wang, G.; Jiang, Y.; Li, Z. Balance between strength and ductility of dilute Fe2B by high-throughput first-principles calculations. Ceram. Int. 2021, 47, 4758–4768. [Google Scholar] [CrossRef]
- Zhang, W.H.; Lv, Z.Q.; Shi, Z.P. Electronic, magnetic and elastic properties of ε-phases Fe3X(X = B, C, N) from density-functional theory calculations. J. Magn. Magn. Mater. 2012, 324, 2271–2276. [Google Scholar] [CrossRef]
- Wei, L.I. Progress of Wear-resistant Steel and Iron Technology. Foundry 2006, 55, 1105–1109. [Google Scholar]
- Li, H.N.; Zhang, B.H.; Qiao, G.Y. Refinement effect of NbC particle additions on the microstructure of high-speed steel rolls. J. Mater. Res. Technol. 2023, 26, 1697–1711. [Google Scholar] [CrossRef]
- Chong, X.; Hu, M.; Wu, P. Tailoring the anisotropic mechanical properties of hexagonal M7X3 (M = Fe, Cr, W, Mo; X = C, B) by multialloying. Acta Mater. 2019, 169, 193–208. [Google Scholar] [CrossRef]
- Lentz, J.; Röttgera, A.; Theisen, W. Hardness and modulus of Fe2B, Fe3(C,B), and Fe23(C,B)6 borides and carboborides in the Fe-C-B system. Mater. Charact. 2018, 135, 192–202. [Google Scholar] [CrossRef]
- Shein, I.; Medvedeva, N.; Ivanovskii, A. Electronic and structural properties of cementite-type M3X (M = Fe, Co, Ni; X = C or B) by first principles calculations. Phys. B Condens. Matter 2006, 371, 126–132. [Google Scholar] [CrossRef]
- Konyaeva, M.; Medvedeva, N. Electronic Structure, Magnetic Properties, and Stability of the Binary and Ternary Carbides (Fe,Cr)3C and (Fe,Cr)7C3. Phys. Solid State 2009, 51, 2084–2089. [Google Scholar] [CrossRef]
- Matthews, S.; Hyland, M.; James, B. Microhardness variation in relation to carbide development in heat treated Cr3C2–NiCr thermal spray coatings. Acta Mater. 2003, 51, 4267–4277. [Google Scholar] [CrossRef]
- Zhou, C.T.; Xiao, B.; Feng, J. First principles study on the elastic properties and electronic structures of (Fe, Cr)3C. Comput. Mater. Sci. 2009, 45, 986–992. [Google Scholar] [CrossRef]
- Razumovskiy, V.I.; Ghosh, G. A first-principles study of cementite (Fe3C) and its alloyed counterparts: Structural properties, stability, and electronic structure. Comput. Mater. Sci. 2015, 110, 169–181. [Google Scholar] [CrossRef]
- Lv, Z.Q.; Fu, W.T.; Sun, S.H. First-principles study on the electronic structure, magnetic properties and phase stability of alloyed cementite with Cr or Mn. J. Magn. Magn. Mater. 2011, 323, 915–919. [Google Scholar] [CrossRef]
- Lv, Z.Q.; Zhang, F.C.; Sun, S.H. First-principles study on the mechanical, electronic and magnetic properties of Fe3C. Comput. Mater. Sci. 2008, 44, 690–694. [Google Scholar] [CrossRef]
- Taylor, K.A.; Hansen, S.S. The boron hardenability effect in thermomechanically processed, direct-quenched 0.2 Pct C steels. Metall. Trans. A 1990, 21, 1697–1708. [Google Scholar] [CrossRef]
- Jiang, D.; Xiao, W.; Liu, D. Structural stability, electronic structures, mechanical properties and debye temperature of W-Re alloys: A first-principles study. Fusion Eng. Des. 2021, 162, 112081. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Xiao, B.; Xing, J.; Feng, J. A comparative study of Cr7C3, Fe3C and Fe2B in cast iron both from ab initio calculations and experiments. J. Phys. D Appl. Phys. 2009, 42, 115415. [Google Scholar] [CrossRef]
- Katsura, T.; Tange, Y. A Simple Derivation of the Birch–Murnaghan Equations of State (EOSs) and Comparison with EOSs Derived from Other Definitions of Finite Strain. Minerals 2019, 9, 745. [Google Scholar] [CrossRef]
- Shang, S.; Kim, D.; Zacherl, C. Effects of alloying elements and temperature on the elastic properties of dilute Ni-base superalloys from first-principles calculations. J. Appl. Phys. 2012, 112, 053515. [Google Scholar] [CrossRef]
- Liu, Y.; Jiang, Y.; Xing, J. Mechanical properties and electronic structures of M23C6 (M = Fe, Cr, Mn)-type multicomponent carbides. J. Alloys Compd. 2015, 648, 874–880. [Google Scholar] [CrossRef]
- Nikolussi, M.; Shang, S.; Gressmann, T. Extreme elastic anisotropy of cementite, Fe3C: First-principles calculations and experimental evidence. Scr. Mater. 2008, 59, 814–817. [Google Scholar] [CrossRef]
- Hill, R. The Elastic Behaviour of a Crystalline Aggregate. Proc. Phys. Soc. Sect. A 1952, 65, 349–354. [Google Scholar] [CrossRef]
- Tian, Y.; Xu, B.; Zhao, Z. Microscopic theory of hardness and design of novel superhard crystals. Int. J. Refract. Met. Hard Mater. 2012, 33, 93–106. [Google Scholar] [CrossRef]
- Wang, D.T.; Zhang, X.Z.; Nagaumi, H. Exploring the Relationship between the Structural Characteristics and Mechanical Behavior of Multicomponent Fe-Containing Phases: Experimental Studies and First-Principles Calculations. Molecules 2023, 28, 7141. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.; Zhou, Y.; Yang, J. Optimization on mechanical properties of Fe7−xCrxC3 carbides by first-principles investigation. J. Alloys Compd. 2013, 560, 49–53. [Google Scholar] [CrossRef]
- Chong, X.; Jiang, Y.; Zhou, R. First principles study the stability, mechanical and electronic properties of manganese carbides. Comput. Mater. Sci. 2014, 87, 19–25. [Google Scholar] [CrossRef]
- Liu, Z.K.; Zhang, H.; Ganeshan, S. Computational modeling of effects of alloying elements on elastic coefficients. Scr. Mater. 2010, 63, 686–691. [Google Scholar] [CrossRef]
- Fruchart, D.; Chaudouet, P.; Fruchart, R. Etudes structurales de composés de type cémentite: Effet de l’hydrogène sur Fe3C suivi par diffraction neutronique. Spectrométrie Mössbauer sur FeCo2B et Co3B dopés au57Fe. J. Solid State Chem. 1984, 51, 246–252. [Google Scholar] [CrossRef]
- Scott, H.P.; Williams, Q.; Knittle, E. Stability and equation of state of Fe3C to 73 GPa: Implications for carbon in the Earth’s core. Geophys. Res. Lett. 2001, 28, 1875–1878. [Google Scholar] [CrossRef]
- Ghosh, G. A first-principles study of cementite (Fe3C) and its alloyed counterparts: Elastic constants, elastic anisotropies, and isotropic elastic moduli. AIP Adv. 2015, 5, 169–181. [Google Scholar] [CrossRef]
- Villars, P.; Cenzual, K.; Pearson, W.B. Pearson’s Crystal Data: Crystal Structure Database for Inorganic Compounds; ASM International: Almere, The Netherlands, 2007. [Google Scholar]
- Li, Y.; Gao, Y.; Xiao, B. The electronic, mechanical properties and theoretical hardness of chromium carbides by first-principles calculations. J. Alloys Compd. 2011, 509, 5242–5249. [Google Scholar] [CrossRef]
- Wang, X.; Liu, L.B.; Wang, M.F. Computational modeling of elastic constants as a function of temperature and composition in Zr–Nb alloys. Calphad 2015, 48, 89–94. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, L.J. Composition-dependent hardness and Young’s modulus in fcc Ni-X (X = Rh, Ta, W, Re, Os, and Ir) alloys: Experimental measurements and CALPHAD modeling. J. Mater. Res. 2019, 34, 3104–3115. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, L.; Guo, Z. Study of low-modulus biomedical β Ti–Nb–Zr alloys based on single-crystal elastic constants modeling. J. Mech. Behav. Biomed. Mater. 2016, 62, 310–318. [Google Scholar] [CrossRef]
- Liang, J.S.; Liu, L.B.; Xu, G.L.; Wang, X.; Zhang, L.G.; Shi, X.; Tao, X.M. Compositional screening of Zr-Nb-Mo alloys with CALPHAD-type model for promising bio-medical implants. Calphad 2017, 56, 196–206. [Google Scholar] [CrossRef]
- Zeng, W.-J.; Hu, K.; Liu, H.-S. Crystal structures and elastic properties of Ti(Cu,Pt)2 and Ti(Cu,Pt)3 phases. Trans. Nonferrous Met. Soc. China 2020, 30, 1839–1848. [Google Scholar] [CrossRef]
- Liu, Z.K. Computational thermodynamics and its applications. Acta Mater. 2020, 200, 745–792. [Google Scholar] [CrossRef]
- Liao, M.Q.; Liu, Y.; Cui, P.C. Modeling of alloying effect on elastic properties in BCC Nb-Ti-V-Zr solid solution: From unary to quaternary. Comput. Mater. Sci. 2020, 172, 109289. [Google Scholar] [CrossRef]
- Marker, C.; Shang, S.L.; Zhao, J.C. Effects of alloying elements on the elastic properties of bcc Ti-X alloys from first-principles calculations. Comput. Mater. Sci. 2018, 142, 215–226. [Google Scholar] [CrossRef]
- Hill, R. A self-consistent mechanics of composite materials. J. Mech. Phys. Solids 1965, 13, 213–222. [Google Scholar] [CrossRef]
- Dodd, S.; Saunders, G.; Cankurtaran, M. Ultrasonic study of the temperature and hydrostatic-pressure dependences of the elastic properties of polycrystalline cementite (Fe3C). Phys. Status Solidi (A) 2003, 198, 272–281. [Google Scholar] [CrossRef]
- Umemoto, M.; Todaka, Y.; Takahashi, T. Characterization of bulk cementite produced by mechanical alloying and spark plasma sintering. J. Metastable Nanocryst. Mater. 2003, 15, 607–614. [Google Scholar] [CrossRef]
- Guo, X.; Li, L.; Liu, Z. Hardness of covalent compounds: Roles of metallic component and d valence electrons. J. Appl. Phys. 2008, 104, 023503. [Google Scholar] [CrossRef]
- Gueddouh, A.; Bentria, B.; Lefkaier, I.K. Effect of spin polarization on the structural properties and bond hardness of FexB (x = 1, 2, 3) compounds first-principles study. Bull. Mater. Sci. 2016, 39, 1427–1434. [Google Scholar] [CrossRef]
- Jiang, C. First-principles study of structural, elastic, and electronic properties of chromium carbides. Appl. Phys. Lett. 2008, 92, 889. [Google Scholar] [CrossRef]
- Ledbetter, H. Polycrystalline elastic constants of in situ cementite (Fe3C). Mater. Sci. Eng. A 2010, 527, 2657–2661. [Google Scholar] [CrossRef]
- Umemoto, M.; Liu, Z.G.; Masuyama, K. Influence of alloy additions on production and properties of bulk cementite. Scr. Mater. 2001, 45, 391–397. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).